| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
Все релятивистские квантовые частицы (поля) абсолютно равноправны в квантовой теории поля; поля обладают свойствами частиц, а частицы—свойствами волн (полей); взаимодействие между частицами происходит в результате обмена квантами полей. В частности, в квантовой электродинамике — квантовой наследнице теории Максвелла — изучаются взаимодействия между электронами и фотонами, Электроны (фермионы с массой  спиновым квантовым числом
спиновым квантовым числом  и зарядом
и зарядом  подчиняются принципу запрета. Фотоны же (бозоны с нулевыми массой покоя и зарядом и со спиновым квантовым числом, равным 1) не подчиняются этому принципу. (Множество фотонов может находиться в одном квантовом состоянии, образуя в классическом пределе электромагнитное поле.)
подчиняются принципу запрета. Фотоны же (бозоны с нулевыми массой покоя и зарядом и со спиновым квантовым числом, равным 1) не подчиняются этому принципу. (Множество фотонов может находиться в одном квантовом состоянии, образуя в классическом пределе электромагнитное поле.)
В отсутствие взаимодействия (если бы, например, заряд электрона равнялся нулю, электрические силы не возникали бы) свойства электрона были бы такими же, как у релятивистского (дираковского) электрона, который характеризуется направлением спина и импульсом. Состояние электрона определяется обычной волной де Бройля, которая удовлетворяет релятивистскому соотношению между энергией и
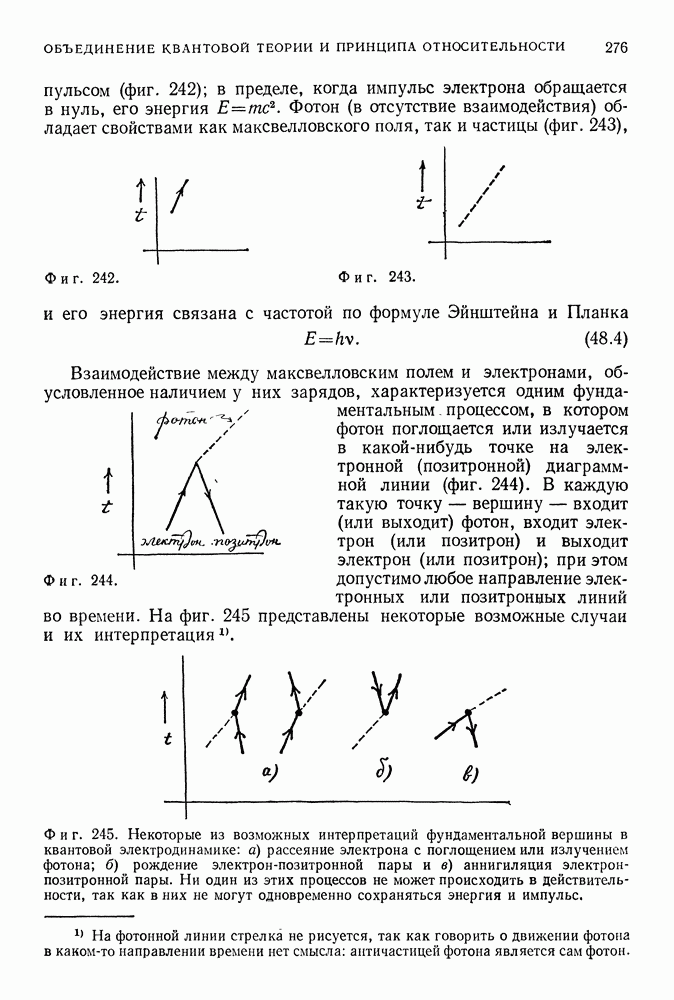
импульсом (фиг. 242); в пределе, когда импульс электрона обращается в нуль, его энергия 

Фиг. 242.

Фиг. 243.
Фотон (в отсутствие взаимодействия) обладает свойствами как максвелловского поля, так и частицы (фиг. 243), и его энергия связана с частотой по формуле Эйнштейна и Планка

Взаимодействие между максвелловским полем и электронами, обусловленное наличием у них зарядов, характеризуется одним фундаментальным процессом, в котором фотон поглощается или излучается в какой-нибудь точке на электронной (позитронной) диаграммной линии (фиг. 244). В каждую такую точку — вершину — входит (или выходит) фотон, входит электрон (или позитрон) и выходит электрон (или позитрон); при этом допустимо любое направление электронных или позитронцых линий во времени. На фиг. 245 представлены некоторые возможные случаи и их интерпретация.

Фиг. 244.

Фиг. 245. Некоторые из возможных интерпретаций фундаментальной вершины в квантовой электродинамике: а) рассеяние электрона с поглощением или излучением фотона; б) рождение электрон-позитронной пары и в) аннигиляция электрон-позитронной пары. Ни один из этих процессов не может происходить в действительности, так как в них не могут одновременно сохраняться энергия и импульс.
Используя эти фундаментальные вершины, можно описать любой процесс взаимодействия электронов и фотонов (если такой процесс возможен). Например, рассеяние фотона на электроне описывается диаграммой, изображенной на фиг. 246, которая соответствует взаимодействию и поглощению фотона электроном в точке 1 с последующим взаимодействием электрона и излучением им фотона в точке 2.
Процесс определяется входящими и выходящими линиями. Так, при рассеянии фотона на электроне фотон и электрон входят в вершину с импульсами и энергиями  а выходят из нее с
а выходят из нее с  из закона сохранения полных энергии и импульса следует, что
из закона сохранения полных энергии и импульса следует, что

Амплитуда вероятности перехода

равна сумме вкладов всех диаграмм, которые можно построить с этими входящими и выходящими линиями, как показано на фиг. 247. [Виртуальные фотоны изображаются пунктирными линиями (иногда искривленными).

Фиг. 246.

Фиг. 247. Входящие и выходящие линии определяют процесс. Любые графы, которые можно нарисовать, используя фундаментальные вершины, и которые начинаются и оканчиваются этими линиями, дают вклад в результат. Некоторые из них представлены здесь.
Эти линии искривлены для наглядности, так как реальные фотоны (и электроны) распространяются как волны и могут взаимодействовать друг с другом в обширных областях пространства-времени.]
Амплитуда вероятности другого процесса — рассеяния фотона на фотоне (взаимодействие света со светом) — содержит, в частности, вклад и от диаграммы, представленной на фиг. 248.
В некотором смысле данная теория является просто переводом старых теорий на новый язык, который является современным и очень удобным, так как с его помощью можно наглядно толковать
корпускулярно-волновые свойства полей и их взаимодействия. Эта теория есть релятивистское квантовое обобщение теории Лоренца — Максвелла, являющейся ее классическим пределом.

Фиг. 248,
Именно эта теория объясняет, почему электрон, находящийся на самой низкой боровской орбите, не излучает энергию, и переходит в классическую теорию излучения при рассмотрении явлений в макроскопических масштабах.
С точки зрения квантовой электродинамики электрон, находящийся на самой близкой от протона боровской орбите, представляет собой систему электрон — протон — фотон в основном состоянии и с наинизшей энергией (фиг. 249).

Фиг. 249.
В этом состоянии система живет вечно. Из возбужденного состояния (скажем,  система может совершить переход (фиг. 250):
система может совершить переход (фиг. 250):


Фиг. 250.
Мир электронов и фотонов удается упорядочить, если предположить, что все разнообразные возможные процессы могут быть описаны диаграммами, содержащими вершины только одного типа (фиг. 251). Такие вершины могут характеризовать любые взаимодействия, приводящие к нарушению движения по инерции. Можно спросить, почему не ввести, например, верщину, изображенную на фиг. 252, и не считать электрон-фотонное рассеяние в качестве элементарного процесса. Ответ гласит, что сделать это можно, однако, поскольку число возможных процессов бесконечно (общий случай — это рассеяние  фотонов
фотонов
на М электронах, фиг. 253), предпочтительнее не вводить нового элементарного взаимодействия для каждого из процессов.
Изящество квантовой электродинамики состоит отчасти в том, что вся она построена на основе одного-единственного фундаментального взаимодействия. Именно этого не удается добиться в ядерных (мезонных) полевых теориях.

Фиг. 251,

Фиг. 252.
В этих теориях пришлось ввести не одну, а десятки фундаментальных вершин, соответствующих обменам различными квантами. Попытка создания ядерного аналога квантовой электродинамики была так мало успешна и натолкнулась на такие трудности, что возникли серьезные сомнения в пригодности полевых теорий для описания внутриядерных явлений.
Рассмотрим в качестве примера, как трактуется кулоновская сила в квантовой электродинамике. Сила, если использовать этот термин, определяется по тому эффекту, который она производит на движение заряженных тел. Исследуем рассеяние двух электронов. В отсутствие взаимодействия они движутся по инерции (фиг. 254). Электрон 1 обладает импульсом  и энергией
и энергией  электрон 2 — импульсом
электрон 2 — импульсом  и энергией
и энергией  Если учесть, что у электронов имеются заряды и что они взаимодействуют через электромагнитное поле, картина становится более интересной.
Если учесть, что у электронов имеются заряды и что они взаимодействуют через электромагнитное поле, картина становится более интересной.

Фиг. 253.

Фиг. 254.

Фиг. 255.
Электрон может излучать и поглощать фотоны, так что может произойти процесс, изображенный на фиг. 255, где представлена диаграмма рассеяния электрона на электроне в результате обмена одним фотоном. В этом процессе входящие электроны (на диаграмме отмечены лишь импульсы частиц) обладают импульсами  Фотон
Фотон
с импульсом  излучается электроном 1 и поглощается электроном 2. Так как импульс сохраняется в каждой вершине, электрон 1 выходит после рассеяния с импульсом
излучается электроном 1 и поглощается электроном 2. Так как импульс сохраняется в каждой вершине, электрон 1 выходит после рассеяния с импульсом  а электрон 2 — с импульсом
а электрон 2 — с импульсом  Таким образом, в каждой вершине сумма импульсов, взятых со знаком плюс для стрелок, направленных к центру, и со знаком минус для стрелок, направленных от центра, равна нулю.
Таким образом, в каждой вершине сумма импульсов, взятых со знаком плюс для стрелок, направленных к центру, и со знаком минус для стрелок, направленных от центра, равна нулю.
Если рассчитать этот процесс для предельного случая, когда электроны покоятся друг относительно друга и относительно наблюдателя  то окажется, что энергия электронов изменяется на такую величину, на какую она изменилась бы под действием кулоновской силы. Далее, рассеяние двух электронов происходит так же, как это следует из теории Шредингера (при малых относительных скоростях электронов) для случая кулоновского рассеяния.
то окажется, что энергия электронов изменяется на такую величину, на какую она изменилась бы под действием кулоновской силы. Далее, рассеяние двух электронов происходит так же, как это следует из теории Шредингера (при малых относительных скоростях электронов) для случая кулоновского рассеяния.

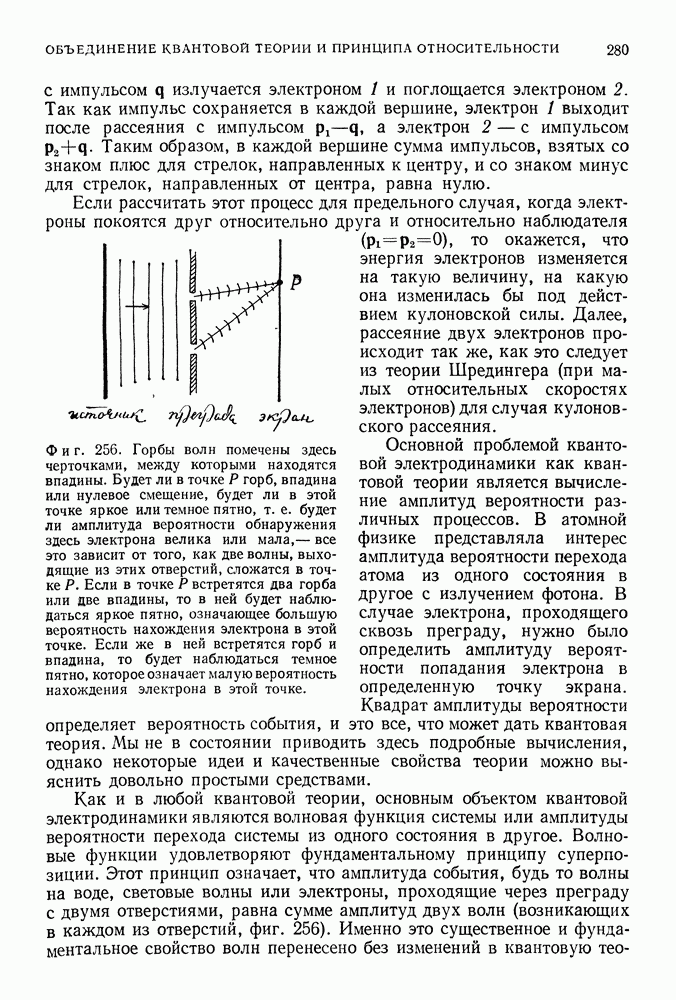
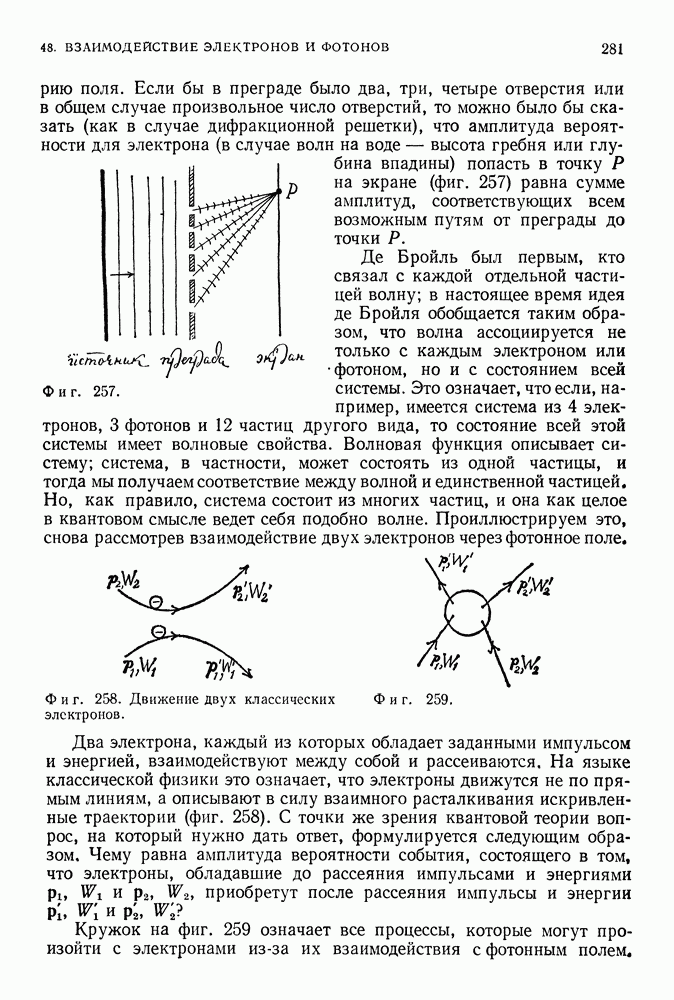
Фиг. 256. Горбы волн помечены здесь черточками, между которыми находятся впадины. Будет ли в точке Р горб, впадина или нулевое смещение, будет ли в этой точке яркое или темное пятно, т. е. будет ли амплитуда вероятности обнаружения здесь электрона велика или мала,— все это зависит от того, как две волны, выходящие из этих отверстий, сложатся в точке Р. Если в точке Р встретятся два горба или две впадины, то в ней будет наблюдаться яркое пятно, означающее большую вероятность нахождения электрона в этой точке. Если же в ней встретятся горб и впадина, то будет наблюдаться темное пятно, которое означает малую вероятность нахождения электрона в этой точке.
Основной проблемой квантовой электродинамики как квантовой теории является вычисление амплитуд вероятности различных процессов. В атомной физике представляла интерес амплитуда вероятности перехода атома из одного состояния в другое с излучением фотона. В случае электрона, проходящего сквозь преграду, нужно было определить амплитуду вероятности попадания электрона в определенную точку экрана. Квадрат амплитуды вероятности определяет вероятность события, и это все, что может дать квантовая теория. Мы не в состоянии приводить здесь подробные вычисления, однако некоторые идеи и качественные свойства теории можно выяснить довольно простыми средствами.
Как и в любой квантовой теории, основным объектом квантовой электродинамики являются волновая функция системы или амплитуды вероятности перехода системы из одного состояния в другое. Волновые функции удовлетворяют фундаментальному принципу суперпозиции. Этот принцип означает, что амплитуда события, будь то волны на воде, световые волны или электроны, проходящие через преграду с двумя отверстиями, равна сумме амплитуд двух волн (возникающих в каждом из отверстий, фиг. 256). Именно это существенное и фундаментальное свойство волн перенесено без изменений в квантовую
теорию поля. Если бы в преграде было два, три, четыре отверстия или в общем случае произвольное число отверстий, то можно было бы сказать (как в случае дифракционной решетки), что амплитуда вероятности для электрона (в случае волн на воде — высота гребня или глубина впадины) попасть в точку Р на экране (фиг. 257) равна сумме амплитуд, соответствующих всем возможным путям от преграды до точки Р.
Де Бройль был первым, кто связал с каждой отдельной частицей волну; в настоящее время идея де Бройля обобщается таким образом, что волна ассоциируется не только с каждым электроном или фотоном, но и с состоянием всей системы. Это означает, что если, например, имеется система из 4 электронов, 3 фотонов и 12 частиц другого вида, то состояние всей этой системы имеет волновые свойства. Волновая функция описывает систему; система, в частности, может состоять из одной частицы, и тогда мы получаем соответствие между волной и единственной частицей, Но, как правило, система состоит из многих частиц, и она как целое в квантовом смысле ведет себя подобно волне. Проиллюстрируем это, снова рассмотрев взаимодействие двух электронов через фотонное поле.

Фиг. 257.

Фиг. 258. Движение двух классических электронов.

Фиг. 259.
Два электрона, каждый из которых обладает заданными импульсом и энергией, взаимодействуют между собой и рассеиваются, На языке классической физики это означает, что электроны движутся не по прямым линиям, а описывают в силу взаимного расталкивания искривленные траектории (фиг. 258). С точки же зрения квантовой теории вопрос, на который нужно дать ответ, формулируется следующим образом, Чему равна амплитуда вероятности события, состоящего в том, что электроны, обладавшие до рассеяния импульсами и энергиями  приобретут после рассеяния импульсы и энергии
приобретут после рассеяния импульсы и энергии  ?
?
Кружок на фиг. 259 означает все процессы, которые могут произойти с электронами из-за их взаимодействия с фотонным полем.
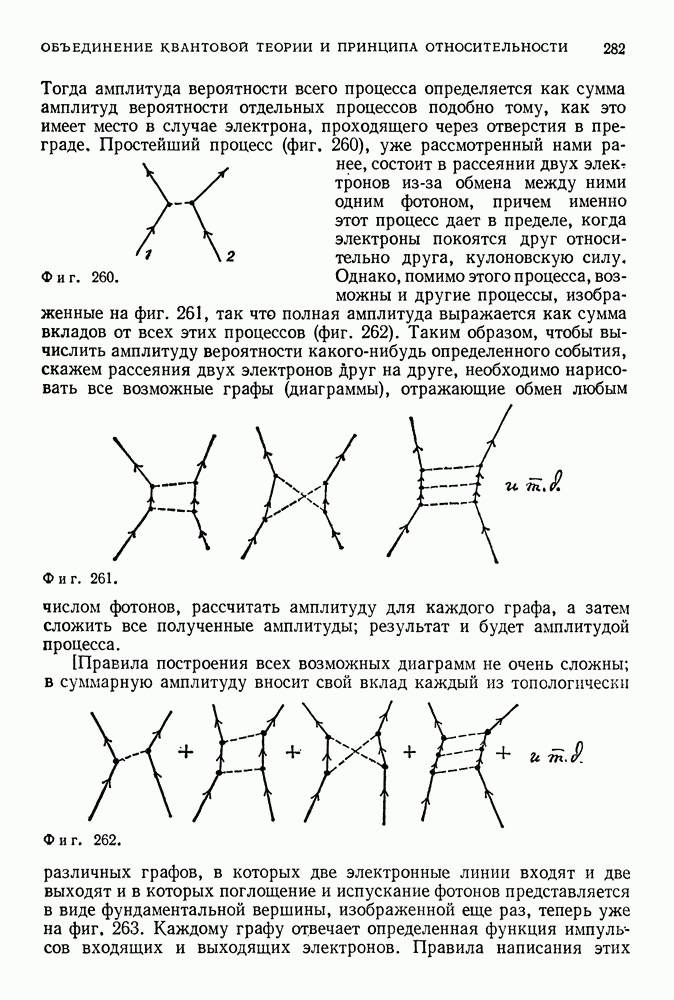
Тогда амплитуда вероятности всего процесса определяется как сумма амплитуд вероятности отдельных процессов подобно тому, как это имеет место в случае электрона, проходящего через отверстия в преграде, Простейший процесс (фиг, 260), уже рассмотренный нами ранее, состоит в рассеянии двух элек? тронов из-за обмена между ними одним фотоном, причем именно этот процесс дает в пределе, когда электроны покоятся друг относительно друга, кулоновскую силу. Однако, помимо этого процесса, возможны и другие процессы, изображенные на фиг. 261, так что полная амплитуда выражается как сумма вкладов от всех этих процессов (фиг. 262).

Фиг. 260.

Фиг. 261.
Таким образом, чтобы вычислить амплитуду вероятности какого-нибудь определенного события, скажем рассеяния двух электронов друг на друге, необходимо нарисовать все возможные графы (диаграммы), отражающие обмен любым числом фотонов, рассчитать амплитуду для каждого графа, а затем сложить все полученные амплитуды; результат и будет амплитудой процесса.

Фиг. 262.
[Правила построения всех возможных диаграмм не очень сложны; в суммарную амплитуду вносит свой вклад каждый из топологически различных графов, в которых две электронные линии входят и две выходят и в которых поглощение и испускание фотонов представляется в виде фундаментальной вершины, изображенной еще раз, теперь уже на фиг, 263. Каждому графу отвечает определенная функция импульсов входящих и выходящих электронов. Правила написания этих
функций (собственно, они и составляют содержание квантовой электродинамики) изложены в различных «поваренных книгах» по теоретической физике. (Следует отметить, что изготовить блюдо по рецепту может любой образованный повар, не обязательно гениальный.) Таким образом, каждой диаграмме соответствует определенная функция начальных и конечных импульсов:

Сумма амплитуд всех графов определяет вероятность процесса


Фиг. 263.

Фиг. 264.
Такая процедура расчетов в квантовой электродинамике особенно успешна в связи с тем, что каждой вершине диаграммы соответствует число (константа связи), определяющее силу электромагнитного взаимодействия:

Поэтому мы всегда можем, не проводя подробных расчетов, оценить вклад одного процесса относительно вкладов других,

Фиг. 265.
Например, диаграмма процесса, изображенная на фиг. 264, содержит две вершины. Стало быть, постоянная связи появляется здесь дважды и вклад от этого графа умножается на

Граф же, изображенный на фиг. 265, который тоже дает вклад в процесс рассеяния двух электронов, содержит четыре вершины, поэтому его вклад умножается на

Таким образом, не проводя расчетов, мы можем сразу же заключить, что вклад второго графа в суммарную амплитуду составляет приблизительно 1% от вклада первого графа. Это позволяет нам оценить суммарную амплитуду процесса, содержащего два входящих и два выходящих электрона, по диаграмме первого порядка, так как такая диаграмма включает минимальное число вершин. (Граф, не содержащий ни одного обмена фотонами, является, конечно, графом более низкого порядка, однако при таком процессе электроны не рассеиваются, а продолжают двигаться по инерции.) Рассчитав вклад графа наинизшего порядка, мы можем быть уверены, что он отличается от правильного результата не больше, чем на  так как введение дополнительных обменов фотонами приводит к умножению вкладов соответствующих графов как минимум на
так как введение дополнительных обменов фотонами приводит к умножению вкладов соответствующих графов как минимум на  Малость этой величины (постоянной тонкой структуры) оправдывает метод разложения полной амплитуды на сумму членов, соответствующих различным процессам обмена фотонами, и позволяет получать чрезвычайно точные результаты при учете лишь вкладов членов наинизшего порядка.
Малость этой величины (постоянной тонкой структуры) оправдывает метод разложения полной амплитуды на сумму членов, соответствующих различным процессам обмена фотонами, и позволяет получать чрезвычайно точные результаты при учете лишь вкладов членов наинизшего порядка.

Фиг. 266.
Такой метод разложения называется теорией возмущений; он получил свое название по аналогии с методом расчета орбит планет. (Для вычисления фактических орбит планет с помощью теории возмущений рассчитывают сначала орбиты, соответствующие действию лишь поля тяготения Солнца, пренебрегая силами взаимодействия планет друг с другом. Далее, получив так называемые невозмущенные орбиты, определяют силы, с которыми планеты действовали бы друг на друга, если бы они двигались по невозмущенным орбитам. Эти силы слегка искажают орбиты планет, которые могут быть снова подправлены, если вычислить силы, действующие между планетами, движущимися по искаженным орбитам.) Подобным же образом в квантовой теории поля при исследовании рассеяния двух электронов расчеты по теории возмущений начинают с вычисления амплитуды, отвечающей двум невозмущенным электронам (фиг. 266). Далее вносятся роправки, обусловленные обменом одним фотоном, затем двумя фотонами и т. д.
Одна из проблем квантовой теории поля ядерных сил (к которой мы обратимся позже) состоит в том, что константы связи ядерных взаимодействий относительно велики. Они не равны  а являются
а являются
числами порядка 1. В результате вклад процессов более высокого порядка (обмен двумя ядерными частицами и т. д.) оказывается того же порядка, что и вклад процессов наинизшего порядка, и расчеты, основанные на сохранении лишь членов разложения наинизшего порядка, теряют всякий смысл. Точные же расчеты настолько сложны, что технически просто невозможно решить уравнения, определяющие движение этих частиц, не используя какие-нибудь разумные разложения. Таким образом, помимо других проблем, связанных с ядерными силами, существует еще и та, что не только неизвестна до конца природа этих сил, но ставится под сомнение даже сама возможность введения понятия силы в масштабах ядер. Известно, однако, что, какова бы ни была природа этих сил, они настолько велики, что методрасчета, успешно применяемый при вычислении орбит планет и в квантовой электродинамике, оказывается здесь непригодным.
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
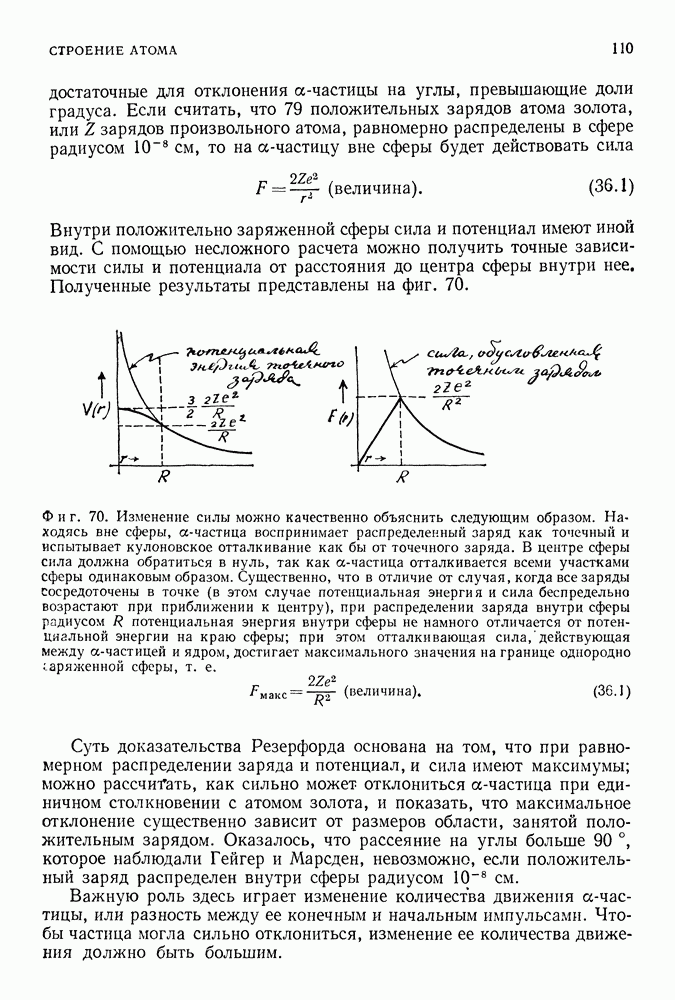
- 36. АТОМ РЕЗЕРФОРДА
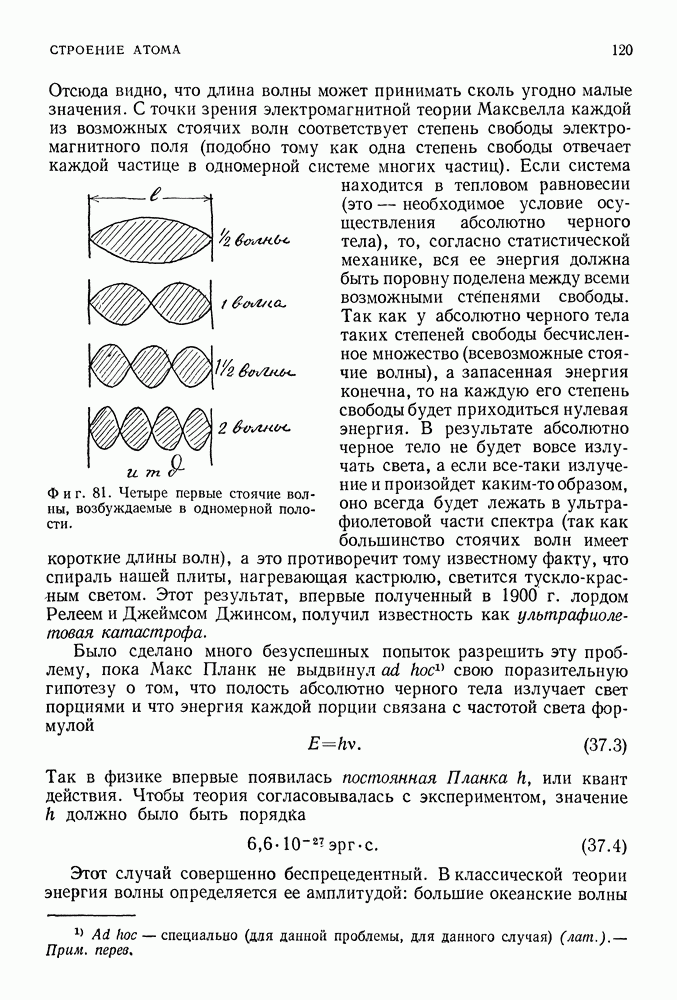
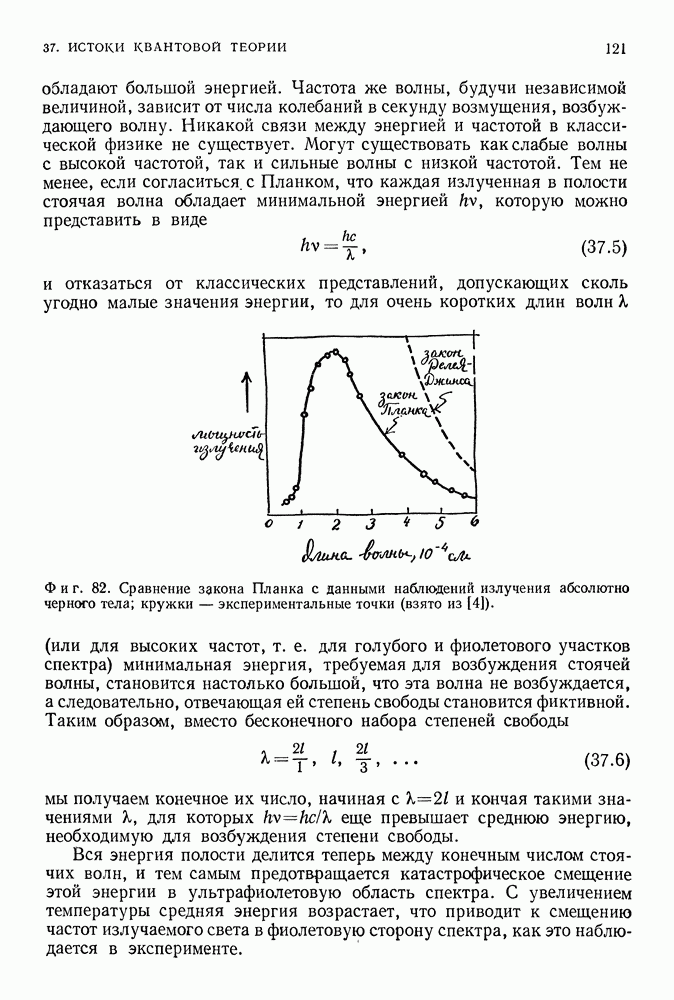
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
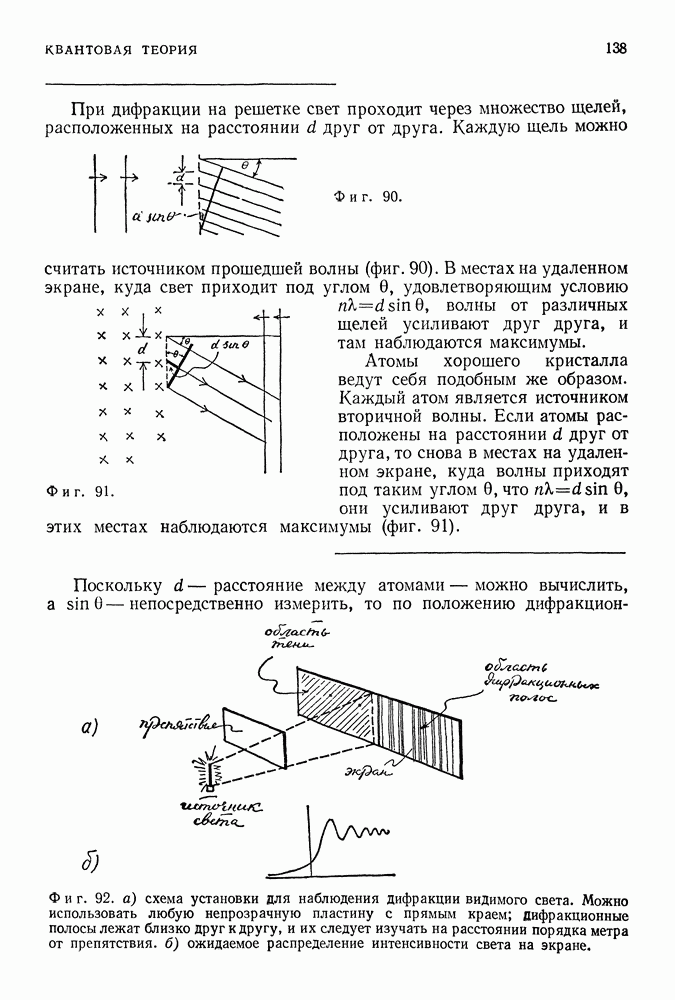
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
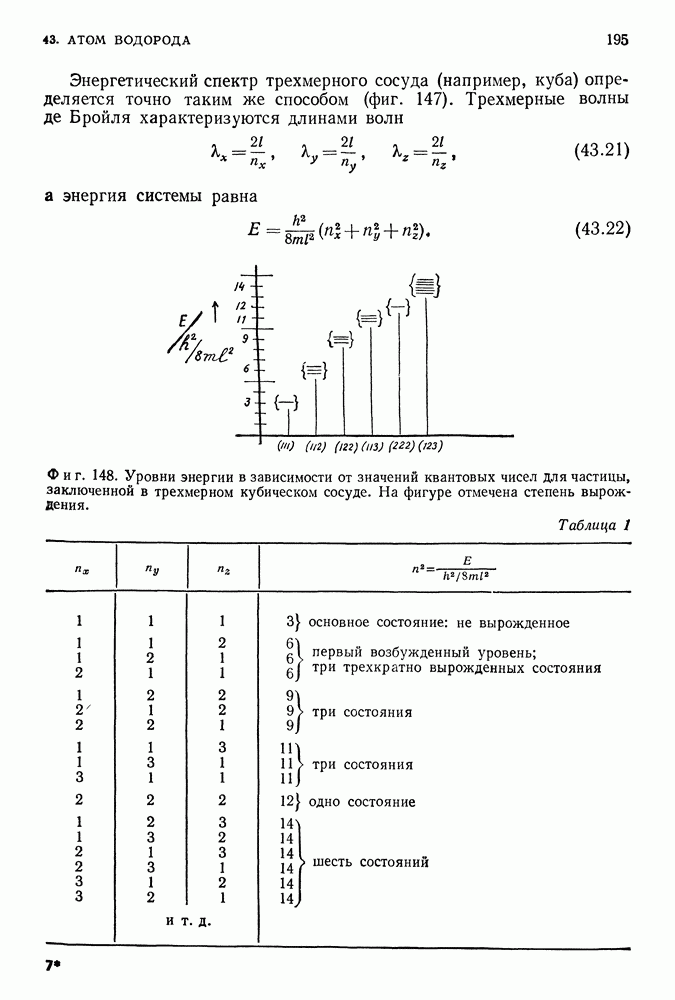
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
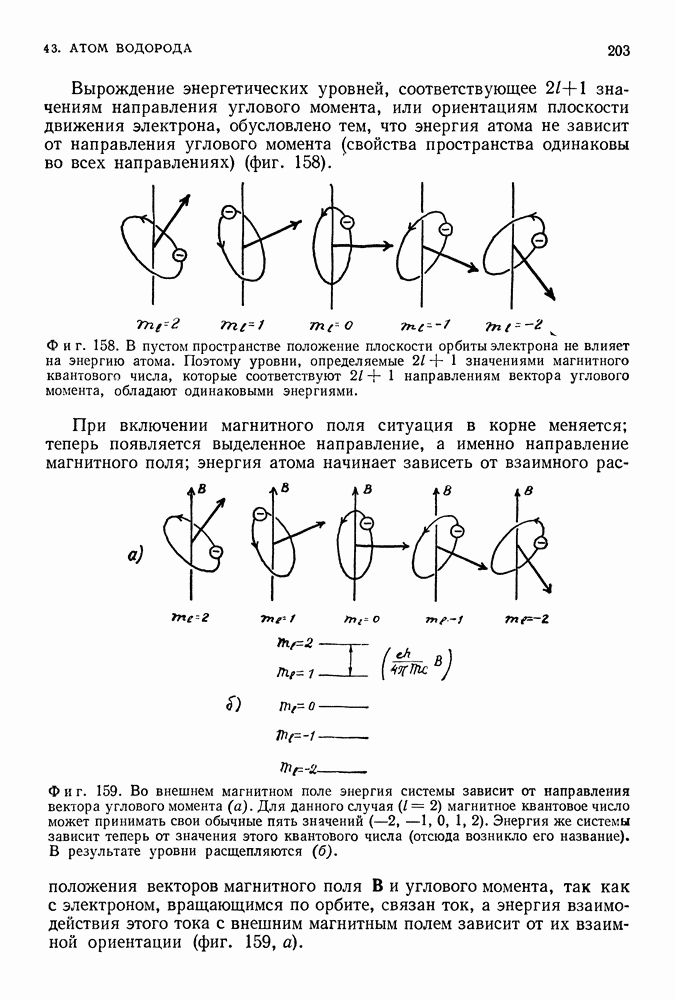
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
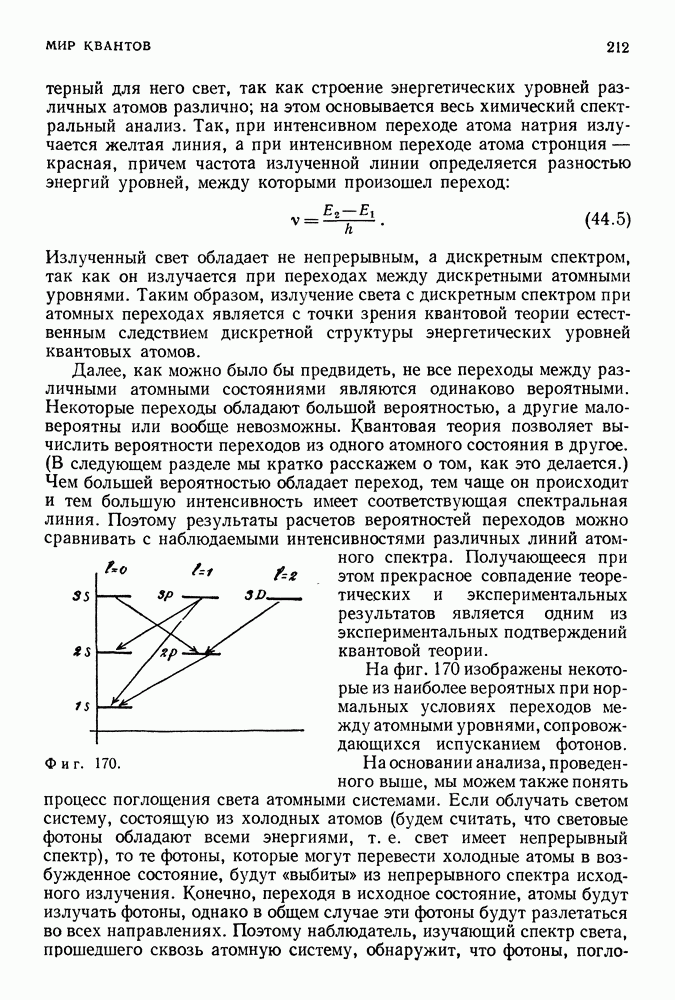
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
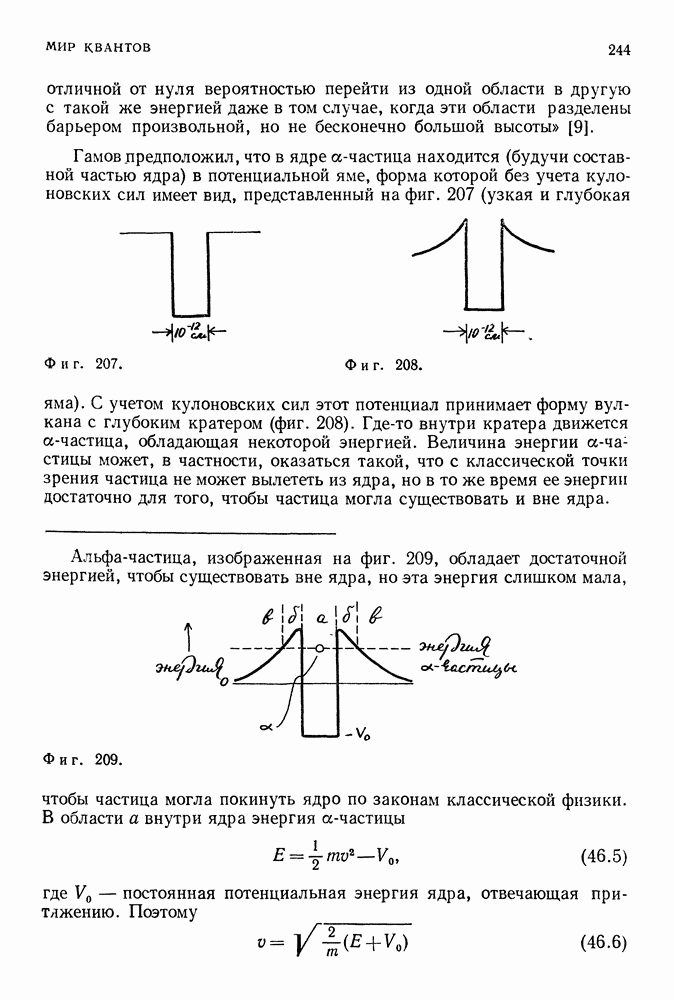
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
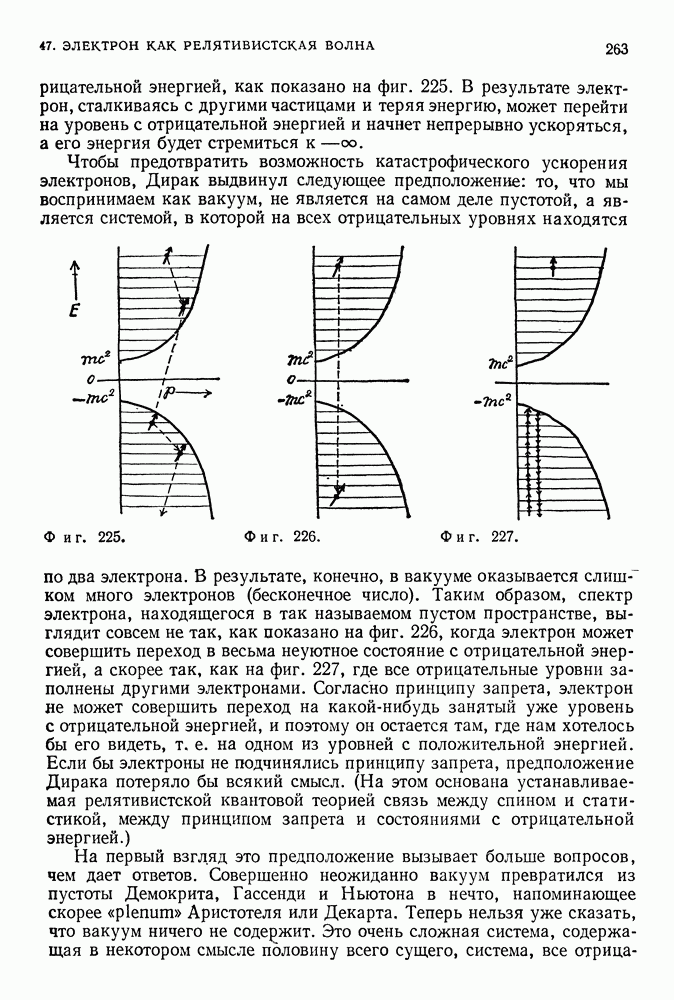
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
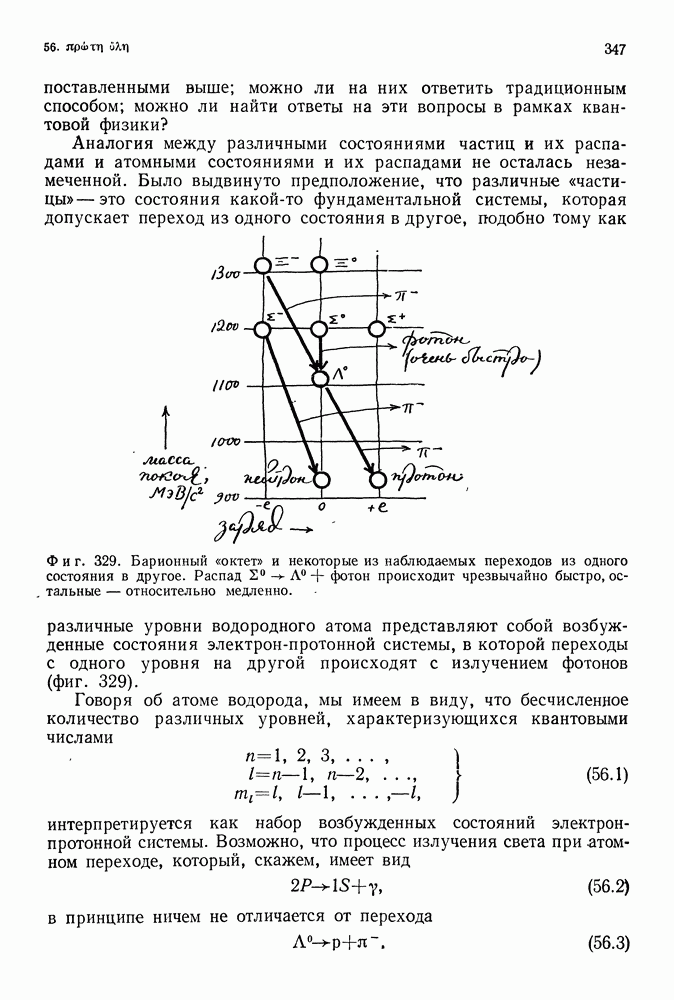
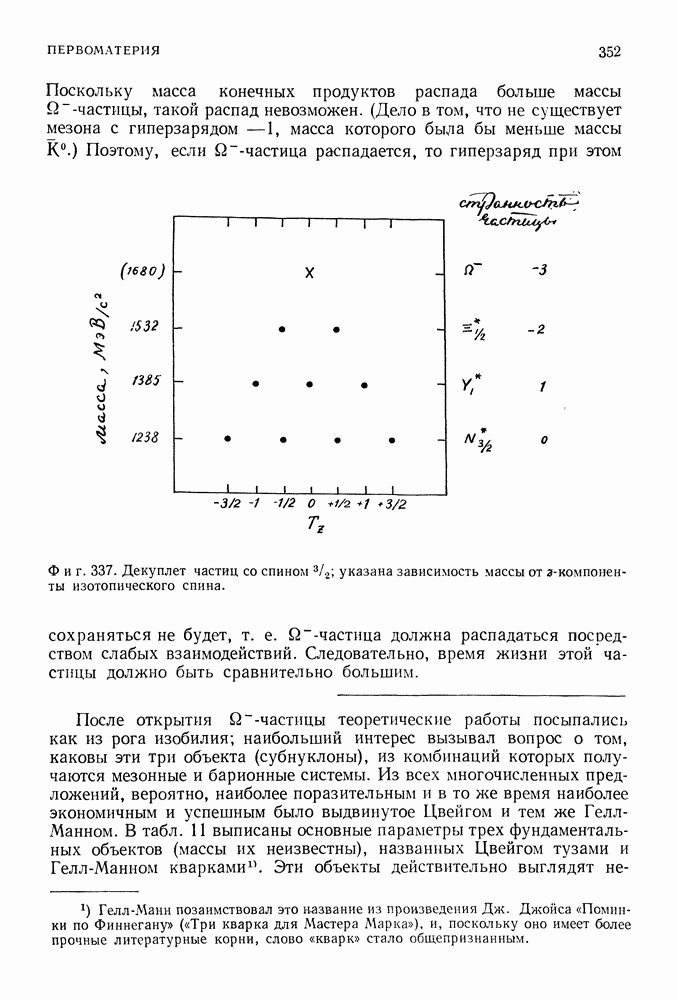
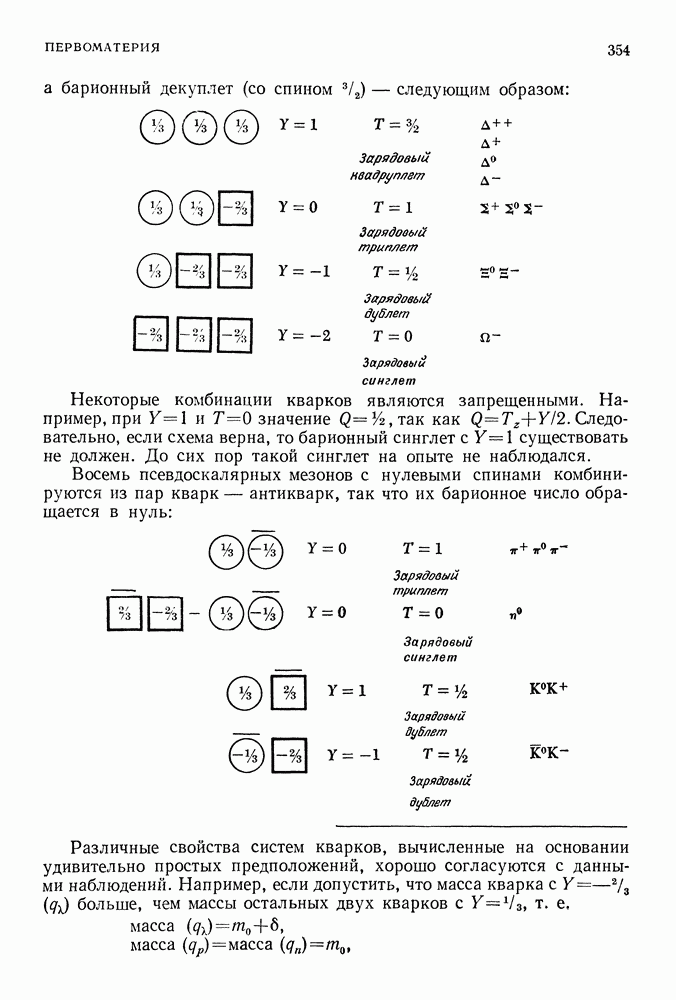
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА