| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
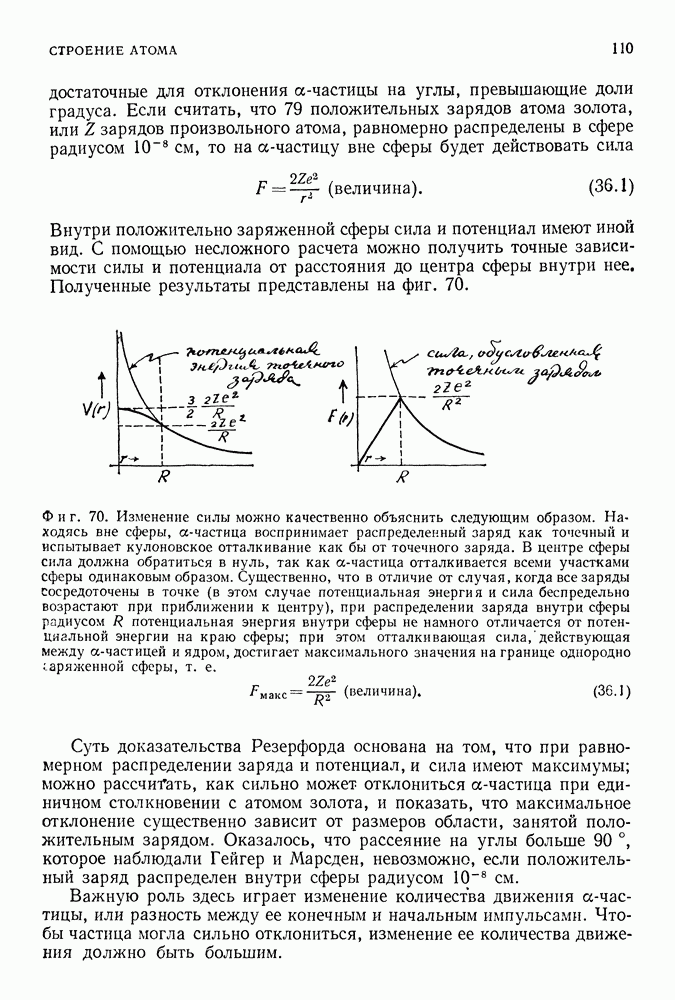
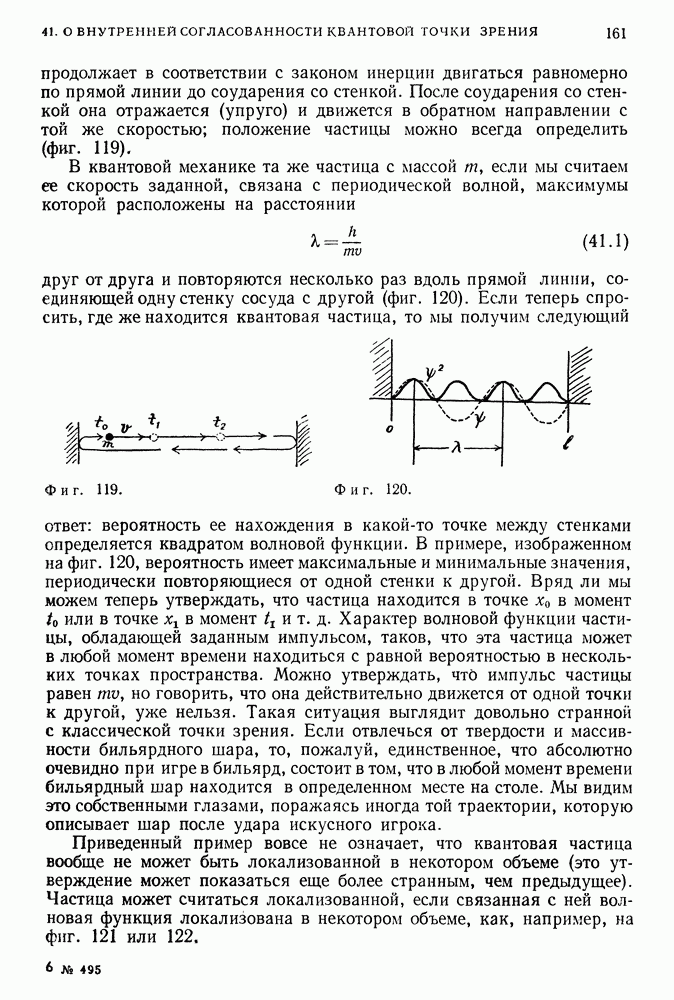
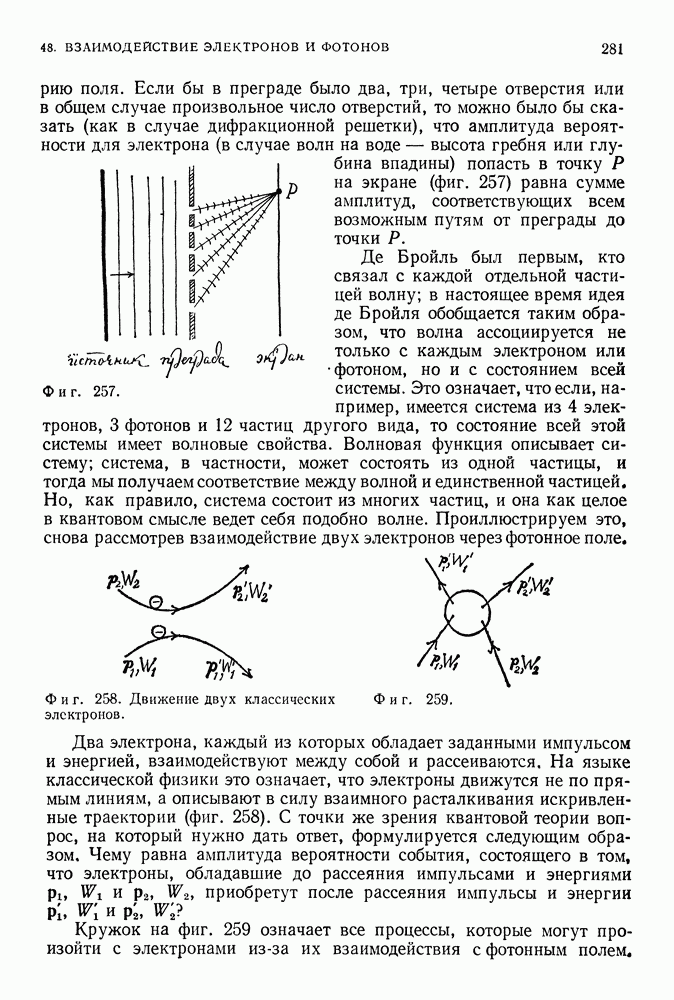
Кулоновская сила, удерживающая электрон в атоме водорода вблизи протона, обладает максимальной возможной симметрией относительно поворотов вокруг точки в пространстве. Вид ее эквипотенциальных поверхностей (сфер) не изменяется (является инвариантом) при повороте системы на любой угол (фиг. 149).

Фиг. 149.
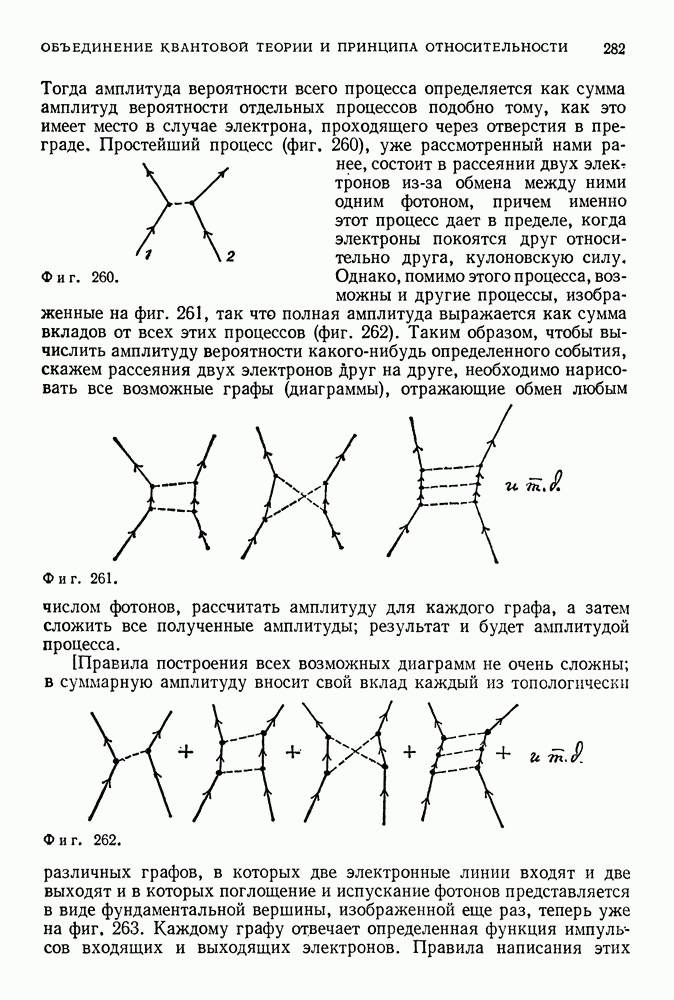
Такая вращательная симметрия физически означает, что сила, действующая между электроном и протоном (как и гравитационная сила), зависит только от расстояния между этими частицами. Если вращать электрон вокруг протона по поверхности сферы, то сила их взаимодействия будет оставаться постоянной. Можно противопоставить этот случай другому гипотетическому случаю, когда величина силы не остается неизменной при вращении системы и соответствующие эквипотенциальные поверхности представляют собой не сферы, а произвольные поверхности, одна из которых изображена на фиг. 150.

Фиг. 150. Когда сила не инвариантна относительно поворотов, сферы не являются эквипотенциальными поверхностями; в этом случае сила зависит не только от расстояния  между двумя телами, но и от их взаимной ориентации.
между двумя телами, но и от их взаимной ориентации.
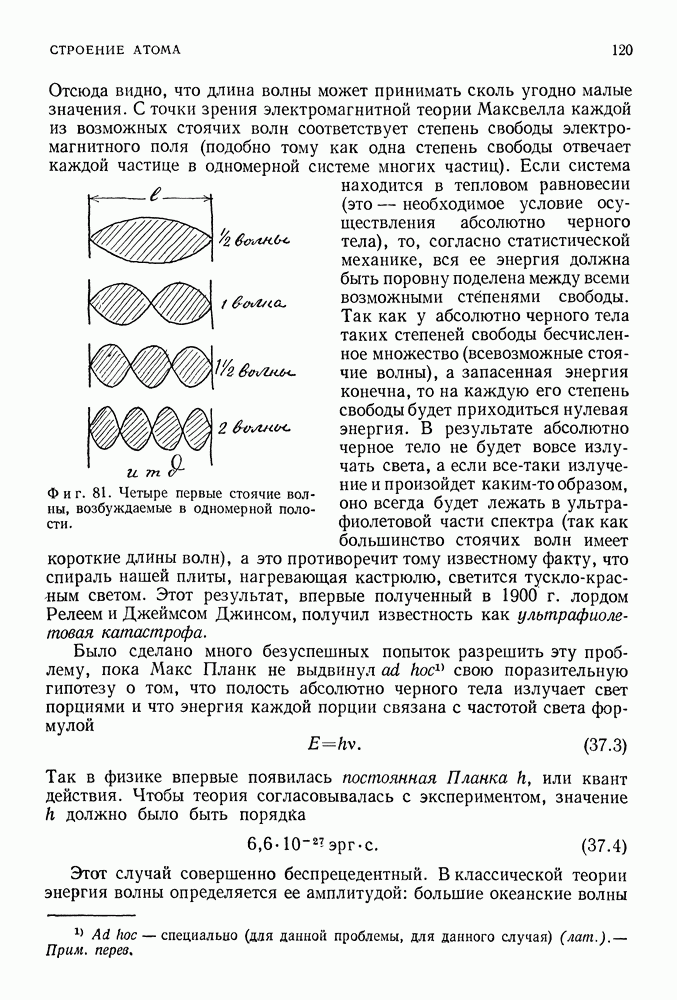
Энергетические уровни одномерной квантовой системы, рассмотренной в гл. 39, характеризуются одним числом  (называемым квантовым числом), которое определяет длину волны соответствующей волны де Бройля:
(называемым квантовым числом), которое определяет длину волны соответствующей волны де Бройля:

и энергию системы

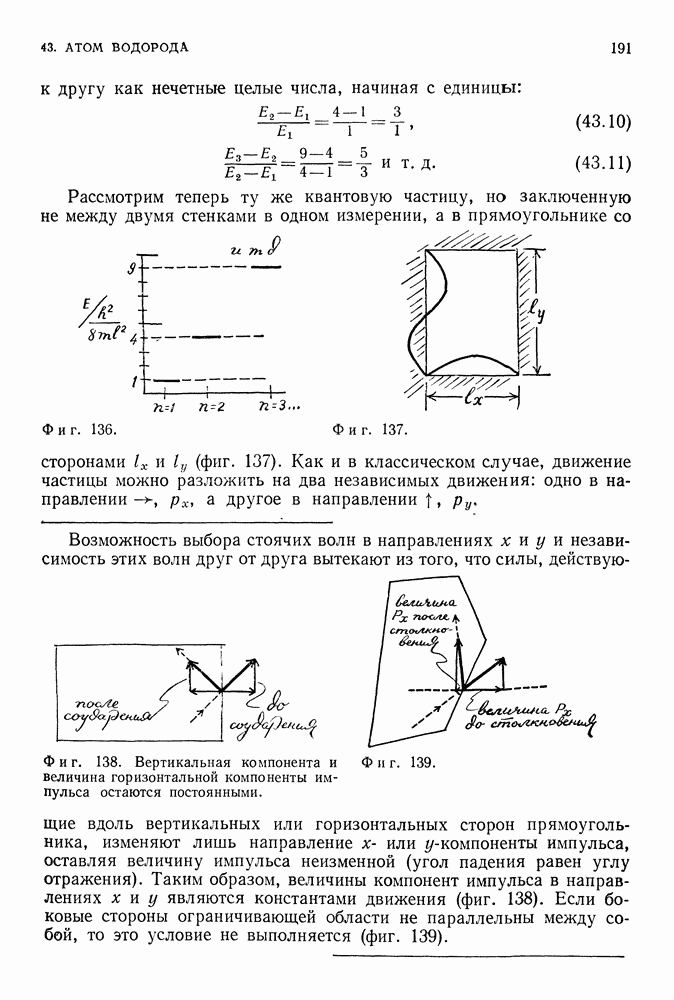
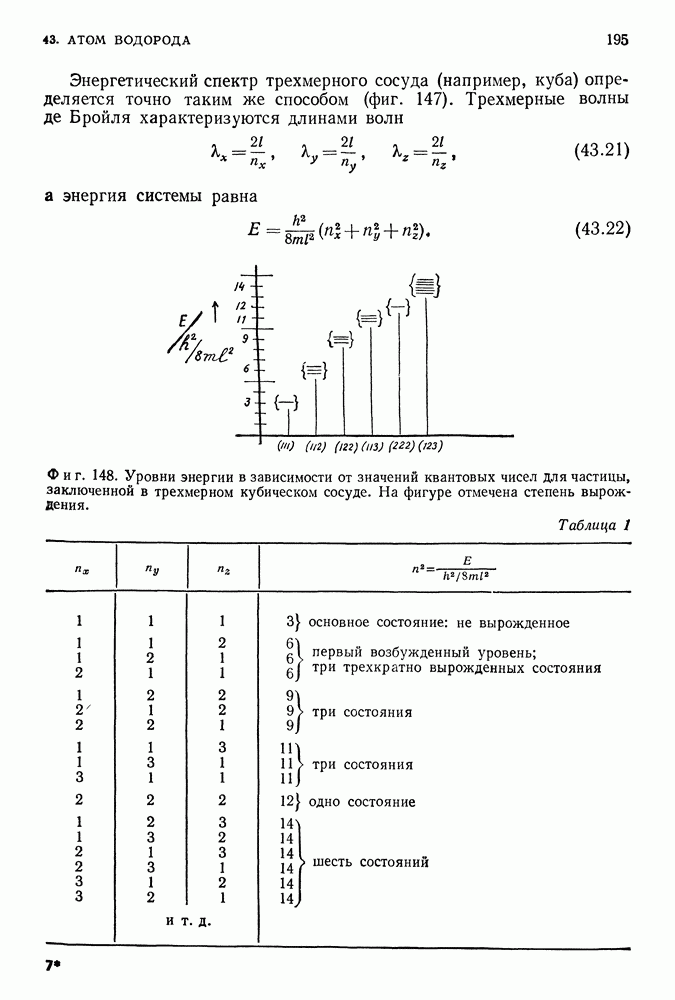
Уровни энергии двумерной квантовой системы, рассмотренной выше, определяются подобным же образом двумя квантовыми числами  а трехмерной системы — тремя числами
а трехмерной системы — тремя числами  Конкретный выбор чисел соответствует тем величинам, которые в данном случае сохраняются, — компонентам импульса в
Конкретный выбор чисел соответствует тем величинам, которые в данном случае сохраняются, — компонентам импульса в  -направлениях.
-направлениях.
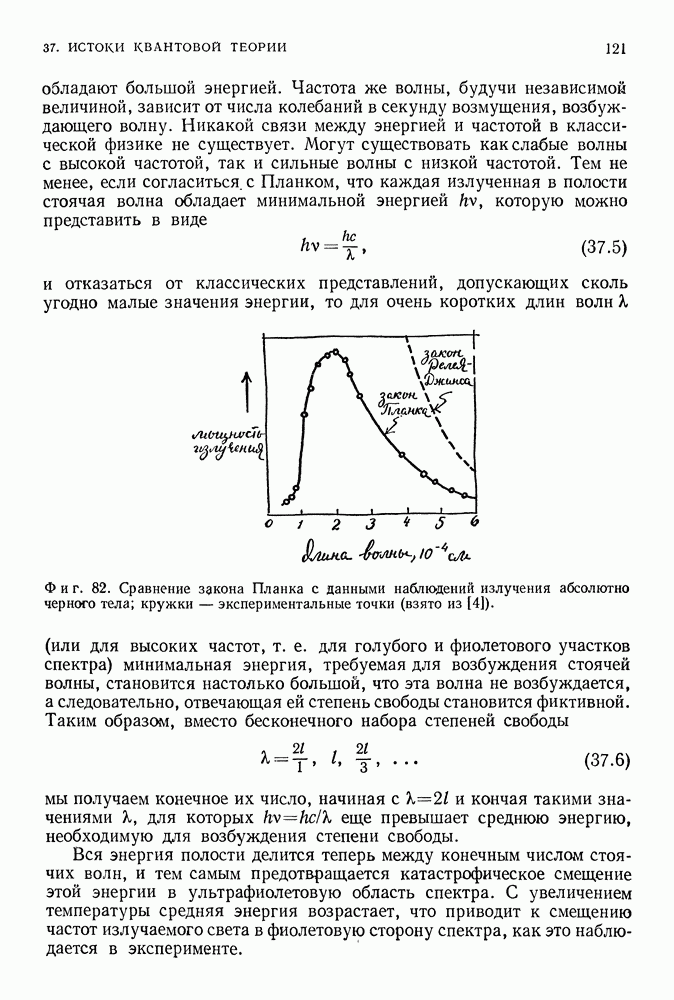
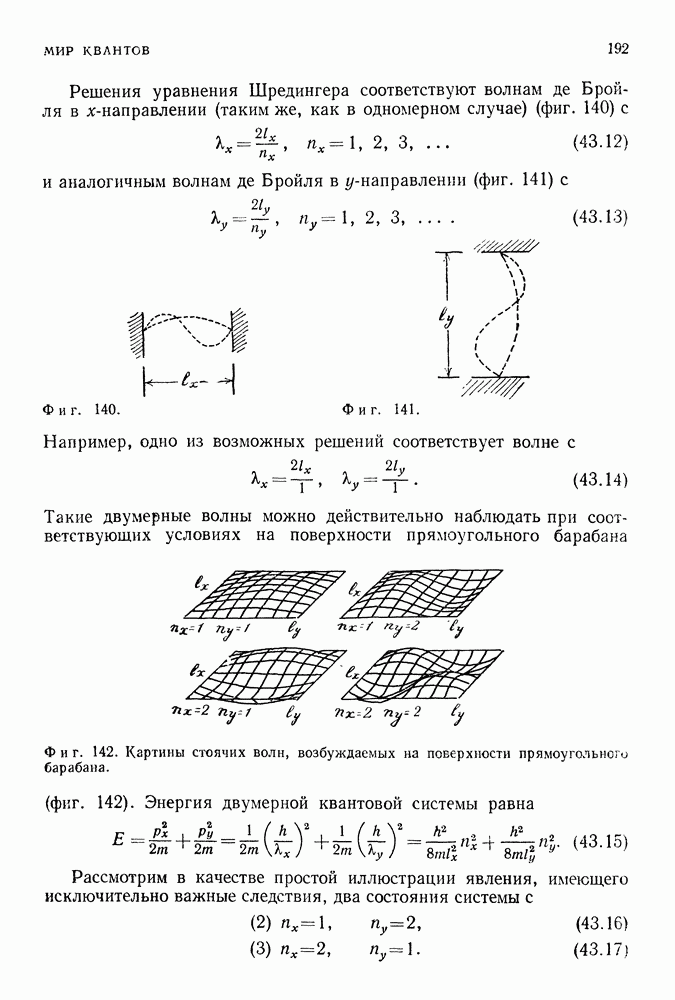
Инвариантность силовых систем относительно вращений (системы обладают симметрией сферы) приводит как в классической, так и в квантовой теориях к сохранению углового момента системы. В случае планетарной системы этот вывод заключен во втором законе Кеплера,

Фиг. 151. В случае круговых орбит сохранение углового момента  (величина) означает, что скорость
(величина) означает, что скорость  должна оставаться неизменной. Это условие содержится в утверждении, что за равные промежутки времени радиус, соединяющий частицу с центром, заметает равные площади. (Площадь, заметенная радиусом
должна оставаться неизменной. Это условие содержится в утверждении, что за равные промежутки времени радиус, соединяющий частицу с центром, заметает равные площади. (Площадь, заметенная радиусом  за время равна
за время равна 
Прямая, соединяющая Солнце с планетой, заметает за равные времена равные площади; этот же закон справедлив и в случае электрона, вращающегося вокруг протона (фиг. 151). В таких силовых системах компоненты импульса в  и
и  -направлениях не являются постоянными движения (как в случае кубической системы, рассмотренной ранее). Поэтому соответствующие им квантовые числа непригодны для характеристики системы. (Эти квантовые числа, если их ввести, будут изменяться со временем.) Чтобы получить некоторые квантовые числа сферически симметричной системы, следует обратиться к ее угловым моментам.
-направлениях не являются постоянными движения (как в случае кубической системы, рассмотренной ранее). Поэтому соответствующие им квантовые числа непригодны для характеристики системы. (Эти квантовые числа, если их ввести, будут изменяться со временем.) Чтобы получить некоторые квантовые числа сферически симметричной системы, следует обратиться к ее угловым моментам.
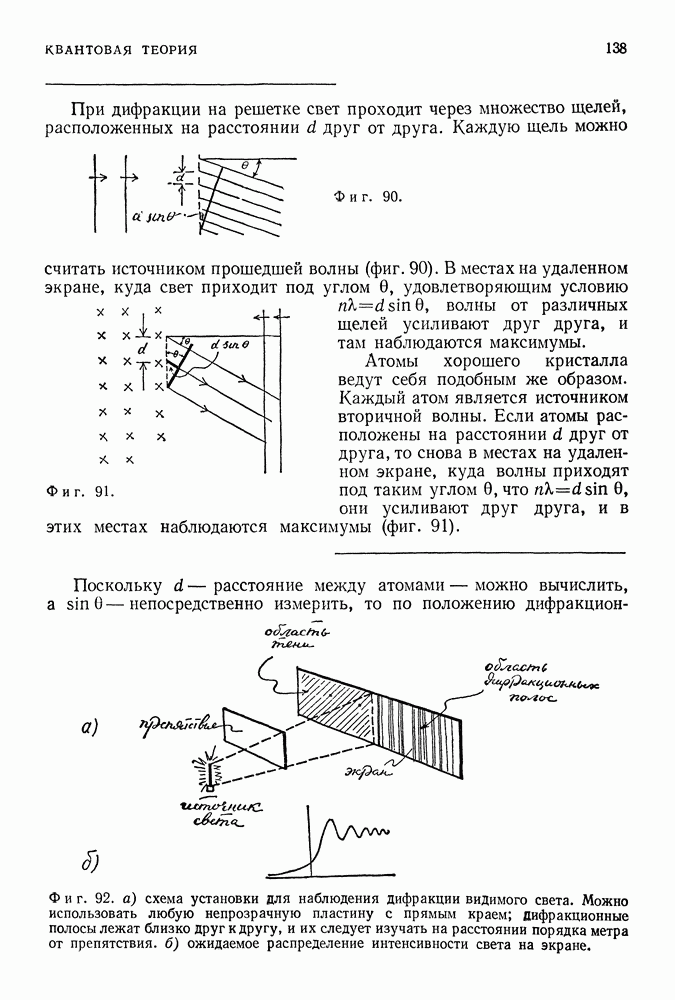
Угловой момент частицы, заключенной в квадратном сосуде, не является константой движения (фиг. 152).

Фиг. 152.

Фиг. 153.
При движении частицы вверх ее угловой момент относительно центра равен  (направлен против движения часовой стрелки), а при движении частицы вниз он равен —
(направлен против движения часовой стрелки), а при движении частицы вниз он равен —  (направлен по движению часовой стрелки). Другими словами, после отражения частицы от стенки ее угловой момент изменяет направление,
(направлен по движению часовой стрелки). Другими словами, после отражения частицы от стенки ее угловой момент изменяет направление,
Если же эта частица заключена в круглом сосуде (вид которого не изменяется при поворотах), то ее угловой момент, равный  направлен против движения часовой стрелки и не изменяется при отражении частицы от стенки сосуда (фиг. 153). Вместе с тем в квадратном сосуде в отличие от круглого сохраняются величины компонент импульса частицы в обоих направлениях.
направлен против движения часовой стрелки и не изменяется при отражении частицы от стенки сосуда (фиг. 153). Вместе с тем в квадратном сосуде в отличие от круглого сохраняются величины компонент импульса частицы в обоих направлениях.
Величине и направлению углового момента соответствуют так называемые азимутальные (или орбитальные) волны де Бройля и азимутальные квантовые числа. В рассматриваемом случае, как и в теории Бора и аналогично случаю частицы, заключенной в кубическом сосуде, в качестве возможных решений уравнения Шредингера могут выступать лишь определенные стоячие волны де Бройля (соответствующие величине и направлению углового момента). Эти волны характеризуются следующими квантовыми числами:

Первое число связано с угловым моментом системы по формуле (табл. 2.):

Таблица 2

Второе число  пробегает все целые значения от
пробегает все целые значения от  до
до  и при заданном I имеет
и при заданном I имеет  значений (табл, 3),
значений (табл, 3),
Таблица 3

Квантовое число  соответствует компоненте углового момента вдоль некоторого направления в пространстве, например направления приложенного магнитного поля:
соответствует компоненте углового момента вдоль некоторого направления в пространстве, например направления приложенного магнитного поля:

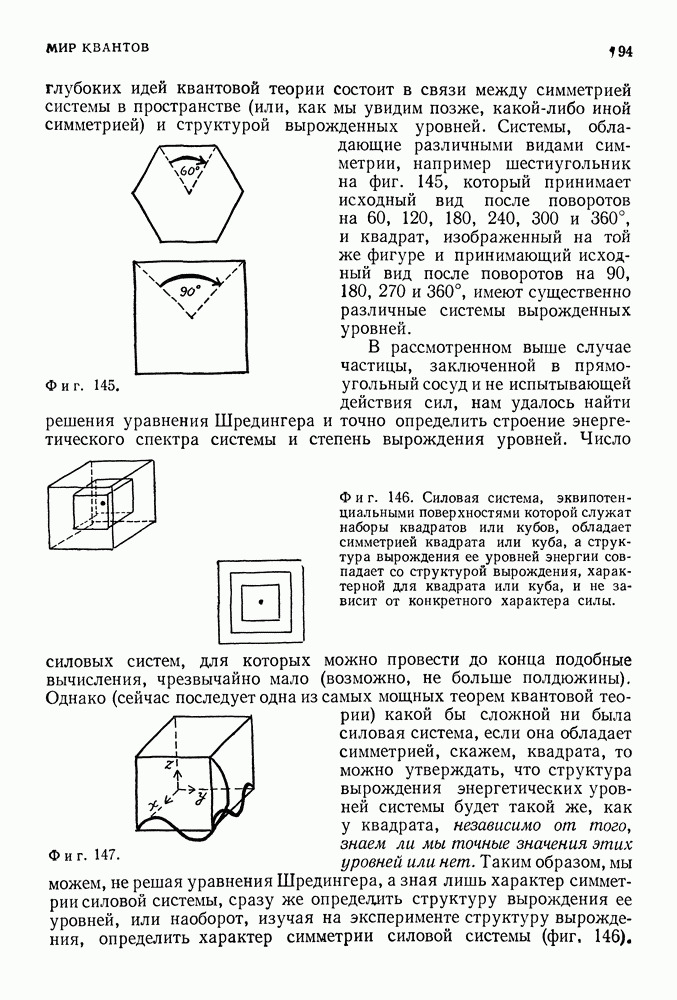
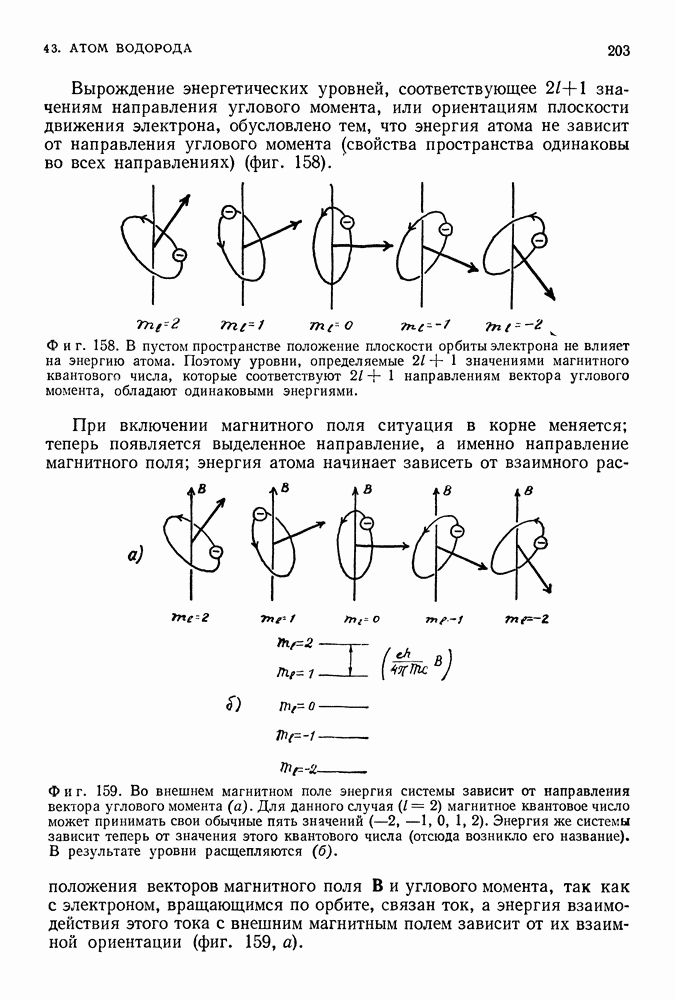
Таким образом, как величина, так и направление углового момента (как и в случае стоячих волн де Бройля в сосуде) принимают в отличие от классического вектора углового момента лишь дискретные значения, определяемые целыми числами (фиг. 154).

Фиг. 154. Величина вектора квантового углового момента характеризуется целым числом I (здесь 1—2), а его компонента в вертикальном направлении — целым числом  (здесь
(здесь  ). Величину
). Величину  можно интерпретировать как компоненту углового момента в вертикальном направлении, так как она не превышает I (компонента вектора не может быть больше самого вектора). В отличие от классического случая вектор квантового момента может иметь лишь строго определенные направления в пространстве. (Исторически такое поведение квантового момента получило название пространственного квантования.)
можно интерпретировать как компоненту углового момента в вертикальном направлении, так как она не превышает I (компонента вектора не может быть больше самого вектора). В отличие от классического случая вектор квантового момента может иметь лишь строго определенные направления в пространстве. (Исторически такое поведение квантового момента получило название пространственного квантования.)
Интересно, понравилось бы это Пифагору?
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
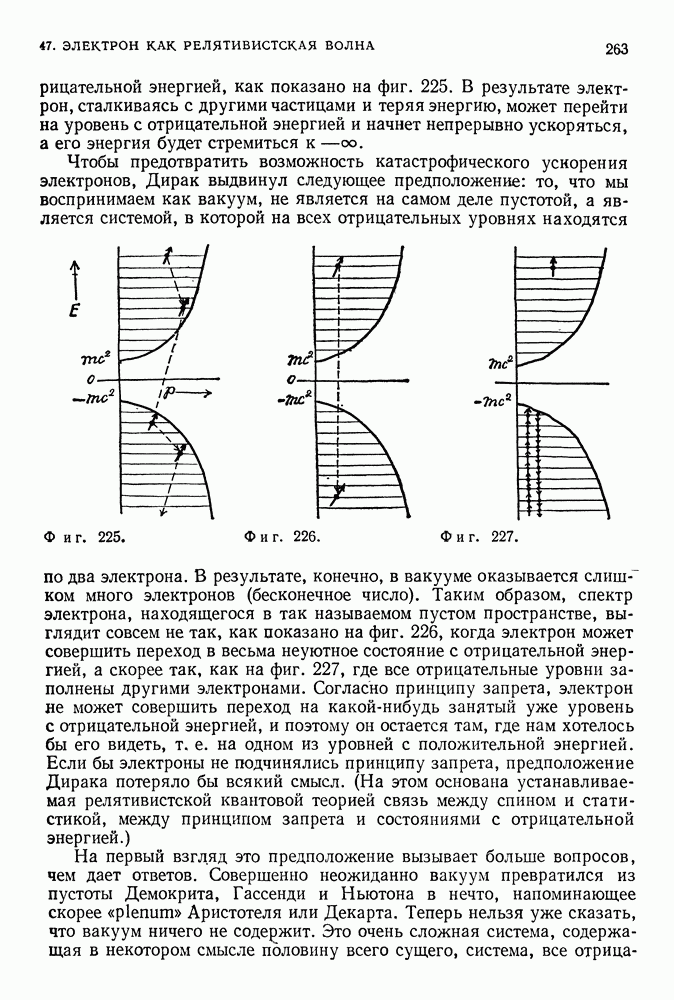
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
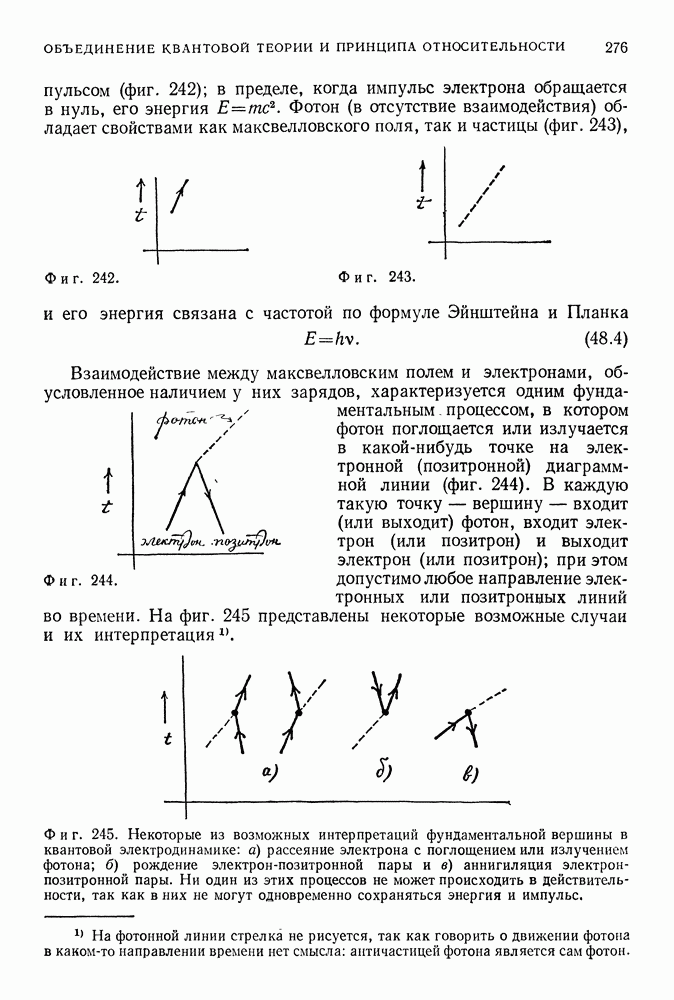
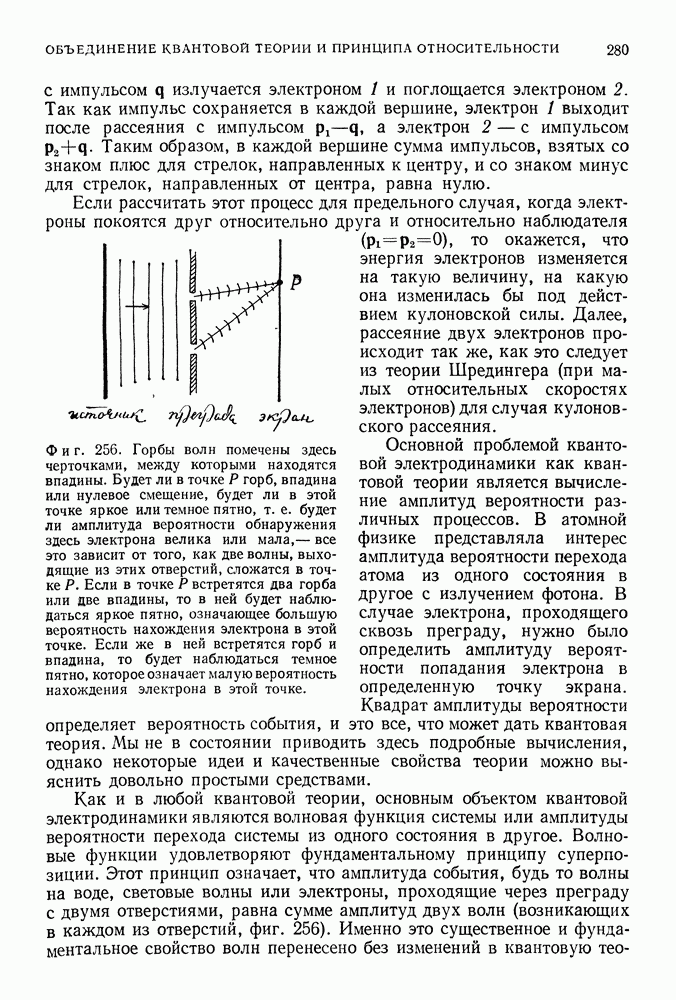
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
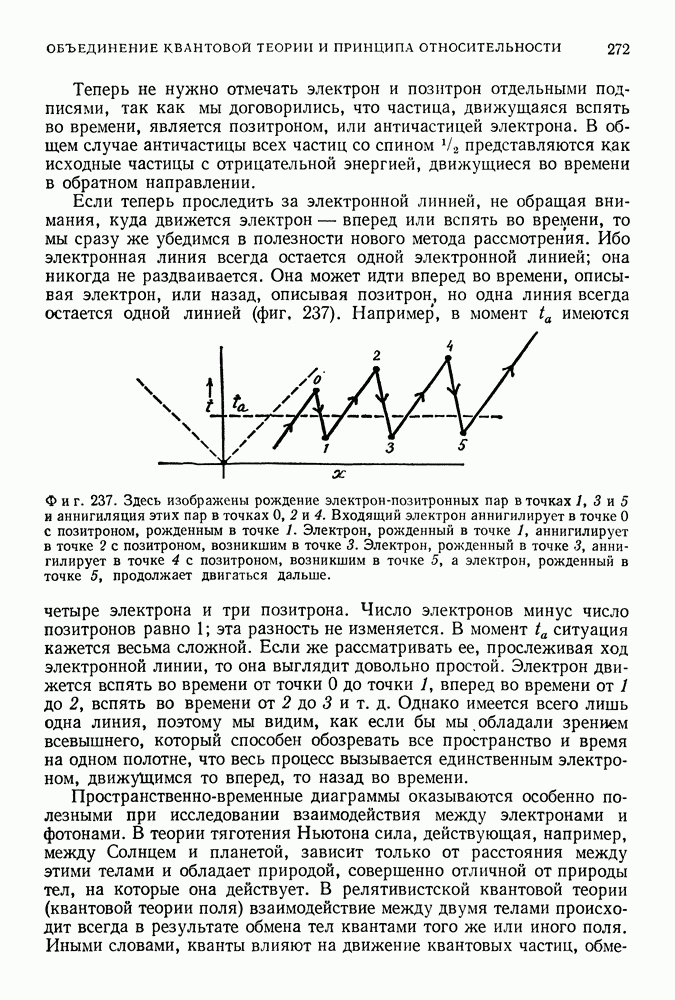
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
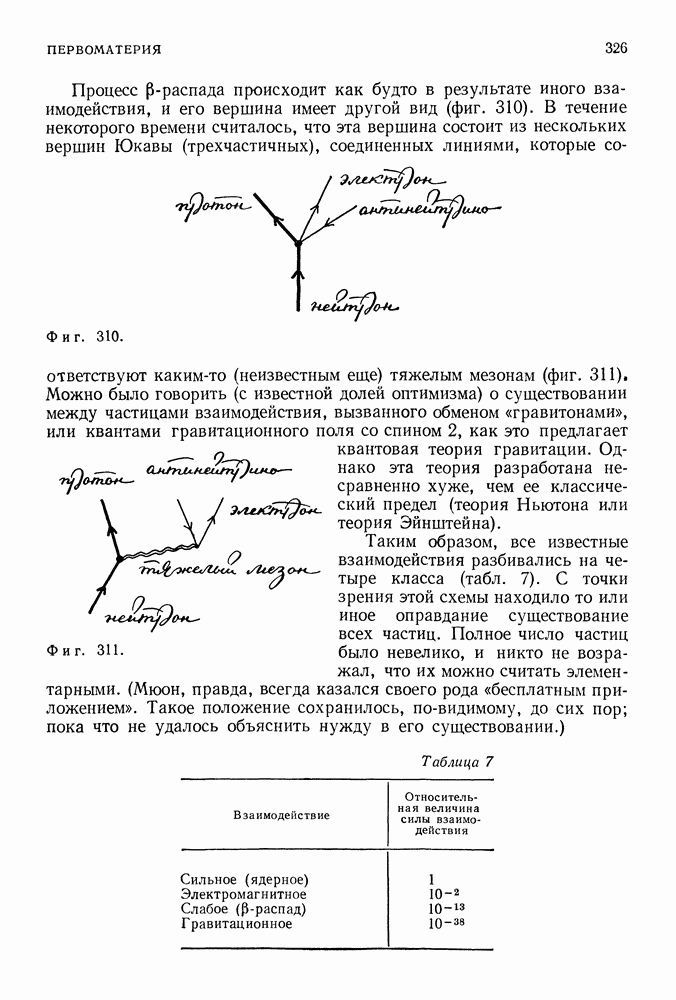
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
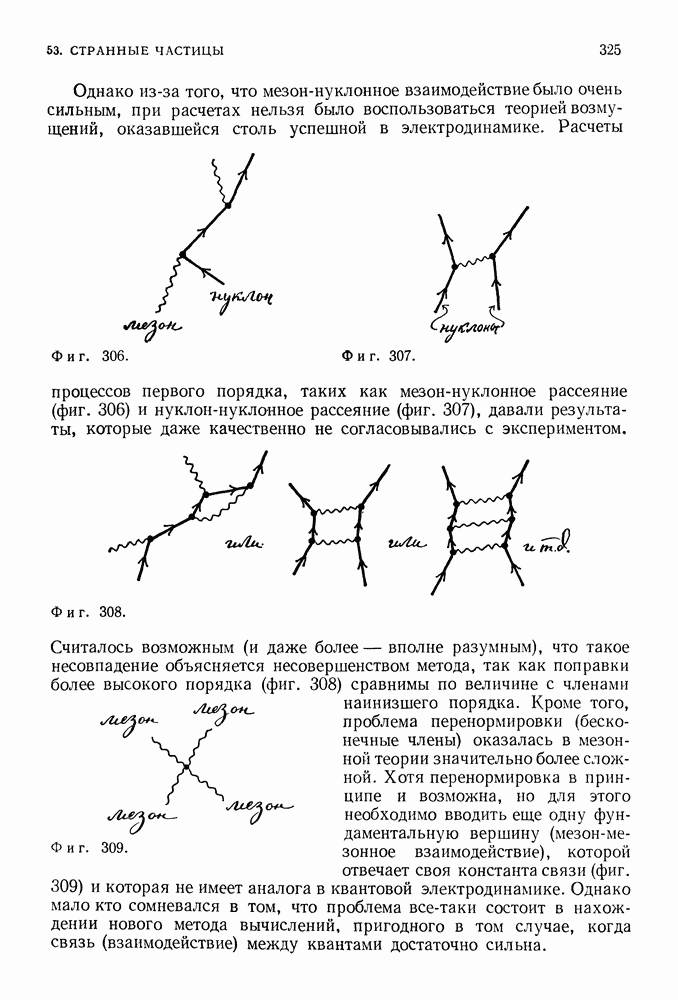
- 53. СТРАННЫЕ ЧАСТИЦЫ
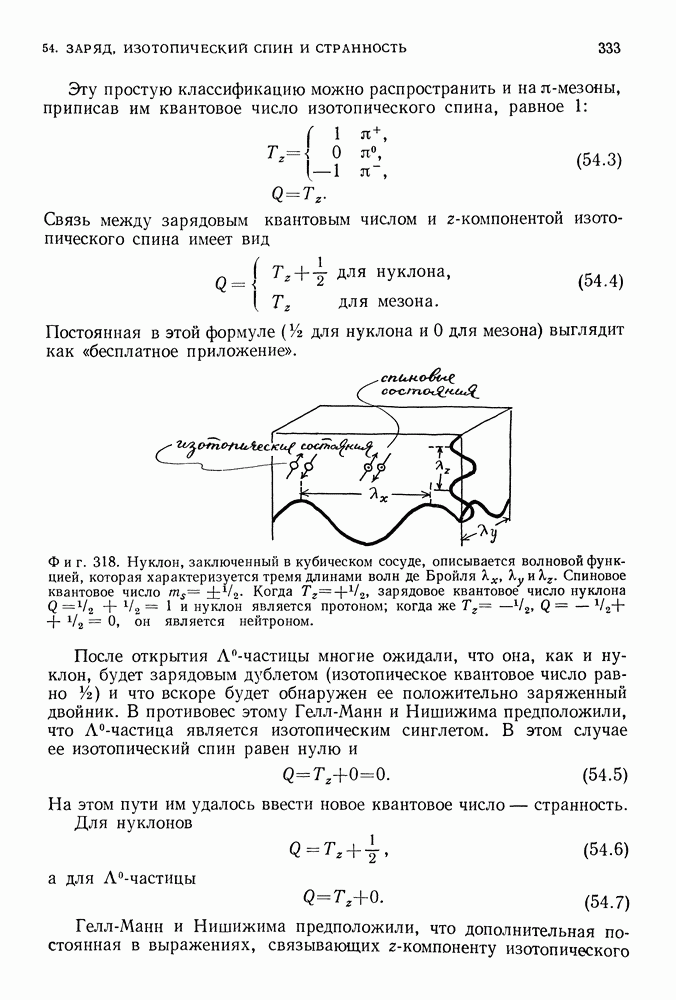
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА