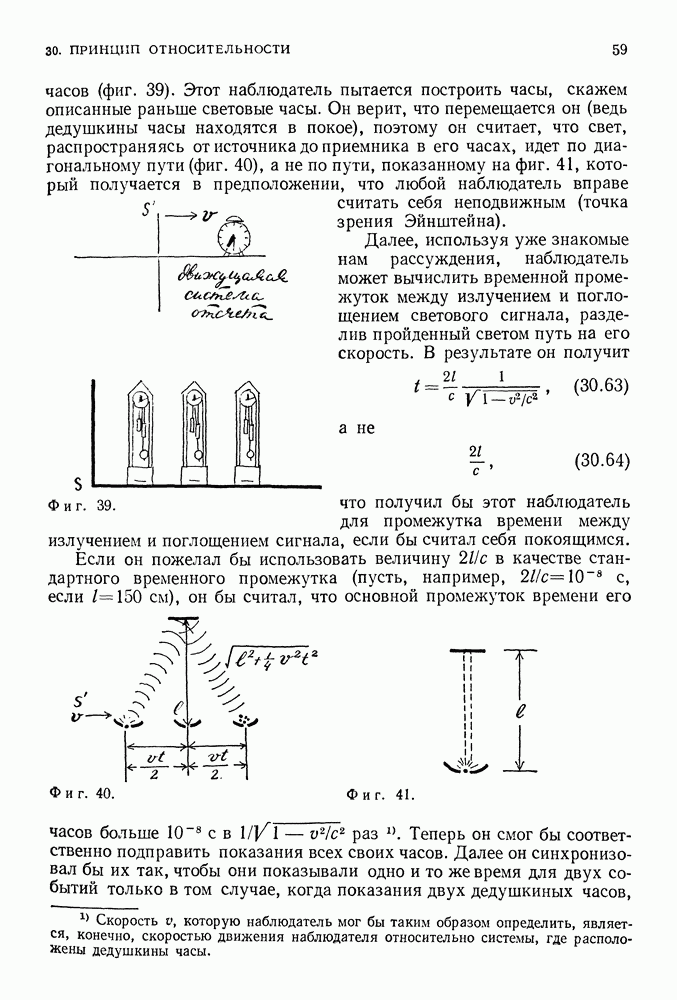
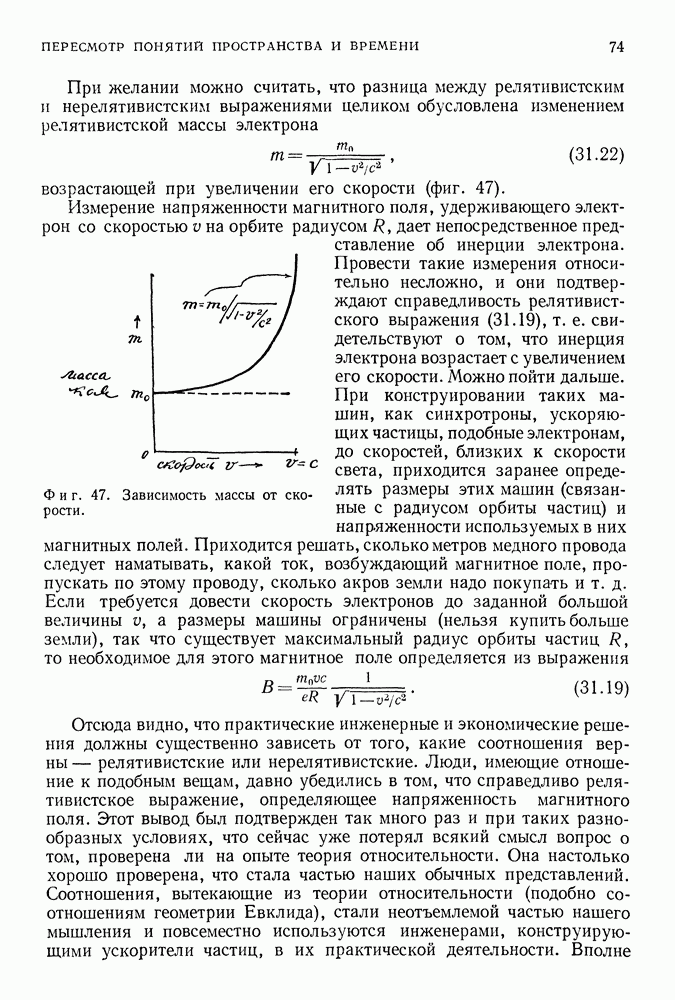
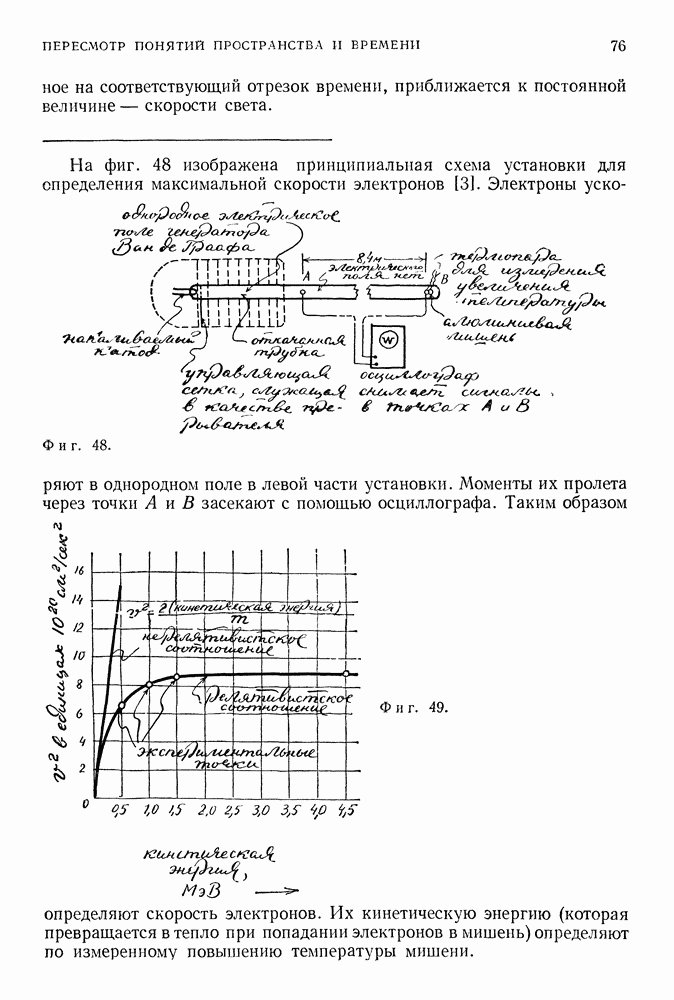
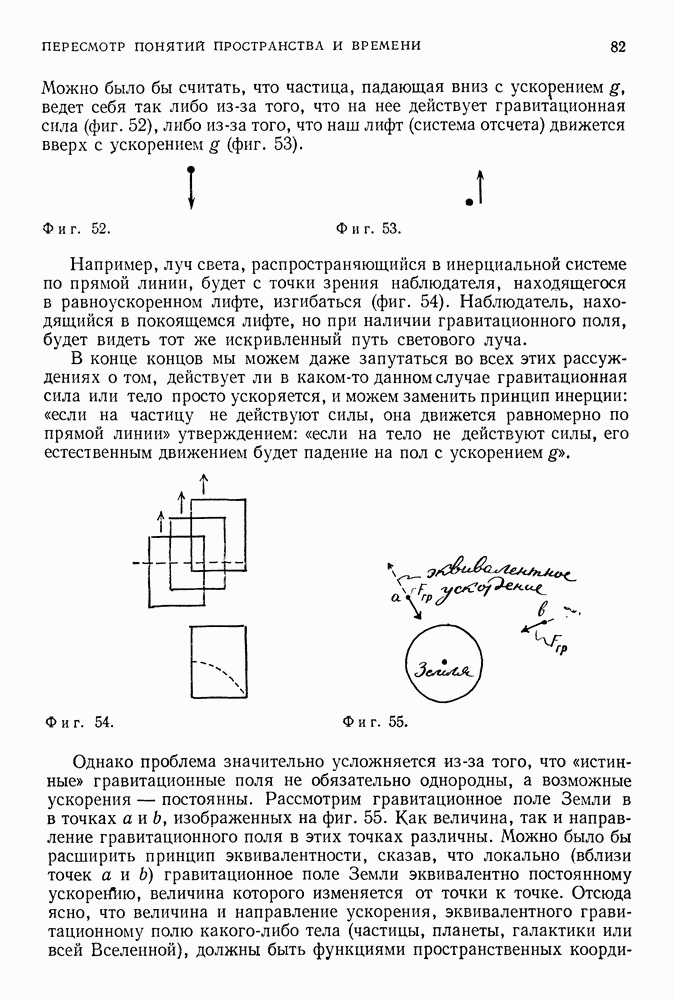
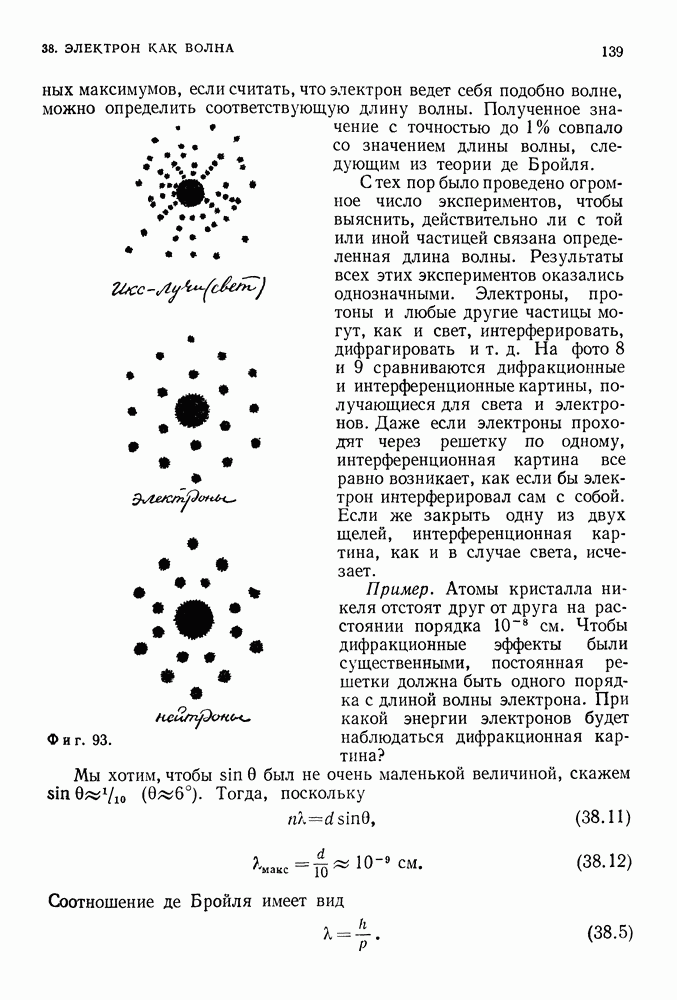
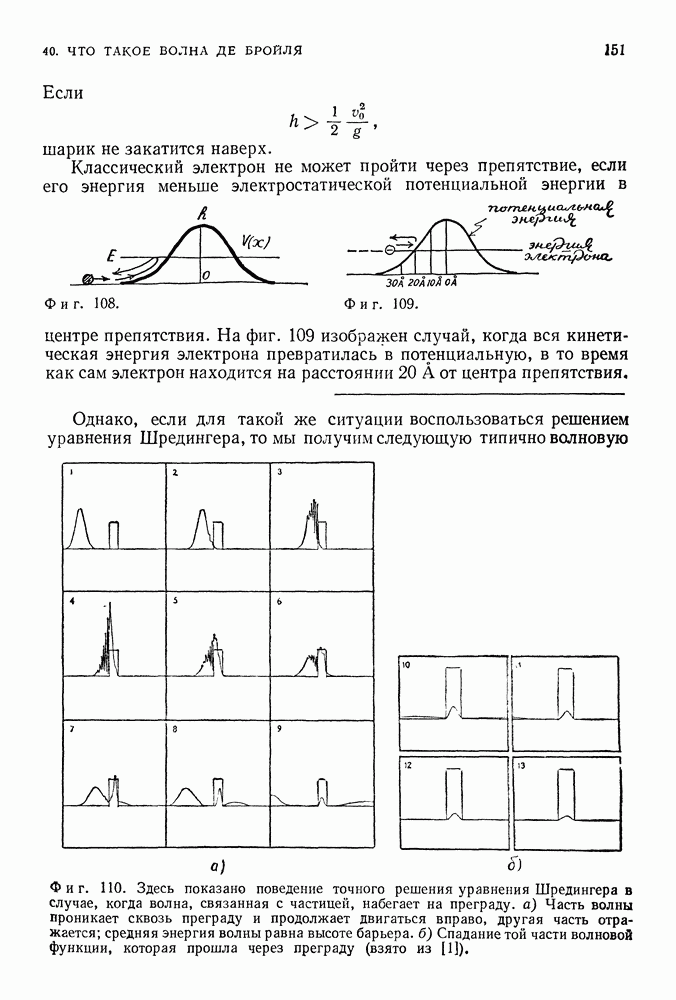
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
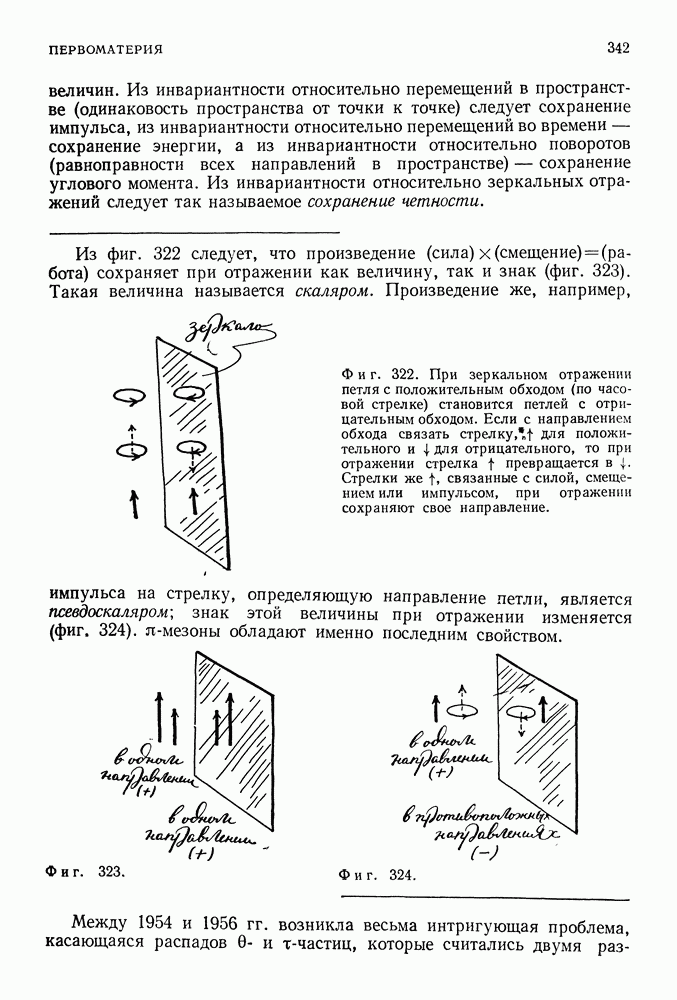
Хотя этот принцип и выглядит довольно странным, по своей сути он чрезвычайно прост. В квантовой теории, где положение объекта характеризуется квадратом амплитуды, а величина его импульса — длиной волны соответствующей волновой функции, этот принцип есть не что иное, как просто факт, характерный для волн: волна, локализованная в пространстве, не может иметь одну длину волны. Недоумение вызывается тем, что, говоря о частице, мы мысленно представляем ее классический образ, а затем удивляемся, когда обнаруживаем, что квантовая частица ведет себя не так, как ее классическая предшественница.
Если настаивать на классическом описании поведения квантовой частицы (в частности, если пытаться приписать ей как положение в пространстве, так и импульс), то максимальные возможные точности одновременного определения ее положения и импульса окажутся связанными между собой с помощью удивительно простого соотношения, впервые предложенного Гейзенбергом и получившего название принципа неопределенности:

где  — неточности, или неопределенности, значений импульса и положения частицы. Произведение неточностей импульса и положения
— неточности, или неопределенности, значений импульса и положения частицы. Произведение неточностей импульса и положения
оказывается порядка величины постоянной Планка. В квантовой теории в отличие от классической невозможно одновременно локализовать квантовую частицу  и приписать ей определенный импульс
и приписать ей определенный импульс  Поэтому такая частица не может обладать и траекторией в том же смысле, что классическая частица. Мы имеем в виду отнюдь не психологическую неопределенность. Эта неопределенность характеризует природу такого объекта, который не может одновременно обладать двумя свойствами—положением и импульсом; объекта, отдаленно напоминающего шторм в атмосфере: если он простирается на большие расстояния, то дуют слабые ветры; если же он сконцентрирован в небольшой области, то возникает ураган или тайфун.
Поэтому такая частица не может обладать и траекторией в том же смысле, что классическая частица. Мы имеем в виду отнюдь не психологическую неопределенность. Эта неопределенность характеризует природу такого объекта, который не может одновременно обладать двумя свойствами—положением и импульсом; объекта, отдаленно напоминающего шторм в атмосфере: если он простирается на большие расстояния, то дуют слабые ветры; если же он сконцентрирован в небольшой области, то возникает ураган или тайфун.
Принцип неопределенности содержит в удивительно простой форме то, что было так трудно сформулировать, используя волну Шредингера. Если имеется волновая функция с заданной длиной волны или с заданным импульсом, то ее положение является полностью неопределенным, так как вероятности нахождения частицы в различных точках пространства равны между собой. С другой стороны, если частица полностью локализована, ее волновая функция должна состоять из суммы всех возможных периодических волн, так что ее длина волны или импульс оказываются абсолютно неопределенными. Точное соотношение между неопределенностями положения и импульса (которое получается непосредственно из волновой теории и не связано особым образом с квантовой механикой, так как оно характеризует природу любых волн — звуковых волн, волн на поверхности воды или волн, бегущих вдоль натянутой пружины) дается в простой форме принципом неопределенности Гейзенберга.
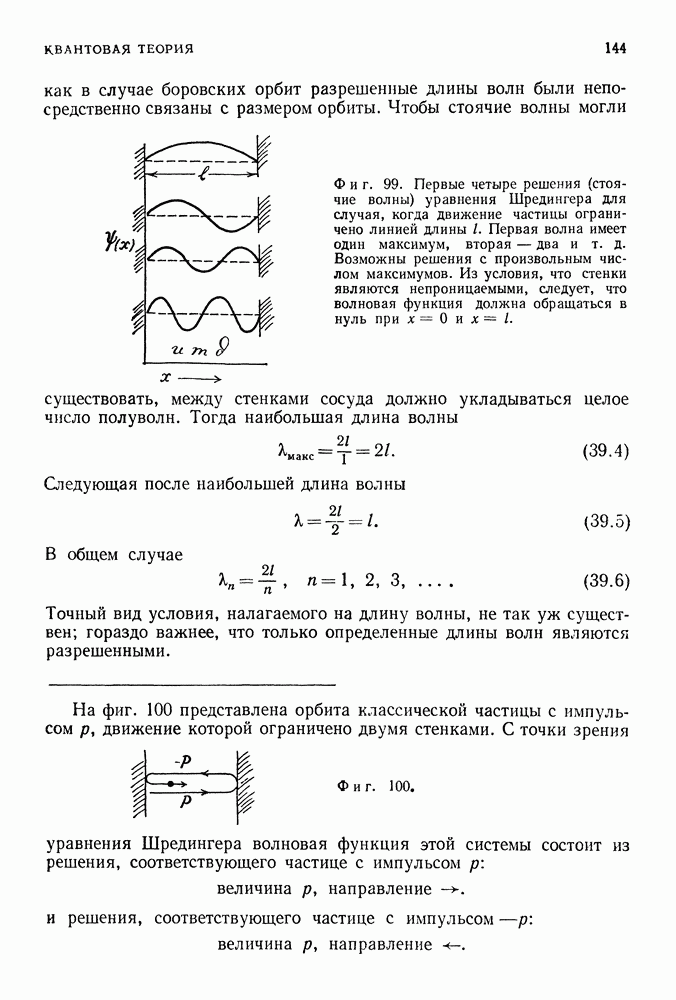
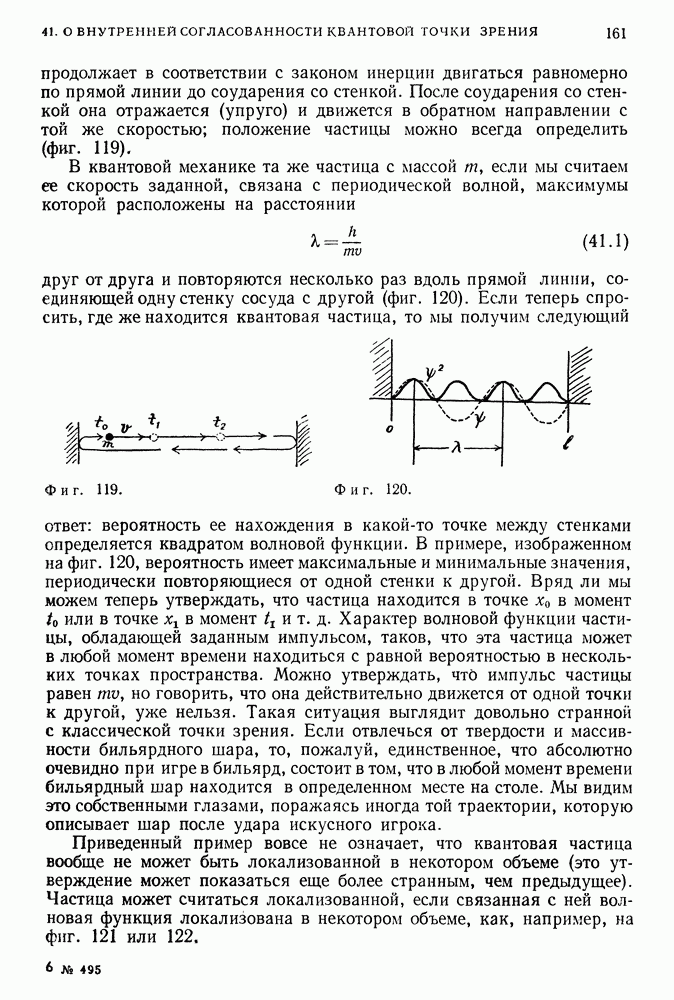
Вспомним рассмотренную ранее частицу, одномерное движение которой происходило между двумя стенками, расположенными на расстоянии  друг от друга. Неопределенность положения такой частицы не превышает расстояния между стенками, так как мы знаем, что частица заключена между ними. Поэтому величина
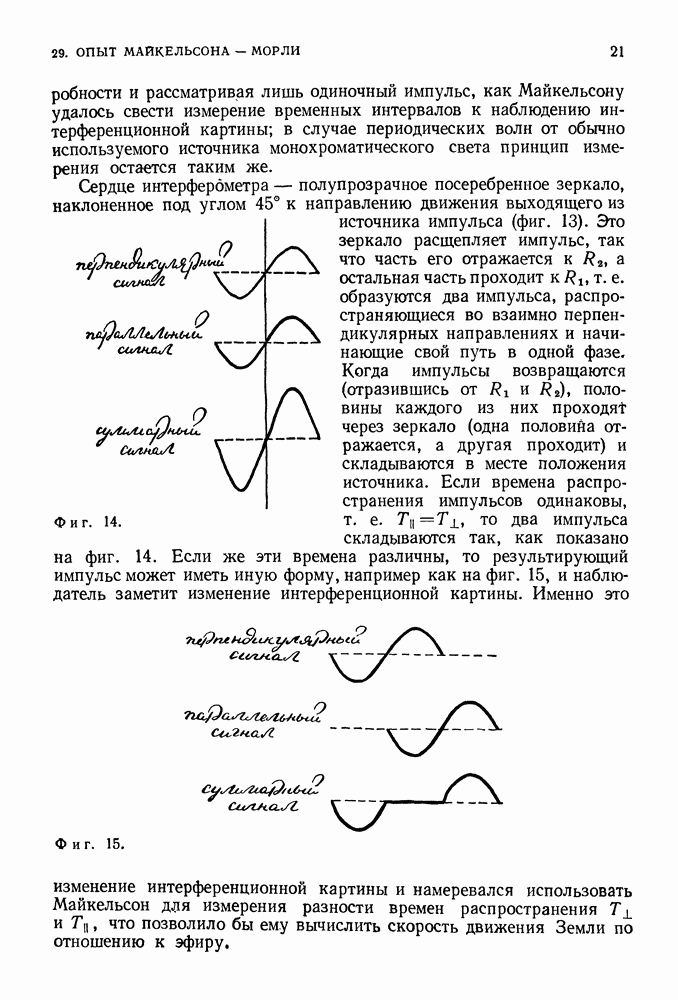
друг от друга. Неопределенность положения такой частицы не превышает расстояния между стенками, так как мы знаем, что частица заключена между ними. Поэтому величина  равна или меньше
равна или меньше 

Положение частицы, конечно, может быть локализовано в более узких пределах. Но если задано, что частица просто заключена между стенками, ее координата х не может выйти за пределы расстояния между этими стенками. Следовательно, неопределенность, или отсутствие
знания, ее координаты х не может превышать величину I. Тогда неопределенность импульса частицы больше или равна 

Импульс связан со скоростью по формуле

следовательно, неопределенность скорости

Если частица—электрон и расстояние между стенками равно  см. то
см. то

Таким образом, если частица с массой электрона локализована в области, размеры которой порядка  то говорить о скорости частицы можно лишь с точностью до
то говорить о скорости частицы можно лишь с точностью до  см/с,
см/с,
Используя результаты, полученные ранее, можно найти соотношение неопределенности для волны Шредингера в случае частицы, заключенной между двумя стенками. Основному состоянию такой системы соответствует смесь в равных долях решений с импульсами

(В классическом случае электрон мечется от стенки к стенке, причем его импульс, оставаясь все время равным по величине  изменяет свое направление при каждом соударении со стенкой.) Так как импульс изменяется от
изменяет свое направление при каждом соударении со стенкой.) Так как импульс изменяется от  до
до  его неопределенность равна
его неопределенность равна

или

Из соотношения де Бройля

а для основного состояния

так что

В то же время

Следовательно,

Этот результат можно использовать для оценки наименьшего значения энергии, которым может обладать квантовая система. Ввиду того что импульс системы — неопределенная величина, эта энергия в общем случае не равна нулю, что радикально отличает квантовую систему от классической. В классическом случае энергия рассматриваемой частицы совпадает с ее кинетической энергией, и когда частица покоится, эта энергия обращается в нуль,  Для квантовой системы, как было показано выше неопределенность импульса находящейся в системе частицы составляет
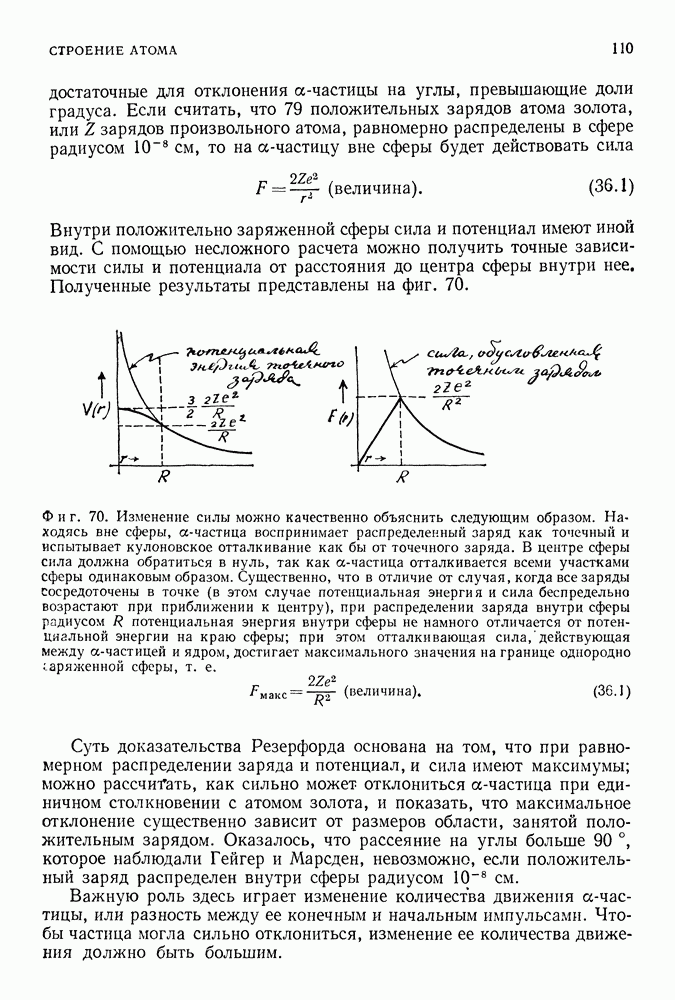
Для квантовой системы, как было показано выше неопределенность импульса находящейся в системе частицы составляет


Фиг. 127.
Импульс такой частицы нельзя определить точно, так как возможные его значения лежат в интервале шириной  Очевидно, если нуль лежит посредине этого интервала (фиг. 127), то импульс будет изменяться по величине в пределах от нуля до
Очевидно, если нуль лежит посредине этого интервала (фиг. 127), то импульс будет изменяться по величине в пределах от нуля до  Следовательно, минимальный возможный импульс, который можно приписать частице, равен в силу принципа неопределенности
Следовательно, минимальный возможный импульс, который можно приписать частице, равен в силу принципа неопределенности

При меньших значениях импульса принцип неопределенности нарушится. Энергию, соответствующую этому импульсу,

можно сравнить с наименьшей энергией, величину которой мы вычислили с помощью уравнения Шредингера, подбирая подходящую стоячую волну между стенками сосуда:

Ценность полученного результата состоит не в численном согласии, а в том, что нам удалось провести грубую оценку величины минимальной энергии, используя лишь принцип неопределенности. Кроме того, нам удалось понять, почему минимальное значение кинетической энергии квантовомеханической системы (в отличие от классической системы) никогда не равно нулю. Соответствующая классическая частица, заключенная между стенками, обладает нулевой кинетической
энергией, когда она находится в покое. Квантовая же частица не может покоиться, если она захвачена между стенками. Ее импульс или скорость существенно неопределенны, что проявляется в увеличении энергии, причем это увеличение в точности совпадает с тем значением, которое получается из строгого решения уравнения Шредингера.
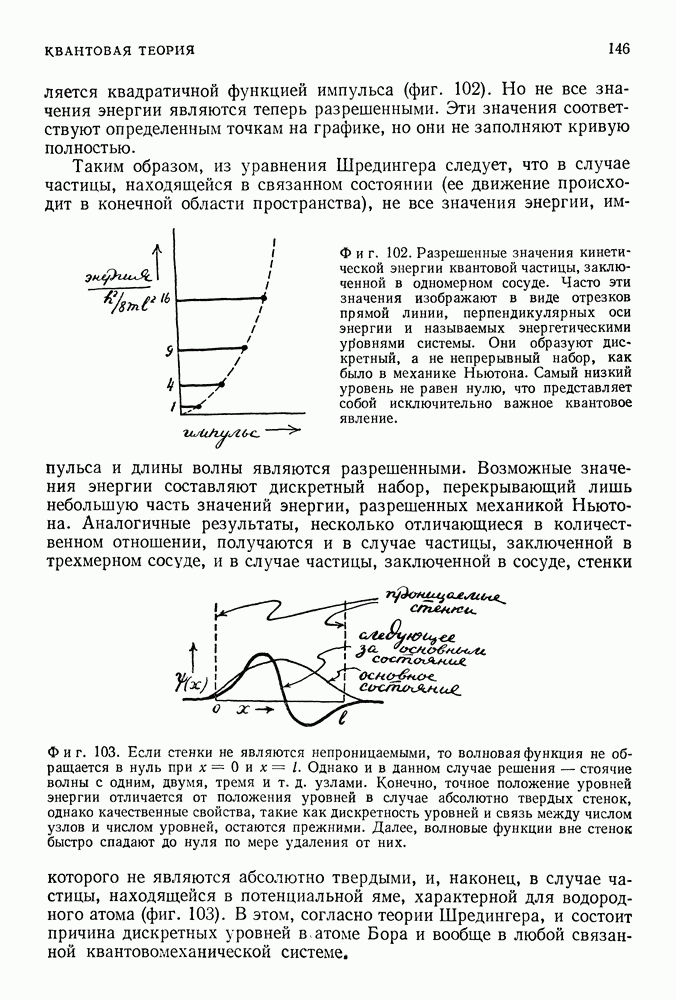
Этот весьма общий результат имеет особенно важные следствия в том разделе квантовой теории, который соответствует классической кинетической теории, т. е. в квантовой статистике. Широко известно, что температура системы, как утверждает кинетическая теория, определяется внутренним движением составляющих систему атомов. Если температура квантовой системы высока, то нечто весьма похожее на это действительно имеет место. Однако при низких температурах квантовые системы не могут прийти к абсолютному покою. Минимальная температура соответствует наинизшему из возможных состояний данной системы. В классическом случае все частицы находятся в покое, а в квантовом — энергия частиц определяется из выражения (41.17), что не соответствует покою частиц.
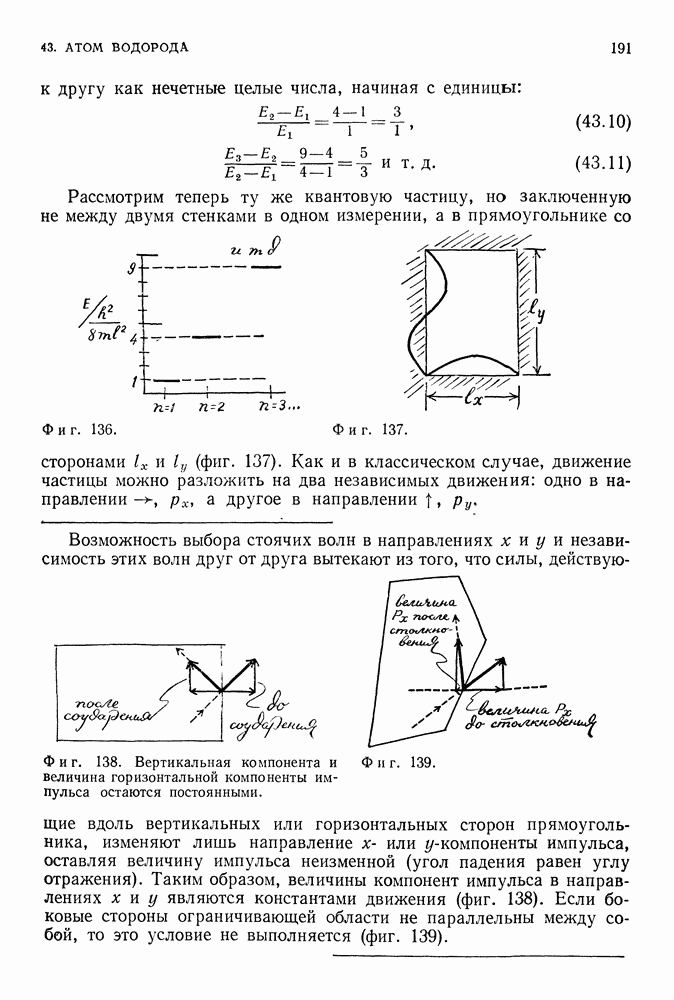
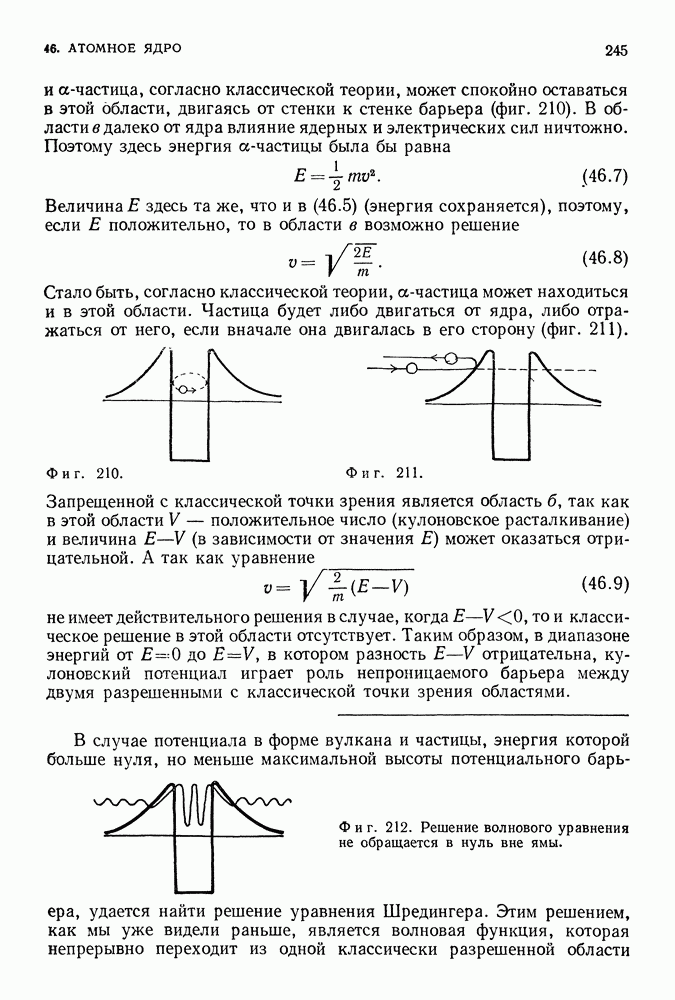
Из всего сказанного может создаться впечатление, что мы уделяем слишком много внимания электронам, заключенным между двумя стенками. Наше внимание к электронам вполне оправдано. А к стенкам? Если проанализировать все рассмотренные ранее случаи, то можно убедиться в том, что вид силовой системы, будь то сосуд или что-нибудь иное, удерживающей электрон в ограниченной области пространства, не так уже существен.

Фиг. 128.
Две стенки, центральная сила или различные препятствия (фиг. 128) приводят к примерно одинаковым результатам. Не столь уж важен вид конкретной системы, которая удерживает электрон. Гораздо важнее, что электрон вообще захвачен, т. е. его волновая функция локализована. В результате эта функция представляется в виде суммы периодических волн и импульс частицы становится неопределенным, причем

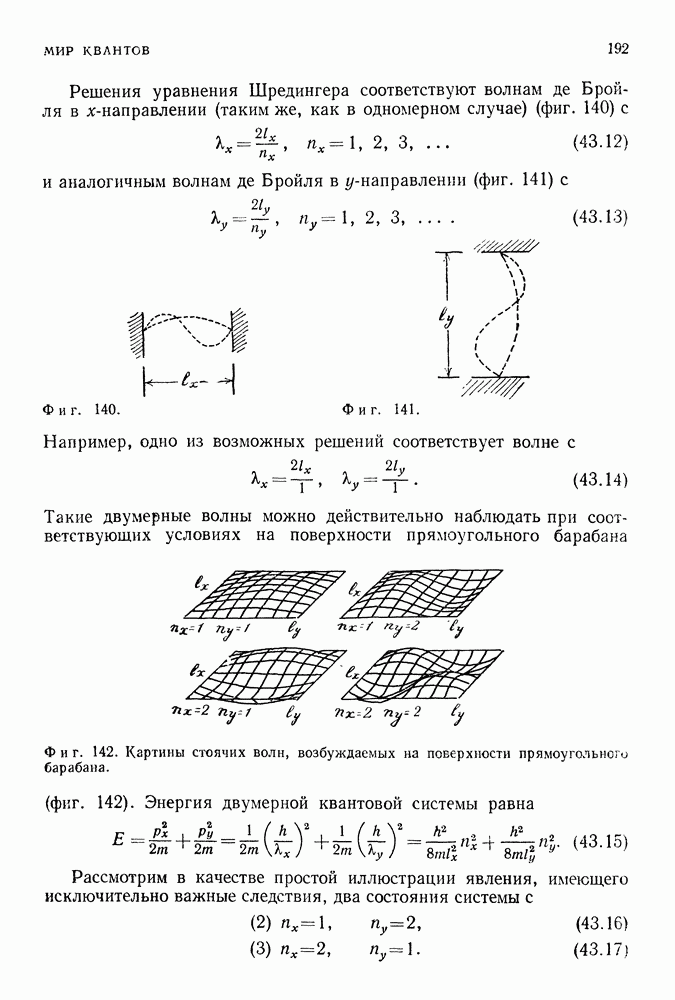
Проанализируем теперь с помощью принципа неопределенности одно типично волновое явление, а именно расширение волны после прохождения ею небольшого отверстия (фиг. 129). Это явление мы уже разбирали геометрическим способом, вычисляя расстояния, на
которых горбы пересекаются с впадинами., В том, что теперь результаты окажутся сходными, нет ничего удивительного. Просто одна и та же теоретическая модель описывается разными словами. Допустим, что электрон попадает в отверстие в экране, двигаясь слева направо. Нас интересует неопределенность положения и скорости электрона в направлении х (перпендикулярном направлению движения). (Соотношение неопределенности выполняется для каждого из трех направлений в отдельности: Ах-Архжк, 

Фиг. 129.
Обозначим ширину щели через  эта величина является максимальной погрешностью определения положения электрона в направлении х, когда он проходил через отверстие, чтобы проникнуть за экран. Отсюда мы можем найти неопределенность импульса или скорости частицы в направлении я:
эта величина является максимальной погрешностью определения положения электрона в направлении х, когда он проходил через отверстие, чтобы проникнуть за экран. Отсюда мы можем найти неопределенность импульса или скорости частицы в направлении я:

Следовательно, если мы допускаем, что электрон проходит сквозь отверстие в экране шириной  мы должны признать, что его скорость при этом станет неопределенной с точностью до величины
мы должны признать, что его скорость при этом станет неопределенной с точностью до величины

В отличие от классической частицы квантовая не может, пройдя сквозь отверстие, дать на экране четкое изображение.
Если она движется со скоростью  в направлении экрана, а расстояние между экраном и отверстием равно
в направлении экрана, а расстояние между экраном и отверстием равно  то она пройдет это расстояние за время
то она пройдет это расстояние за время

За это время частица сместится в направлении х на величину

Угловой разброс определяется как отношение величины смещения к длине 

или

Таким образом, угловой разброс (интерпретируемый как половина углового расстояния до первого дифракционного минимума) равен длине волны, деленной на ширину отверстия, что совпадает с результатом, полученным ранее для света.
А что можно сказать об обычных массивных частицах? Являются ли они квантовыми частицами или частицами ньютоновского типа? Следует ли пользоваться механикой Ньютона в случае объектов обычных размеров и квантовой механикой в случае объектов, размеры которых малы? Мы можем считать все частицы, все тела (даже Землю) квантовыми. Однако, если размеры и масса частицы соизмеримы с размерами и массами, которые обычно наблюдаются в макроскопических явлениях, то квантовые эффекты — волновые свойства, неопределенности положения и скорости — становятся слишком малыми, чтобы быть обнаружимыми в обычных условиях.
Рассмотрим, например, частицу, о которой мы говорили выше. Допустим, что эта частица — металлический шарик от подшипника с массой в одну тысячную грамма (очень маленький шарик). Если мы локализуем его положение с точностью, доступной нашему зрению, в поле микроскопа, скажем с точностью до одной тысячной сантиметра, то

так что

или

Следовательно, неопределенность скорости такого шарика составляет величину порядка  см/с.
см/с.
Этот пример дает однозначный ответ на вопрос о том, имеем ли мы дело с несколькими теориями или с одной. Когда масса и размеры тела становятся обычными, результаты квантовой теории настолько близко совпадают с результатами классической теории, что различить эти результаты оказывается практически невозможно. Квантовые явления, или волновые свойства материи, проявляются лишь тогда, когда
мы имеем дело с частицами, массы которых порядка массы электрона, и с расстояниями порядка размеров атома. Даже в случае тела, масса которого  локализованного на длине
локализованного на длине  см, неопределенность скорости оказывается слишком маленькой величиной, чтобы быть обнаруженной при обычных наблюдениях.
см, неопределенность скорости оказывается слишком маленькой величиной, чтобы быть обнаруженной при обычных наблюдениях.
Соотношения неопределенности Гейзенберга связывают не только положение и импульс системы, но и другие ее параметры, которые в классической теории считались независимыми. Одним из наиболее интересных и полезных для наших целей соотношений является связь между неопределенностями энергии и времени. Обычно ее записывают в виде

Если система находится в определенном состоянии в течение длительного промежутка времени, то энергия этой системы известна с большой точностью; если же она находится в этом состоянии в течение очень короткого интервала времени, то ее энергия становится неопределенной; этот факт точно описывается соотношением, приведенным выше.
Это соотношение обычно применяют при рассмотрении перехода квантовой системы из одного состояния в другое. Допустим, например, что время жизни какой-то частицы равно  , т. е. между моментом рождения этой частицы и моментом ее распада проходит время порядка
, т. е. между моментом рождения этой частицы и моментом ее распада проходит время порядка  с. Тогда максимальная точность, с которой может быть известна энергия этой частицы, равна
с. Тогда максимальная точность, с которой может быть известна энергия этой частицы, равна

что составляет весьма небольшую величину. Как мы увидим позднее, существуют так называемые элементарные частицы, время жизни которых порядка  с (время между моментом рождения частицы и моментом ее аннигиляции). Таким образом, промежуток времени, в течение которого частица находится в определенном состоянии, очень мал, и неопределенность энергии оценивается как
с (время между моментом рождения частицы и моментом ее аннигиляции). Таким образом, промежуток времени, в течение которого частица находится в определенном состоянии, очень мал, и неопределенность энергии оценивается как

Эта величина, 4-106 эВ (миллион электронвольт кратко обозначается символом МэВ), огромна; вот почему, как мы увидим позже, таким элементарным частицам, иногда называемым резонансами, приписывают не точное значение энергии, а целый спектр значений в довольно широком диапазоне.
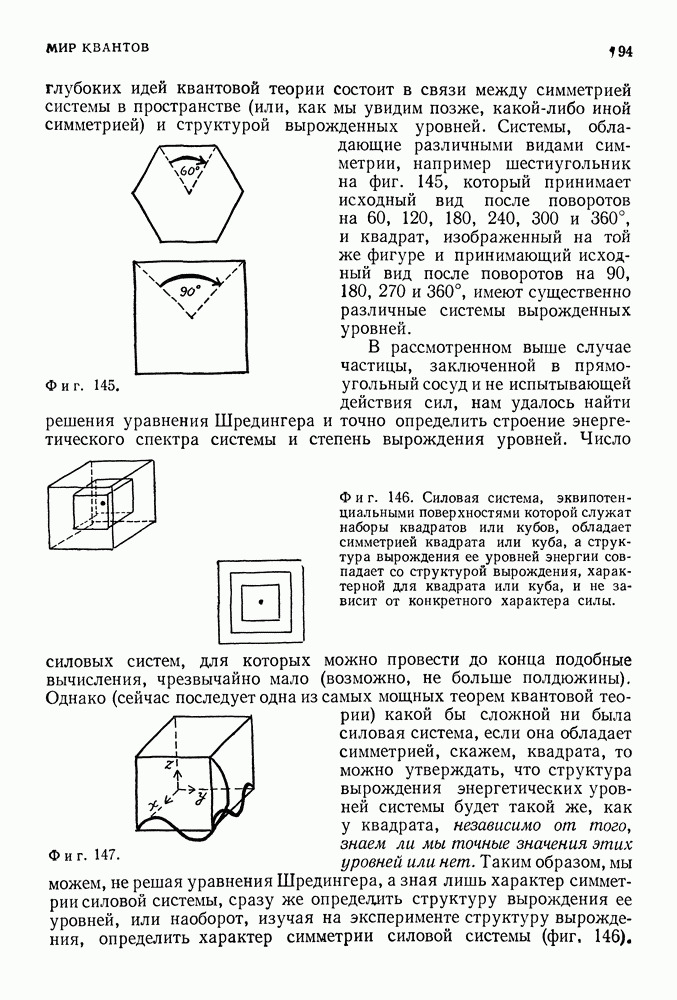
Из соотношения (41.28) можно также получить так называемую естественную ширину уровней квантовой системы. Если, например, атом переходит с уровня 1 на уровень 0 (фиг. 130), то энергию уровня
1 нельзя считать определенной, так как атом находится на нем в те чение конечного промежутка времени. Время жизни уровня для типичной квантовой системы порядка  с.
с.

Фиг. 130.
Тогда разброс значений энергии этого уровня определяется из выражения:

Это типичная естественная ширина энергетических уровней атомной системы.
| << Предыдущий параграф | Следующий параграф >> |
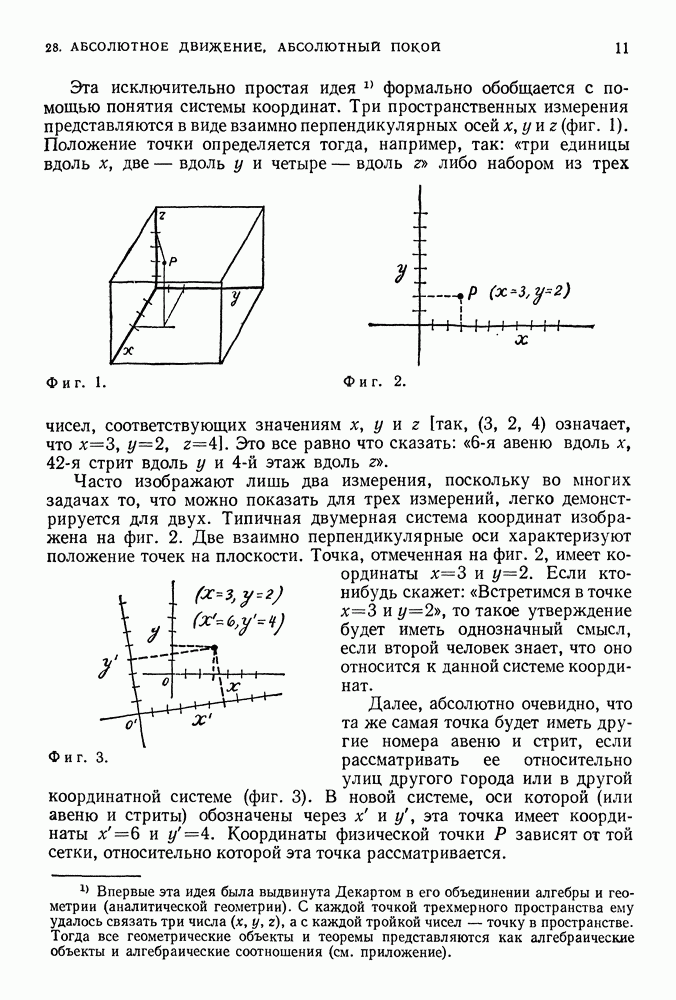
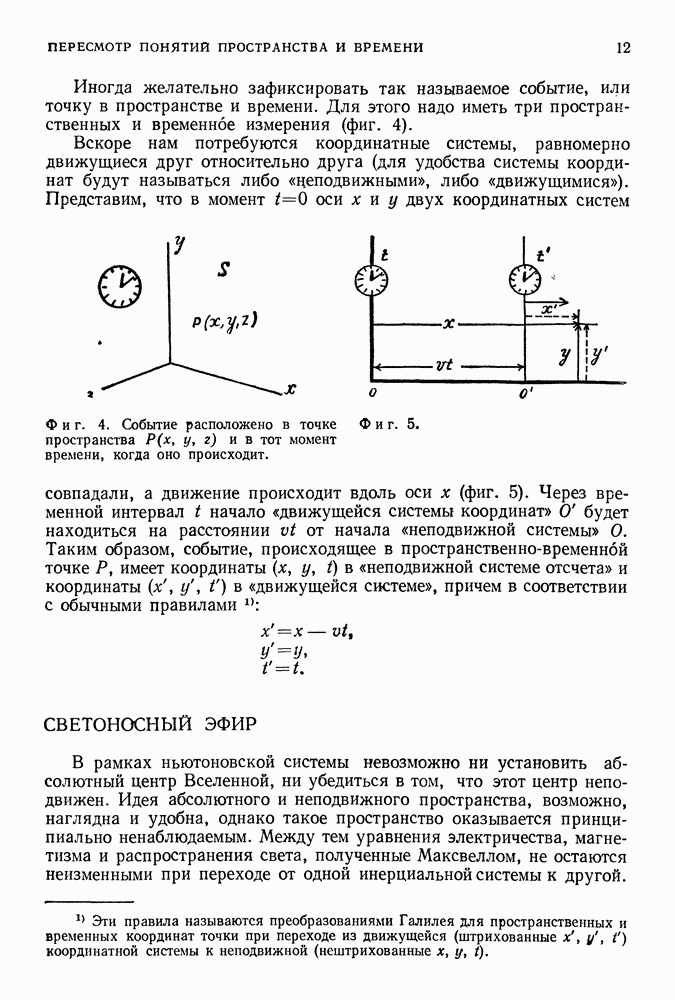
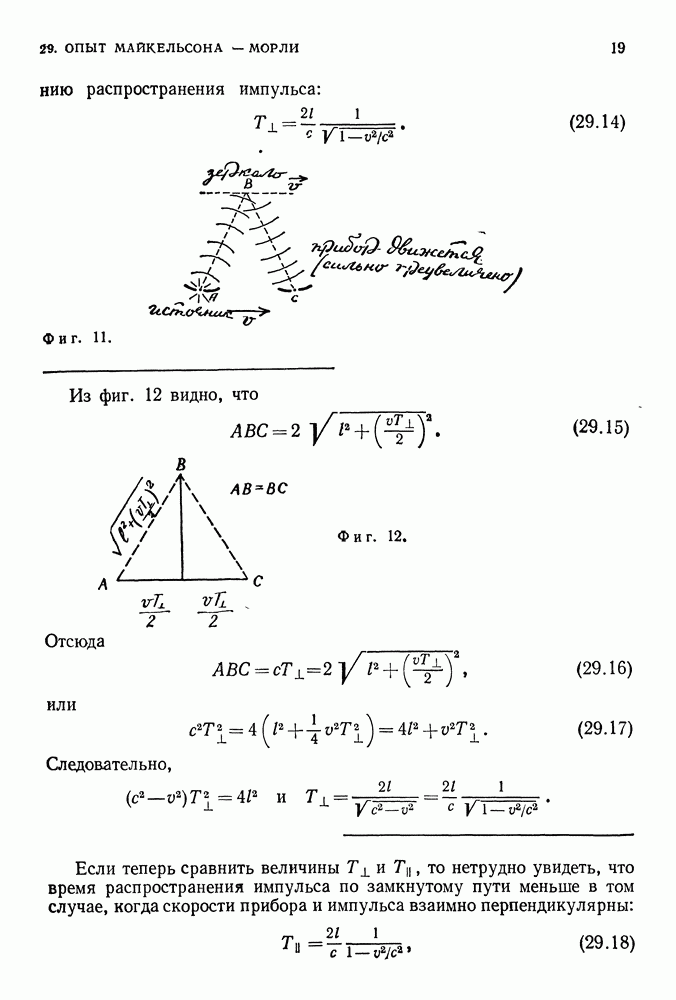
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
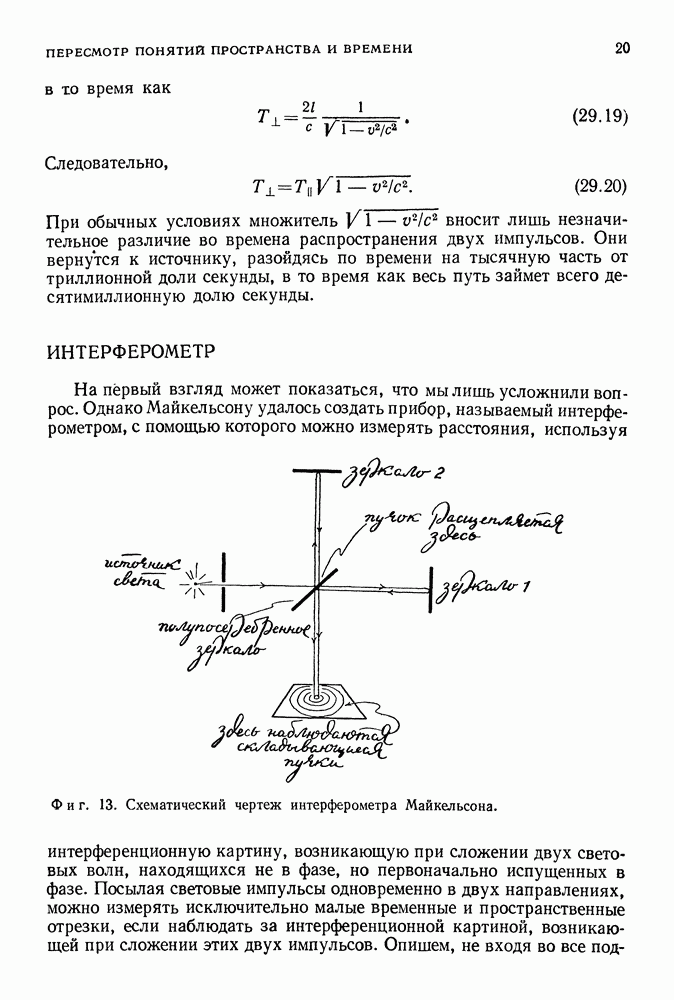
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
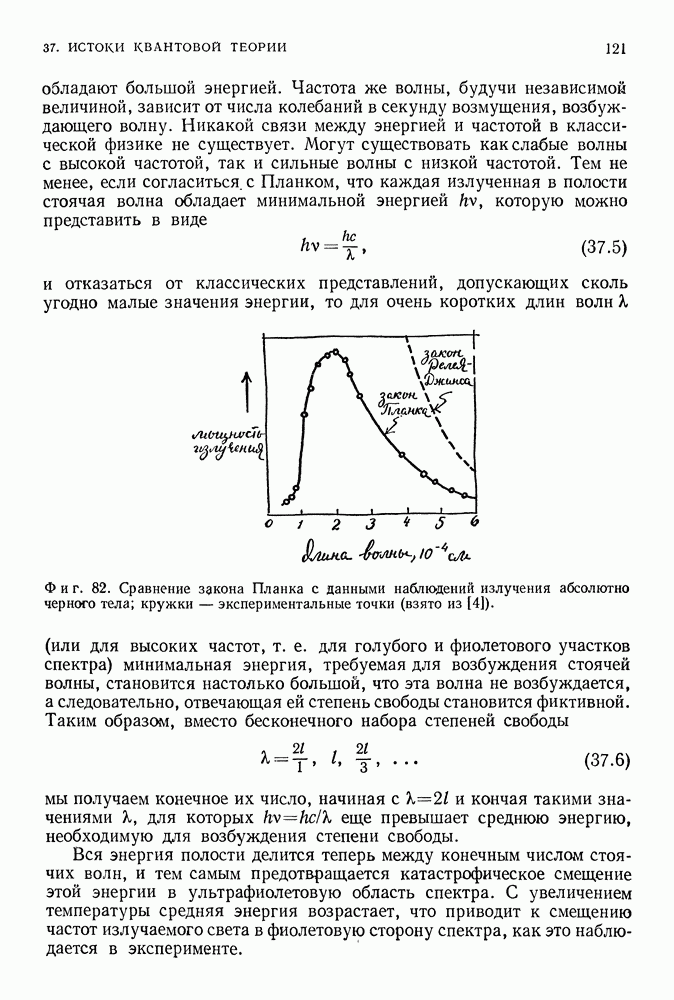
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
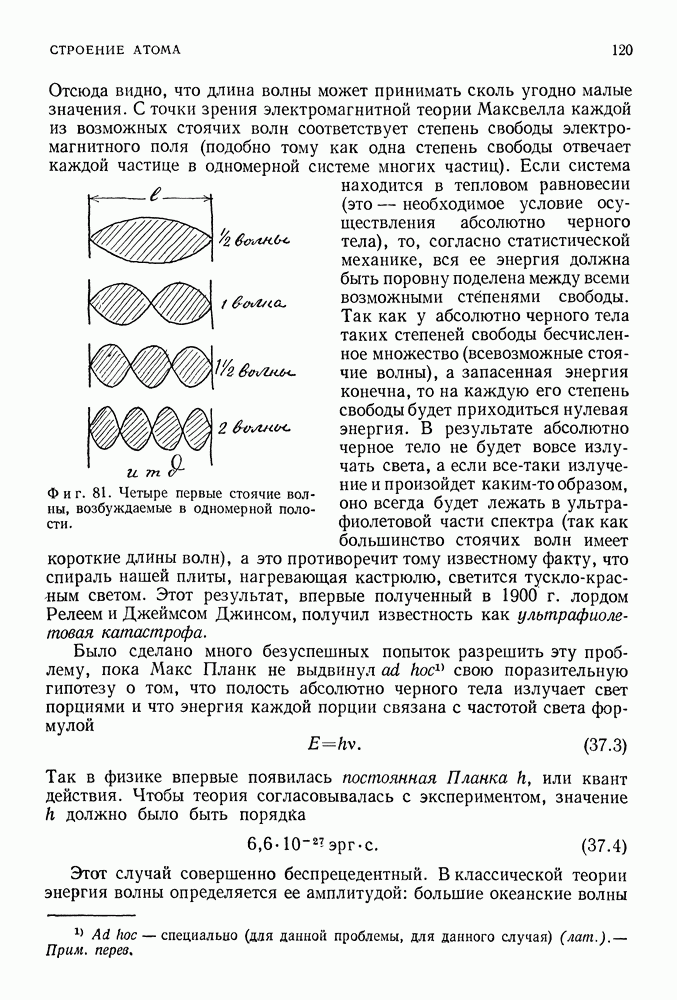
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
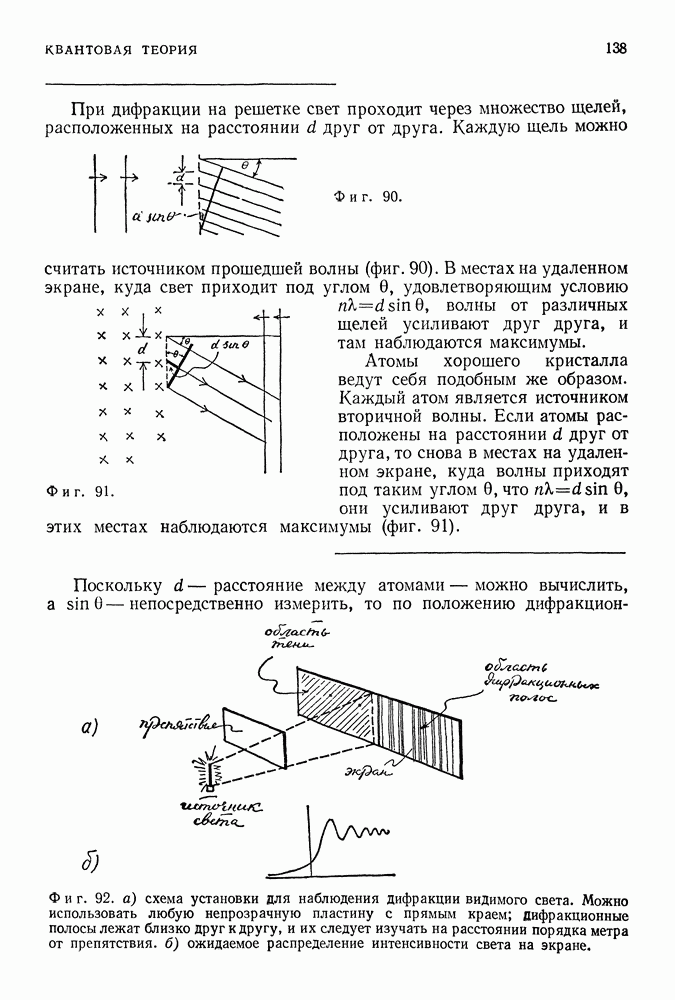
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
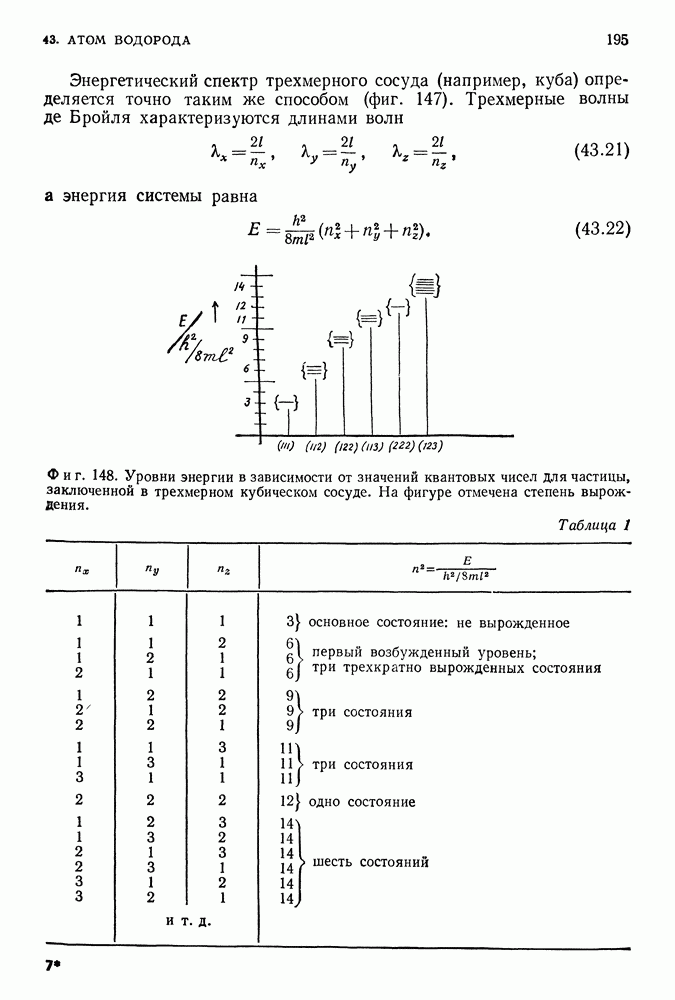
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
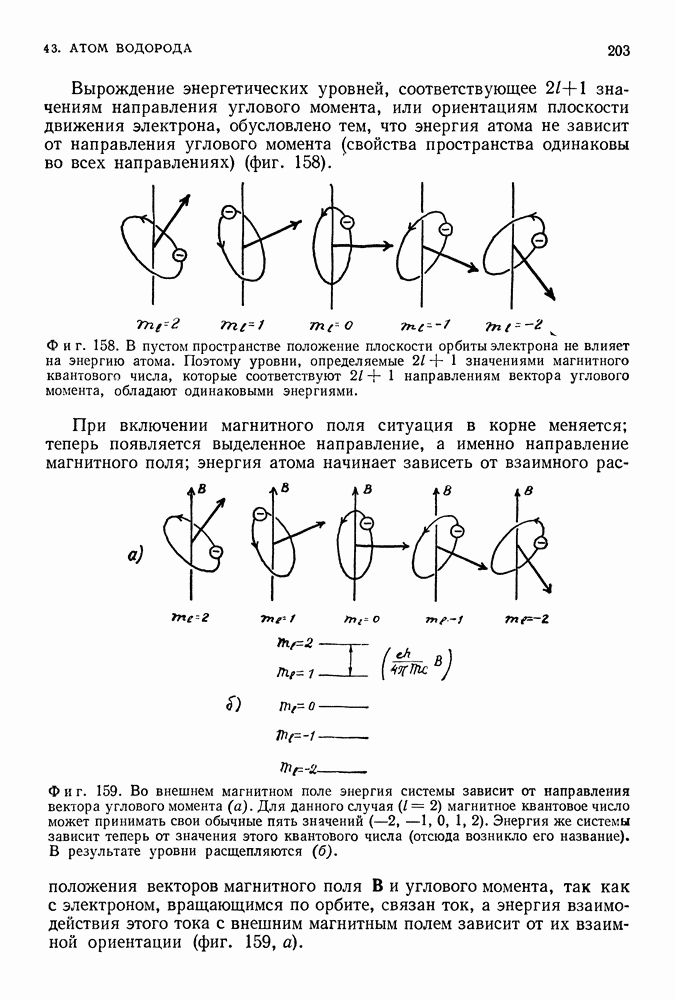
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
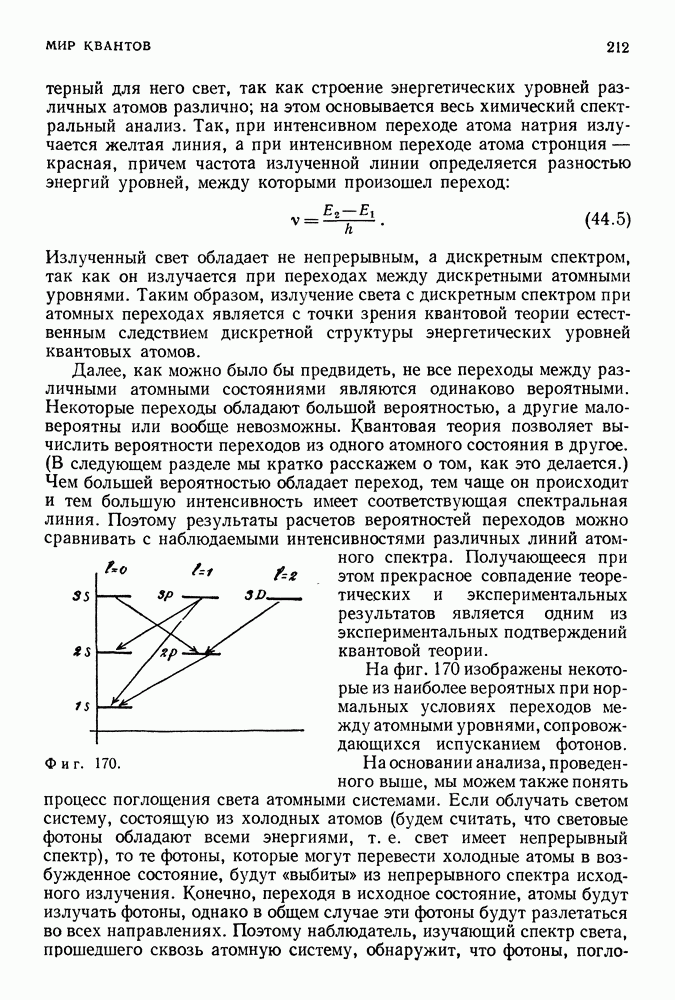
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
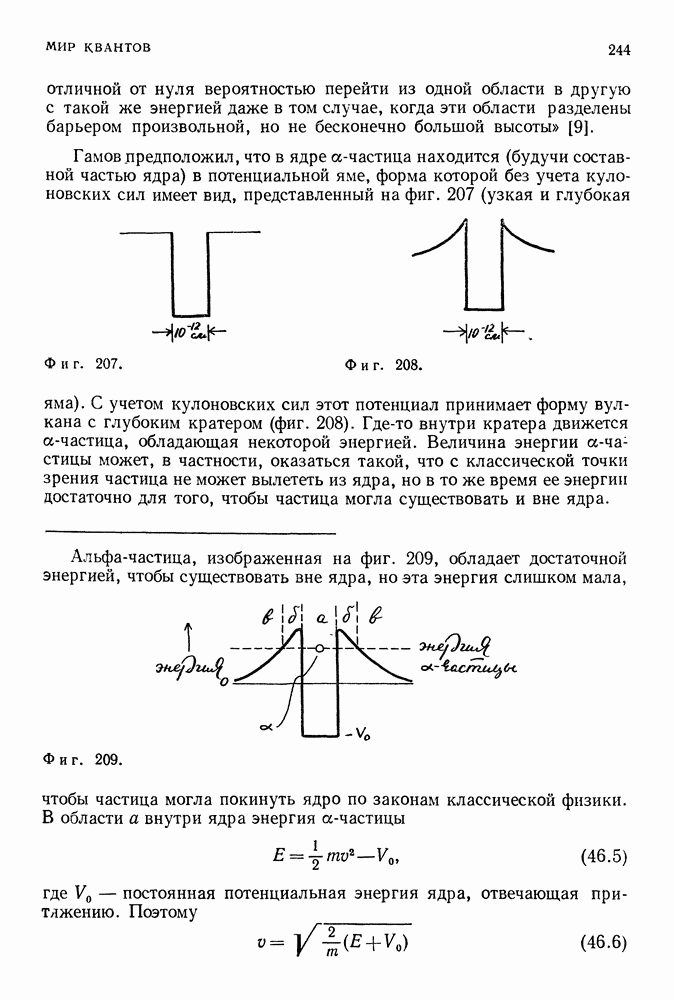
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
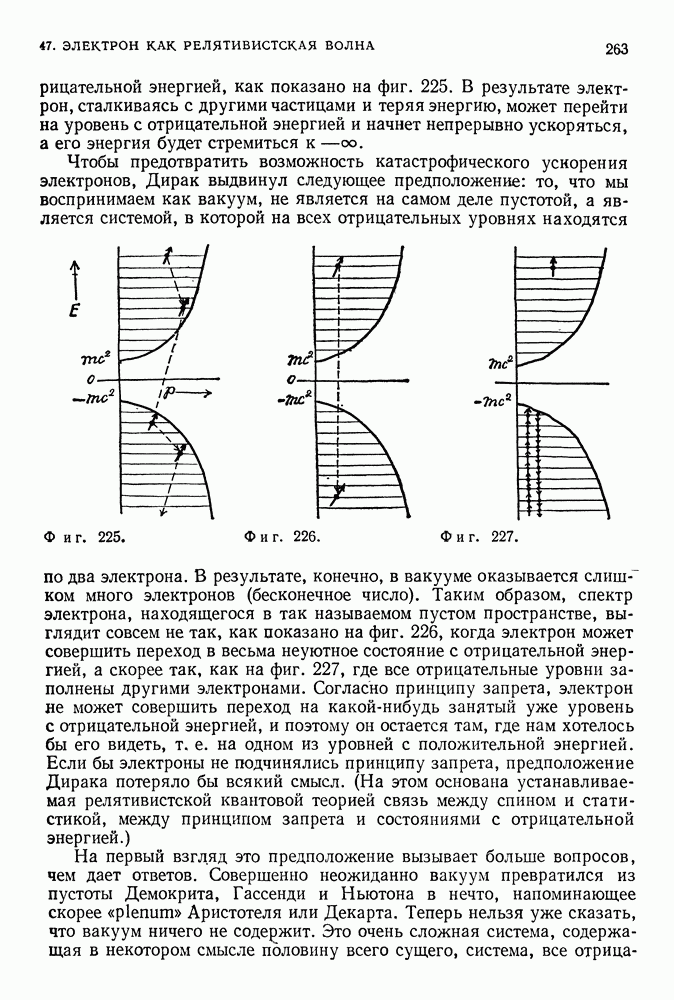
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
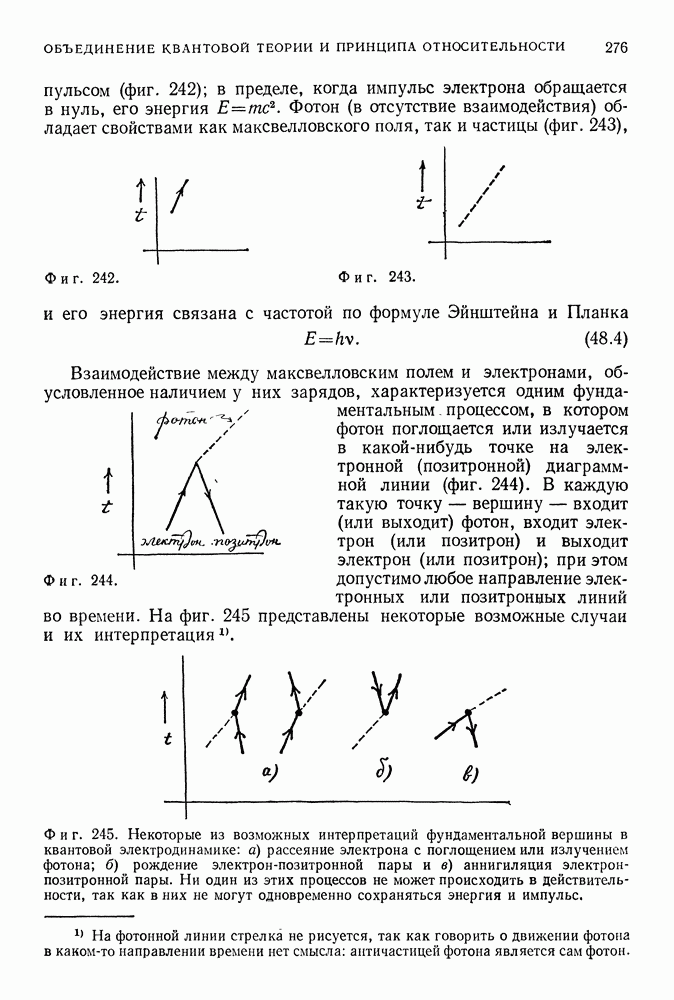
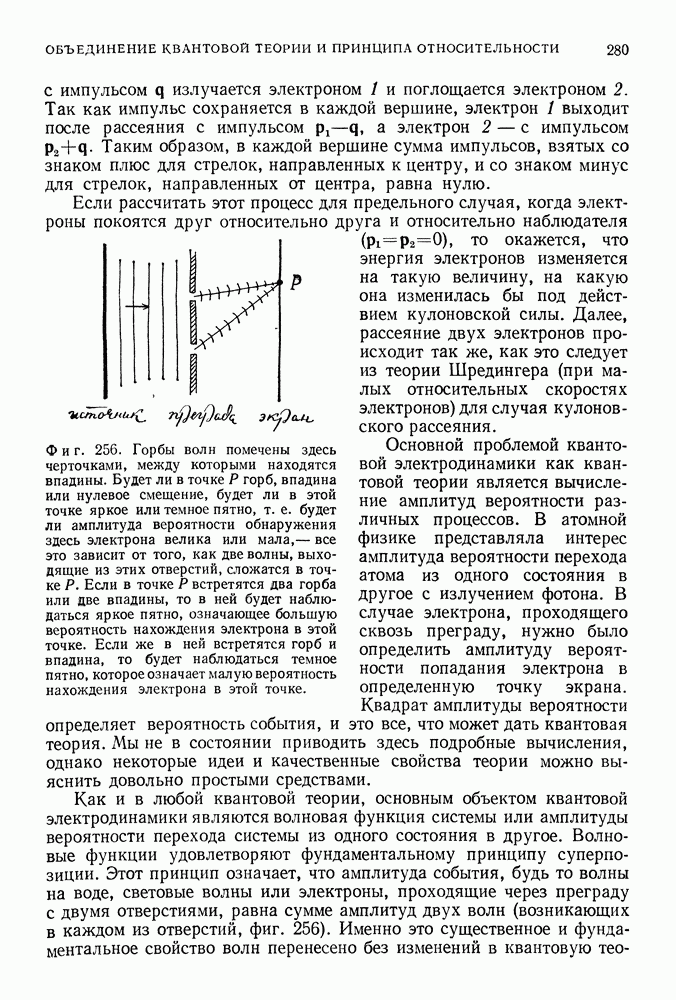
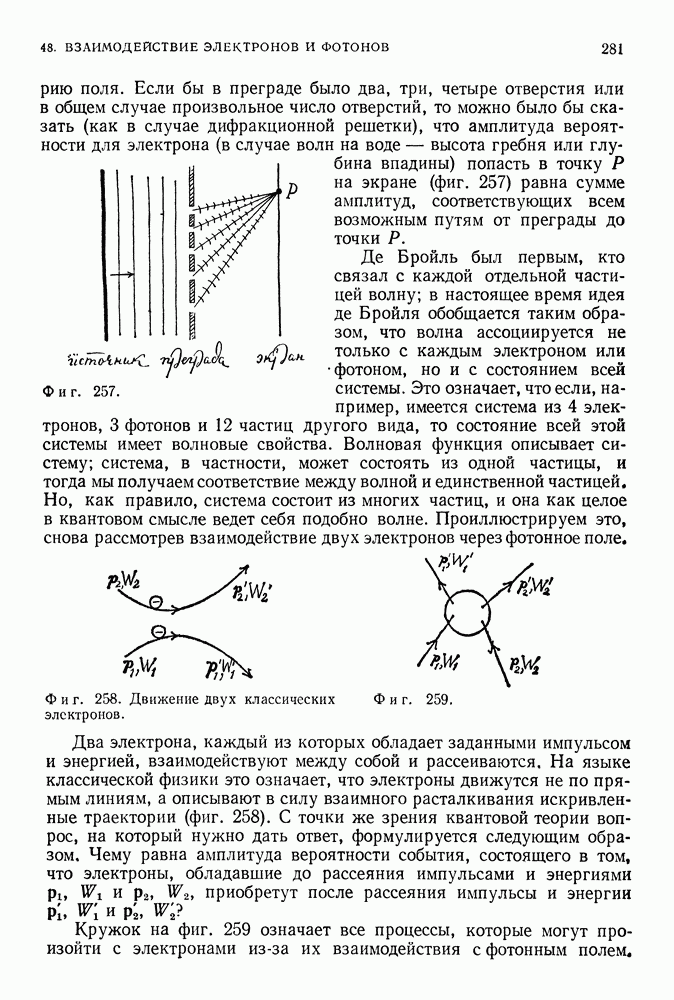
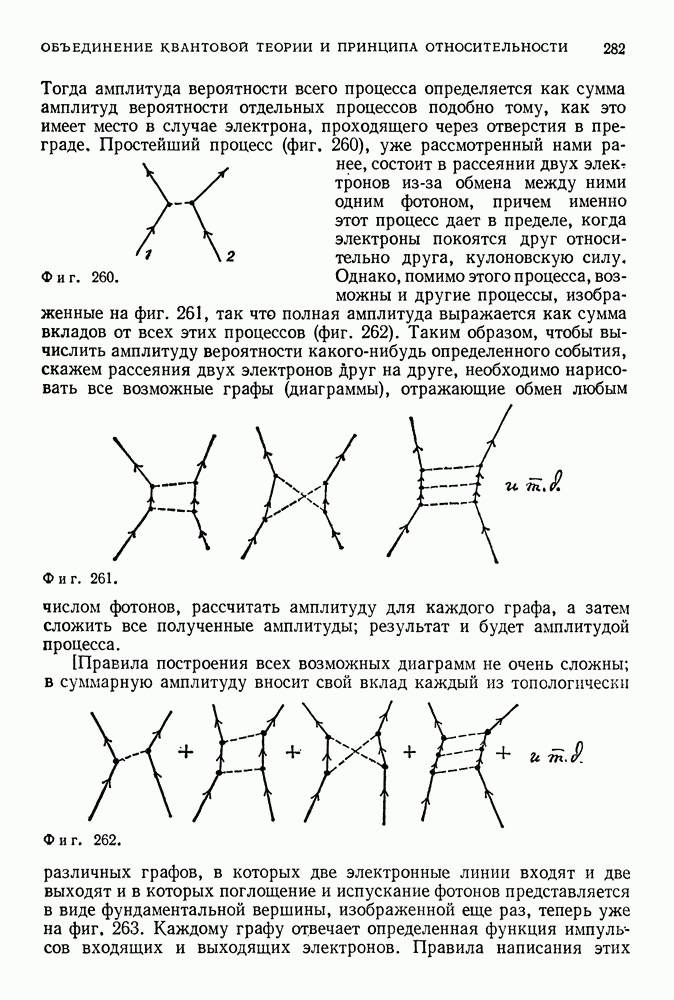
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
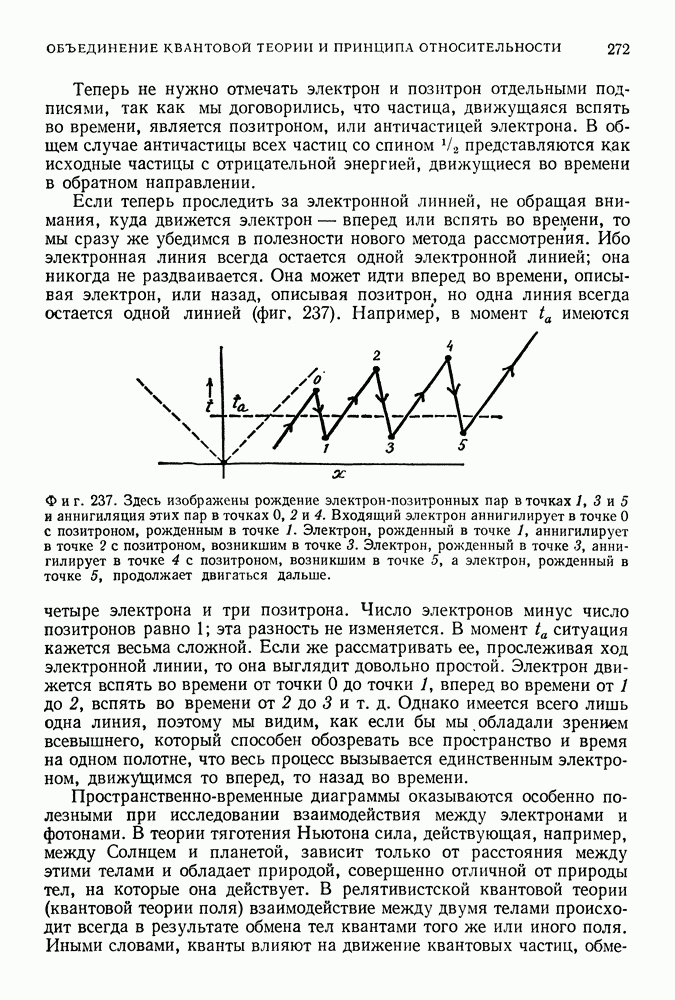
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
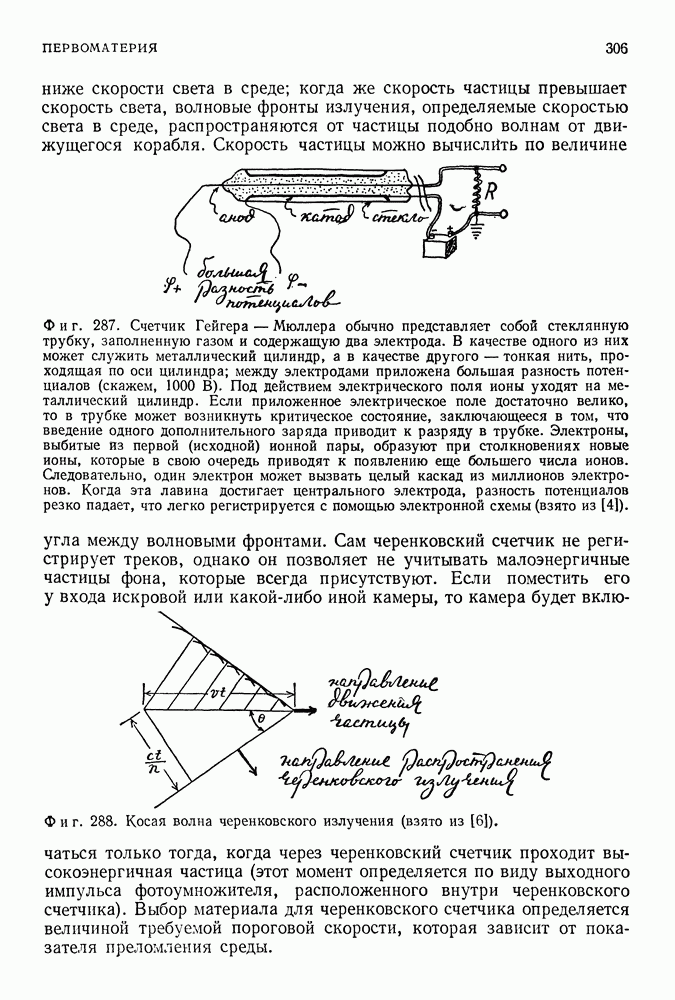
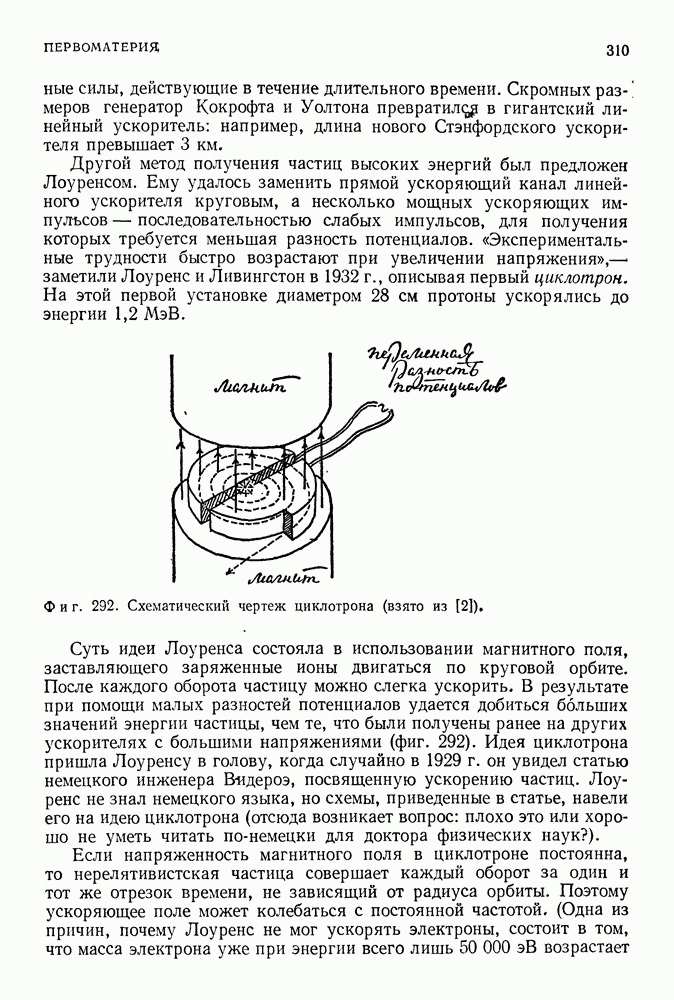
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
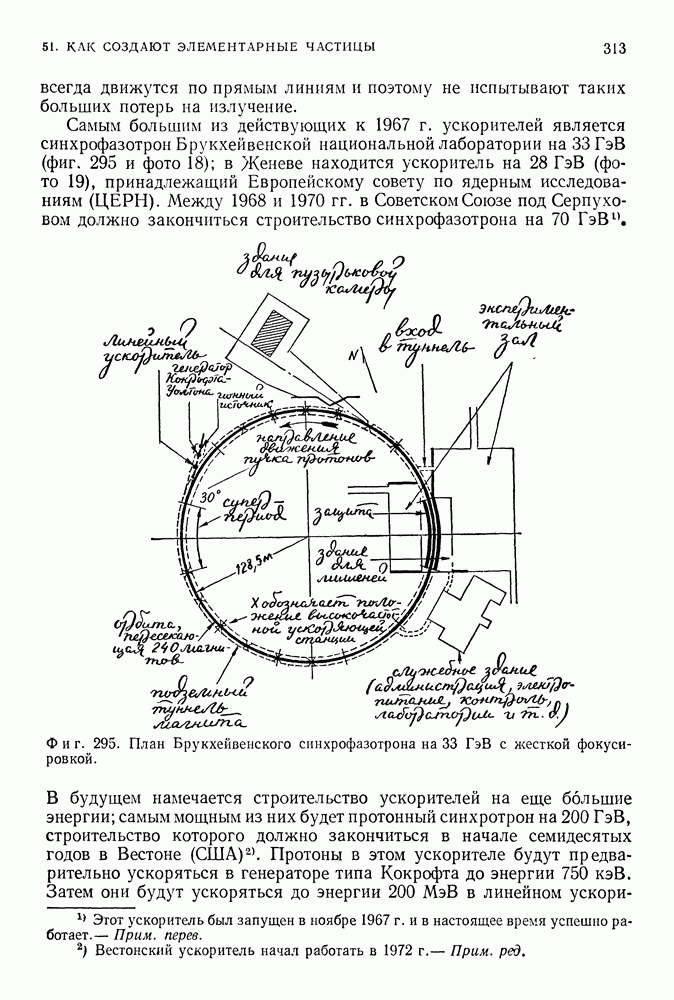
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА