| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
В качестве наглядного примера рассмотрим систему из  квантовых частиц, заключенных в одномерном сосуде длиной
квантовых частиц, заключенных в одномерном сосуде длиной  Если обобщить этот случай на трехмерный сосуд — куб, то можно получить простую модель поведения электронов в металлах, которая по крайней мере качественно описывает большинство свойств обычных металлов: их реакцию на внешние электрическое и магнитное поля, их удельные теплоемкости и т. д.
Если обобщить этот случай на трехмерный сосуд — куб, то можно получить простую модель поведения электронов в металлах, которая по крайней мере качественно описывает большинство свойств обычных металлов: их реакцию на внешние электрическое и магнитное поля, их удельные теплоемкости и т. д.
Как мы уже установили ранее, волновыми функциями квантовой частицы, заключенной в одномерном сосуде, являются стоячие волны де Бройля с длинами волн

а энергия этой частицы

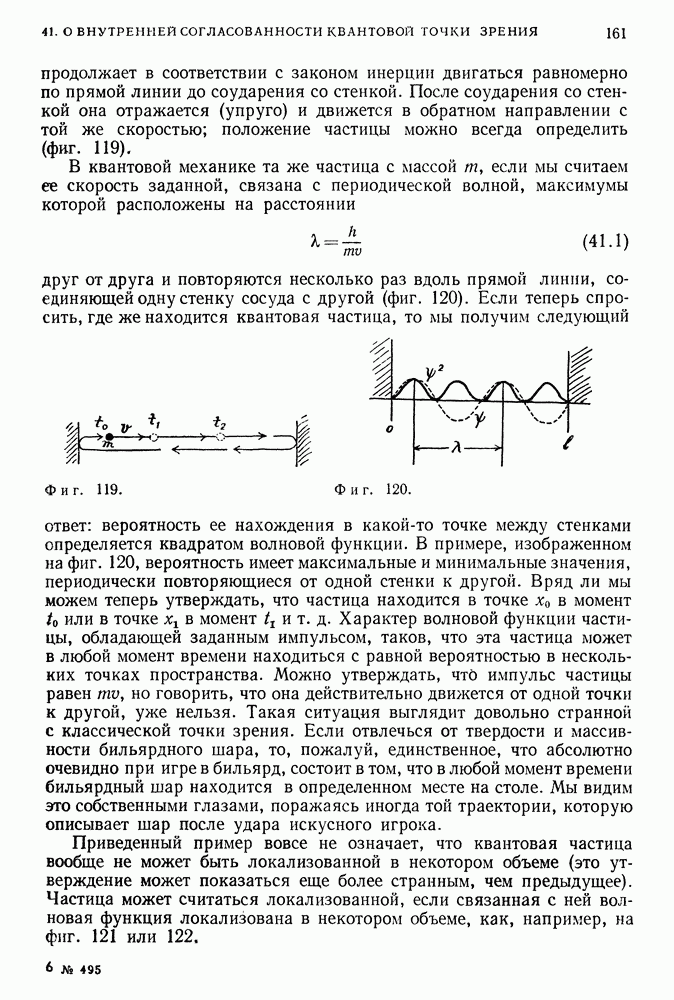
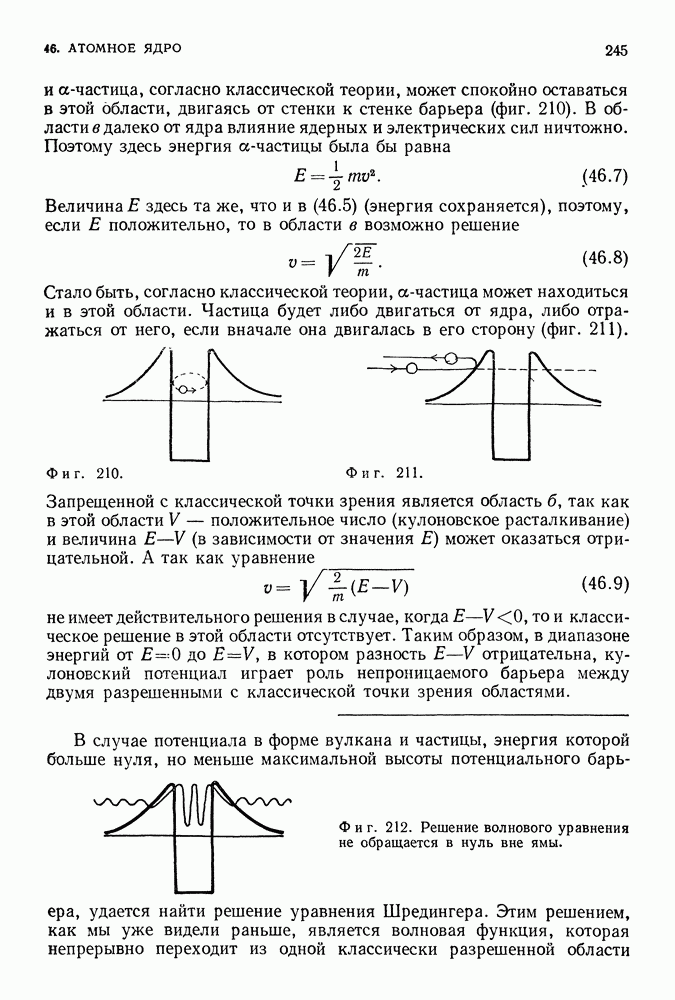
В случае одной частицы наинизшее состояние системы характеризуется значением  (фиг, 183):
(фиг, 183):

Если в сосуде находится несколько невзаимодействующих друг с другом частиц (между частицами не действуют силы), то полную волновую функцию системы можно сконструировать, приписывая каждой частице одну из упомянутых выше стоячих волн де Бройля,

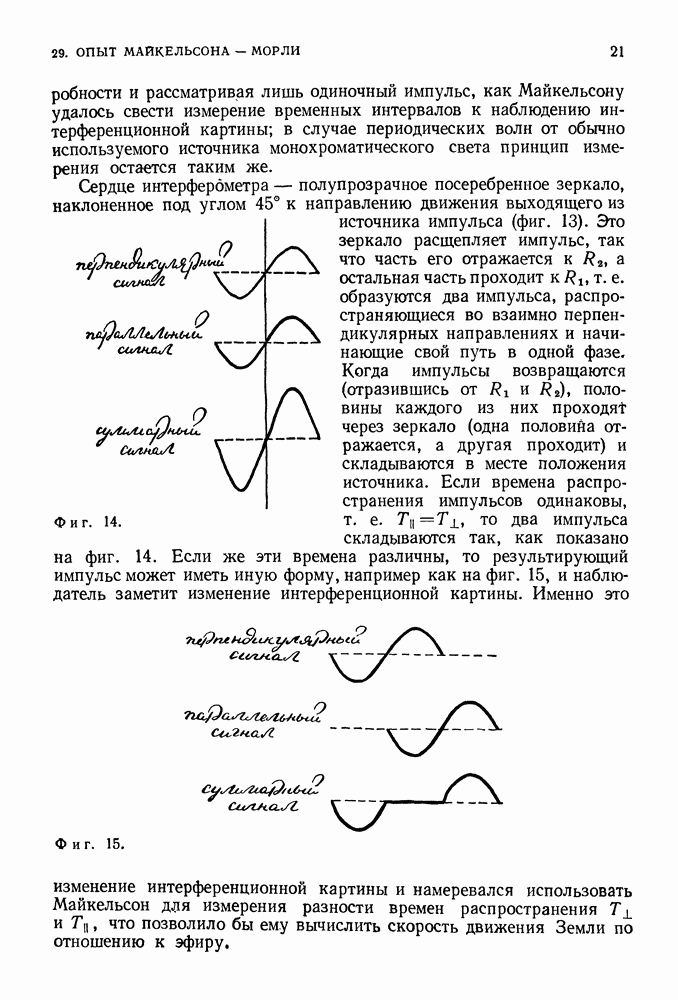
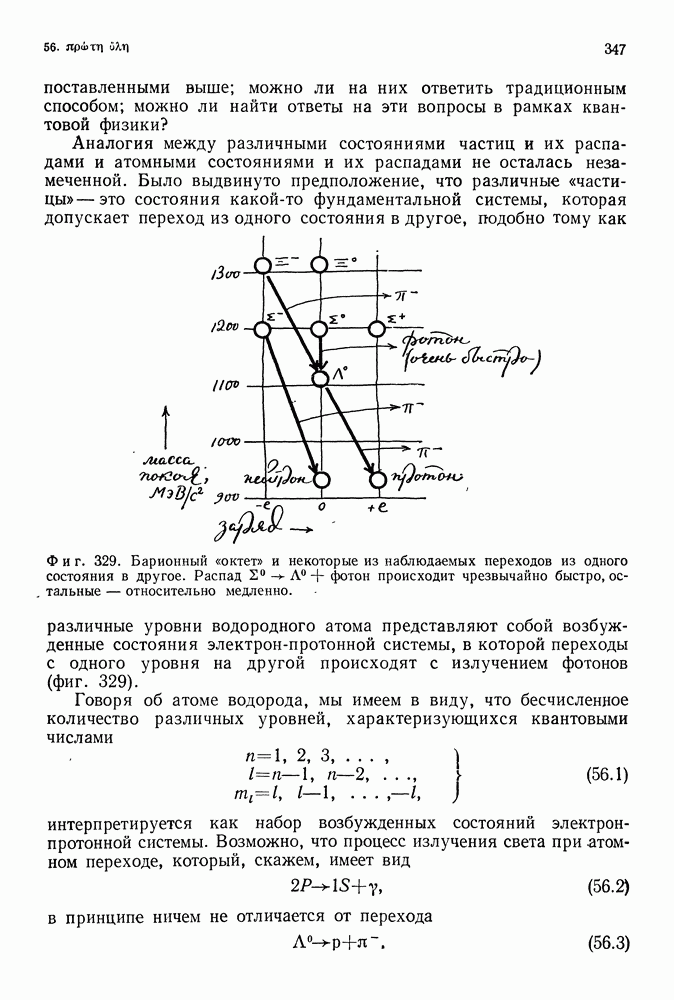
Фиг. 183.
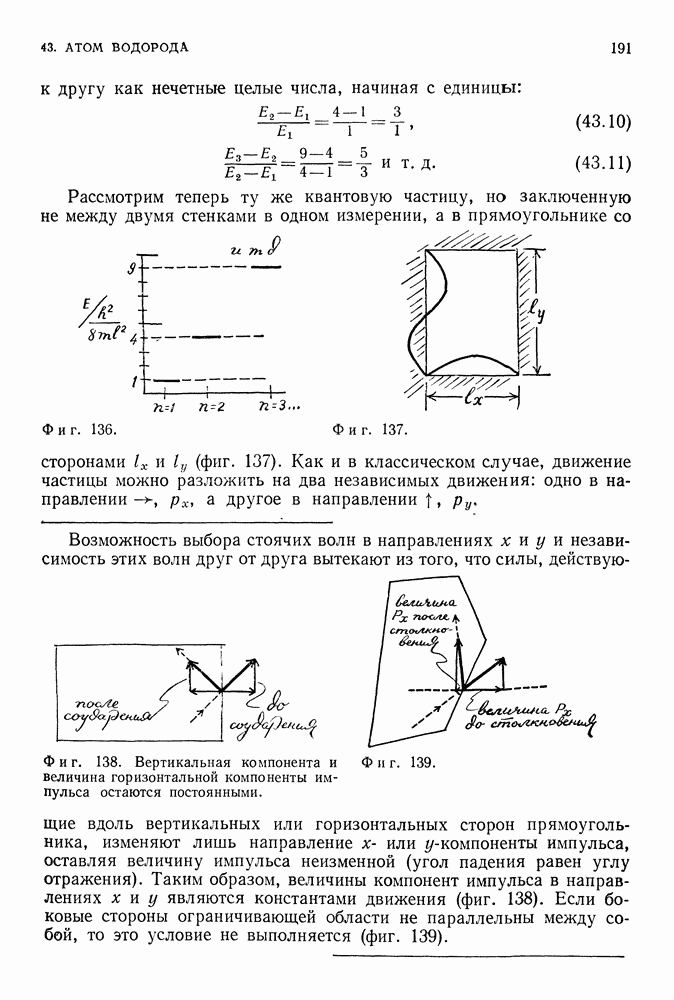
Представим теперь, что в сосуде заключены две квантовые частицы. Если эти частицы бозоны, то наинизшему состоянию системы будет соответствовать случай, когда обе частицы описываются стоячей волной де Бройля с длиной волны 21 (фиг. 184):

Если же они фермионы, то, согласно принципу запрета, они не могут характеризоваться одинаковыми квантовыми числами.

Фиг. 184.

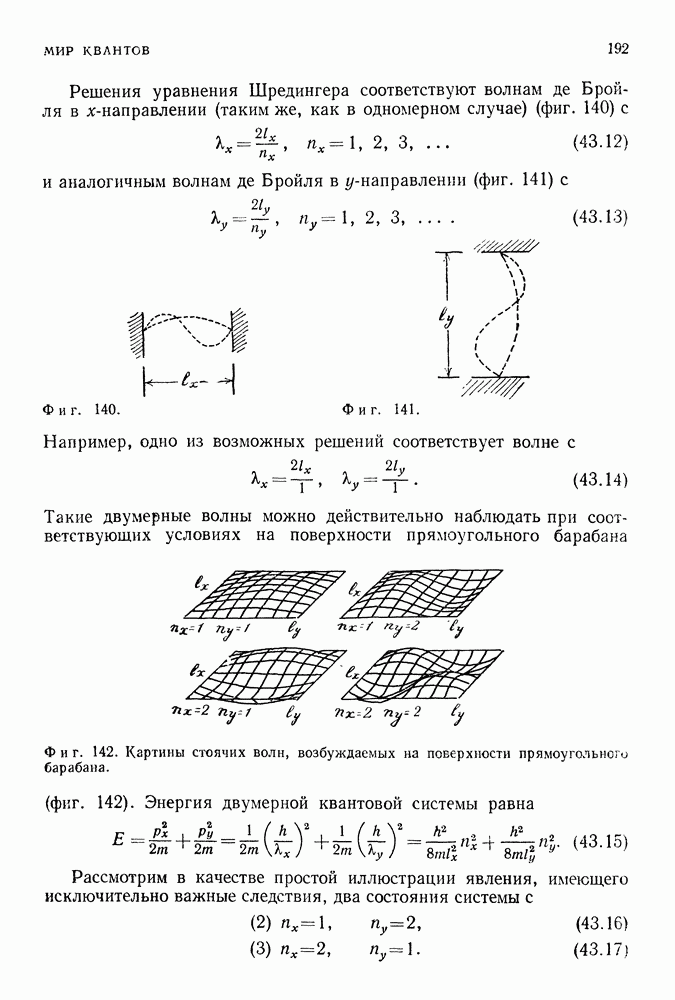
Фиг. 185.

Фиг. 186.
Поэтому, если частицы описываются одинаковыми волнами де Бройля, их спины должны быть направлены в противоположные стороны (фиг. 185):

При добавлении третьего, четвертого или  бозона увеличивается лишь число частиц, находящихся в наинизшем состоянии, которое описывается волной де Бройля с длиной волны 21 (фиг, 186):
бозона увеличивается лишь число частиц, находящихся в наинизшем состоянии, которое описывается волной де Бройля с длиной волны 21 (фиг, 186):

(Именно благодаря этому свойству бозонов с их помощью можно построить классическую волну. Чем большее число бозонов описывается одной и той же волновой функцией, тем больше становится вероятность их нахождения в заданном квантовом состоянии, что придает системе свойство классического непрерывного поля, например электромагнитного.)
Если же к двум фермионам добавляется третий, четвертый или  фермион, то наблюдается совсем иная картина. Третий фермион не может быть описан волной де Бройля с длиной волны
фермион, то наблюдается совсем иная картина. Третий фермион не может быть описан волной де Бройля с длиной волны  так как в этом, случае в какую сторону ни был бы направлен его спин, характеризующие его квантовые числа совпадали бы с квантовыми числами какой-либо из двух начальных частиц, — а это невозможно на основании принципа запрета.
так как в этом, случае в какую сторону ни был бы направлен его спин, характеризующие его квантовые числа совпадали бы с квантовыми числами какой-либо из двух начальных частиц, — а это невозможно на основании принципа запрета.

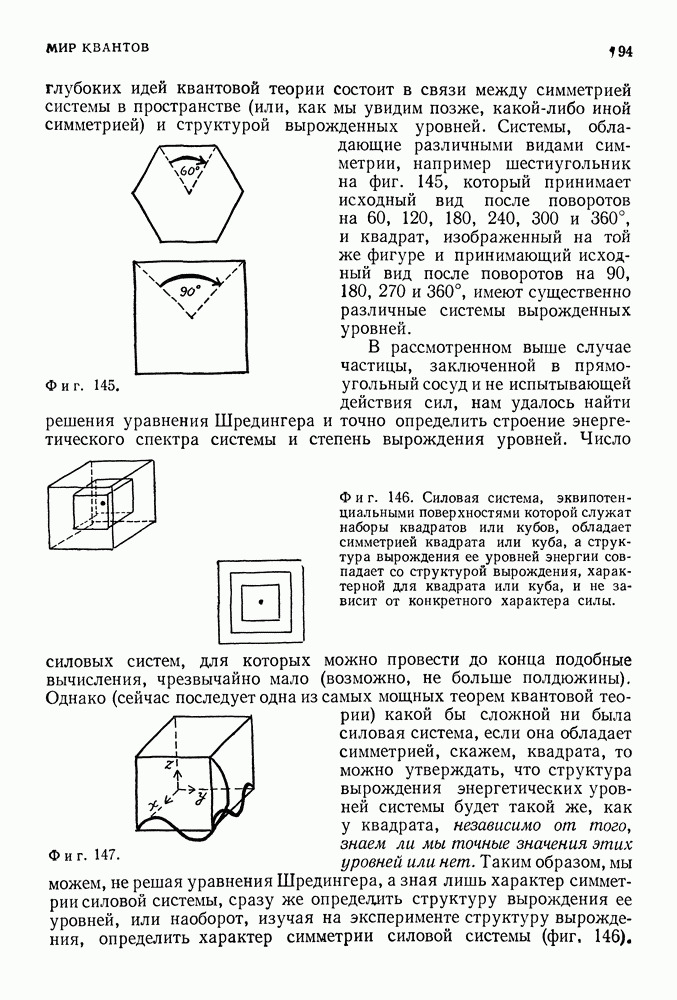
Фиг. 187.

Фиг. 188
Поэтому для описания третьего фермиона следует выбрать следующую волну де Бройля. В результате основное состояние системы из трех фермионов характеризуется следующими параметрами (фиг. 187):

В случае  фермионов (фиг. 188)
фермионов (фиг. 188)

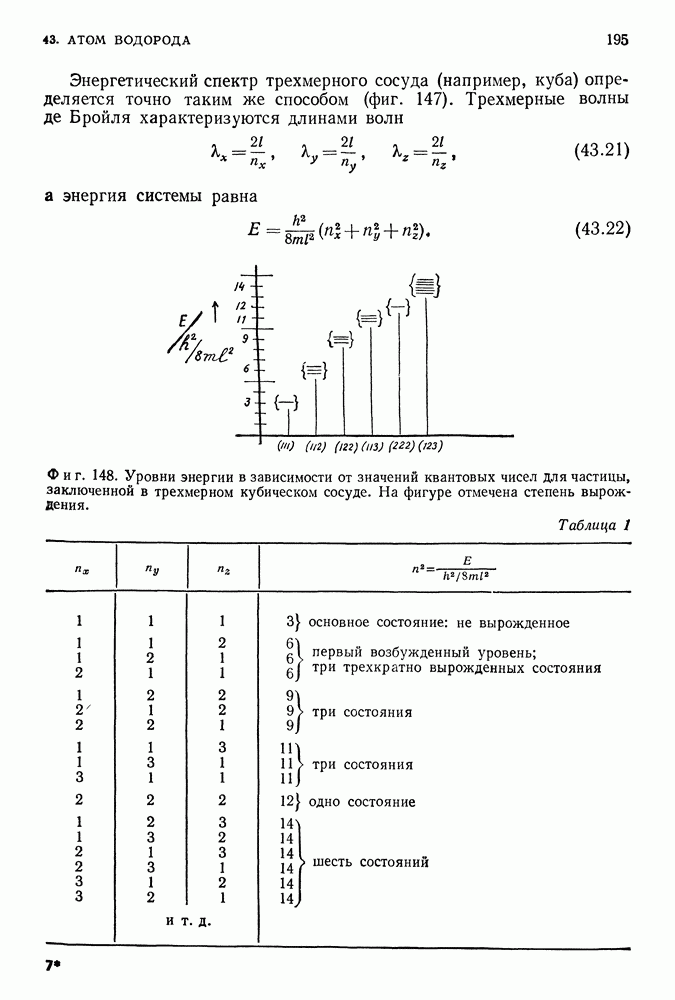
а энергия системы

Таким образом, влияние принципа запрета на волновую функцию системы из большого числа фермионов сказывается в том,  фермионы не могут все находиться в наинизшем квантовом состоянии (фиг. 189). Наинизшая энергия этой системы значительно превышает соответствующую энергию системы из такого же числа бозонов. В результате энергия основного состояния электронов в металле оказывается чрезвычайно большой величиной, и для дальнейших взаимодействий
фермионы не могут все находиться в наинизшем квантовом состоянии (фиг. 189). Наинизшая энергия этой системы значительно превышает соответствующую энергию системы из такого же числа бозонов. В результате энергия основного состояния электронов в металле оказывается чрезвычайно большой величиной, и для дальнейших взаимодействий 
таются свободными лишь такие уровни, которые располагаются выше последнего занятого. Волновая функция системы взаимодействующих частиц отличается от рассмотренной выше волновой функции из-за наличия сил, действующих между частицами.

Фиг. 189. Сравнение одночастичных уровней, заполненных 8 фермионами и 8 бозонами. Для бозонов  (основное состояние), а для фермионов
(основное состояние), а для фермионов  (основное состояние).
(основное состояние).
Однако, как мы убедимся при обсуждении периодической таблицы элементов, многие ее качественные свойства остаются прежними.
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
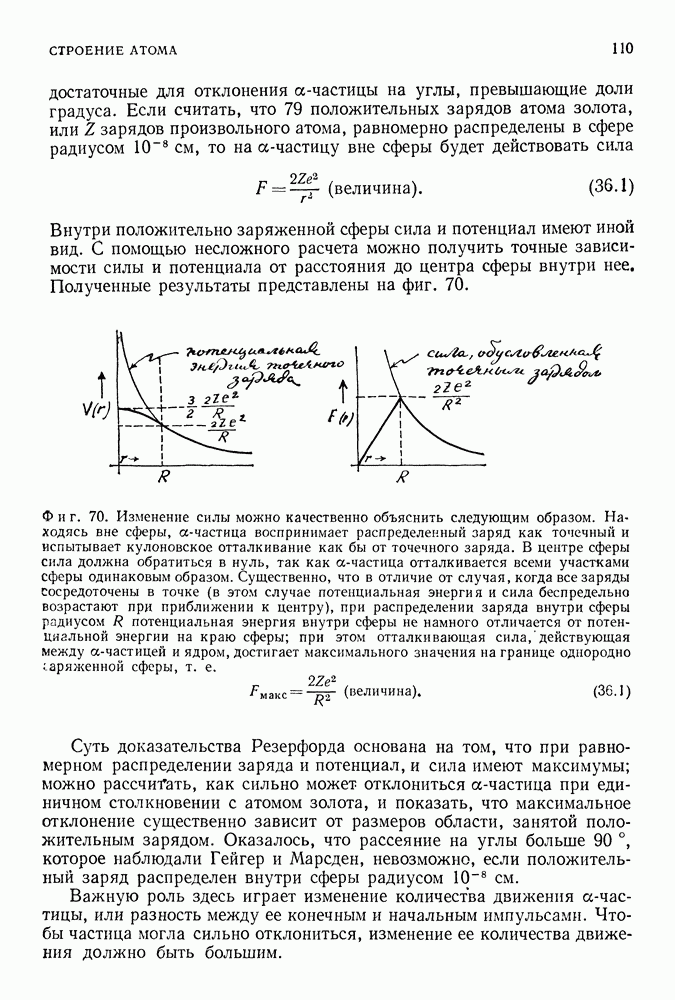
- 36. АТОМ РЕЗЕРФОРДА
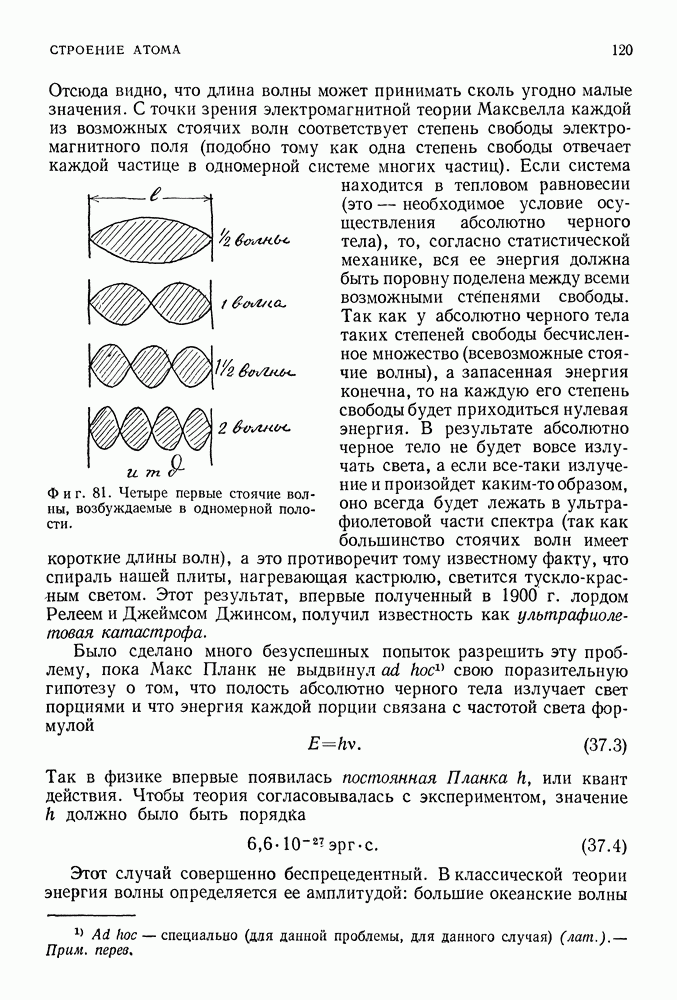
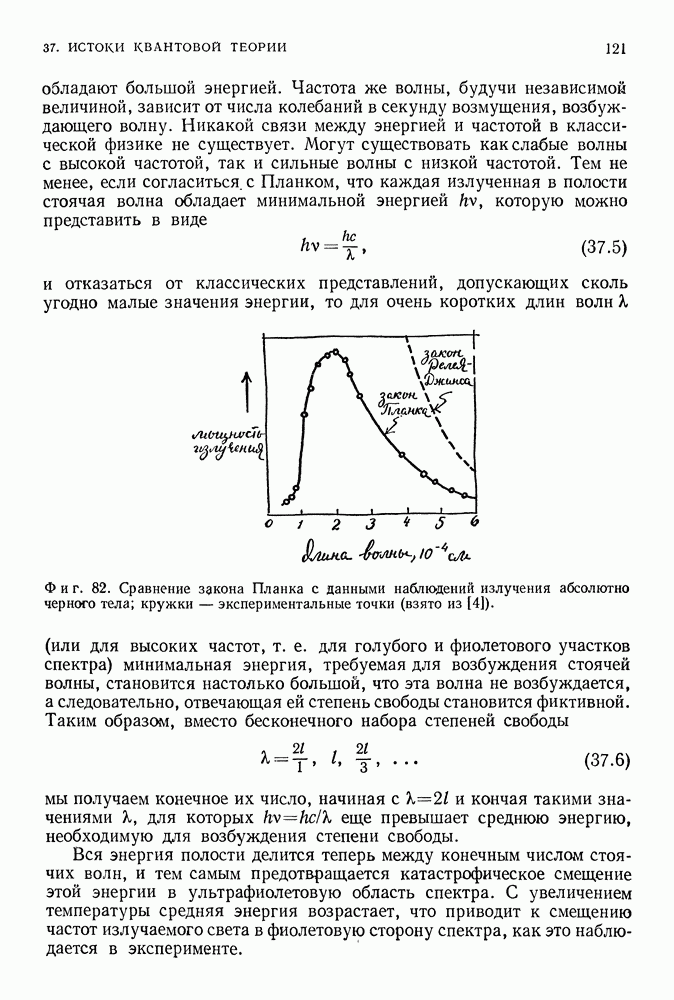
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
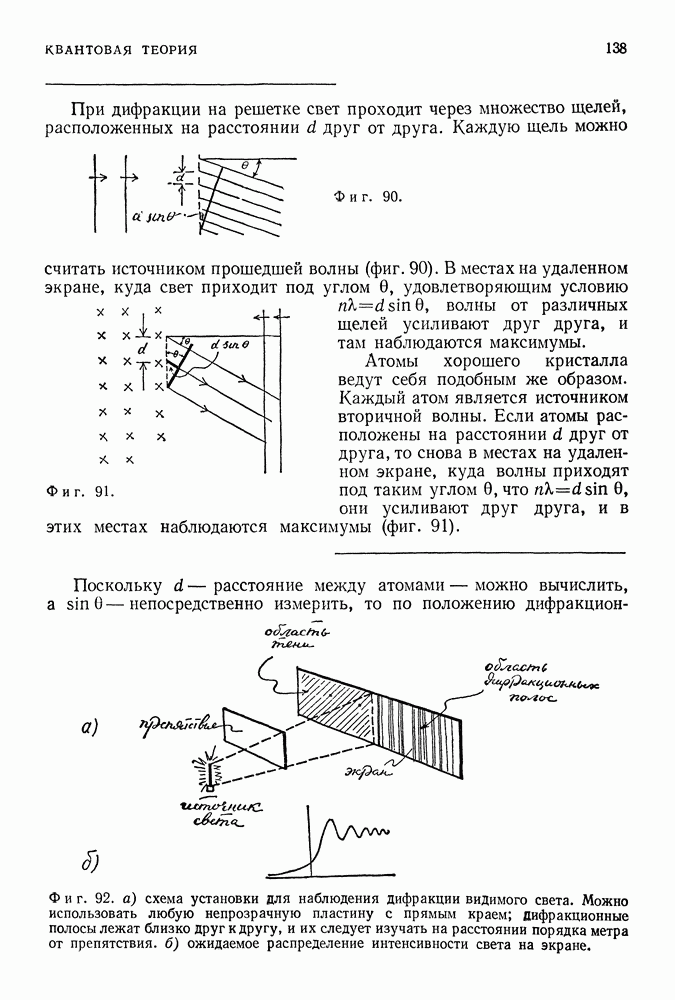
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
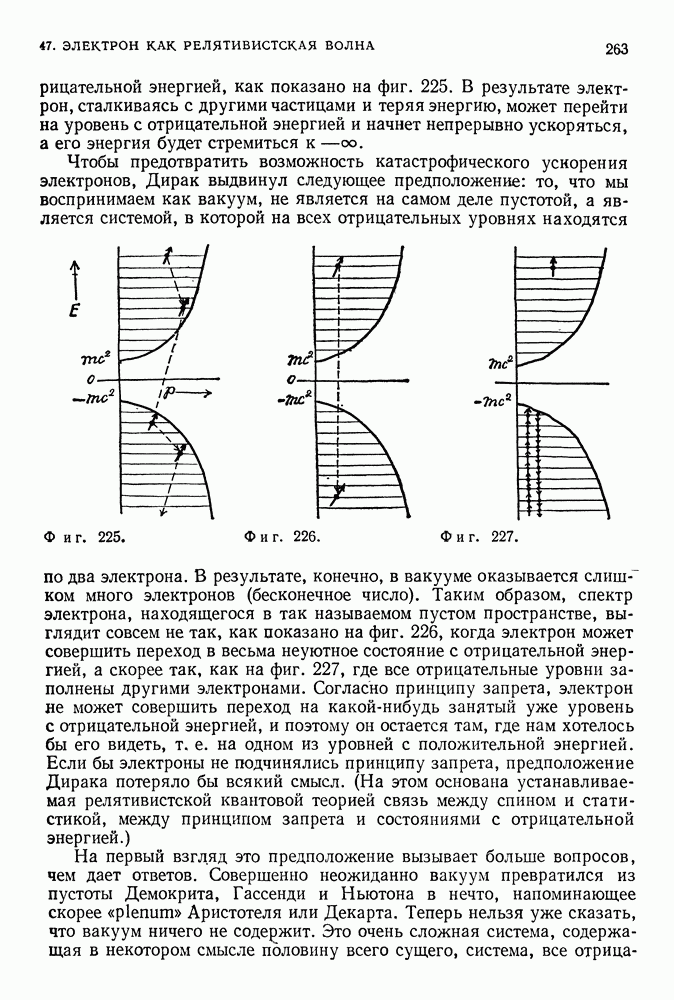
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
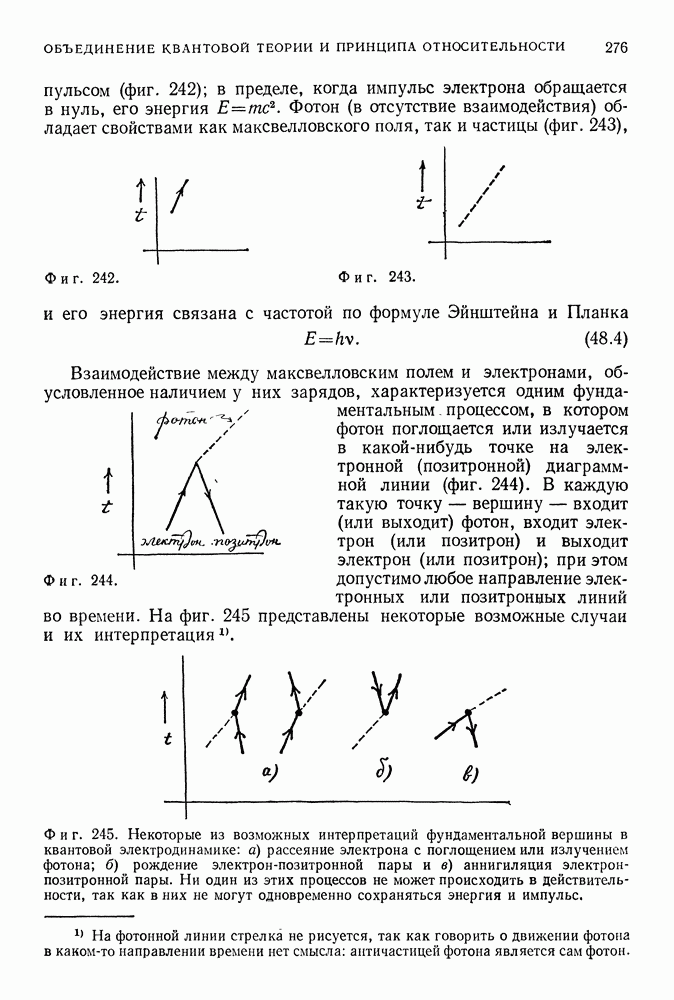
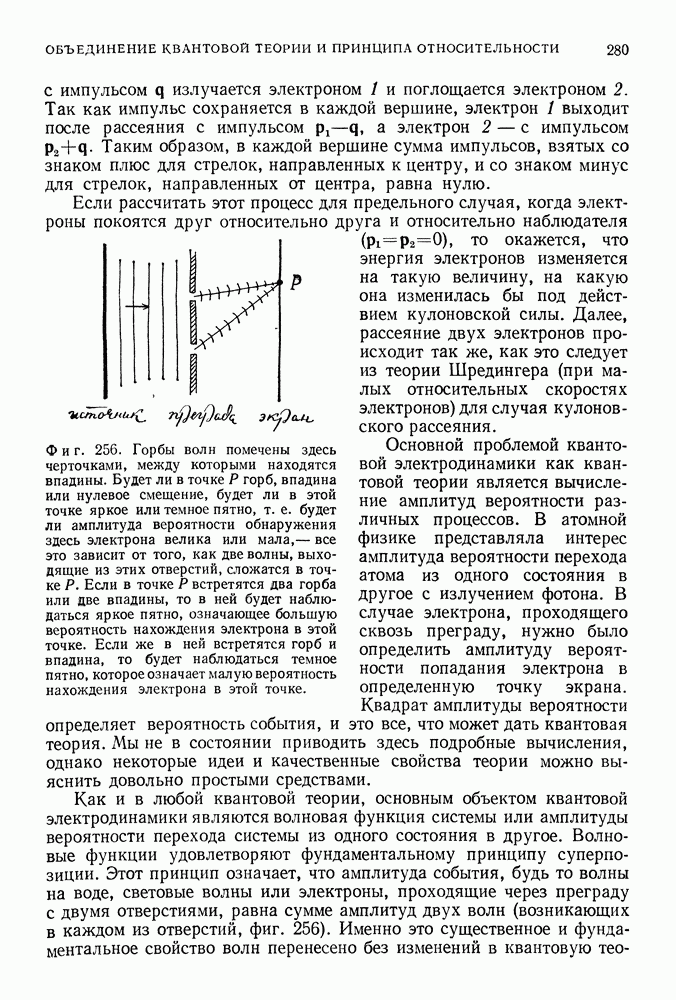
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
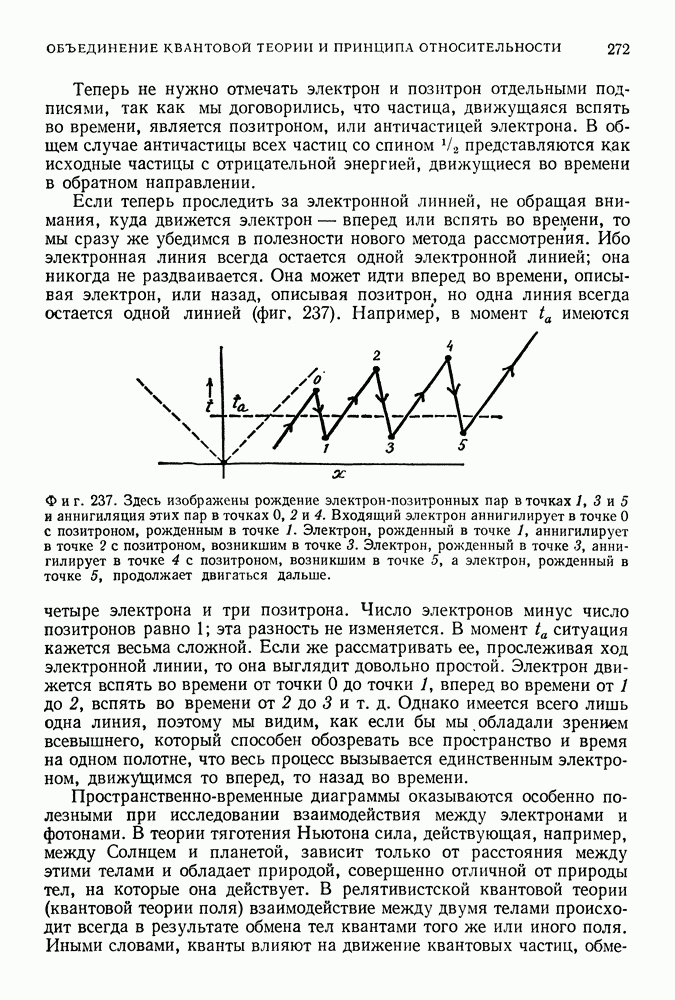
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
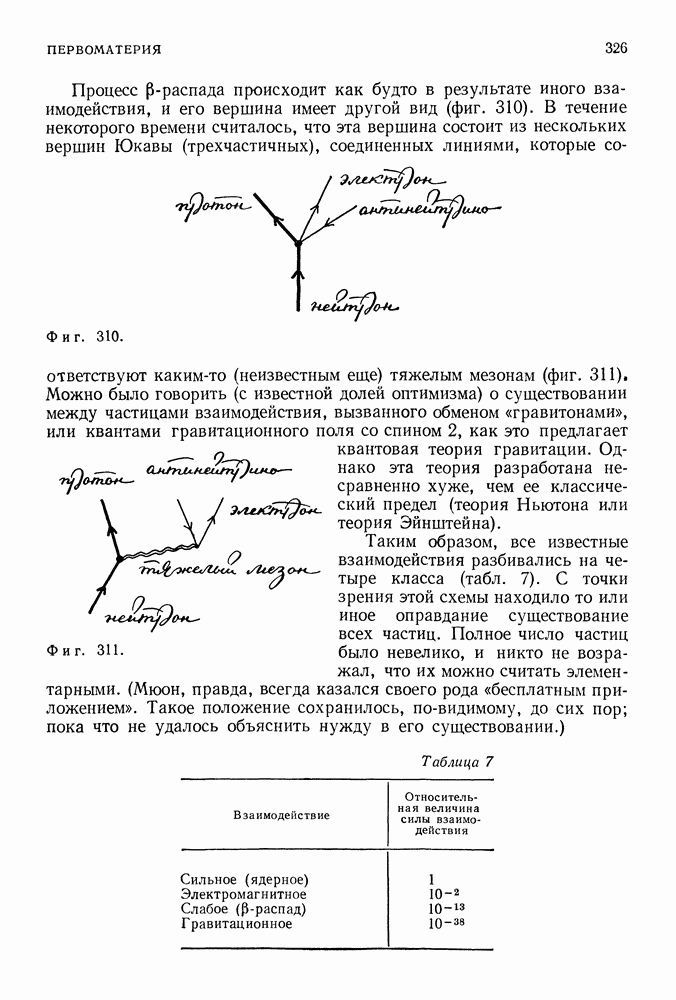
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
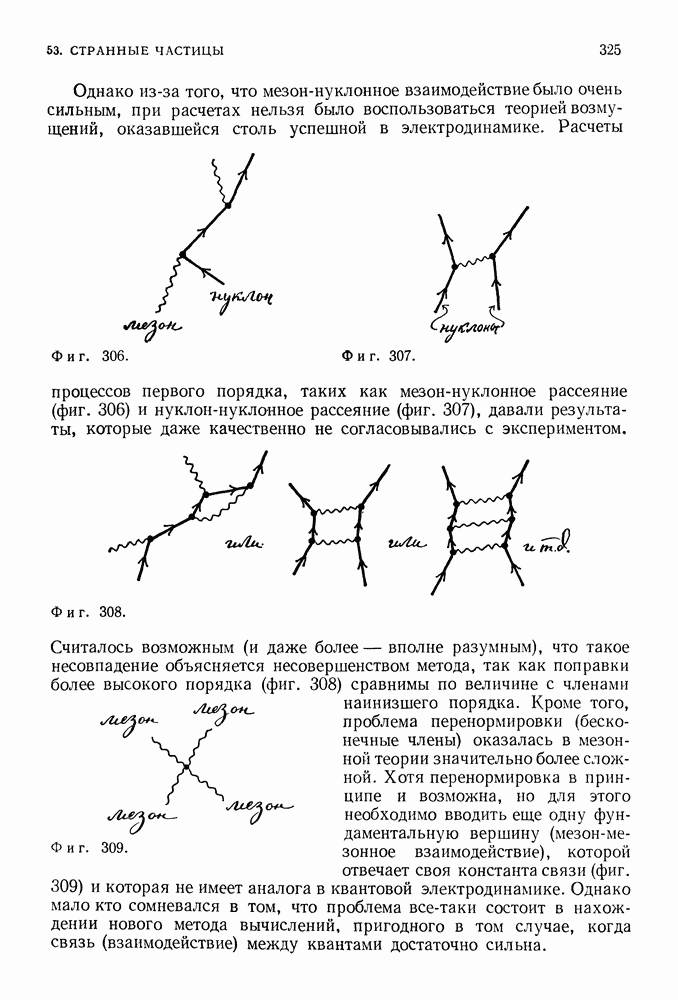
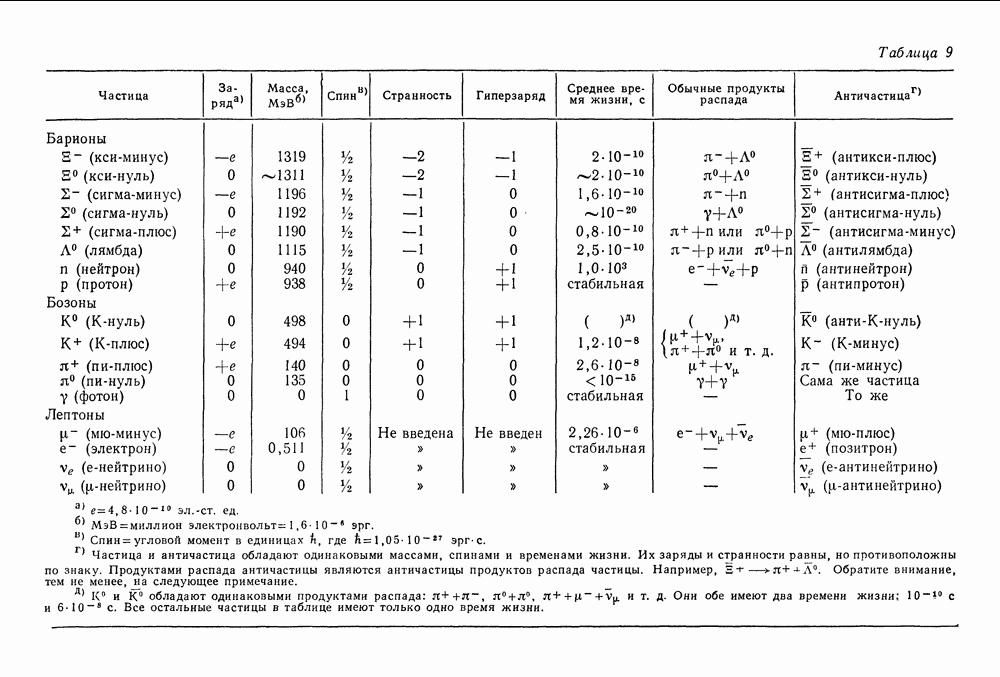
- 53. СТРАННЫЕ ЧАСТИЦЫ
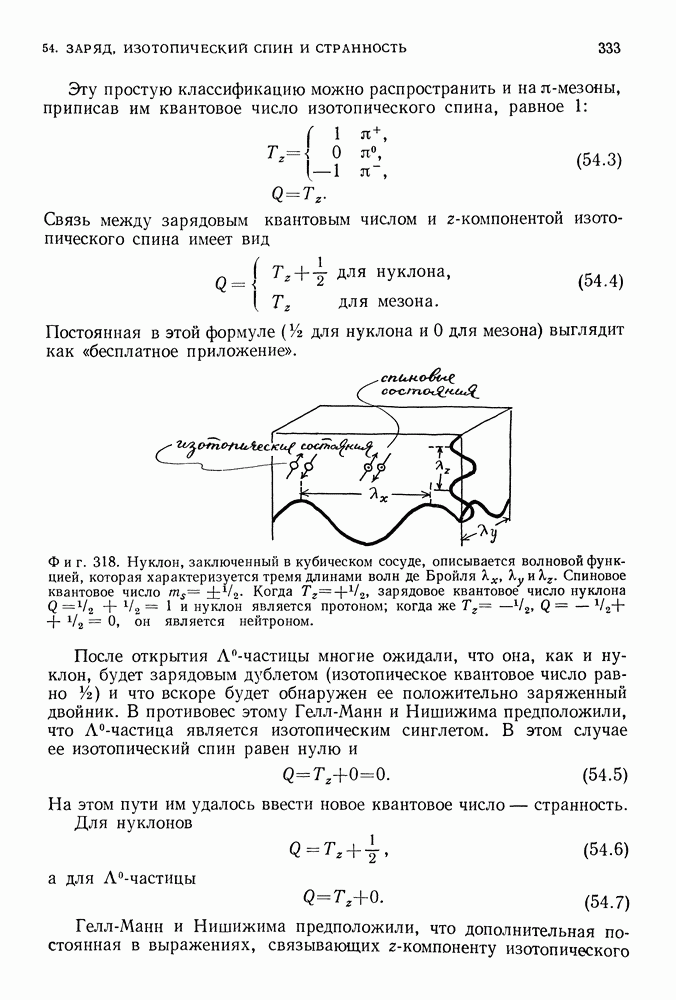
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА