| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
Электрон в магнитном поле
Рассмотрим снова движение электрона, находящегося в однородном магнитном поле. Мы ожидаем, что при малых скоростях электрона описанное ранее движение будет совпадать с тем, что мы получим сейчас. При больших скоростях существенную роль должны играть так называемые релятивистские поправки. Эта задача представляет интерес не только для сравнения нерелятивистских и релятивистских результатов, но имеет и чисто практическое значение. Дело в том, что в установках, ускоряющих электроны до релятивистских скоростей, часто используют постоянные однородные магнитные поля, удерживающие эти электроны на круговых орбитах.
Выражение для силы, действующей на движущийся электрон со стороны магнитного поля, было получено нами ранее:

Второй закон движения в форме Ньютона имеет вид

В рассматриваемом случае электрон движется по круговой орбите с ускорением  Поскольку скорость электрона остается постоянной
Поскольку скорость электрона остается постоянной
(изменяется лишь направление скорости), данный случай особенно прост для исследования, так как величина  не изменяется в процессе движения.
не изменяется в процессе движения.
В результате релятивистский закон движения можно записать в виде

и

Поэтому

Комбинируя второй закон Ньютона с выражением для силы, действующей на электрон со стороны магнитного поля, получаем

Отсюда находим напряженность магнитного поля, необходимую для удержания частицы на орбите радиусом 

которую можно сравнить с определенной ранее напряженностью поля в нерелятивистском случае:

Эти напряженности отличаются множителем

Смысл полученного результата состоит в том, что в релятивистском случае требуется большее магнитное поле для удержания частицы с заданной скоростью на орбите заданного радиуса. Этот результат нетрудно понять. При заданных  и
и  ускорение электрона равно
ускорение электрона равно  Произведение ускорения на массу дает требуемую силу. В релятивистском случае масса (или инерция) электрона возрастает при увеличении его скорости. Поэтому при заданном ускорении, т. е. при заданных
Произведение ускорения на массу дает требуемую силу. В релятивистском случае масса (или инерция) электрона возрастает при увеличении его скорости. Поэтому при заданном ускорении, т. е. при заданных  и
и  требуется большая сила. Но поскольку сила пропорциональна напряженности магнитного поля В, мы получаем, что в релятивистском случае требуется большее магнитное поле для удержания частицы с заданной скоростью на орбите заданного радиуса.
требуется большая сила. Но поскольку сила пропорциональна напряженности магнитного поля В, мы получаем, что в релятивистском случае требуется большее магнитное поле для удержания частицы с заданной скоростью на орбите заданного радиуса.
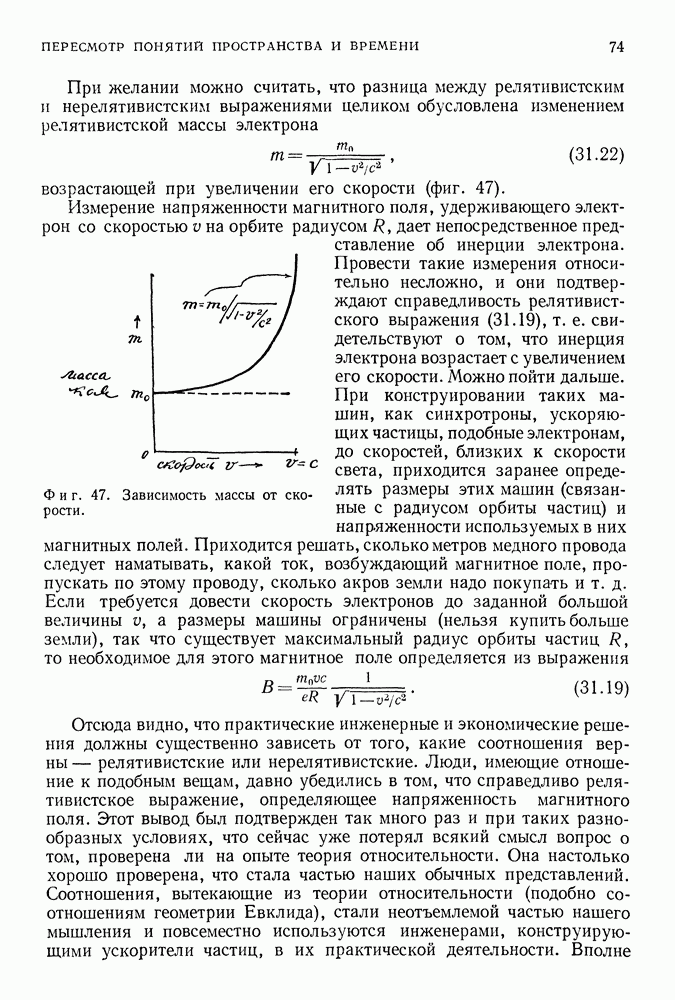
При желании можно считать, что разница между релятивистским и нерелятивистским выражениями целиком обусловлена изменением релятивистской массы электрона

возрастающей при увеличении его скорости (фиг. 47).
Измерение напряженности магнитного поля, удерживающего электрон со скоростью  на орбите радиусом
на орбите радиусом  дает непосредственное представление об инерции электрона. Провести такие измерения относительно несложно, и они подтверждают справедливость релятивистского выражения (31.19), т. е. свидетельствуют о том, что инерция электрона возрастает с увеличением его скорости. Можно пойти дальше. При конструировании таких машин, как синхротроны, ускоряющих частицы, подобные электронам, до скоростей, близких к скорости света, приходится заранее определять размеры этих машин (связанные с радиусом орбиты частиц) и напряженности используемых в них магнитных полей. Приходится решать, сколько метров медного провода следует наматывать, какой ток, возбуждающий магнитное поле, пропускать по этому проводу, сколько акров земли надо покупать и т. д. Если требуется довести скорость электронов до заданной большой величины
дает непосредственное представление об инерции электрона. Провести такие измерения относительно несложно, и они подтверждают справедливость релятивистского выражения (31.19), т. е. свидетельствуют о том, что инерция электрона возрастает с увеличением его скорости. Можно пойти дальше. При конструировании таких машин, как синхротроны, ускоряющих частицы, подобные электронам, до скоростей, близких к скорости света, приходится заранее определять размеры этих машин (связанные с радиусом орбиты частиц) и напряженности используемых в них магнитных полей. Приходится решать, сколько метров медного провода следует наматывать, какой ток, возбуждающий магнитное поле, пропускать по этому проводу, сколько акров земли надо покупать и т. д. Если требуется довести скорость электронов до заданной большой величины  а размеры машины ограничены (нельзя купить больше земли), так что существует максимальный радиус орбиты частиц
а размеры машины ограничены (нельзя купить больше земли), так что существует максимальный радиус орбиты частиц  то необходимое для этого магнитное поле определяется из выражения
то необходимое для этого магнитное поле определяется из выражения


Фиг. 47. Зависимость массы от скорости.
Отсюда видно, что практические инженерные и экономические решения должны существенно зависеть от того, какие соотношения верны — релятивистские или нерелятивистские. Люди, имеющие отношение к подобным вещам, давно убедились в том, что справедливо релятивистское выражение, определяющее напряженность магнитного поля. Этот вывод был подтвержден так много раз и при таких разнообразных условиях, что сейчас уже потерял всякий смысл вопрос о том, проверена ли на опыте теория относительности. Она настолько хорошо проверена, что стала частью наших обычных представлений. Соотношения, вытекающие из теории относительности (подобно соотношениям геометрии Евклида), стали неотъемлемой частью нашего мышления и повсеместно используются инженерами, конструирующими ускорители частиц, в их практической деятельности. Вполне
возможно, что в будущем по неизвестным сейчас причинам эти представления (как и любые другие) придется уточнять. Но в настоящее время теория относительности внесла такую ясность в рассматриваемый круг явлений, что подобно геометрии Евклида в пространстве она заслужила титул «правдивой».
Максимальная скорость
Рассмотрим теперь поведение частицы, на которую действует постоянная однородная сила в заданном направлении. С точки зрения теории Ньютона такая частица будет испытывать постоянное ускорение, а ее скорость со временем будет неограниченно возрастать. Релятивистские уравнения можно записать в виде

где релятивистский импульс

В релятивистском случае импульс и энергия частицы, подверженной действию постоянной силы, непрерывно нарастают. Скорость же частицы не может превысить с.
Чтобы показать это, выразим из уравнения (31.3) скорость через импульс. 

При заданной массе покоя и при больших значениях импульса это выражение можно приблизительно представить в виде

Таким образом, в пределе бесконечно больших значений импульса скорость  приближается к с, но никогда не превышает эту величину.
приближается к с, но никогда не превышает эту величину.
Если действительно приложить к электрону постоянную силу (как, например, в эксперименте «Максимальная скорость»  а затем измерить его скорость (измеряя, например, промежуток времени, за который электрон пролетает известное расстояние) и одновременно энергию, то можно убедиться, что скорость частицы связана с ее энергией или импульсом не в соответствии с ньютоновским выражением
а затем измерить его скорость (измеряя, например, промежуток времени, за который электрон пролетает известное расстояние) и одновременно энергию, то можно убедиться, что скорость частицы связана с ее энергией или импульсом не в соответствии с ньютоновским выражением

а по формуле

Таким образом, мы получили следующий практический результат: несмотря на то, что импульс и энергия электрона непрерывно увеличиваются, его скорость, т. е. пройденное электроном расстояние,
деленное на соответствующий отрезок времени, приближается к постоянной величине — скорости света.
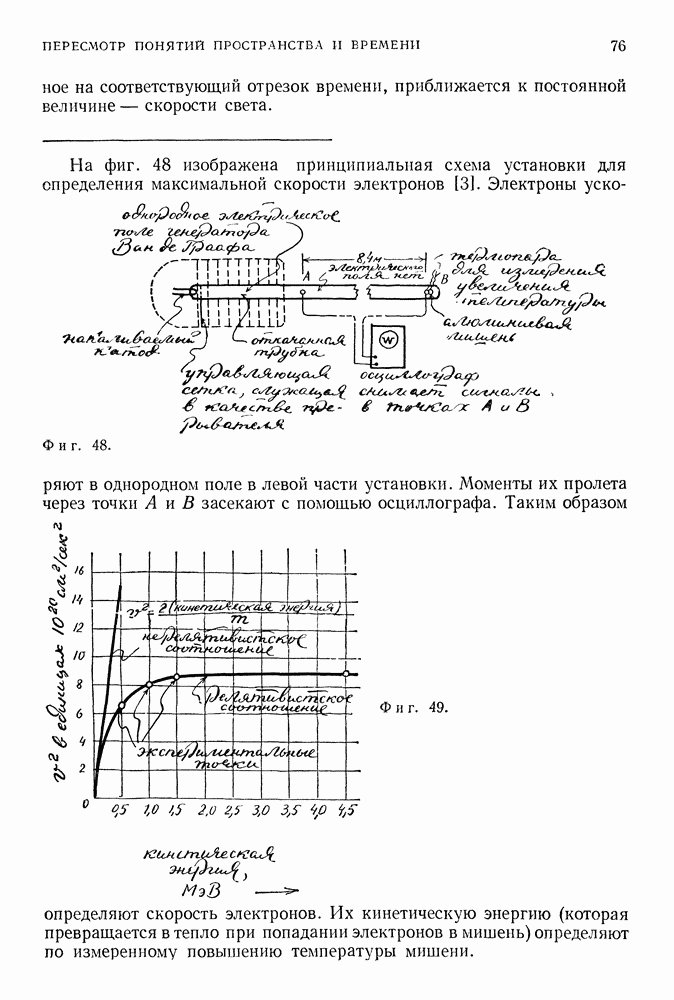
На фиг. 48 изображена принципиальная схема установки для определения максимальной скорости электронов [3].

Фиг. 48.
Электроны ускоряют в однородном поле в левой части установки. Моменты их пролета через точки А и В засекают с помощью осциллографа. Таким образом определяют скорость электронов.

Фиг. 49.
Их кинетическую энергию (которая превращается в тепло при попадании электронов в мишень) определяют по измеренному повышению температуры мишени.
Если построить затем график зависимости кинетической энергии от  то он будет соответствовать не соотношению
то он будет соответствовать не соотношению

(прямая линия на фиг. 49), а релятивистскому выражению

| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
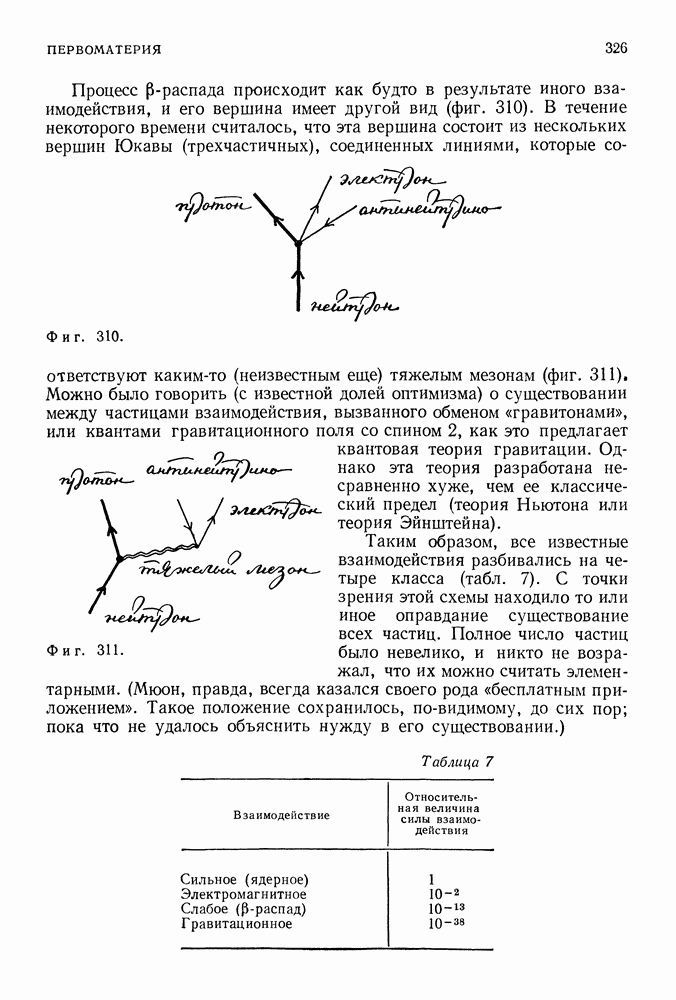
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
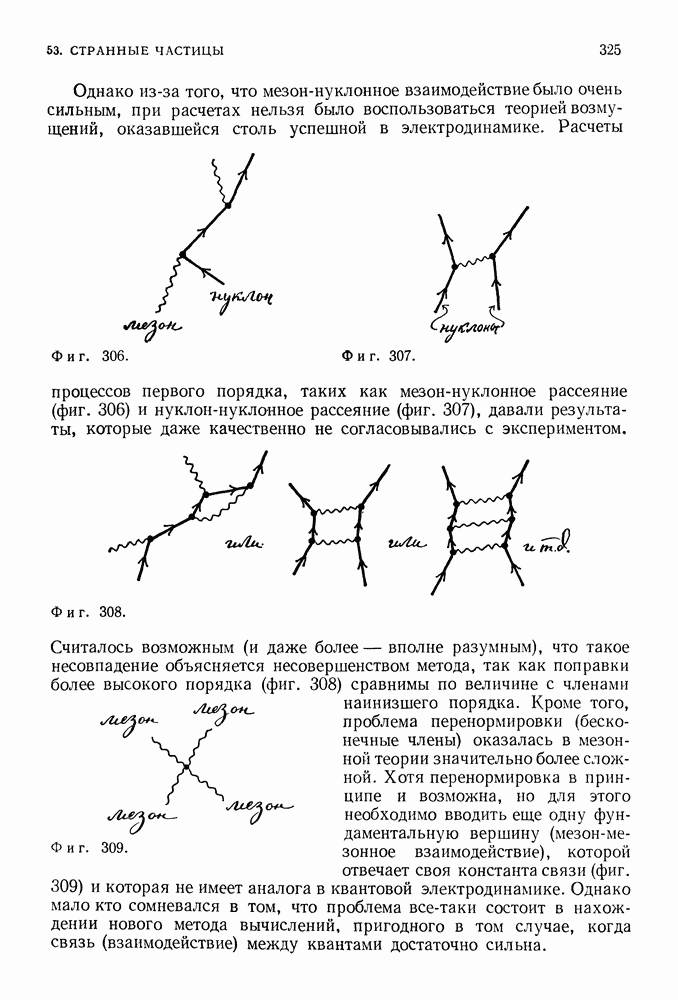
- 53. СТРАННЫЕ ЧАСТИЦЫ
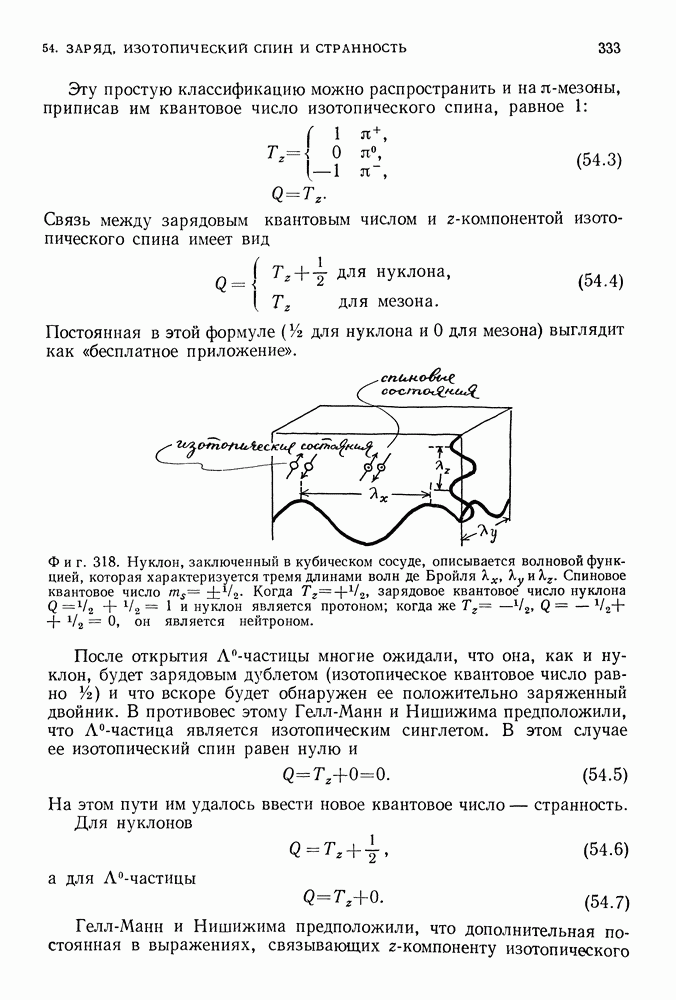
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА