| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СЛОЖЕНИЕ СКОРОСТЕЙ
Какова скорость тела, измеренная наблюдателем в неподвижной системе  если с точки зрения наблюдателя в движущейся системе
если с точки зрения наблюдателя в движущейся системе  его скорость равна и (фиг. 37)?
его скорость равна и (фиг. 37)?

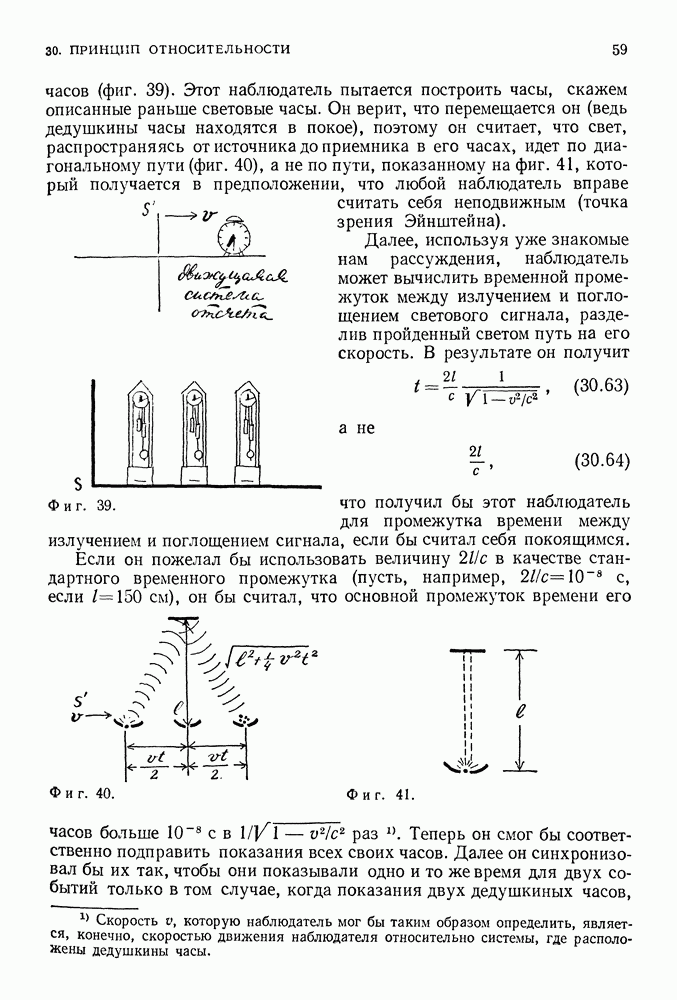
Фиг. 37. Теле движется со скоростью и относительно 
Мы привыкли считать, что относительно тело движется со скоростью  поскольку в то время, как тело удаляется от начала координат системы
поскольку в то время, как тело удаляется от начала координат системы  со скоростью и, сама система
со скоростью и, сама система  удаляется от начала системы
удаляется от начала системы  со скоростью
со скоростью  Теперь, однако, мы уже не удивимся, если этот результат окажется неверным с точки зрения теории относительности. Результат
Теперь, однако, мы уже не удивимся, если этот результат окажется неверным с точки зрения теории относительности. Результат  опирается на гипотезу,
опирается на гипотезу,
что расстояние и время, измеренные в системе  совпадают с расстоянием и временем, полученными в системе
совпадают с расстоянием и временем, полученными в системе 
Скорость и есть пройденное телом расстояние, деленное на промежуток времени, причем и то и другое измерены наблюдателем, находящимся в системе 

Чтобы получить скорость тела в системе  необходимо разделить пройденный телом путь на промежуток времени, оба измеренные наблюдателем в системе
необходимо разделить пройденный телом путь на промежуток времени, оба измеренные наблюдателем в системе 
С точки зрения наблюдателя в движущейся системе  тело за время
тело за время  удаляется от начала координат О на расстояние
удаляется от начала координат О на расстояние  поэтому
поэтому

С точки зрения наблюдателя в покоящейся системе  тело за время
тело за время  удаляется от начала координат О на расстояние
удаляется от начала координат О на расстояние  поэтому
поэтому

Согласно правилу Эйнштейна, связь между расстояниями от начала системы  до предмета с точки зрения двух наблюдателей имеет
до предмета с точки зрения двух наблюдателей имеет

(для неподвижного наблюдателя все длины в движущейся системе сократились). Тогда

Это соотношение можно записать в виде

поскольку  Но
Но  есть расстояние, деленное на время, или скорость тела в движущейся системе отсчета. Поэтому
есть расстояние, деленное на время, или скорость тела в движущейся системе отсчета. Поэтому

Величина  есть отношение промежутков времени, измеренных наблюдателями в движущейся и неподвижной системах отсчета в точке нахождения движущегося
есть отношение промежутков времени, измеренных наблюдателями в движущейся и неподвижной системах отсчета в точке нахождения движущегося 

Подставляя (30.53) в (30.52), получаем

С точки зрения наблюдателя в 

но для точки  расположенной на движущемся теле,
расположенной на движущемся теле,  где а — скорость тела в системе
где а — скорость тела в системе  Поэтому
Поэтому

или

 Подставляя это выражение в (30.52), получаем
Подставляя это выражение в (30.52), получаем

Чтобы различать релятивистское и обычное сложения скоростей, можно при желании ввести новый символ -Н для релятивистского сложения. Тогда сумма скоростей и и  в теории относительности запишется в виде
в теории относительности запишется в виде

Это выражение связано с обычным сложением по формуле

Представляет некоторый интерес изучить свойства такого правила сложения. Предположим, например, что и и  равны по величине половине скорости света. При обычных представлениях о длине и времени мы заключили бы, что сумма этих скоростей, одна вторая плюс одна вторая, равна единице. В релятивистском же случае такой вывод оказывается неверным. Действительно, если
равны по величине половине скорости света. При обычных представлениях о длине и времени мы заключили бы, что сумма этих скоростей, одна вторая плюс одна вторая, равна единице. В релятивистском же случае такой вывод оказывается неверным. Действительно, если  то
то

Иными словами, как это ни парадоксально, сумма двух половинок равна четырем пятым. Конечно, такое правило сложения есть просто переопределение символа «плюс».
Рассмотрим теперь интересный случай, когда объектом, движущимся относительно системы  является луч света, поэтому скорость этого объекта в системе
является луч света, поэтому скорость этого объекта в системе  равна с. Чему равна его скорость, измеренная в системе
равна с. Чему равна его скорость, измеренная в системе  ? В данном случае
? В данном случае  Скорость же
Скорость же  может быть любой величиной, меньшей скорости света. Тогда, если
может быть любой величиной, меньшей скорости света. Тогда, если 

Таким образом, при релятивистском сложении любой скорости со скоростью света получается снова скорость света. Конечно, этот результат не является неожиданным, если наша теория согласована, так как она опирается на постулат, что. свет в любой системе отсчета распространяется с одной и той же скоростью.
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
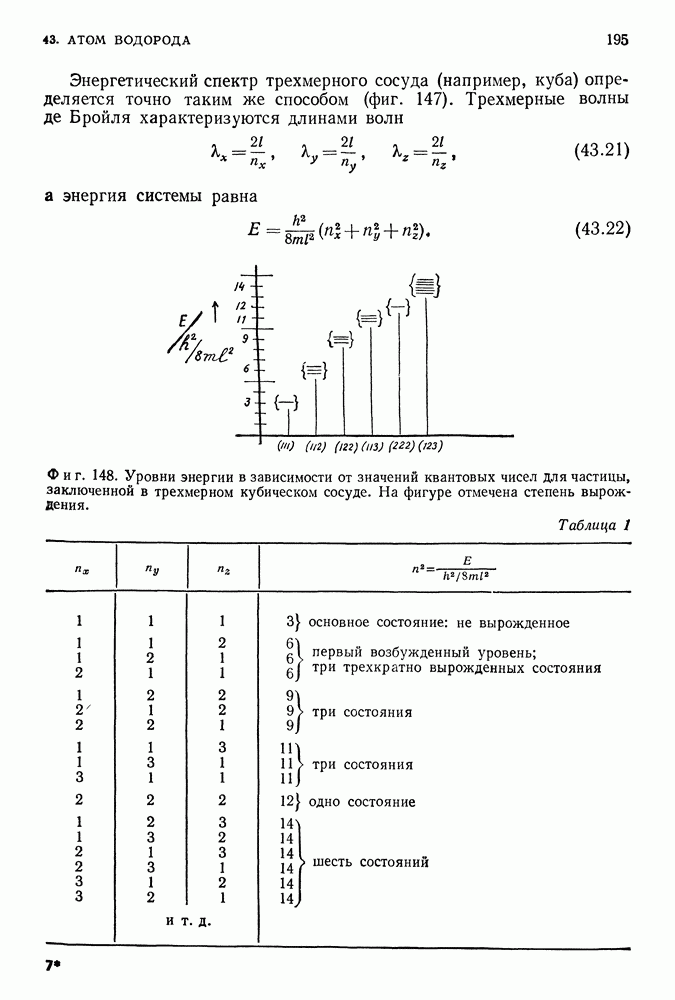
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
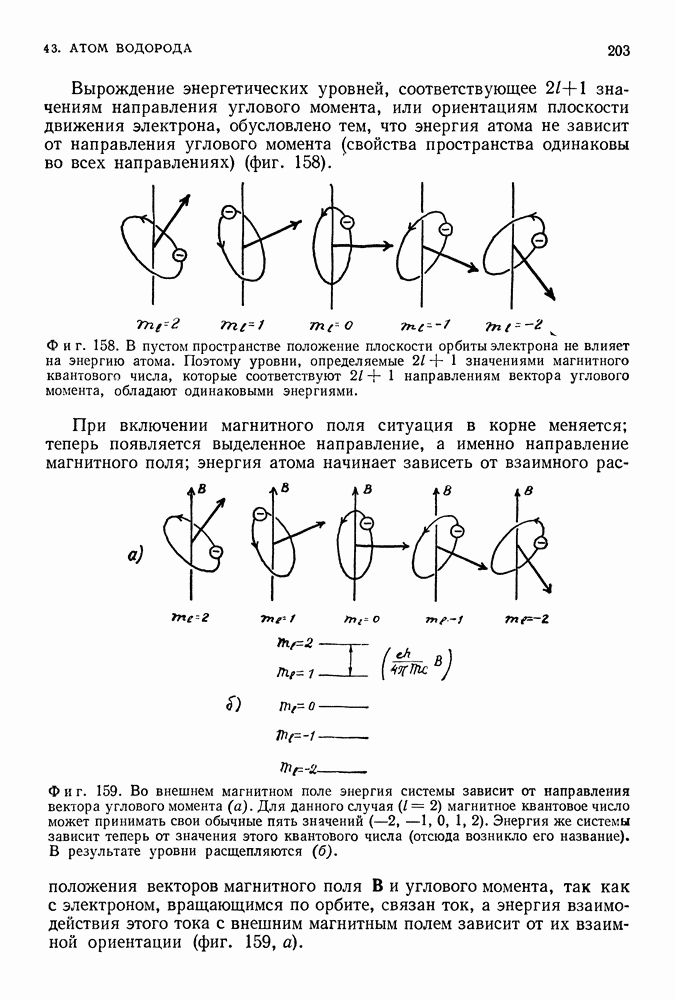
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
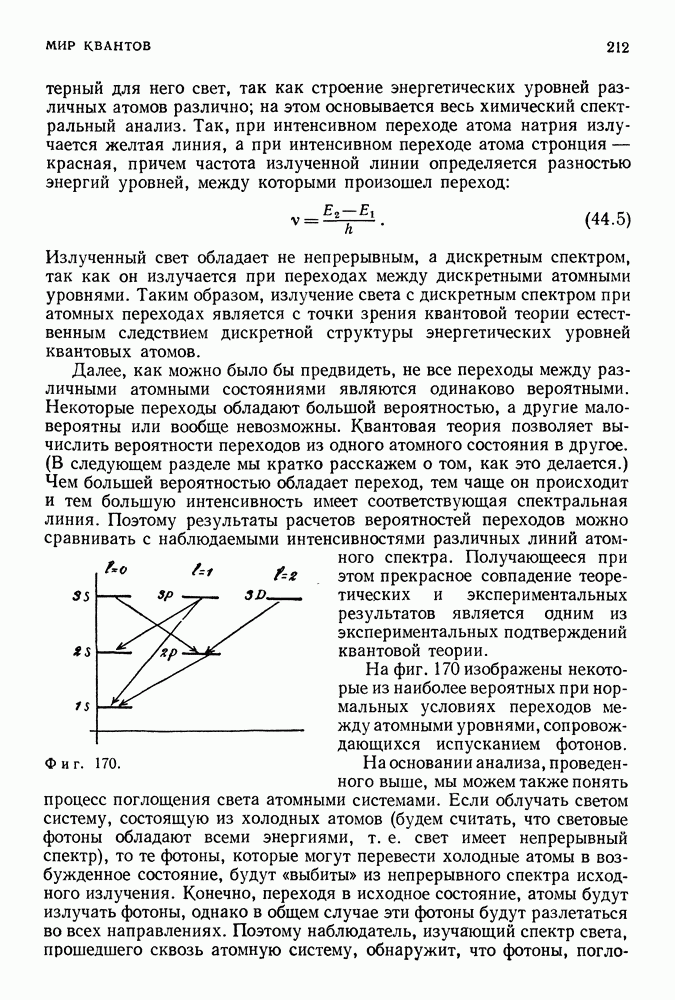
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
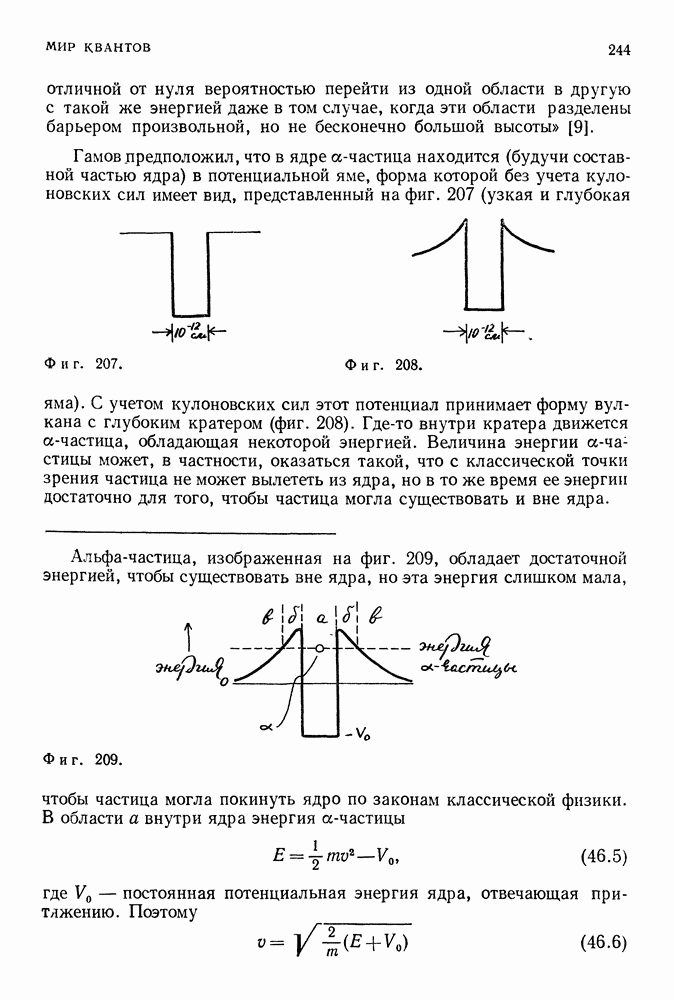
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
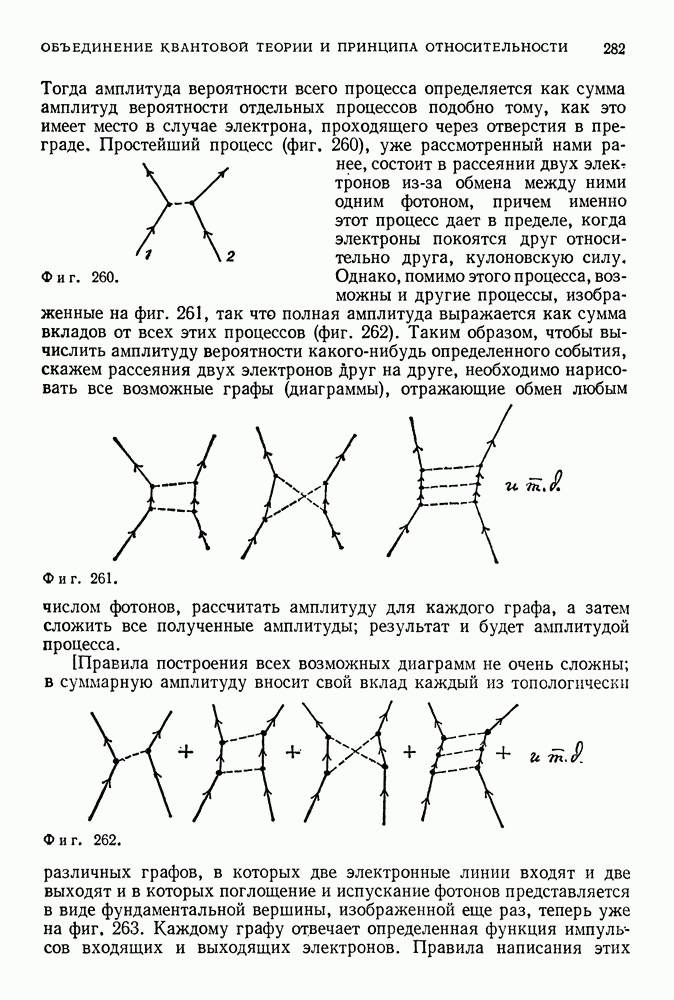
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
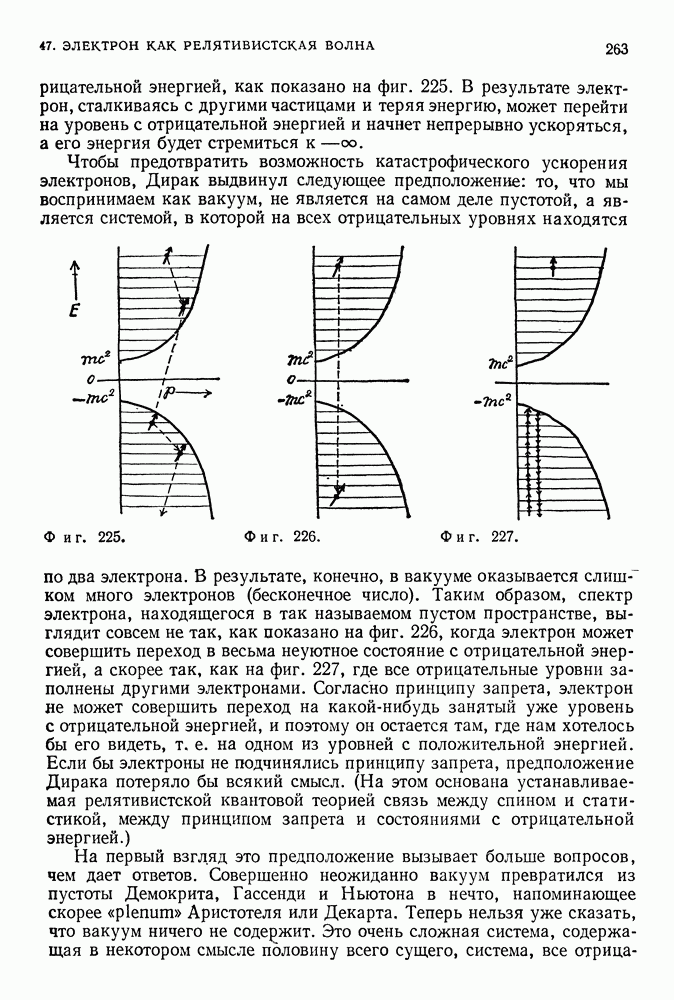
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
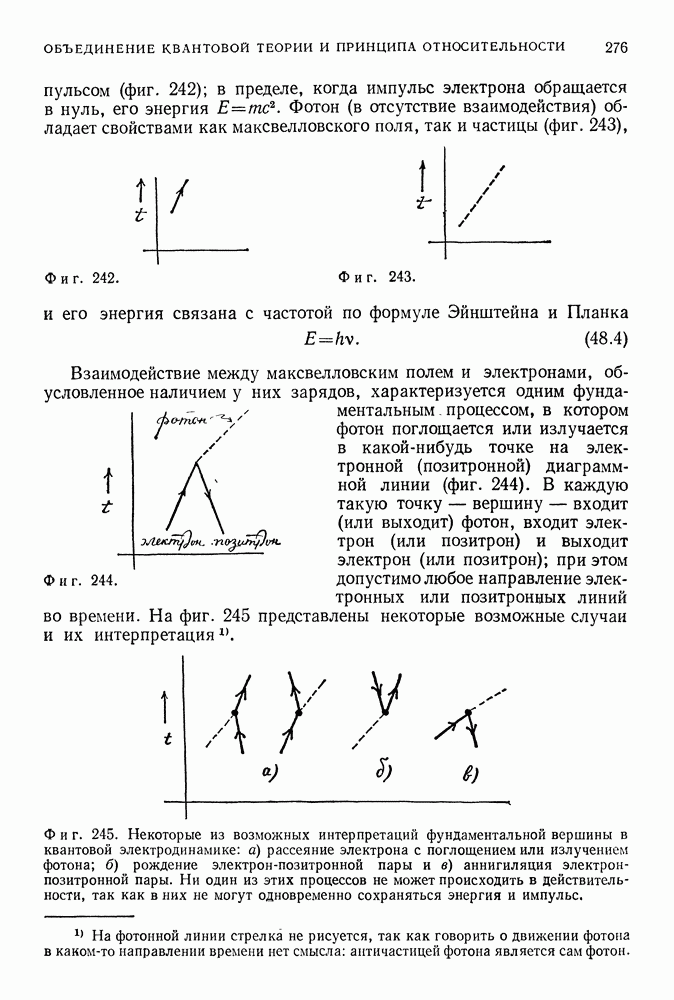
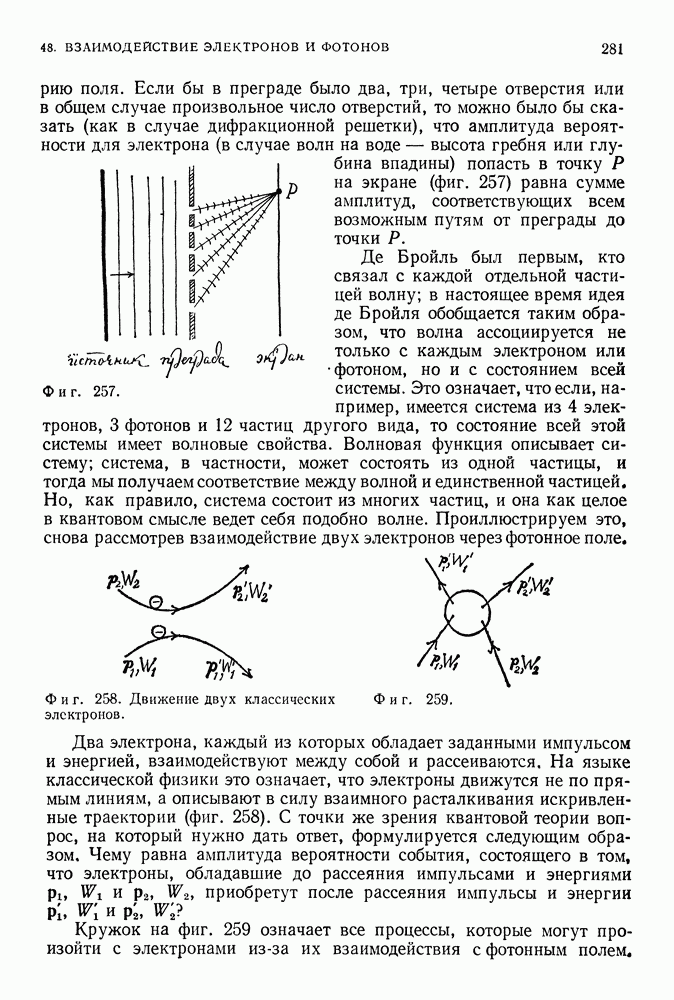
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
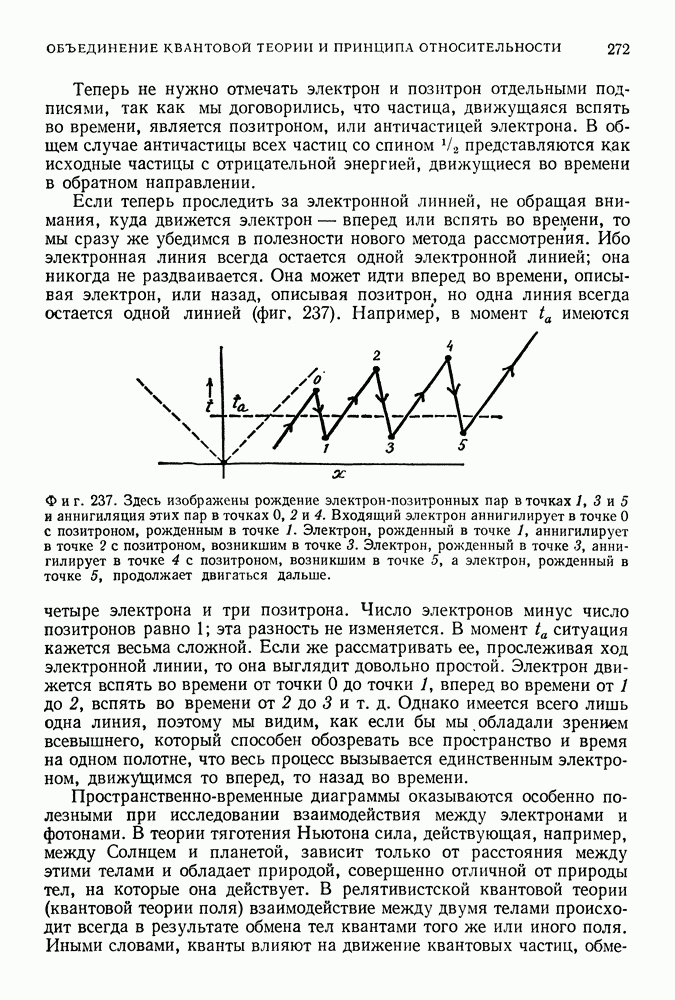
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
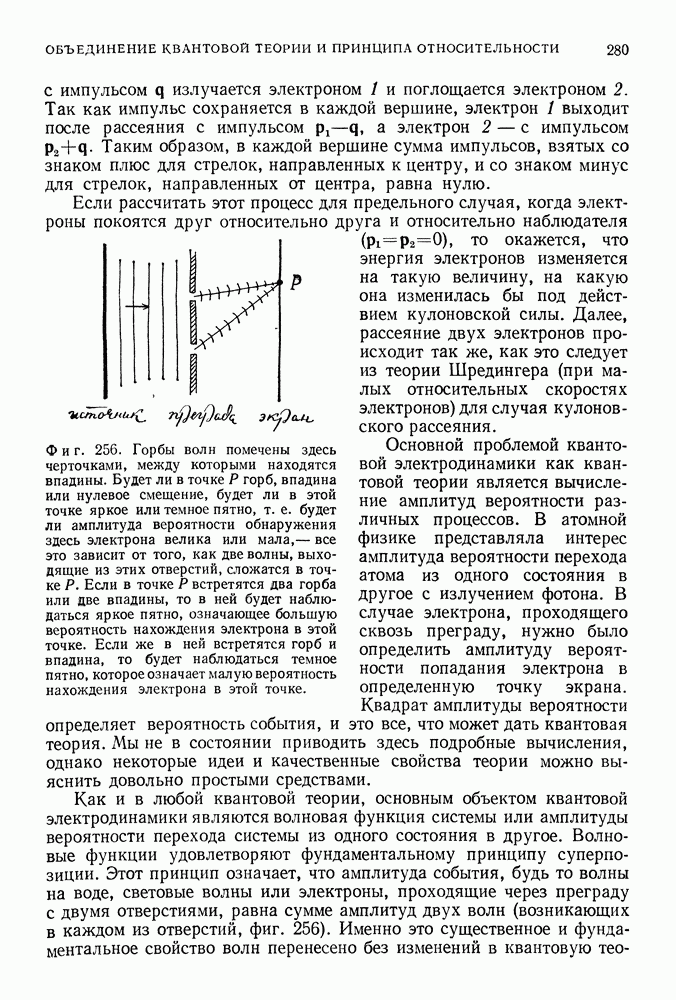
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
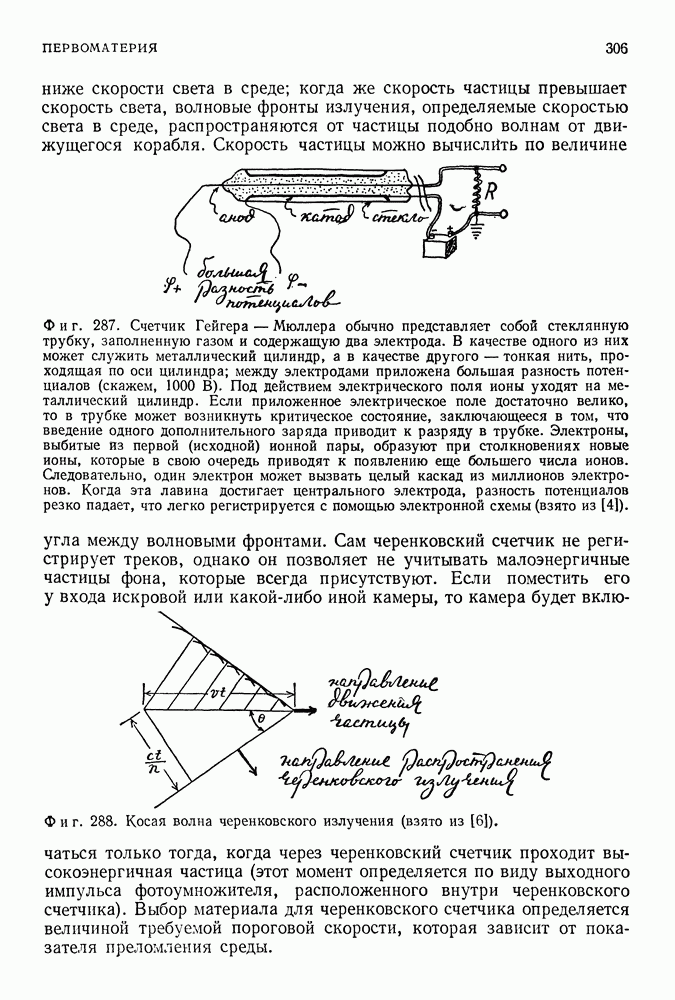
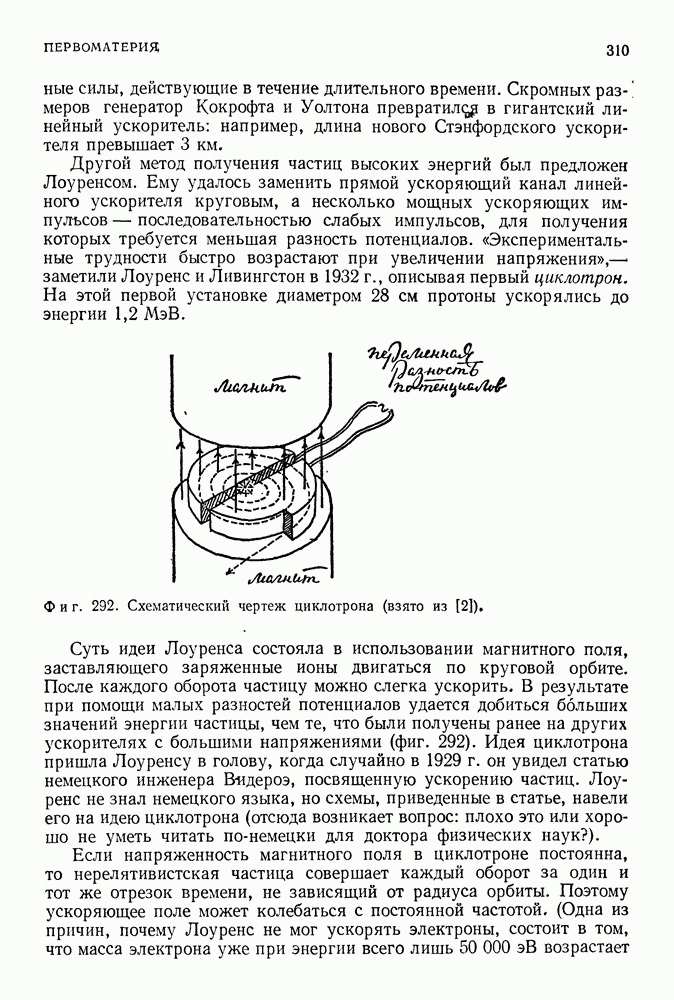
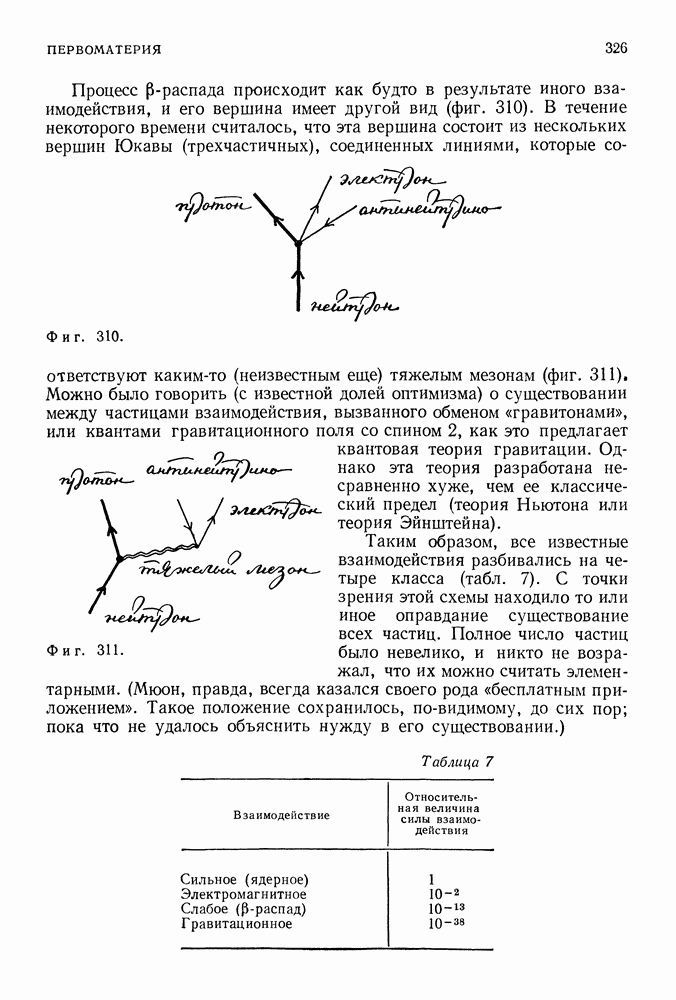
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
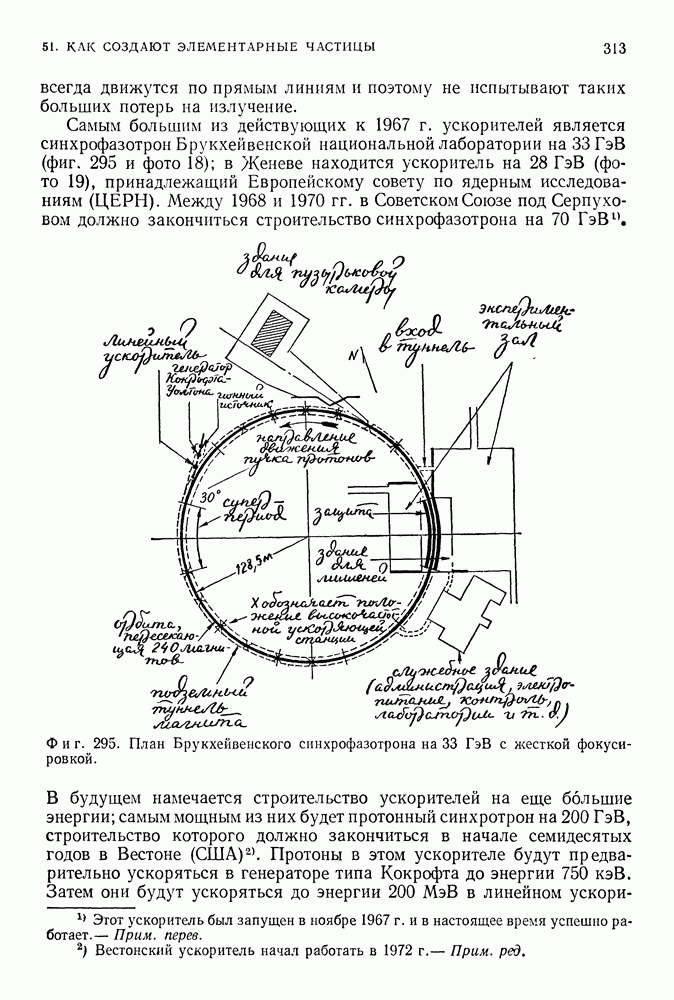
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
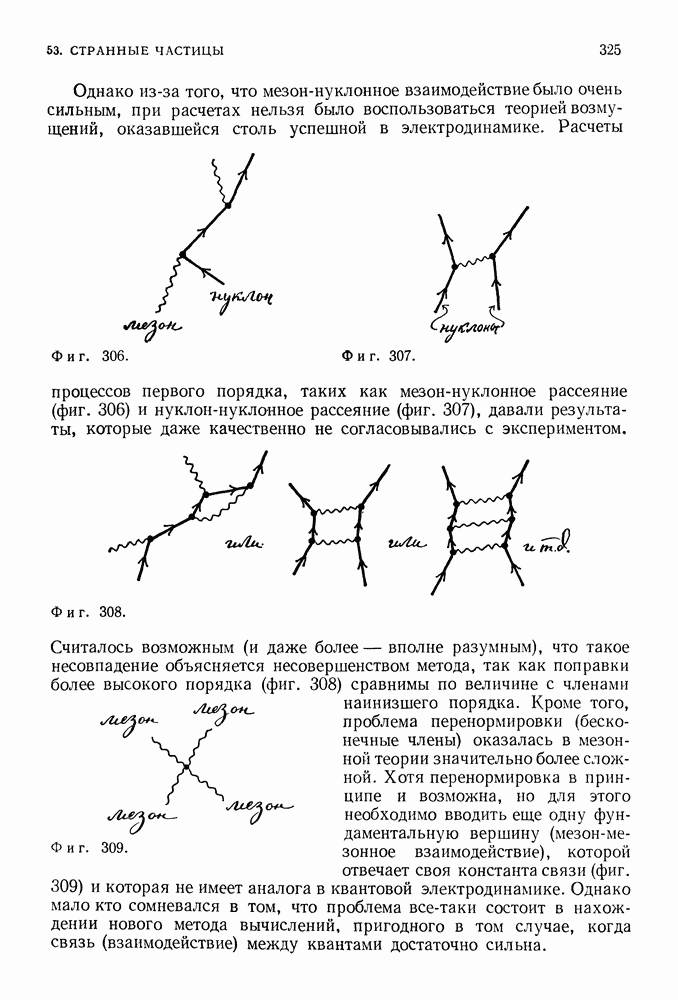
- 53. СТРАННЫЕ ЧАСТИЦЫ
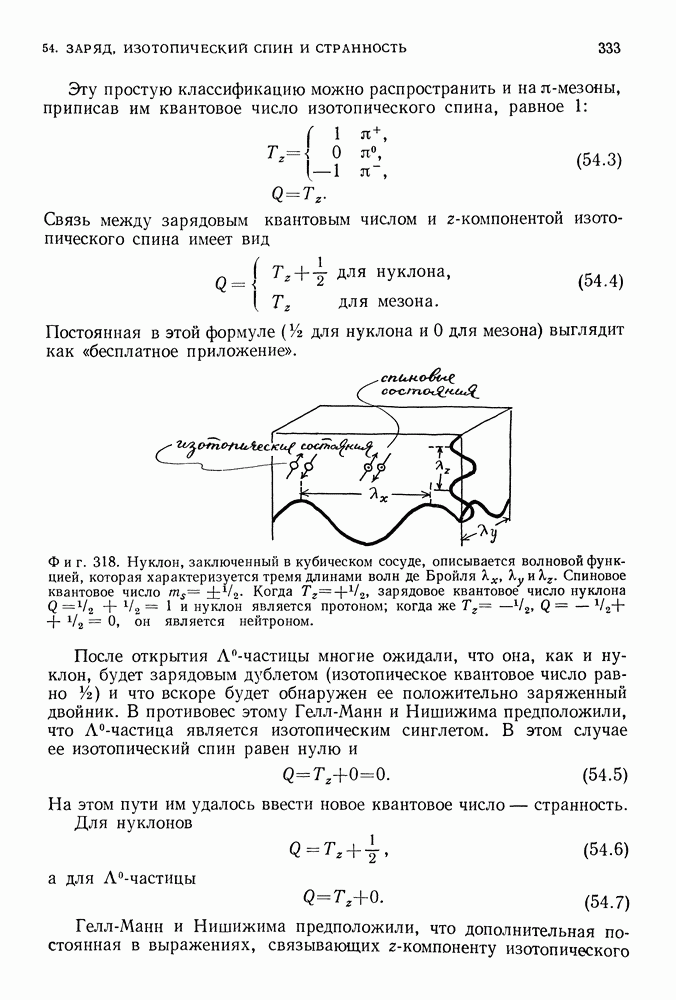
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА