| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
Взглянем снова на уравнения Ньютона в релятивистской форме:

За исключением определения импульса, эти уравнения в точности совпадают с уравнениями из ньютоновских «Начал»: произведение силы на отрезок времени, в течение которого она действует, равно изменению импульса. По этой причине структура многих соотношений, полученных нами ранее из нерелятивистских уравнений (фактически всех тех следствий из второго закона, в которых не используется определение  как произведения
как произведения  остается в силе и в релятивистском случае, что дает наглядный пример того, как может сохраниться структура соотношений теории, даже если интерпретация символов в них изменилась.
остается в силе и в релятивистском случае, что дает наглядный пример того, как может сохраниться структура соотношений теории, даже если интерпретация символов в них изменилась.
Один из наиболее важных результатов теории Ньютона состоит в том, что в отсутствие сил импульс сохраняется. Этот результат остается справедливым и в релятивистской теории. В отсутствие сил изменение количества движения  равно нулю и, следовательно, релятивистский импульс остается постоянным. Таким же образом можно показать, что релятивистский импульс сохраняется и при столкновениях частиц,
равно нулю и, следовательно, релятивистский импульс остается постоянным. Таким же образом можно показать, что релятивистский импульс сохраняется и при столкновениях частиц,
если выполняется (в смысле, указанном выше) третий закон Ньютона (действие равно противодействию). Следовательно, и в релятивистской теории мы можем определить центр масс системы и доказать теорему, что в отсутствие внешних сил этот центр масс движется с постоянной скоростью, и т. д.
При изучении теории Ньютона мы видели, что изменение импульса, или «движущая сила» в терминах средневековой механики, связано с силой, действующей в течение заданного отрезка времени. Мы ввели понятия работы и энергии как величин, связанных с силой, действующей вдоль определенного расстояния, и нам удалось так определить кинетическую энергию, что работа, совершенная над частицей, оказалась равной изменению ее кинетической энергии. Мы можем снова ввести понятие силы, действующей вдоль определенного расстояния, и, как и раньше, определить работу. Если над релятивистской частицей совершается работа, то существует некая величина, которая при этом изменяется. Эта величина связана с энергией из механики Ньютона, или с «живой силой» из средневековой механики. Мы снова будем называть ее кинетической энергией. Однако зависимость энергии от скорости имеет теперь иной вид, чем в нерелятивистском случае, так как связь между импульсом и скоростью изменилась. В нерелятивистском случае

так как

Если на частицу не действуют силы, ее кинетическая энергия равна полной энергии частицы:

В релятивистском же случае мы получаем следующее выражение

которое можно переписать в виде

Иными словами, если на заданном пути на релятивистскую частицу действует сила, то изменяется величина

При малом значении импульса выражение (31.8) приближенно записывается в виде

Таким образом, релятивистская энергия свободной частицы при малых скоростях равна  (что совпадает с выражением для кинетической энергии в нерелятивистском случае) плюс дополнительный член
(что совпадает с выражением для кинетической энергии в нерелятивистском случае) плюс дополнительный член  являющийся постоянной величиной. Если импульс частицы равен
являющийся постоянной величиной. Если импульс частицы равен

Эта формула, безусловно, является самой знаменитой формулой физики
В 1905 г. вскоре после выхода своей первой работы Эйнштейн опубликовал вторую статью, озаглавленную «Зависит ли инерция тела от содержащейся в нем энергии?» В ней он проанализировал процесс излучения телом света. В заключение Эйнштейн писал:
«Если тело отдает энергию Е 2) в виде излучения, то его масса уменьшается на  При этом, очевидно, несущественно, что энергия, взятая у тела, прямо переходит в лучистую энергию излучения, так что мы приходим к более общему выводу. Масса тела есть мера содержащейся в нем энергии; если энергия изменяется на величину
При этом, очевидно, несущественно, что энергия, взятая у тела, прямо переходит в лучистую энергию излучения, так что мы приходим к более общему выводу. Масса тела есть мера содержащейся в нем энергии; если энергия изменяется на величину  , то масса меняется соответственно на величину
, то масса меняется соответственно на величину  причем здесь энергия измеряется в эргах, а масса — в граммах» [1].
причем здесь энергия измеряется в эргах, а масса — в граммах» [1].
Далее он пророчески заключил:
«Не исключена возможность того, что теорию удастся проверить для веществ, энергия которых меняется в большой степени (например, для солей радия)» [2].
В области малых скоростей в релятивистском выражении для энергии появляется дополнительный постоянный член  связанный с массой покоя частицы. Мы можем рассматривать эту дополнительную энергию как своего рода потенциальную энергию, обусловленную наличием у частицы массы покоя. Если эту энергию можно как обычную потенциальную энергию превратить в кинетическую энергию, то ее можно превратить и в работу. Если же нет, то максимальная работа, которую способно совершить тело, равна величине
связанный с массой покоя частицы. Мы можем рассматривать эту дополнительную энергию как своего рода потенциальную энергию, обусловленную наличием у частицы массы покоя. Если эту энергию можно как обычную потенциальную энергию превратить в кинетическую энергию, то ее можно превратить и в работу. Если же нет, то максимальная работа, которую способно совершить тело, равна величине

которую можно назвать релятивистской кинетической энергией. Используя (31.9), получаем, что

Если массу тела удалось бы как-нибудь уменьшить, мы тем самым превратили бы ее в энергию и работу. Такое превращение возможно далеко не во всех случаях; ведь и тепло не всегда удается превратить в работу. Однако в некоторых случаях, например в упомянутом Эйнштейном случае солей радия (теперь же нам известно много и других случаев), масса действительно превращается в энергию. Возможность такого превращения объединила два казавшихся самостоятельными понятия, а именно понятия массы и энергии. Теперь уже нельзя утверждать, что масса и энергия сохраняются независимо друг от друга. Поэтому мы еще шире обобщаем понятие энергии, объединяя его с понятием массы. Энергия сохраняется, если она включает в себя массу покоя системы  Вещество тем не менее не всегда переходит в форму энергии. В нёкоторых случаях оно переходит, а в других нет. Правила, которым подчиняются эти превращения, составляют предмет активно развивающейся области современной физики.
Вещество тем не менее не всегда переходит в форму энергии. В нёкоторых случаях оно переходит, а в других нет. Правила, которым подчиняются эти превращения, составляют предмет активно развивающейся области современной физики.
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
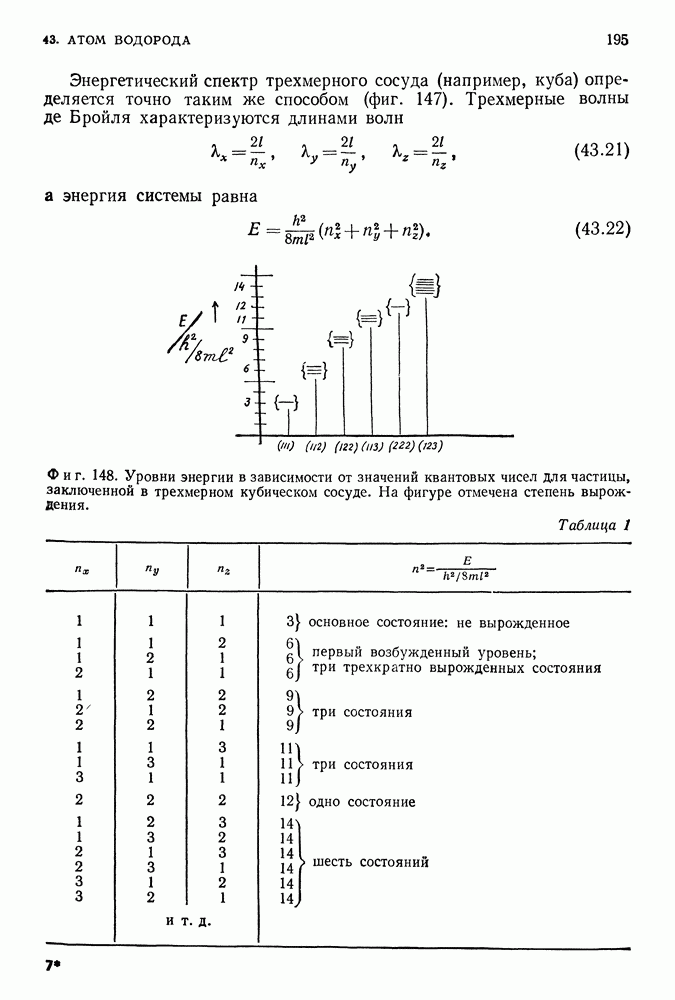
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
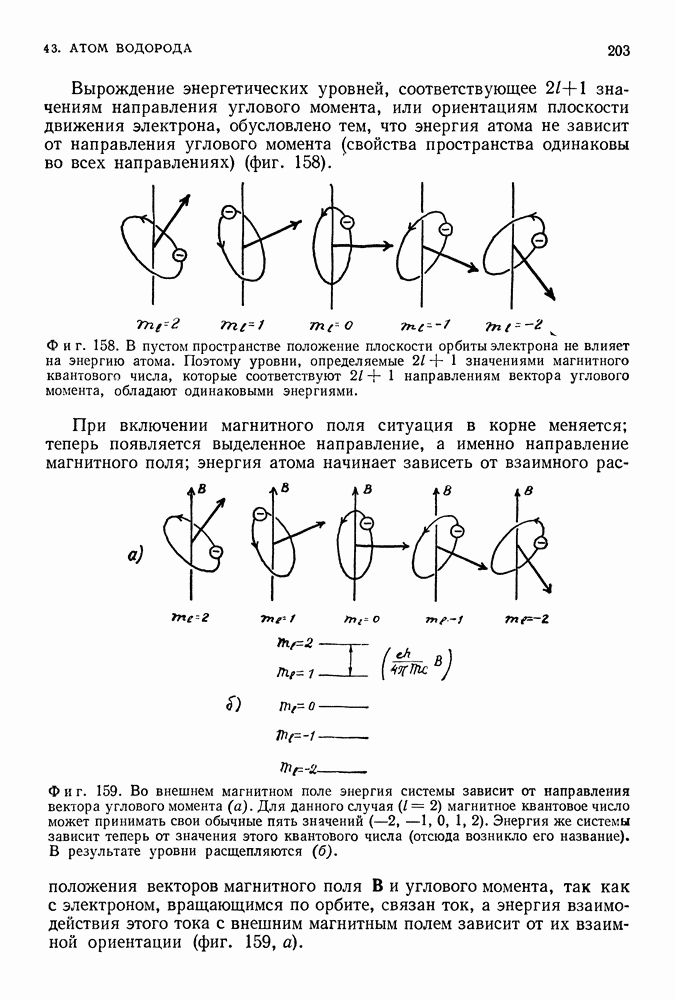
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
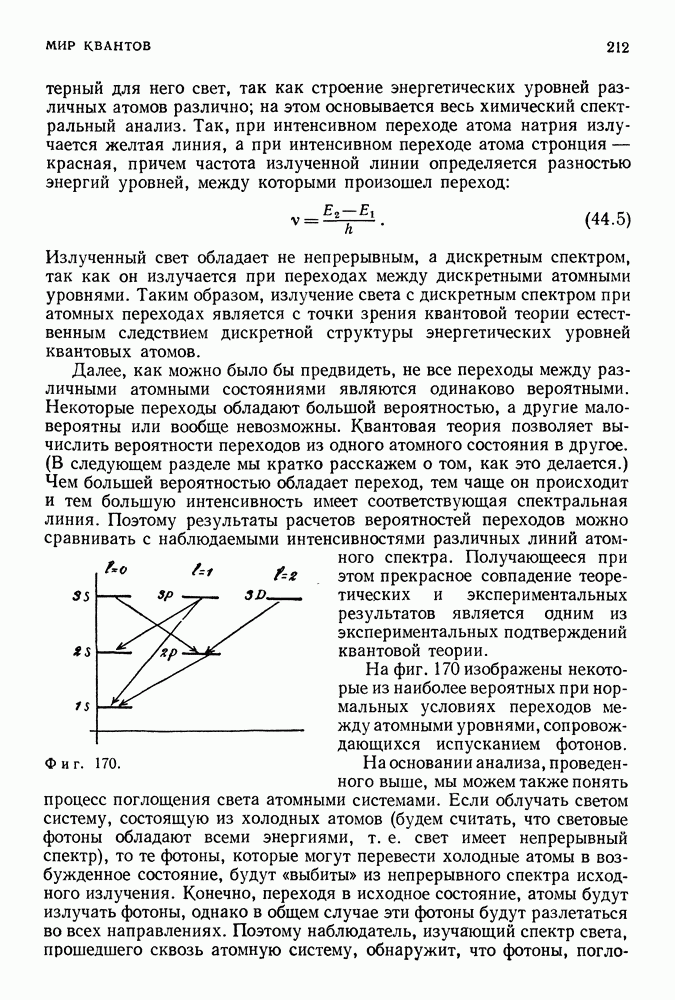
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
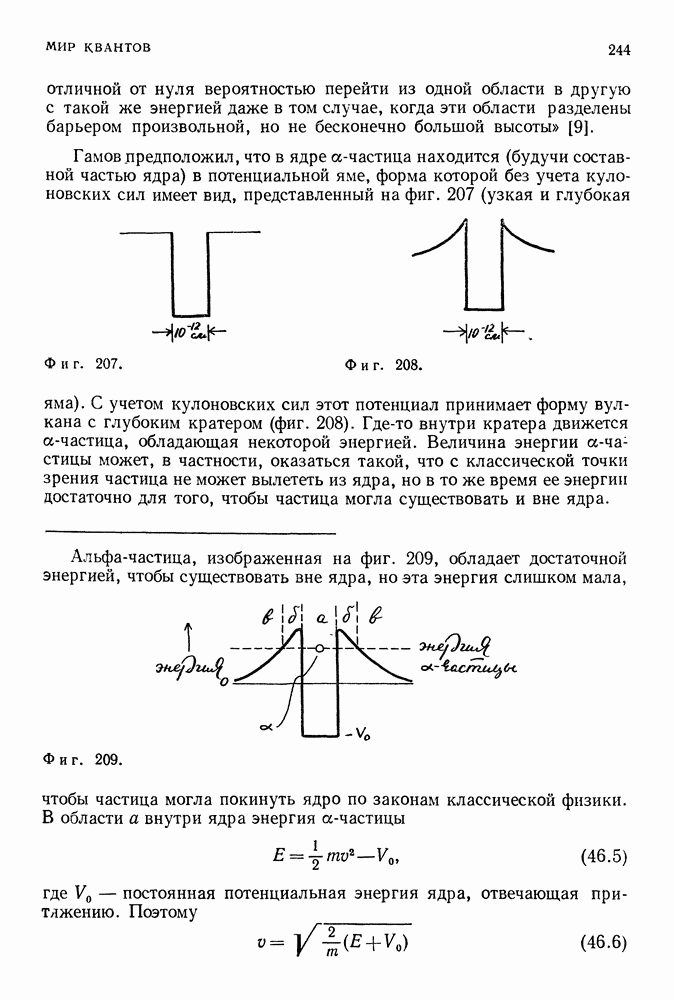
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
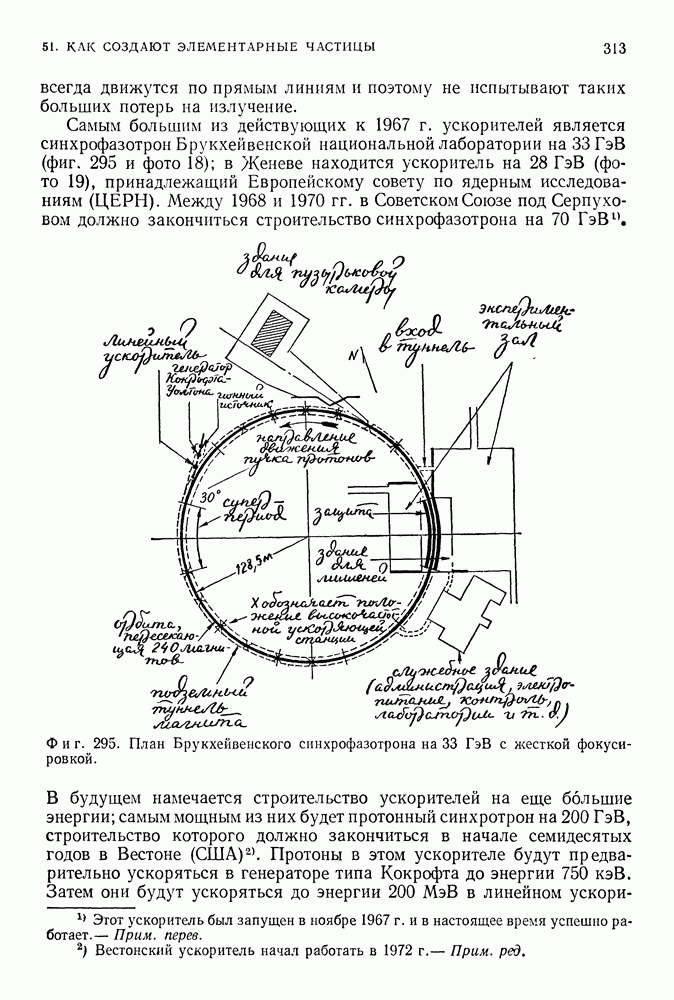
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА