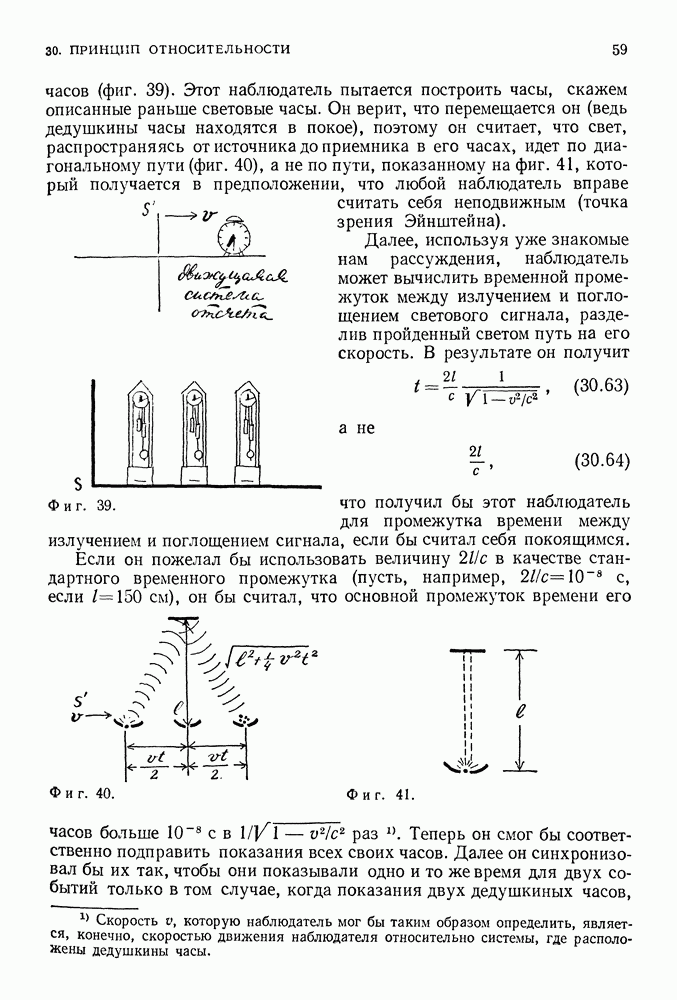
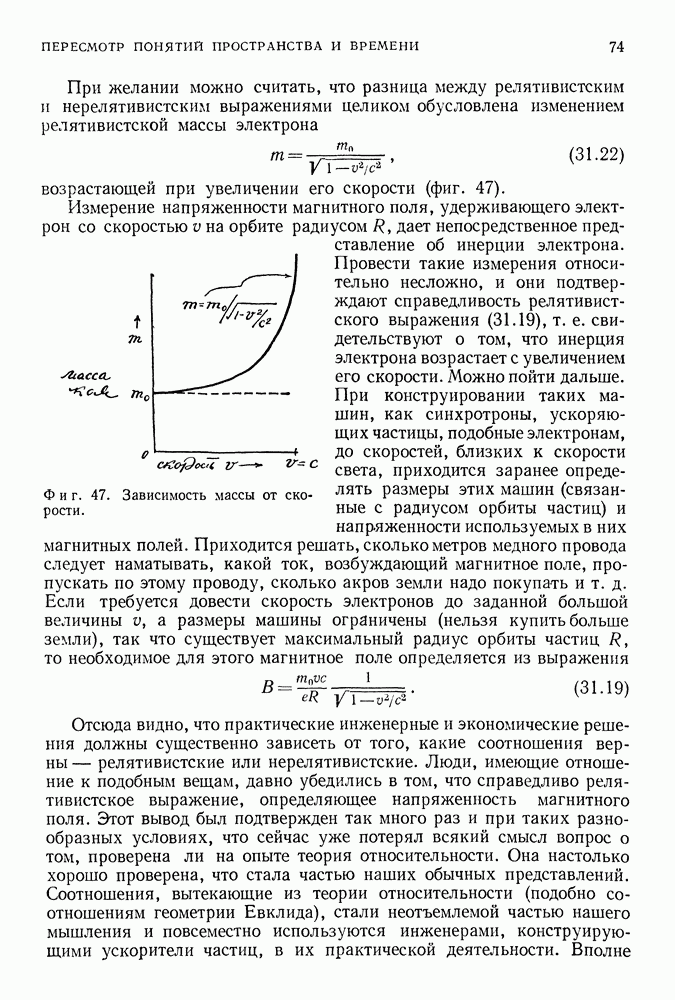
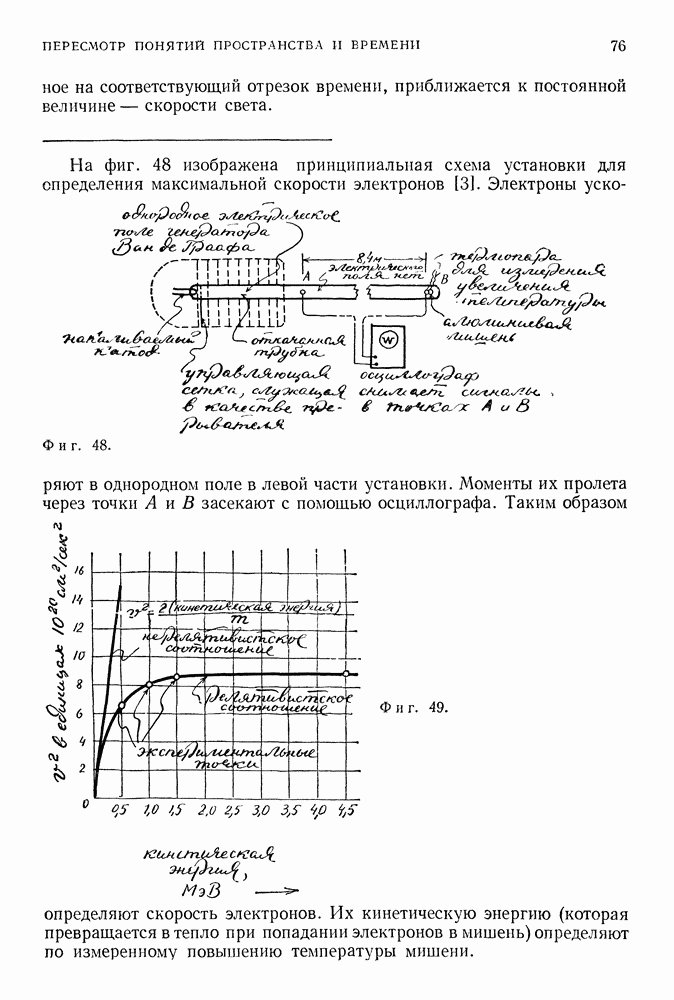
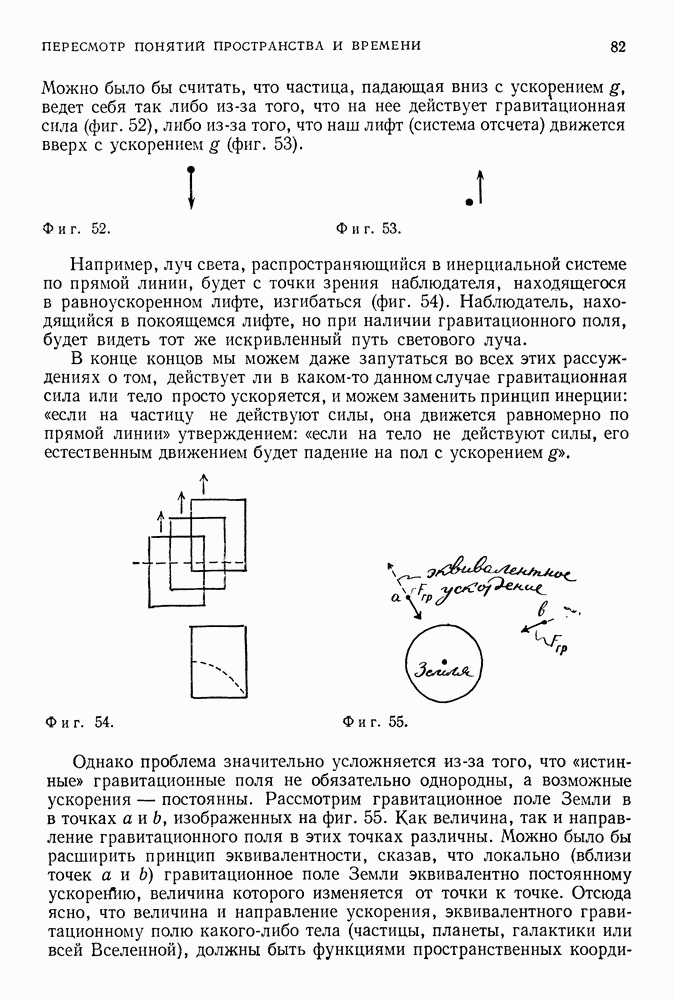
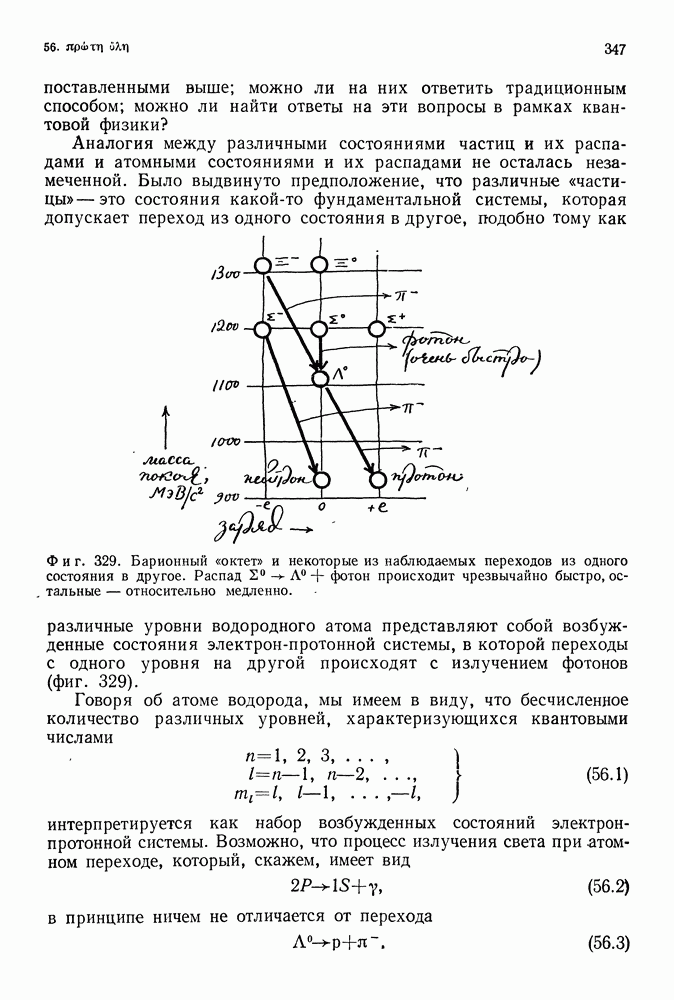
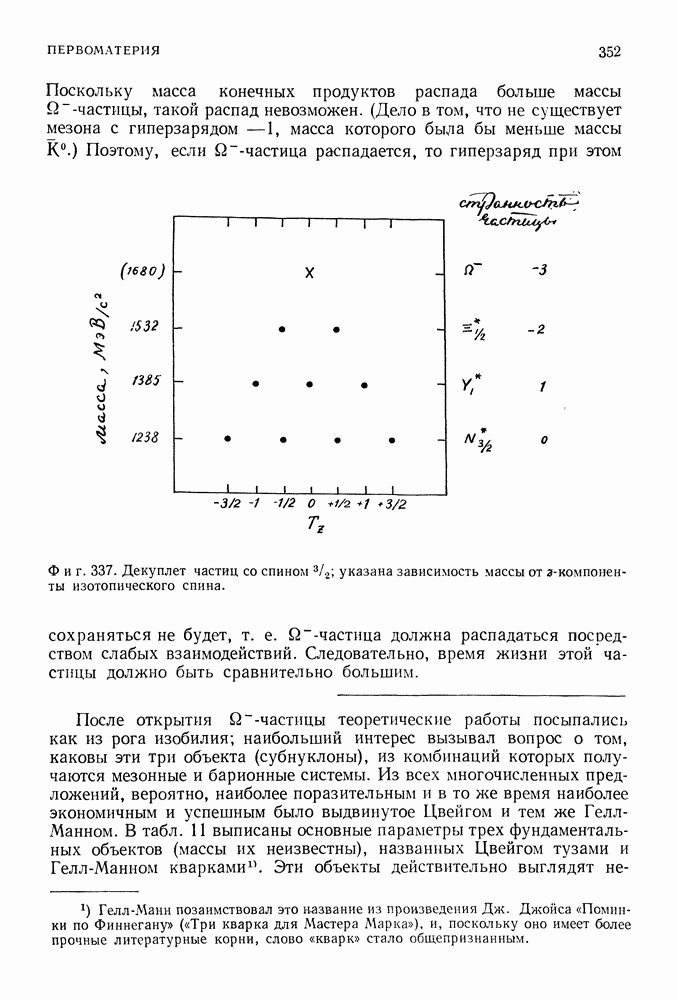
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СВЯЗАННЫЕ РЕШЕНИЯ
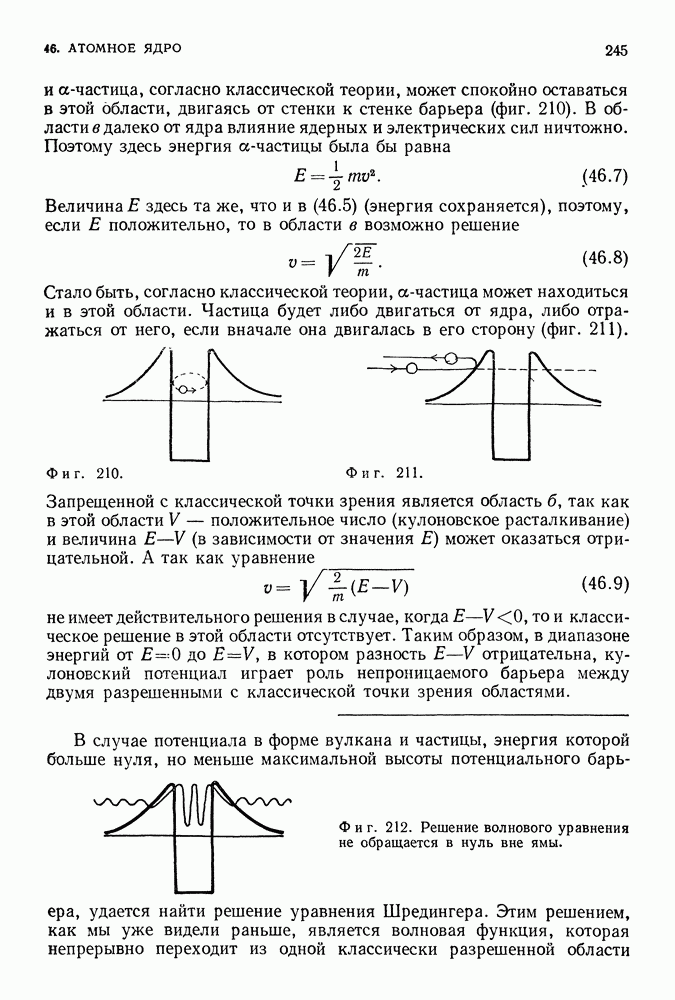
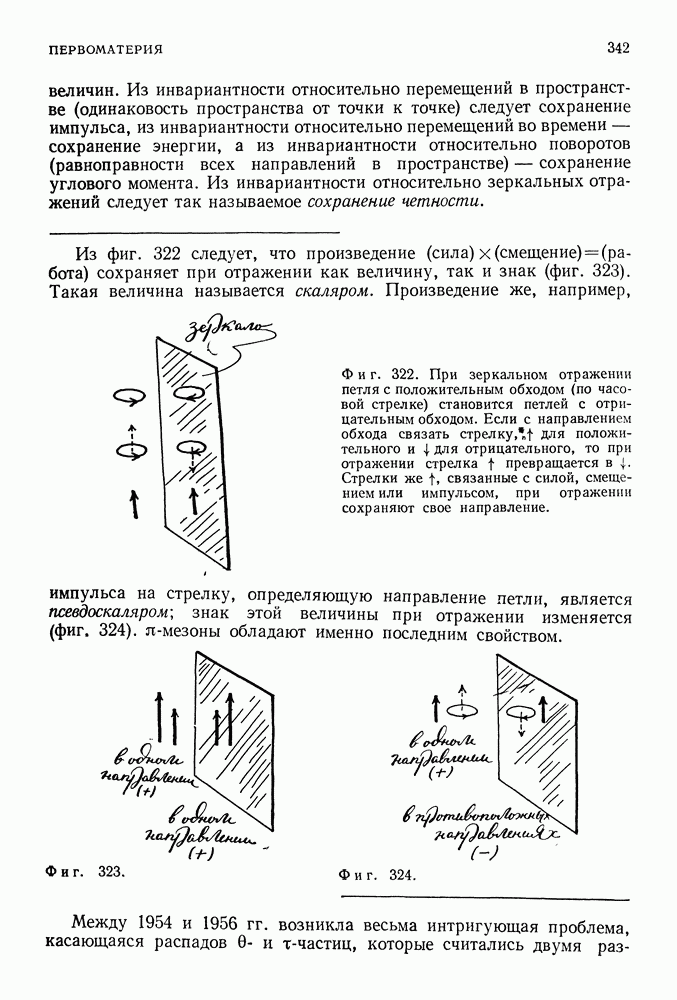
В случае свободной системы уравнение Шредингера (как и второй закон классической механики) имеет решение для любой энергии, т. е. частица в этом случае может двигаться с произвольной скоростью. В случае же связанной системы, когда движение частицы ограничено определенной областью пространства, проявляется характерная черта квантовой механики, отличающая ее от классической механики. Как правило, для связанной системы оказываются возможными не любые уровни энергии. Причина этого тесно связана с тем объяснением, которое ранее дал де Бройль: чтобы орбита была устойчивой, на ее длине должно укладываться целое число волн.
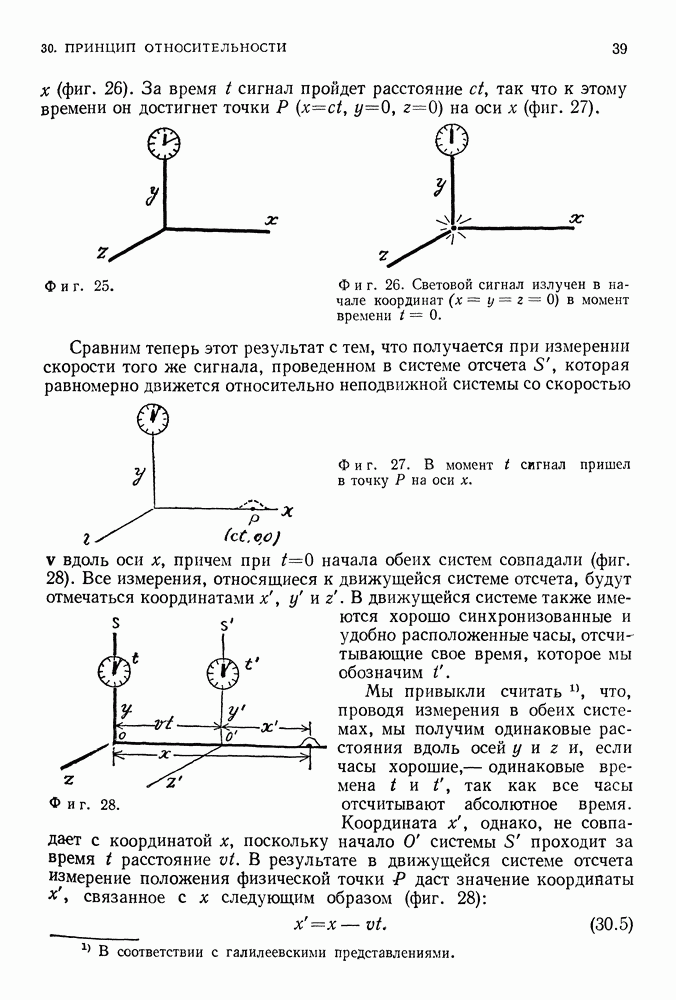
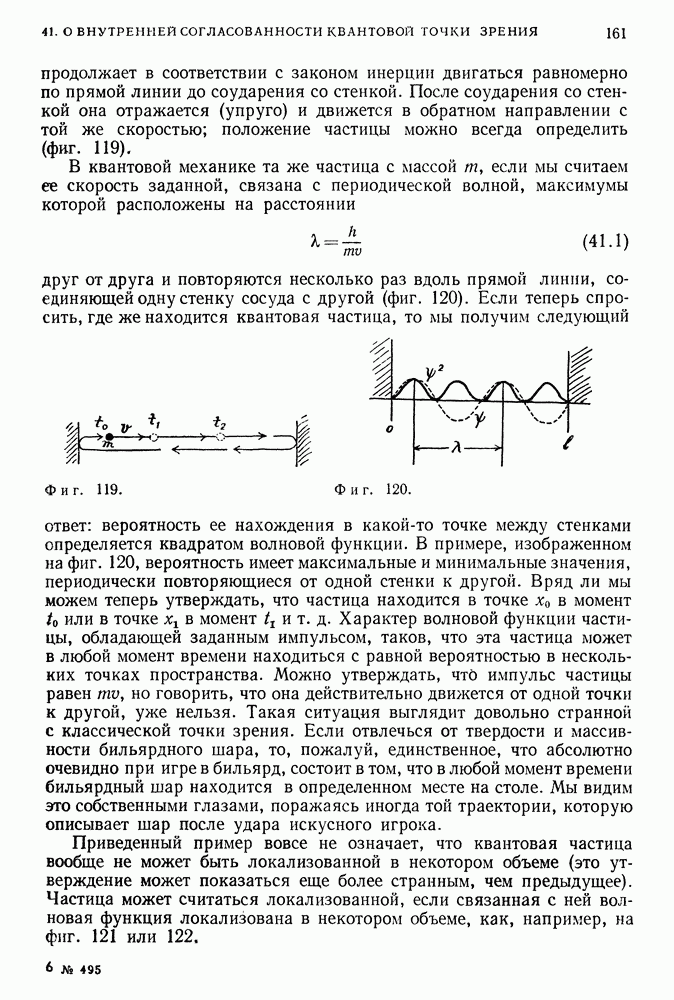
Мы иллюстрировали это раньше на примере воровских орбит. Теперь мы рассмотрим это свойство более подробно для случая (очень характерного для квантовой физики), когда частица при движении в одном измерении «захвачена» сосудом, стенки которого не позволяют ей выйти наружу. Частица с массой  движется вдоль прямой линии между двумя стенками, расположенными на расстоянии
движется вдоль прямой линии между двумя стенками, расположенными на расстоянии  друг от друга.
друг от друга.

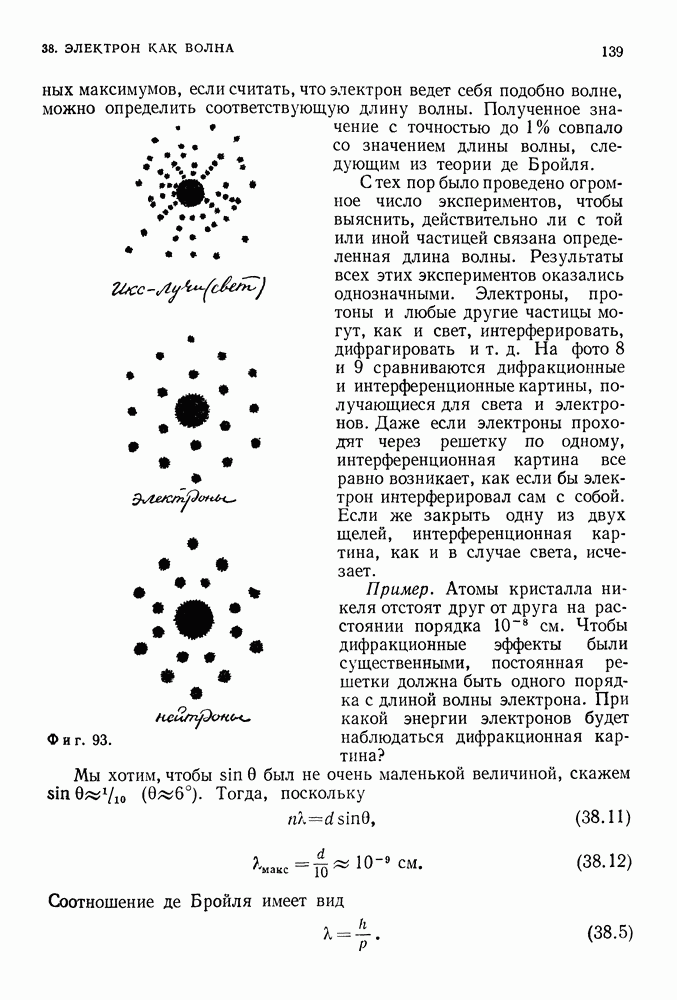
Фиг. 97.
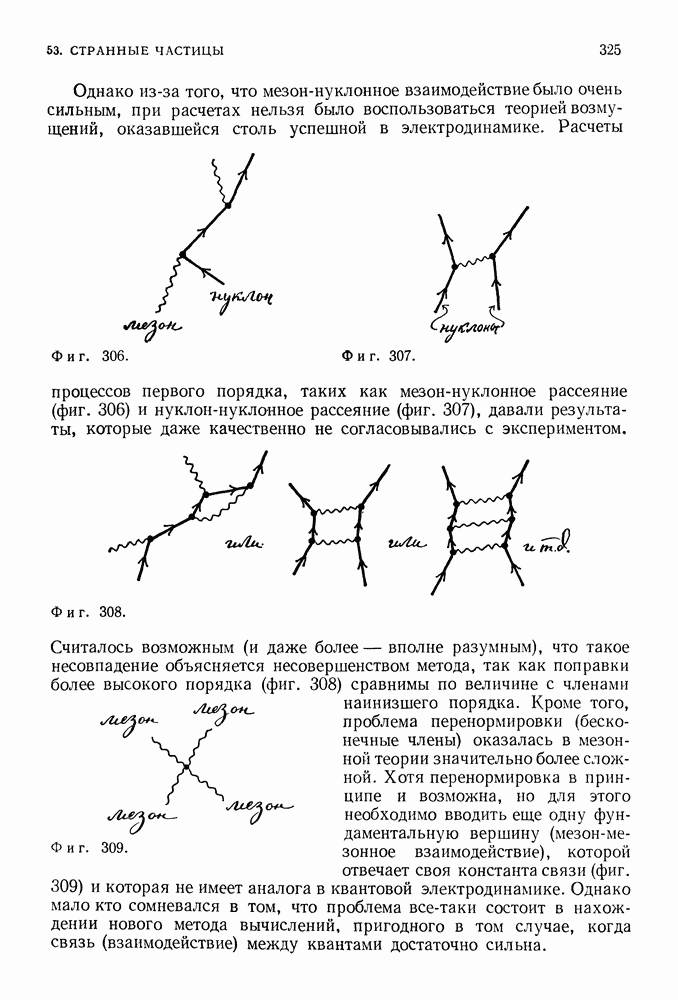
С точки зрения теории Ньютона ситуация крайне проста. Частица может двигаться с любой скоростью; она ударяется о стенку, отскакивает от нее, ударяется о другую стенку и т. д. (фиг. 97), Энергия частицы связана с ее импульсом формулой (39.2)

(Можно, например, вычислить величину импульса, передаваемого частице вблизи стенки, как это делалось при анализе модели газа в кинетической теории.) Ничто не ограничивает величину энергии, которая с ростом скорости возрастает от нуля, когда скорость равна нулю, до любого большого числа (фиг. 98) при условии, конечно, что скорость не настолько велика, чтобы частица или стенка разрушились при столкновении.

Фиг. 98. В теории Ньютона энергия пропорциональна квадрату скорости; при увеличении скорости частицы энергия непрерывно изменяется от нуля до сколь угодно больших значений.
С точки зрения квантовой физики та же ситуация выглядит по-иному. В качестве решений уравнения Шредингера возможны лишь такие, в которых стоячая волна де Бройля укладывается целое число раз между двумя стенками сосуда. Условие, что стенки удерживают частицу, на языке уравнения Шредингера равнозначно требованию, чтобы амплитуда волны на стенках равнялась нулю. (Это соответствует условию упругого отражения в теории Ньютона.) На фиг. 99 представлены четыре возможных решения уравнения Шредингера (стоячие волны) для данного случая.
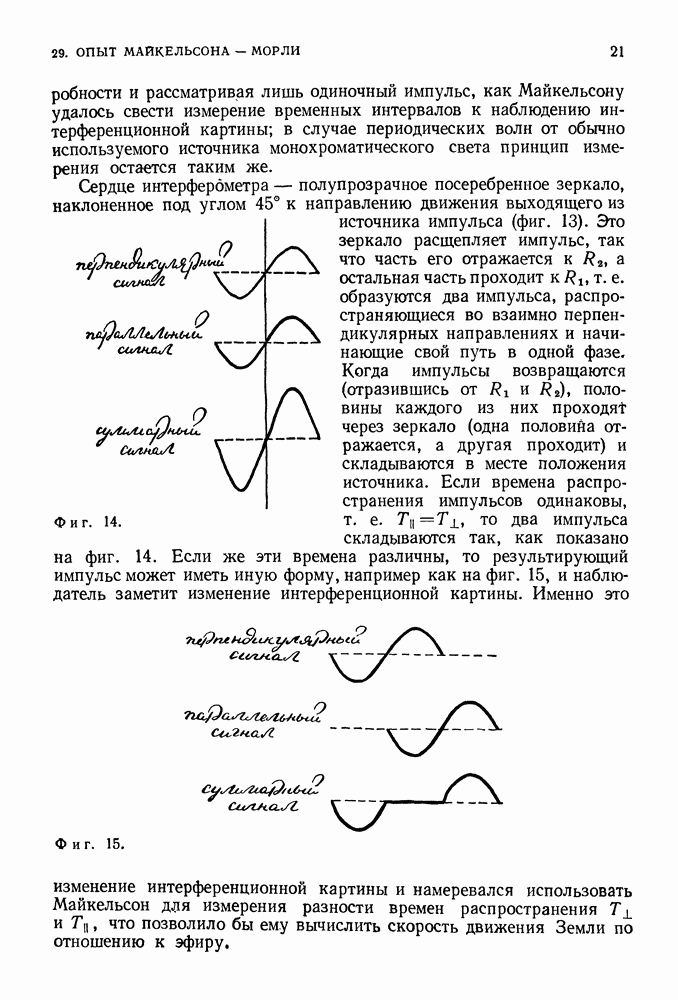
Отличительная особенность этих решений уравнения Шредингера состоит в том, что в данном случае разрешенными являются только определенные длины волн, а именно волны, длины которых непосредственно связаны с размерами сосуда (шириной  подобно тому
подобно тому
как в случае боровских орбит разрешенные длины волн были непосредственно связаны с размером орбиты.

Фиг. 99. Первые четыре решения (стоячие волны) уравнения Шредингера для случая, когда движение частицы ограничено линией длины  Первая волна имеет один максимум, вторая — два и т. д. Возможны решения с произвольным числом максимумов. Из условия, что стенки являются непроницаемыми, следует, что волновая функция должна обращаться в нуль при
Первая волна имеет один максимум, вторая — два и т. д. Возможны решения с произвольным числом максимумов. Из условия, что стенки являются непроницаемыми, следует, что волновая функция должна обращаться в нуль при 
Чтобы стоячие волны могли существовать, между стенками сосуда должно укладываться целое число полуволн. Тогда наибольшая длина волны

Следующая после наибольшей длина волны

В общем случае

Точный вид условия, налагаемого на длину волны, не так уж существен; гораздо важнее, что только определенные длины волн являются разрешенными.
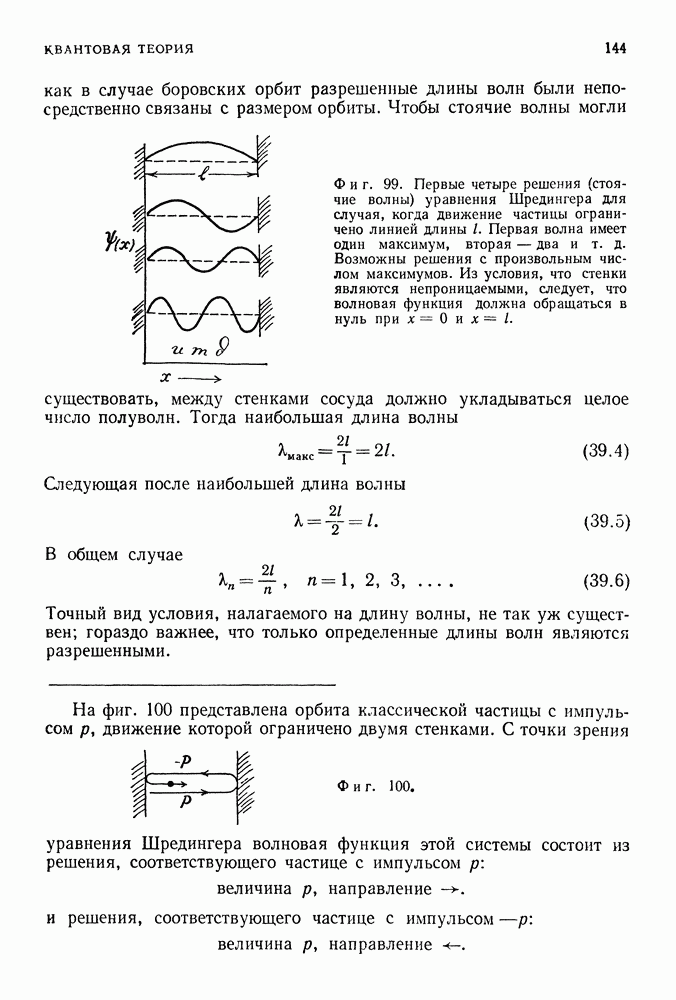
На фиг. 100 представлена орбита классической частицы с импульсом  движение которой ограничено двумя стенками.
движение которой ограничено двумя стенками.

Фиг. 100.
С точки зрения уравнения Шредингера волновая функция этой системы состоит из решения, соответствующего частице с импульсом 

и решения, соответствующего частице с импульсом 

Обе эти частицы, хотя они и движутся в противоположных направлениях, обладают одинаковыми по величине импульсами, а следовательно, и одинаковыми длинами волн де Бройля (39.3)

и одинаковыми энергиями

Согласно принципу суперпозиции, сумма этих решений тоже является решением уравнения Шредингера с той же самой энергией.

Фиг. 101.
Решение, составленное из и  и обращающееся в нуль на стенках, имеет вид
и обращающееся в нуль на стенках, имеет вид

Как уже отмечалось, величина  определяется из условия существования стоячих волн. Основное состояние системы описывается волновой функцией, изображенной на фиг. 101.
определяется из условия существования стоячих волн. Основное состояние системы описывается волновой функцией, изображенной на фиг. 101.
Поскольку длина волны связана с величиной импульса по формуле

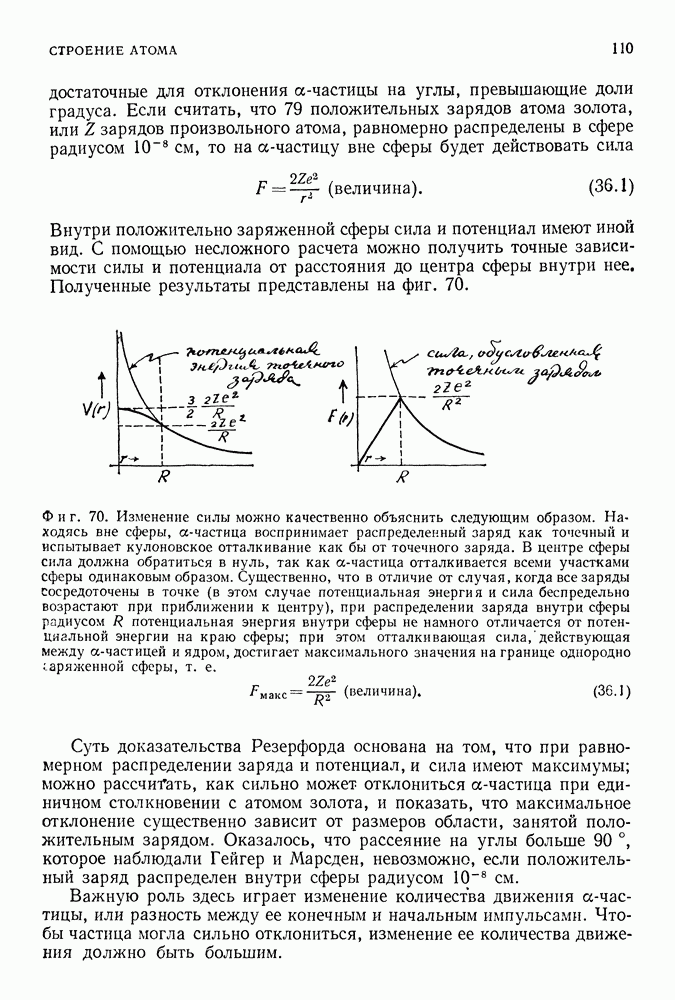
условиям, налагаемым на длину волны, будут соответствовать ограничения, определяющие возможные значения импульса частицы:

А так как импульс частицы связан с ее энергией,

возможные значения энергии данной квантовой системы тоже ограничены:

Как и раньше, здесь важен не столько точный вид формулы, как то, что не все значения энергии разрешены. Если мы теперь нарисуем Подобно тому, как это делалось выше, график зависимости энергии от импульса для квантовой системы, то увидим, что энергия снова
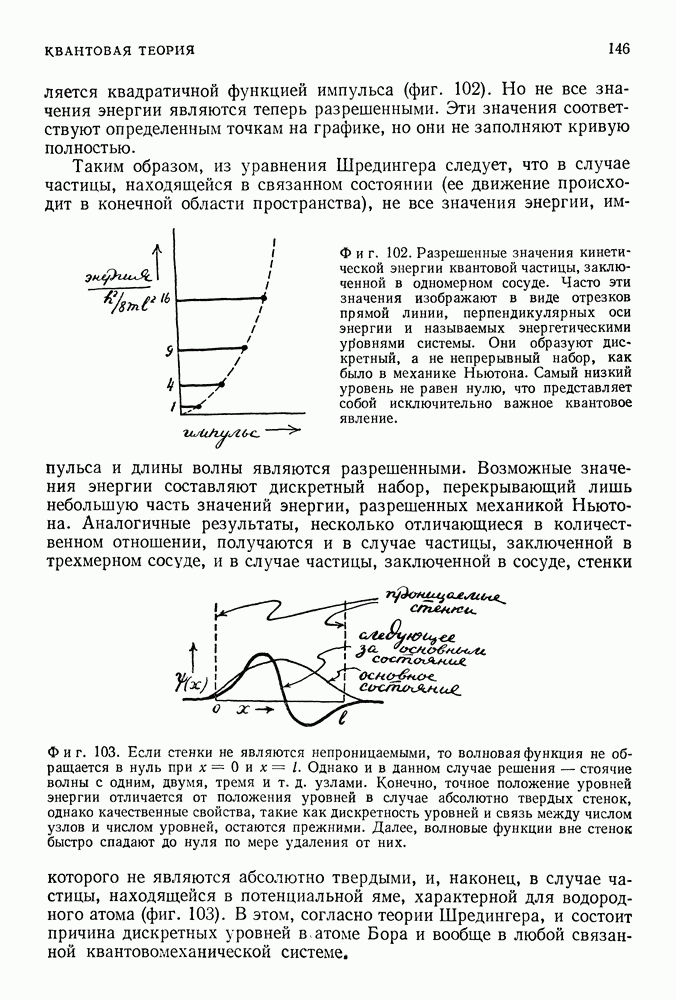
является квадратичной функцией импульса (фиг. 102). Но не все значения энергии являются теперь разрешенными. Эти значения соответствуют определенным точкам на графике, но они не заполняют кривую полностью.
Таким образом, из уравнения Шредингера следует, что в случае частицы, находящейся в связанном состоянии (ее движение происходит в конечной области пространства), не все значения энергии, импульса и длины волны являются разрешенными.

Фиг. 102. Разрешенные значения кинетической энергии квантовой частицы, заключенной в одномерном сосуде. Часто эти значения изображают в виде отрезков прямой линии, перпендикулярных оси энергии и называемых энергетическими уровнями системы. Они образуют дискретный, а не непрерывный набор, как было в механике Ньютона. Самый низкий уровень не равен нулю, что представляет собой исключительно важное квантовое явление.
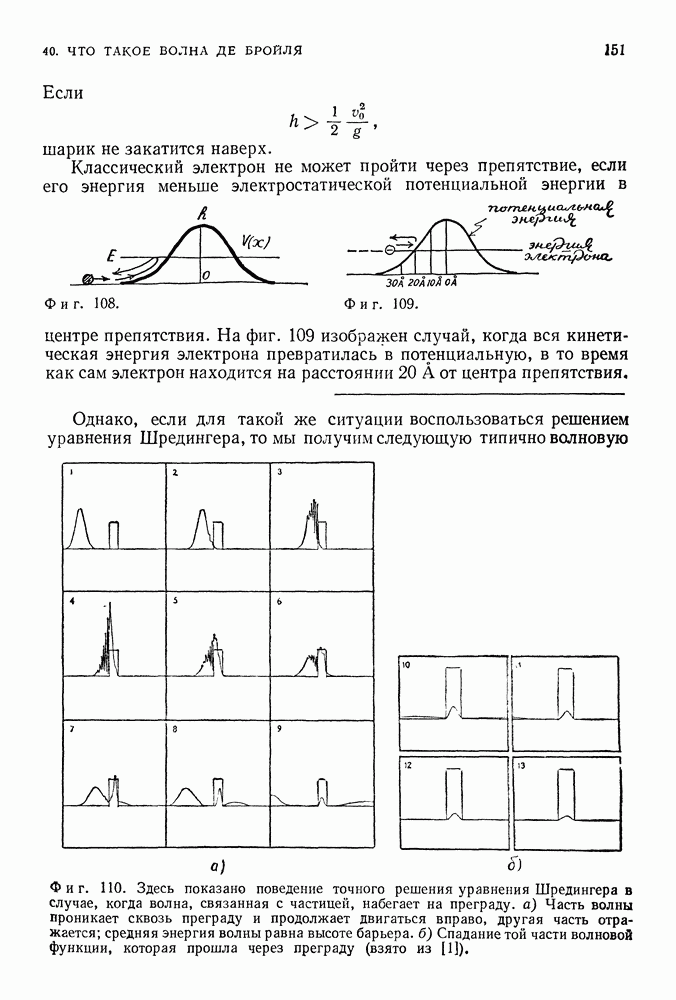
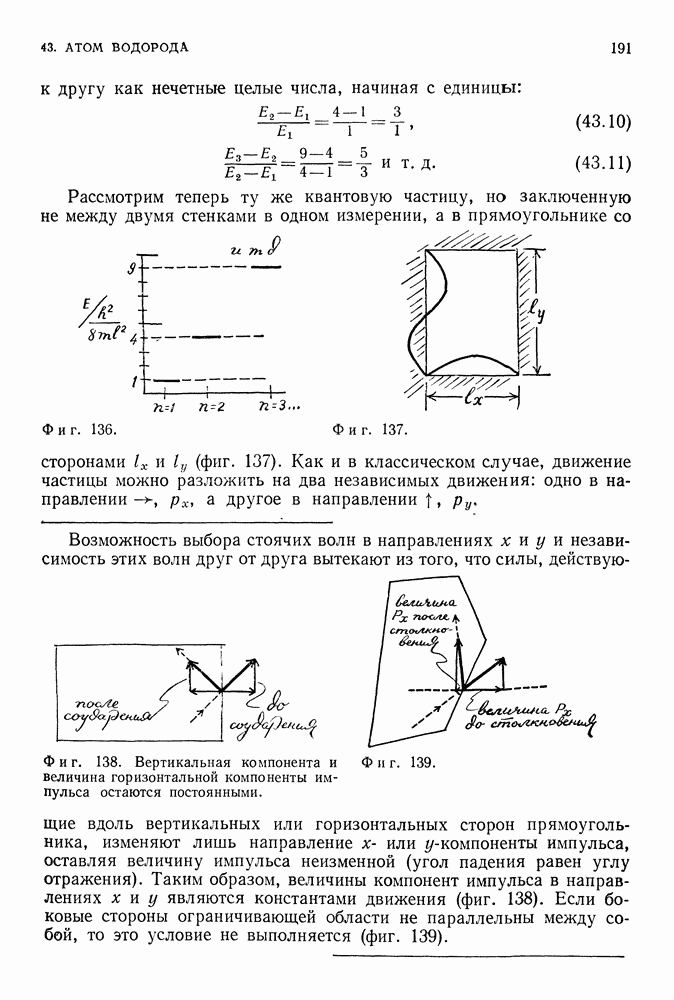
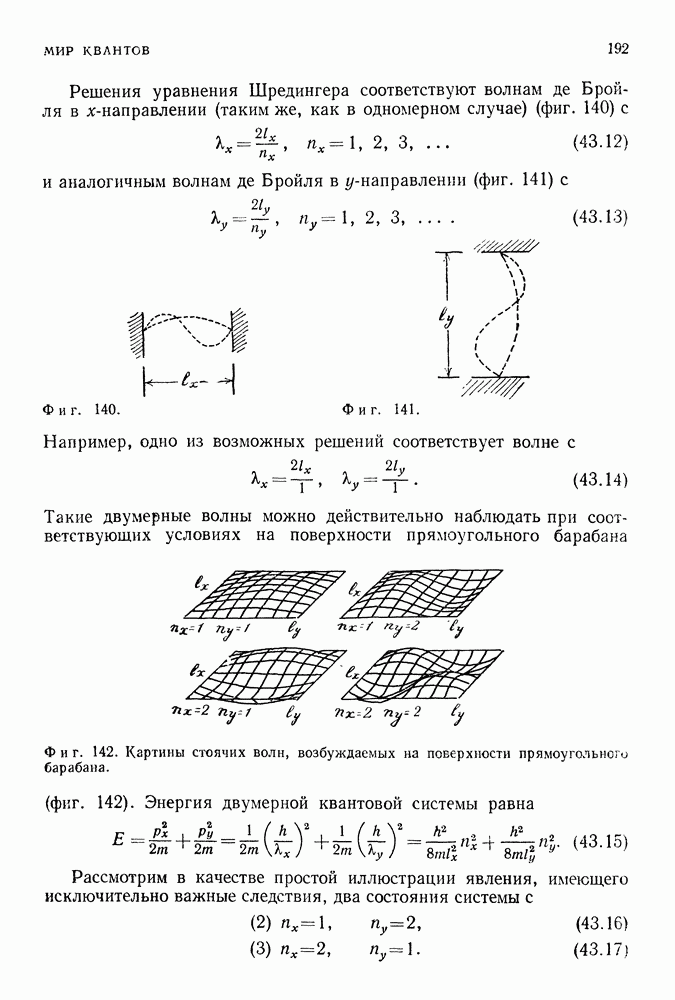
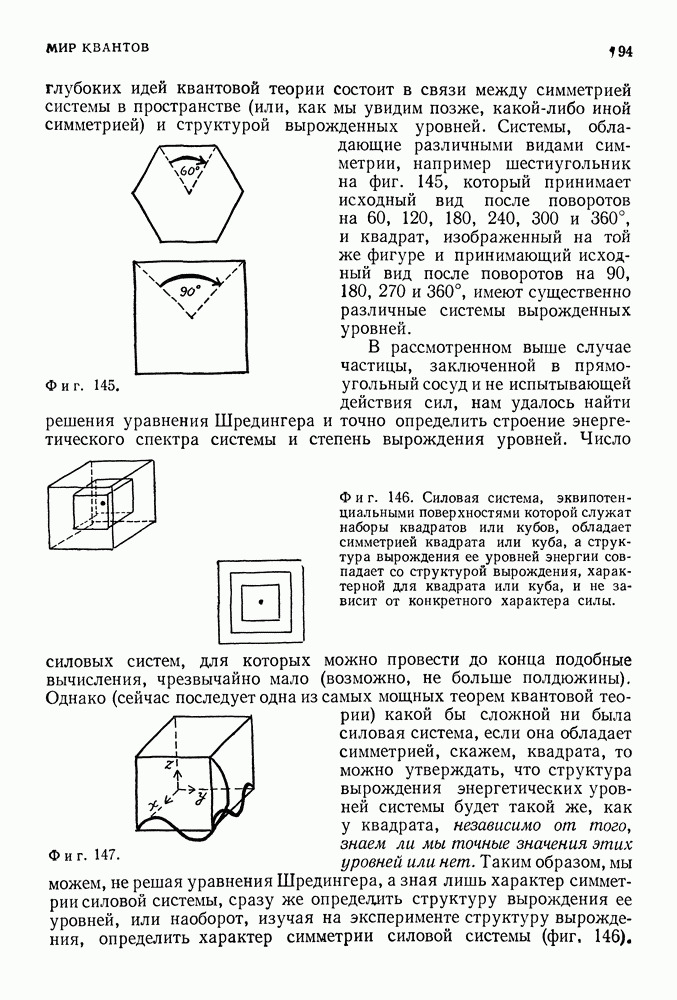
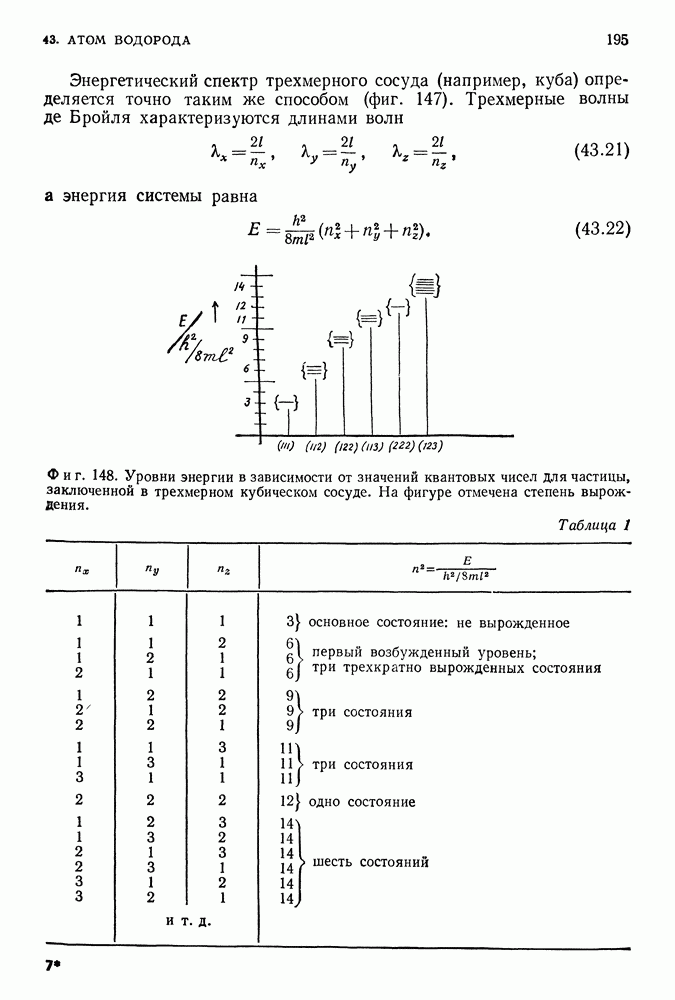
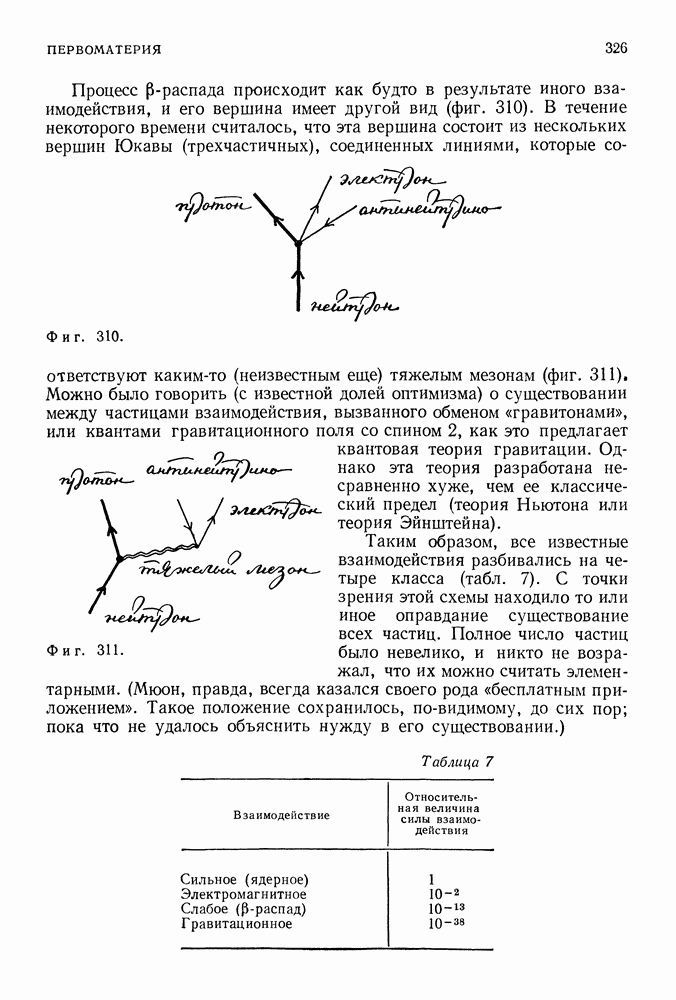
Возможные значения энергии составляют дискретный набор, перекрывающий лишь небольшую часть значений энергии, разрешенных механикой Ньютона. Аналогичные результаты, несколько отличающиеся в количественном отношении, получаются и в случае частицы, заключенной в трехмерном сосуде, и в случае частицы, заключенной в сосуде, стенки которого не являются абсолютно твердыми, и, наконец, в случае частицы, находящейся в потенциальной яме, характерной для водородного атома (фиг. 103).

Фиг. 103. Если стенки не являются непроницаемыми, то волновая функция не обращается в нуль при  Однако и в данном случае решения — стоячие волны с одним, двумя, тремя и т. д. узлами. Конечно, точное положение уровней энергии отличается от положения уровней в случае абсолютно твердых стенок, однако качественные свойства, такие как дискретность уровней и связь между числом узлов и числом уровней, остаются прежними. Далее, волновые функции вне стенок быстро спадают до нуля по мере удаления от них.
Однако и в данном случае решения — стоячие волны с одним, двумя, тремя и т. д. узлами. Конечно, точное положение уровней энергии отличается от положения уровней в случае абсолютно твердых стенок, однако качественные свойства, такие как дискретность уровней и связь между числом узлов и числом уровней, остаются прежними. Далее, волновые функции вне стенок быстро спадают до нуля по мере удаления от них.
В этом, согласно теории Шредингера, и состоит причина дискретных уровней в, атоме Бора и вообще в любой связанной квантовомеханической системе
Пример 1. Движение частицы с массой  ограничено линией, длина которой 1 см. Разрешенные энергии частицы
ограничено линией, длина которой 1 см. Разрешенные энергии частицы

Скорость частицы на наинизшем уровне равна примерно  см/с, т. е. она фактически неподвижна. Электрон же, масса которого
см/с, т. е. она фактически неподвижна. Электрон же, масса которого  и движение которого ограничено линией длиной
и движение которого ограничено линией длиной  имеет разрешенные энергии
имеет разрешенные энергии

при этом скорость электрона в основном состоянии будет порядка  см/с.
см/с.
Длина волны частицы с энергией Е и массой 

Если частица — электрон с энергией 1 эВ, то

Частица же с массой  движущаяся со скоростью 1 см/с, обладает длиной волны
движущаяся со скоростью 1 см/с, обладает длиной волны

Пример 2. Движение шарика от подшипника с массой  ограничено линией длиной 10 см. Как изменится скорость шарика при переходе его с основного квантового уровня на следующий?
ограничено линией длиной 10 см. Как изменится скорость шарика при переходе его с основного квантового уровня на следующий?

Когда  изменяется с 1 на 2,
изменяется с 1 на 2,

Заметить это изменение скорости совершенно невозможно. Следовательно, если на шарик действует сила, он будет плавно двигаться в соответствии с ньютоновскими законами, и никаких «скачков» скорости мы не обнаружим. Если же вместо шарика мы имеем электрон, движение которого ограничено атомной «линией» длиной 10 см, то

что составляет весьма ощутимую величину,
| << Предыдущий параграф | Следующий параграф >> |
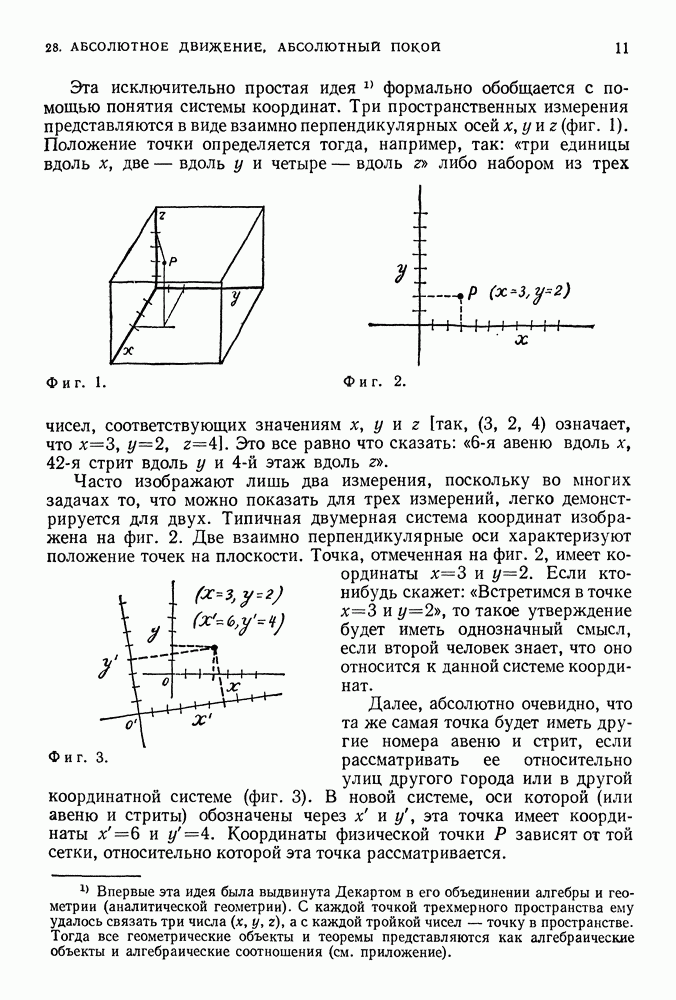
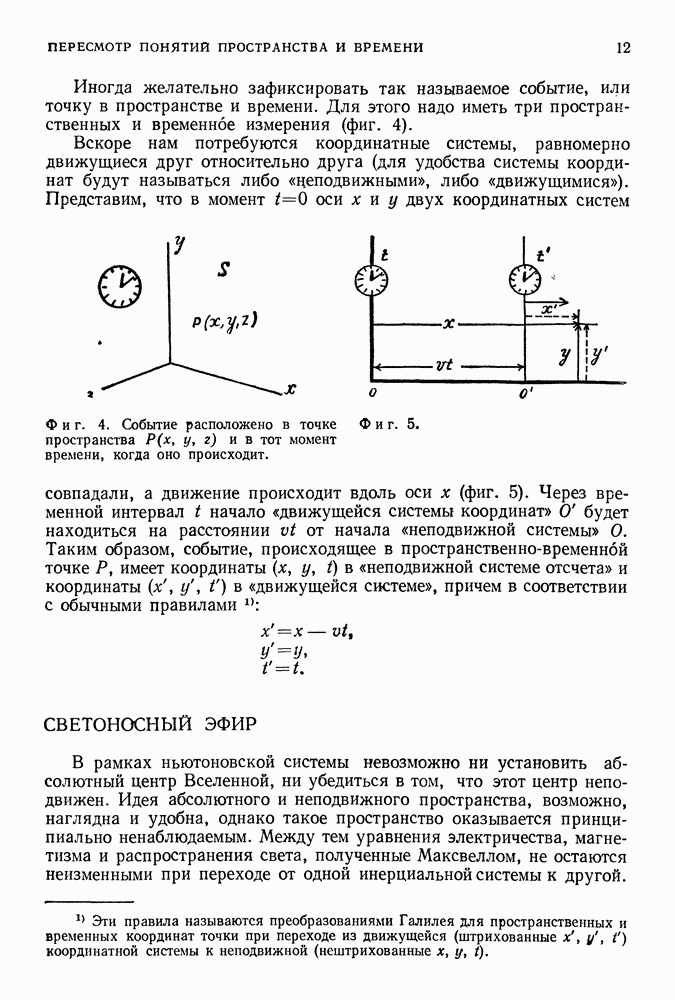
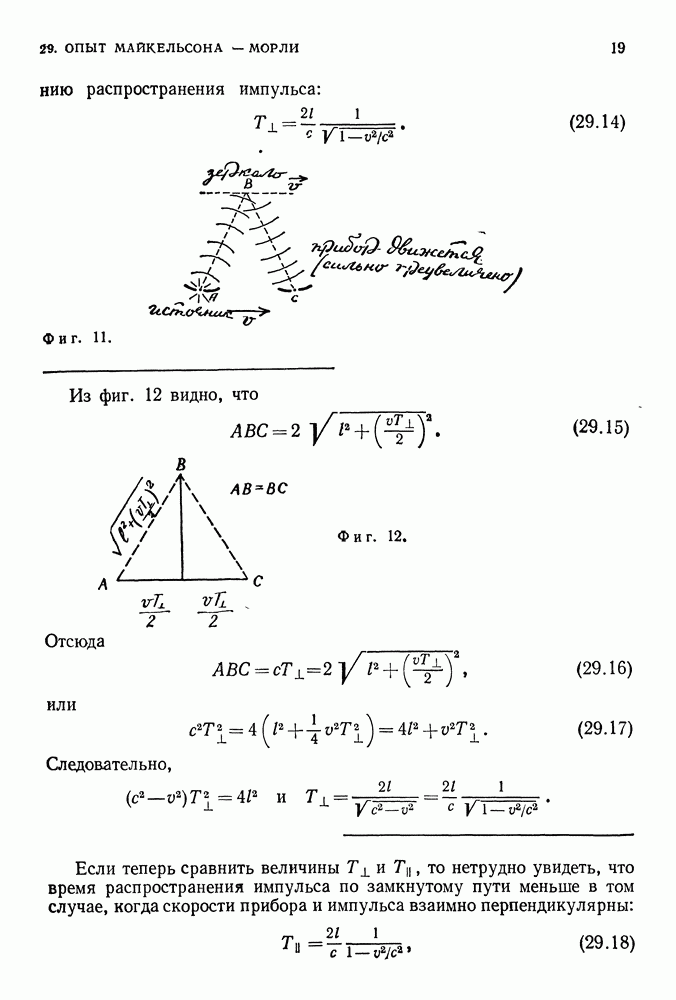
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
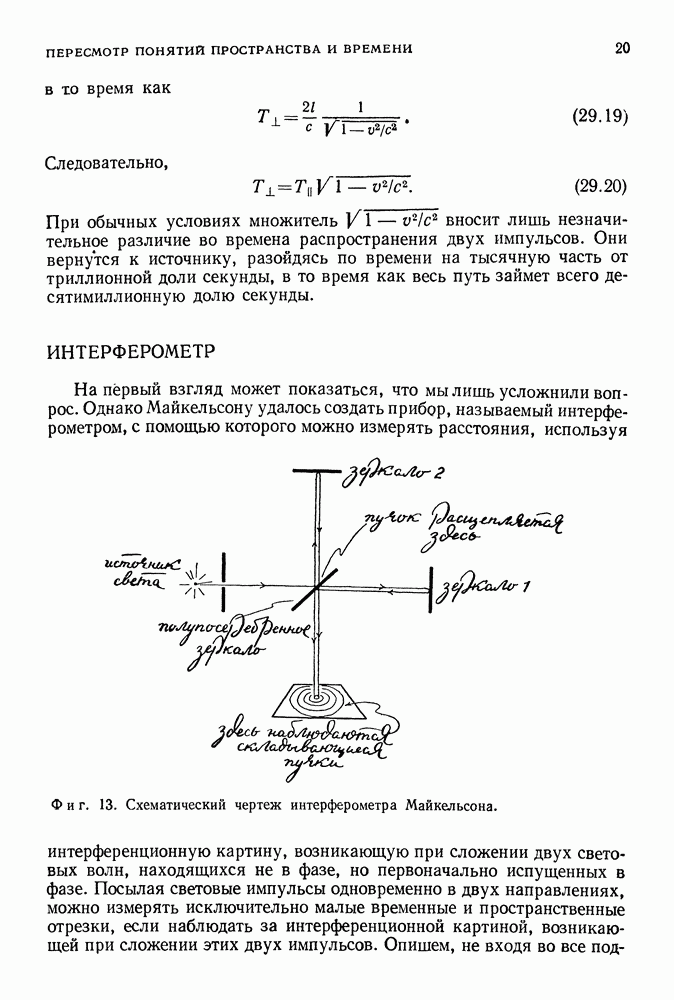
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
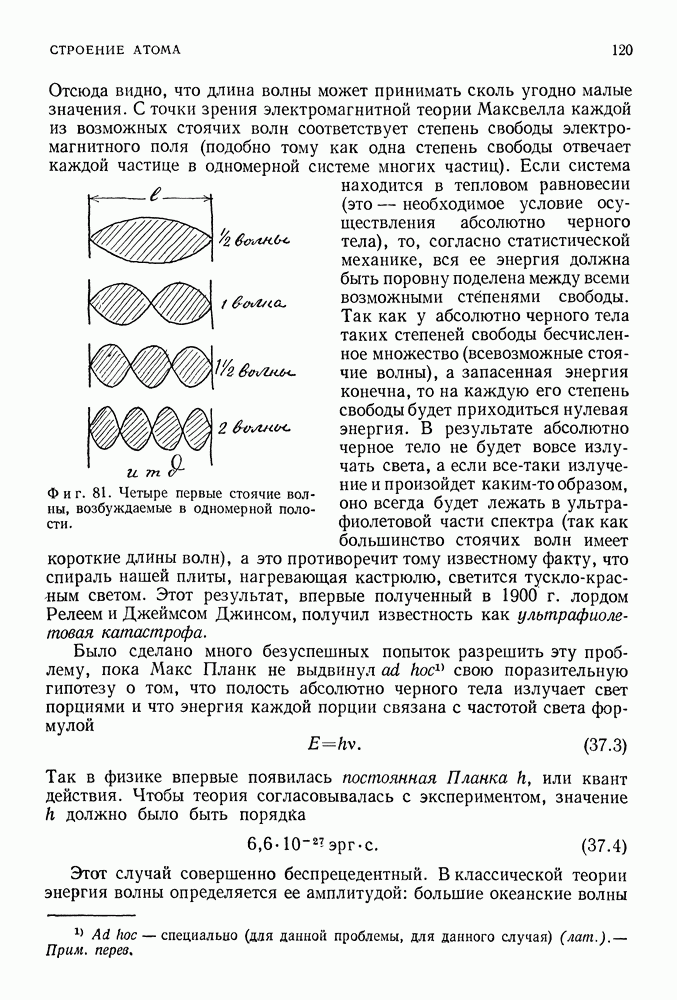
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
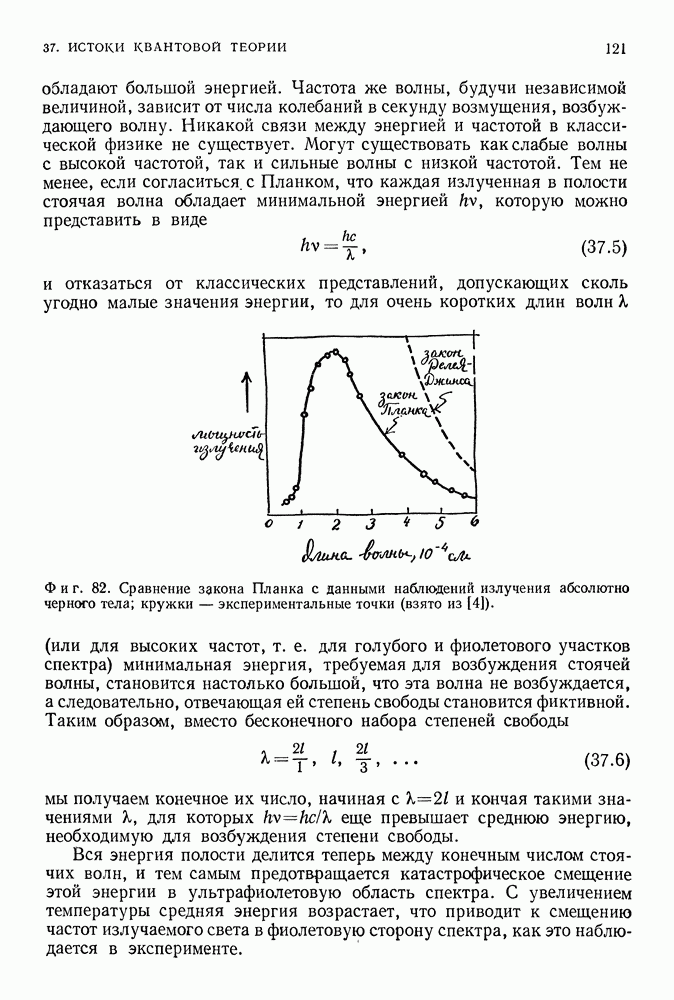
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
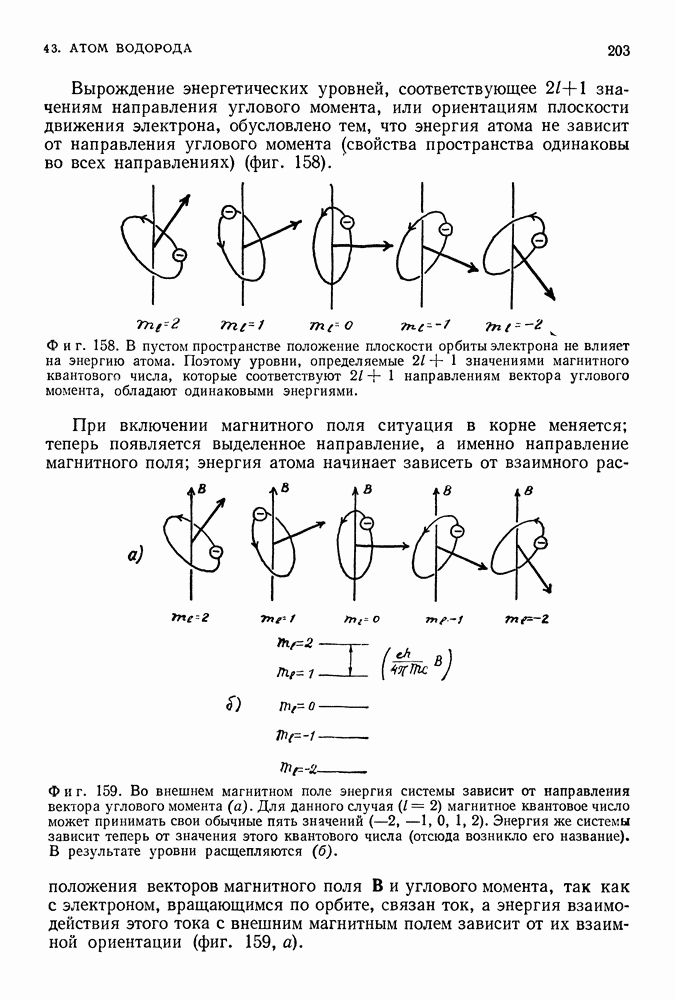
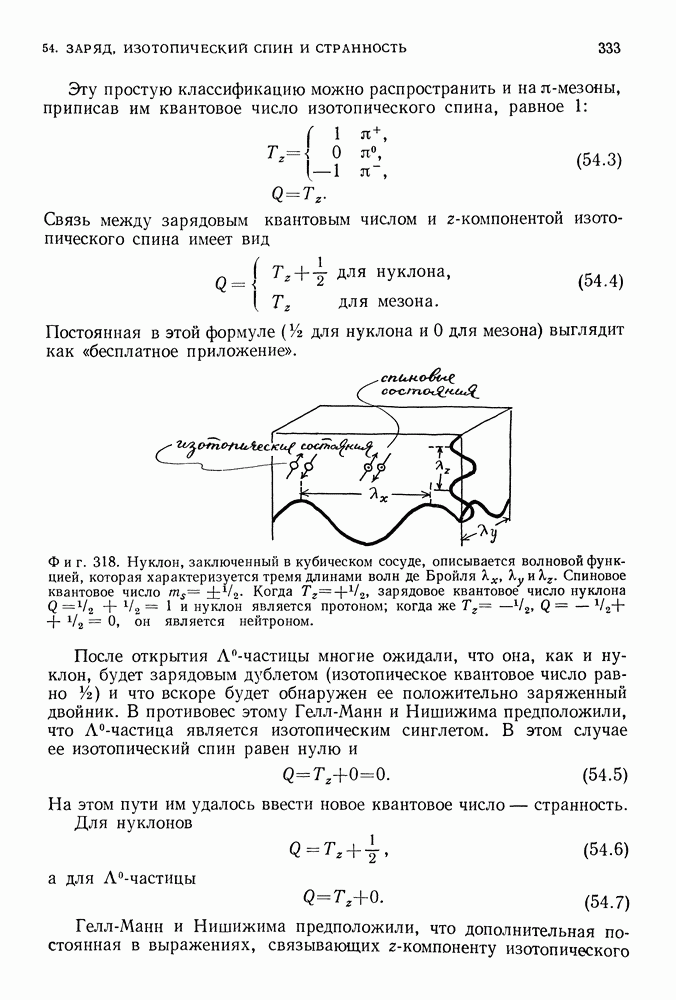
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
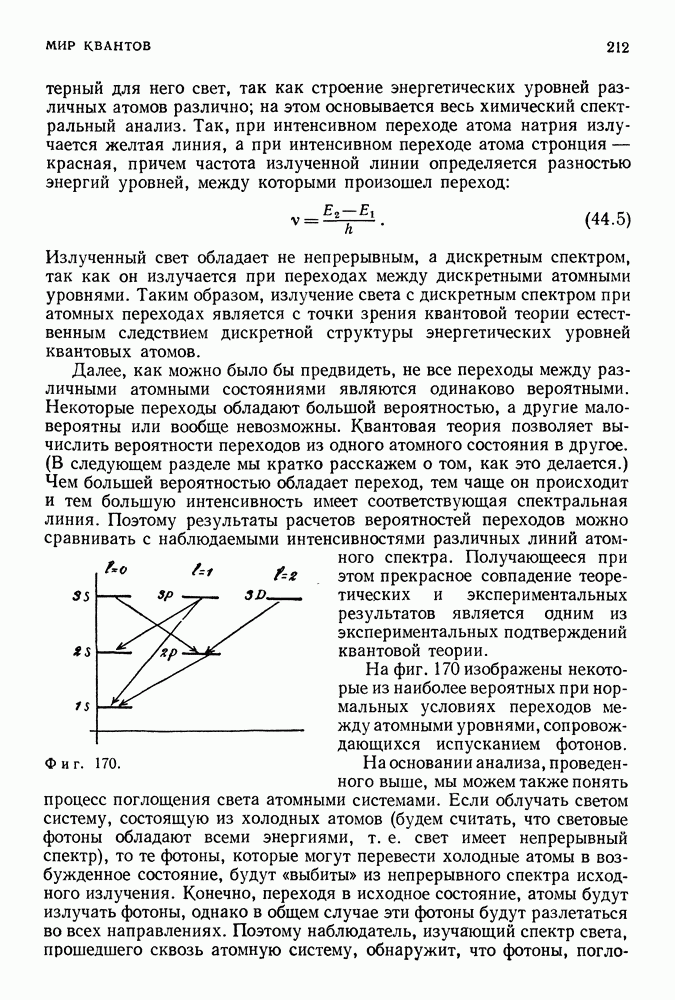
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
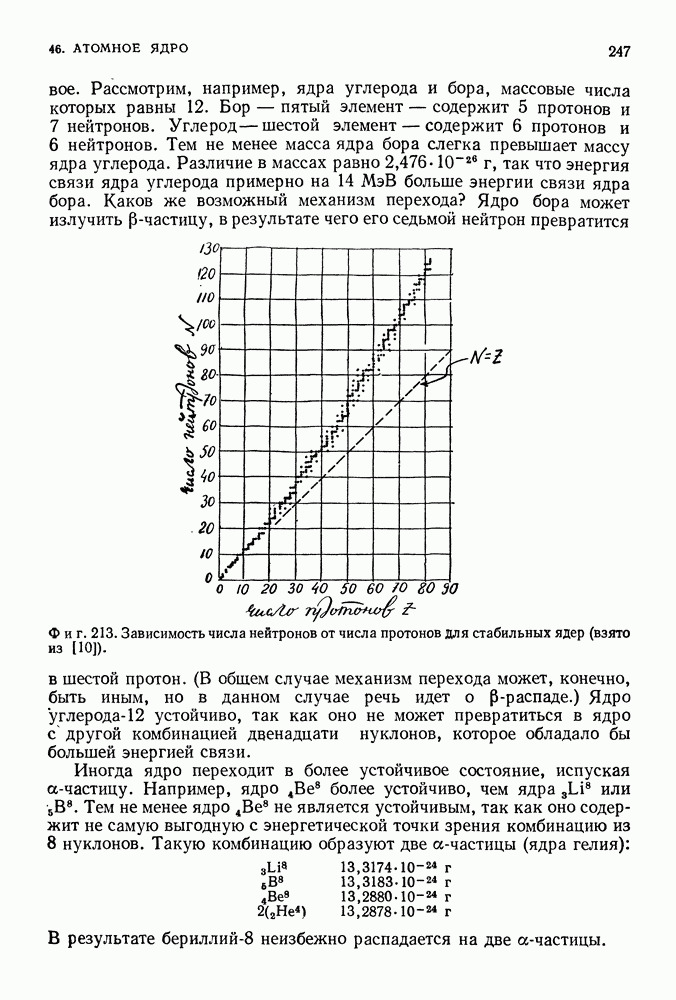
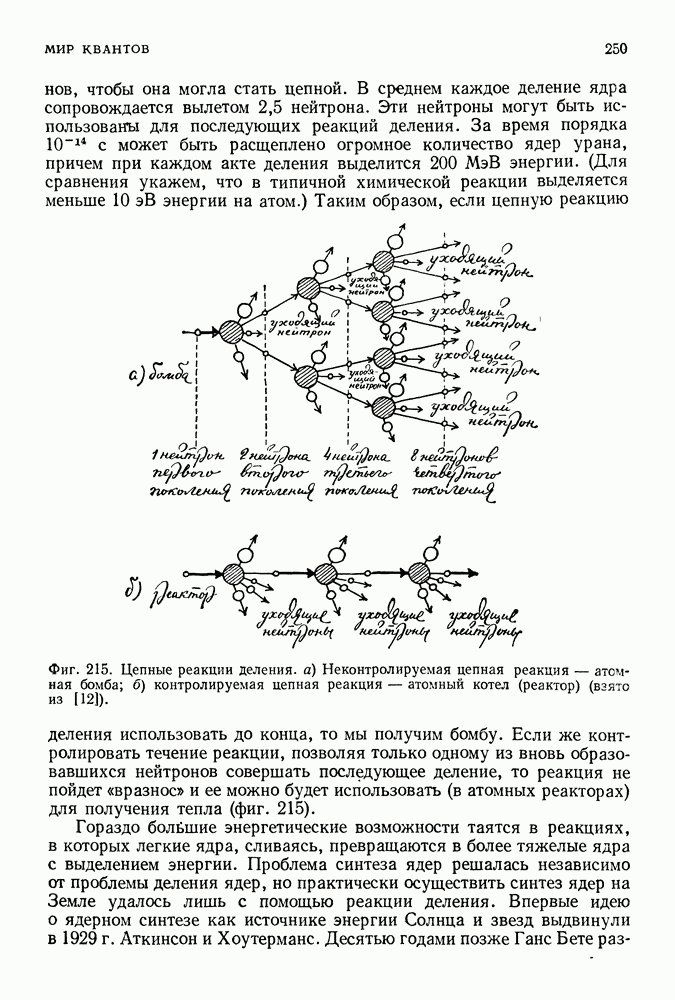
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
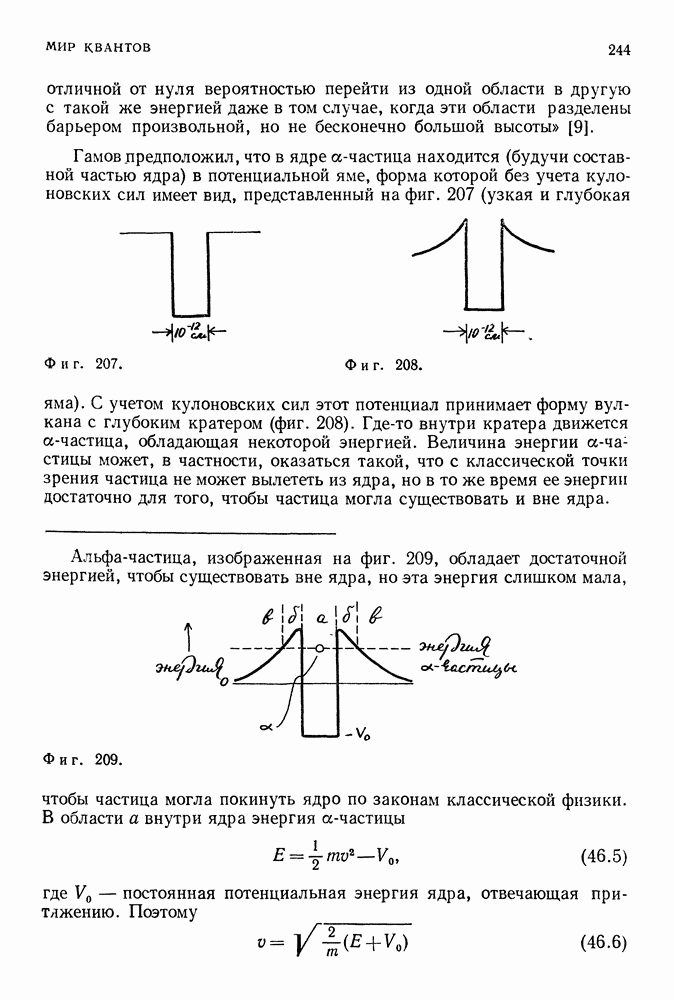
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
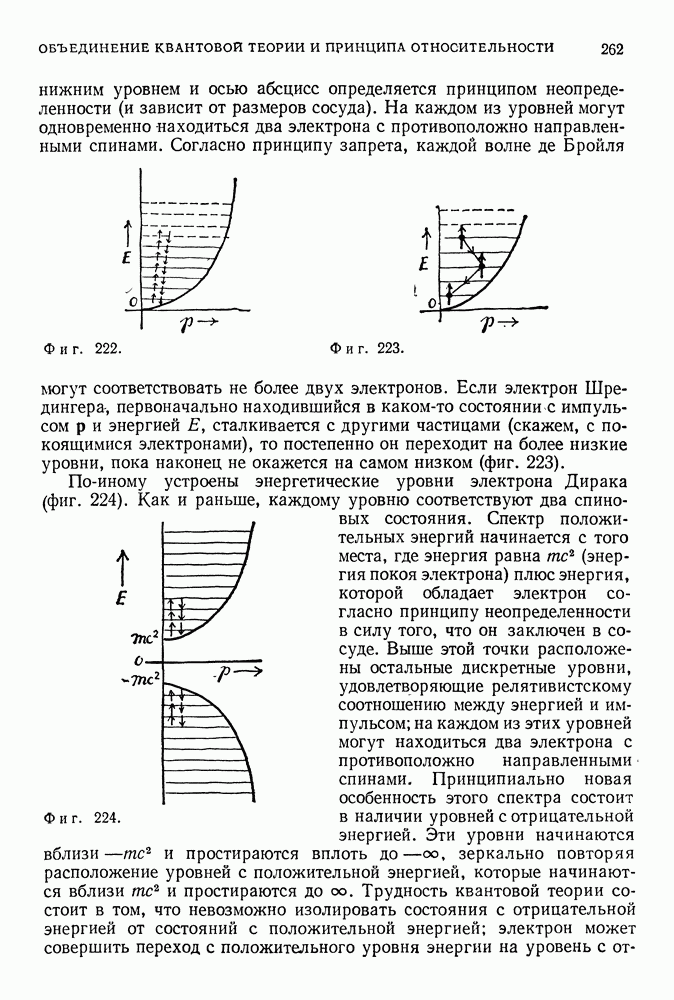
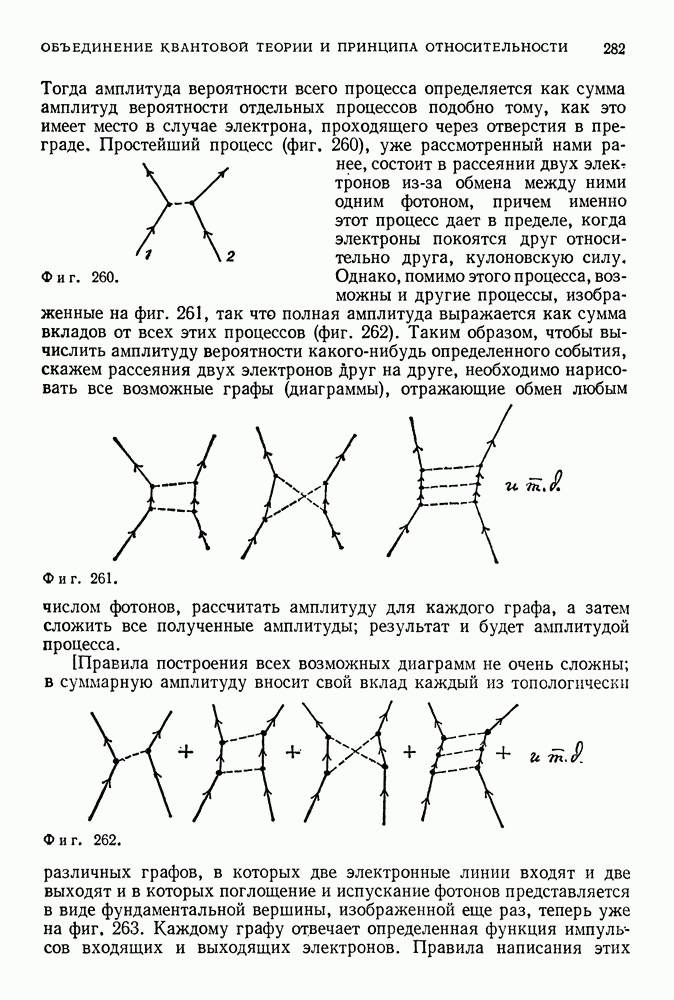
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
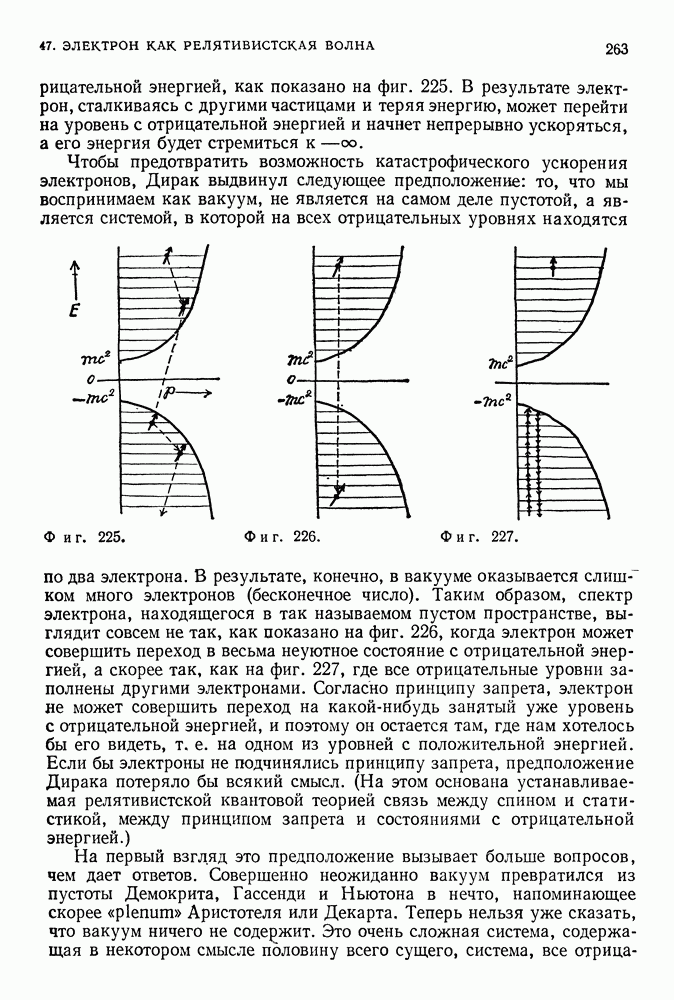
- ВАКУУМ ДИРАКА
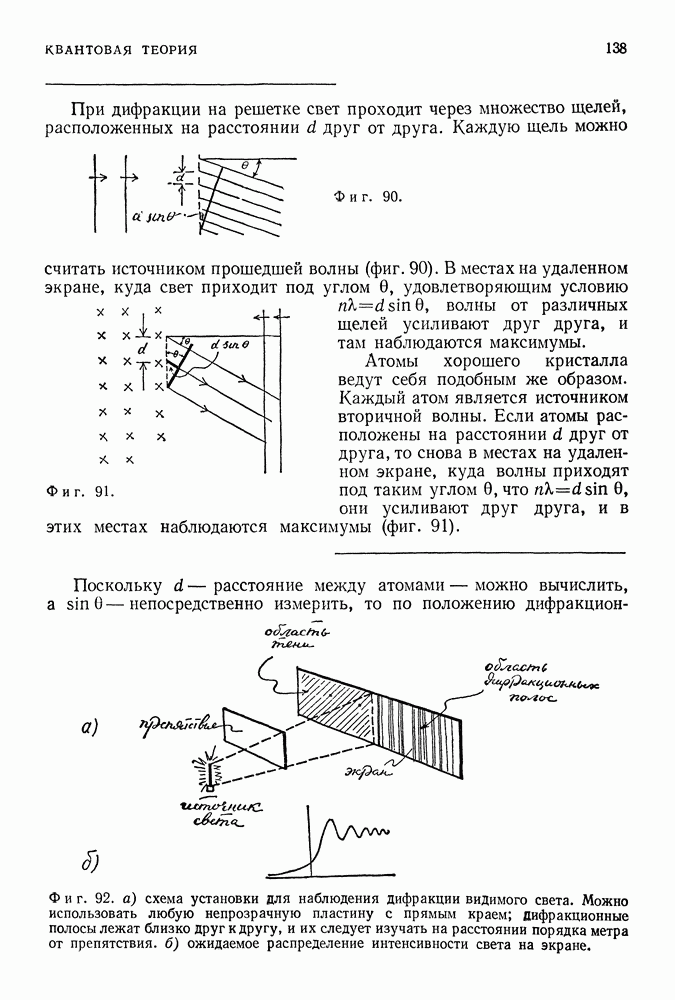
- АНТИВЕЩЕСТВО
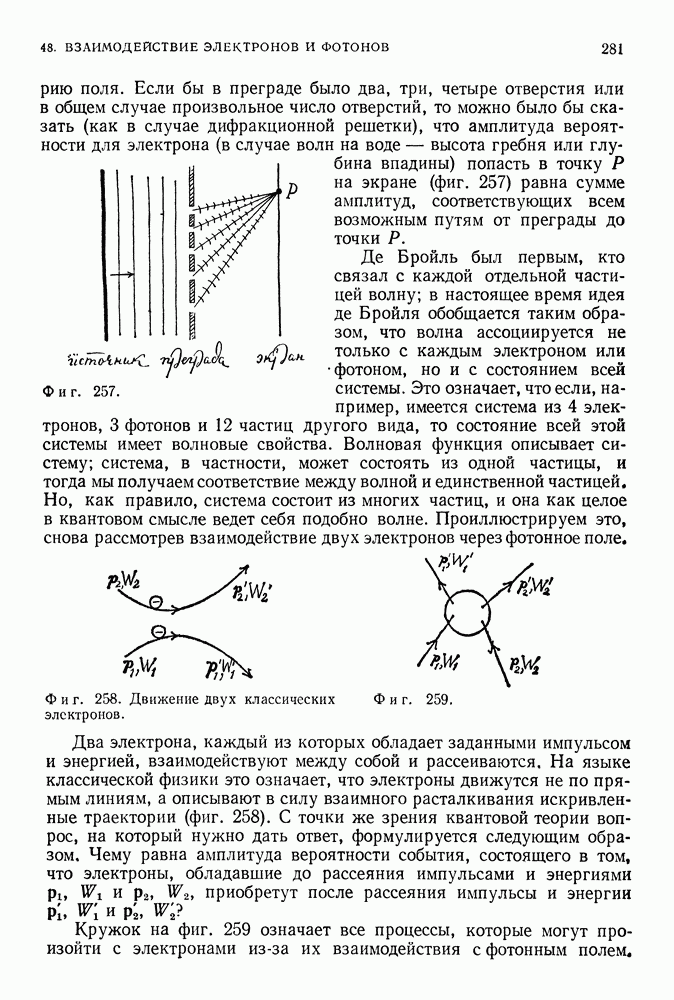
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
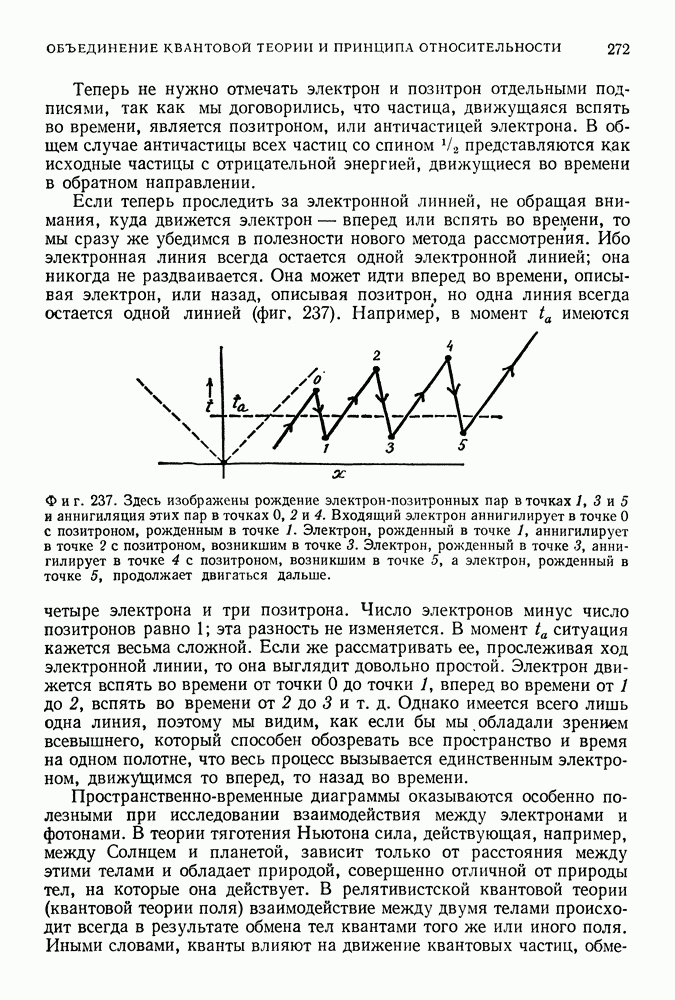
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
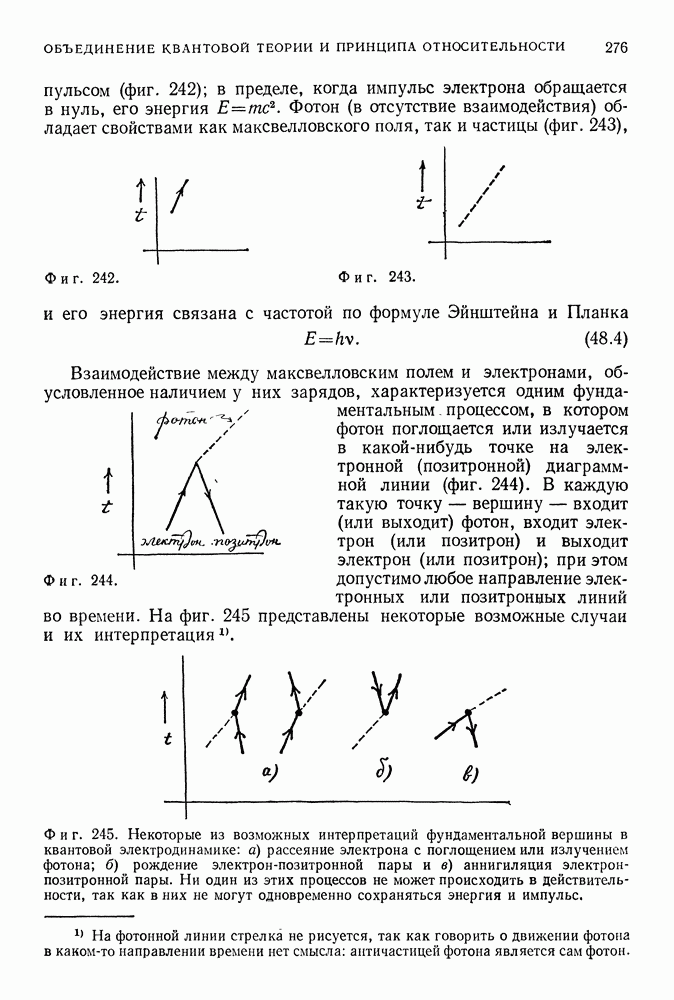
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
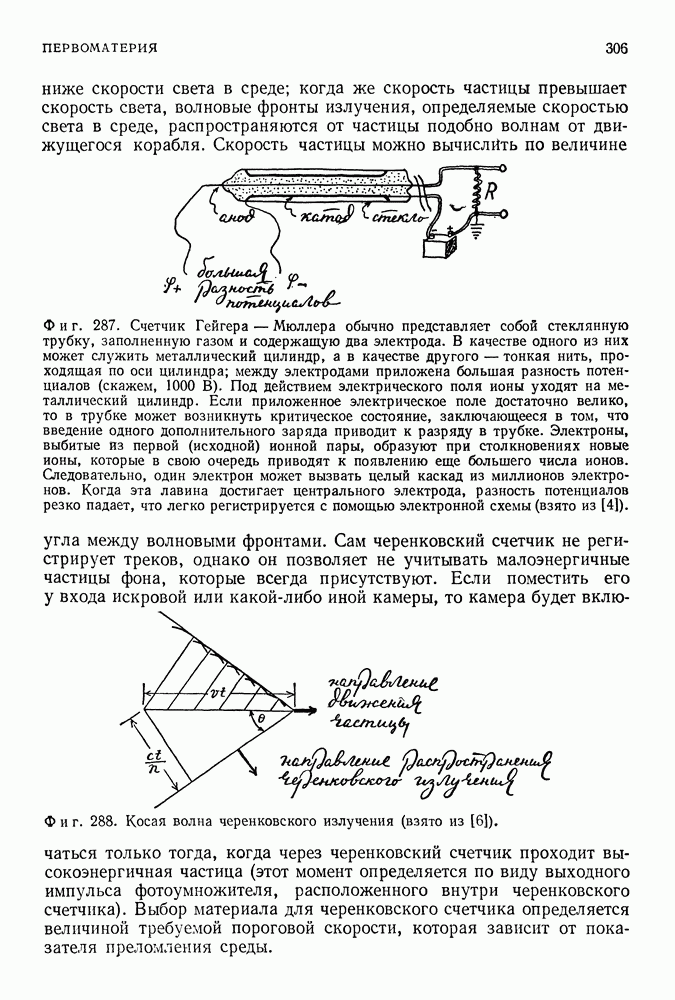
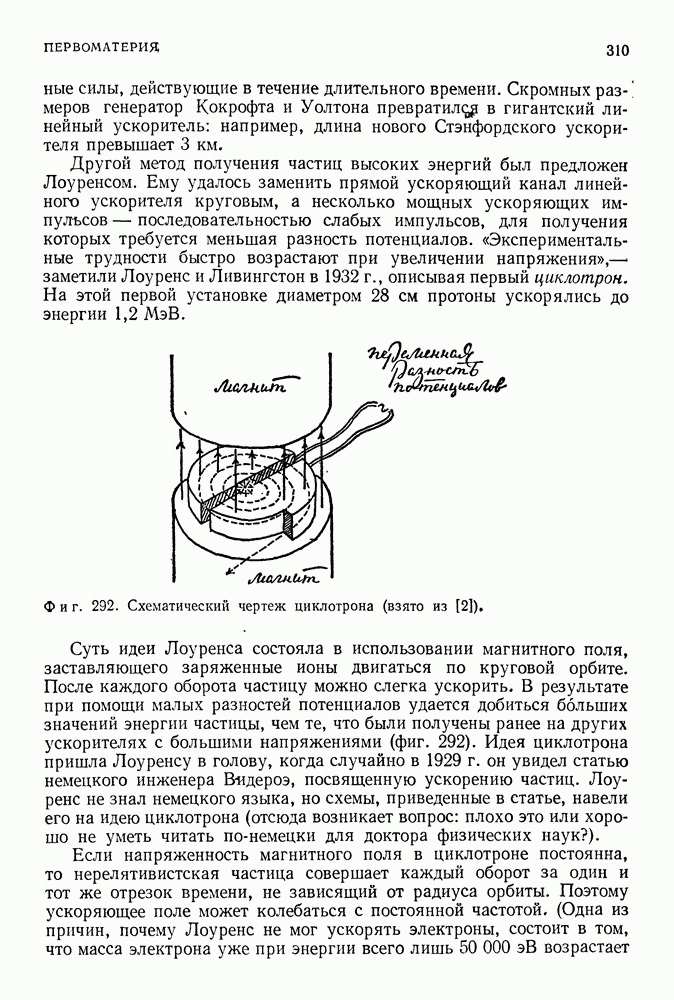
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
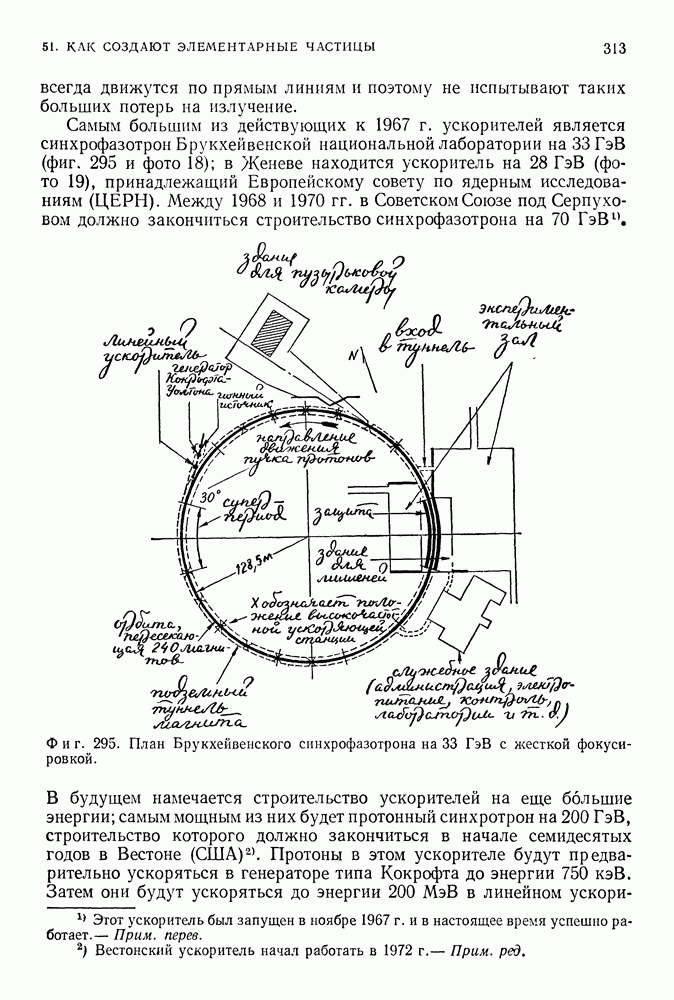
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА