| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
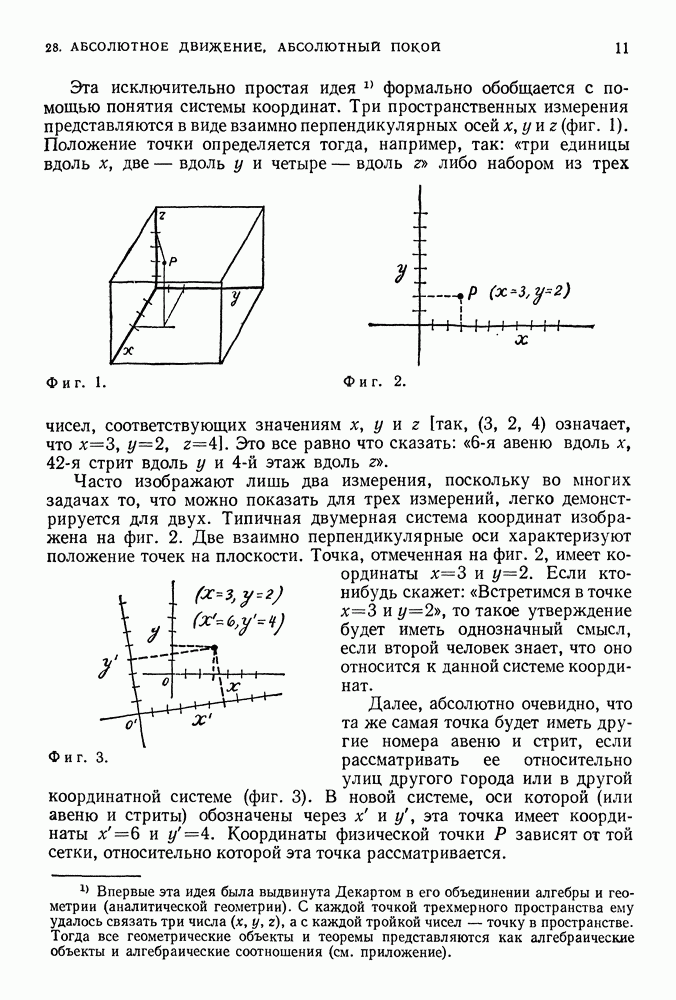
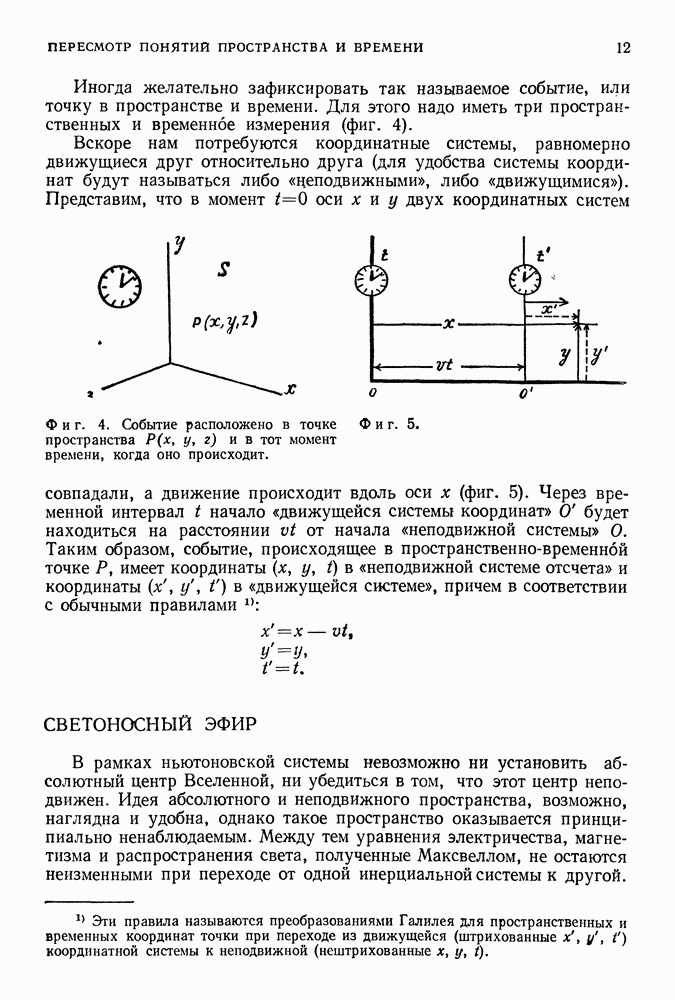
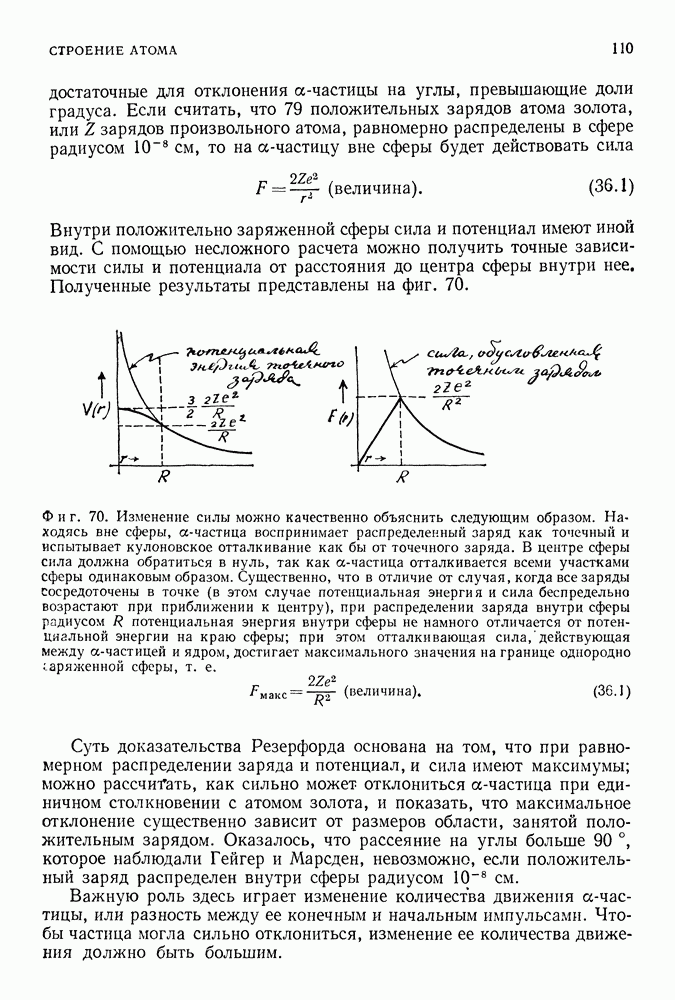
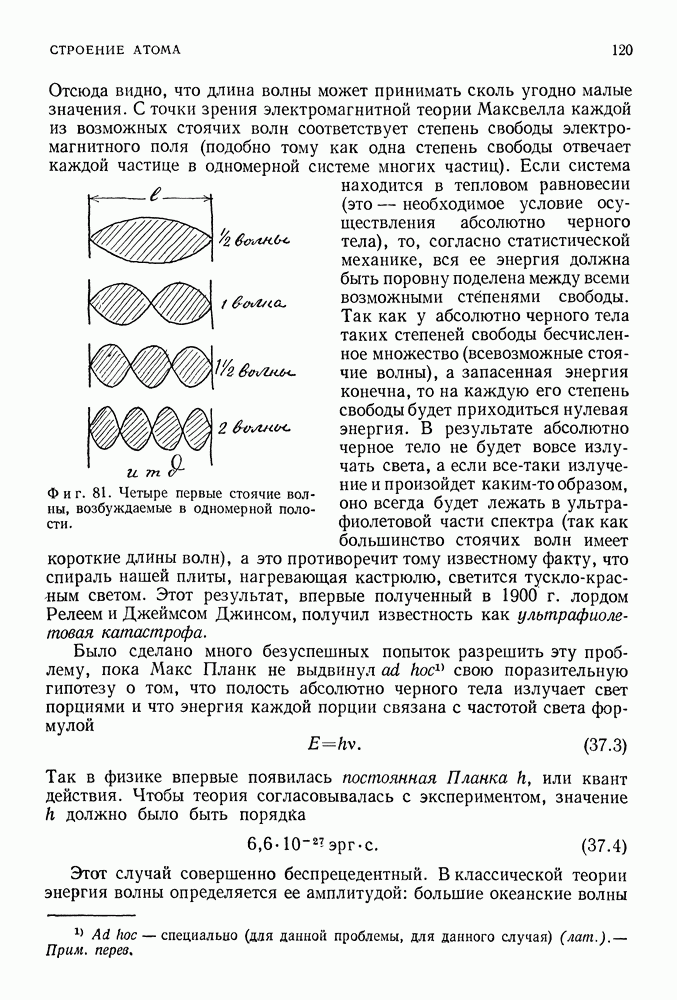
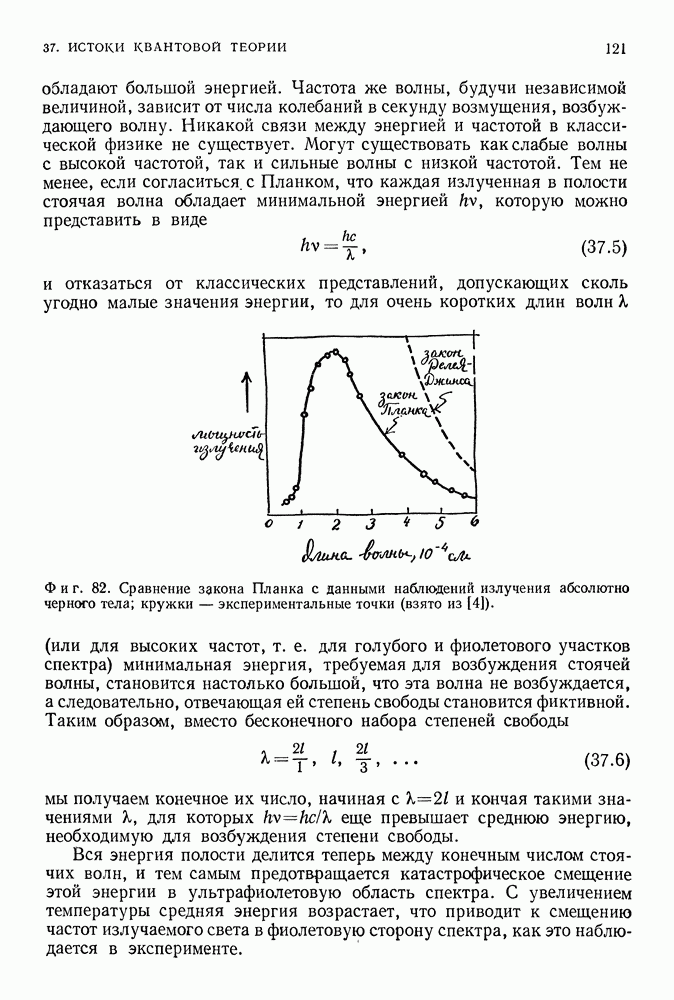
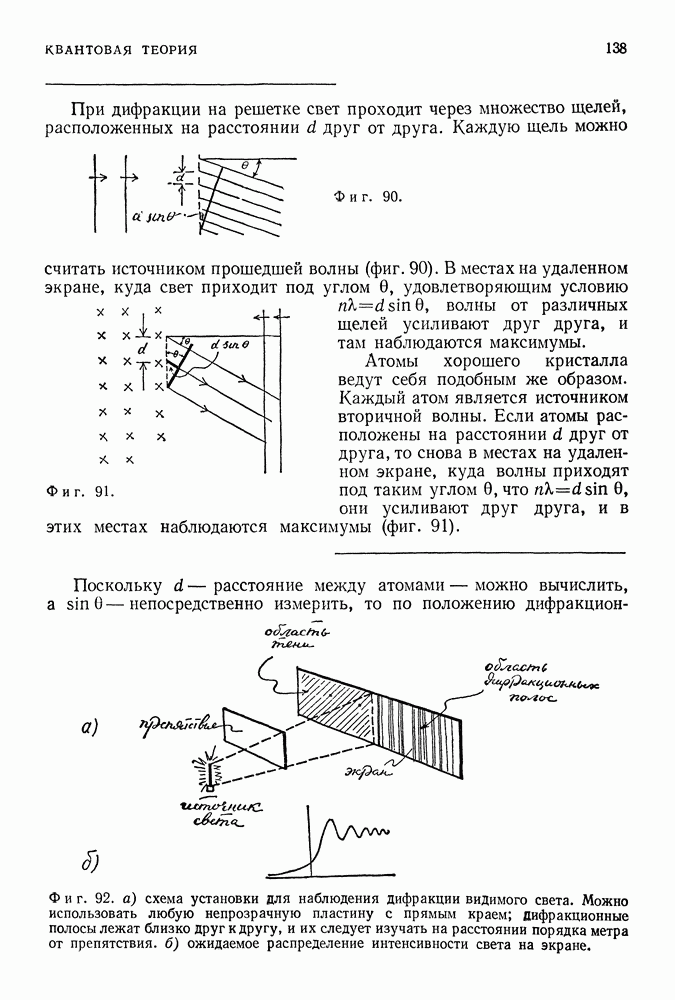
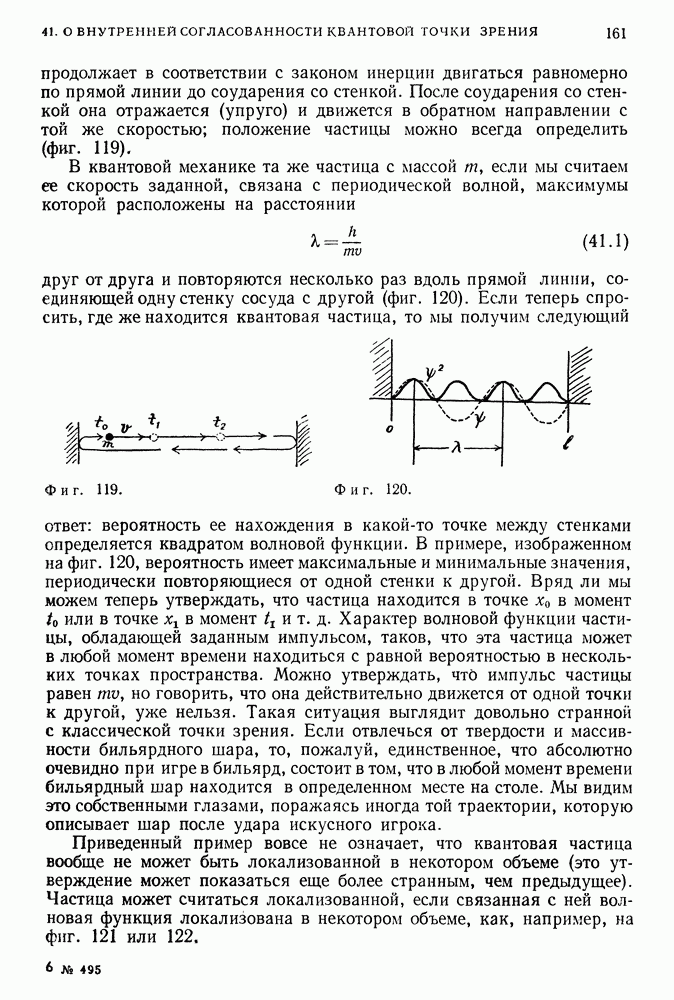
Ранее мы получили структуру энергетических уровней частицы, заключенной между двумя стенками, подбирая такие стоячие волны между этими стенками, которым отвечали все более короткие длины волн. Структура уровней атома водорода получается с помощью примерно такого же способа, однако соответствующие расчеты в случае атома водорода значительно сложнее, так как 1) он является трехмерной системой и 2) вместо сосуда следует рассматривать притягивающую силу, величина которой изменяется с расстоянием. Прежде всего рассмотрим некоторые новые свойства структуры энергетических уровней, появляющиеся в случае двух- или трехмерной квантовой системы, обобщая проанализированную ранее систему (частица заключена между двумя стенками).

Фиг. 135.
Для одномерной квантовой системы, ограниченной двумя стенками (фиг. 135), возможные решения уравнения Шредингера соответствуют волнам де Бройля с длинами волн

и с энергиями

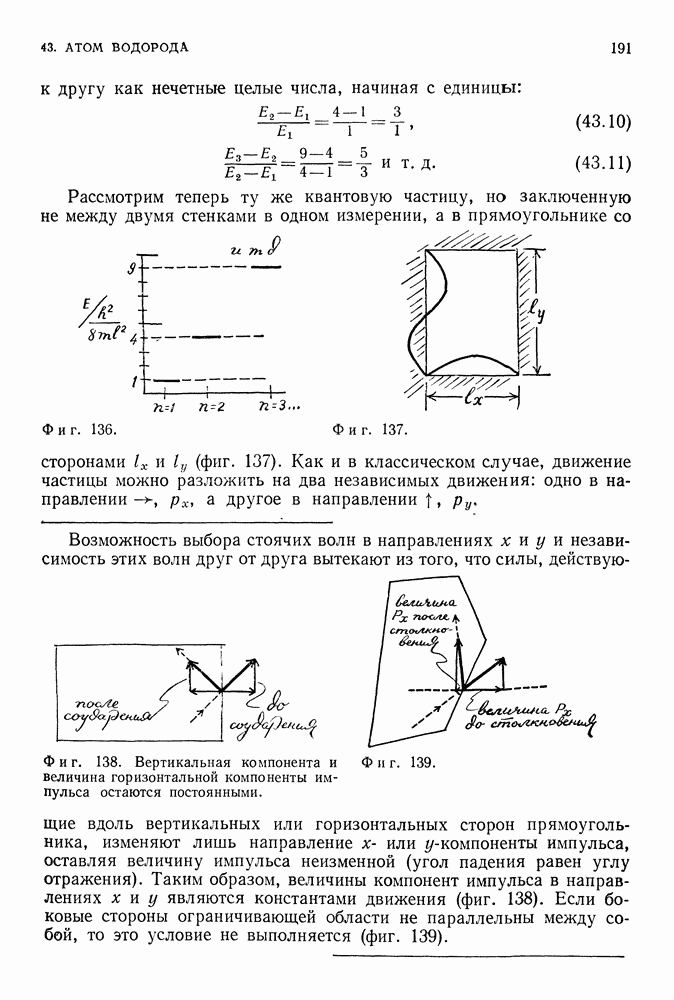
На фиг. 136 изображена диаграмма значений энергии в зависимости от  Разности значений энергии на соседних уровнях относятся друг
Разности значений энергии на соседних уровнях относятся друг
к другу как нечетные целые числа, начиная с единицы:

Рассмотрим теперь ту же квантовую частицу, но заключенную не между двумя стенками в одном измерении, а в прямоугольнике со сторонами  (фиг. 137).
(фиг. 137).

Фиг. 136.

Фиг. 137.
Как и в классическом случае, движение частицы можно разложить на два независимых движения: одно в направлении  а другое в направлении
а другое в направлении 
Возможность выбора стоячих волн в направлениях х и у и независимость этих волн друг от друга вытекают из того, что силы, действующие вдоль вертикальных или горизонтальных сторон прямоугольника, изменяют лишь направление  или
или  -компоненты импульса, оставляя величину импульса неизменной (угол падения равен углу отражения).
-компоненты импульса, оставляя величину импульса неизменной (угол падения равен углу отражения).

Фиг. 138. Вертикальная компонента и величина горизонтальной компоненты импульса остаются постоянными.

Фиг. 139.
Таким образом, величины компонент импульса в направлениях х и у являются константами движения (фиг. 138). Если боковые стороны ограничивающей области не параллельны между собой, то это условие не выполняется (фиг. 139).
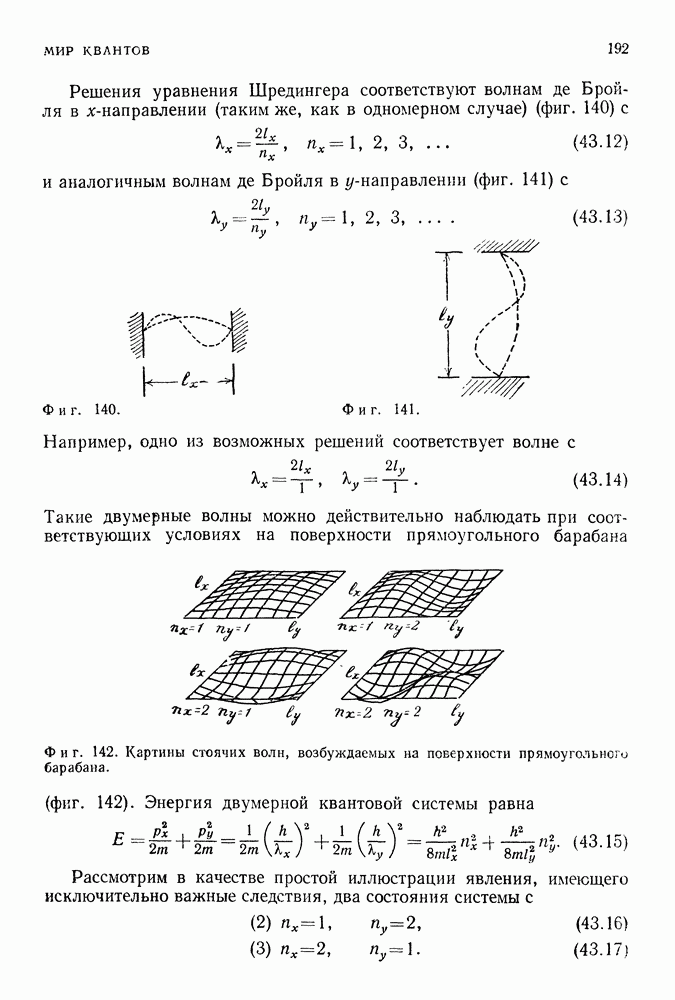
Решения уравнения Шредингера соответствуют волнам де Бройля в х-направлении (таким же, как в одномерном случае) (фиг. 140) с

и аналогичным волнам де Бройля в у-направлении (фиг. 141) с


Фиг. 140.

Фиг. 141.
Например, одно из возможных решений соответствует волне с

Такие двумерные волны можно действительно наблюдать при соответствующих условиях на поверхности прямоугольного барабана (фиг. 142).

Фиг. 142. Картины стоячих волн, возбуждаемых на поверхности прямоугольного барабана.
Энергия двумерной квантовой системы равна

Рассмотрим в качестве простой иллюстрации явления, имеющего исключительно важные следствия, два состояния системы с

Если стороны прямоугольника равны между собой  то в обоих этих состояниях система обладает одинаковой энергией:
то в обоих этих состояниях система обладает одинаковой энергией:

В этом случае общее выражение для энергии системы имеет вид

Отсюда видно, что всем комбинациям  таким, что сумма равна одному и тому же числу, отвечает одно и то же значение энергии.
таким, что сумма равна одному и тому же числу, отвечает одно и то же значение энергии.

Фиг. 143. Зависимость нескольких первых энергетических уровней от квантовых чисел, если частица заключена в двумерном прямоугольном сосуде, у которого  (сплошные линии) и
(сплошные линии) и  (штриховая линия).
(штриховая линия).
Два или большее число квантовых состояний, обладающих одинаковыми энергиями, называются вырожденными; это слово было позаимствовано из обиходного языка, только его наделили специальным техническим значением.

Фиг. 144. При повороте на  прямоугольник занимает другое положение — он выглядит по-иному. Квадрат же, повернутый на те
прямоугольник занимает другое положение — он выглядит по-иному. Квадрат же, повернутый на те  ничем не отличается от исходной фигуры. Можно возразить, что, хотя квадрат и выглядит после поворота точно так же, как и вначале, «на самом деле» он занимает после поворота иное положение. Конечно, если как-то пометить стороны квадрата, то удастся определить различие в положениях. Идея же состоит в том, что физические величины — импульс, энергия и т. д. — не зависят от этих невидимых отметок. Вполне достаточно знать, что
ничем не отличается от исходной фигуры. Можно возразить, что, хотя квадрат и выглядит после поворота точно так же, как и вначале, «на самом деле» он занимает после поворота иное положение. Конечно, если как-то пометить стороны квадрата, то удастся определить различие в положениях. Идея же состоит в том, что физические величины — импульс, энергия и т. д. — не зависят от этих невидимых отметок. Вполне достаточно знать, что  и что противоположные стороны параллельны.
и что противоположные стороны параллельны.
Состояния, первоначально имевшие различные энергии, становятся вырожденными, когда прямоугольник превращается в квадрат (фиг. 143).
Квадрат обладает симметрией, которой нет у прямоугольника; если повернуть квадрат на 90°, то он, в отличие от прямоугольника, будет выглядеть так же, как и до поворота (фиг, 144). Одна из наиболее
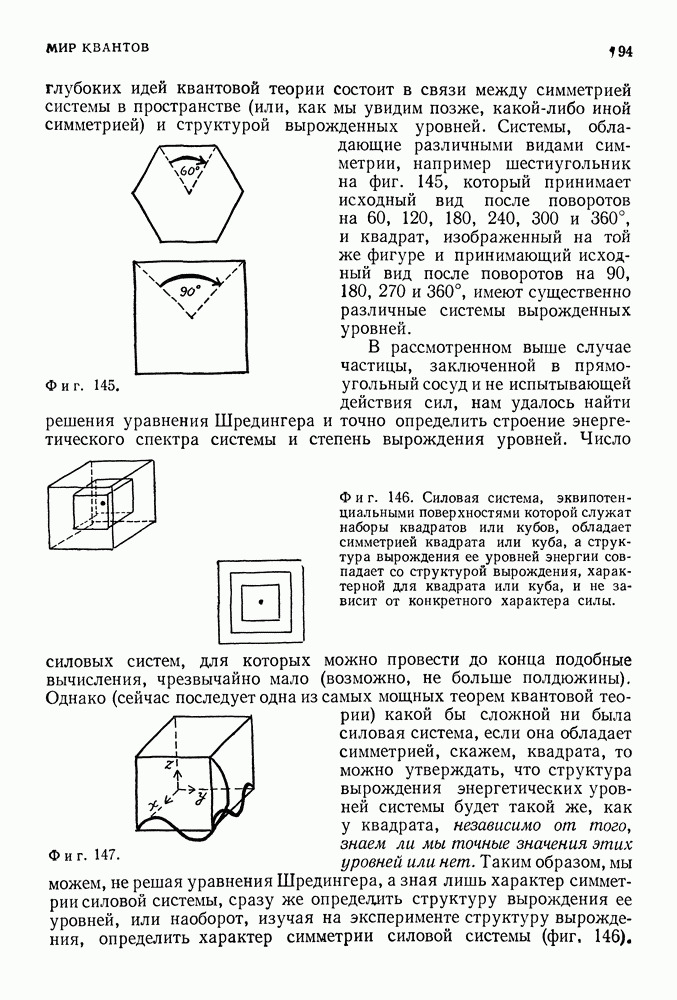
глубоких идей квантовой теории состоит в связи между симметрией системы в пространстве (или, как мы увидим позже, какой-либо иной симметрией) и структурой вырожденных уровней. Системы, обладающие различными видами симметрии, например шестиугольник на фиг. 145, который принимает исходный вид после поворотов на 60, 120, 180, 240, 300 и 360°, и квадрат, изображенный на той же фигуре и принимающий исходный вид после поворотов на 90, 180, 270 и 360°, имеют существенно различные системы вырожденных уровней.
В рассмотренном выше случае частицы, заключенной в прямоугольный сосуд и не испытывающей действия сил, нам удалось найти решения уравнения Шредингера и точно определить строение энергетического спектра системы и степень вырождения уровней.

Фиг. 145.

Фиг. 146. Силовая система, эквипотенциальными поверхностями которой служат наборы квадратов или кубов, обладает симметрией квадрата или куба, а структура вырождения ее уровней энергии совпадает со структурой вырождения, характерной для квадрата или куба, и не зависит от конкретного характера силы.

Фиг. 147.
Число силовых систем, для которых можно провести до конца подобные вычисления, чрезвычайно мало (возможно, не больше полдюжины). Однако (сейчас последует одна из самых мощных теорем квантовой теории) какой бы сложной ни была силовая система, если она обладает симметрией, скажем, квадрата, то можно утверждать, что структура вырождения энергетических уровней системы будет такой же, как у квадрата, независимо от того, знаем ли мы точные значения этих уровней или нет. Таким образом, мы можем, не решая уравнения Шредингера, а зная лишь характер симметрии силовой системы, сразу же определять структуру вырождения ее уровней, или наоборот, изучая на эксперименте структуру вырождения, определить характер симметрии силовой системы (фиг, 146).
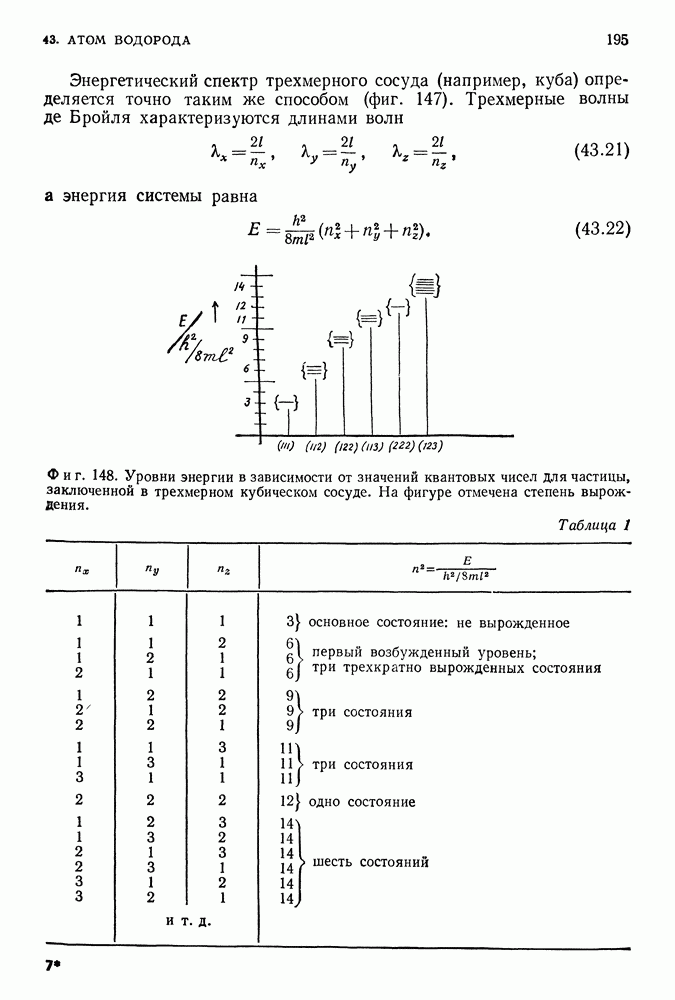
Энергетический спектр трехмерного сосуда (например, куба) определяется точно таким же способом (фиг. 147). Трехмерные волны де Бройля характеризуются длинами волн

а энергия системы равна


Фиг. 148. Уровни энергии в зависимости от значений квантовых чисел для частицы, заключенной в трехмерном кубическом сосуде. На фигуре отмечена степень вырождения.
Таблица 1

Таким образом, все комбинации  для которых сумма
для которых сумма

есть одно и то же число, соответствуют одинаковому значению энергии (фиг. 148 и табл. 1).
| << Предыдущий параграф | Следующий параграф >> |
- 28. АБСОЛЮТНОЕ ДВИЖЕНИЕ, АБСОЛЮТНЫЙ ПОКОЙ
- СИСТЕМЫ ОТСЧЕТА
- СВЕТОНОСНЫЙ ЭФИР
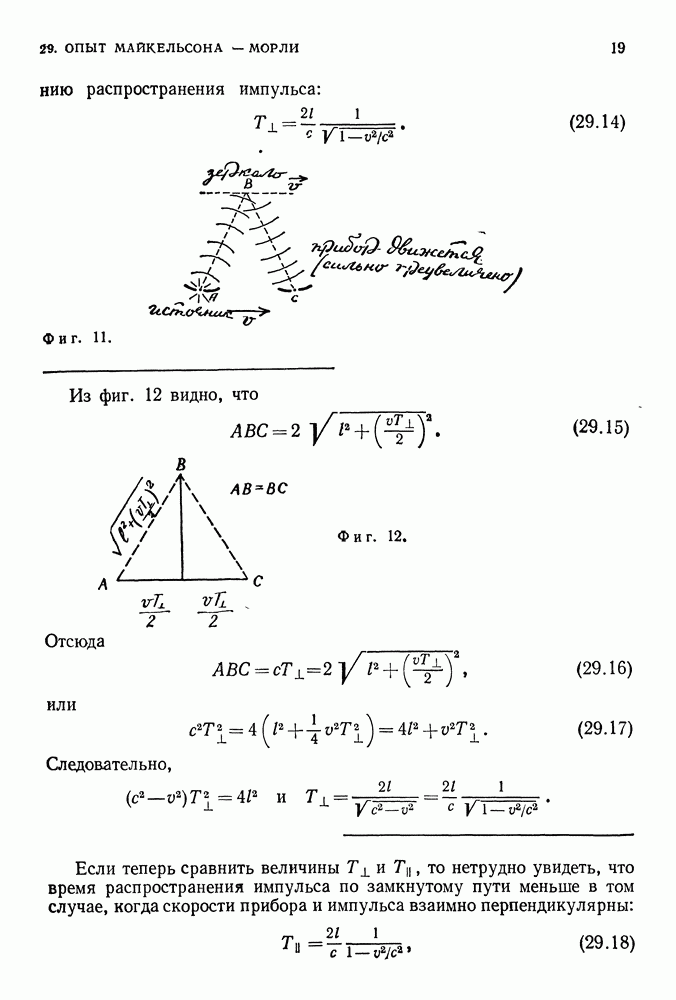
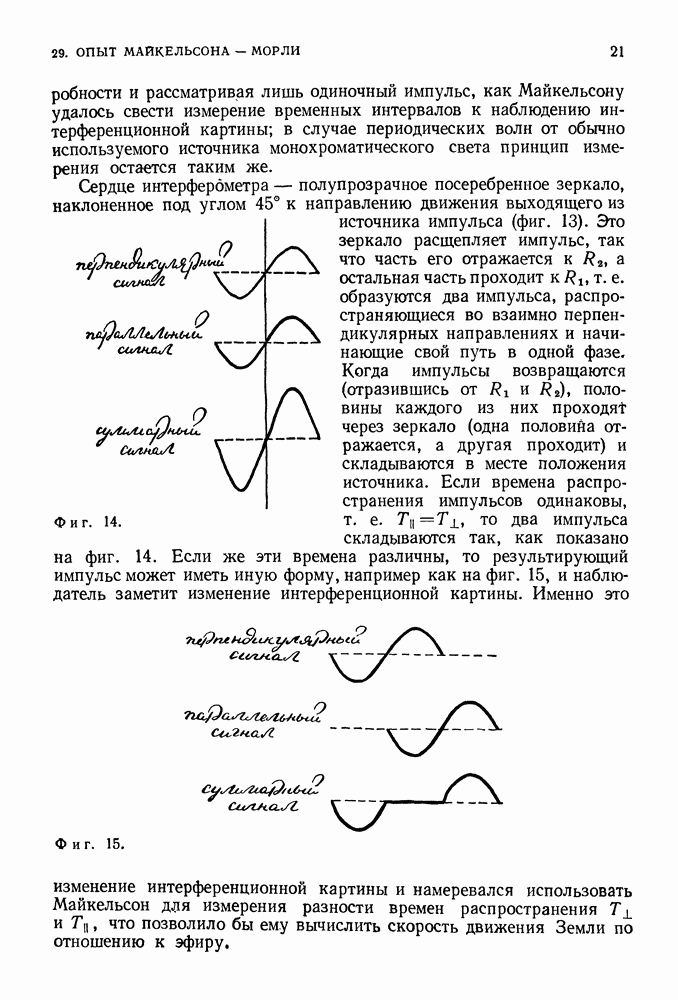
- 29. ОПЫТ МАЙКЕЛЬСОНА-МОРЛИ
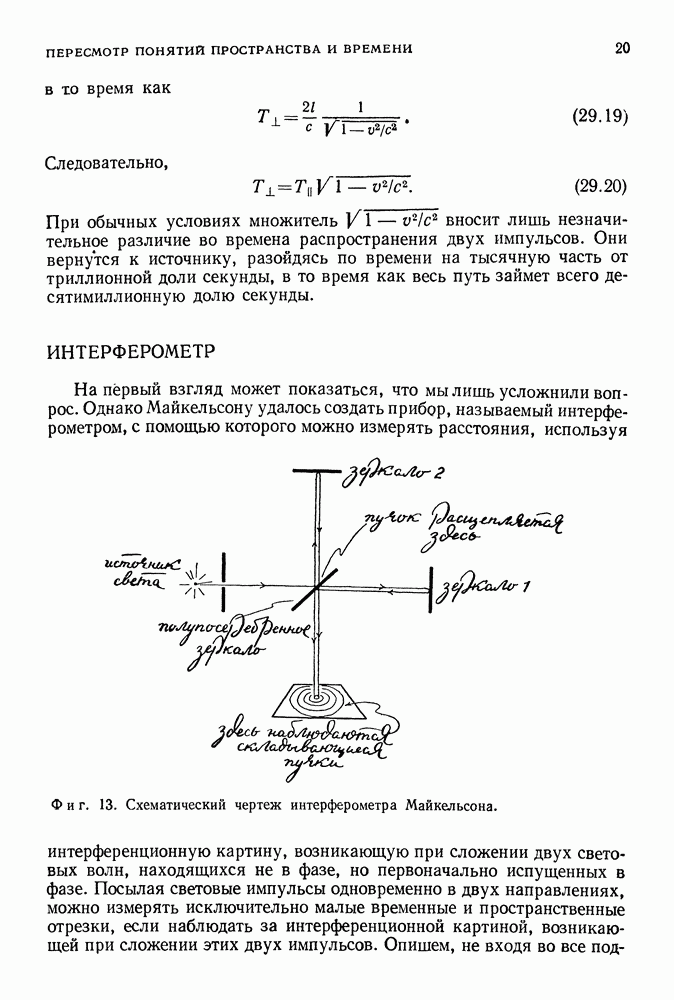
- ИНТЕРФЕРОМЕТР
- РЕЗУЛЬТАТЫ
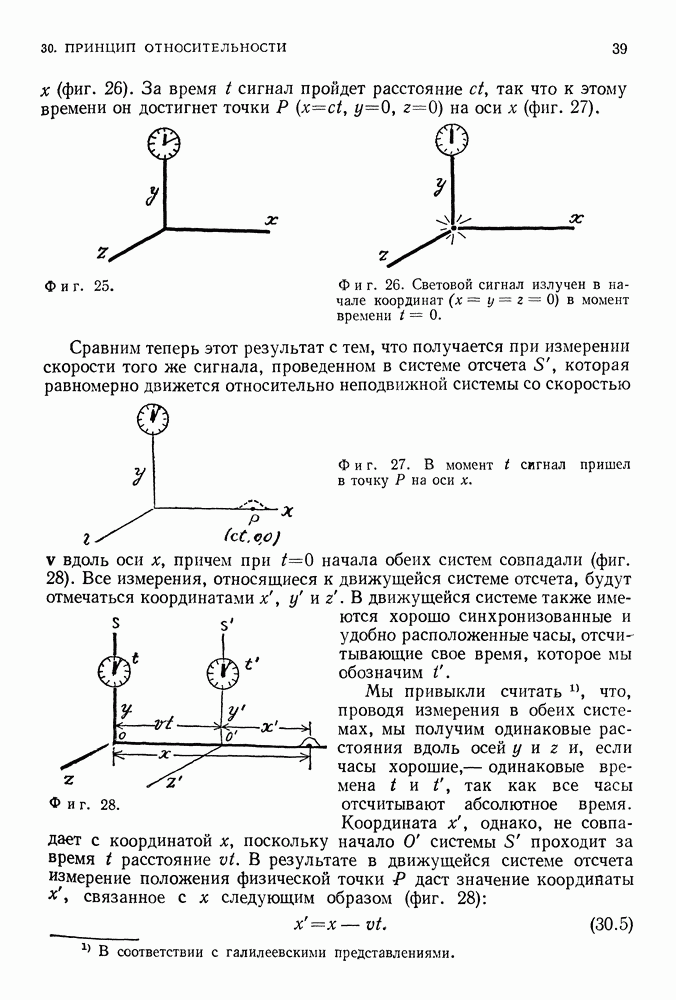
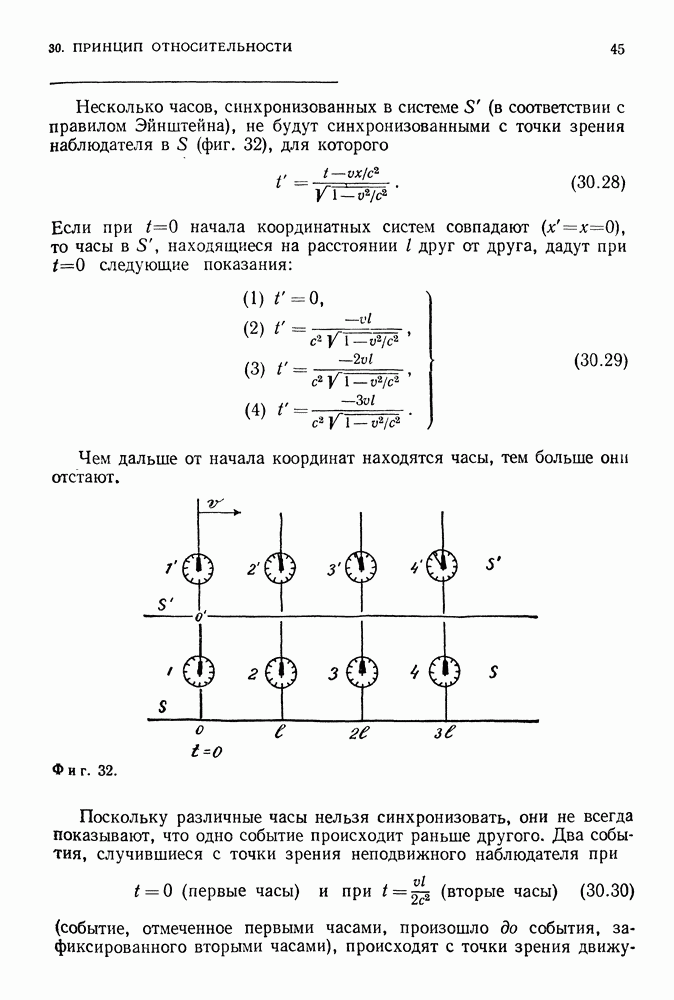
- 30. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
- ЗАГОВОР
- СКОРОСТЬ СВЕТА
- TEMPS PERDU
- О ПРОСТРАНСТВЕННЫХ И ВРЕМЕННЫХ ПРОМЕЖУТКАХ, ОПРЕДЕЛЯЕМЫХ В СИСТЕМАХ ОТСЧЕТА, РАВНОМЕРНО ДВИЖУЩИХСЯ ДРУГ ОТНОСИТЕЛЬНО ДРУГА
- ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- СЛОЖЕНИЕ СКОРОСТЕЙ
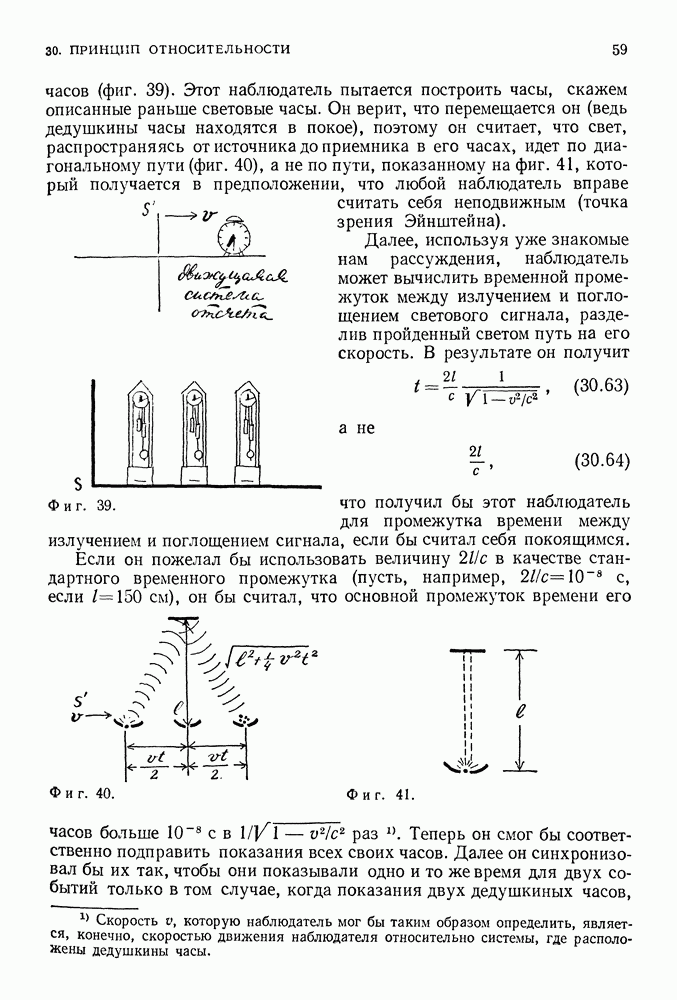
- ДЕДУШКИНЫ ЧАСЫ ВО ВНЕШНЕМ ПРОСТРАНСТВЕ
- 31. ОБЪЕДИНЕНИЕ ЗАКОНОВ НЬЮТОНА И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- РЕЛЯТИВИСТСКОЕ СООТНОШЕНИЕ МЕЖДУ ЭНЕРГИЕЙ И ИМПУЛЬСОМ
- О ДВИЖЕНИИ РЕЛЯТИВИСТСКИХ ЭЛЕКТРОНОВ
- 32. ПАРАДОКС БЛИЗНЕЦОВ
- 33. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (ТЕОРИЯ ТЯГОТЕНИЯ ЭЙНШТЕЙНА)
- ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
- СТРОЕНИЕ АТОМА
- 34. СЕРЕБРЯНЫЕ НИТИ
- ДИСКРЕТНЫЕ СПЕКТРАЛЬНЫЕ ЛИНИИ
- ИКС-ЛУЧИ
- РАДИОАКТИВНОСТЬ
- 35. ОТКРЫТИЕ ЭЛЕКТРОНА
- ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ МАТЕРИИ
- АТОМ ТОМСОНА
- 36. АТОМ РЕЗЕРФОРДА
- 37. ИСТОКИ КВАНТОВОЙ ТЕОРИИ
- КВАНТ ДЕЙСТВИЯ МАКСА ПЛАНКА
- ФОТОН АЛЬБЕРТА ЭЙНШТЕЙНА
- ВОДОРОДНЫЙ АТОМ БОРА
- КВАНТОВАЯ ТЕОРИЯ
- 38. ЭЛЕКТРОН КАК ВОЛНА
- ОПЫТ ДЭВИССОНА — ДЖЕРМЕРА
- 39. УРАВНЕНИЕ ШРЕДИНГЕРА — ЗАКОН ДВИЖЕНИЯ ДЛЯ КВАНТОВЫХ СИСТЕМ
- СВОБОДНЫЕ РЕШЕНИЯ
- СВЯЗАННЫЕ РЕШЕНИЯ
- 40. ЧТО ТАКОЕ ВОЛНА ДЕ БРОЙЛЯ
- ИНТЕРПРЕТАЦИЯ ШРЕДИНГЕРА: ПЛОТНОСТЬ ВЕЩЕСТВА
- ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ
- ДРУГИЕ ВОЗМОЖНЫЕ ИНТЕРПРЕТАЦИИ
- 41. О ВНУТРЕННЕЙ СОГЛАСОВАННОСТИ КВАНТОВОМЕХАНИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ
- ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА
- МЫСЛЕННЫЕ ЭКСПЕРИМЕНТЫ ГЕЙЗЕНБЕРГА
- О РОЛИ НЕНАБЛЮДАЕМЫХ ВЕЛИЧИН В ФИЗИЧЕСКОЙ ТЕОРИИ
- ДУАЛИЗМ ВОЛНА — ЧАСТИЦА
- 42. ПЕРЕХОД ОТ КВАНТОВОЙ ТОЧКИ ЗРЕНИЯ К КЛАССИЧЕСКОЙ
- МИР КВАНТОВ
- 43. АТОМ ВОДОРОДА
- О ПРИРОДЕ ВЫРОЖДЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ КВАНТОВЫХ СИСТЕМ
- СФЕРИЧЕСКАЯ СИММЕТРИЯ КУЛОНОВСКОЙ СИЛЫ. АЗИМУТАЛЬНЫЕ КВАНТОВЫЕ ЧИСЛА
- УРОВНИ ЭНЕРГИИ АТОМА ВОДОРОДА
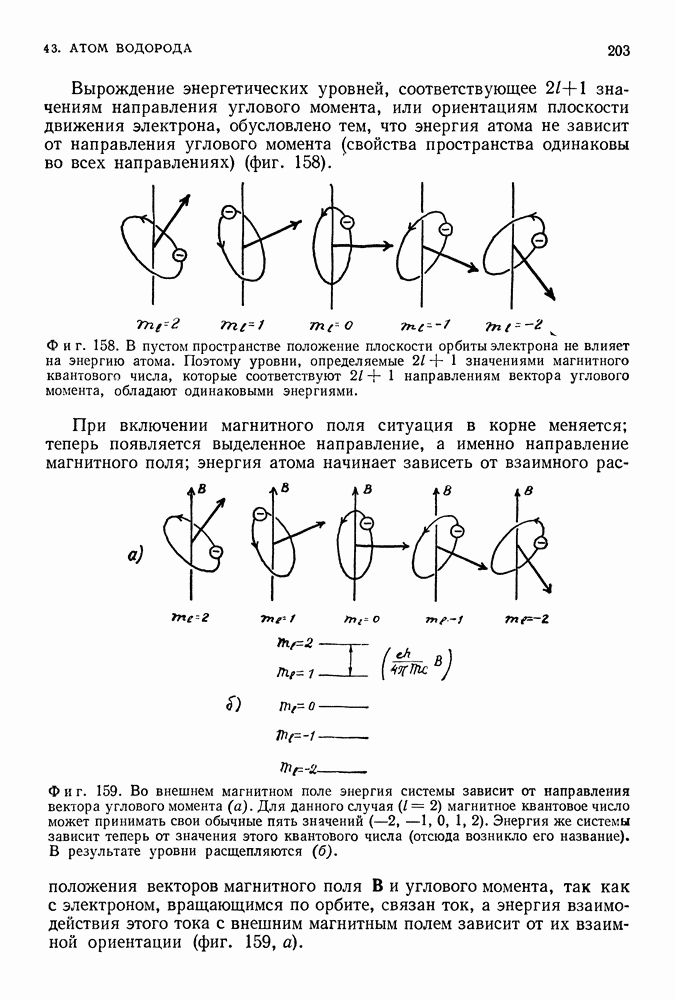
- ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- СПИН ЭЛЕКТРОНА
- 44. ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ И ФОТОНОВ С АТОМНЫМИ СИСТЕМАМИ
- СВЕТ
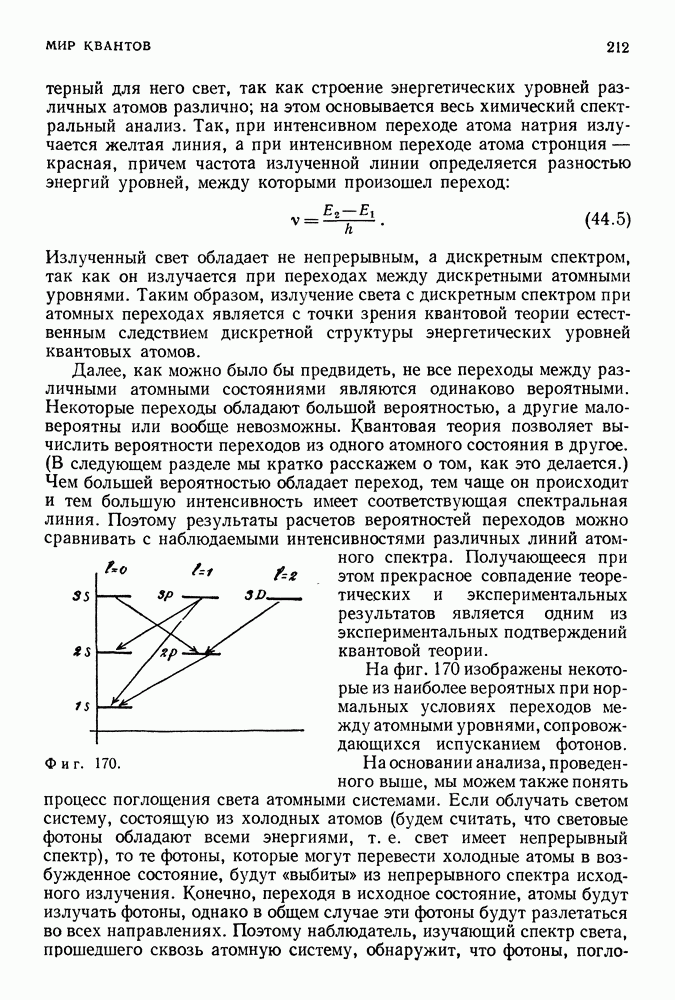
- ВЕРОЯТНОСТИ ПЕРЕХОДОВ
- 45. КВАНТОВЫЕ СИСТЕМЫ МНОГИХ ЧАСТИЦ
- СИММЕТРИЯ ВОЛНОВОЙ ФУНКЦИИ ОТНОСИТЕЛЬНО ПЕРЕСТАНОВКИ ТОЖДЕСТВЕННЫХ ЧАСТИЦ
- НЕВЗАИМОДЕЙСТВУЮЩИЕ ЭЛЕКТРОНЫ, ЗАКЛЮЧЕННЫЕ В СОСУДЕ, — ПРОСТЕЙШАЯ МОДЕЛЬ МЕТАЛЛА
- ПЕРИОДИЧЕСКАЯ ТАБЛИЦА ЭЛЕМЕНТОВ
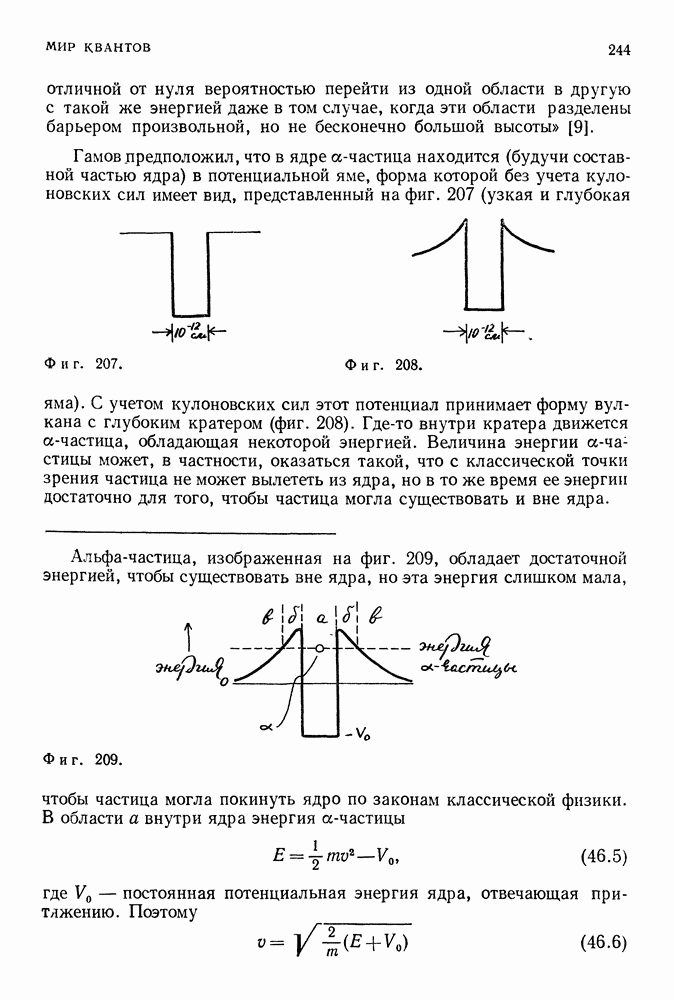
- 46. АТОМНОЕ ЯДРО
- КАК ЯДЕРНЫЕ ЧАСТИЦЫ УДЕРЖИВАЮТСЯ ВМЕСТЕ?
- ЯДЕРНЫЕ СИЛЫ И МОДЕЛИ ЯДЕР
- ЯДЕРНЫЕ ПРОЦЕССЫ И УСТОЙЧИВОСТЬ
- ОГОНЬ ЗВЕЗД
- ОБЪЕДИНЕНИЕ КВАНТОВОЙ ТЕОРИИ И ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ
- 47. ЭЛЕКТРОН КАК РЕЛЯТИВИСТСКАЯ ВОЛНА
- ЭЛЕКТРОН ДИРАКА
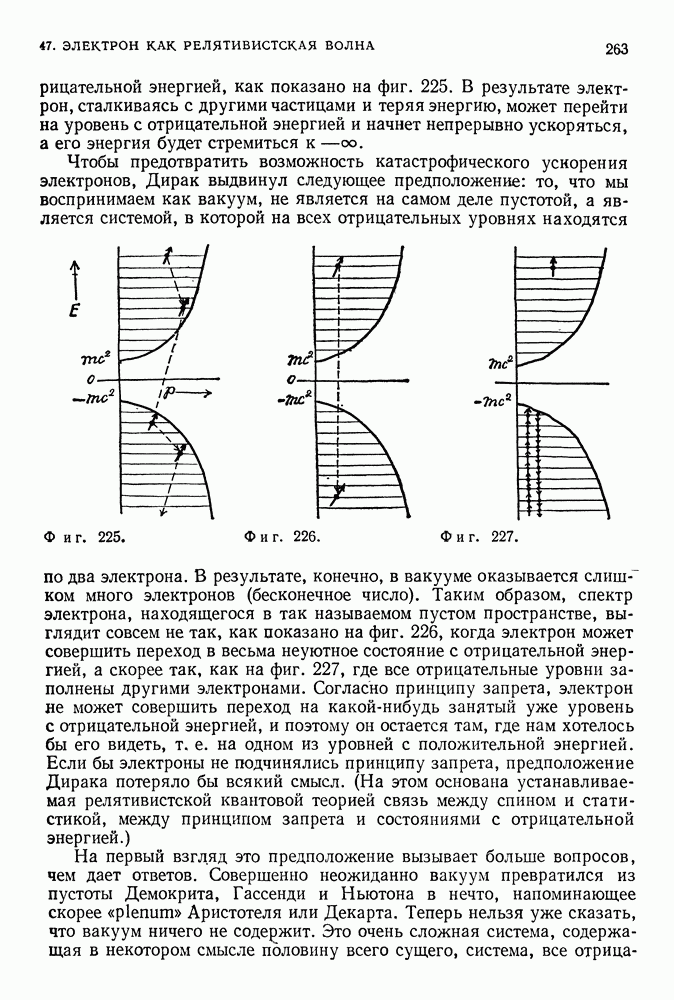
- ВАКУУМ ДИРАКА
- АНТИВЕЩЕСТВО
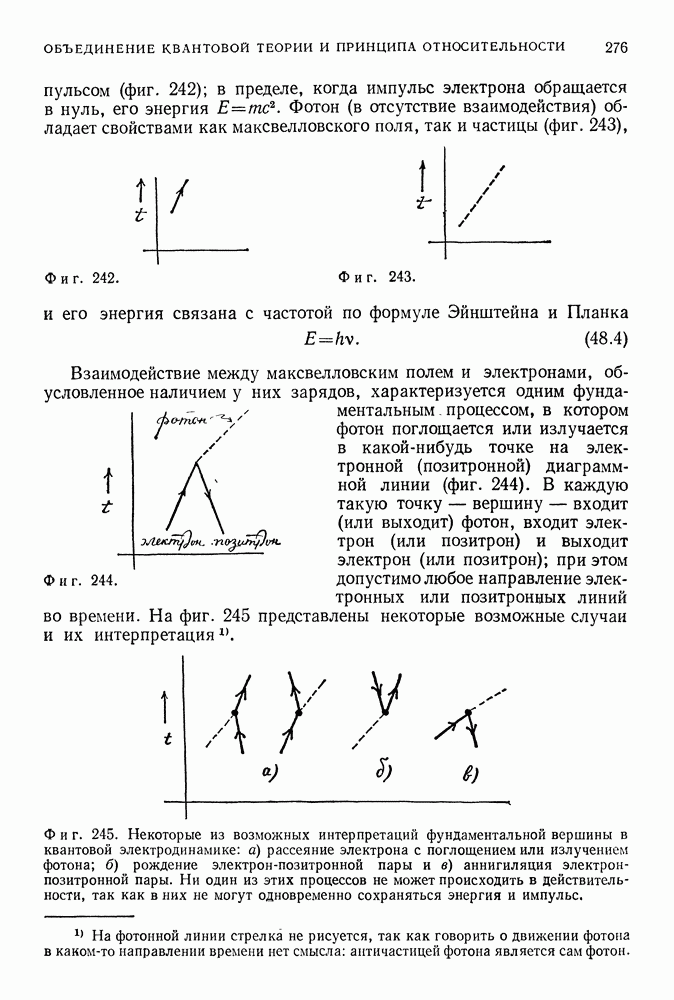
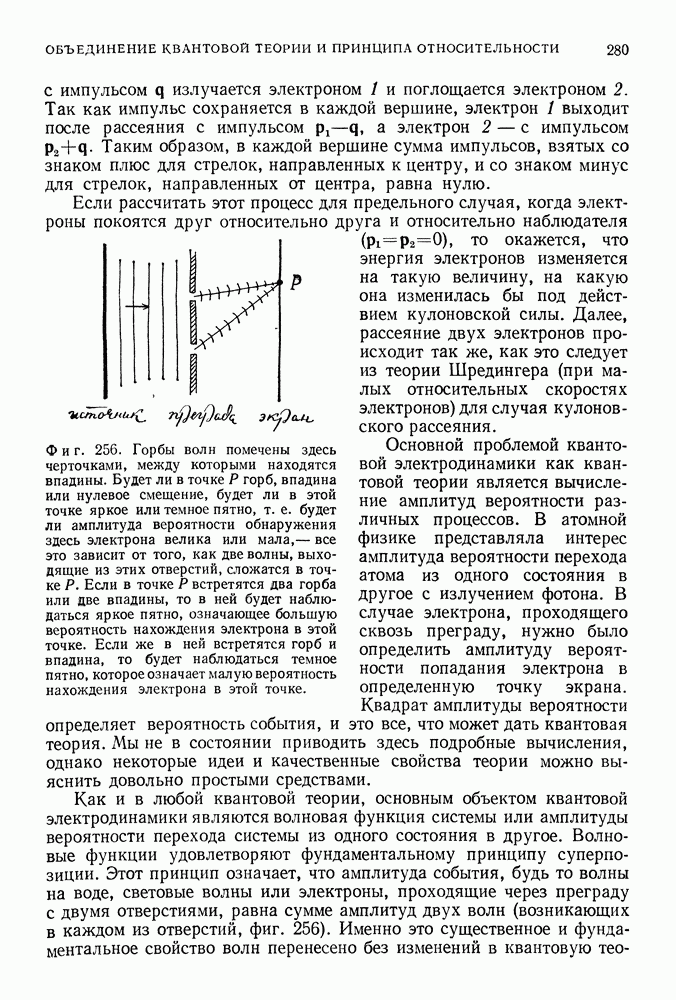
- 48. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОНОВ И ФОТОНОВ
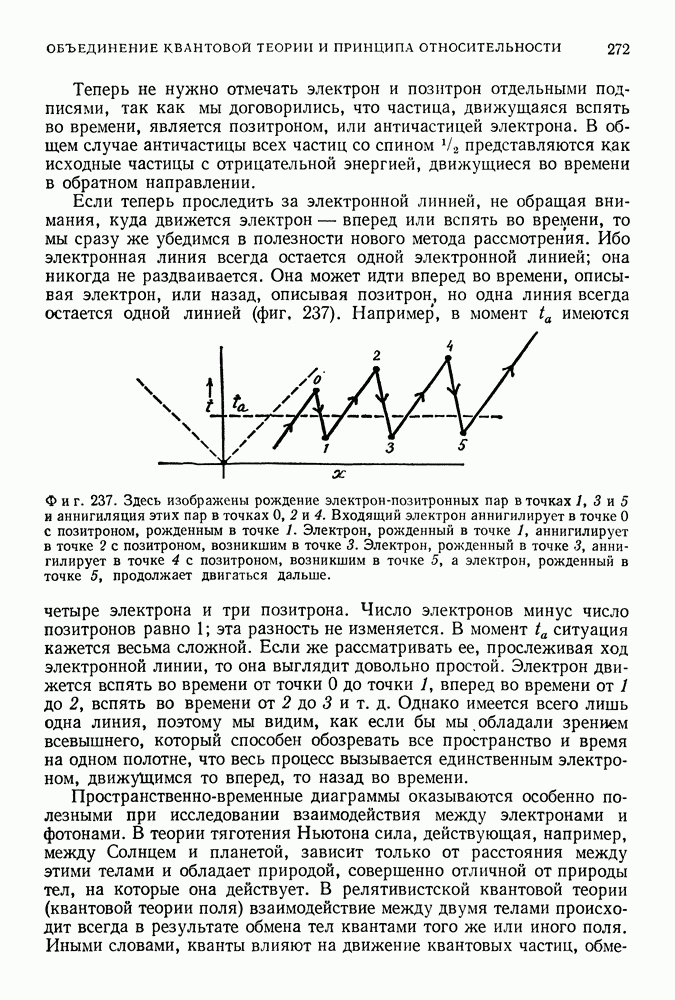
- ПРОСТРАНСТВЕННО-ВРЕМЕННЫЕ ДИАГРАММЫ
- КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- РАДИАЦИОННЫЕ ПОПРАВКИ И МЕТОД ПЕРЕНОРМИРОВОК
- ПЕРВОМАТЕРИЯ
- 49. ЧТО ТАКОЕ ЭЛЕМЕНТАРНАЯ ЧАСТИЦА
- 50. КАК НАБЛЮДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 51. КАК СОЗДАЮТ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- 52. ЧТО УДЕРЖИВАЕТ ЧАСТИЦЫ ЯДРА ВМЕСТЕ
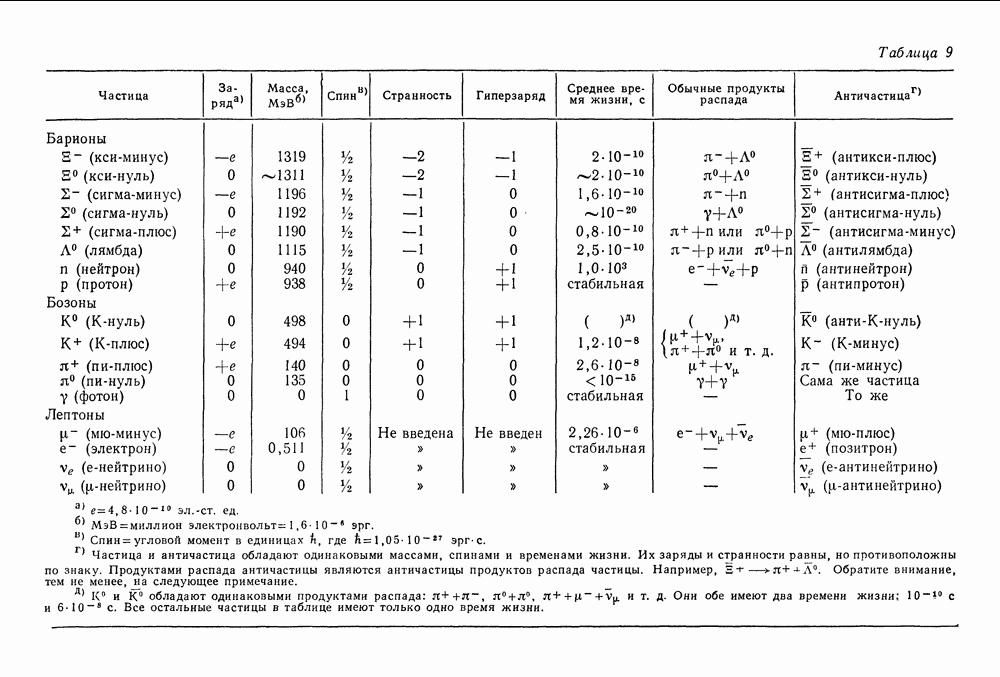
- 53. СТРАННЫЕ ЧАСТИЦЫ
- 54. ЗАРЯД, ИЗОТОПИЧЕСКИЙ СПИН И СТРАННОСТЬ
- 55. СИММЕТРИЯ: ОТ ПИФАГОРА ДО ПАУЛИ
- 56. ПЕРВОМАТЕРИЯ
- ВОПРОСЫ И ЗАДАЧИ
- ОТВЕТЫ НА НЕКОТОРЫЕ ЗАДАЧИ
- ЛИТЕРАТУРА