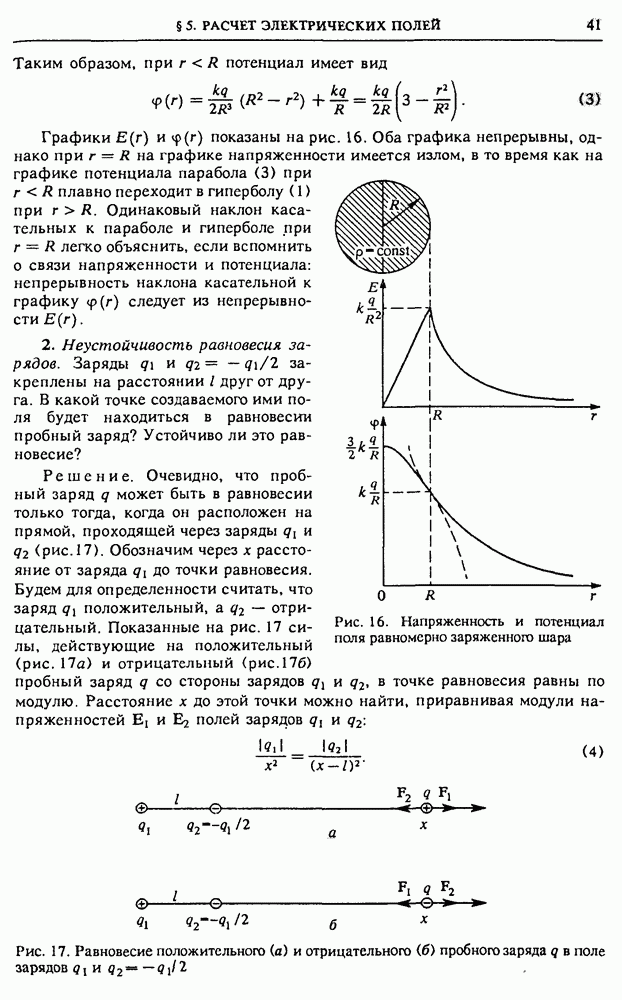
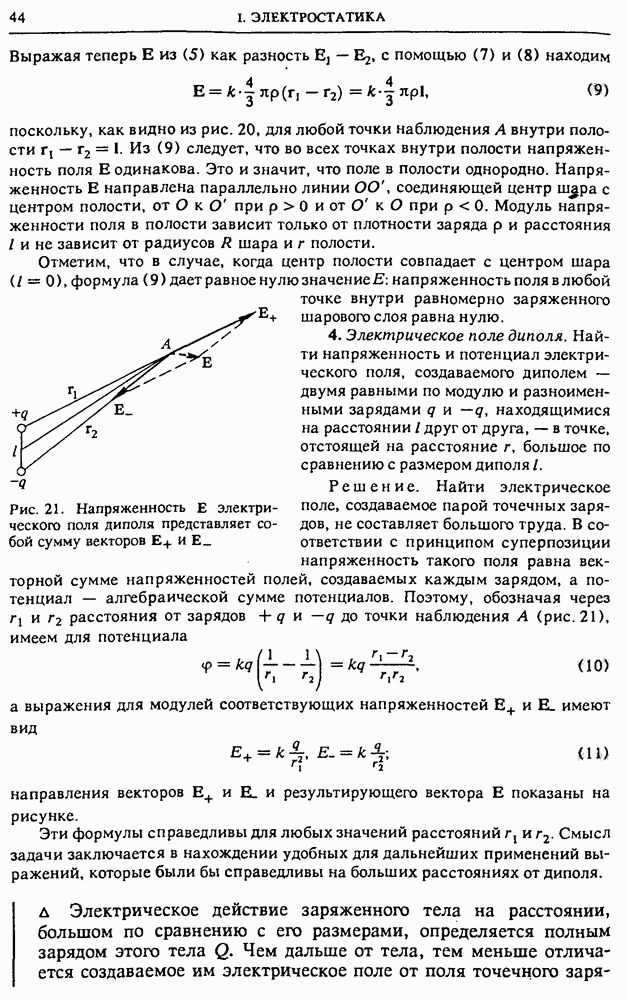
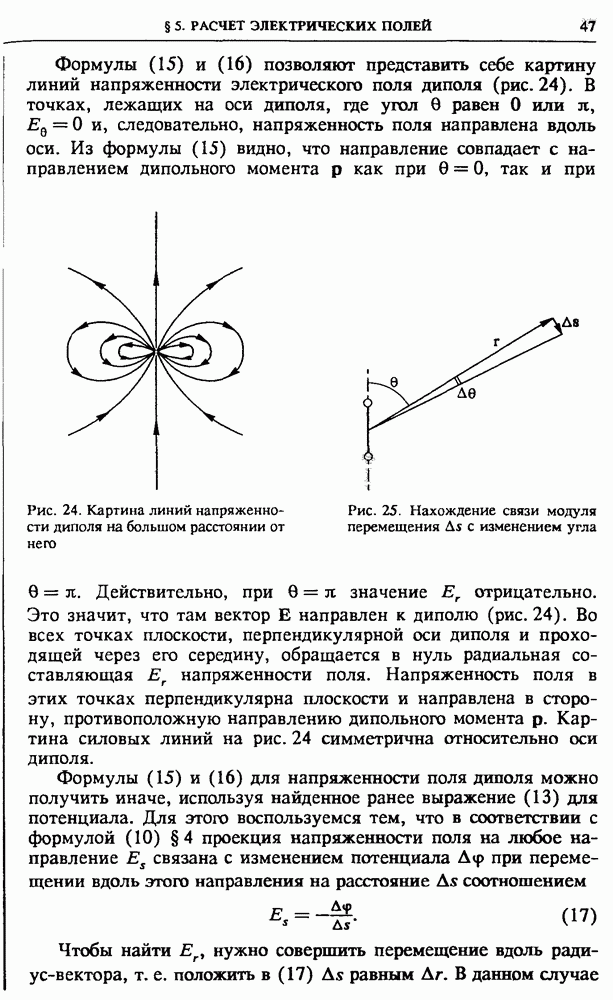
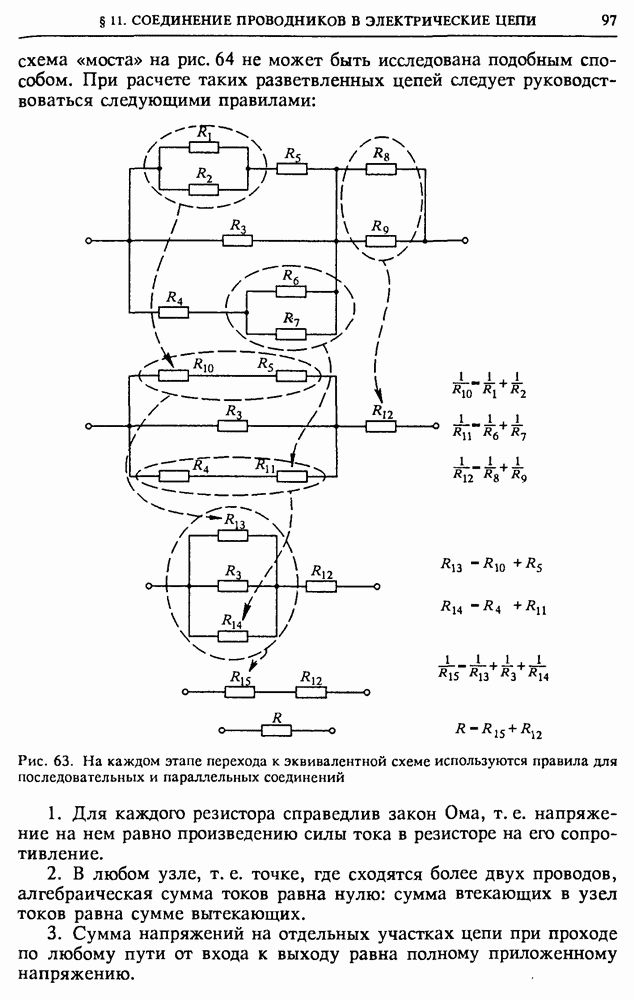
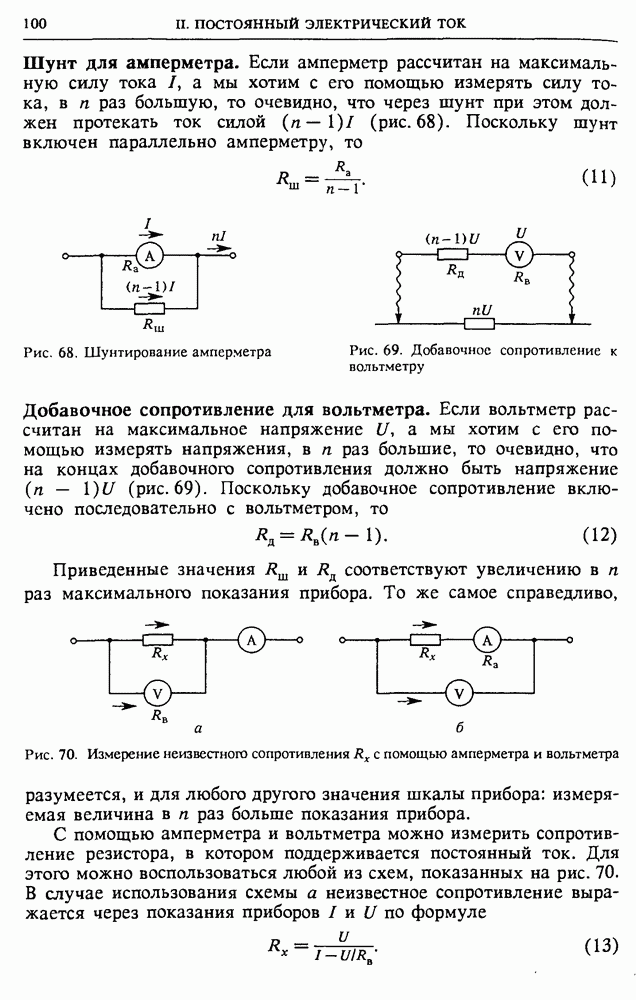
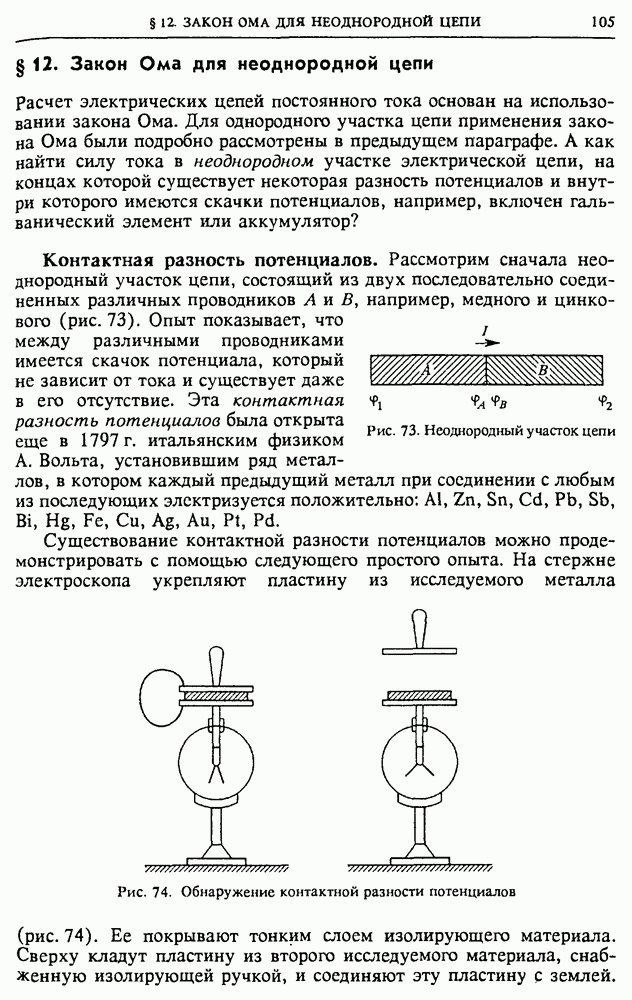
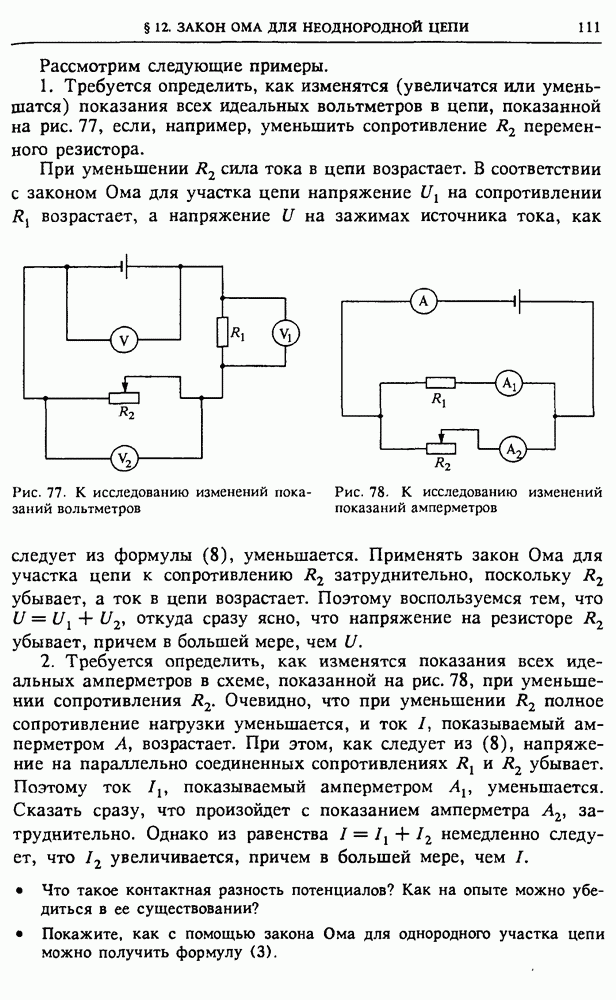
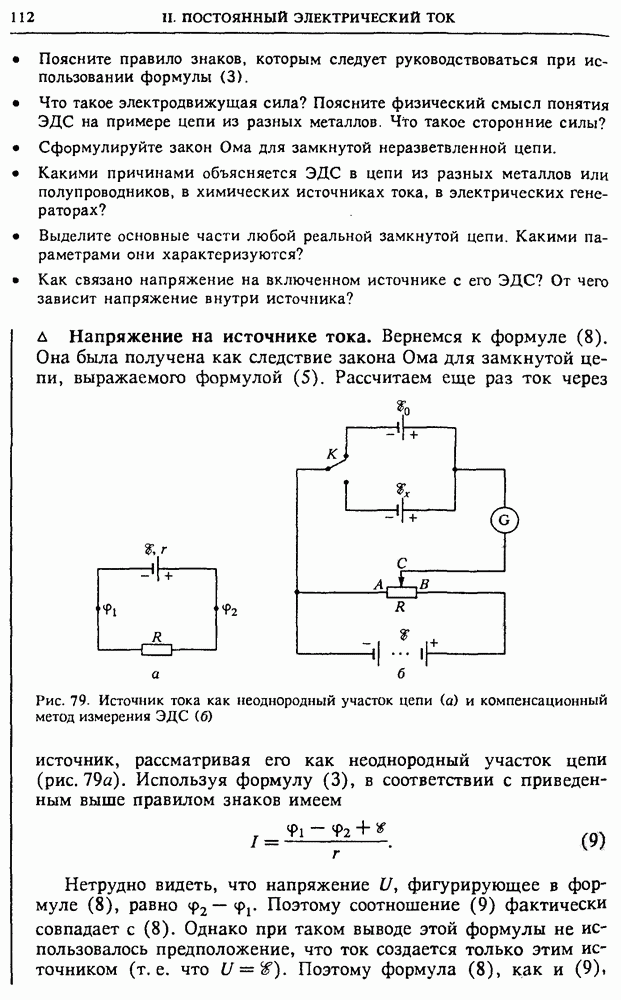
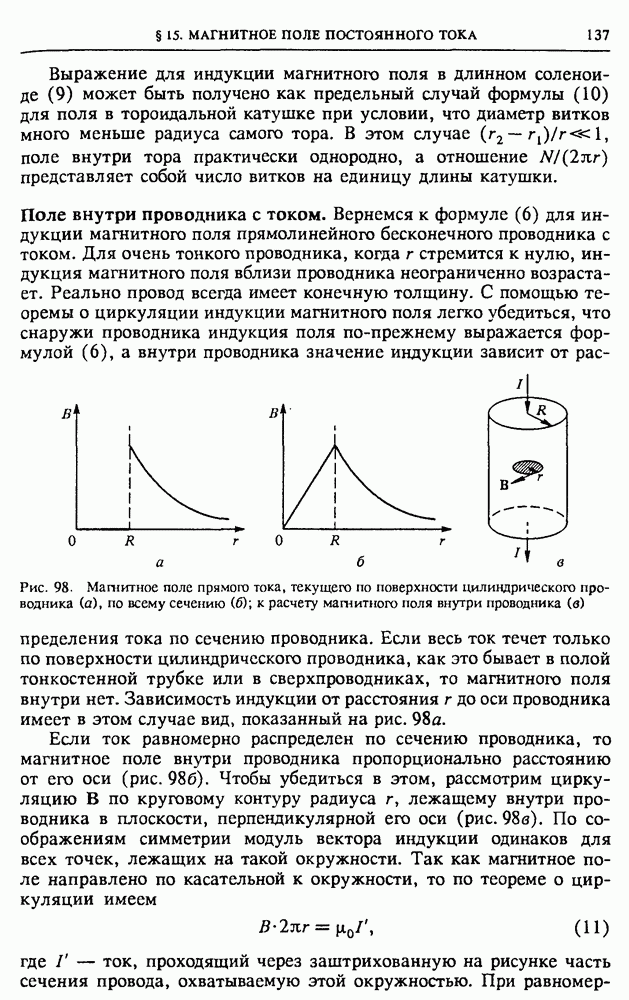
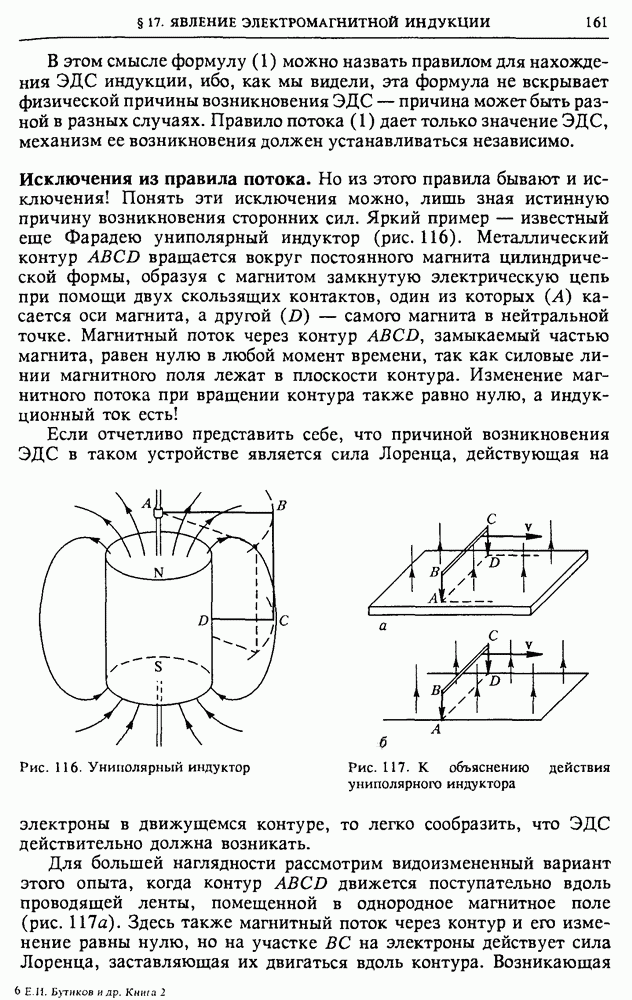
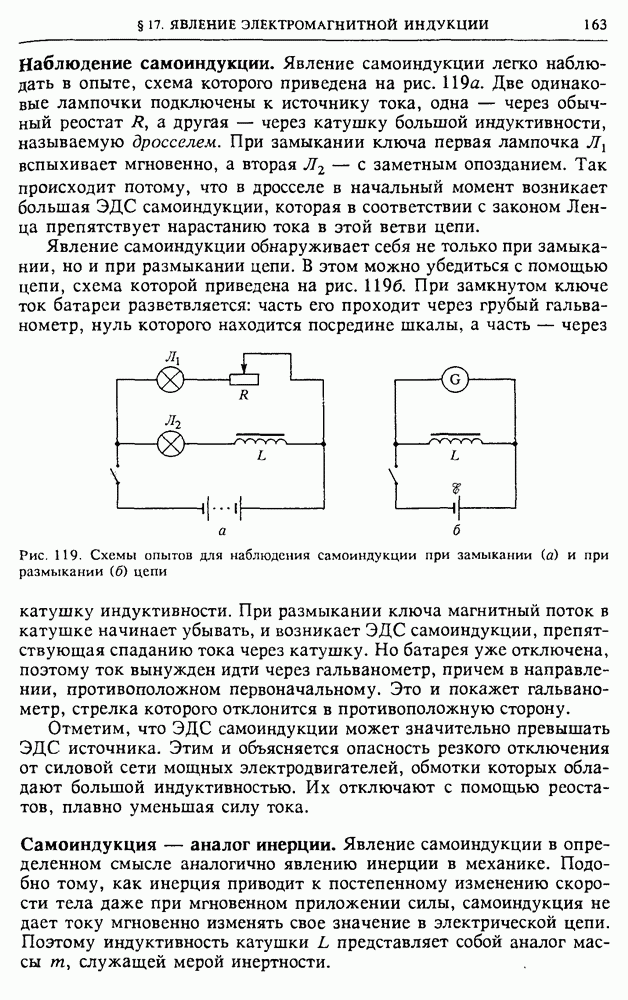
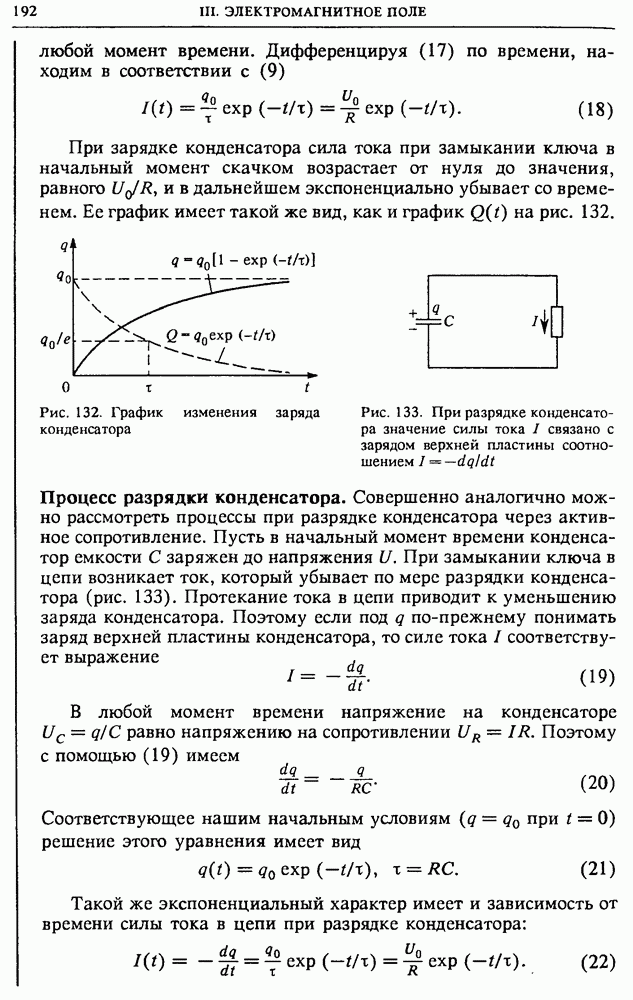
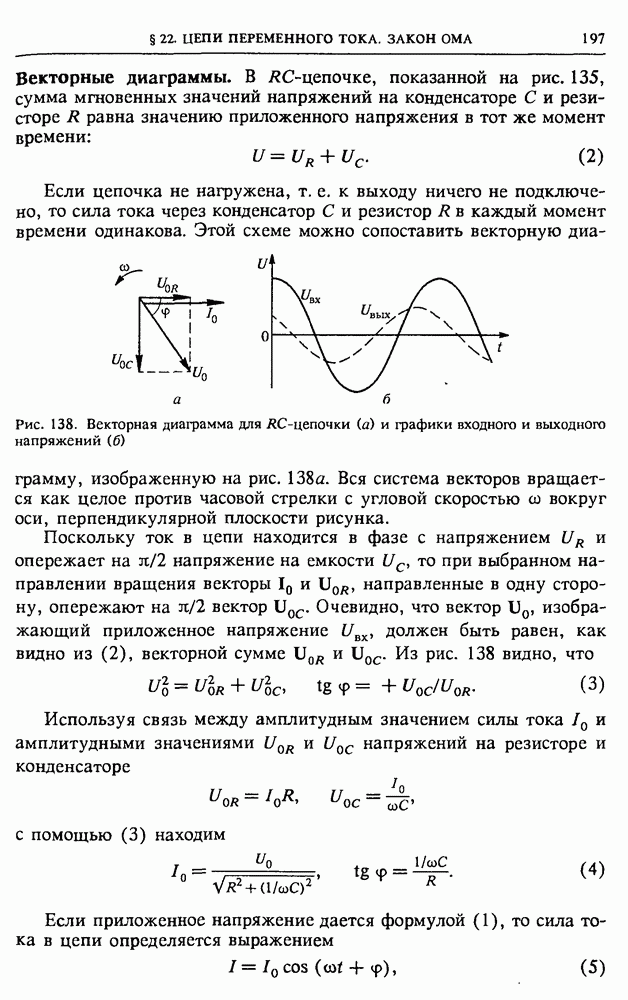
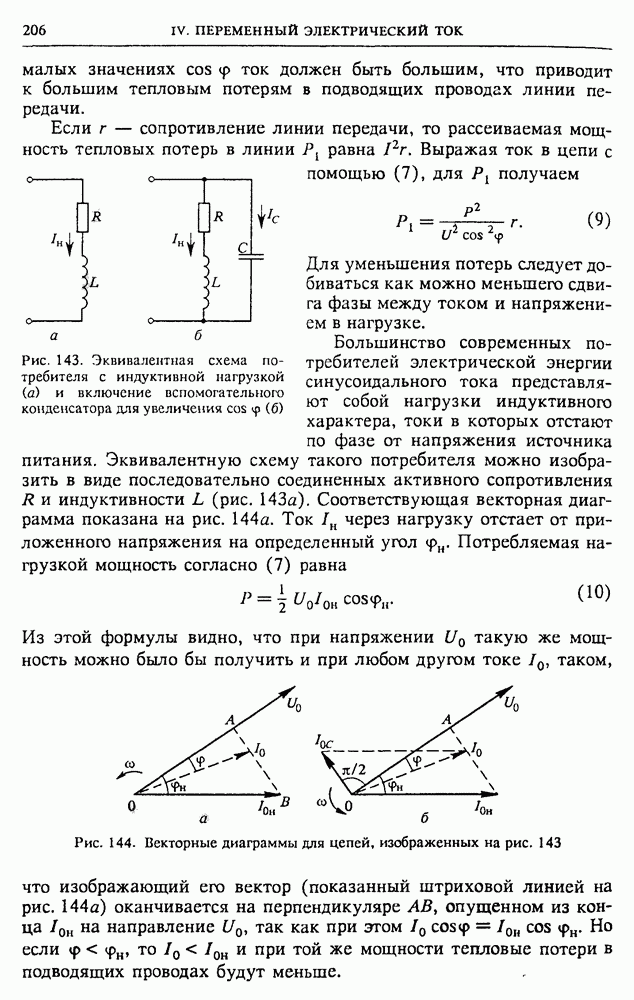
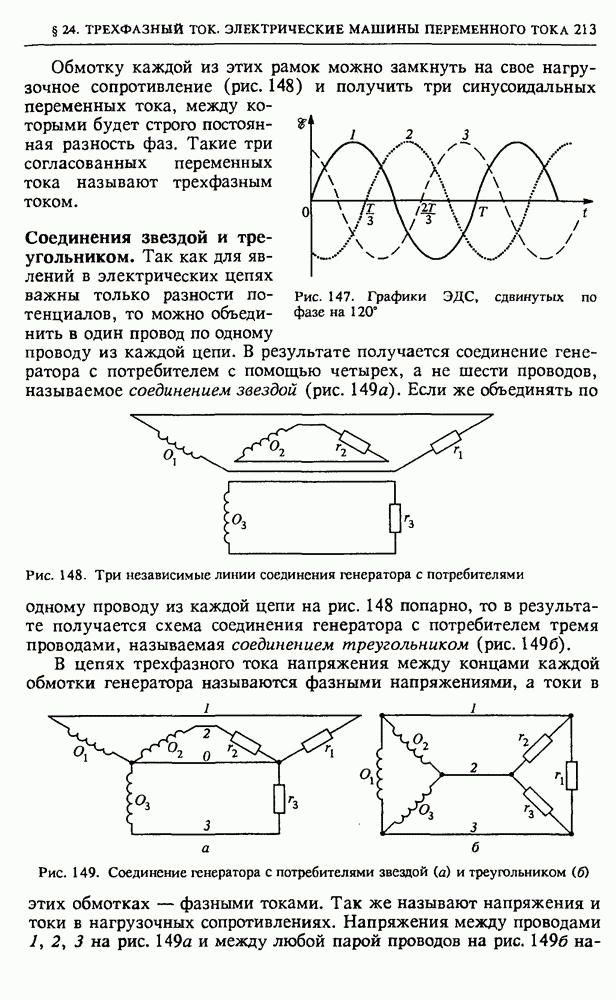
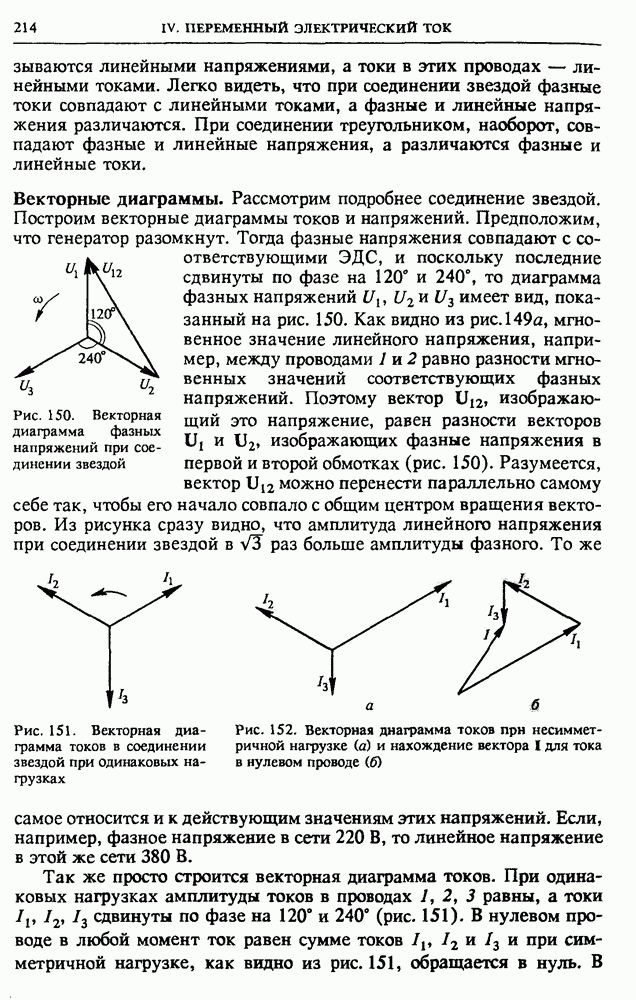
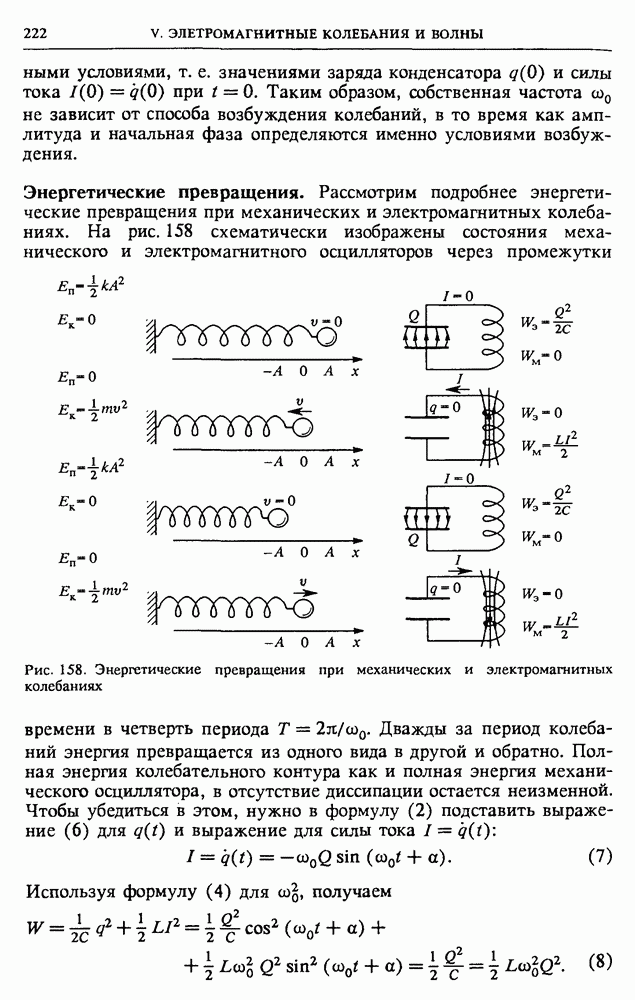
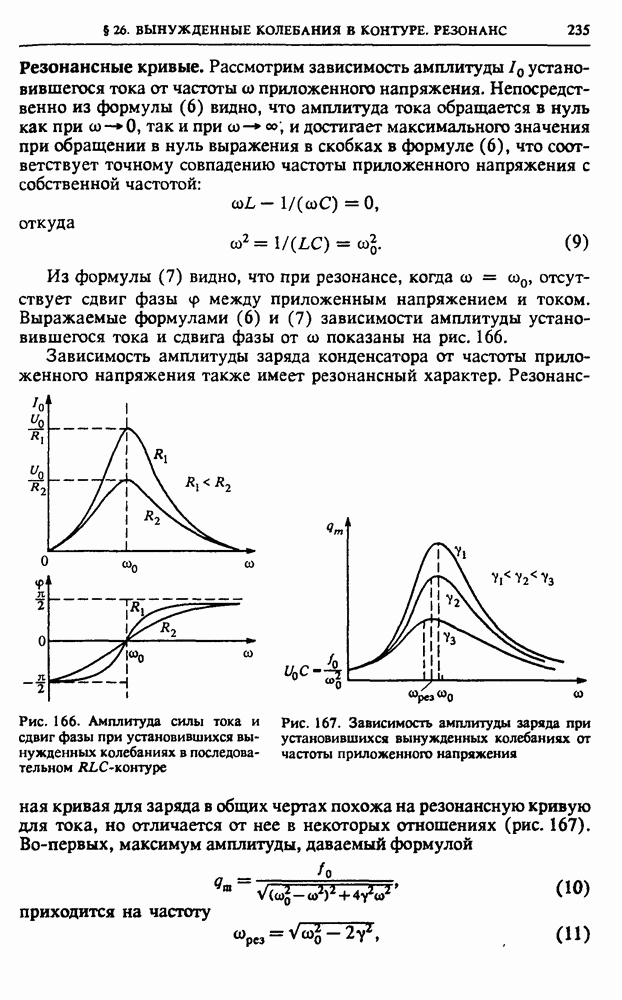
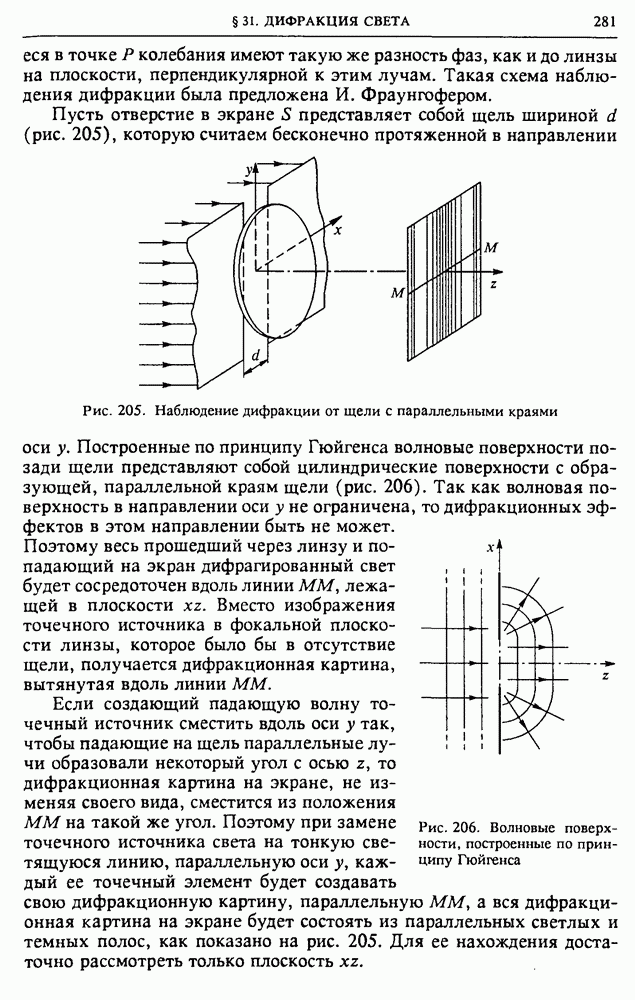
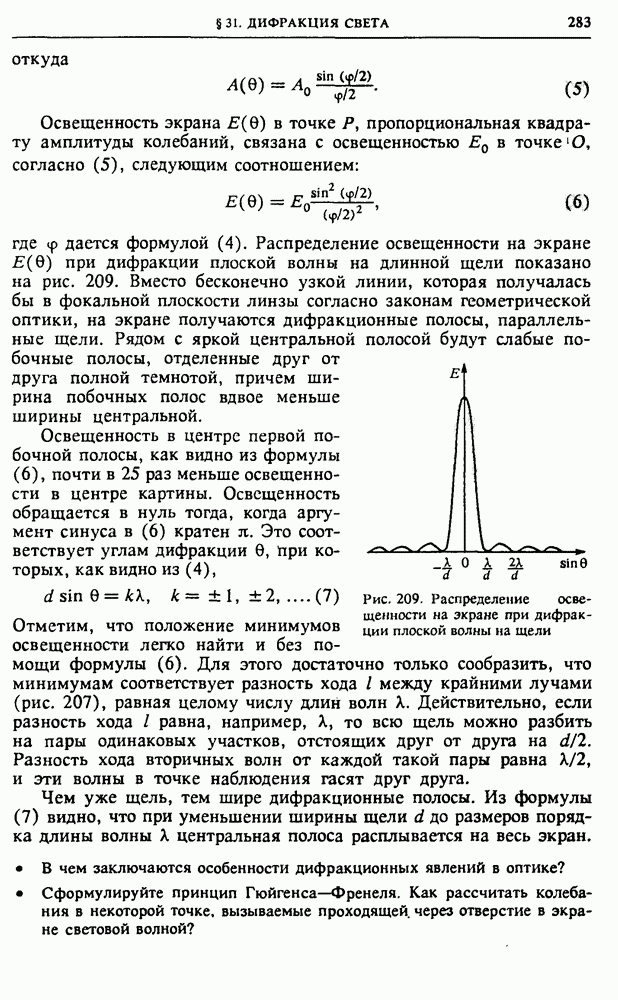
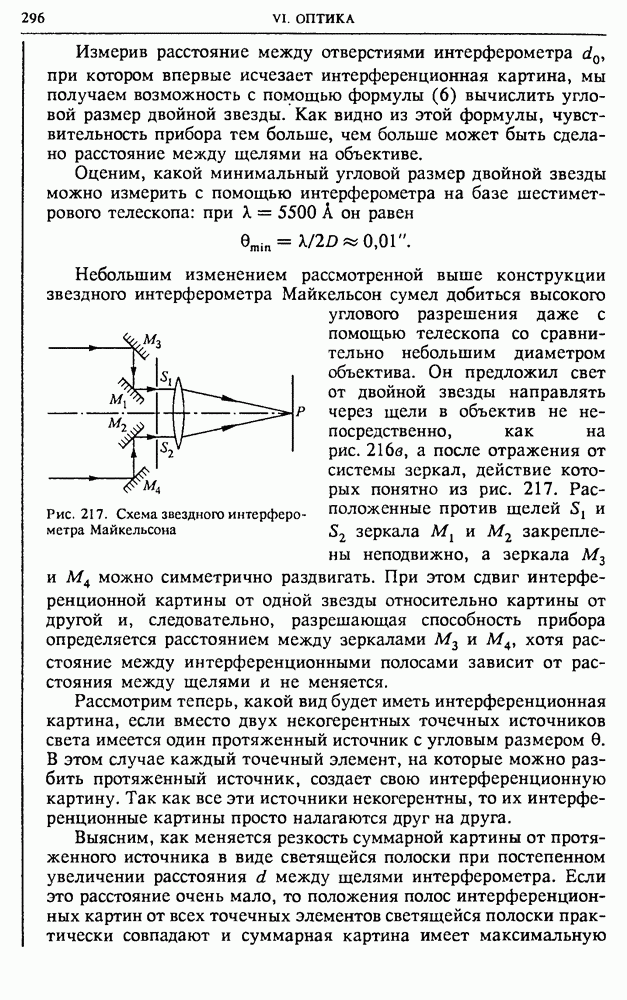
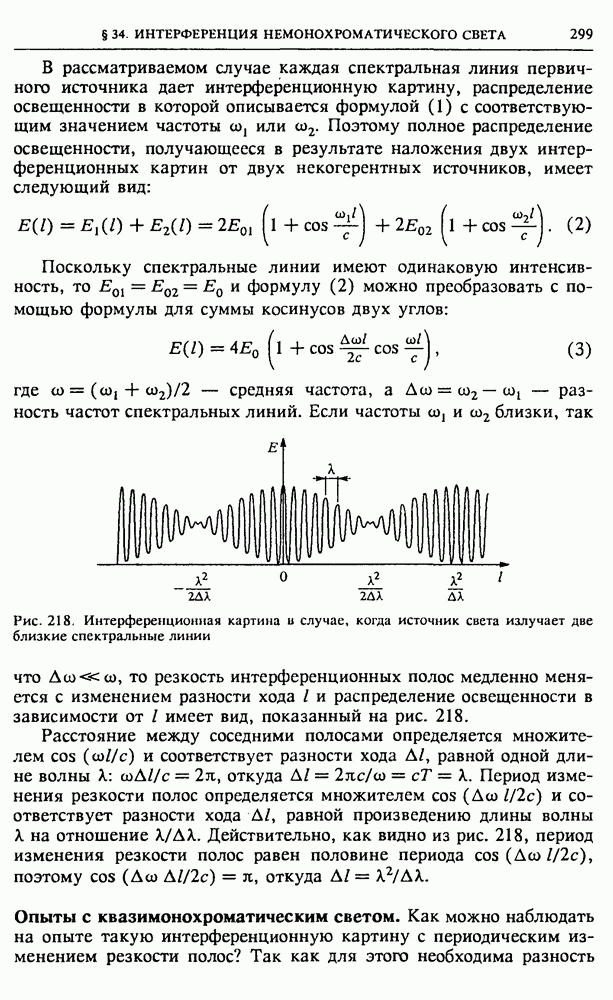
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. Энергия электрического поля
Заряженный конденсатор обладает энергией. Проще всего выражение для этой энергии получить, рассматривая плоский конденсатор.
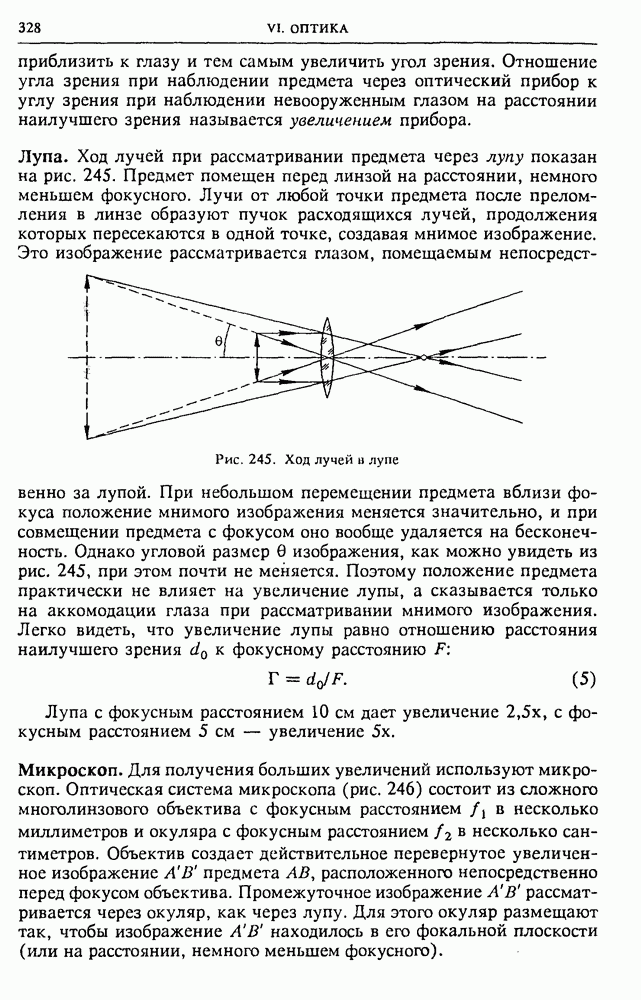
Энергия плоского конденсатора. Предположим, что пластины конденсатора, несущие равные и противоположные по знаку заряды, сначала расположены на расстоянии  Затем одной из пластин мысленно дадим возможность перемещаться в направлении к другой пластине вплоть до полного их совмещения, коща заряды пластин компенсируются и конденсатор фактически исчезнет. При этом исчезает и энергия конденсатора, поэтому работа действующей на пластину электрической силы, совершаемая при ее перемещении, как раз и равна первоначальному запасу энергии конденсатора. Подсчитаем эту работу.
Затем одной из пластин мысленно дадим возможность перемещаться в направлении к другой пластине вплоть до полного их совмещения, коща заряды пластин компенсируются и конденсатор фактически исчезнет. При этом исчезает и энергия конденсатора, поэтому работа действующей на пластину электрической силы, совершаемая при ее перемещении, как раз и равна первоначальному запасу энергии конденсатора. Подсчитаем эту работу.
Сила, действующая на пластину, равна произведению ее заряда  на напряженность однородного электрического поля, создаваемого другой пластиной. Эта напряженность, как мы видели в § 7, равна половине полной напряженности Е электрического поля внутри конденсатора, создаваемой зарядами обеих пластин. Поэтому искомая работа
на напряженность однородного электрического поля, создаваемого другой пластиной. Эта напряженность, как мы видели в § 7, равна половине полной напряженности Е электрического поля внутри конденсатора, создаваемой зарядами обеих пластин. Поэтому искомая работа  где
где  — напряжение между
— напряжение между
пластинами. Таким образом, выражение для энергии конденсатора через его заряд  и напряжение
и напряжение  имеет вид
имеет вид

Поскольку заряд конденсатора  и напряжение
и напряжение  связаны соотношением
связаны соотношением  то формулу (1) можно переписать в эквивалентной форме так, чтобы энергия выражалась либо только через заряд
то формулу (1) можно переписать в эквивалентной форме так, чтобы энергия выражалась либо только через заряд  либо только через напряжение
либо только через напряжение 

Энергия конденсатора. Эта формула справедлива для конденсатора любой формы. В этом можно убедиться, рассматривая работу, которую необходимо совершить для того, чтобы зарядить конденсатор, перенося заряд маленькими порциями с одной обкладки на другую. При вычислении этой работы следует учесть, что первая порция заряда  переносится через нулевую разность потенциалов, последняя — через полную разность потенциалов
переносится через нулевую разность потенциалов, последняя — через полную разность потенциалов  а в каждый момент разность потенциалов пропорциональна уже перенесенному заряду.
а в каждый момент разность потенциалов пропорциональна уже перенесенному заряду.
Формулы (1) или (2) для энергии заряженного конденсатора можно, разумеется, получить как частный случай общей формулы (12) § 4, справедливой для энергии системы любых заряженных тел:

Энергию заряженного конденсатора можно трактовать не только как потенциальную энергию взаимодействия зарядов, но и как энергию создаваемого этими зарядами электрического поля, заключенного в пространстве между обкладками конденсатора. Обратимся опять для простоты к плоскому конденсатору, где электрическое поле однородно. Подставляя  в выражение для энергии
в выражение для энергии  получаем
получаем

где  — объем между обкладками конденсатора, заполненный электрическим полем.
— объем между обкладками конденсатора, заполненный электрическим полем.
Плотность энергии электрического поля. Энергия заряженного конденсатора оказывается пропорциональной занимаемому электрическим полем объему. Очевидно, что множитель, стоящий перед V в формуле (4), имеет смысл энергии, заключенной в единичном объеме, т. е. объемной плотности  энергии электрического поля:
энергии электрического поля:

В СИ эта формула имеет вид

В системе единиц СГСЭ

Выражения  для объемной плотности энергии справедливы при любой конфигурации электрического поля.
для объемной плотности энергии справедливы при любой конфигурации электрического поля.
Энергия заряженного шара. Рассмотрим, например, энергию уединенного шара радиуса  по поверхности которого равномерно распределен заряд
по поверхности которого равномерно распределен заряд  . Такую систему можно рассматривать как предельный случай сферического конденсатора, радиус внешней обкладки которого стремится к бесконечности, а емкость принимает значение, равное радиусу шара
. Такую систему можно рассматривать как предельный случай сферического конденсатора, радиус внешней обкладки которого стремится к бесконечности, а емкость принимает значение, равное радиусу шара  (в системе единиц СГСЭ). Применяя для энергии формулу
(в системе единиц СГСЭ). Применяя для энергии формулу  получаем
получаем

Если рассматривать эту энергию как энергию поля, создаваемого шаром, то можно считать, что вся она локализована в окружающем шар пространстве, а не внутри его, так как там напряженность поля Е равна нулю. Наибольшее значение объемная плотность имеет вблизи поверхности шара и очень быстро убывает при удалении от нее — как  .
.
Собственная энергия точечного заряда. Таким образом, электростатическую энергию можно рассматривать либо как энергию взаимодействия зарядов, либо как энергию создаваемого этими зарядами поля.
Однако, рассматривая энергию двух разноименных точечных зарядов, мы приходим к противоречию. Согласно формуле (12) § 4 эта энергия отрицательна:  а если ее рассматривать как энергию поля этих зарядов, то энергия получается положительной, так как плотность энергии поля, пропорциональная
а если ее рассматривать как энергию поля этих зарядов, то энергия получается положительной, так как плотность энергии поля, пропорциональная  нигде не принимает отрицательных значений. В чем же здесь дело? Объясняется это тем, что в формуле (12) для энергии точечных зарядов учитывается лишь их взаимодействие, но не учитывается взаимодействие отдельных элементов каждого такого заряда между собой. Действительно, если мы имеем дело лишь с одним единственным точечным зарядом
нигде не принимает отрицательных значений. В чем же здесь дело? Объясняется это тем, что в формуле (12) для энергии точечных зарядов учитывается лишь их взаимодействие, но не учитывается взаимодействие отдельных элементов каждого такого заряда между собой. Действительно, если мы имеем дело лишь с одним единственным точечным зарядом  то энергия, вычисляемая по формуле (12), равна нулю, в то время как энергия электрического поля этого заряда имеет положительное (бесконечное для истинно точечного заряда) значение, равное так называемой собственной энергии заряда
то энергия, вычисляемая по формуле (12), равна нулю, в то время как энергия электрического поля этого заряда имеет положительное (бесконечное для истинно точечного заряда) значение, равное так называемой собственной энергии заряда  .
.
Чтобы убедиться в этом, обратимся к формуле (8) для энергии заряженного шара. Если устремить в ней  к нулю, то мы и придем к точечному заряду. С уменьшением
к нулю, то мы и придем к точечному заряду. С уменьшением  плотность энергии растет настолько быстро, что, как видно из (8), полная энергия поля оказывается бесконечно большой. В классической электродинамике собственная энергия точечного заряда бесконечна.
плотность энергии растет настолько быстро, что, как видно из (8), полная энергия поля оказывается бесконечно большой. В классической электродинамике собственная энергия точечного заряда бесконечна.
Собственная энергия произвольного заряда может рассматриваться как энергия взаимодействия его частей. Эта энергия зависит, конечно, от размеров и формы заряда. Часть ее освободилась бы при «взрыве» и разлете «осколков» заряда под действием кулоновских сил отталкивания, превратившись в кинетическую энергию «осколков», другая ее часть осталась бы в форме собственной энергии этих «осколков».
Рассмотрим теперь полную, т. е. собственную и взаимную, энергию двух зарядов  Пусть каждый из этих зарядов в отдельности создает соответственно поле
Пусть каждый из этих зарядов в отдельности создает соответственно поле  так что результирующее поле
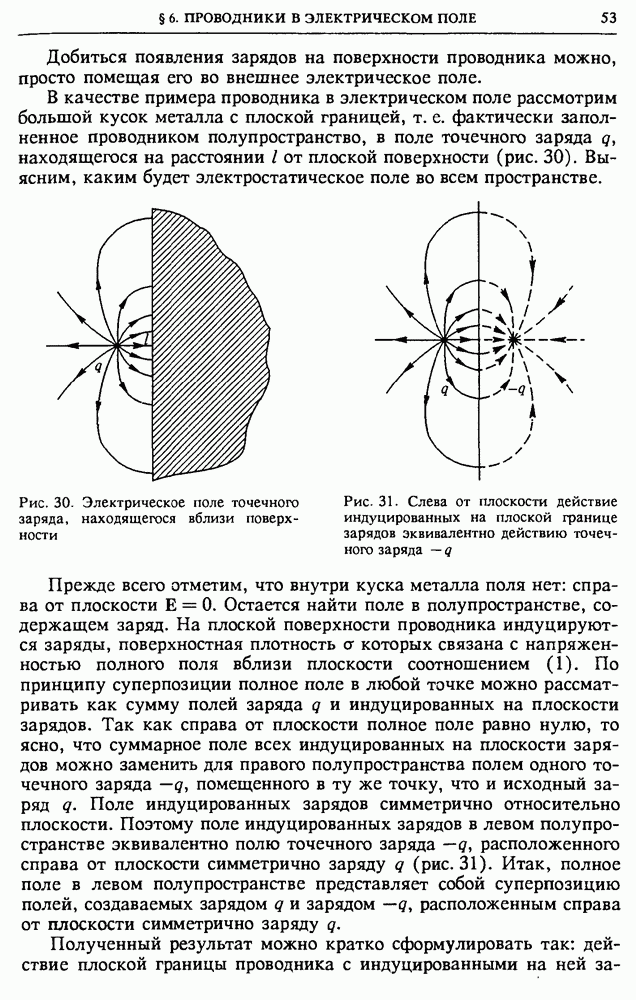
так что результирующее поле  Объемная плотность энергии поля распадается на три слагаемых в соответствии с выражением
Объемная плотность энергии поля распадается на три слагаемых в соответствии с выражением

Первые два слагаемых в правой части соответствуют объемной плотности собственных энергий зарядов  а третье слагаемое соответствует энергии взаимодействия зарядов друг с другом. Именно эта часть полной энергии системы и дается формулой (12) § 4. Из очевидного неравенства
а третье слагаемое соответствует энергии взаимодействия зарядов друг с другом. Именно эта часть полной энергии системы и дается формулой (12) § 4. Из очевидного неравенства  следует, что
следует, что  Таким образом, положительная собственная энергия зарядов всегда больше или в крайнем случае равна их взаимной энергии. Насмотря на то, что взаимная энергия может принимать как положительные, так и отрицательные значения, полная энергия, пропорциональная
Таким образом, положительная собственная энергия зарядов всегда больше или в крайнем случае равна их взаимной энергии. Насмотря на то, что взаимная энергия может принимать как положительные, так и отрицательные значения, полная энергия, пропорциональная  всегда положительна.
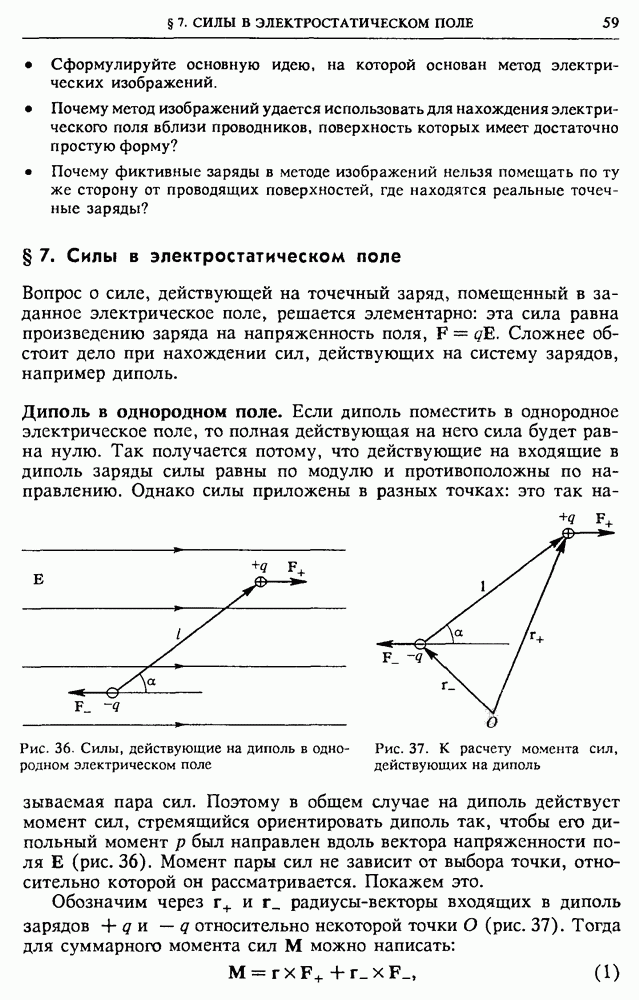
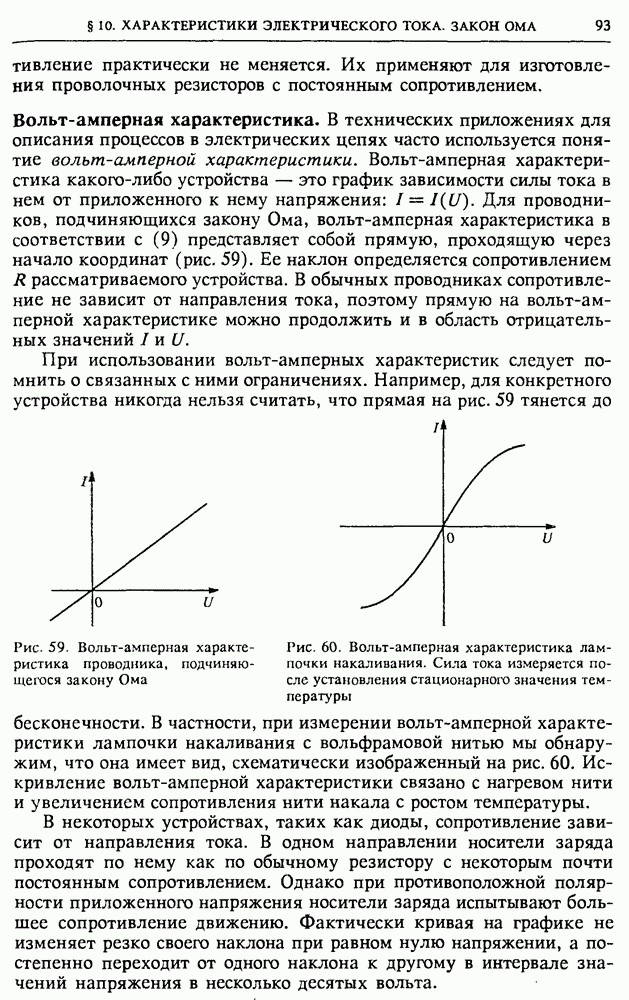
всегда положительна.
При всех возможных перемещениях зарядов, не изменяющих их формы и размеров, собственная энергия зарядов остается постоянной. Поэтому при таких перемещениях изменение полной энергии системы зарядов равно изменению их взаимной энергии. Так как во всех физических явлениях существенно именно изменение энергии системы, то постоянная часть — собственная энергия зарядов — может быть отброшена. В этом смысле и следует понимать утверждение об эквивалентности энергии взаимодействия зарядов и энергии создаваемого ими поля. Итак, мы можем сопоставлять системе зарядов либо полную энергию — энергию поля, либо энергию взаимодействия и будем получать при этом, вообще говоря, разные значения. Но, рассматривая переход системы из одного состояния в другое, мы для изменения энергии всегда получим одну и ту же величину.
Обратим внимание, что при использовании формулы (12) § 4 для системы точечных зарядов и проводников мы получаем, как видно
из самого вывода формулы, собственную энергию проводников и взаимную потенциальную энергию всех входящих в систему зарядов, т. е. полную энергию поля за вычетом неизменной собственной энергии точечных зарядов.
Собственная энергия проводника. Собственная энергия проводников, в отличие от собственной энергии точечных зарядов, не является постоянной. Она может измениться при изменении конфигурации системы вследствие перемещения зарядов в проводниках. Поэтому эта энергия не может быть отброшена при вычислении изменения энергии системы.
В том случае, когда система состоит только из проводников, а точечных зарядов нет, формула (12) §4 дает полную энергию системы, т. е. сумму собственных энергий всех проводников и энергии их взаимодействия. Мы получаем одно и то же значение независимо от того, рассматриваем ли энергию поля или энергию системы зарядов. Примером такой системы является конденсатор, где, как мы видели, оба подхода дают одинаковый результат 
Очевидно, что при наличии точечных зарядов и проводников не имеет смысла рассматривать по отдельности собственную энергию проводников и взаимную потенциальную энергию всех зарядов, так как работа внешних сил определяет изменение суммы этих энергий. Исключить из рассмотрения можно только неизменную собственную энергию точечных зарядов.
Энергетические превращения в конденсаторах. Для анализа энергетических превращений, которые могут происходить в электрическом поле, рассмотрим плоский конденсатор с воздушным зазором, подсоединенный к источнику с постоянным напряжением  Будем раздвигать пластины конденсатора от расстояния
Будем раздвигать пластины конденсатора от расстояния  до расстояния
до расстояния  в двух случаях: предварительно отсоединив конденсатор от источника питания и не отсоединяя конденсатор от источника.
в двух случаях: предварительно отсоединив конденсатор от источника питания и не отсоединяя конденсатор от источника.
В первом случае заряд на обкладках конденсатора все время остается неизменным:  хотя емкость С и напряжение
хотя емкость С и напряжение  изменяются при движении пластин. Зная напряжение на конденсаторе в начальный момент, находим величину этого заряда (в единицах СИ):
изменяются при движении пластин. Зная напряжение на конденсаторе в начальный момент, находим величину этого заряда (в единицах СИ):

Так как разноименно заряженные пластины конденсатора притягиваются, для их раздвижения необходимо совершить положительную механическую работу. Если при раздвижении расстояние между пластинами все время остается много меньше их линейных размеров, то сила притяжения пластин не зависит от расстояния между ними.
Для равномерного перемещения пластины внешняя сила должна уравновесить силу притяжения, и поэтому совершаемая при перемещении пластины на расстояние  механическая работа равна
механическая работа равна

так как  где
где  — неизменная напряженность поля, создаваемого зарядами обеих обкладок. Подставляя в (11) заряд из (10) и
— неизменная напряженность поля, создаваемого зарядами обеих обкладок. Подставляя в (11) заряд из (10) и  находим
находим

Второй случай отличается от рассмотренного тем, что при движении пластин остается неизменным не заряд конденсатора, а напряжение на нем:  Поскольку расстояние между обкладками увеличивается, то напряженность поля убывает, а следовательно, убывает и заряд на пластинах. Поэтому сила притяжения пластин не остается постоянной, как в первом случае, а убывает, причем, как нетрудно убедиться, обратно пропорционально квадрату расстояния. Вычислить работу этой переменной силы можно с помощью закона сохранения и превращения энергии.
Поскольку расстояние между обкладками увеличивается, то напряженность поля убывает, а следовательно, убывает и заряд на пластинах. Поэтому сила притяжения пластин не остается постоянной, как в первом случае, а убывает, причем, как нетрудно убедиться, обратно пропорционально квадрату расстояния. Вычислить работу этой переменной силы можно с помощью закона сохранения и превращения энергии.
Применим его сначала к более простому первому случаю. Изменение энергии  конденсатора происходит только за счет механической работы, совершаемой внешними силами:
конденсатора происходит только за счет механической работы, совершаемой внешними силами:  Поскольку заряд конденсатора остается неизменным, для энергии конденсатора удобно воспользоваться формулой
Поскольку заряд конденсатора остается неизменным, для энергии конденсатора удобно воспользоваться формулой  Таким образом,
Таким образом,

что при подстановке выражения для емкости и для заряда (10) приводит к окончательной формуле (12). Обратим внимание, что этот результат можно получить и рассматривая энергию конденсатора как энергию электрического поля между его обкладками. Так как напряженность поля и, следовательно, плотность энергии остаются неизменными, а объем, занимаемый полем, возрастает, то увеличение энергии равно произведению плотности энергии  на приращение объема
на приращение объема 
Во втором случае энергия конденсатора изменяется как за счет механической работы, так и за счет работы, совершаемой источником питания:

Определив независимо изменение энергии конденсатора и работу источника, можно с помощью закона сохранения энергии (13) найти механическую работу.
Поскольку в этом случае остается неизменным напряжение, для расчета энергии конденсатора удобно использовать формулу  Для изменения энергии получаем
Для изменения энергии получаем

При изменении заряда на обкладках конденсатора на величину  источник питания совершает работу
источник питания совершает работу  Заряд конденсатора определяется соотношением
Заряд конденсатора определяется соотношением  Тогда
Тогда

и с помощью выражения (13) получаем

Отметим, что из (15) и (14) видно, что

т. е. работа источника равна удвоенному изменению энергии конденсатора.
Интересно отметить, что как работа источника, так и изменение энергии конденсатора получились отрицательными. Это вполне понятно: совершаемая механическая работа положительна и должна была бы привести к увеличению энергии конденсатора (как и происходит в первом случае). Но энергия конденсатора убывает, и, следовательно, источник должен «принять на себя» энергию, равную убыли энергии конденсатора и механической работе внешних сил. Если процессы в источнике обратимы (аккумулятор), то он будет заряжаться, в противном случае источник просто нагревается.
Чтобы лучше разобраться в сути явлений, рассмотрим противоположный случай: присоединенные к источнику пластины конденсатора сближают от расстояния  до расстояния
до расстояния  Поскольку пластины притягиваются, работа внешних сил отрицательна, ибо для равномерного перемещения пластин внешняя сила должна быть направлена в сторону, противоположную перемещению. Энергия конденсатора при сближении пластин возрастает. Итак, механическая работа внешних сил отрицательна, а энергия конденсатора возросла, следовательно, источник совершил положительную работу. Половина этой работы равна увеличению энергии конденсатора, вторая половина передана внешним телам в виде механической работы при сближении пластин. Все приведенные выше формулы применимы, разумеется, при любом направлении перемещения пластин.
Поскольку пластины притягиваются, работа внешних сил отрицательна, ибо для равномерного перемещения пластин внешняя сила должна быть направлена в сторону, противоположную перемещению. Энергия конденсатора при сближении пластин возрастает. Итак, механическая работа внешних сил отрицательна, а энергия конденсатора возросла, следовательно, источник совершил положительную работу. Половина этой работы равна увеличению энергии конденсатора, вторая половина передана внешним телам в виде механической работы при сближении пластин. Все приведенные выше формулы применимы, разумеется, при любом направлении перемещения пластин.
Во всех рассуждениях мы пренебрегали сопротивлением проводов, соединяющих конденсатор с источником. Если учитывать выделяющуюся в проводах при движении зарядов теплоту  уравнение
уравнение
баланса энергии принимает вид

Изменение энергии конденсатора и работа источника выражаются, конечно, прежними формулами (14) и (15). Теплота всегда выделяется независимо от того, сближаются или раздвигаются пластины, поэтому  Значение
Значение  можно вычислить, если известна скорость движения пластин. Чем больше скорость движения, тем больше выделяющаяся теплота. При бесконечно медленном движении пластин
можно вычислить, если известна скорость движения пластин. Чем больше скорость движения, тем больше выделяющаяся теплота. При бесконечно медленном движении пластин 
Изменение энергии и работа источника. Выше мы отметили, что работа источника питания при раздвижении пластин равна удвоенному изменению энергии конденсатора. Этот факт носит универсальный характер: если любым способом изменить энергию подсоединенного к источнику питания конденсатора, то работа, совершаемая при этом источником питания, равна удвоенному значению изменения энергии конденсатора:

Как в этом убедиться? Поскольку конденсатор все время остается присоединенным к источнику питания, напряжение на конденсаторе равно  как в начале, так и в конце процесса (хотя во время процесса напряжение на конденсаторе может быть и меньше). Если заряд конденсатора во время процесса изменился на величину
как в начале, так и в конце процесса (хотя во время процесса напряжение на конденсаторе может быть и меньше). Если заряд конденсатора во время процесса изменился на величину  то его энергия изменилась на величину
то его энергия изменилась на величину

При этом источник питания совершил работу

Чтобы не возникало подозрений в том, что половина энергии «бесследно исчезла», напишем уравнение баланса энергии:

где  — механическая работа, совершенная при этом процессе силами, действующими на внешние тела,
— механическая работа, совершенная при этом процессе силами, действующими на внешние тела,  выделившаяся теплота. Очевидно, что
выделившаяся теплота. Очевидно, что  и равно оставшейся половине работы источника. Существуют такие процессы, в которых либо
и равно оставшейся половине работы источника. Существуют такие процессы, в которых либо  либо
либо  Но, как видно из (16) и (17), изменение энергии конденсатора, соединенного с источником, обязательно сопровождается либо совершением механической работы, либо выделением теплоты.
Но, как видно из (16) и (17), изменение энергии конденсатора, соединенного с источником, обязательно сопровождается либо совершением механической работы, либо выделением теплоты.
• Получите формулу для энергии заряженного конденсатора, рассматривая работу, совершаемую при его зарядке путем переноса заряда с одной обкладки на другую.
• Поясните качественно, почему объемная плотность энергии электрического поля пропорциональна квадрату его напряженности.
• Что такое собственная энергия точечного заряда? Как в электростатике преодолевается трудность, связанная с бесконечным значением собственной энергии точечных зарядов?
• Поясните, почему два первых слагаемых в правой части формулы (9) соответствуют объемной плотности собственных энергий точечных зарядов  а третье слагаемое — энергии взаимодействия зарядов друг с другом.
а третье слагаемое — энергии взаимодействия зарядов друг с другом.
• Как связаны между собой изменение энергии конденсатора при каком-либо процессе и работа источника питания, к которому подсоединен этот конденсатор в течение всего процесса?
• При каких условиях изменение энергии конденсатора, соединенного с источником питания, не сопровождается выделением теплоты?
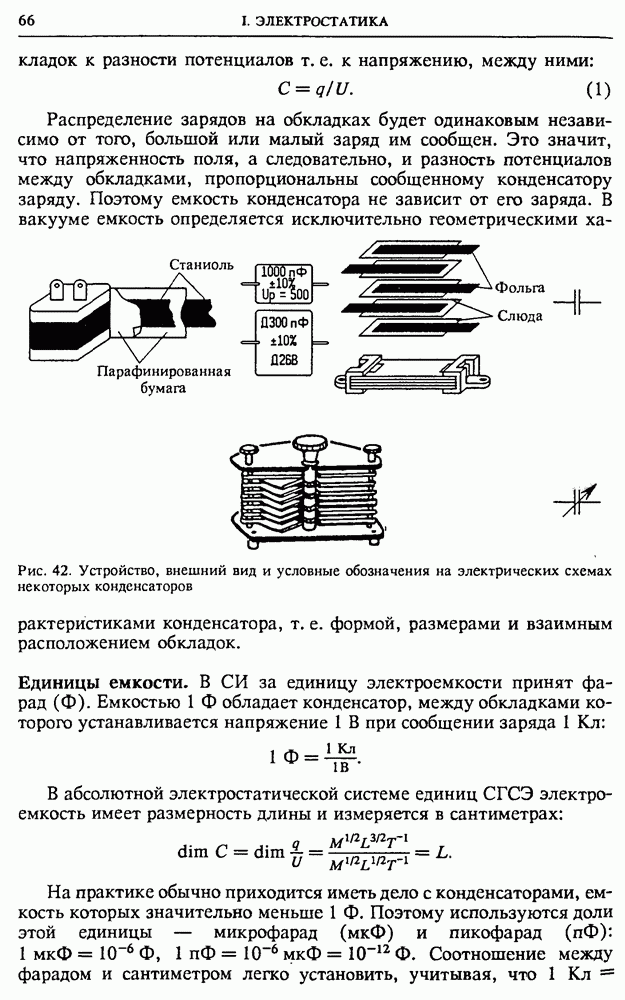
Конденсатор с диэлектриком. Рассмотрим теперь энергетические превращения в конденсаторах при наличии диэлектрика между обкладками, считая для простоты его диэлектрическую проницаемость  постоянной. Емкость конденсатора с диэлектриком в
постоянной. Емкость конденсатора с диэлектриком в  раз больше, чем емкость С такого же конденсатора без диэлектрика. Конденсатор с зарядом
раз больше, чем емкость С такого же конденсатора без диэлектрика. Конденсатор с зарядом  отсоединенный от источника питания, обладает энергией
отсоединенный от источника питания, обладает энергией 

Рис. 52. Втягивание пластины из диэлектрика в плоский конденсатор
При заполнении пространства между обкладками диэлектриком с проницаемостью  энергия конденсатора уменьшится в
энергия конденсатора уменьшится в  раз:
раз:  Отсюда сразу можно сделать вывод о том, что диэлектрик втягивается в электрическое поле.
Отсюда сразу можно сделать вывод о том, что диэлектрик втягивается в электрическое поле.
Втягивающая сила при неизменном заряде конденсатора убывает по мере заполнения диэлектриком пространства между обкладками. Если на пластинах конденсатора поддерживается постоянное напряжение, то сила, втягивающая диэлектрик, не зависит от длины втянутой части.
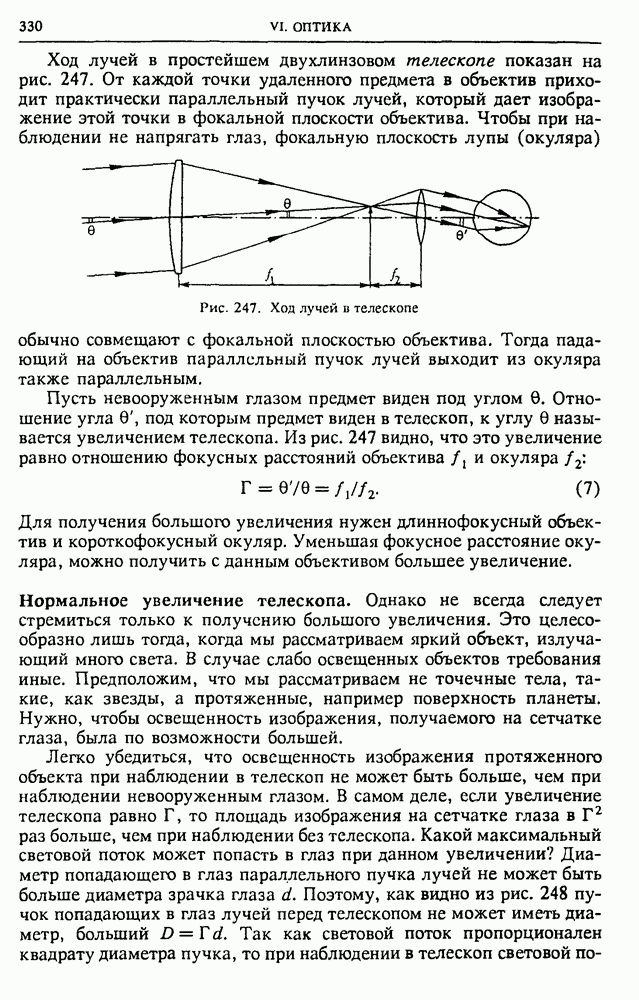
Для нахождения силы, действующей на диэлектрик со стороны электрического поля, рассмотрим втягивание твердого диэлектрика в горизонтально расположенный конденсатор, соединенный с источником постоянного напряжения  (рис. 52). Пусть под действием интересующей нас втягивающей силы
(рис. 52). Пусть под действием интересующей нас втягивающей силы  и какой-то внешней силы
и какой-то внешней силы  кусок диэлектрика находится в
кусок диэлектрика находится в
равновесии и длина втянутой части при этом равна х. Допустим, что диэлектрик вдвинулся на расстояние  Внешняя сила
Внешняя сила  при этом совершает отрицательную работу, равную
при этом совершает отрицательную работу, равную  Из закона сохранения энергии следует, что изменение энергии конденсатора
Из закона сохранения энергии следует, что изменение энергии конденсатора  равно сумме работы источника Аист и работы внешней силы
равно сумме работы источника Аист и работы внешней силы 

Как мы знаем,  поэтому уравнение (18) можно переписать в виде
поэтому уравнение (18) можно переписать в виде

Изменение энергии конденсатора при вдвигании диэлектрика на расстояние  равно
равно

где I — поперечный размер пластины.
С помощью формул (19) и (20) находим

т. е. сила при вдвигании диэлектрика постоянна при неизменном напряжении.
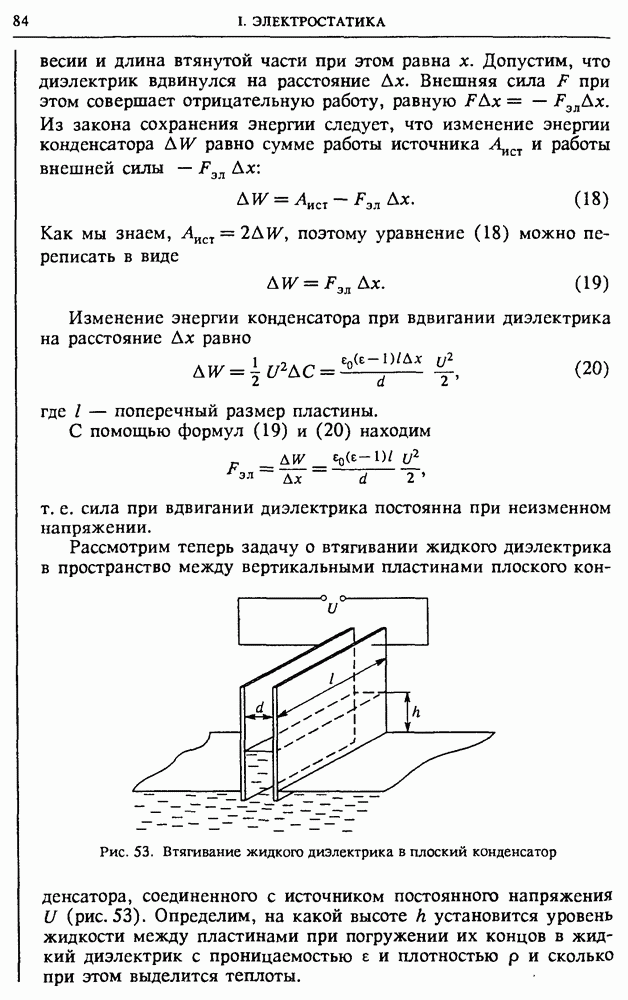
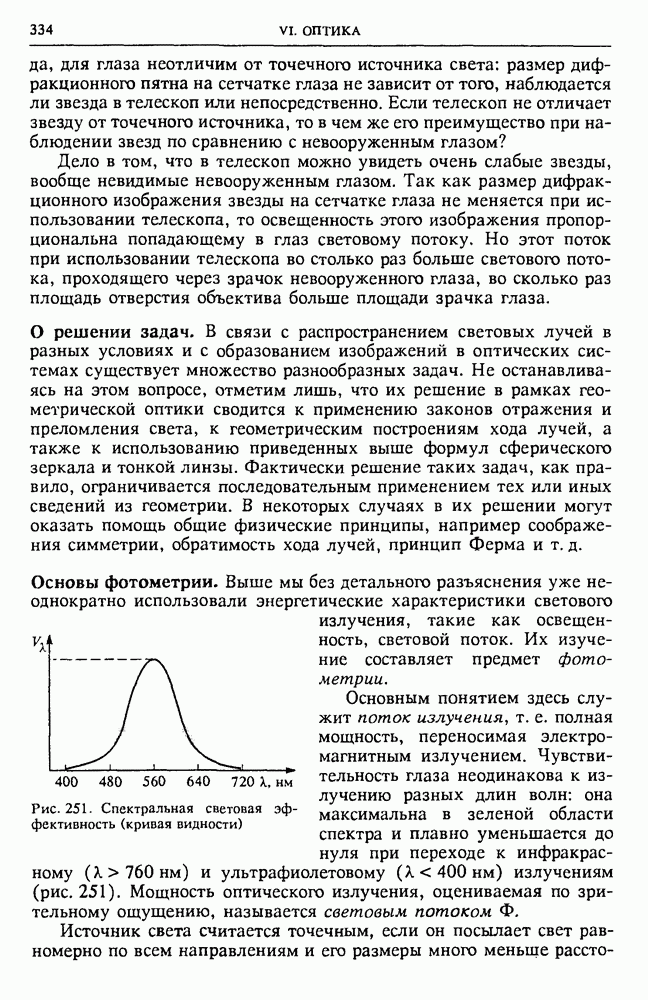
Рассмотрим теперь задачу о втягивании жидкого диэлектрика в пространство между вертикальными пластинами плоского конденсатора, соединенного с источником постоянного напряжения  (рис. 53).
(рис. 53).

Рис. 53. Втягивание жидкого диэлектрика в плоский конденсатор
Определим, на какой высоте  установится уровень жидкости между пластинами при погружении их концов в жидкий диэлектрик с проницаемостью
установится уровень жидкости между пластинами при погружении их концов в жидкий диэлектрик с проницаемостью  и плотностью
и плотностью  и сколько при этом выделится теплоты.
и сколько при этом выделится теплоты.
В состоянии равновесия сила, втягивающая диэлектрик в пространство между пластинами, уравновешивается силой тяжести Р, действующей на поднятую жидкость:  Для нахождения высоты подъема жидкого диэлектрика приравняем вычисленную втягивающую силу весу поднявшейся жидкости и получим
Для нахождения высоты подъема жидкого диэлектрика приравняем вычисленную втягивающую силу весу поднявшейся жидкости и получим

Для нахождения выделившейся при подъеме жидкости теплоты проще всего исходить из закона сохранения энергии. Поскольку поднятый столб жидкости покоится, совершенная источником работа равна сумме изменений энергий конденсатора и потенциальной энергии диэлектрика в поле тяжести, а также выделившейся теплоты 

Учитывая, что  и пользуясь соотношением (21), находим
и пользуясь соотношением (21), находим

Таким образом, работа источника питания разделилась пополам: одна половина пошла на увеличение электростатической энергии конденсатора; вторая половина разделилась поровну между увеличением потенциальной энергии диэлектрика в поле тяжести и выделившейся теплотой. Как происходило выделение этой теплоты? При погружении пластин конденсатора в диэлектрик жидкость начинает подниматься, приобретая кинетическую энергию, и по инерции проскакивает положение равновесия. Возникают колебания, которые постепенно затухают из-за вязкости жидкости, и кинетическая энергия превращается в теплоту. Если вязкость достаточно велика, то колебаний может и не быть — вся теплота выделяется при подъеме жидкости до положения равновесия.
• Сформулируйте закон сохранения энергии для процесса, в котором наряду с изменением электростатической энергии изменяется еще какая-либо энергия и происходит выделение теплоты.
• Поясните физический механизм возникновения сил, втягивающих диэлектрик в пространство между пластинами заряженного конденсатора.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
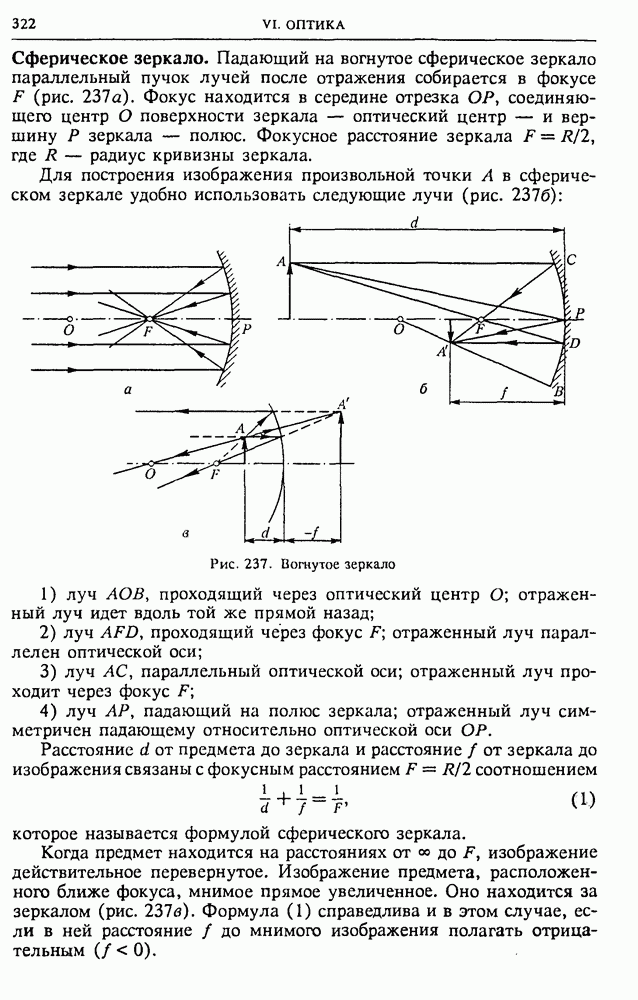
- § 36. Геометрическая оптика
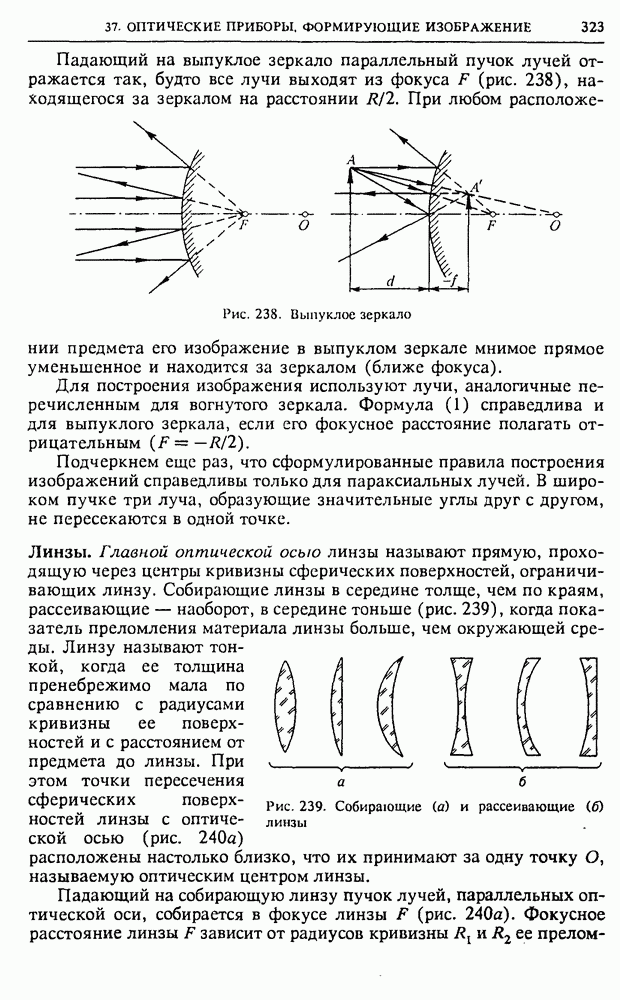
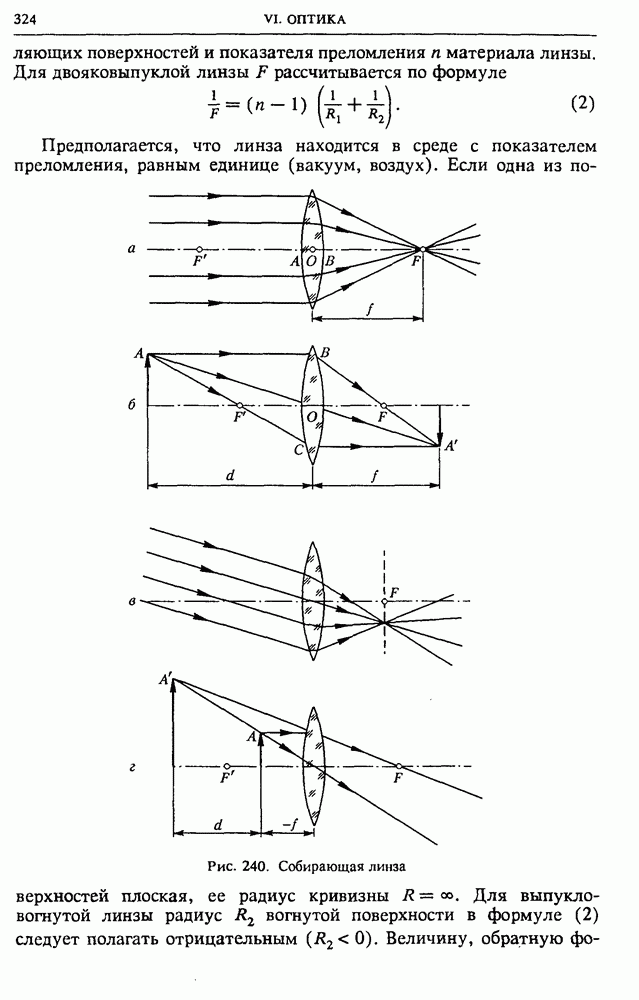
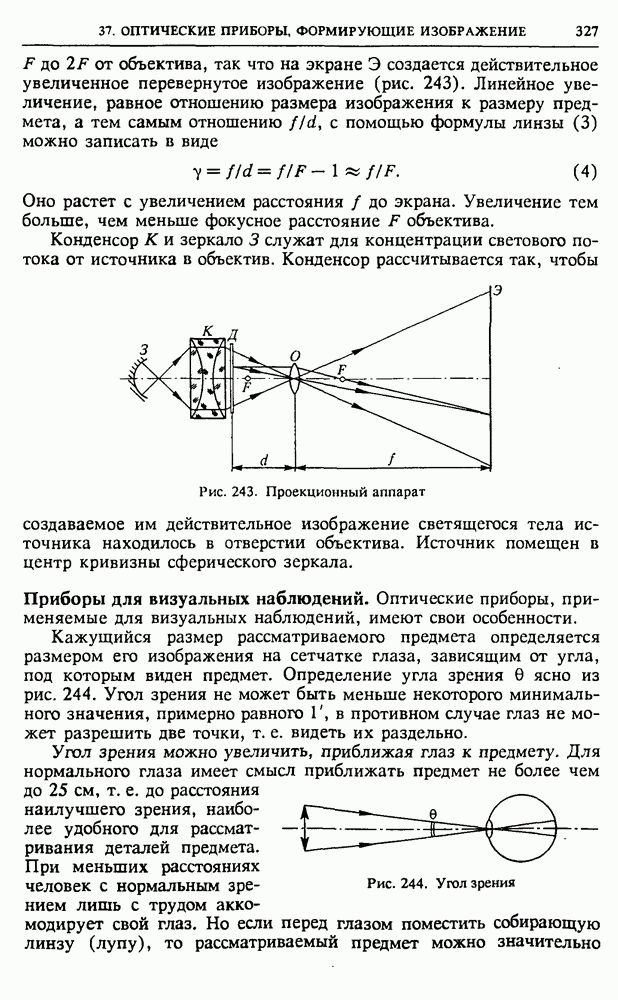
- § 37. Оптические приборы, формирующие изображение