§ 4. Потенциал электростатического поля. Энергия системы зарядов

Электростатическое поле — это потенциальное поле. Понятие о потенциальных силовых полях было введено в курсе механики. Поле называется потенциальным, если работа сил этого поля при перемещении из одной точки в другую не зависит от формы траектории, а определяется только начальным и конечным положениями.

Потенциальным является любое центральное поле, в котором сила зависит только от расстояния до силового центра и направлена по радиусу. Доказательство этого утверждения рассматривалось в курсе механики. Электростатическое поле, создаваемое уединенным точечным зарядом, описывается законом Кулона. Это поле сферически-симметрично и представляет собой частный случай центрального поля. Отсюда следует потенциальный характер электростатического поля точечного заряда.

В соответствии с принципом суперпозиции напряженность электростатического поля, создаваемого любым, сколь угодно сложным распределением неподвижных зарядов, представляет собой векторную сумму напряженностей полей, создаваемых каждым зарядом в отдельности. Сила, действующая на перемещаемый пробный заряд, определяется полной напряженностью поля. Поэтому работа при перемещении пробного заряда равна сумме работ сил, действующих со стороны отдельных точечных зарядов. Работа каждой такой силы не зависит от формы траектории. Поэтому и суммарная работа — работа результирующей силы — также не зависит от траектории, что и доказывает потенциальный характер любого электростатического поля.

Потенциальная энергия. Для заряда в электростатическом поле, как и в случае любого потенциального поля, можно ввести понятие потенциальной энергии. Потенциальная энергия заряда в любой точке поля определяется как работа, совершаемая силами поля при перемещении заряда из этой точки в некоторую фиксированную точку, потенциальная энергия в которой принята равной нулю. Можно сказать и иначе: эта потенциальная энергия равна работе, совершаемой внешними силами при переносе заряда из выбранной фиксированной точки в данную точку поля. Выбор фиксированной точки нулевого значения потенциальной энергии произволен. Поэтому потенциальная энергия заряда в поле определена с точностью до некоторой аддитивной постоянной. Такая неоднозначность потенциальной энергии никак не сказывается на физических результатах, поскольку во всех конкретных расчетах имеет значение только изменение энергии при переносе заряда из одной точки поля в другую.

Потенциал электрического поля. Действующая на заряд сила в электрическом поле Е пропорциональна заряду: Поэтому и совершаемая при некотором перемещении заряда работа, и его

потенциальная энергия также пропорциональны заряду Вследствие этого удобно рассматривать потенциальную энергию в расчете на единицу заряда. Возникающая при этом энергетическая характеристика электростатического поля называется потенциалом.

Потенциал в некоторой точке поля определяется как отношение работы А, совершаемой силами поля при перемещении пробного заряда из данной точки поля в фиксированную точку, потенциал которой принят равным нулю, к этому заряду:

Физический смысл имеет только разность потенциалов между какими-либо точками, а не сами по себе значения потенциалов этих точек.

Потенциал поля точечного заряда. Для электростатического поля точечного заряда удобно в качестве точки с нулевым потенциалом выбрать бесконечно удаленную точку. Тогда выражение для потенциала точки, отстоящей на расстояние от заряда создающего поле, имеет вид

Напомним, что в системе единиц СГСЭ и в СИ. Соответственно формула (2) записывается в одном из двух видов:

Подчеркнем, что в формулах (2) и (2а) для потенциала стоит заряд создающий поле (а не модуль заряда, как в формулах (4) и (4а) предыдущего параграфа для модуля напряженности поля). Потенциал поля, создаваемого положительным зарядом всюду положителен, так как работа сил этого поля при перемещении положительного пробного заряда в бесконечность из любой точки поля положительна. Аналогично, потенциал поля отрицательного заряда всюду отрицателен. Все это, как и сами формулы (2) и (2а), справедливо, разумеется, при выборе точки нулевого потенциала на бесконечности.

Такой же формулой (2) выражается и потенциал поля снаружи равномерно заряженного шара, так как его поле неотличимо от поля такого же точечного заряда, помещенного в центр шара. Во всех точках внутри такого шара, где напряженность поля равна нулю, потенциал одинаков и имеет такое же значение, как и на поверхности шара.

Потенциальная энергия некоторого заряда помещенного в электростатическое поле, равна произведению на потенциал той точки поля, где находится этот заряд:

Если заряд находится в поле, создаваемом другим точечным зарядом то его потенциальная энергия, с учетом (2), имеет вид

При одноименных зарядах т. е. при отталкивании, потенциальная энергия положительна и убывает при разведении зарядов. При разноименных зарядах, т. е. при притяжении, электростатическая потенциальная энергия, как и потенциальная энергия в гравитационном поле, отрицательна и возрастает при разведении зарядов.

Принцип суперпозиции для потенциала. В соответствии с принципом суперпозиции потенциал произвольной точки поля нескольких зарядов, как следует из определения потенциала, равен алгебраической сумме потенциалов, создаваемых в этой точке всеми зарядами:

При этом точка нулевого потенциала выбирается общей для всех зарядов.

Работа электрического поля. Напряжение. Работа, совершаемая силами электростатического поля при перемещении некоторого заряда из одной точки в другую, равна произведению переносимого заряда на разность потенциалов между начальной и конечной точками:

Выражение (6) следует из определения потенциала.

Разность потенциалов между двумя точками обычно называют напряжением между точками (или просто напряжением)

Как видно из (6), работа сил поля при перемещении заряда из одной точки в другую равна произведению переносимого заряда на напряжение:

Потенциал, разность потенциалов и напряжение измеряются в одних и тех же единицах. В СГСЭ эта единица не имеет специального названия, а в СИ единица напряжения называется вольт При перемещении заряда в один кулон между точками с разностью потенциалов один вольт электрические силы совершают работу один джоуль:

Эквипотенциальные поверхности. Наглядное графическое изображение электростатических полей возможно не только с помощью картины силовых линий, дающей представление о напряженности в каждой точке поля, но и с помощью эквипотенциальных поверхностей. Эквипотенциальная поверхность это множество точек, в которых потенциал имеет одно и то же значение.

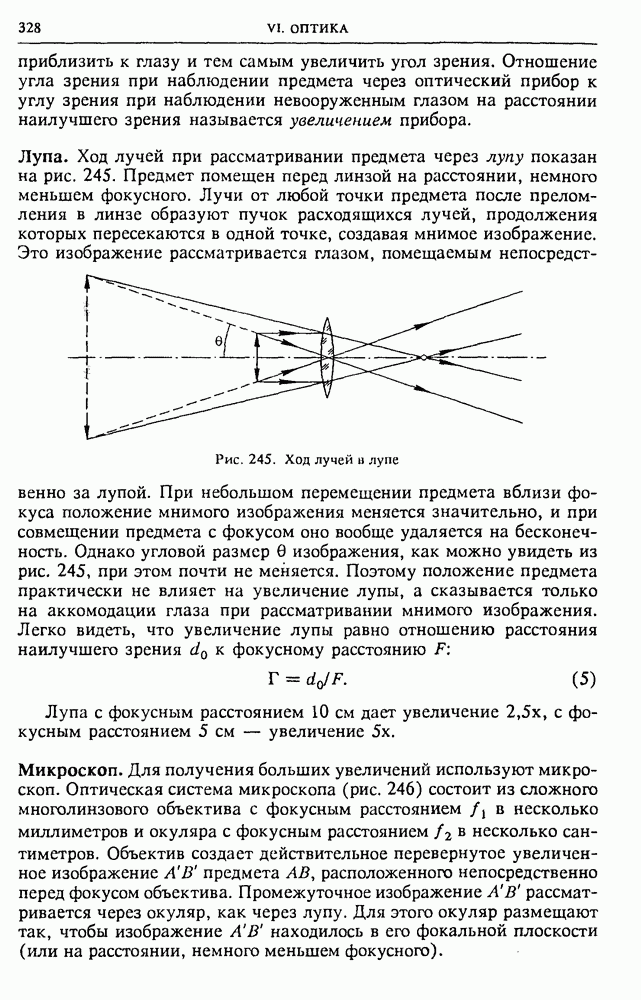
Рис. 13. Линии напряженности и эквипотенциальные поверхности электрического паля точечного зарада

Обычно изображают сечение этих поверхностей какой-либо плоскостью (плоскостью чертежа), поэтому на рисунках они выглядят линиями. Например, для электростатического поля точечного заряда эквипотенциальные поверхности представляют собой концентрические сферы с общим центром в точке, где находится создающий поле заряд. На рис. 13 сечения этих сфер выглядят как концентрические окружности.

Силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям. Действительно, если мысленно перемещать пробный заряд по эквипотенциальной поверхности, то работа, как видно из (8), равна нулю. Таким образом, сила электрического поля работы не совершает, а это возможно, если сила перпендикулярна перемещению.

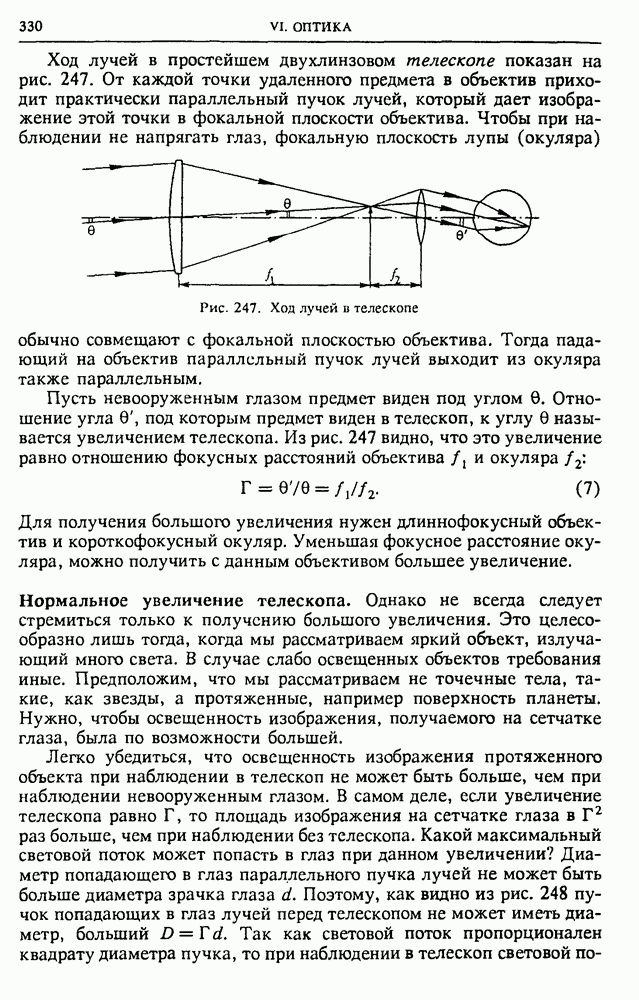
Два способа изображения электростатических полей — силовыми линиями и эквипотенциальными поверхностями — эквивалентны: имея одну из этих картин, можно легко построить другую. Особенно наглядны рисунки, на которых изображены обе эти картины (рис. 14).

Рис. 14. Линии напряженности и эквипотенциальные поверхности поля разноименных (а) и одноименных (б) одинаковых по модулю точечных зарядов

Связь напряженности и потенциала. Напряженность электростатического поля и его потенциал связаны друг с другом. Эту связь легко найти, рассматривая работу сил поля при столь малом перемещении пробного заряда, чтобы напряженность поля можно было считать постоянной. С одной стороны, эта работа равна скалярному произведению силы на перемещение, т. е. . С другой стороны, эта работа, в соответствии с (8), равна произведению заряда на разность потенциалов, т. е. Знак минус здесь возникает потому, что приращение потенциала по определению равно разности значений потенциала в конечной и начальной точках: Приравнивая оба выражения для работы, получаем

Скалярное произведение можно представить как произведение проекции напряженности на направление вектора перемещения и модуля этого перемещения

Направление перемещения можно выбрать произвольно. Выбирая его вдоль одной из осей координат, из (10) получаем выражение для проекции вектора Е на соответствующую ось:

Подчеркнем, что в числителях этих выражений, в соответствии с (9), стоят приращения потенциала при малых перемещениях вдоль соответствующих осей координат.

Энергия системы зарядов. До сих пор мы рассматривали потенциальную энергию некоторого заряда, помещенного в электростатическое поле, создаваемое другими зарядами, расположение которых в пространстве считалось неизменным. Однако по физической природе пробные заряды и заряды — источники поля ничем не отличаются, а потенциальная энергия заряда в поле — это энергия взаимодействия этих зарядов. Поэтому в некоторых случаях бывает удобно придать выражению для потенциальной энергии симметричный вид, чтобы все заряды — и источники поля, и пробные — фигурировали как равноправные. Для двух взаимодействующих точечных зарядов такой симметричный вид выражения потенциальной энергии уже был найден — это формула (4). В ней принимается, что потенциальная энергия равна нулю, когда заряды разведены на бесконечно большое расстояние.

В более сложных случаях, когда рассматривается несколько взаимодействующих зарядов, принимается, что потенциальная энергия взаимодействия равна нулю при каком-либо определенном взаимном расположении этих зарядов. Удобно (хотя и необязательно) в

качестве этой конфигурации выбрать такое расположение, когда все взаимодействующие заряды удалены друг от друга на бесконечные расстояния. Потенциальная энергия системы во всякой иной конфигурации определяется как работа, совершаемая всеми силами взаимодействия при переходе системы из этой конфигурации в положение с нулевой потенциальной энергией. В то же время эта потенциальная энергия равна работе, совершаемой внешними силами при переносе всех зарядов из положения с нулевой потенциальной энергией в заданную конфигурацию.

Энергия взаимодействия системы неподвижных точечных зарядов выражается формулой

где — потенциал поля, создаваемого всеми зарядами, кроме в той точке, где находится заряд:

Здесь — расстояние между зарядами.

Для доказательства формулы (12) можно использовать метод математической индукции. Прежде всего отметим, что для

2 эта формула совпадает с полученной ранее формулой (4): сумма по содержит два слагаемых:

где в соответствии с (13)

Подставляя эти значения в (14), получаем формулу (4).

Теперь предположим, что формула (12) справедлива для точечных зарядов, и докажем ее справедливость для системы зарядов. При внесении заряда из бесконечности энергия системы изменится на величину, равную работе, совершаемой внешними силами:

Здесь согласно предположению, определяется формулой (12), а работа, совершаемая внешними силами при перемещении заряда из бесконечности в точку поля с потенциалом равна где

— потенциал этой точки поля, создаваемый всеми зарядами, кроме

После внесения заряда изменяются потенциалы всех точек поля, кроме той, где находится этот заряд. Потенциал точки, в которой находится заряд, теперь будет равен

Выразим энергию системы зарядов (15) через новые значения потенциалов с помощью соотношений (17):

Сумма произведений на второе слагаемое в скобках в правой части этого равенства, в силу формулы (16), равна Поэтому

Таким образом, формула (12) для энергии системы точечных зарядов доказана.

• Докажите, что электростатическое поле, создаваемое уединенным точечным зарядом, потенциально.

Докажите, что поле, создаваемое любым распределением неподвижных электрических зарядов, потенциально.

• Что означает принцип суперпозиции применительно к энергетической характеристике электростатического поля — потенциалу?

• Докажите справедливость формулы (6), рассматривая работу поля при перемещении заряда из начальной точки I в бесконечность, а затем из бесконечности в точку 2.

• Чему равна работа сил электростатического поля при перемещении заряда по замкнутому контуру?

• Докажите, что поле потенциально, если работа сил этого поля при перемещении по любому замкнутому контуру равна нулю.

• Нарисуйте картину силовых линий и эквипотенциальных поверхностей однородного электростатического поля.

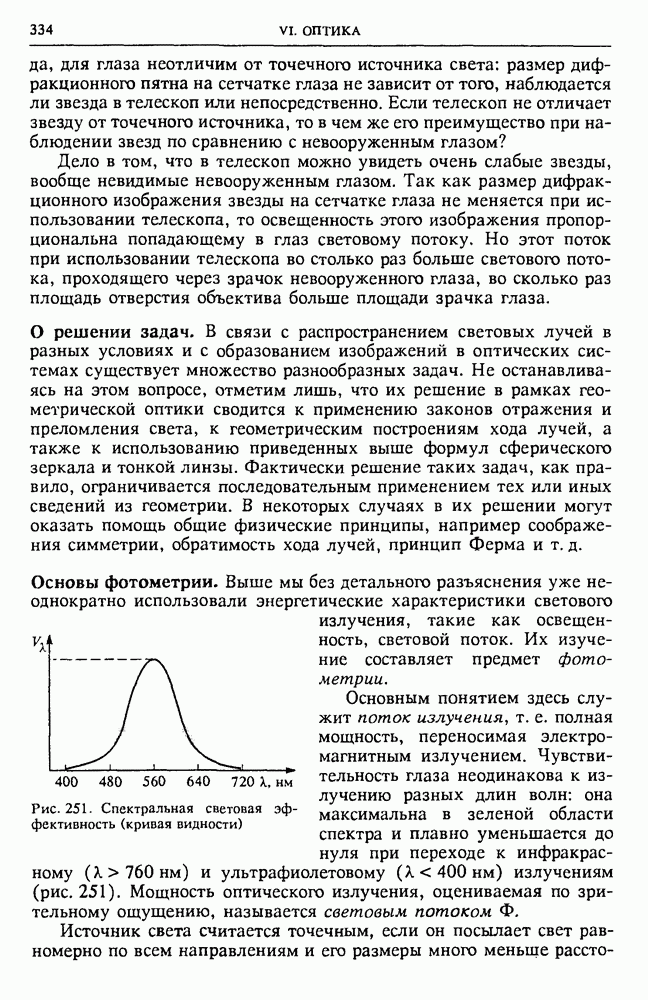
• Может ли существовать электростатическое поле, силовые линии которого представляют собой параллельные прямые с переменной густотой (рис. 15)?

Рис. 15

• В чем различие понятия потенциальной энергии пробного заряда, находящегося в электростатическом поле двух зарядов, и понятия потенциальной энергии всех трех зарядов?

Вывод формулы. Докажем справедливость формулы (2) для потенциала уединенного точечного заряда. Потенциал в точке Р, находящейся на расстоянии от заряда равен работе, совершаемой силами поля при перемещении единичного положительного заряда из точки Р в бесконечно удаленную точку. Поскольку сила, действующая на единичный заряд, равна напряженности поля Е, то выражение для интересующей нас работы, равной потенциалу в точке Р, запишется в виде

Интегрирование здесь может выполняться вдоль любого пути, проходящего из точки Р в бесконечность, так как работа сил потенциального поля не зависит от формы траектории. Выберем этот путь вдоль прямой, проходящей из заряда через данную точку Р на бесконечность. Поскольку напряженность поля Е направлена вдоль этой прямой (от заряда при и к заряду при то скалярное произведение можно записать как

если начало координат выбрано в точке, где находится заряд Интегрирование в (18) теперь выполняется в пределах от до

О модели точечного заряда. Обратим внимание на то, что и напряженность, и потенциал поля точечного заряда неограниченно возрастают (стремятся к бесконечности) при приближении точки Р к тому месту, где расположен создающий поле заряд. Физически это бессмысленно, так как соответствует обращению в бесконечность и силы, действующей на пробный заряд, и его потенциальной энергии. Все это говорит о том, что сама модель точечного заряда имеет ограниченную область применимости.

В какой мере для элементарных частиц можно использовать модель точечного заряда? Эксперименты на больших ускорителях показали, что нуклоны обладают внутренней структурой. Заряд в них распределен некоторым образом по объему, причем не только у протона, но даже и у нейтрона, который в целом электрически нейтрален. Что касается электронов, то для них модель точечного заряда «работает» вплоть до расстояний порядка так называемого классического радиуса электрона см.

Напряженность как градиент потенциала. Вернемся теперь к формулам выражающим напряженность любого электростатического поля через его потенциал. Из формул (11) следует, что проекции вектора Е напряженности поля на оси координат можно рассматривать как взятые с противоположным знаком производные по соответствующим координатам от потенциала скалярной функции координат При вычислении любой из этих производных, например по х, две другие переменные, у и нужно считать фиксированными. Такие производные функции нескольких переменных в математике называют частными производными и обозначают как Вектор, проекции которого равны частным производным скалярной функции по соответствующим координатам, называется градиентом этой скалярной функции. Таким образом, напряженность Е электрического поля — это взятый со знаком минус градиент потенциала. Записывают это следующим образом:

Здесь V — символический вектор, проекции которого на оси координат — операции дифференцирования:

— орты декартовой системы координат.

Чем быстрее меняется в пространстве потенциал, тем больше модуль его градиента, т. е. модуль напряженности электрического поля. «Смотрит» вектор напряженности в том направлении, в котором потенциал убывает быстрее всего, т. е. перпендикулярно эквипотенциальным поверхностям. Увидеть, что вектор Е направлен именно таким образом, можно с помощью формулы (9): если из рассматриваемой точки совершить одинаковые по модулю перемещения во всевозможных направлениях, то наибольшее изменение потенциала произойдет тогда, когда это перемещение направлено вдоль вектора Е.

• На каком свойстве электростатического поля основан выбор пути интегрирования в формуле (18)?

• Почему для поля точечного заряда точку нулевого значения потенциала нельзя выбрать в том месте, где находится сам заряд?

• Объясните, почему напряженность электрического поля направлена в сторону наибыстрейшего убывания потенциала.