| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Расчет электрических полей
Расчеты электрических полей, создаваемых заданным распределением зарядов, основаны на использовании принципа суперпозиции. Эти расчеты существенно упрощаются при наличии какой-либо
симметрии в распределении создающих поле зарядов. Рассмотрим примеры таких расчетов в конкретных задачах.
Задачи
1. Поле заряженного шара. Шар радиуса  равномерно заряжен по объему. Полный заряд шара
равномерно заряжен по объему. Полный заряд шара  Найти напряженность и потенциал электрического поля, создаваемого таким шаром.
Найти напряженность и потенциал электрического поля, создаваемого таким шаром.
Решение. Так как распределение создающих поле зарядов сферически-симметрично, то и создаваемое ими электростатическое поле должно обладать такой же симметрией. Это значит, что потенциал и модуль напряженности зависят только от расстояния  до центра заряженного шара, а вектор напряженности во всех точках имеет радиальное направление. Однако зависимость от
до центра заряженного шара, а вектор напряженности во всех точках имеет радиальное направление. Однако зависимость от  величин
величин  будет разной для внешней
будет разной для внешней  и внутренней
и внутренней  областей.
областей.
Симметрия системы позволяет применить теорему Гаусса для расчета напряженности поля  Для области
Для области  этот расчет ничем не отличается от описанного в предыдущем параграфе расчета напряженности поля шара, равномерно заряженного по поверхности. Напряженность поля и, следовательно, потенциал, оказываются точно такими же, как у точечного заряда
этот расчет ничем не отличается от описанного в предыдущем параграфе расчета напряженности поля шара, равномерно заряженного по поверхности. Напряженность поля и, следовательно, потенциал, оказываются точно такими же, как у точечного заряда  помещенного в центр шара:
помещенного в центр шара:

Для нахождения напряженности поля внутри шара рассмотрим поток напряженности через сферическую поверхность радиуса  концентрическую с шаром. Поскольку силовые линии всюду пересекают эту поверхность под прямым углом, то поток
концентрическую с шаром. Поскольку силовые линии всюду пересекают эту поверхность под прямым углом, то поток  вектора Е через нее равен
вектора Е через нее равен  По теореме Гаусса этот же поток пропорционален полному заряду
По теореме Гаусса этот же поток пропорционален полному заряду  находящемуся внутри сферы:
находящемуся внутри сферы:  При постоянной плотности заряд пропорционален объему, т. е.
При постоянной плотности заряд пропорционален объему, т. е.  Поэтому
Поэтому  Приравнивая эти выражения для потока, имеем
Приравнивая эти выражения для потока, имеем

откуда

Видно, что напряженность поля внутри равномерно заряженного шара пропорциональна расстоянию  от его центра. На поверхности шара, т. е. при
от его центра. На поверхности шара, т. е. при  значения напряженности поля
значения напряженности поля  даваемые формулами (1) и (2), совпадают.
даваемые формулами (1) и (2), совпадают.
Потенциал  для внутренней точки может быть найден как работа сил поля при перемещении единичного заряда из этой точки в бесконечность. Фактически требуется вычислить только работу при перемещении до поверхности, так как работа при перемещении от поверхности в бесконечность равна значению потенциала на поверхности шара:
для внутренней точки может быть найден как работа сил поля при перемещении единичного заряда из этой точки в бесконечность. Фактически требуется вычислить только работу при перемещении до поверхности, так как работа при перемещении от поверхности в бесконечность равна значению потенциала на поверхности шара:  При линейной зависимости силы от расстояния в (2) работа при перемещении изданной точки, находящейся на расстоянии
При линейной зависимости силы от расстояния в (2) работа при перемещении изданной точки, находящейся на расстоянии  от центра шара, до поверхности равна
от центра шара, до поверхности равна

Таким образом, при  потенциал имеет вид
потенциал имеет вид

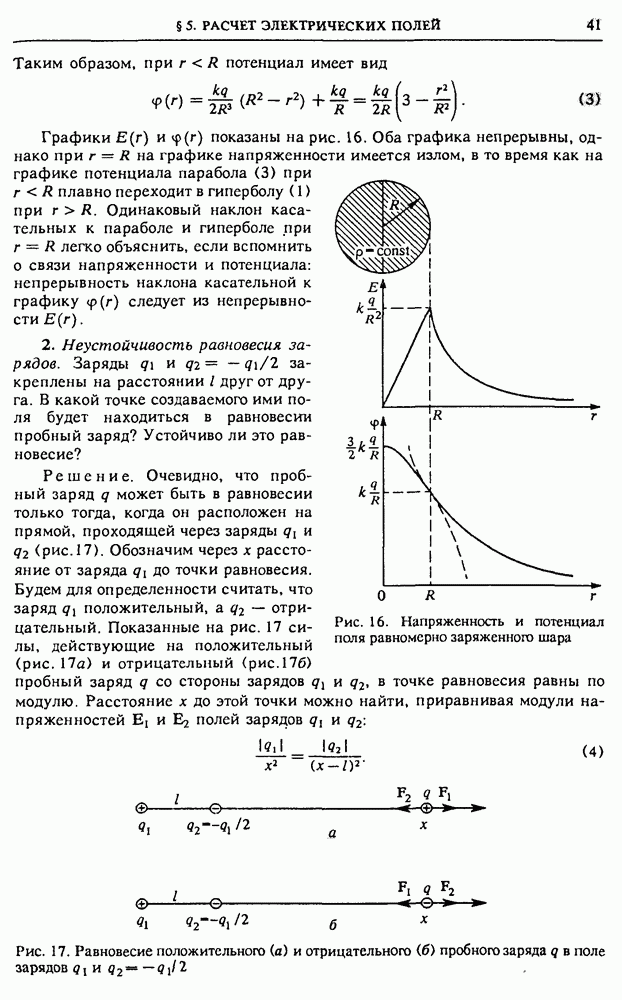
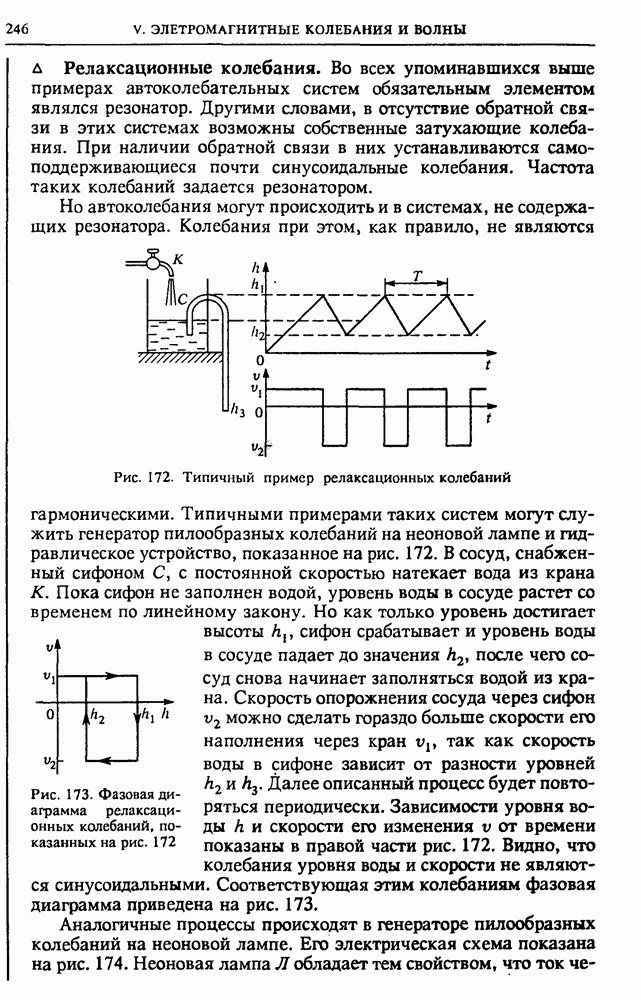
Графики  показаны на рис. 16. Оба графика непрерывны, однако при
показаны на рис. 16. Оба графика непрерывны, однако при  на графике напряженности имеется излом, в то время как на графике потенциала парабола (3) при
на графике напряженности имеется излом, в то время как на графике потенциала парабола (3) при  плавно переходит в гиперболу (1) при
плавно переходит в гиперболу (1) при  Одинаковый наклон касательных к параболе и гиперболе при
Одинаковый наклон касательных к параболе и гиперболе при  легко объяснить, если вспомнить о связи напряженности и потенциала: непрерывность наклона касательной к графику
легко объяснить, если вспомнить о связи напряженности и потенциала: непрерывность наклона касательной к графику  следует из непрерывности
следует из непрерывности 
2. Неустойчивость равновесия зарядов. Заряды  закреплены на расстоянии
закреплены на расстоянии  друг от друга. В какой точке создаваемого ими поля будет находиться в равновесии пробный заряд? Устойчиво ли это равновесие?
друг от друга. В какой точке создаваемого ими поля будет находиться в равновесии пробный заряд? Устойчиво ли это равновесие?

Рис. 16. Напряженность и потенциал псшя равномерно заряженного шара
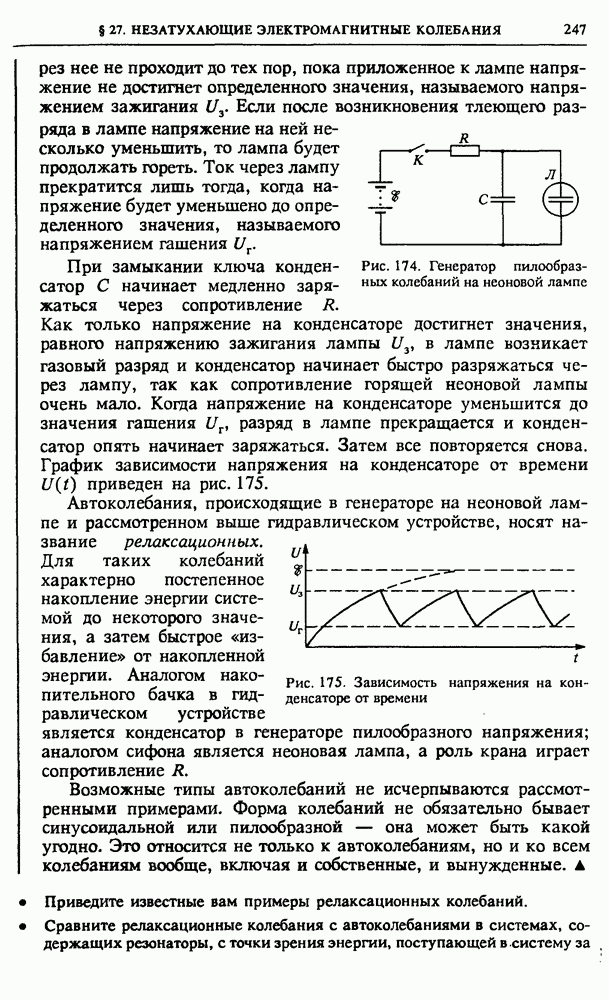
Решение. Очевидно, что пробный заряд  может быть в равновесии только тогда, когда он расположен на прямой, проходящей через заряды
может быть в равновесии только тогда, когда он расположен на прямой, проходящей через заряды  (рис. 17). Обозначим через х расстояние от заряда
(рис. 17). Обозначим через х расстояние от заряда  до точки равновесия.
до точки равновесия.
Будем для определенности считать, что заряд  положительный, а
положительный, а  отрицательный. Показанные на рис. 17 силы, действующие на положительный (рис. 17а) и отрицательный
отрицательный. Показанные на рис. 17 силы, действующие на положительный (рис. 17а) и отрицательный  пробный заряд
пробный заряд  со стороны зарядов
со стороны зарядов  в точке равновесия равны по модулю. Расстояние х до этой точки можно найти, приравнивая модули напряженностей
в точке равновесия равны по модулю. Расстояние х до этой точки можно найти, приравнивая модули напряженностей  полей зарядов
полей зарядов 


Рис. 17. Равновесие положительного (а) и отрицательного (б) пробного заряда  в поле зарядов
в поле зарядов 
Учитывая, что  приходим к квадратному уравнению для искомого расстояния
приходим к квадратному уравнению для искомого расстояния 

откуда 
Положению равновесия пробного заряда соответствует корень  Второй корень соответствует положению равновесия в случае, когда
Второй корень соответствует положению равновесия в случае, когда  так как уравнение (4) справедливо и при одноименных зарядах
так как уравнение (4) справедливо и при одноименных зарядах 
Для выяснения вопроса об устойчивости равновесия можно рассмотреть силы, действующие на пробный заряд при его небольшом смещении из положения равновесия. Рассмотрим сначала смещение в направлении, перпендикулярном прямой, проходящей через 

Рис. 18. По отношению к поперечным смещениям равновесие положительного пробного заряда устойчиво, а отрицательного — неустойчиво
Из рис. 18 видно, что на положительный пробный заряд будет действовать сила (равнодействующая  и
и  направленная к положению равновесия. Так получается потому, что силы
направленная к положению равновесия. Так получается потому, что силы  вблизи точки равновесия почти равны по модулю, но несколько отличаются по направлению. На отрицательный пробный заряд будет действовать сила (равнодействующая
вблизи точки равновесия почти равны по модулю, но несколько отличаются по направлению. На отрицательный пробный заряд будет действовать сила (равнодействующая  направленная от положения равновесия.
направленная от положения равновесия.
Отсюда, однако, нельзя сделать вывод отом, что равновесие положительного пробного заряда будет устойчивым, а отрицательного — неустойчивым. В самом деле, если рассмотреть малые смещения из точки равновесия вдоль прямой, проходящей через  все будет наоборот: на положительный заряд будет действовать сила, направленная от точки равновесия
все будет наоборот: на положительный заряд будет действовать сила, направленная от точки равновесия  а на отрицательный — к положению равновесия (рис. 19б).
а на отрицательный — к положению равновесия (рис. 19б).

Рис. 19. По отношению к продольным смещениям равновесие положительного пробного заряда неустойчиво (а), а отрицательного — устойчиво
Это легко понять, заметив, что при таком смещении относительное изменение расстояния  больше, чем до.
больше, чем до.
Таким образом, в электростатическом поле двух точечных зарядов равновесие пробного заряда не может быть устойчивым: всегда найдутся такие
смещения из положения равновесия, при которых на пробный заряд будет действовать сила, «уводящая» его дальше от этого положения.
Подмеченное на этом примере обстоятельство имеет совершенно общий характер: невозможно устойчивое равновесие заряда под действием только электростатических сил.
Устойчивое равновесие в потенциальном поле соответствует минимуму потенциальной энергии. Невозможность устойчивого равновесия пробного заряда в электростатическом поле означает, что потенциал  любого поля, который может быть представлен как сумма членов вида
любого поля, который может быть представлен как сумма членов вида  где
где  — радиус-вектор
— радиус-вектор  заряда, создающего поле, не имеет минимумов и максимумов на любом конечном расстоянии.
заряда, создающего поле, не имеет минимумов и максимумов на любом конечном расстоянии.

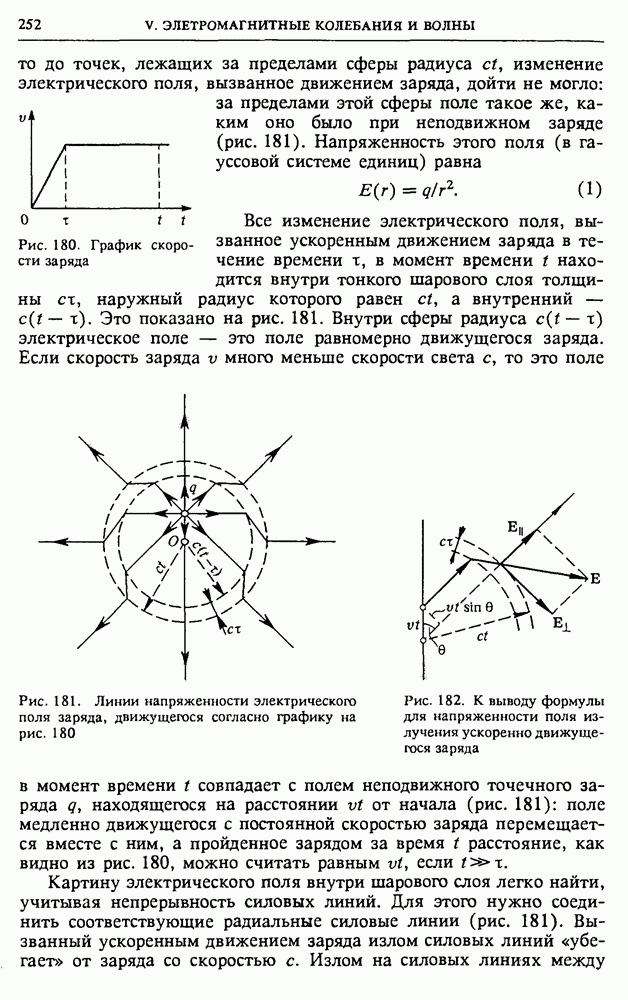
Рис. 20. Нахождение электростатического поля в сферической полости равномерно заряженного шара
Вопрос. Объясните, почему можно утверждать, что  не может иметь не только минимума, но и максимума.
не может иметь не только минимума, но и максимума.
3. Однородное поле в полости. Докажите, что электростатическое поле внутри сферической полости в равномерно заряженном по объему шаре однородно. Найдите напряженность этого поля, если расстояние от центра шара до центра полости I, а объемная плотность заряда шара 
Решение. Искомую напряженность поля внутри полости проще всего найти с помощью принципа суперпозиции. Идея заключается в следующем. Если бы полости не было, поле Е, в точке А (рис. 20) создавалось бы всем равномерно заряженным шаром. Такое поле нам известно (см. задачу 1). Но эту напряженность  можно рассматривать как векторную сумму искомой напряженности Е поля, создаваемого шаром с полостью, и напряженности
можно рассматривать как векторную сумму искомой напряженности Е поля, создаваемого шаром с полостью, и напряженности  поля, создаваемого меньшим шаром, после удаления которого и образуется данная полость:
поля, создаваемого меньшим шаром, после удаления которого и образуется данная полость:

Теперь остается только подставить соответствующие выражения для Е, и 
Обозначим через  вектор, проведенный в произвольную точку наблюдения А из центра О заряженного шара, а через
вектор, проведенный в произвольную точку наблюдения А из центра О заряженного шара, а через  — вектор, проведенный в точку А из центра полости О. Вектор 1 проведен из О в О. Запишем формулу (2) задачи 1 в векторном виде:
— вектор, проведенный в точку А из центра полости О. Вектор 1 проведен из О в О. Запишем формулу (2) задачи 1 в векторном виде: 

где  — радиус шара. Подставляя сюда заряд
— радиус шара. Подставляя сюда заряд  шара (без полости)
шара (без полости)  перепишем (6) следующим образом:
перепишем (6) следующим образом:

Очевидно, что точно такой же формулой выражается напряженность  поля, создаваемого меньшим шаром, после удаления которого образуется полость:
поля, создаваемого меньшим шаром, после удаления которого образуется полость:

Выражая теперь Е из (5) как разность Е] — с помощью (7) и (8) находим

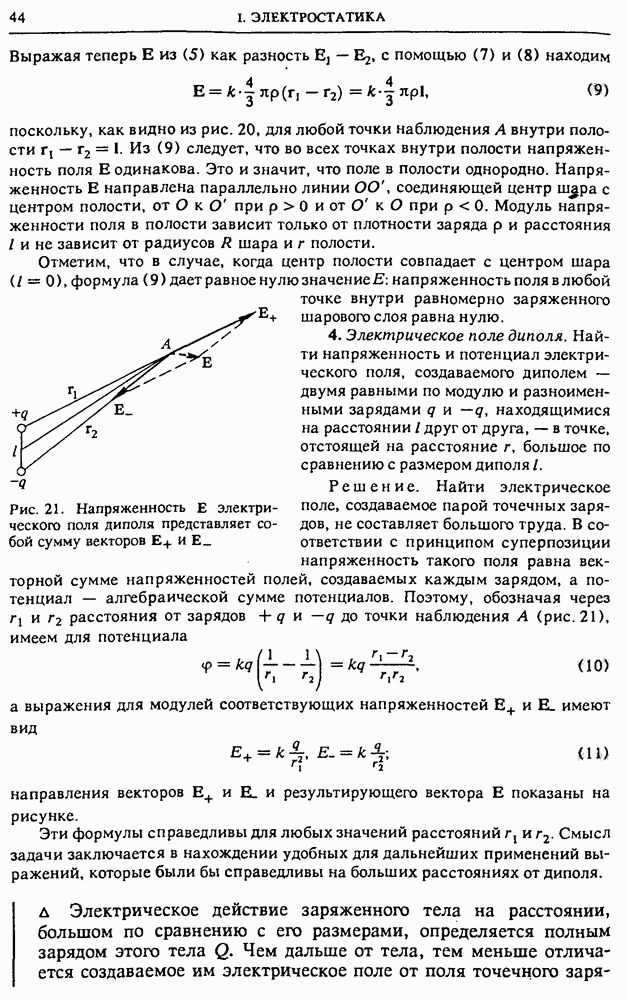
поскольку, как видно из рис. 20, для любой точки наблюдения А внутри полости  Из (9) следует, что во всех точках внутри полости напряженность поля Е одинакова. Это и значит, что поле в полости однородно. Напряженность Е направлена параллельно линии
Из (9) следует, что во всех точках внутри полости напряженность поля Е одинакова. Это и значит, что поле в полости однородно. Напряженность Е направлена параллельно линии  соединяющей центр
соединяющей центр  с центром полости, от О к О при
с центром полости, от О к О при  и от О к О при
и от О к О при  Модуль напряженности поля в полости зависит только от плотности заряда
Модуль напряженности поля в полости зависит только от плотности заряда  и расстояния
и расстояния  и не зависит от радиусов
и не зависит от радиусов  шара и
шара и  полости.
полости.
Отметим, что в случае, когда центр полости совпадает с центром шара  формула (9) дает равное нулю значение: напряженность поля в любой точке внутри равномерно заряженного шарового слоя равна нулю.
формула (9) дает равное нулю значение: напряженность поля в любой точке внутри равномерно заряженного шарового слоя равна нулю.
4. Электрическое поле диполя. Найти напряженность и потенциал электрического поля, создаваемого диполем — двумя равными по модулю и разноименными зарядами  и
и  находящимися на расстоянии
находящимися на расстоянии  друг от друга, — в точке, отстоящей на расстояние
друг от друга, — в точке, отстоящей на расстояние  большое по сравнению с размером диполя I.
большое по сравнению с размером диполя I.

Рис. 21. Напряженность Е электрического поля диполя представляет собой сумму векторов 
Решение. Найти электрическое поле, создаваемое парой точечных зарядов, не составляет большого труда. В соответствии с принципом суперпозиции напряженность такого поля равна векторной сумме напряженностей полей, создаваемых каждым зарядом, а потенциал — алгебраической сумме потенциалов. Поэтому, обозначая через  расстояния от зарядов
расстояния от зарядов  и —
и —  до точки наблюдения А (рис. 21), имеем для потенциала
до точки наблюдения А (рис. 21), имеем для потенциала

а выражения для модулей соответствующих напряженностей  имеют вид
имеют вид

направления векторов  и результирующего вектора Е показаны на рисунке.
и результирующего вектора Е показаны на рисунке.
Эти формулы справедливы для любых значений расстояний  Смысл задачи заключается в нахождении удобных для дальнейших применений выражений, которые были бы справедливы на больших расстояниях от диполя.
Смысл задачи заключается в нахождении удобных для дальнейших применений выражений, которые были бы справедливы на больших расстояниях от диполя.
Электрическое действие заряженного тела на расстоянии, большом по сравнению с его размерами, определяется полным зарядом этого тела  Чем дальше от тела, тем меньше отличается создаваемое им электрическое поле от поля точечного
Чем дальше от тела, тем меньше отличается создаваемое им электрическое поле от поля точечного
заряда: это поле почти сферически-симметрично, его потенциал убывает с расстоянием как  а напряженность — как
а напряженность — как 
Если же тело в целом электрически нейтрально, т. е. его полный заряд  равен нулю, то это вовсе не означает, что оно совсем не создает электрического поля.
равен нулю, то это вовсе не означает, что оно совсем не создает электрического поля.
В самом деле, электрически нейтральные молекулы вещества именно благодаря электростатическому взаимодействию между собой объединяются и образуют кристаллы или жидкости.

Рис. 22. Вычисление потенциала диполя в точке А
Для расчета электрического поля простейшей электрически нейтральной системы — диполя удобно несколько преобразовать выражения (10) и (11). Диполь принято характеризовать дипольным моментом  модуль которого равен произведению
модуль которого равен произведению  а направление выбирается вдоль оси диполя от отрицательного заряда к положительному (рис. 22). Далее удобно вместо
а направление выбирается вдоль оси диполя от отрицательного заряда к положительному (рис. 22). Далее удобно вместо  ввести расстояние
ввести расстояние  от середины диполя и угол 8 между вектором дипольного момента и направлением на точку наблюдения. Как видно из рис. 22, при
от середины диполя и угол 8 между вектором дипольного момента и направлением на точку наблюдения. Как видно из рис. 22, при  разность расстояний
разность расстояний  можно записать в виде
можно записать в виде

В то же время произведение  в знаменателе формулы (10) можно заменить на
в знаменателе формулы (10) можно заменить на  В результате формула (10) для потенциала принимает вид
В результате формула (10) для потенциала принимает вид

В отличие от потенциала поля точечного заряда, убывающего как  потенциал электрического поля диполя убывает с расстоянием быстрее — как
потенциал электрического поля диполя убывает с расстоянием быстрее — как  Разумеется, поле диполя обладает осевой, а не сферической, симметрией, поэтому его потенциал зависит не только от расстояния
Разумеется, поле диполя обладает осевой, а не сферической, симметрией, поэтому его потенциал зависит не только от расстояния  но и от направления на точку наблюдения, характеризуемого углом 8.
но и от направления на точку наблюдения, характеризуемого углом 8.
При получении формулы для напряженности удобно представить результирующий вектор Е на рис. 21 не как сумму векторов  а как сумму двух взаимно перпендикулярных составляющих, одна из которых,
а как сумму двух взаимно перпендикулярных составляющих, одна из которых,  направлена вдоль радиуса-вектора
направлена вдоль радиуса-вектора  характеризующего положение точки А относительно середины диполя, а другая,
характеризующего положение точки А относительно середины диполя, а другая,  перпендикулярна ей (рис. 23). На больших расстояниях от диполя, когда
перпендикулярна ей (рис. 23). На больших расстояниях от диполя, когда  , векторы
, векторы  направлены почти в противоположные стороны и мало отличаются по
направлены почти в противоположные стороны и мало отличаются по
модулю. При приближенном нахождении  нужно учитывать разницу векторов
нужно учитывать разницу векторов  по модулю, но можно пренебречь тем, что они направлены не строго в противоположные стороны.
по модулю, но можно пренебречь тем, что они направлены не строго в противоположные стороны.

Рис. 23. Напряженность Е поля диполя как сумма векторов 
Наоборот, при вычислении  можно пренебречь различием векторов
можно пренебречь различием векторов  по модулю, но нужно обязательно учесть их неколлинеарность.
по модулю, но нужно обязательно учесть их неколлинеарность.
Записав с помощью формул (11) выражение для  в виде
в виде

можно при  как и при вычислении потенциала, заменить в знаменателе
как и при вычислении потенциала, заменить в знаменателе  на
на  , а в числителе — сумму
, а в числителе — сумму  на
на  и разность
и разность  на
на  . В результате из (14) получаем
. В результате из (14) получаем

При вычислении  следует учесть, что угол между векторами
следует учесть, что угол между векторами  отличается от
отличается от  на малую величину
на малую величину  для которой, как видно из рис. 23, справедливо
для которой, как видно из рис. 23, справедливо

Учитывая, что для  можно приближенно написать
можно приближенно написать  а в выражении для
а в выражении для  заменить
заменить  на
на  окончательно получаем
окончательно получаем

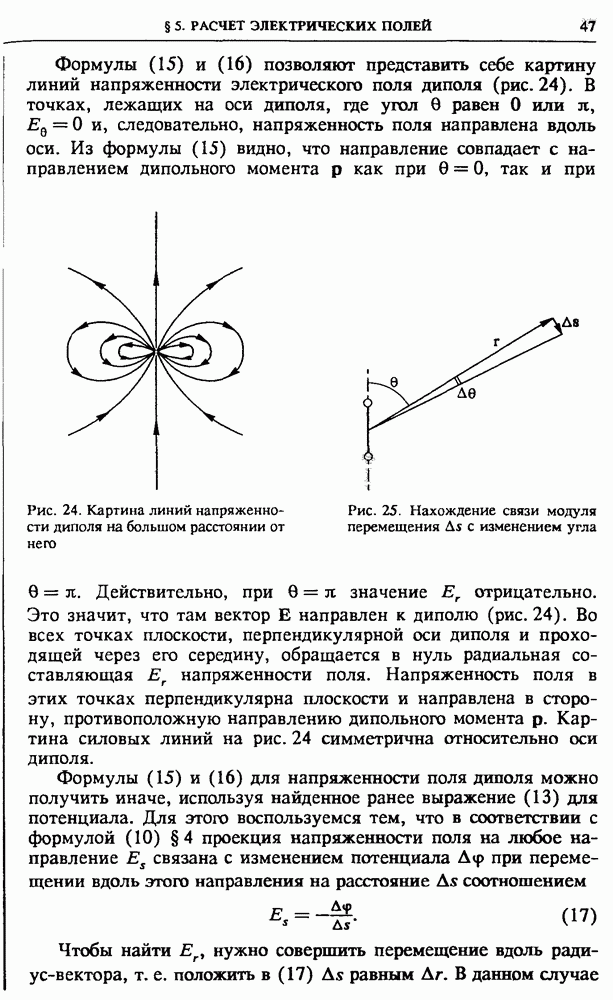
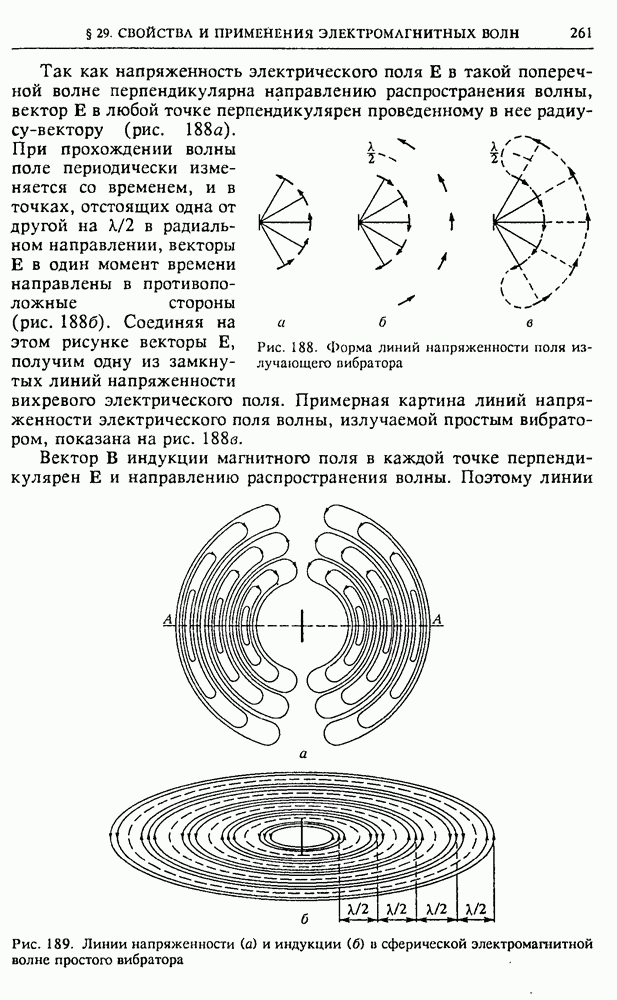
Формулы (15) и (16) позволяют представить себе картину линий напряженности электрического поля диполя (рис. 24). В точках, лежащих на оси диполя,  угол
угол  равен 0 или
равен 0 или  , следовательно, напряженность поля направлена вдоль оси. Из формулы (15) видно, что направление совпадает с направлением дипольного момента
, следовательно, напряженность поля направлена вдоль оси. Из формулы (15) видно, что направление совпадает с направлением дипольного момента  как при
как при  так и при
так и при 

Рис. 24. Картина линий напряженности диполя на большом расстоянии от него

Рис. 25. Нахождение связи модуля перемещения  с изменением угла
с изменением угла
Действительно, при  значение
значение  отрицательно. Это значит, что там вектор Е направлен к диполю (рис. 24). Во всех точках плоскости, перпендикулярной оси диполя и проходящей через его середину, обращается в нуль радиальная составляющая
отрицательно. Это значит, что там вектор Е направлен к диполю (рис. 24). Во всех точках плоскости, перпендикулярной оси диполя и проходящей через его середину, обращается в нуль радиальная составляющая  напряженности поля. Напряженность поля в этих точках перпендикулярна плоскости и направлена в сторону, противоположную направлению дипольного момента
напряженности поля. Напряженность поля в этих точках перпендикулярна плоскости и направлена в сторону, противоположную направлению дипольного момента  Картина силовых линий на рис. 24 симметрична относительно оси диполя.
Картина силовых линий на рис. 24 симметрична относительно оси диполя.
Формулы (15) и (16) для напряженности поля диполя можно получить иначе, используя найденное ранее выражение (13) для потенциала. Для этого воспользуемся тем, что в соответствии с формулой (10) §4 проекция напряженности поля на любое направление  связана с изменением потенциала
связана с изменением потенциала  при перемещении вдоль этого направления на расстояние
при перемещении вдоль этого направления на расстояние  соотношением
соотношением

Чтобы найти  нужно совершить перемещение вдоль радиус-вектора, т. е. положить в
нужно совершить перемещение вдоль радиус-вектора, т. е. положить в  равным
равным  . В данном случае
. В данном случае
это сводится к дифференцированию выражения (13) для  по
по  при фиксированном 0. В результате получаем формулу (15).
при фиксированном 0. В результате получаем формулу (15).
Совершенно аналогично, для нахождения  нужно совершить перемещение
нужно совершить перемещение  перпендикулярно радиусу-вектору
перпендикулярно радиусу-вектору  в направлении возрастания угла
в направлении возрастания угла  . При этом, как видно из рис. 25, перемещение
. При этом, как видно из рис. 25, перемещение  и вычисление по формуле
и вычисление по формуле

с помощью выражения (13) для потенциала приводит к (16).
Формулы (15) и (16) важны потому, что они определяют электрическое поле на большом расстоянии не только для настоящего диполя, т. е. двух точечных разноименных зарядов  но и для любой электрически нейтральной системы зарядов, у которой центры распределения положительных и отрицательных зарядов не совпадают. Другими словами, на достаточно большом расстоянии любое тело с суммарным зарядом
но и для любой электрически нейтральной системы зарядов, у которой центры распределения положительных и отрицательных зарядов не совпадают. Другими словами, на достаточно большом расстоянии любое тело с суммарным зарядом  будет похоже не на точечный заряд, а на диполь. Для него можно подобрать диполь с моментом
будет похоже не на точечный заряд, а на диполь. Для него можно подобрать диполь с моментом  так, чтобы создаваемое диполем поле на большом расстоянии было практически эквивалентно полю такого тела со сложным распределением заряда.
так, чтобы создаваемое диполем поле на большом расстоянии было практически эквивалентно полю такого тела со сложным распределением заряда.
• Поясните на качественном уровне (без формул), почему сила, действующая на пробный заряд внутри равномерно заряженного шара, пропорциональна расстоянию до центра шара. Почему в центре шара эта сила равна нулю?
• Почему на графике напряженности поля равномерно заряженного шара есть излом при  а на графике потенциала излома нет?
а на графике потенциала излома нет?
• Рассмотрите характер равновесия пробного заряда в задаче 2, если заряд  отрицательный,
отрицательный,  — положительный, а также для случая, когда
— положительный, а также для случая, когда  одного знака.
одного знака.
• При решении задачи 3 мы опирались на принцип суперпозиции, применяя его не к совокупности точечных зарядов, а к распределенным по объему зарядам. Приведите обоснование такой возможности.
• Почему для напряженности поля, создаваемого в точке А меньшим шаром, можно использовать ту же формулу (7), заменив в ней  на
на 
• В каких случаях тело со сложным распределением заряда можно на большом расстоянии приближенно заменить точечным зарядом, а в каких — диполем?
• По какому закону убывает с расстоянием напряженность поля и потенциал электрического поля диполя? Сравните с полем точечного заряда.
• Как по-вашему, может ли создавать какое-либо электрическое поле тело, у которого равны нулю и полный заряд, и дипольный момент?
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
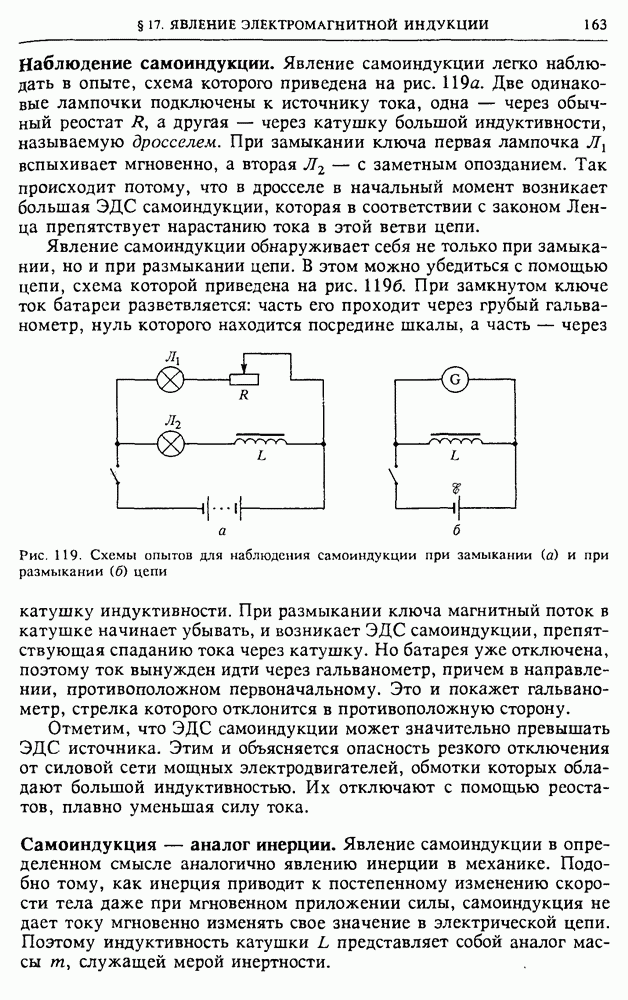
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
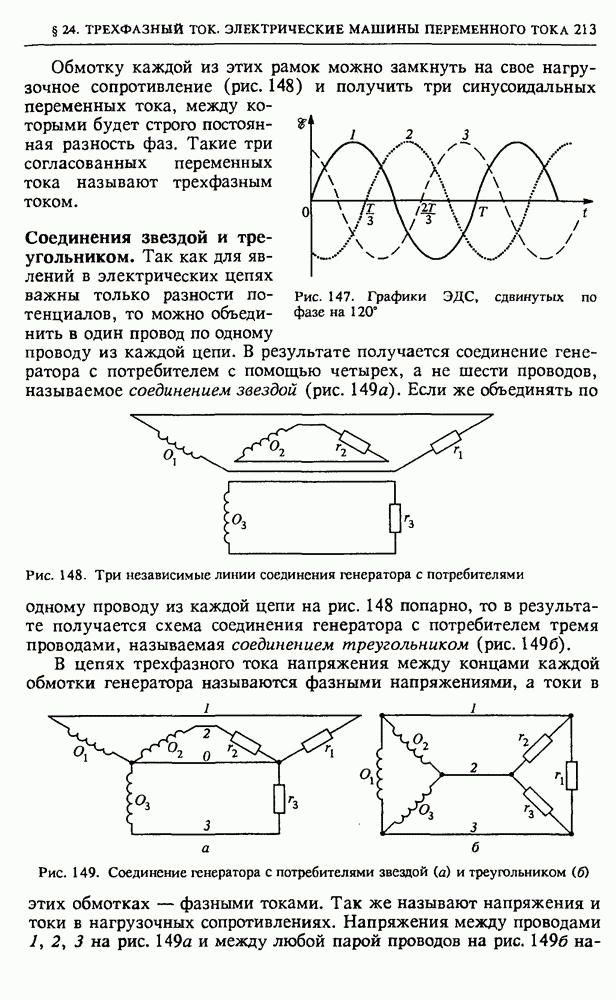
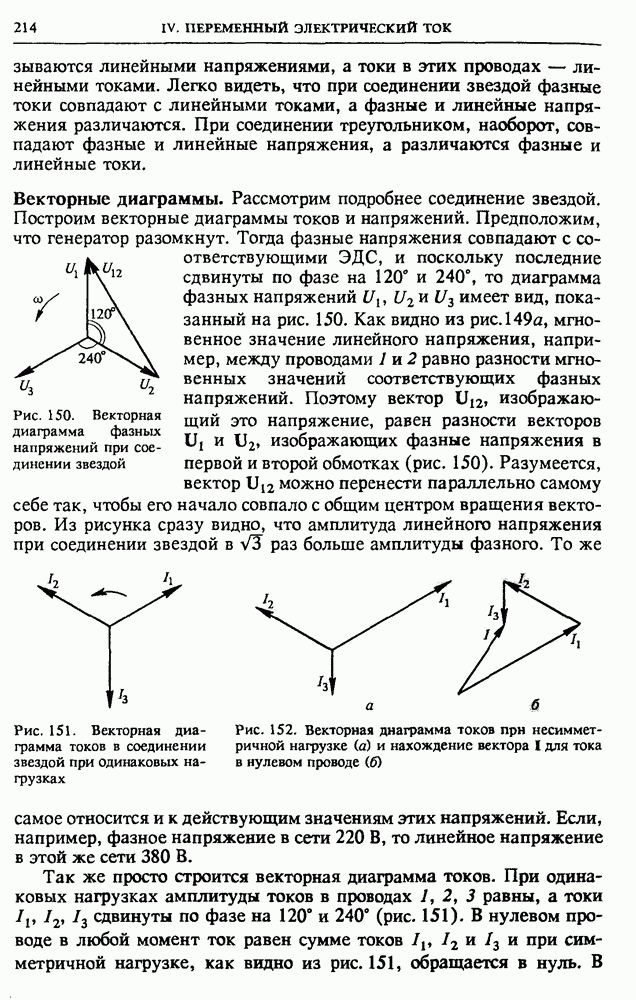
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
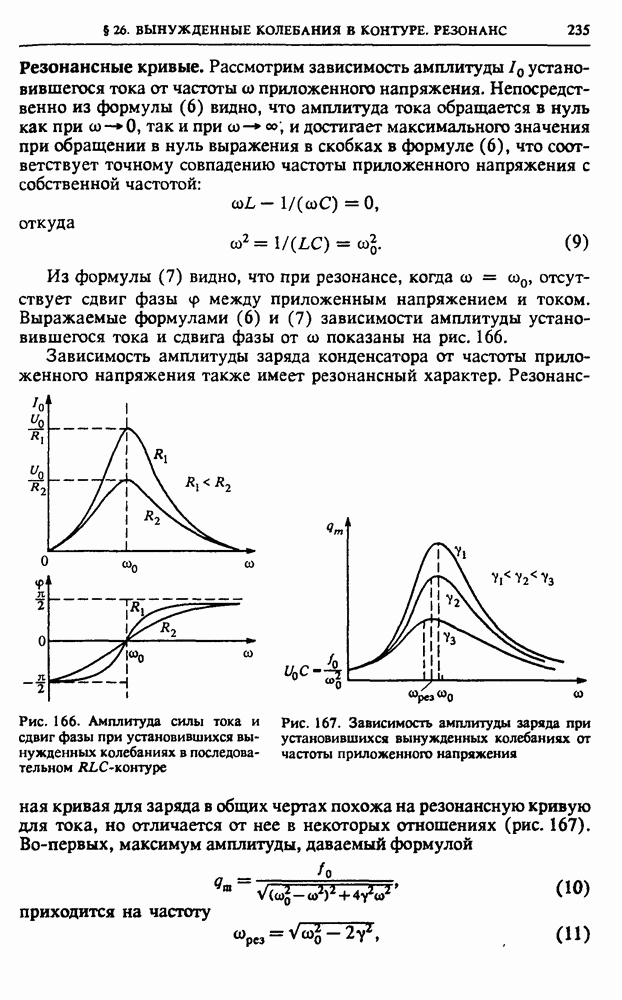
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение