| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Проводники в электрическом поле
Характерным свойством проводников является наличие в них свободных зарядов (электронов или ионов), способных перемещаться по всему объему тела.
Напряженность поля внутри проводника. В равновесии заряды располагаются таким образом, чтобы равнодействующая всех сил, действующих на каждый из зарядов, обращалась в нуль. Поэтому необходимым условием электростатического равновесия является равенство нулю напряженности электрического поля внутри проводника. Если бы внутри проводника существовало электрическое поле, то свободные заряды пришли бы в движение, т. е. равновесие было бы нарушено. Условие  должно быть выполнено для всех точек внутри проводника независимо от того, заряжен он сам или помещен во внешнее электростатическое поле.
должно быть выполнено для всех точек внутри проводника независимо от того, заряжен он сам или помещен во внешнее электростатическое поле.
Условие отсутствия электростатического поля внутри проводника приводит к тому, что нескомпенсированные заряды могут располагаться только на его поверхности. В этом легко убедиться с помощью теоремы Гаусса. Рассмотрим произвольную замкнутую поверхность, ограничивающую некоторый объем внутри проводника. Во всех точках этой поверхности напряженность электрического поля равна нулю. Следовательно, равен нулю и поток напряженности поля через эту поверхность. Тогда по теореме Гаусса равен нулю и полный заряд в объеме, ограниченном рассматриваемой поверхностью. Так как поверхность произвольна, то результат применим к любому участку внутри проводника вплоть до его границы. Итак, нескомпенсированные заряды могут располагаться только на поверхности проводника.
Проводники и закон Кулона. Отсутствие зарядов во внутренних частях проводника может быть использовано для проверки закона Кулона на опыте. Если бы в законе Кулона

показатель степени  не равнялся бы точно двум, то не была бы справедлива теорема Гаусса и во внутренних частях заряженного проводника должны были бы находиться заряды. Интересно, что отсутствие зарядов во внутренних частях заряженного металлического проводника было экспериментально установлено Г. Кавендишем за 12 лет до того, как Кулон сформулировал закон взаимодействия точечных зарядов.
не равнялся бы точно двум, то не была бы справедлива теорема Гаусса и во внутренних частях заряженного проводника должны были бы находиться заряды. Интересно, что отсутствие зарядов во внутренних частях заряженного металлического проводника было экспериментально установлено Г. Кавендишем за 12 лет до того, как Кулон сформулировал закон взаимодействия точечных зарядов.
Идея опыта Кавендиша ясна из рис. 26. Металлический шар 1 укреплен на изолирующей подставке 2. Две металлические полусферы 3, изолированные от земли и от шара, укреплялись на подвижных подставках и могли быть соединены в одну сферу,
охватывающую шар 1. В одной из полусфер имелось малое отверстие, в которое можно было вставлять изолированный проводник 4, чтобы соединять шар со сферой. Соединенные с шаром полусферы заряжали некоторым зарядом 5, о величине которого можно было судить по показаниям электрометра. Затем соединяющий шар с полусферами проводник 4 удаляли, полусферы раздвигали и разряжали. После этого электрометр подсоединяли к шару 1 и проверяли, имеется ли на нем какой-либо заряд. Опыт всегда показывал, что на шаре нет никаких следов заряда. Проверку закона Кулона таким способом можно произвести с большей точностью, чем при непосредственном измерении силы взаимодействия между заряженными телами, так как очень трудно создать условия, отвечающие требованию, чтобы заряды были точечными.

Рис. 26. Опыт Кавендиша
Напряженность поля и поверхностная плотность зарядов. С помощью теоремы Гаусса легко найти выражение для напряженности электрического поля в непосредственной близости от поверхности проводника. Прежде всего отметим, что во всех точках проводника потенциал одинаков и, следовательно, его граница является эквипотенциальной поверхностью, а силовые линии перпендикулярны его поверхности. Возьмем на поверхности проводника настолько малый участок  чтобы его можно было считать плоским, а поверхностную плотность заряда
чтобы его можно было считать плоским, а поверхностную плотность заряда  — постоянной. Проведем мысленно малую замкнутую цилиндрическую поверхность, образующие которой перпендикулярны к поверхности проводника, а основания параллельны
— постоянной. Проведем мысленно малую замкнутую цилиндрическую поверхность, образующие которой перпендикулярны к поверхности проводника, а основания параллельны  (рис. 27). Нижнее основание расположено целиком внутри проводника, где поле отсутствует, а верхнее — в непосредственной близости от поверхности проводника, где силовые линии еще перпендикулярны ей.
(рис. 27). Нижнее основание расположено целиком внутри проводника, где поле отсутствует, а верхнее — в непосредственной близости от поверхности проводника, где силовые линии еще перпендикулярны ей.

Рис. 27. К вычислению напряженности поля вблизи поверхности проводника
При таком выборе замкнутой поверхности поток напряженности проходит только через верхнее основание и равен  По теореме Гаусса
По теореме Гаусса

откуда

В  и формула (1) принимает вид
и формула (1) принимает вид

В системе единиц СГСЭ к = 1 и для напряженности поля вблизи поверхности проводника имеем

Подчеркнем, что формула (1) дает выражение для напряженности полного электростатического поля, существующего вблизи поверхности проводника, независимо от того, создается ли это поле только самим заряженным проводником или еще и другими зарядами. Из (1) видно, что напряженность результирующего поля вблизи поверхности проводника связана только с плотностью зарядов на его поверхности.
Распределение зарядов по поверхности проводника. От чего зависит плотность заряда на поверхности проводника? В случае уединенного заряженного проводящего тела эта плотность тем больше, чем больше полный заряд  проводника. Если это тело — шар, то заряд
проводника. Если это тело — шар, то заряд  распределен по его поверхности равномерно, так что поверхностная плотность всюду одинакова:
распределен по его поверхности равномерно, так что поверхностная плотность всюду одинакова:

Так как напряженность электрического поля, создаваемого равномерно заряженным шаром вблизи его поверхности, равна

то при подстановке сюда заряда  выраженного через плотность а из (4), приходим к формуле
выраженного через плотность а из (4), приходим к формуле  Алка, справедливой в общем случае, а не только для заряженного шара. Поверхностную плотность заряда а можно выразить не через заряд
Алка, справедливой в общем случае, а не только для заряженного шара. Поверхностную плотность заряда а можно выразить не через заряд  , а через потенциал шара
, а через потенциал шара  Подставляя
Подставляя  к в (4), получаем
к в (4), получаем

При заданном потенциале поверхностная плотность заряда а обратно пропорциональна радиусу шара 
Этот результат имеет общий характер. Какой бы сложной формой ни обладало проводящее тело, потенциал во всех точках одинаков:  Поэтому поверхностная плотность заряда будет больше в тех местах, не меньше
Поэтому поверхностная плотность заряда будет больше в тех местах, не меньше  поверхность искривлена сильнее. Очевидно, что в этих же местах будет больше и напряженность электрического поля.
поверхность искривлена сильнее. Очевидно, что в этих же местах будет больше и напряженность электрического поля.
Зависимость напряженности поля от кривизны поверхности можно продемонстрировать в простых опытах. Воспользуемся гибкой
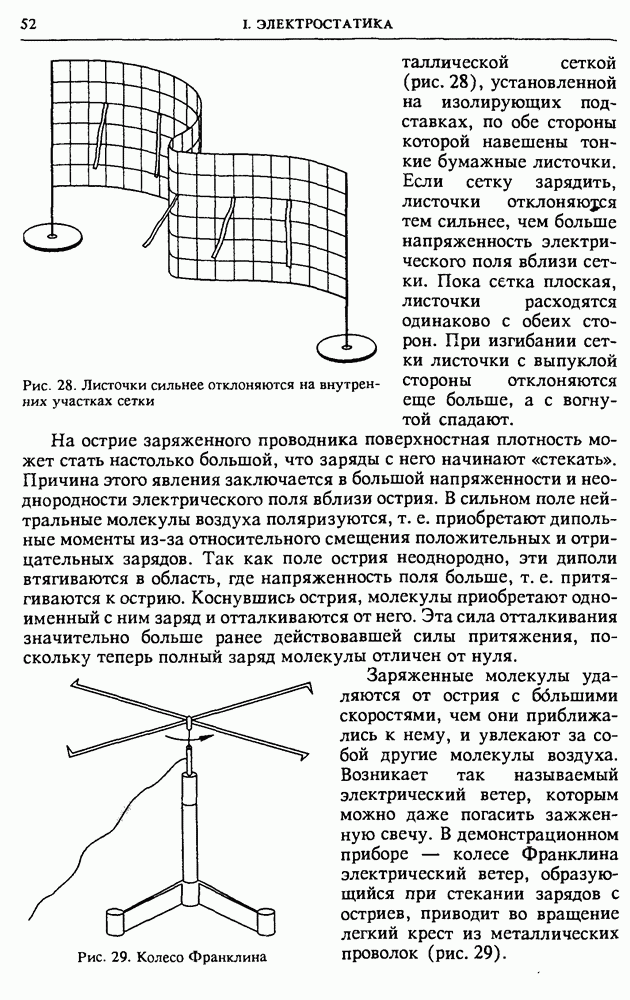
металлической сеткой (рис. 28), установленной на изолирующих подставках, по обе стороны которой навешены тонкие бумажные листочки. Если сетку зарядить, листочки отклоняются тем сильнее, чем больше напряженность электрического поля вблизи сетки. Пока сетка плоская, листочки расходятся одинаково с обеих сторон. При изгибании сетки листочки с выпуклой стороны отклоняются еще больше, а с вогнутой спадают.

Рис. 28. Листочки сильнее отклоняются на внутренних участках сетки
На острие заряженного проводника поверхностная плотность может стать настолько большой, что заряды с него начинают «стекать». Причина этого явления заключается в большой напряженности и неоднородности электрического поля вблизи острия. В сильном поле нейтральные молекулы воздуха поляризуются, т. е. приобретают дипольные моменты из-за относительного смещения положительных и отрицательных зарядов. Так как поле острия неоднородно, эти диполи втягиваются в область, где напряженность поля больше, т. е. притягиваются к острию. Коснувшись острия, молекулы приобретают одноименный с ним заряд и отталкиваются от него. Эта сила отталкивания значительно больше ранее действовавшей силы притяжения, поскольку теперь полный заряд молекулы отличен от нуля.

Рис. 29. Колесо Франклина
Заряженные молекулы удаляются от острия с большими скоростями, чем они приближались к нему, и увлекают за собой другие молекулы воздуха. Возникает так называемый электрический ветер, которым можно даже погасить зажженную свечу. В демонстрационном приборе — колесе Франклина электрический ветер, образующийся при стекании зарядов с остриев, приводит во вращение легкий крест из металлических проволок (рис. 29).
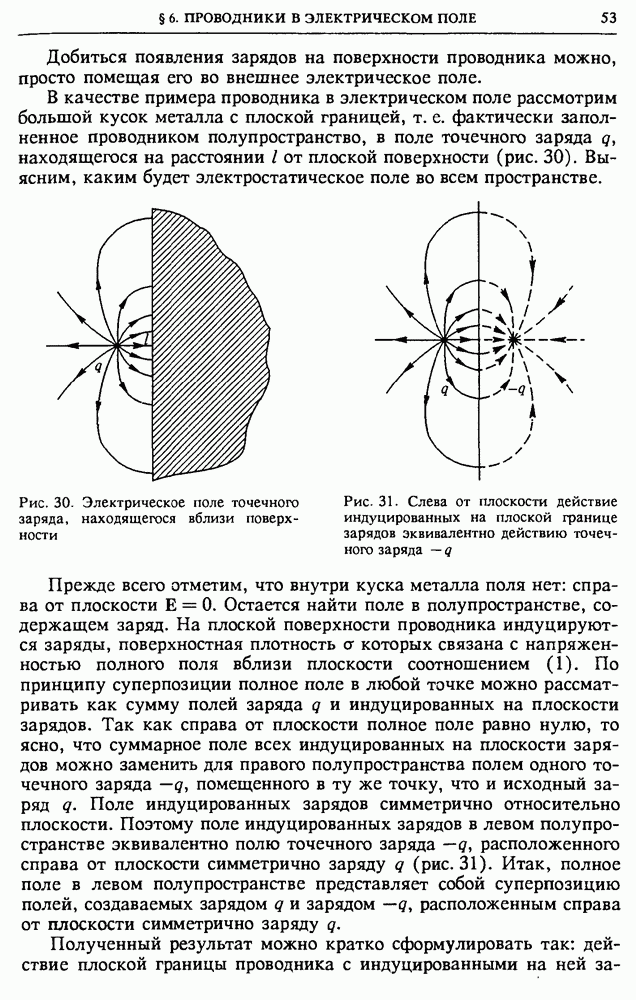
Добиться появления зарядов на поверхности проводника можно, просто помещая его во внешнее электрическое поле.
В качестве примера проводника в электрическом поле рассмотрим большой кусок металла с плоской границей, т. е. фактически заполненное проводником полупространство, в поле точечного заряда  находящегося на расстоянии
находящегося на расстоянии  от плоской поверхности (рис. 30). Выясним, каким будет электростатическое поле во всем пространстве.
от плоской поверхности (рис. 30). Выясним, каким будет электростатическое поле во всем пространстве.

Рис. 30. Электрическое поле точечного заряда, находящегося вблизи поверхности

Рис. 31. Слева от плоскости действие индуцированных на плоской границе зарядов эквивалентно действию точечного заряда — 
Прежде всего отметим, что внутри куска металла поля нет: справа от плоскости  Остается найти поле в полупространстве, содержащем заряд. На плоской поверхности проводника индуцируются заряды, поверхностная плотность
Остается найти поле в полупространстве, содержащем заряд. На плоской поверхности проводника индуцируются заряды, поверхностная плотность  которых связана с напряженностью полного поля вблизи плоскости соотношением (1). По принципу суперпозиции полное поле в любой точке можно рассматривать как сумму полей заряда
которых связана с напряженностью полного поля вблизи плоскости соотношением (1). По принципу суперпозиции полное поле в любой точке можно рассматривать как сумму полей заряда  и индуцированных на плоскости зарядов. Так как справа от плоскости полное поле равно нулю, то ясно, что суммарное поле всех индуцированных на плоскости зарядов можно заменить для правого полупространства полем одного точечного заряда —
и индуцированных на плоскости зарядов. Так как справа от плоскости полное поле равно нулю, то ясно, что суммарное поле всех индуцированных на плоскости зарядов можно заменить для правого полупространства полем одного точечного заряда —  помещенного в ту же точку, что и исходный заряд
помещенного в ту же точку, что и исходный заряд  Поле индуцированных зарядов симметрично относительно плоскости. Поэтому поле индуцированных зарядов в левом полупространстве эквивалентно полю точечного заряда
Поле индуцированных зарядов симметрично относительно плоскости. Поэтому поле индуцированных зарядов в левом полупространстве эквивалентно полю точечного заряда  расположенного справа от плоскости симметрично заряду
расположенного справа от плоскости симметрично заряду  (рис. 31). Итак, полное поле в левом полупространстве представляет собой суперпозицию полей, создаваемых зарядом
(рис. 31). Итак, полное поле в левом полупространстве представляет собой суперпозицию полей, создаваемых зарядом  и зарядом
и зарядом  расположенным справа от плоскости симметрично заряду
расположенным справа от плоскости симметрично заряду 
Полученный результат можно кратко сформулировать так: действие плоской границы проводника с индуцированными на ней
зарядами можно заменить действием точечного заряда  являющегося как бы зеркальным изображением данного заряда
являющегося как бы зеркальным изображением данного заряда  в проводящей плоскости. Поэтому описанный способ нахождения поля носит название метода изображений.
в проводящей плоскости. Поэтому описанный способ нахождения поля носит название метода изображений.
Распределение зарядов на поверхности. Зная электрическое поле, можно рассчитать поверхностную плотность индуцированных на проводнике зарядов и силу, действующую на точечный заряд д. Поскольку все силовые линии, выходящие из заряда  оканчиваются на проводящей плоскости, то полный индуцированный на ней заряд равен
оканчиваются на проводящей плоскости, то полный индуцированный на ней заряд равен  Разумеется, этот заряд распределен неравномерно.
Разумеется, этот заряд распределен неравномерно.

Рис. 32. К расчету поверхностной плотности индуцировашых зарядов
Поверхностную плотность индуцированных зарядов легко определить с помощью соотношения (1). Напряженность поля вблизи поверхности проводника направлена по нормали к ней. Очевидно, что в рассматриваемом случае поле обладает осевой симметрией: при вращении вокруг линии, соединяющей заряды  картина поля не меняется. Поэтому плотность заряда на поверхности зависит только от расстояния
картина поля не меняется. Поэтому плотность заряда на поверхности зависит только от расстояния  от оси симметрии:
от оси симметрии:  Простой расчет, идея которого понятна из рис. 32, приводит к результату (в единицах СИ):
Простой расчет, идея которого понятна из рис. 32, приводит к результату (в единицах СИ):

Какая сила действует на заряд  Для нахождения силы нужно знать напряженность поля, в котором находится этот заряд. В данном случае это поле создается зарядами, индуцированными на проводнике. Точно такое же поле создавал бы заряд-изображение
Для нахождения силы нужно знать напряженность поля, в котором находится этот заряд. В данном случае это поле создается зарядами, индуцированными на проводнике. Точно такое же поле создавал бы заряд-изображение  Таким образом, заряд
Таким образом, заряд  притягивается к проводнику с такой же силой, как и к заряду
притягивается к проводнику с такой же силой, как и к заряду  находящемуся на расстоянии
находящемуся на расстоянии  от него.
от него.
Энергия заряда вблизи проводника. А какую работу нужно совершить, чтобы удалить заряд  на бесконечность? Может показаться, что искомая работа будет такой же, как и при раздвижении на бесконечность зарядов
на бесконечность? Может показаться, что искомая работа будет такой же, как и при раздвижении на бесконечность зарядов  и
и  находящихся на расстоянии
находящихся на расстоянии  друг от друга:
друг от друга:

Однако это неверно! В этом можно убедиться с помощью следующего простого рассуждения. При удалении заряда  от поверхности металла будет удаляться в противоположную сторону и его
от поверхности металла будет удаляться в противоположную сторону и его
«изображение»  ибо в каждый момент сила, действующая на заряд, определяется зарядом-изображением
ибо в каждый момент сила, действующая на заряд, определяется зарядом-изображением  расположенным симметрично
расположенным симметрично  «тносительно поверхности металла. Поэтому по формуле (8) определяется работа, которая совершается внешними силами, действующими на оба заряда. Нам же необходимо найти работу только одной из этих сил, действующей на заряд
«тносительно поверхности металла. Поэтому по формуле (8) определяется работа, которая совершается внешними силами, действующими на оба заряда. Нам же необходимо найти работу только одной из этих сил, действующей на заряд  ведь на самом деле никакого заряда —
ведь на самом деле никакого заряда —  нет, а есть заряды, индуцированные на поверхности металла, которые при удалении заряда
нет, а есть заряды, индуцированные на поверхности металла, которые при удалении заряда  растекаются по эквипотенциальной поверхности, так что при их перемещении никакой работы не совершается.
растекаются по эквипотенциальной поверхности, так что при их перемещении никакой работы не совершается.
Таким образом, интересующая нас работа А будет в два раза меньше, чем работа А в (8):

Энергия системы точечных зарядов и проводников. Расчитать эту работу можно и с помощью общей формулы (12) из § 4 для энергии системы зарядов, которая справедлива и тогда, когда наряду с точечными зарядами в систему входят проводники. При этом в слагаемых, соответствующих проводникам,  есть полный заряд проводника, а
есть полный заряд проводника, а  — его потенциал, создаваемый как другими зарядами, так и его собственным. Докажем это.
— его потенциал, создаваемый как другими зарядами, так и его собственным. Докажем это.
Пусть в системе из  зарядов есть один заряженный проводник с зарядом
зарядов есть один заряженный проводник с зарядом  и потенциалом
и потенциалом  а все остальные заряды точечные. Тогда формула для энергии этой системы должна иметь вид
а все остальные заряды точечные. Тогда формула для энергии этой системы должна иметь вид

Чтобы показать справедливость этой формулы, разобьем мысленно заряд проводника  на большое число М малых частей так, чтобы каждую часть
на большое число М малых частей так, чтобы каждую часть  можно было считать точечным зарядом, и представим энергию всей системы как энергию
можно было считать точечным зарядом, и представим энергию всей системы как энергию  точечных зарядов. В соответствии с формулой (12) § 4 имеем
точечных зарядов. В соответствии с формулой (12) § 4 имеем

Поскольку все точки проводника имеют одинаковый потенциал  ), во второй сумме в этой формуле
), во второй сумме в этой формуле  можно вынести за знак суммы:
можно вынести за знак суммы:

Сумма всех  представляет собой полный заряд
представляет собой полный заряд  проводника. Таким образом, формула (10) доказана.
проводника. Таким образом, формула (10) доказана.
Из приведенного вывода ясцо, что потенциал проводника  создается как точечными зарядами др так и зарядом самого проводника
создается как точечными зарядами др так и зарядом самого проводника  Действительно, в формуле (11) есть потенциал поля, создаваемого всеми зарядами, кроме
Действительно, в формуле (11) есть потенциал поля, создаваемого всеми зарядами, кроме  т. е. всеми точечными зарядами
т. е. всеми точечными зарядами  и зарядом проводника
и зарядом проводника  за исключением малой его части
за исключением малой его части  которая может быть выбрана сколь угодно малой по сравнению с
которая может быть выбрана сколь угодно малой по сравнению с  Разумеется, формула (10) остается в силе и в том случае, когда в рассматриваемой системе есть только заряженные проводники и нет точечных зарядов.
Разумеется, формула (10) остается в силе и в том случае, когда в рассматриваемой системе есть только заряженные проводники и нет точечных зарядов.
Применим общую формулу (10) к рассмотренной выше системе, состоящей из точечного заряда  и проводника с бесконечной плоской поверхностью на расстоянии
и проводника с бесконечной плоской поверхностью на расстоянии  от заряда
от заряда  Потенциал
Потенциал  этого проводника равен нулю, так как проводник простирается до бесконечности, и соответствующее слагаемое в формуле (10) отсутствует. Поэтому энергия рассматриваемой системы равна
этого проводника равен нулю, так как проводник простирается до бесконечности, и соответствующее слагаемое в формуле (10) отсутствует. Поэтому энергия рассматриваемой системы равна  где
где  — потенциал, создаваемый индуцированными на проводнике зарядами (т. е. зарядом-изображением
— потенциал, создаваемый индуцированными на проводнике зарядами (т. е. зарядом-изображением  в точке, где находится заряд
в точке, где находится заряд  Итак,
Итак,

Работа А, которую совершают внешние силы при удалении точечного заряда  на бесконечность, равна происходящему при этом изменению энергии системы, т. е.
на бесконечность, равна происходящему при этом изменению энергии системы, т. е.  что совпадает с (9).
что совпадает с (9).
• Докажите, что потенциал всех точек проводника, включая его границу, одинаков независимо от того, заряжен он сам или помещен во внешнее электрическое поле.
• Докажите, что силовые линии электростатического поля вблизи проводника перпендикулярны его поверхности.
• Как связаны между собой поверхностная плотность заряда и напряженность поля вблизи поверхности проводника?
• Объясните, почему диполь втягивается в область, где напряженность электрического поля больше.
• Докажите формулу (7) для поверхностной плотности заряда, индуцируемого точечным зарядом на проводящей плоскости.
• Почему в задаче о заряде вблизи проводящей плоскости формальное применение метода изображений дает правильный результат для действующей силы и вдвое завышенный результат — для работы?
• В чем отличие смысла входящих в формулу (10) величин  в слагаемых, относящихся к точечным зарядам и к проводникам?
в слагаемых, относящихся к точечным зарядам и к проводникам?
Еще о методе изображений. Мы рассмотрели простейший случай: точечный заряд вблизи бесконечной плоской поверхности проводника, и сумели просто угадать решение — заменили поле индуцированных зарядов полем фиктивного точечного заряда-изображения, расположенного по другую сторону границы проводника. А можно ли применять метод изображений для проводников более сложной формы? Для ответа на этот вопрос рассмотрим разобранный выше пример с несколько иной точки зрения.

Рис. 33. Линии напряженности и сечения эквипотенциальных поверхностей поля двух разноименных точечных зарядов
Предположим, что имеются два точечных заряда  и
и  на расстоянии 21 друг от друга. Поле такой системы зарядов хорошо известно. На рис. 33 показаны силовые линии и сечения эквипотенциальных поверхностей. Одна из эквипотенциальных поверхностей — плоскость, перпендикулярная соединяющему заряды отрезку и делящая его пополам. Действительно, потенциал любой точки этой плоскости
на расстоянии 21 друг от друга. Поле такой системы зарядов хорошо известно. На рис. 33 показаны силовые линии и сечения эквипотенциальных поверхностей. Одна из эквипотенциальных поверхностей — плоскость, перпендикулярная соединяющему заряды отрезку и делящая его пополам. Действительно, потенциал любой точки этой плоскости

так как расстояния любой точки этой плоскости от зарядов  и
и  одинаковы
одинаковы  Совместим с этой плоскостью тонкий проводящий экран. Поскольку все точки проводника, помещенного в электростатическое поле, имеют одинаковый потенциал, картина поля не изменится вне экрана, а внутри него напряженность поля равна нулю. Уберем теперь заряд
Совместим с этой плоскостью тонкий проводящий экран. Поскольку все точки проводника, помещенного в электростатическое поле, имеют одинаковый потенциал, картина поля не изменится вне экрана, а внутри него напряженность поля равна нулю. Уберем теперь заряд  Справа от экрана поля не будет, слева все останется без изменения. Но получившаяся система — как раз то, что нам нужно рассмотреть! Справа от экрана поля нет, слева напряженность в любой точке определяется векторной суммой напряженностей полей, создаваемых зарядами
Справа от экрана поля не будет, слева все останется без изменения. Но получившаяся система — как раз то, что нам нужно рассмотреть! Справа от экрана поля нет, слева напряженность в любой точке определяется векторной суммой напряженностей полей, создаваемых зарядами  а потенциал — алгебраической суммой потенциалов этих полей.
а потенциал — алгебраической суммой потенциалов этих полей.
Теперь можно сформулировать основную идею метода изображений: нужно подобрать точечные заряды, которые создавали бы такие же поля, как и индуцированные на поверхностях проводников заряды. Положение и величина этих фиктивных зарядов должны выбираться таким образом, чтобы одна из эквипотенциальных поверхностей поля, создаваемого заданными и фиктивными подобранными зарядами, совпадала бы с поверхностью
проводника. Подчеркнем, что с помощью этих зарядов находится поле только вне проводников. Внутри проводников поля нет.
Метод изображений в некоторых случаях позволяет очень просто находить решения весьма сложных на первый взгляд электростатических задач. Для примера рассмотрим поле точечного заряда  находящегося внутри проводящего прямого двугранного угла (рис. 34а).
находящегося внутри проводящего прямого двугранного угла (рис. 34а).

Рис. 34. Электрическое поле внутри двугранного угла (а) совпадает с полем четырех зарядов (б)

Рис. 35. Такую задачу методом изображений решить нельзя
Все электрическое поле сосредоточено только внутри угла,  расположен заряд
расположен заряд  по другую сторону проводящей поверхности поля нет. Нетрудно убедиться, что эквипотенциальность поверхности двугранного угла будет обеспечена, если ввести еще три фиктивных точечных заряда. Поэтому поле внутри угла представляет собой суперпозицию полей четырех изображенных на рис. 34б зарядов.
по другую сторону проводящей поверхности поля нет. Нетрудно убедиться, что эквипотенциальность поверхности двугранного угла будет обеспечена, если ввести еще три фиктивных точечных заряда. Поэтому поле внутри угла представляет собой суперпозицию полей четырех изображенных на рис. 34б зарядов.
Сила, с которой заряд притягивается к проводнику, может быть представлена как векторная сумма сил его взаимодействия с тремя фиктивными зарядами.
Но, несмотря на свою привлекательность, метод изображений далеко не универсален. Достаточно поместить точечный заряд  снаружи проводящего двугранного угла (рис. 35), чтобы задачу уже невозможно было решить таким методом. Хотя система четырех точечных зарядов, изображенная на рис. 34б, и в этом случае обеспечивает эквипотенциальность поверхности двугранного угла, она не дает решения задачи. Дело в том, что фиктивные заряды можно помещать только по другую от реального заряда сторону проводящей поверхности. В той точке, где находится точечный заряд, напряженность поля обращается в бесконечность. Поэтому если мы поместим фиктивный точечный заряд по одну сторону с реальным зарядом, то в точке нахождения фиктивного заряда напряженность поля обращается в бесконечность, чего на самом деле нет.
снаружи проводящего двугранного угла (рис. 35), чтобы задачу уже невозможно было решить таким методом. Хотя система четырех точечных зарядов, изображенная на рис. 34б, и в этом случае обеспечивает эквипотенциальность поверхности двугранного угла, она не дает решения задачи. Дело в том, что фиктивные заряды можно помещать только по другую от реального заряда сторону проводящей поверхности. В той точке, где находится точечный заряд, напряженность поля обращается в бесконечность. Поэтому если мы поместим фиктивный точечный заряд по одну сторону с реальным зарядом, то в точке нахождения фиктивного заряда напряженность поля обращается в бесконечность, чего на самом деле нет.
• Сформулируйте основную идею, на которой основан метод электрических изображений.
• Почему метод изображений удается использовать для нахождения электрического поля вблизи проводников, поверхность которых имеет достаточно простую форму?
• Почему фиктивные заряды в методе изображений нельзя помещать по ту же сторону от проводящих поверхностей, где находятся реальные точечные заряды?
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
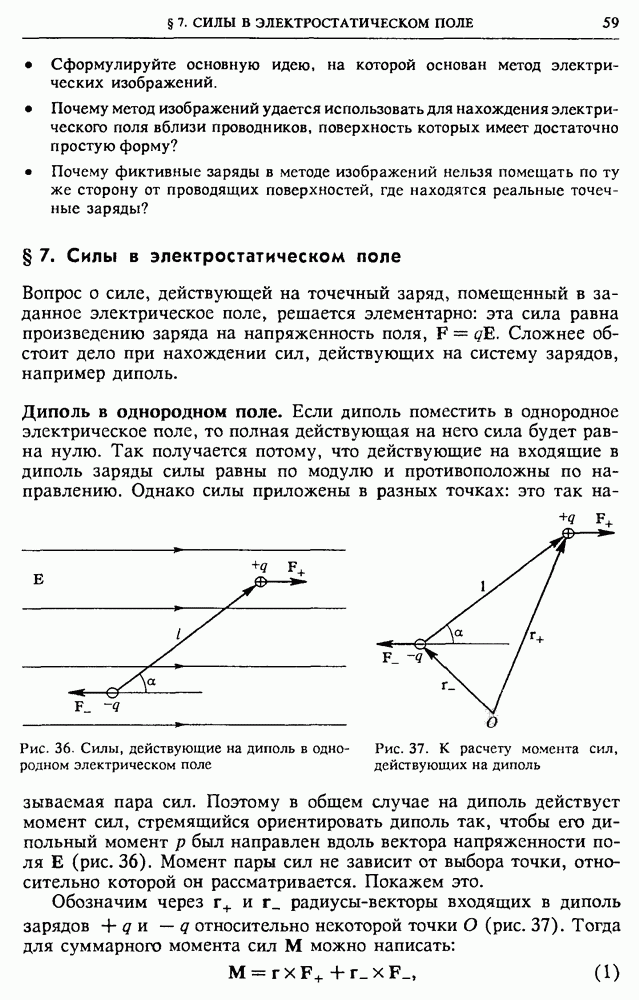
- § 7. Силы в электростатическом поле
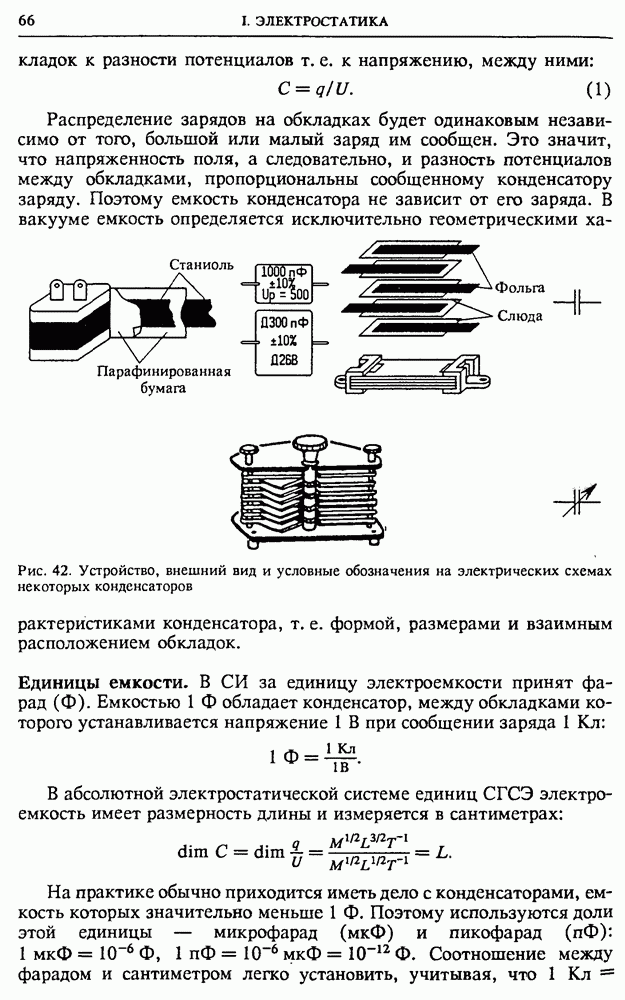
- § 8. Конденсаторы. Электроемкость
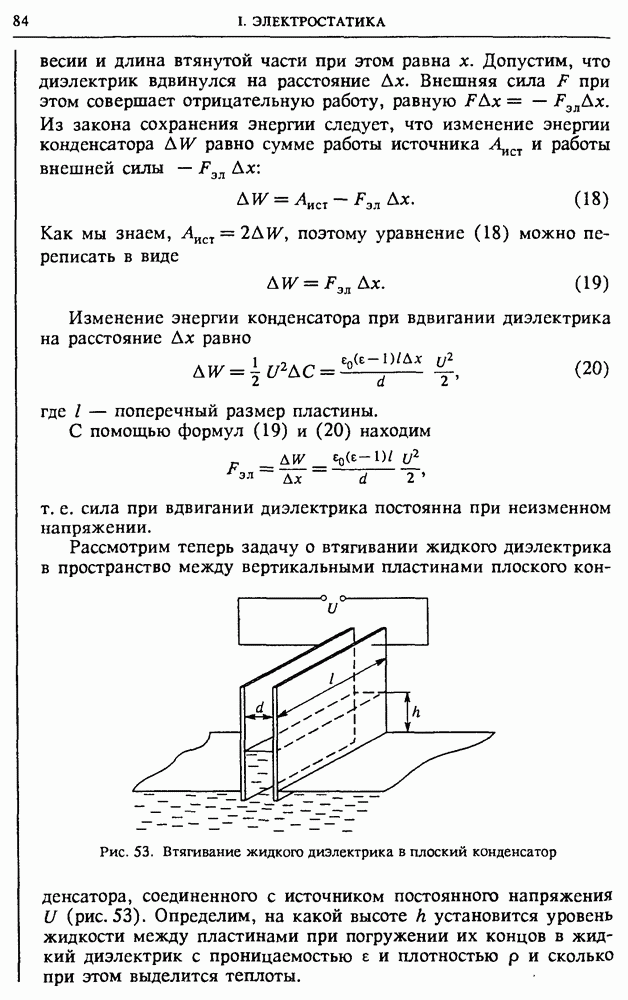
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
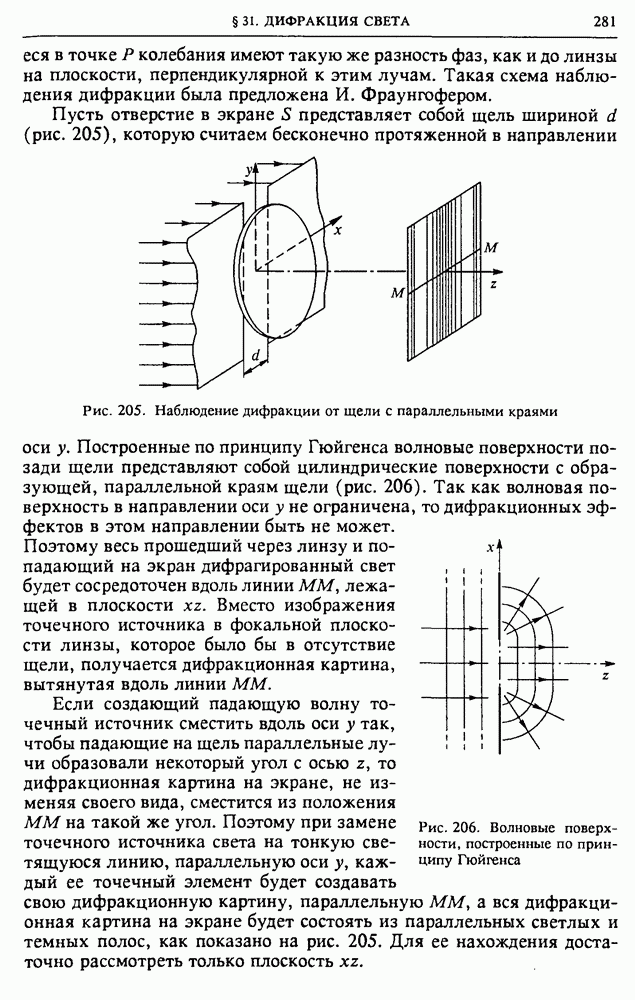
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
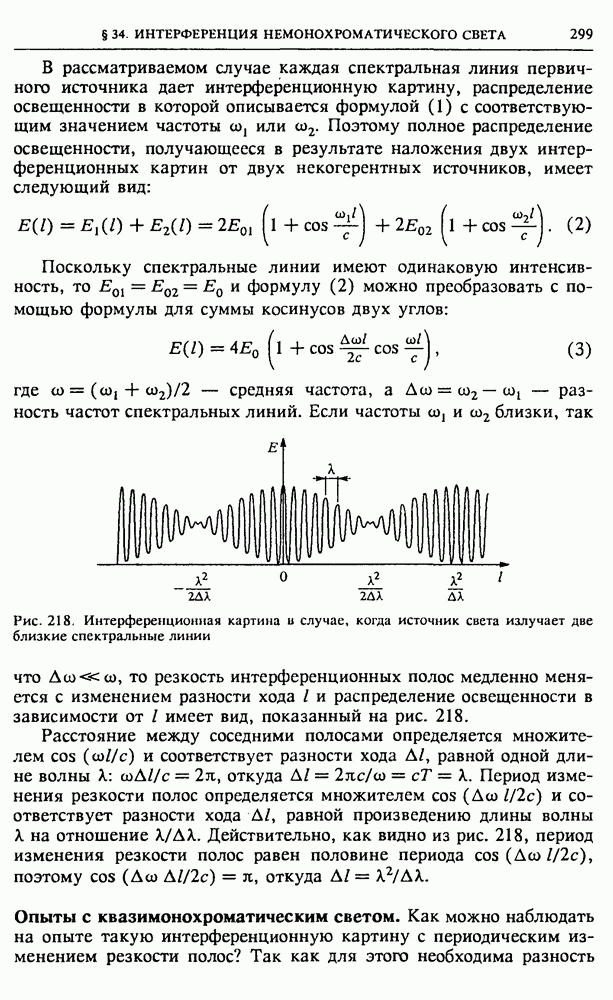
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение