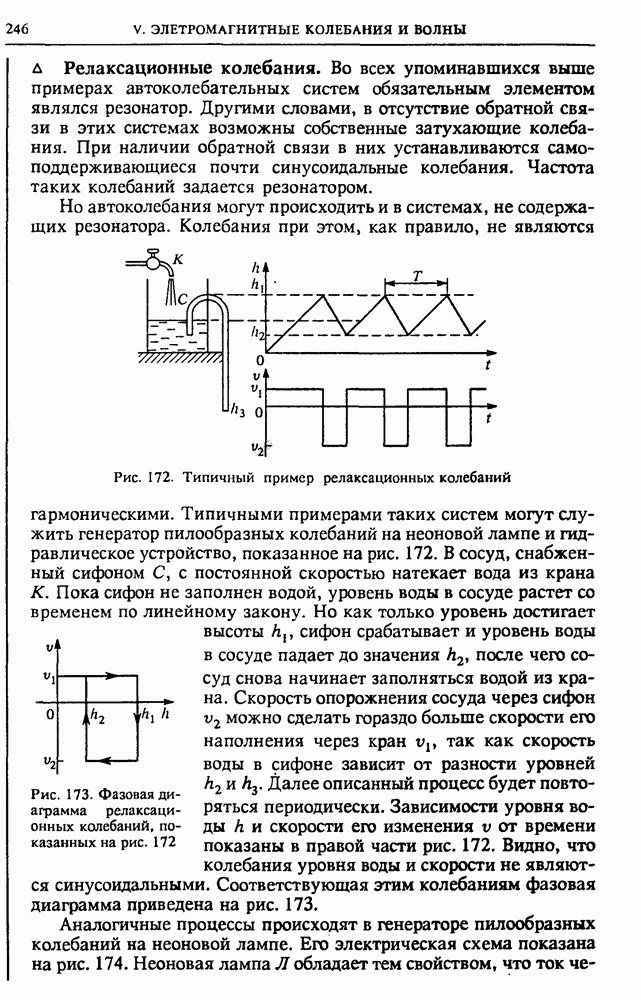
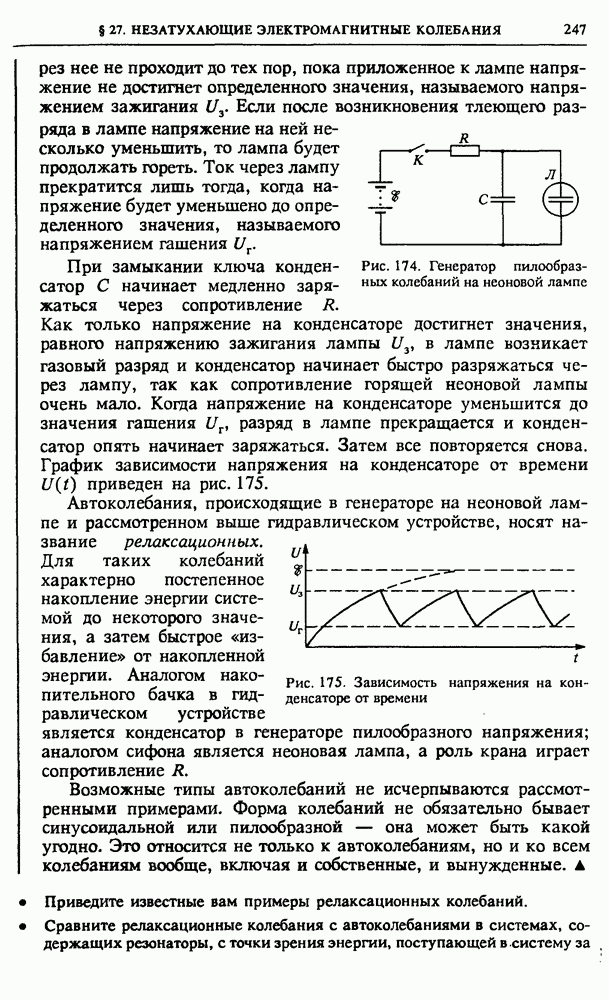
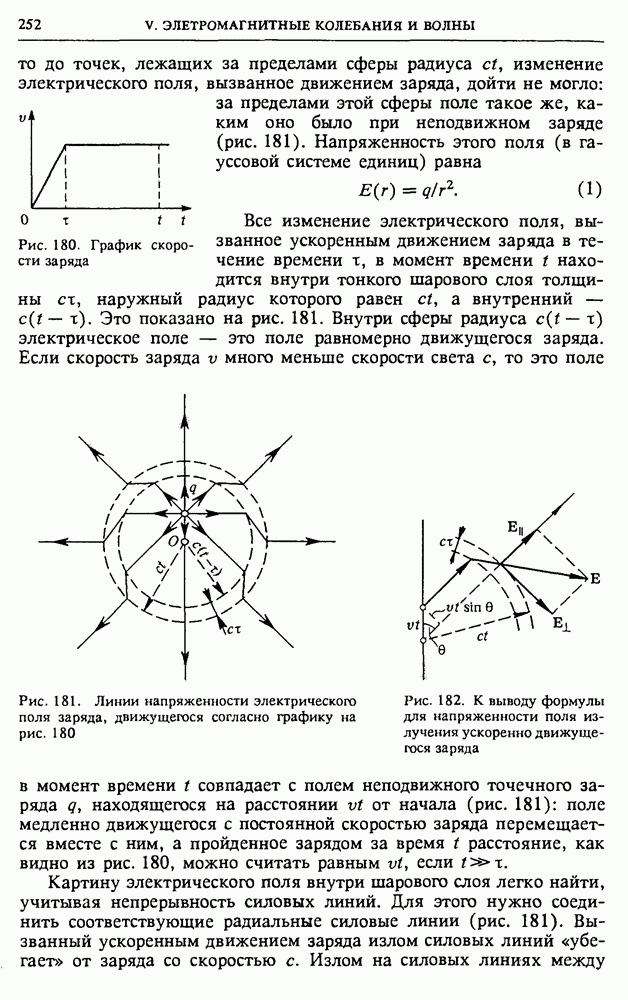
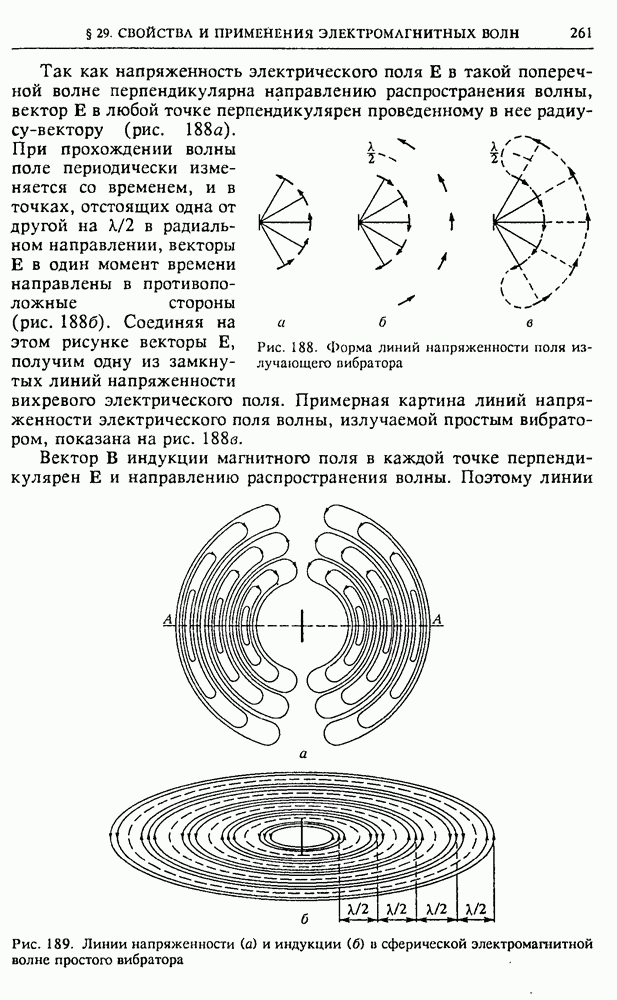
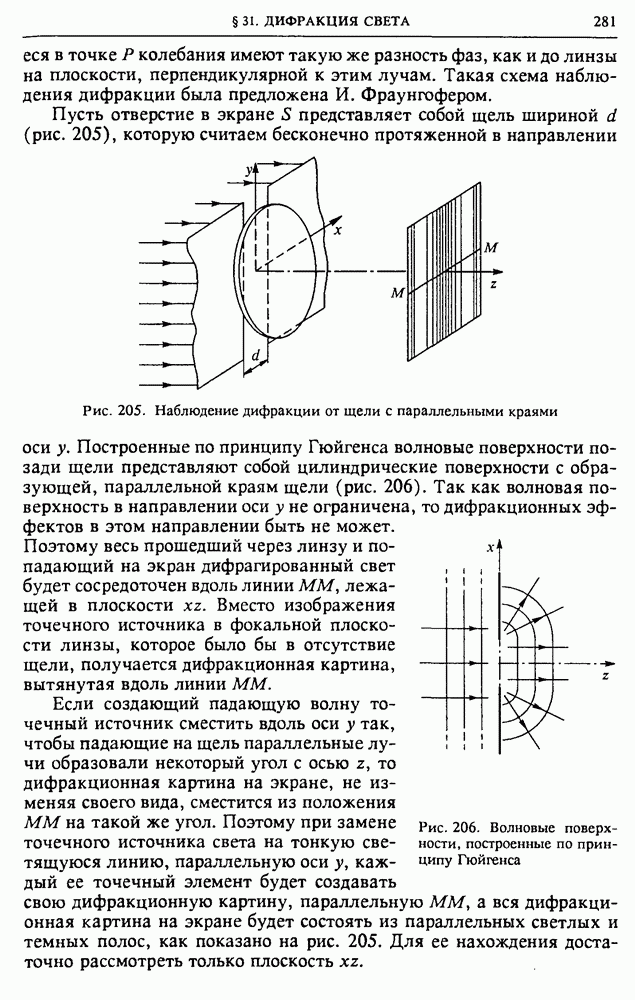
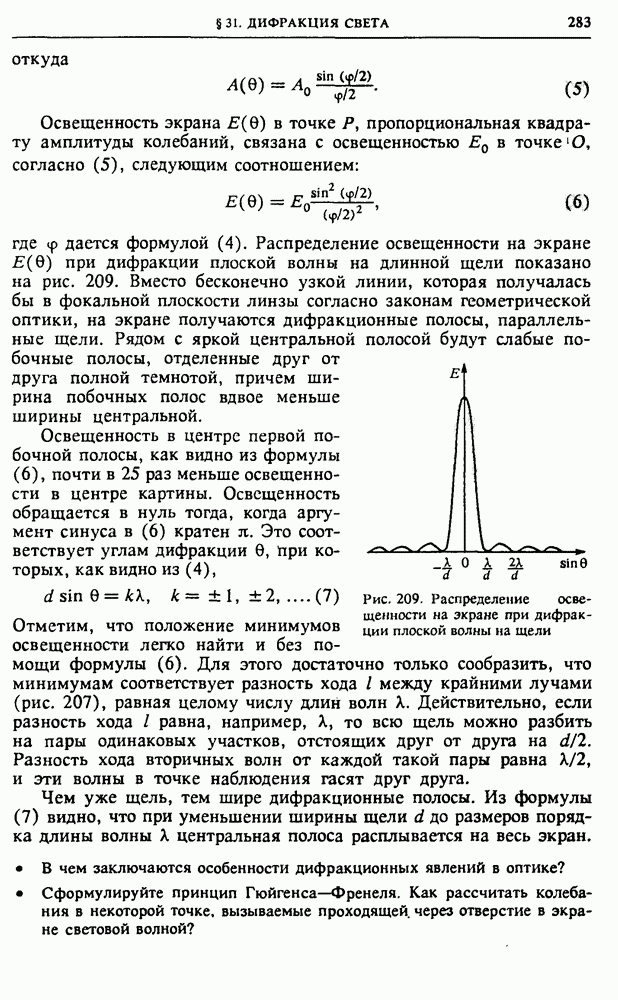
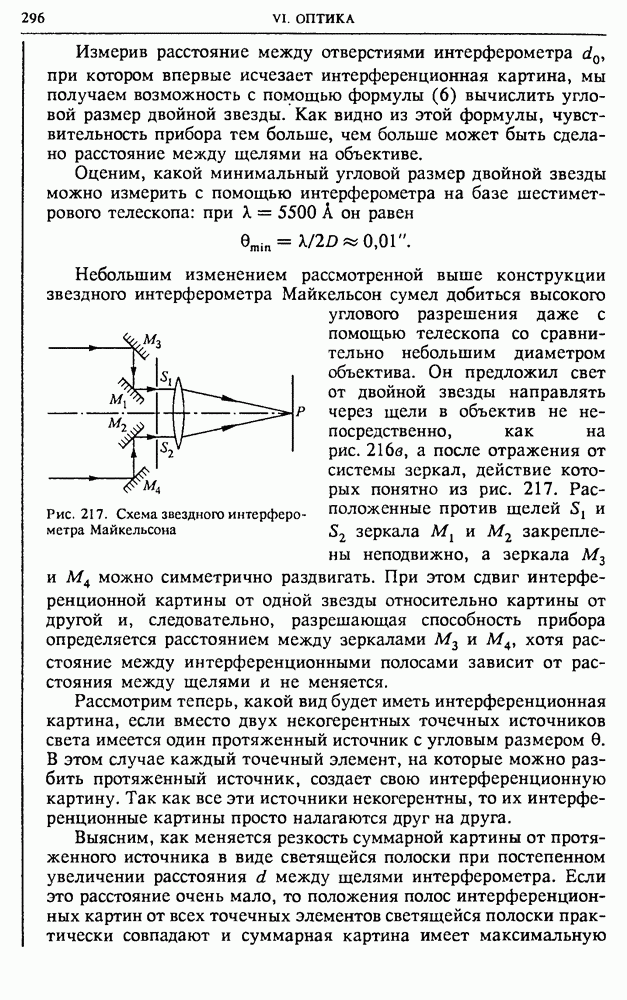
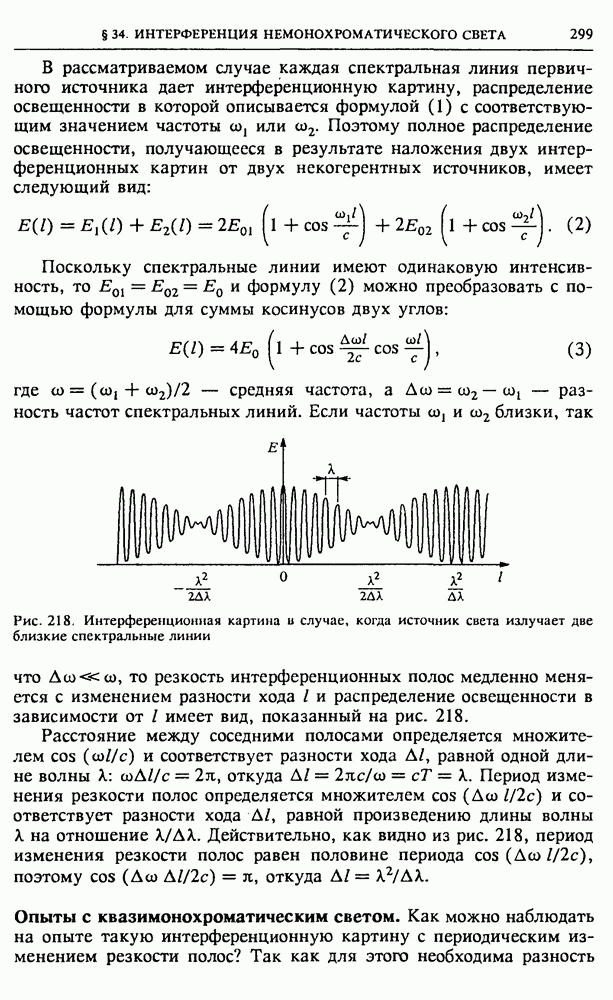
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 23. Работа и мощность переменного тока. Передача электроэнергии
Как мы видели, в цепи синусоидального переменного тока, вообще говоря, возникает сдвиг по фазе между приложенным напряжением и током:

Мгновенная мощность. Сдвиг фаз  зависит от соотношения между активным и реактивными сопротивлениями и тем самым от частоты
зависит от соотношения между активным и реактивными сопротивлениями и тем самым от частоты  Поскольку напряжение и ток в цепи изменяются с частотой
Поскольку напряжение и ток в цепи изменяются с частотой  , то при подсчете работы тока нужно рассматривать настолько малый промежуток времени
, то при подсчете работы тока нужно рассматривать настолько малый промежуток времени  чтобы значения напряжения и тока можно было считать постоянными:
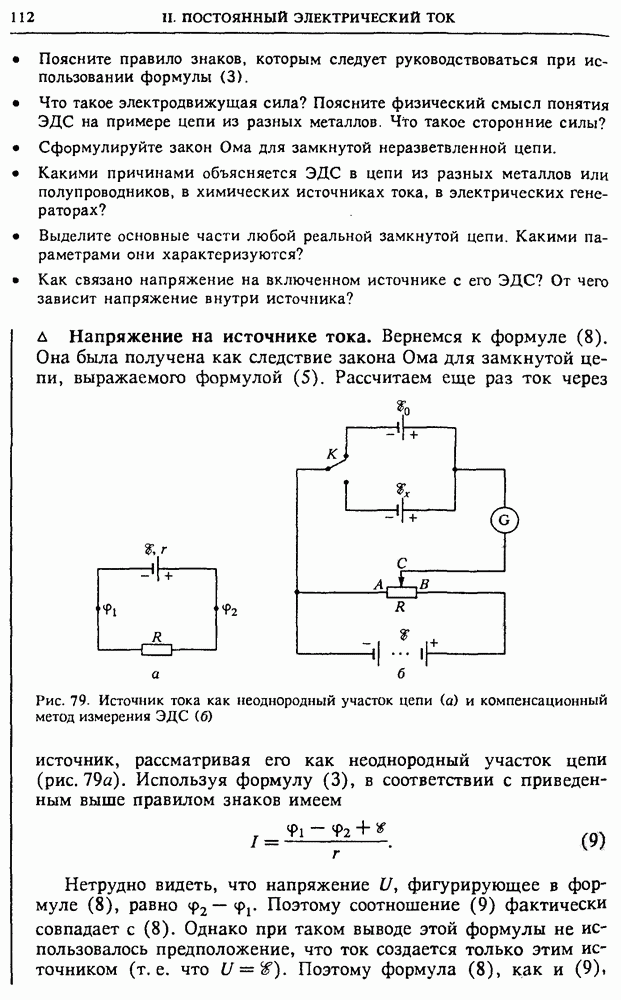
чтобы значения напряжения и тока можно было считать постоянными:

Отсюда получается следующее выражение для мгновенной мощности тока:

Подставив сюда значения  из (1), получаем
из (1), получаем

Воспользовавшись тригонометрическим тождеством

перепишем (4) в следующем виде:

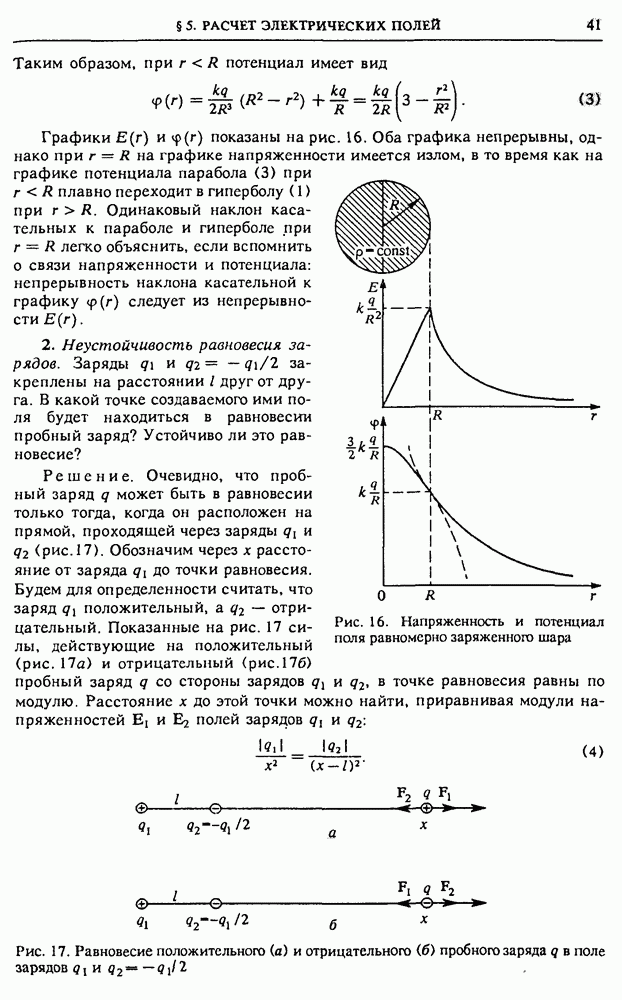
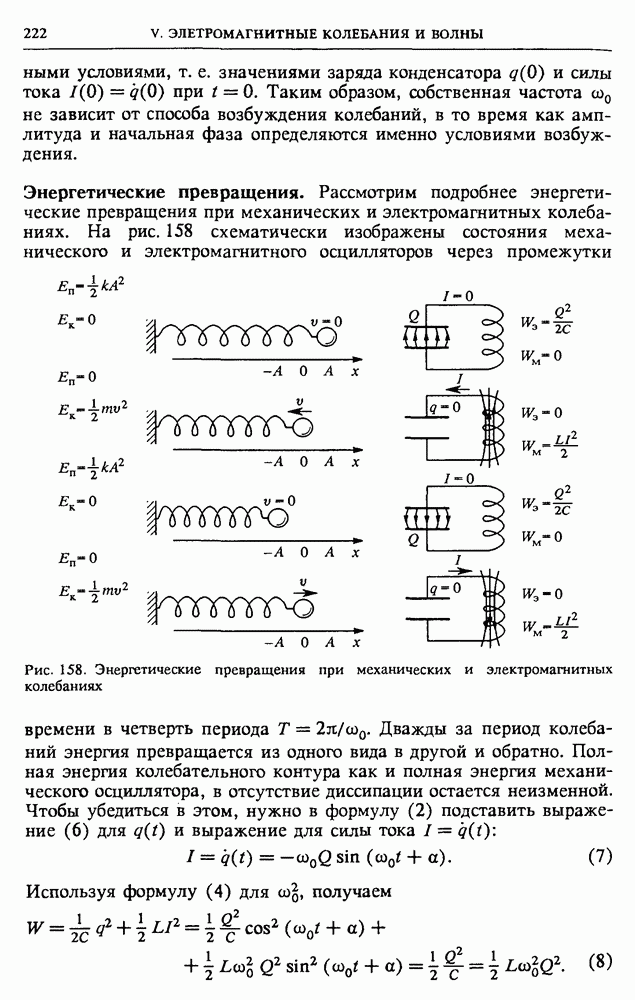
Выражение для мгновенной мощности (5) состоит из двух слагаемых: одно из них не зависит от времени, а второе осциллирует с удвоенной частотой  Это значит, что дважды за каждый период изменения приложенного напряжения изменяется направление потока энергии: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течение другой части возвращается обратно. Средний за период поток энергии положителен, т. е. энергия поступает в цепь от источника.
Это значит, что дважды за каждый период изменения приложенного напряжения изменяется направление потока энергии: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течение другой части возвращается обратно. Средний за период поток энергии положителен, т. е. энергия поступает в цепь от источника.
Средняя мощность. Действующие значения. Если интересоваться работой переменного тока за промежуток времени, сравнимый с периодом  то в выражении (15) для мощности следует учитывать оба слагаемых. При вычислении работы, совершаемой током за промежуток времени, значительно превышающий период, вклад второго слагаемого будет пренебрежимо малым. В этом случае вместо (5) можно пользоваться выражением для средней мощности Р:
то в выражении (15) для мощности следует учитывать оба слагаемых. При вычислении работы, совершаемой током за промежуток времени, значительно превышающий период, вклад второго слагаемого будет пренебрежимо малым. В этом случае вместо (5) можно пользоваться выражением для средней мощности Р:

Часто эту формулу записывают в виде

где I и  — так называемые действующие значения силы тока и напряжения, в
— так называемые действующие значения силы тока и напряжения, в  раз меньшие соответствующих амплитудных значений:
раз меньшие соответствующих амплитудных значений:

Использование действующих значений вместо амплитудных удобно потому, что в нагрузке с чисто активным сопротивлением, где  выражение (7) для мощности будет таким же, как и для постоянного тока.
выражение (7) для мощности будет таким же, как и для постоянного тока.
Потери в линиях передачи. Потребителю обычно подается напряжение определенной величины  поэтому одна и та же мощность Р будет потребляться при разных значениях тока в цепи I в зависимости от сдвига фазы между током и напряжением. При
поэтому одна и та же мощность Р будет потребляться при разных значениях тока в цепи I в зависимости от сдвига фазы между током и напряжением. При
малых значениях  ток должен быть большим, что приводит к большим тепловым потерям в подводящих проводах линии передачи.
ток должен быть большим, что приводит к большим тепловым потерям в подводящих проводах линии передачи.
Если  — сопротивление линии передачи, то рассеиваемая мощность тепловых потерь в линии
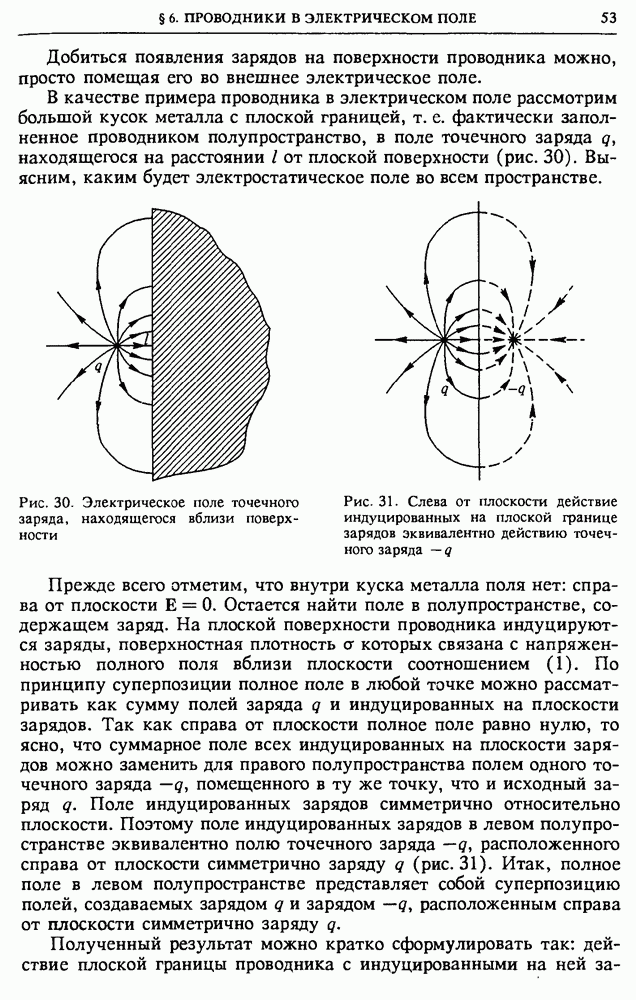
— сопротивление линии передачи, то рассеиваемая мощность тепловых потерь в линии  равна
равна  . Выражая ток в цепи с помощью (7), для
. Выражая ток в цепи с помощью (7), для  получаем
получаем

Для уменьшения потерь следует добиваться как можно меньшего сдвига фазы между током и напряжением в нагрузке.
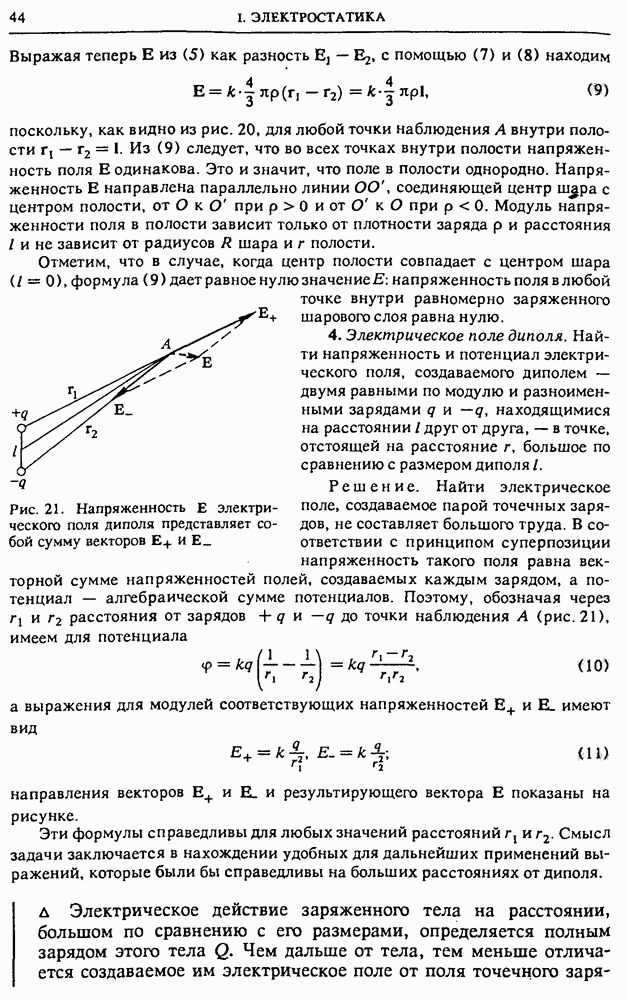
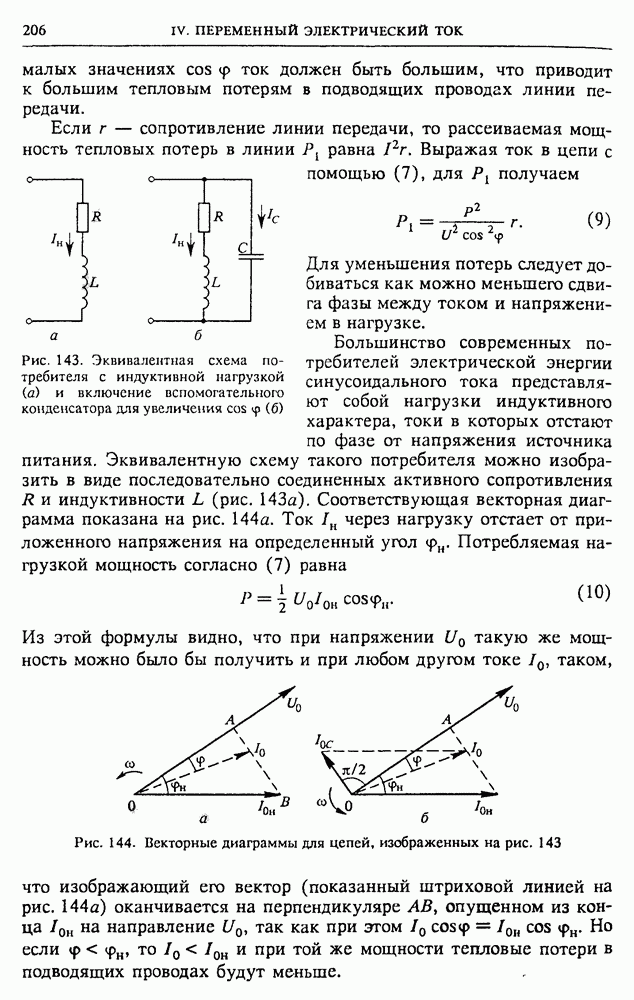
Большинство современных потребителей электрической энергии синусоидального тока представляют собой нагрузки индуктивного характера, токи в которых отстают по фазе от напряжения источника питания. Эквивалентную схему такого потребителя можно изобразить в виде последовательно соединенных активного сопротивления  и индуктивности
и индуктивности  (рис. 143а). Соответствующая векторная диаграмма показана на рис. 144а. Ток
(рис. 143а). Соответствующая векторная диаграмма показана на рис. 144а. Ток  через нагрузку отстает от приложенного напряжения на определенный угол
через нагрузку отстает от приложенного напряжения на определенный угол  Потребляемая нагрузкой мощность согласно (7) равна
Потребляемая нагрузкой мощность согласно (7) равна


Рис. 143. Эквивалентная схема потребителя с индуктивной нагрузкой (а) и включение вспомогательного конденсатора для увеличения 

Рис. 144. Векторные диаграммы для цепей, изображенных на рис. 143
Из этой формулы видно, что при напряжении  такую же мощность можно было бы получить и при любом другом токе
такую же мощность можно было бы получить и при любом другом токе  таком, что изображающий его вектор (показанный штриховой линией на рис. 144а) оканчивается на перпендикуляре
таком, что изображающий его вектор (показанный штриховой линией на рис. 144а) оканчивается на перпендикуляре  опущенном из конца
опущенном из конца  на направление
на направление  так как при этом
так как при этом  Но если
Но если  то
то  и при той же мощности тепловые потери в подводящих проводах будут меньше.
и при той же мощности тепловые потери в подводящих проводах будут меньше.
Уменьшение потерь. Как же добиться того, чтобы сдвиг фаз между напряжением и током в цепи уменьшился? Легко сообразить, что для этого можно подсоединить параллельно нагрузке вспомогательный конденсатор (рис. 1436). Векторная диаграмма в этом случае будет иметь вид, изображенный на рис. 144б. Векторы, изображающие приложенное напряжение  и ток через нагрузку
и ток через нагрузку  останутся неизменными, а полный ток в неразветвленной цепи, равный сумме токов через нагрузку и вспомогательный конденсатор, будет изображаться вектором
останутся неизменными, а полный ток в неразветвленной цепи, равный сумме токов через нагрузку и вспомогательный конденсатор, будет изображаться вектором  Подбирая емкость конденсатора, можно добиться того, чтобы сдвиг по фазе принял заданное значение 9.
Подбирая емкость конденсатора, можно добиться того, чтобы сдвиг по фазе принял заданное значение 9.
Из рис. 1446 видно, что длина вектора  равна
равна

Но  и с помощью (10) находим
и с помощью (10) находим  Амплитудное значение тока в конденсаторе
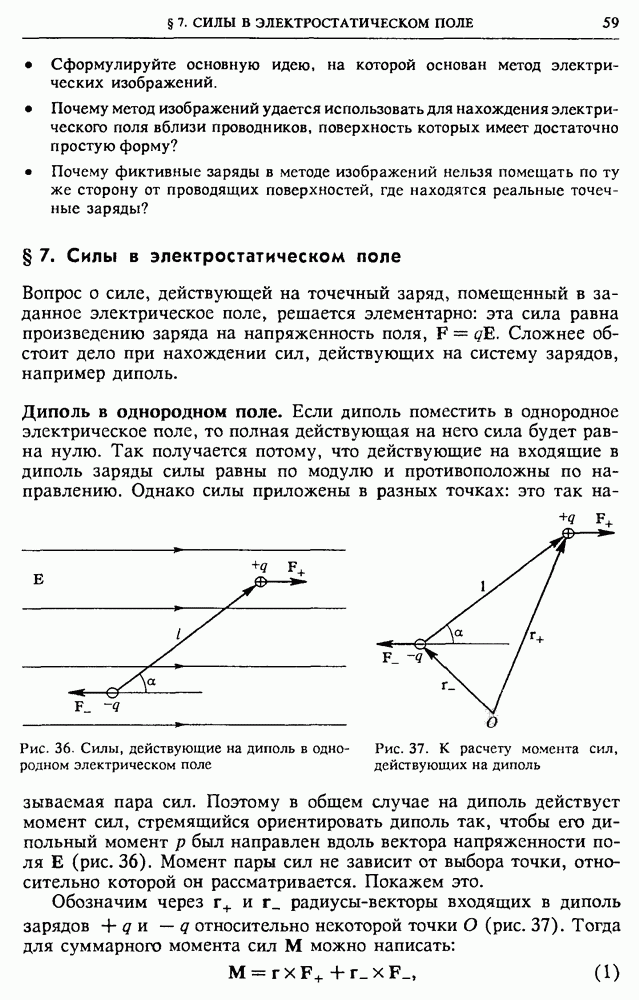
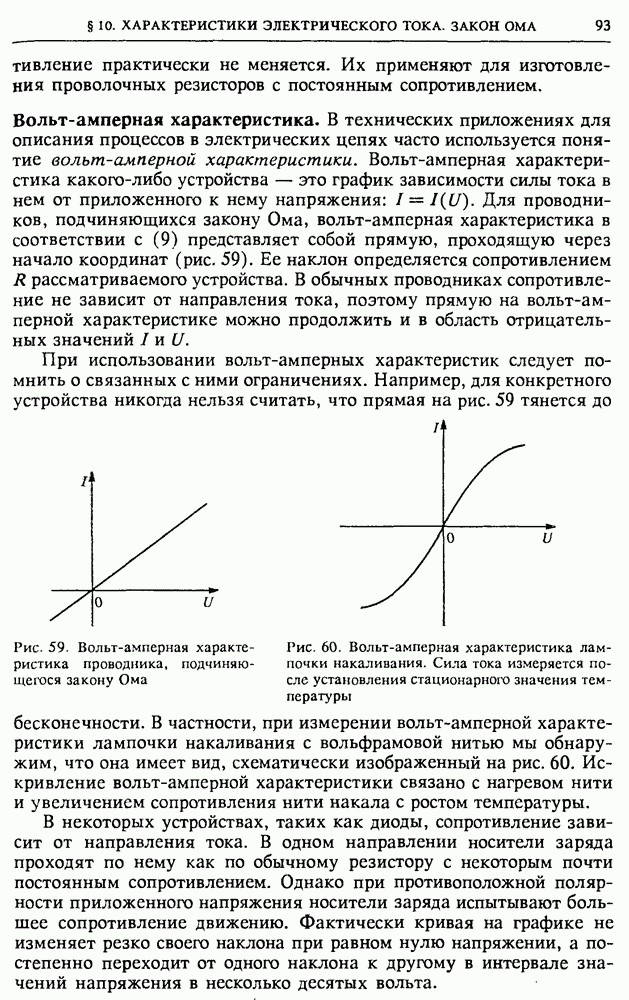
Амплитудное значение тока в конденсаторе  связано с амплитудным значением подаваемого напряжения формулой
связано с амплитудным значением подаваемого напряжения формулой  Подставляя
Подставляя  в (11), находим
в (11), находим

Таким образом, существует достаточно простой и эффективный способ снижения потерь в линиях передачи энергии переменного тока, связанных с реактивным характером сопротивления нагрузки: подключение конденсатора к индуктивной нагрузке позволяет получить равное нулю значение сдвига фаз 9.
Высоковольтные линии передачи. Но даже в том случае, когда сопротивление нагрузки является чисто активным и сдвиг фаз между напряжением и током отсутствует, т. е.  тепловые потери в линии передачи все равно неизбежны. Можно ли их каким-либо способом уменьшить? Ответ на этот вопрос дает формула (9). Из нее видно, что при заданном значении передаваемой потребителю мощности Р уменьшить тепловые потери в линии можно, либо уменьшая сопротивление
тепловые потери в линии передачи все равно неизбежны. Можно ли их каким-либо способом уменьшить? Ответ на этот вопрос дает формула (9). Из нее видно, что при заданном значении передаваемой потребителю мощности Р уменьшить тепловые потери в линии можно, либо уменьшая сопротивление  проводов линии передачи, либо повышая напряжение
проводов линии передачи, либо повышая напряжение  переменного тока, подаваемого потребителю. Уменьшение сопротивления линии в настоящее время возможно лишь до известных пределов, поэтому до создания эффективных сверхпроводящих линий электропередачи с потерями приходится бороться повышением напряжения.
переменного тока, подаваемого потребителю. Уменьшение сопротивления линии в настоящее время возможно лишь до известных пределов, поэтому до создания эффективных сверхпроводящих линий электропередачи с потерями приходится бороться повышением напряжения.
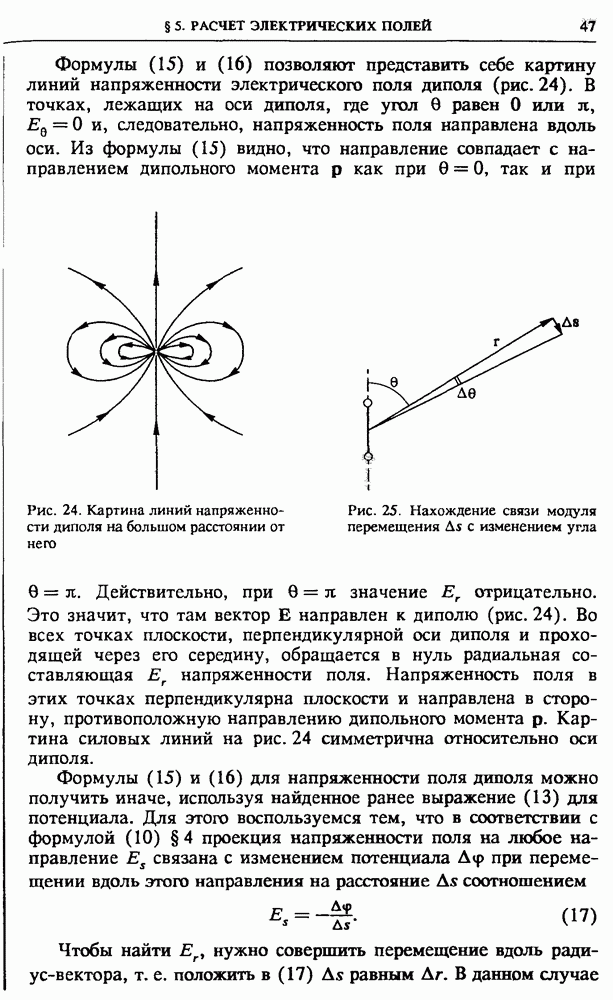
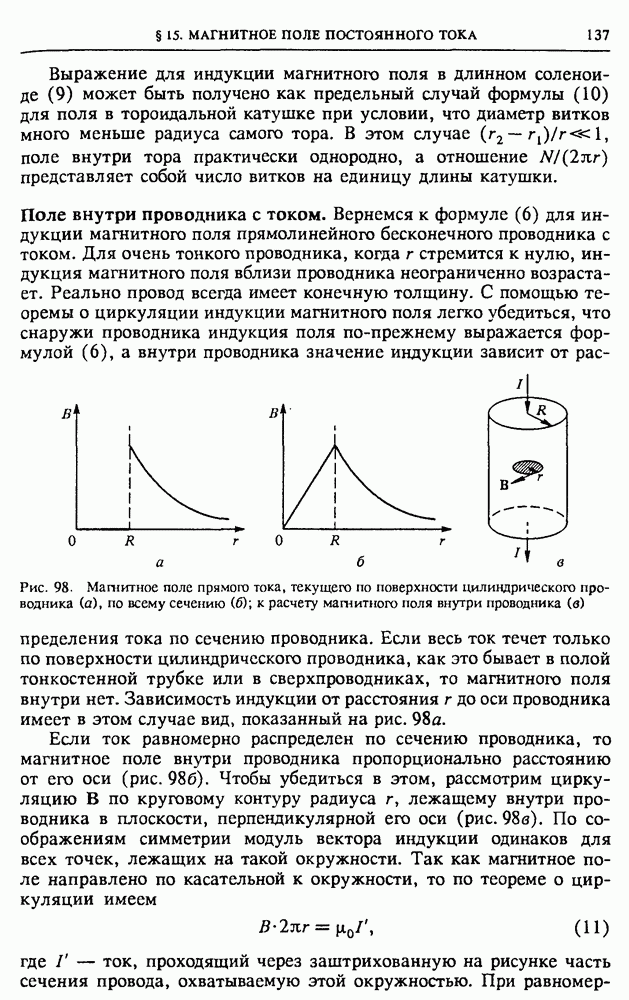
Трансформатор. Для преобразования напряжения на электростанциях и у потребителей используются трансформаторы (рис. 145). Трансформатор имеет сердечник замкнутой формы из магнитомягкого (легко перемагничиваемого) материала, который несет на себе две обмотки: первичную и вторичную. Концы первичной обмотки (вход трансформатора) подключают к сети
переменного тока, а концы вторичной обмотки (выход) — к потребителю электрической энергии. ЭДС электромагнитной индукции, возникающая во вторичной обмотке, пропорциональна числу витков в ней.

Рис. 145. Трансформатор: общий вид, схематическое устройство и условное изображение на схемах
Поэтому, изменяя это число витков, можно изменять в широких пределах напряжение на выходе трансформатора.
Рассмотрим принцип действия трансформатора. Пусть сначала вторичная обмотка трансформатора разомкнута, а на первичную подается переменное синусоидальное напряжение. Это режим холостого хода. Как и всякую катушку индуктивности, первичную обмотку трансформатора можно рассматривать как последовательно соединенные индуктивность  и активное сопротивление
и активное сопротивление  Напряжение
Напряжение  на индуктивном сопротивлении
на индуктивном сопротивлении  первичной обмотки опережает по фазе ток и, следовательно, напряжение
первичной обмотки опережает по фазе ток и, следовательно, напряжение  на ее активном сопротивлении на угол, равный
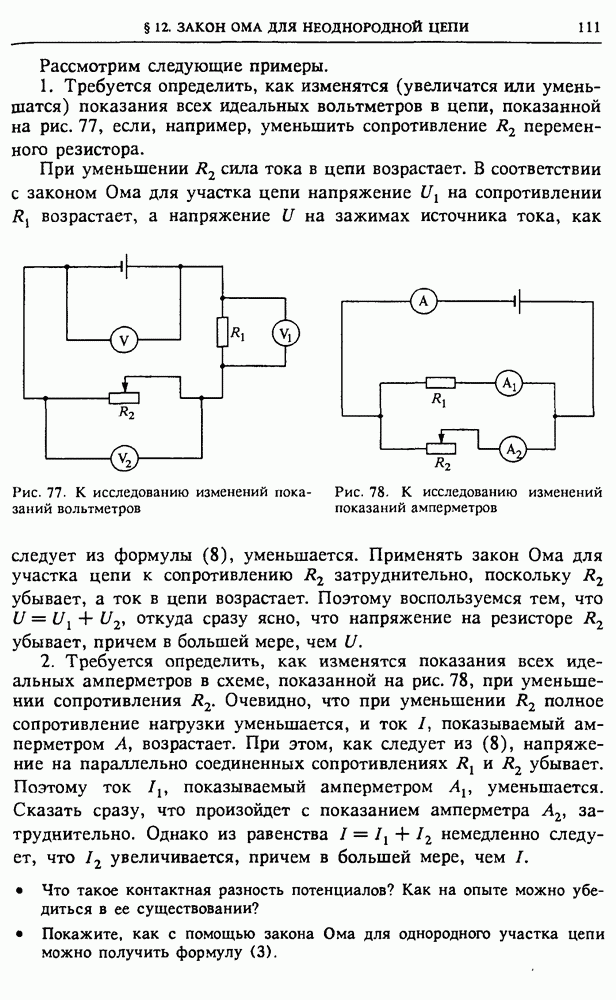
на ее активном сопротивлении на угол, равный  Поэтому амплитудные значения поданного на первичную обмотку напряжения
Поэтому амплитудные значения поданного на первичную обмотку напряжения  и напряжений на
и напряжений на  и
и  связаны соотношением
связаны соотношением

Разумеется, непосредственно измерить  и
и  по отдельности невозможно, так как первичная обмотка, строго говоря, не есть последовательно соединенные индуктивность
по отдельности невозможно, так как первичная обмотка, строго говоря, не есть последовательно соединенные индуктивность  и активное сопротивление
и активное сопротивление  каждый элемент обмотки обладает одновременно индуктивностью и сопротивлением. Это так называемая цепь с распределенными параметрами. Но при расчете можно заменить реальную обмотку на цепь с сосредоточенными параметрами — катушку индуктивности и резистор, соединенные последовательно, поскольку через каждый элемент исходной цепи идет один и тот же ток.
каждый элемент обмотки обладает одновременно индуктивностью и сопротивлением. Это так называемая цепь с распределенными параметрами. Но при расчете можно заменить реальную обмотку на цепь с сосредоточенными параметрами — катушку индуктивности и резистор, соединенные последовательно, поскольку через каждый элемент исходной цепи идет один и тот же ток.
Напряжение на индуктивности  в каждый момент времени компенсирует возникающую в первичной обмотке ЭДС самоиндукции
в каждый момент времени компенсирует возникающую в первичной обмотке ЭДС самоиндукции  поэтому
поэтому

Если весь магнитный поток, создаваемый током первичной обмотки, целиком, т. е. без рассеяния, пронизывает вторичную
обмотку, то индуцируемая в каждом витке вторичной обмотки ЭДС будет такой же, как и в каждом витке первичной обмотки. Поэтому отношение электродвижущих сил в первичной и вторичной обмотках равно отношению чисел витков:

На выходе разомкнутой вторичной обмотки существует напряжение, равное индуцируемой в ней ЭДС:

Подставляя сюда из (15) и учитывая (14), получаем

Режим холостого хода. Таким образом, значение напряжения на  разомкнутой вторичной обмотке трансформатора пропорционально не подаваемому на первичную обмотку напряжению
разомкнутой вторичной обмотке трансформатора пропорционально не подаваемому на первичную обмотку напряжению  а лишь напряжению на индуктивном сопротивлении первичной обмотки
а лишь напряжению на индуктивном сопротивлении первичной обмотки  Отсюда сразу становится ясна роль сердечника трансформатора. В самом деле, из формулы (13) следует, что напряжение на индуктивности
Отсюда сразу становится ясна роль сердечника трансформатора. В самом деле, из формулы (13) следует, что напряжение на индуктивности  будет тем ближе к подаваемому на вход трансформатора напряжению
будет тем ближе к подаваемому на вход трансформатора напряжению  чем больше будет индуктивное сопротивление первичной обмотки
чем больше будет индуктивное сопротивление первичной обмотки  по сравнению с ее активным сопротивлением
по сравнению с ее активным сопротивлением  Наличие сердечника из материала с высокой магнитной проницаемостью приводит к многократному увеличению индуктивности
Наличие сердечника из материала с высокой магнитной проницаемостью приводит к многократному увеличению индуктивности  . У такого трансформатора на холостом ходу
. У такого трансформатора на холостом ходу  Знак минус означает, что эти напряжения находятся в противофазе. Благодаря большому индуктивному сопротивлению первичной обмотки ток в ней при разомкнутой вторичной цепи мал.
Знак минус означает, что эти напряжения находятся в противофазе. Благодаря большому индуктивному сопротивлению первичной обмотки ток в ней при разомкнутой вторичной цепи мал.
Трансформатор под нагрузкой. При замыкании вторичной цепи трансформатора на некоторую нагрузку во вторичной обмотке появляется ток. Создаваемый этим током магнитный поток направлен так, что, согласно закону Ленца, препятствует изменению магнитного потока, создаваемого током в первичной обмотке. Если бы при этом ток в первичной обмотке остался неизменным, то это привело бы к уменьшению магнитного потока. Значит, включение нагрузки во вторичную цепь эквивалентно уменьшению индуктивности первичной цепи.
Но уменьшение индуктивного сопротивления немедленно приводит к увеличению тока в первичной обмотке, к уменьшению сдвига по фазе между напряжением и током и, следовательно, к увеличению потребляемой от внешней цепи мощности. Таким образом, если на холостом ходу трансформатор представляет собой почти чисто
индуктивное сопротивление, то по мере увеличения нагрузки трансформатора, т. е. тока во вторичной цепи, характер сопротивления первичной обмотки трансформатора становится ближе к активному.
Если потери энергии в самом трансформаторе малы, то на основании закона сохранения энергии потребляемая трансформатором мощность целиком передается нагрузке. Тогда с помощью (6) можно написать

где  — сдвиги фаз между током и напряжением в первичной и вторичной цепях.
— сдвиги фаз между током и напряжением в первичной и вторичной цепях.
Приведенное выше рассмотрение работы трансформатора относится к идеализированному случаю трансформатора без потерь. В реальном трансформаторе всегда имеются потери, связанные с выделением джоулевой теплоты в обмотках, с токами Фуко, с необратимыми явлениями при перемагничивании сердечника и с рассеянием магнитного потока. Но в современных трансформаторах суммарные потери не превышают нескольких процентов от передаваемой мощности. Коэффициент полезного действия трансформаторов очень высок и лежит в пределах 95-99,5%.
Выпрямление переменного тока. Для многих практических применений необходимо преобразовать переменный синусоидальный ток в ток одного направления. Этой цели служат выпрямители, действие которых основано на односторонней проводимости ламповых и полупроводниковых диодов.
Понять действие выпрямителя можно, не вникая в физическую природу самого механизма односторонней проводимости.
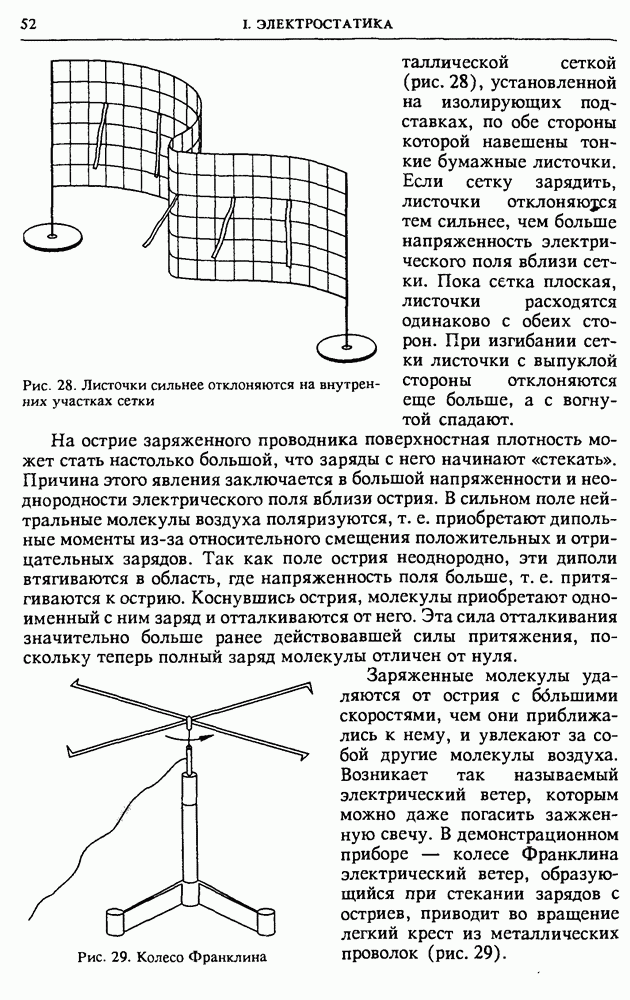
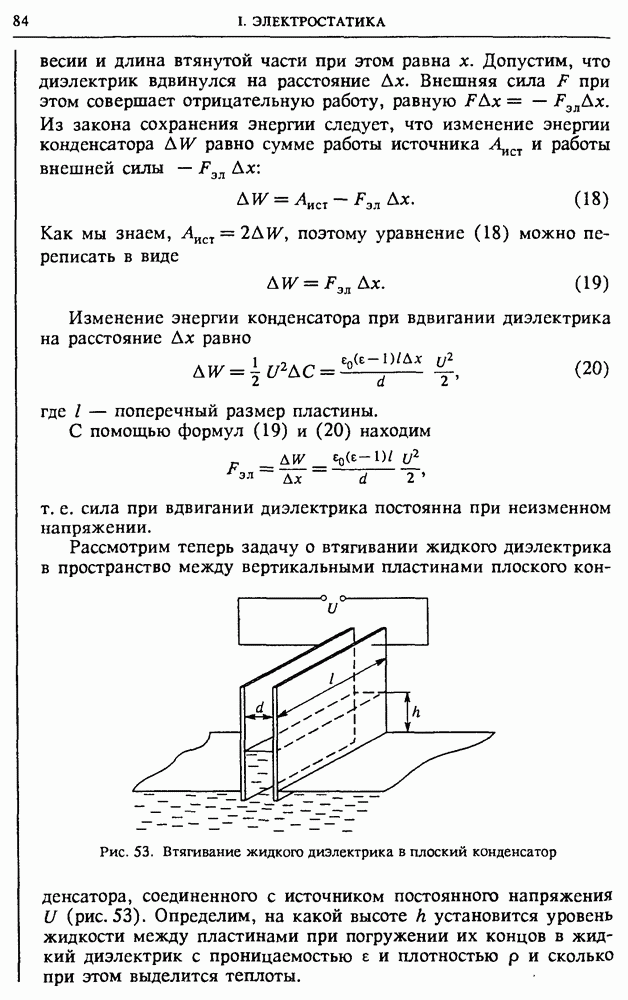
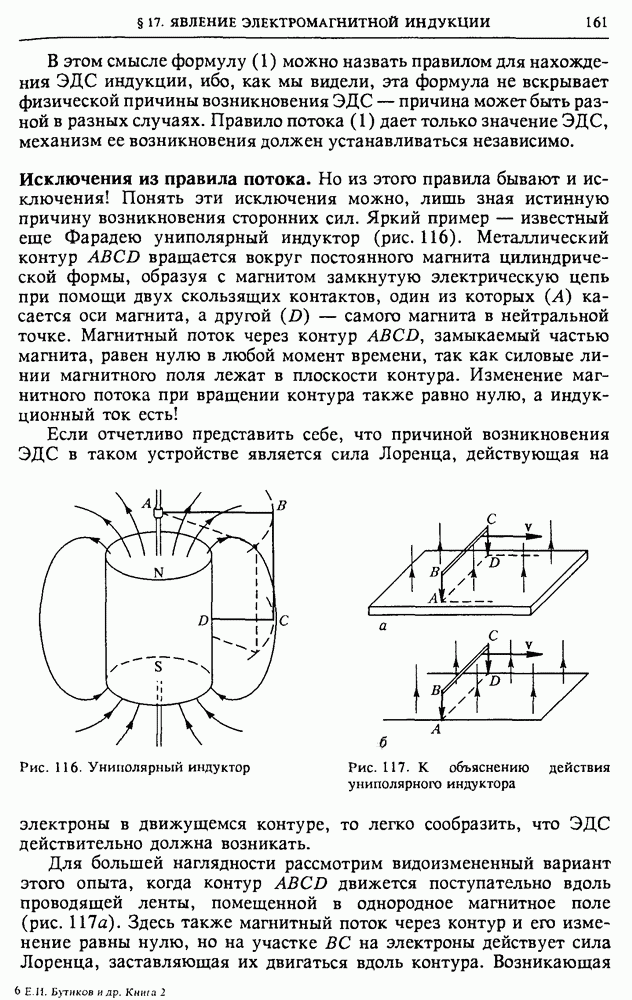
Простейшая схема выпрямителя приведена на рис. 146а. Это однополупериодный выпрямитель, в котором ток через нагрузку  течет только в течение одной половины каждого периода приложенного синусоидального напряжения.
течет только в течение одной половины каждого периода приложенного синусоидального напряжения.

Рис. 146. Схемы выпрямителей: однополупериодного (а), двухполупериодного (б) и с удвоением напряжения (в)
В мостиковой схеме выпрямителя, показанной на рис. 1466, ток через нагрузку идет в одном и том же направлении в течение обеих половин каждого периода. Но в таком двухполупериодном выпрямителе ток все-таки тоже пульсирует. Для сглаживания этих
пульсаций используют так называемые электрические фильтры, если требуется не только получить ток одного направления, но и постоянное напряжение.
В приведенных на рис. 146 а,б схемах максимальное значение напряжения на нагрузке (при идеальных диодах) равно амплитудному значению приложенного синусоидального напряжения. В показанной на рис. 146 в схеме выпрямителя напряжение на нагрузке практически вдвое больше амплитудного значения приложенного напряжения, если время разрядки конденсаторов через сопротивление нагрузки  значительно превышает период Т синусоидального напряжения. Это так называемая схема с удвоением напряжения.
значительно превышает период Т синусоидального напряжения. Это так называемая схема с удвоением напряжения.
Задачи
1. Активное сопротивление  первичной обмотки трансформатора составляет
первичной обмотки трансформатора составляет  ее индуктивного сопротивления
ее индуктивного сопротивления  Какое напряжение будет на разомкнутой вторичной обмотке, имеющей вдвое больше витков, если первичную обмотку включить в сеть напряжением 220 В?
Какое напряжение будет на разомкнутой вторичной обмотке, имеющей вдвое больше витков, если первичную обмотку включить в сеть напряжением 220 В?
Решение. Напряжение  на разомкнутой вторичной обмотке связано с напряжением
на разомкнутой вторичной обмотке связано с напряжением  на индуктивном сопротивлении первичной обмотки соотношением (17). Поэтому в рассматриваемом случае для действующих значений имеем
на индуктивном сопротивлении первичной обмотки соотношением (17). Поэтому в рассматриваемом случае для действующих значений имеем  Напряжение на индуктивности и сопротивлении в первичной обмотке сдвинуты по фазе на
Напряжение на индуктивности и сопротивлении в первичной обмотке сдвинуты по фазе на  а их действующие значения
а их действующие значения  и
и  связаны с действующим значением
связаны с действующим значением  приложенного напряжения тем же соотношением (13), что и соответствующие амплитудные значения. Отношение
приложенного напряжения тем же соотношением (13), что и соответствующие амплитудные значения. Отношение  в соответствии с условием задачи, равно 0,1. Поэтому
в соответствии с условием задачи, равно 0,1. Поэтому

На разомкнутой вторичной обмотке получаем

Выходное напряжение оказывается всего на 0,5% меньше значения 440 В, которое соответствовало бы идеализированному случаю чисто индуктивного сопротивления первичной обмотки.
2. Последовательно с электрокипятильником, включенным в осветительную сеть с частотой  Гц, подключили дроссель. При этом потребляемая кипятильником мощность упала в два раза. Найдите индуктивность
Гц, подключили дроссель. При этом потребляемая кипятильником мощность упала в два раза. Найдите индуктивность  дросселя, если сопротивление кипятильника
дросселя, если сопротивление кипятильника  Ом.
Ом.
Решение. По условию задачи потребляемая кипятильником мощность после подключения дросселя уменьшилась вдвое. Значит, напряжение на нем уменьшилось в  раз. Если построить векторную диаграмму для последовательно соединенных активного сопротивления кипятильника и индуктивного сопротивления дросселя, то легко убедиться, что напряжения на кипятильнике и на дросселе одинаковы и в
раз. Если построить векторную диаграмму для последовательно соединенных активного сопротивления кипятильника и индуктивного сопротивления дросселя, то легко убедиться, что напряжения на кипятильнике и на дросселе одинаковы и в  раз меньше сетевого напряжения. Но это означает, что
раз меньше сетевого напряжения. Но это означает, что  Отсюда
Отсюда

• При каких условиях выражение (2) можно использовать для расчета работы переменного тока? Ведь оно, строго говоря, было получено для постоянного тока.
• Нарисуйте примерный график зависимости от времени мгновенной мощности в цепи переменного тока для случаев  (активная нагрузка),
(активная нагрузка),  (реактивная нагрузка) и
(реактивная нагрузка) и 
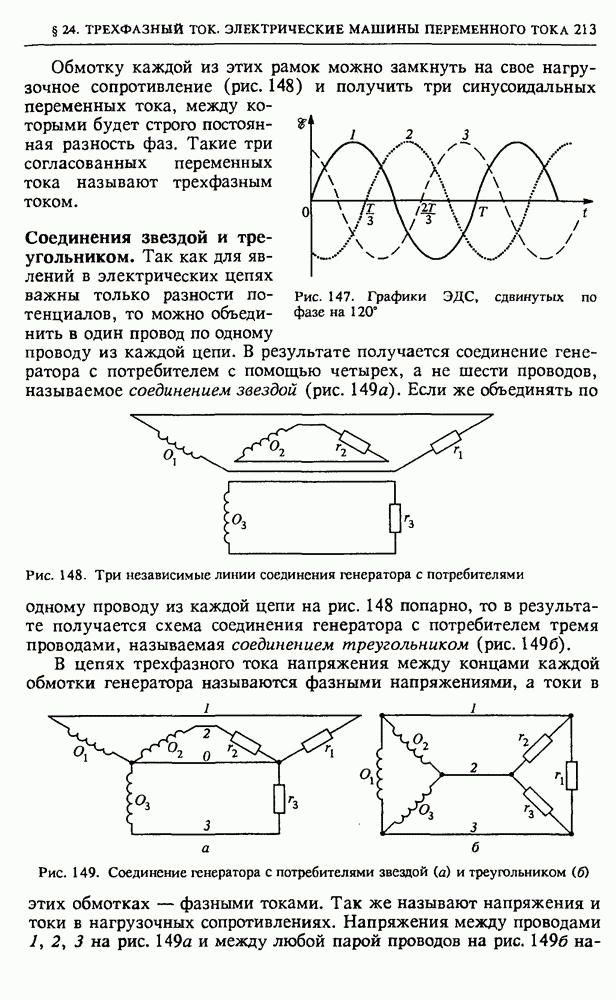
• В каких случаях при расчете работы переменного тока можно пользоваться выражением (6) для средней мощности, а не выражением (5) для мгновенной мощности?
• Каким образом можно уменьшить тепловые потери в линиях электропередачи, изменяя характер сопротивления нагрузки? Почему в сетях переменного тока потребитель энергии должен обладать практически активным в целом сопротивлением?
• В чем преимущество использования линий высокого напряжения для передачи электроэнергии?
• Какую роль в трансформаторе играет сердечник из материала с высокой магнитной проницаемостью? Почему железный сердечник трансформатора собирают из отдельных изолированных пластин?
• Из формулы (17) следует, что коэффициент трансформации напряжения определяется отношением чисел витков  Казалось бы, при отношении
Казалось бы, при отношении  потери в трансформаторе будут тем меньше, чем меньше значения
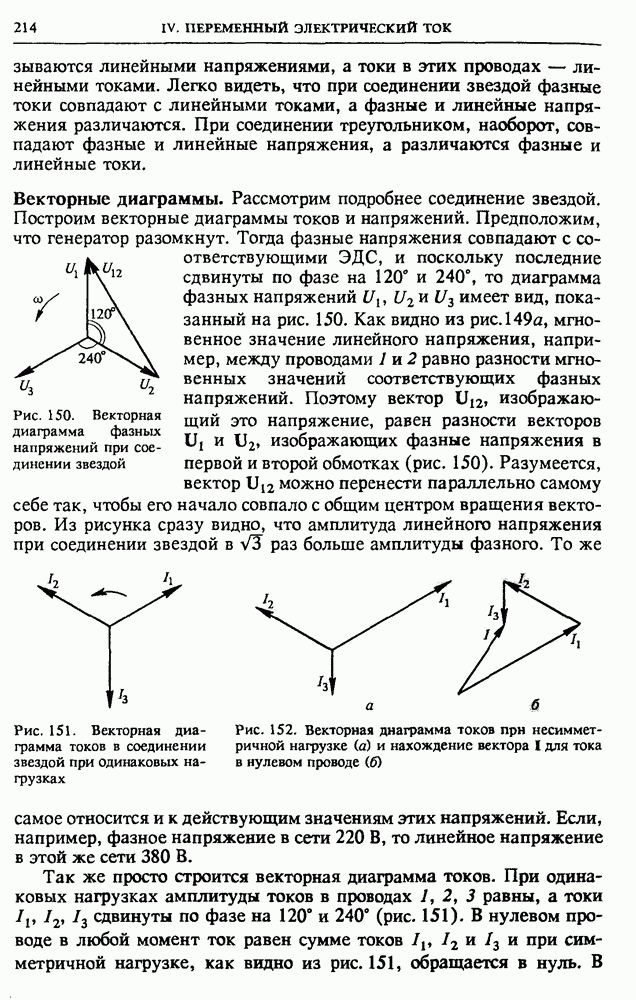
потери в трансформаторе будут тем меньше, чем меньше значения  так как с увеличением числа витков растет активное сопротивление. Почему же у трансформаторов обмотки обычно содержат большое число витков?
так как с увеличением числа витков растет активное сопротивление. Почему же у трансформаторов обмотки обычно содержат большое число витков?
• Можно ли включать трансформатор в сеть постоянного тока?
• Нарисуйте графики зависимости силы тока от времени в нагрузке выпрямителей, схемы которых показаны на рис. 146 а,б.
• Объясните, почему в схеме выпрямителя на рис. 146 в происходит удвоение напряжения на нагрузке. Предложите схему выпрямителя, в котором на нагрузке происходило бы утроение напряжения.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
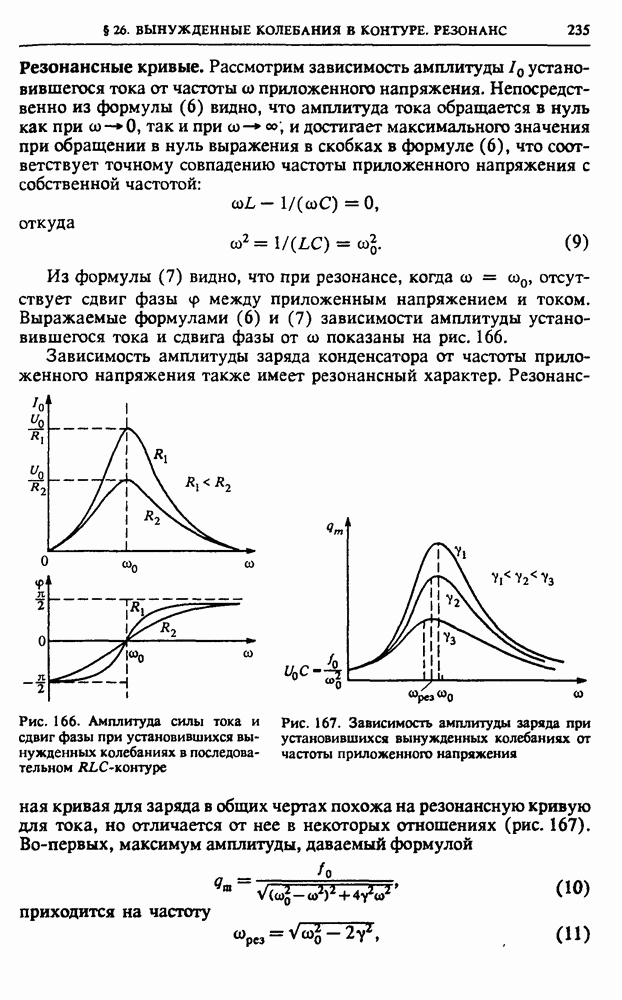
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
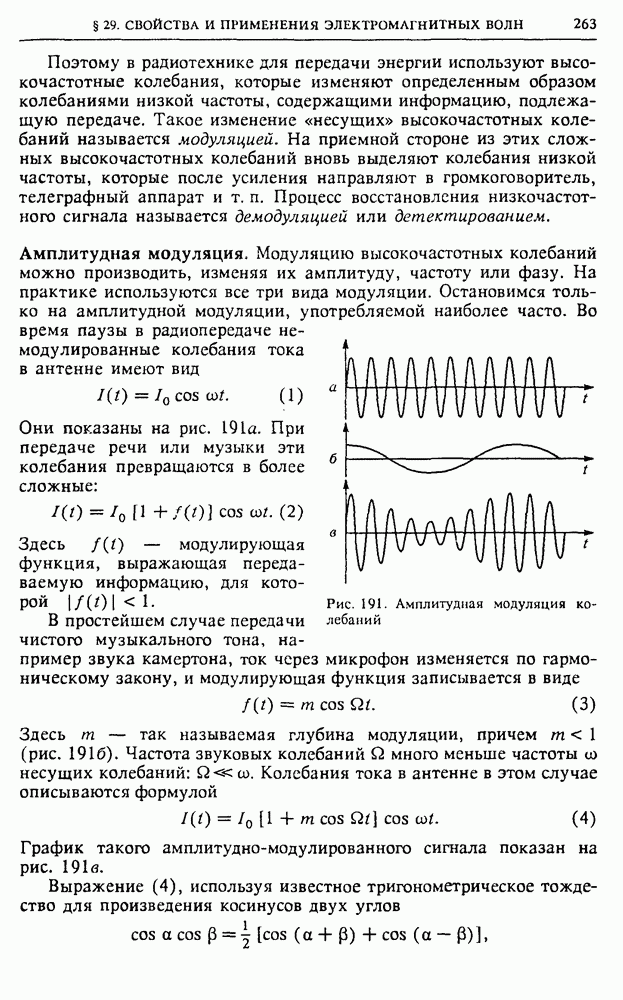
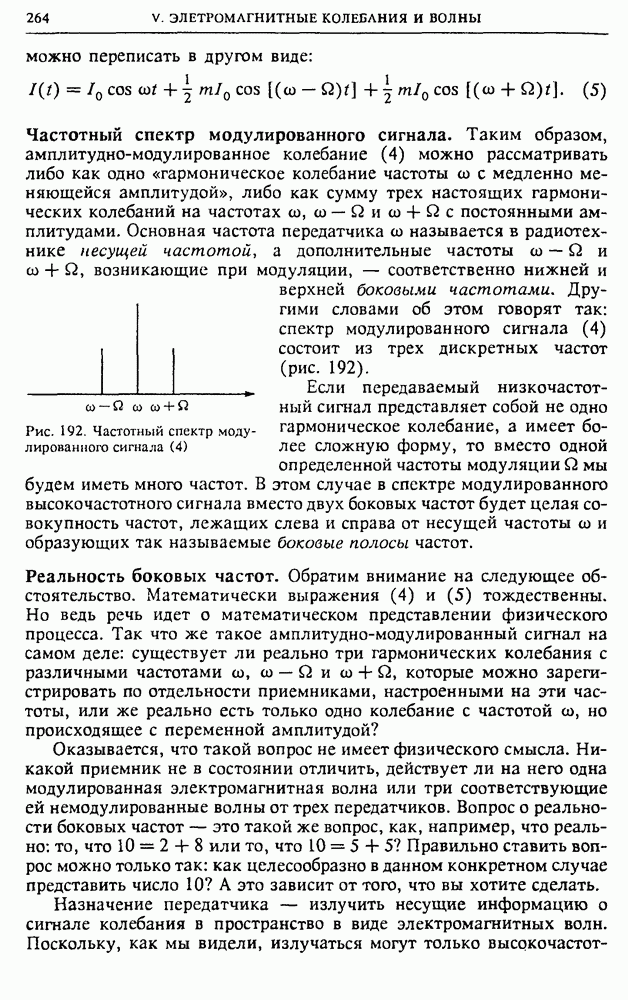
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
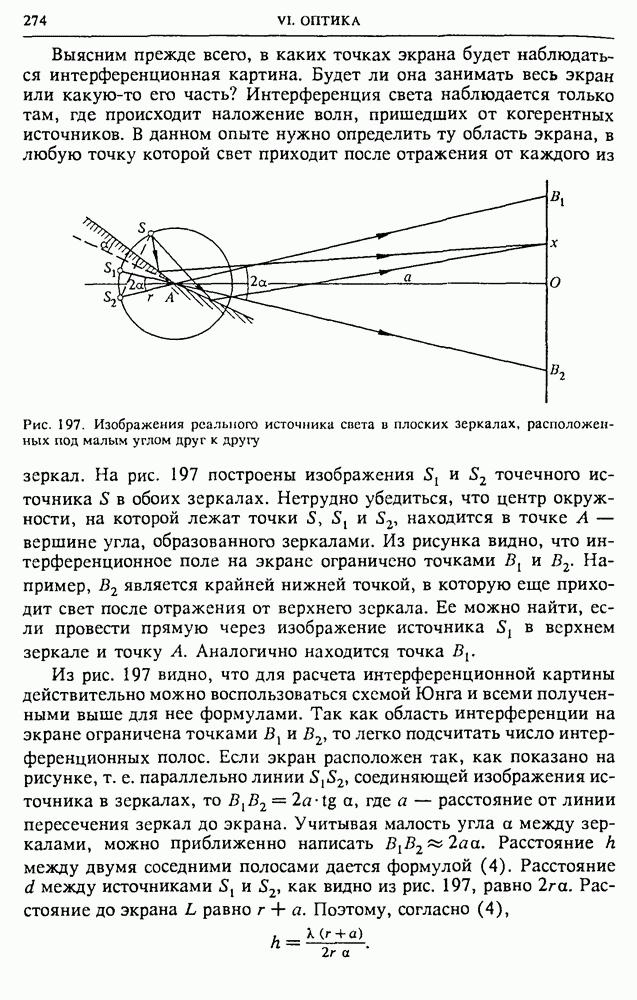
- § 30. Свет как электромагнитные волны. Интерференция
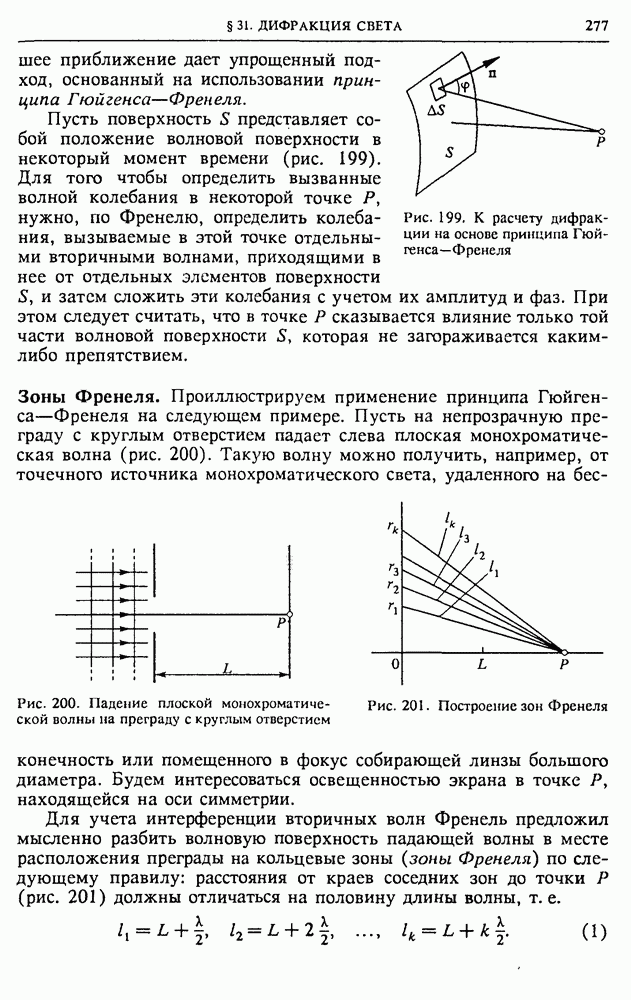
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
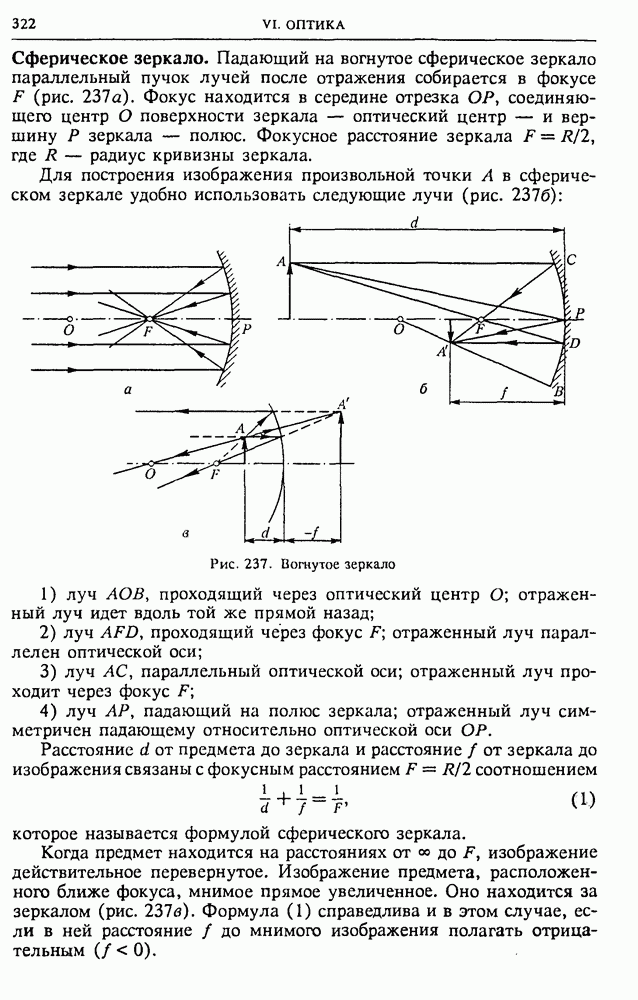
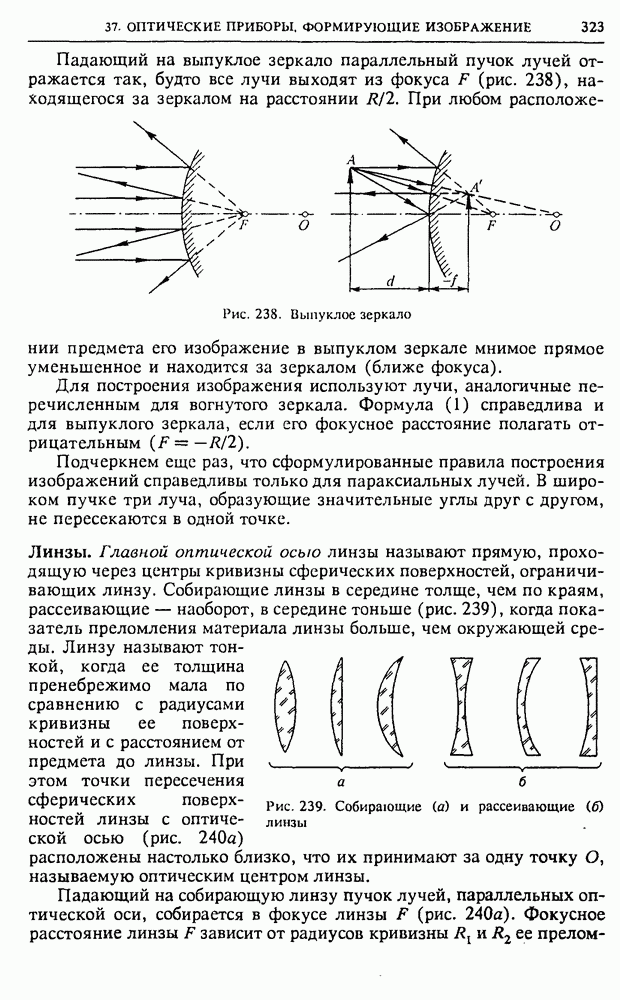
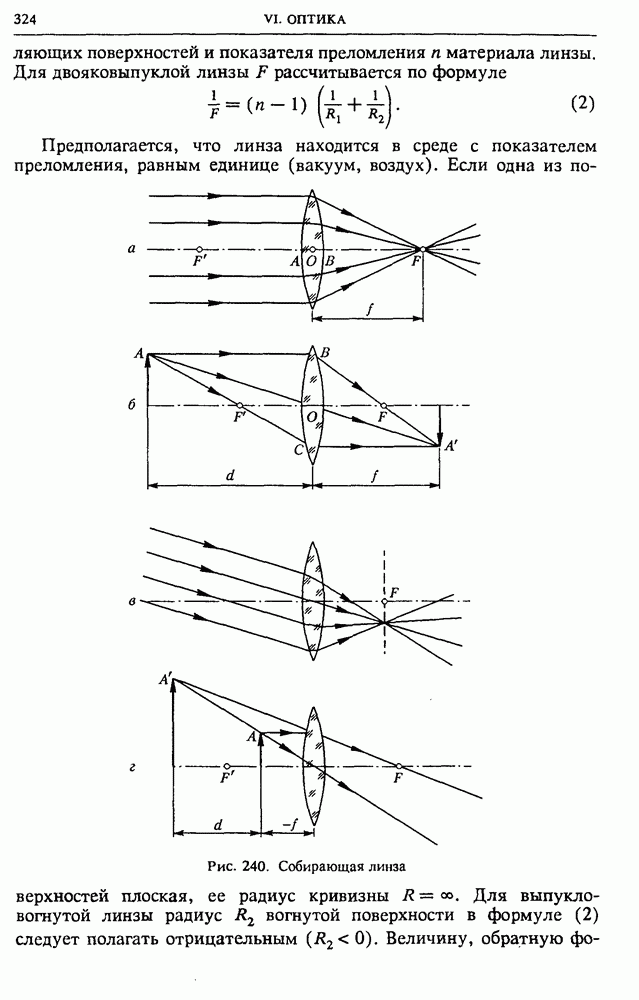
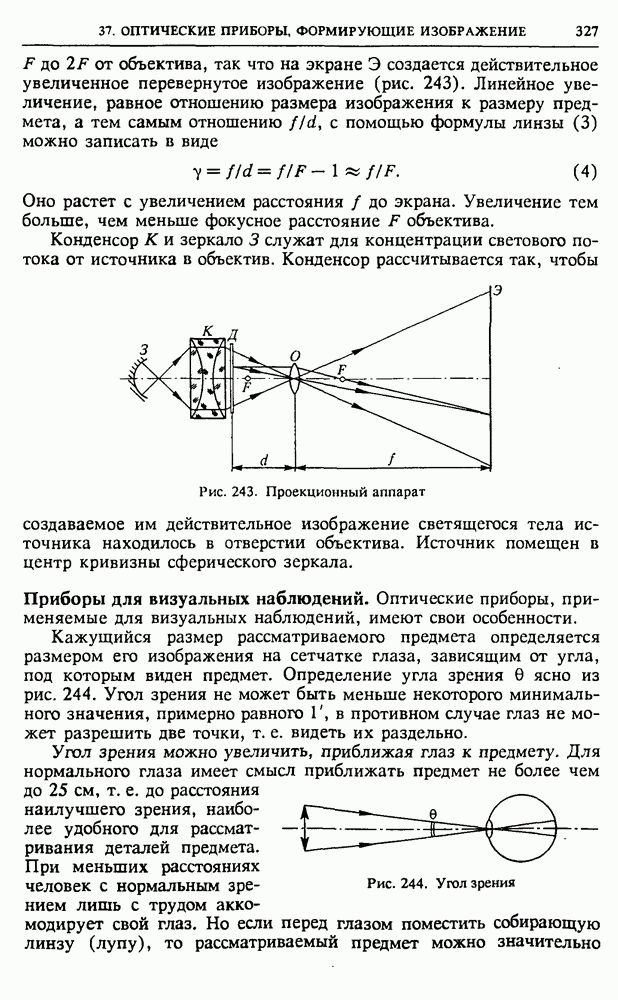
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение