| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 31. Дифракция света
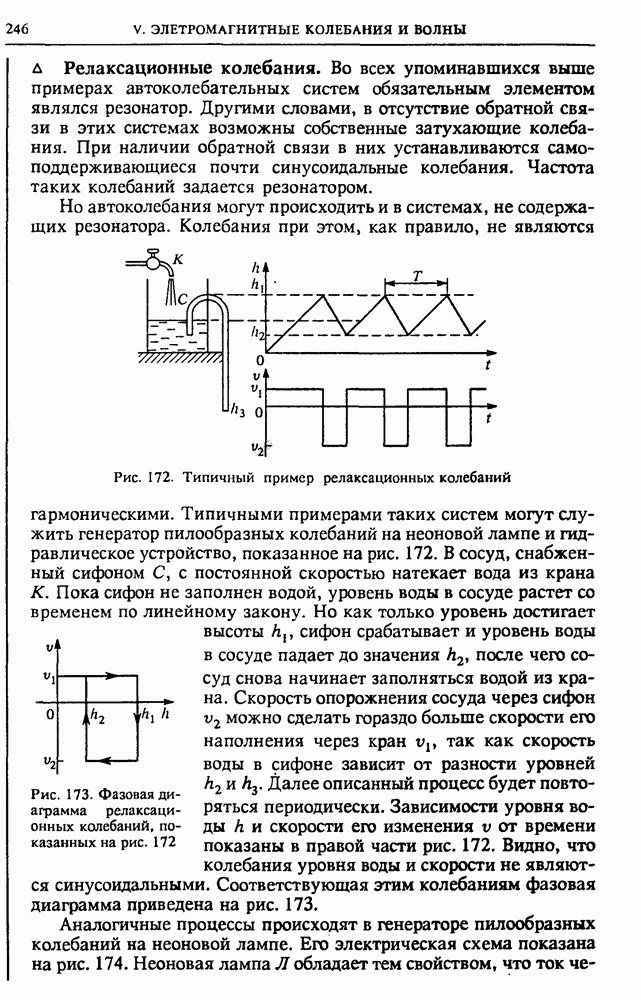
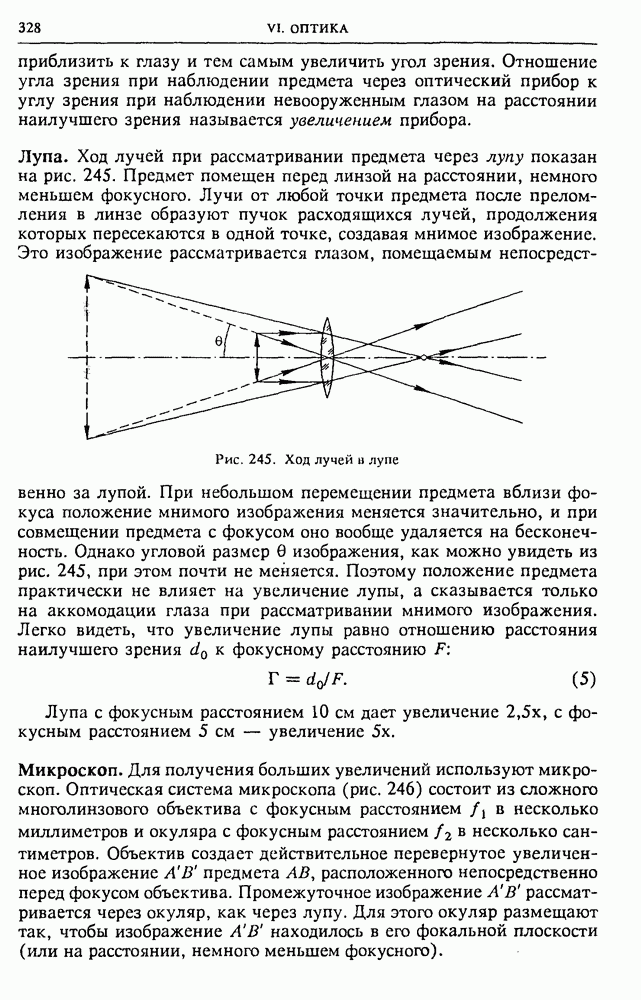
Наряду с интерференцией другим примером общего для всех волновых процессов явления может служить дифракция — огибание волнами препятствий. Для световых волн дифракция проявляется в отклонении от прямолинейного распространения и загибании света в область геометрической тени.
Характерной особенностью дифракционных явлений в оптике оказывается то, что здесь, как правило, длина волны света почти всегда много меньше размеров преград на пути световых волн. Поэтому наблюдать дифракцию света можно только на достаточно больших расстояниях от преграды. Проявление дифракции состоит в том, что распределение освещенности отличается от простой картины, предсказываемой геометрической оптикой на основе прямолинейного распространения света.
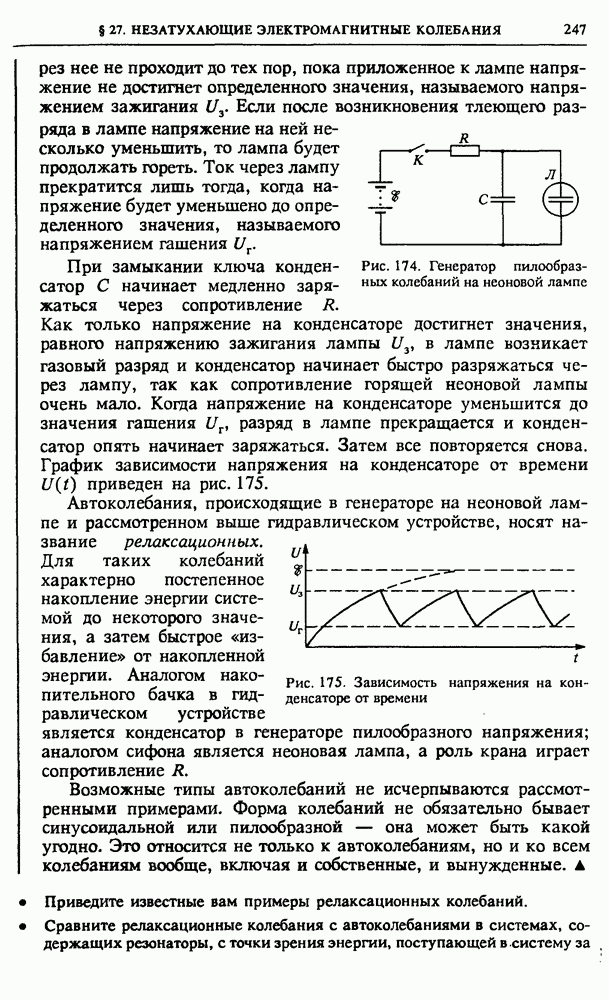
Принцип Гюйгенса—Френеля. Строгий расчет дифракционной картины представляет собой очень сложную математическую задачу. Но в некоторых практически важных случаях достаточно

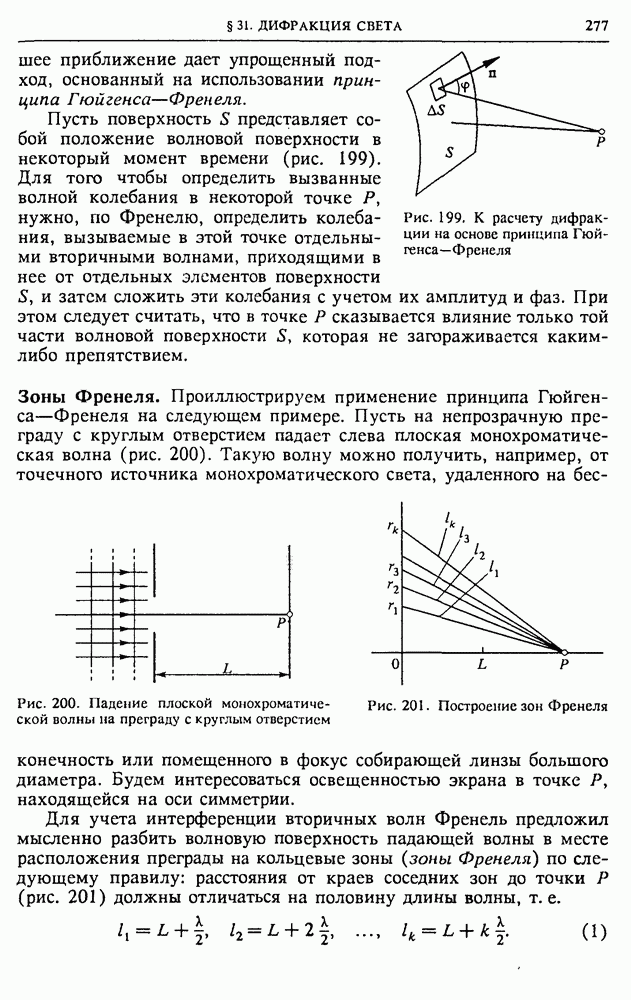
Рис. 199. К расчету дифракции на основе принципа Гюйгенса-Френеля
хорошее приближение дает упрощенный подход, основанный на использовании принципа Гюйгенса—Френеля.
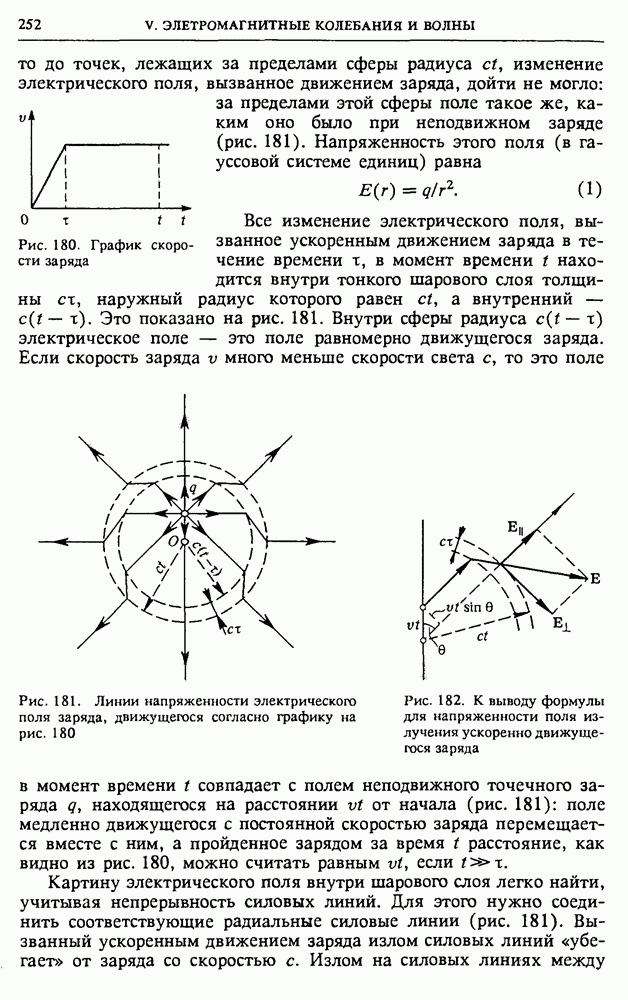
Пусть поверхность  представляет собой положение волновой поверхности в некоторый момент времени (рис. 199).
представляет собой положение волновой поверхности в некоторый момент времени (рис. 199).
Для того чтобы определить вызванные волной колебания в некоторой точке Р, нужно, по Френелю, определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от отдельных элементов поверхности  и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует считать, что в точке Р сказывается влияние только той части волновой поверхности
и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует считать, что в точке Р сказывается влияние только той части волновой поверхности  которая не загораживается каким-либо препятствием.
которая не загораживается каким-либо препятствием.
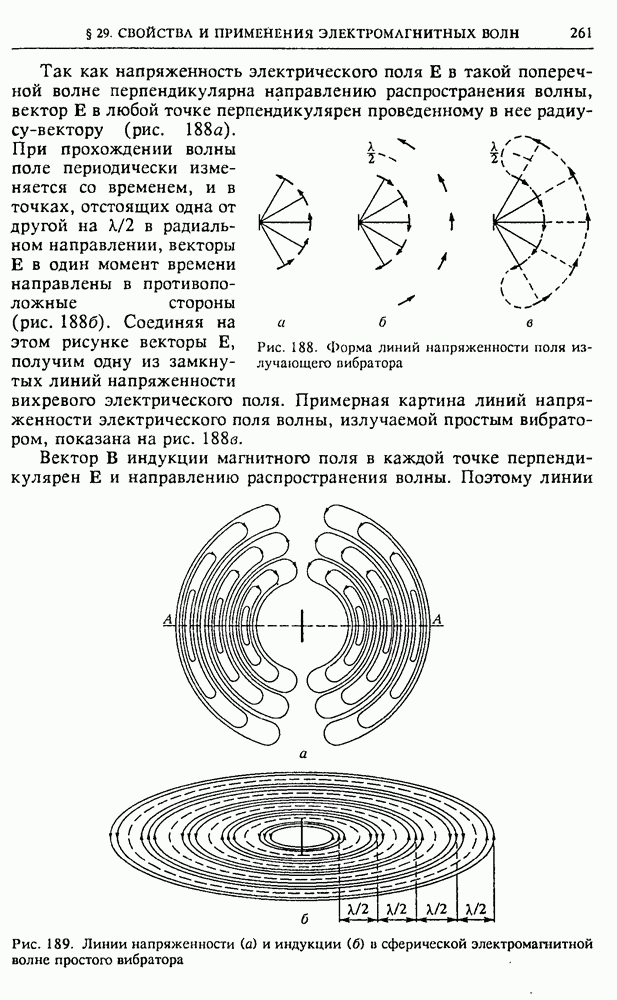
Зоны Френеля. Проиллюстрируем применение принципа Гюйгенса—Френеля на следующем примере. Пусть на непрозрачную преграду с круглым отверстием падает слева плоская монохроматическая волна (рис. 200). Такую волну можно получить, например, от точечного источника монохроматического света, удаленного на бесконечность или помещенного в фокус собирающей линзы большого диаметра.

Рис. 200. Падение плоской монохроматической волны на преграду с круглым отверстием

Рис. 201. Построение зон Френеля
Будем интересоваться освещенностью экрана в точке Р, находящейся на оси симметрии.
Для учета интерференции вторичных волн Френель предложил мысленно разбить волновую поверхность падающей волны в месте расположения преграды на кольцевые зоны (зоны Френеля) по следующему правилу: расстояния от краев соседних зон до точки Р (рис. 201) должны отличаться на половину длины волны, т. е.

Если смотреть на волновую поверхность из точки Р, то зоны Френеля будут выглядеть так, как показано на рис. 202. Из рис. 201 легко найти радиусы зон Френеля:

Видно, что радиус  зоны пропорционален
зоны пропорционален  если
если  При выполнении этого условия площади зон Френеля можно считать одинаковыми. Результат интерференции вторичных волн в точке Р, как мы увидим ниже, определяется тем, сколько зон Френеля открывает круглое отверстие на волновой поверхности.
При выполнении этого условия площади зон Френеля можно считать одинаковыми. Результат интерференции вторичных волн в точке Р, как мы увидим ниже, определяется тем, сколько зон Френеля открывает круглое отверстие на волновой поверхности.

Рис. 202. Зоны Френеля
Дифракция Френеля на круглом отверстии. Предположим, что отверстие в преграде представляет собой диафрагму, диаметр которой можно изменять. Пусть сначала радиус отверстия много меньше радиуса первой зоны Френеля. Тогда можно считать, что колебания от всех точек волновой поверхности в этом маленьком отверстии приходят в точку Р практически в одинаковой фазе. Изобразим колебание поля в точке Р, вызванное этой вторичной волной, с помощью векторной диаграммы (рис. 203а). Этому колебанию на ней сопоставляется вектор  который вращается с угловой скоростью
который вращается с угловой скоростью  , равной циклической частоте падающей волны, в направлении против часовой стрелки. Увеличим отверстие диафрагмы еще немного, так чтобы площадь его удвоилась. Колебания, приходящие в точку Р от вновь открытого участка волновой поверхности, несколько отстают по фазе и изображаются на диаграмме вектором
, равной циклической частоте падающей волны, в направлении против часовой стрелки. Увеличим отверстие диафрагмы еще немного, так чтобы площадь его удвоилась. Колебания, приходящие в точку Р от вновь открытого участка волновой поверхности, несколько отстают по фазе и изображаются на диаграмме вектором  Длина этого вектора равна длине вектора
Длина этого вектора равна длине вектора  так как равны между собой площади соответствующих им участков волновой поверхности. Продолжая увеличивать отверстие диафрагмы, будем откладывать на диаграмме векторы, соответствующие приходящим в точку Р колебаниям от вновь открываемых участков волновой поверхности. Колебаниям, приходящим в Я от участка, прилегающего к границе первой зоны Френеля, будет соответствовать вектор
так как равны между собой площади соответствующих им участков волновой поверхности. Продолжая увеличивать отверстие диафрагмы, будем откладывать на диаграмме векторы, соответствующие приходящим в точку Р колебаниям от вновь открываемых участков волновой поверхности. Колебаниям, приходящим в Я от участка, прилегающего к границе первой зоны Френеля, будет соответствовать вектор  повернутый относительно
повернутый относительно  на
на  так как, согласно определению зон Френеля, разность хода соответствующих им вторичных волн равна
так как, согласно определению зон Френеля, разность хода соответствующих им вторичных волн равна 

Рис. 203. Расчет амплитуды результирующего колебания в точке Р с помощью векторных диаграмм: а — в отверстии укладывается одна зона Френеля;  — две зоны Френеля
— две зоны Френеля
Результирующее колебание в точке Р, создаваемое волной, которая прошла через круглое отверстие, совпадающее с первой зоной Френеля, изображается вектором  (рис. 203а). Будем увеличивать отверстие диафрагмы дальше. Когда на нем будут умещаться две первые зоны Френеля, векторная диаграмма колебаний в точке Р примет вид, изображенный на рис. 2036. При строгом равенстве амплитуд складываемых колебаний
(рис. 203а). Будем увеличивать отверстие диафрагмы дальше. Когда на нем будут умещаться две первые зоны Френеля, векторная диаграмма колебаний в точке Р примет вид, изображенный на рис. 2036. При строгом равенстве амплитуд складываемых колебаний  амплитуда результирующего колебания
амплитуда результирующего колебания  должна была бы равняться нулю, т. е. вторичные волны при двух открытых зонах Френеля полностью гасили бы друг друга в точке Р. Однако действие даже одинаковых по площади участков волновой поверхности в точке Р несколько убывает по мере увеличения угла
должна была бы равняться нулю, т. е. вторичные волны при двух открытых зонах Френеля полностью гасили бы друг друга в точке Р. Однако действие даже одинаковых по площади участков волновой поверхности в точке Р несколько убывает по мере увеличения угла  между направлением на точку Р и нормалью к волновой поверхности (см. рис. 199). Поэтому в действительности амплитуда
между направлением на точку Р и нормалью к волновой поверхности (см. рис. 199). Поэтому в действительности амплитуда  имеет конечное, хотя и очень малое значение.
имеет конечное, хотя и очень малое значение.
Таким образом, освещенность экрана в точке Р, пропорциональная квадрату амплитуды результирующего колебания, будет по мере увеличения отверстия круглой диафрагмы меняться немонотонно. Пока открывается первая зона Френеля, освещенность в Р увеличивается и становится максимальной при полностью открытой первой зоне. По мере открывания второй зоны Френеля освещенность убывает и при полностью открытой второй зоне уменьшается почти до нуля. Затем освещенность будет увеличиваться снова, и т. д.
Эти на первый взгляд парадоксальные результаты, предсказываемые на основе принципа Гюйгенса—Френеля, хорошо согласуются с экспериментом. Подчеркнем, что они находятся в вопиющем противоречии с предсказаниями геометрической оптики, согласно которой при падении плоской волны освещенность в точке Р, лежащей на оси круглого отверстия, не зависит от диаметра отверстия.
Дифракция Френеля на круглом диске. Пятно Араго—Пуассона. Наиболее неожиданным в полученных выше результатах является, пожалуй, то, что при двух открытых зонах Френеля (и вообще при небольшом четном числе открытых зон) освещенность в точке Р близка к нулю. Не менее неожиданным является то, что в точке Р позади непрозрачного круглого экрана, расположенного на месте преграды с отверстием, освещенность не будет равна нулю, как это следовало бы из геометрической оптики. Если при этом непрозрачный круглый экран перекрывает лишь несколько первых зон Френеля, то в точке Р освещенность будет почти такой же, как и без экрана.
В этом можно убедиться, если рассматривать вектор А, изображающий колебания напряженности поля в точке Р при полностью открытой волновой поверхности, как сумму двух векторов, один из которых изображает колебания от открытого участка волновой поверхности, а другой — от тех зон Френеля, которые перекрыты экраном. В центре геометрической тени оказывается свет — так называемое пятно Араго—Пуассона.
Это предсказание теории Френеля произвело сильное впечатление на его современников. В 1818 г. член конкурсного комитета Французской академии С. Пуассон, рассматривавший представленный на премию мемуар Френеля, пришел к выводу о том, что в центре тени маленького диска должно находиться светлое пятно, но счел этот вывод столь абсурдным, что выдвинул его как возражение против волновой теории света, развивавшейся Френелем. Однако другой член того же комитета Араго выполнил эксперимент, показавший, что это удивительное предсказание правильно.
Расстояния, на которых сказывается дифракция. Теперь не представляет труда оценить те условия наблюдения, при которых дифракционные явления становятся существенными и картина распределения освещенности на экране заметно отличается от предсказываемой геометрической оптикой. По геометрической оптике распределение освещенности на экране должно соответствовать форме отверстия, так что освещенность экрана равна нулю в области геометрической тени, а в точке Р такая же, как и в отсутствие преграды. Но мы видели, что в случае, когда на отверстии укладывается лишь несколько зон Френеля, освещенность в точке Р совсем иная. Это дает возможность оценить то расстояние  от отверстия до точки наблюдения, на котором именно дифракционные явления определяют наблюдаемую картину. Для этого в формуле (2) следует считать к
от отверстия до точки наблюдения, на котором именно дифракционные явления определяют наблюдаемую картину. Для этого в формуле (2) следует считать к  положить равным размеру отверстия (или преграды)
положить равным размеру отверстия (или преграды)  В результате находим
В результате находим

Построения Френеля позволяют легко рассчитать освещенность позади непрозрачного круглого экрана или экрана с круглым отверстием только в точках, лежащих на оси симметрии. Найти вид всей дифракционной картины на экране очень трудно.
Дифракция Фраунгофера. Но можно осуществить такие условия наблюдения дифракции света, при которых возможен полный расчет распределения освещенности в дифракционной картине на экране.
Пусть плоская монохроматическая волна от бесконечно удаленного точечного источника падает на экран  с отверстием, а дифракционная картина наблюдается на экране в фокальной плоскости линзы (рис. 204). Так как в каждой точке фокальной плоскости линзы, например Р на рис. 204, сходятся лучи, которые до линзы были параллельны между собой, то наблюдаемая здесь картина называется дифракцией в параллельных лучах. Как мы увидим в дальнейшем, линза не вносит дополнительной разности хода между параллельными до линзы лучами. Поэтому
с отверстием, а дифракционная картина наблюдается на экране в фокальной плоскости линзы (рис. 204). Так как в каждой точке фокальной плоскости линзы, например Р на рис. 204, сходятся лучи, которые до линзы были параллельны между собой, то наблюдаемая здесь картина называется дифракцией в параллельных лучах. Как мы увидим в дальнейшем, линза не вносит дополнительной разности хода между параллельными до линзы лучами. Поэтому

Рис. 204. Наблюдение дифракции в параллельных лучах
складывающиеся в точке Р колебания имеют такую же разность фаз, как и до линзы на плоскости, перпендикулярной к этим лучам. Такая схема наблюдения дифракции была предложена И. Фраунгофером.
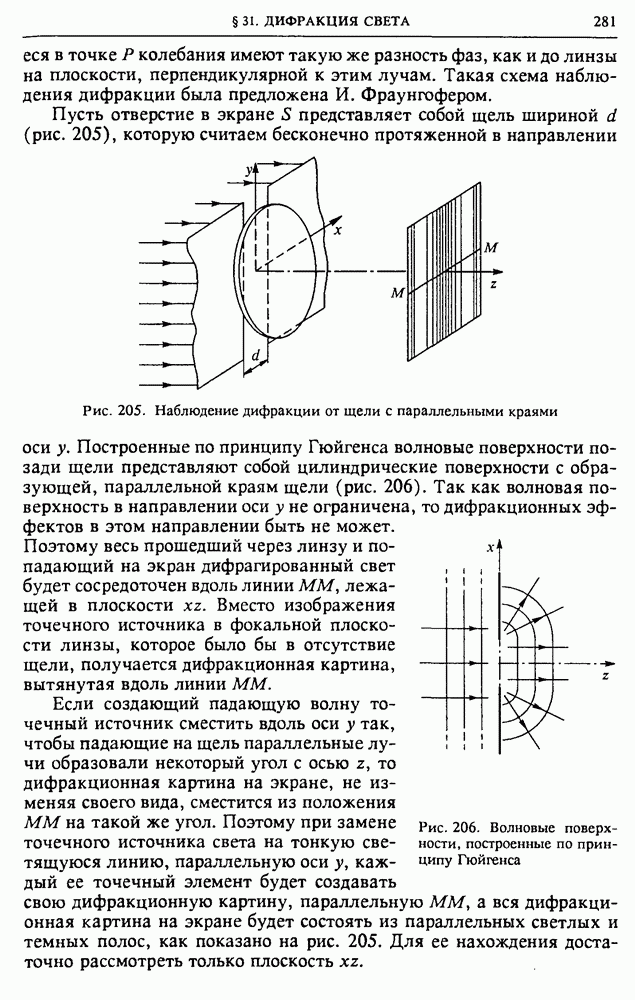
Пусть отверстие в экране  представляет собой щель шириной
представляет собой щель шириной  (рис. 205), которую считаем бесконечно протяженной в направлении оси у.
(рис. 205), которую считаем бесконечно протяженной в направлении оси у.

Рис. 205. Наблюдение дифракции от щели с параллельными краями
Построенные по принципу Гюйгенса волновые поверхности позади щели представляют собой цилиндрические поверхности с образующей, параллельной краям щели (рис. 206). Так как волновая поверхность в направлении оси у не ограничена, то дифракционных эффектов в этом направлении быть не может.
Поэтому весь прошедший через линзу и попадающий на экран дифрагированный свет будет сосредоточен вдоль линии  лежащей в плоскости
лежащей в плоскости  Вместо изображения точечного источника в фокальной плоскости линзы, которое было бы в отсутствие щели, получается дифракционная картина, вытянутая вдоль линии
Вместо изображения точечного источника в фокальной плоскости линзы, которое было бы в отсутствие щели, получается дифракционная картина, вытянутая вдоль линии 

Рис. 206. Волновые поверхности, построенные по принципу Гюйгенса
Если создающий падающую волну точечный источник сместить вдоль оси у так, чтобы падающие на щель параллельные лучи образовали некоторый угол с осью  то дифракционная картина на экране, не изменяя своего вида, сместится из положения
то дифракционная картина на экране, не изменяя своего вида, сместится из положения  на такой же угол. Поэтому при замене точечного источника света на тонкую светящуюся линию, параллельную оси у, каждый ее точечный элемент будет создавать свою дифракционную картину, параллельную
на такой же угол. Поэтому при замене точечного источника света на тонкую светящуюся линию, параллельную оси у, каждый ее точечный элемент будет создавать свою дифракционную картину, параллельную  а вся дифракционная картина на экране будет состоять из параллельных светлых и темных полос, как показано на рис. 205. Для ее нахождения достаточно рассмотреть только плоскость
а вся дифракционная картина на экране будет состоять из параллельных светлых и темных полос, как показано на рис. 205. Для ее нахождения достаточно рассмотреть только плоскость 
Согласно принципу Гюйгенса—Френеля волновую поверхность падающей волны в щели на оси х следует разбить на столь малые участки, чтобы колебания в точке наблюдения Р, вызываемые вторичными волнами от всех точек одного участка, имели почти одинаковую фазу. Колебания в точке Р, вызываемые вторичными волнами, распространяющимися под углом  от разных участков (рис. 207), следует просуммировать с учетом сдвигов по фазе. Это удобно сделать с помощью векторной диаграммы, построенной на рис. 208.
от разных участков (рис. 207), следует просуммировать с учетом сдвигов по фазе. Это удобно сделать с помощью векторной диаграммы, построенной на рис. 208.

Рис. 207. К расчету суммарного колебания в точке Р
Вектор  изображает колебания, приходящие в точку Р от участка
изображает колебания, приходящие в точку Р от участка  лежащего вблизи нижнего края щели. Вектор
лежащего вблизи нижнего края щели. Вектор  изображающий колебания от соседнего участка
изображающий колебания от соседнего участка  повернут относительно
повернут относительно  на некоторый небольшой угол. Вектор
на некоторый небольшой угол. Вектор  изображающий колебания от последнего участка
изображающий колебания от последнего участка  лежащего у верхнего края щели, повернут относительно вектора
лежащего у верхнего края щели, повернут относительно вектора  на угол
на угол  соответствующий разности хода
соответствующий разности хода  (рис. 207) между лучами, приходящими от краев щели. Чтобы найти сдвиг по фазе между колебаниями в точке Р, вызванными волнами с разностью хода
(рис. 207) между лучами, приходящими от краев щели. Чтобы найти сдвиг по фазе между колебаниями в точке Р, вызванными волнами с разностью хода  следует учесть, что сдвиг по фазе равен
следует учесть, что сдвиг по фазе равен  при разности хода X:
при разности хода X:


Рис. 208. Сложение колебаний с помощью векторной диаграммы
Найдем длину суммарного вектора  которая равна амплитуде колебаний в точке наблюдения Р. Легко видеть, что вектор
которая равна амплитуде колебаний в точке наблюдения Р. Легко видеть, что вектор  представляет собой хорду окружности с центром в точке С (рис. 208). Прежде всего отметим, что длина дуги, стягиваемой хордой
представляет собой хорду окружности с центром в точке С (рис. 208). Прежде всего отметим, что длина дуги, стягиваемой хордой  равна амплитуде колебаний
равна амплитуде колебаний  в точке О на экране, так как в эту точку вторичные волны от всех участков
в точке О на экране, так как в эту точку вторичные волны от всех участков  распространяясь под углом
распространяясь под углом  приходят в одинаковой фазе и все векторы
приходят в одинаковой фазе и все векторы  имеют для точки О одинаковые направления. Длину дуги
имеют для точки О одинаковые направления. Длину дуги  и длину хорды
и длину хорды  легко связать между собой из геометрических соображений. Из рис. 208 видно, что
легко связать между собой из геометрических соображений. Из рис. 208 видно, что

откуда

Освещенность экрана  в точке Р, пропорциональная квадрату амплитуды колебаний, связана с освещенностью
в точке Р, пропорциональная квадрату амплитуды колебаний, связана с освещенностью  в точке О, согласно (5), следующим соотношением:
в точке О, согласно (5), следующим соотношением:

где  дается формулой (4). Распределение освещенности на экране
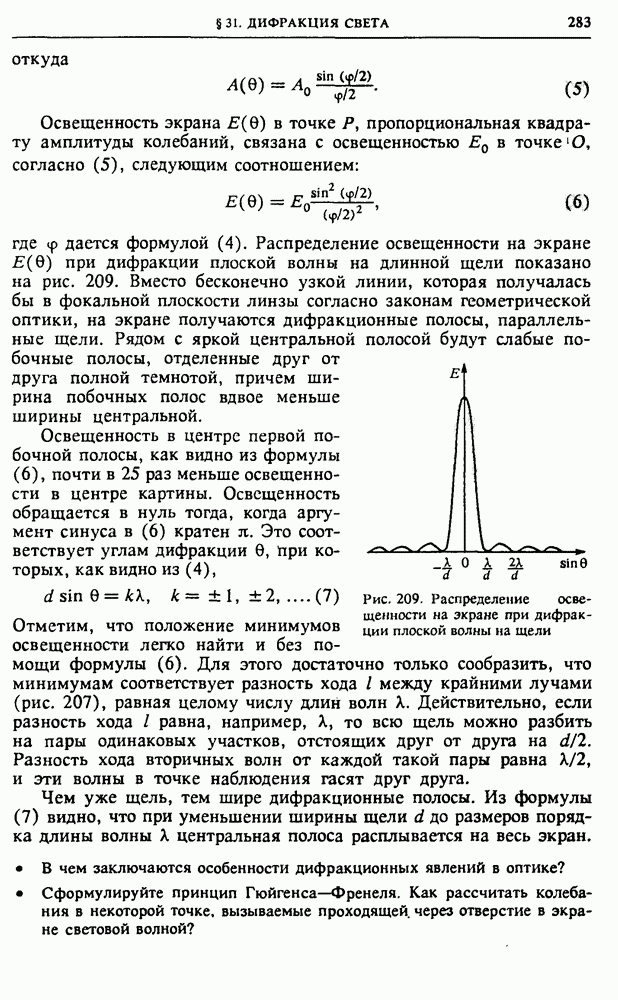
дается формулой (4). Распределение освещенности на экране  при дифракции плоской волны на длинной щели показано на рис. 209. Вместо бесконечно узкой линии, которая получалась бы в фокальной плоскости линзы согласно законам геометрической оптики, на экране получаются дифракционные полосы, параллельные щели. Рядом с яркой центральной полосой будут слабые побочные полосы, отделенные друг от друга полной темнотой, причем ширина побочных полос вдвое меньше ширины центральной.
при дифракции плоской волны на длинной щели показано на рис. 209. Вместо бесконечно узкой линии, которая получалась бы в фокальной плоскости линзы согласно законам геометрической оптики, на экране получаются дифракционные полосы, параллельные щели. Рядом с яркой центральной полосой будут слабые побочные полосы, отделенные друг от друга полной темнотой, причем ширина побочных полос вдвое меньше ширины центральной.

Рис. 209. Распределение освещенности на экране при дифракции плоской волны на щели
Освещенность в центре первой побочной полосы, как видно из формулы (6), почти в 25 раз меньше освещенности в центре картины. Освещенность обращается в нуль тогда, когда аргумент синуса в (6) кратен  Это соответствует углам дифракции 0, При которых, как видно из (4),
Это соответствует углам дифракции 0, При которых, как видно из (4),

Отметим, что положение минимумов освещенности легко найти и без помощи формулы (6). Для этого достаточно только сообразить, что минимумам соответствует разность хода I между крайними лучами (рис. 207), равная целому числу длин волн X. Действительно, если разность хода I равна, например, X, то всю щель можно разбить на пары одинаковых участков, отстоящих друг от друга на  Разность хода вторичных волн от каждой такой пары равна
Разность хода вторичных волн от каждой такой пары равна  и эти волны в точке наблюдения гасят друг друга.
и эти волны в точке наблюдения гасят друг друга.
Чем уже щель, тем шире дифракционные полосы. Из формулы (7) видно, что при уменьшении ширины щели  до размеров порядка длины волны X центральная полоса расплывается на весь экран.
до размеров порядка длины волны X центральная полоса расплывается на весь экран.
• В чем заключаются особенности дифракционных явлений в оптике?
• Сформулируйте принцип Гюйгенса—Френеля. Как рассчитать колебания в некоторой точке, вызываемые проходящей через отверстие в экране световой волной?
• Что такое зоны Френеля? Как осуществляется их построение?
• Докажите, опираясь на формулу (2), что площади зон Френеля одинаковы.
• Как объяснить периодические изменения освещенности в центре дифракционной картины от круглого отверстия при монотонном изменении диаметра отверстия или расстояния от отверстия до экрана?
• Как оценить расстояние от препятствия (экрана или отверстия в нем) до точки наблюдения, - при котором становятся заметными дифракционные явления?
• Чем отличаются условия наблюдения дифракции Фраунгофера и дифракции Френеля?
• Покажите, что дифракция Френеля и дифракция Фраунгофера не представляют собой разные физические явления, а соответствуют разным условиям наблюдения одного и того же явления. Сравните дифракцию Френеля при  с дифракцией Фраунгофера.
с дифракцией Фраунгофера.
• Как изменятся ширина центральной полосы при дифракции Фраунгофера на щели и освещенность в ее середине, если ширину щели увеличить вдвое? Изменится ли при этом отношение освещенностей в побочных и центральной дифракционных полосах?
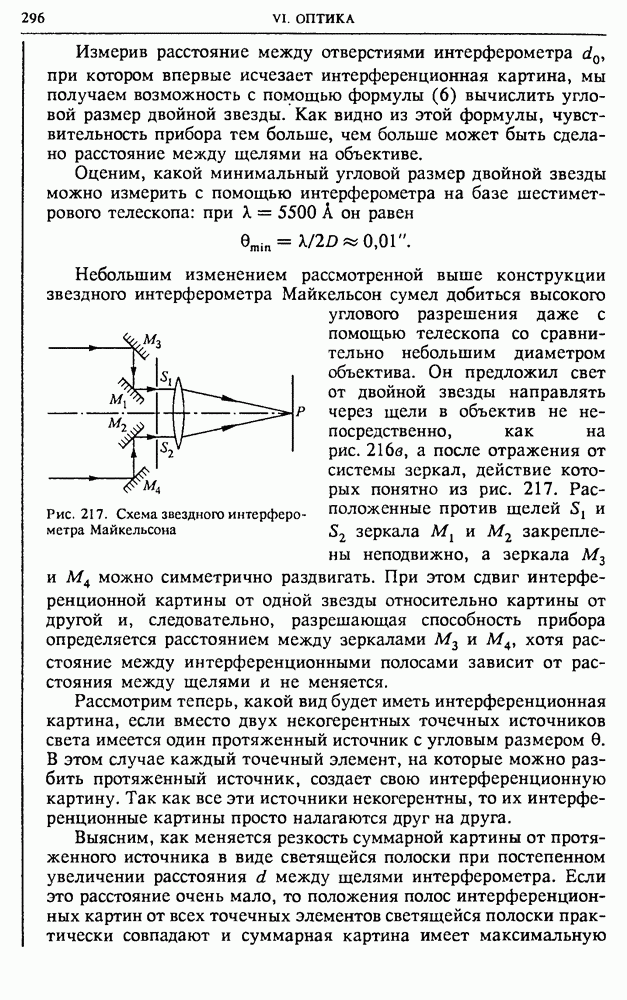
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
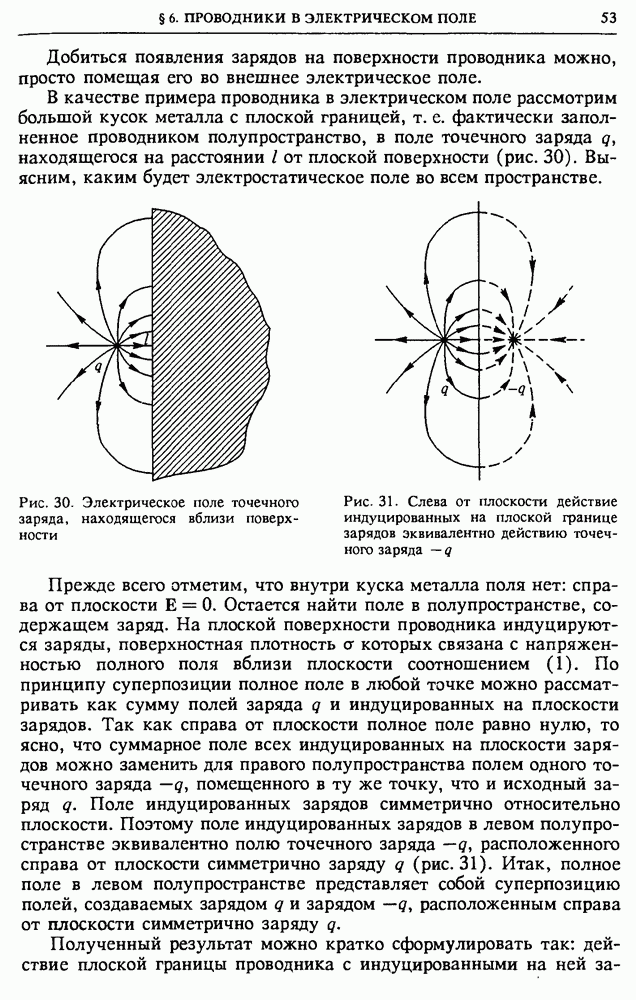
- § 6. Проводники в электрическом поле
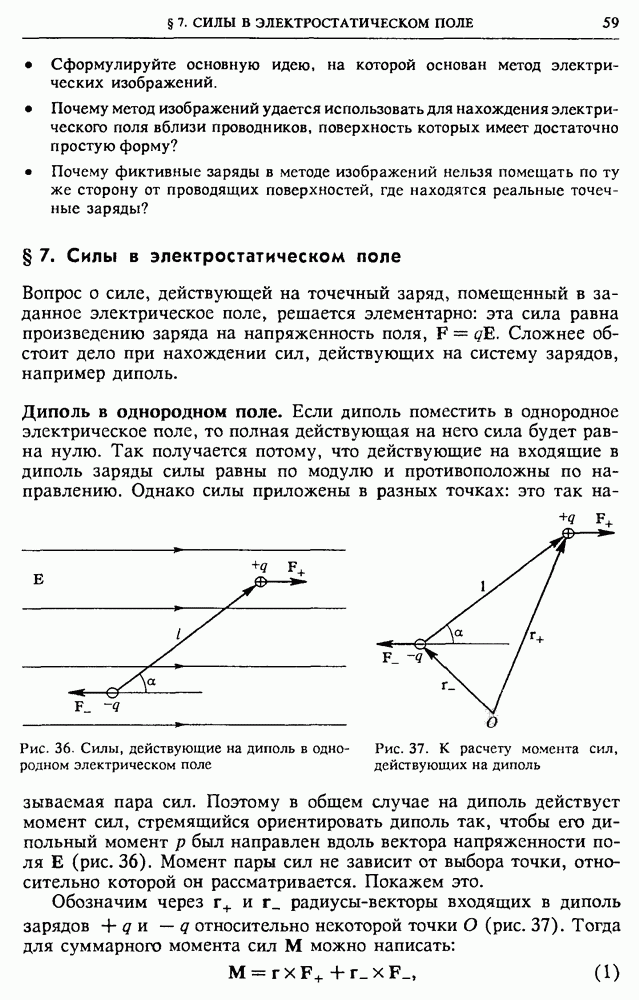
- § 7. Силы в электростатическом поле
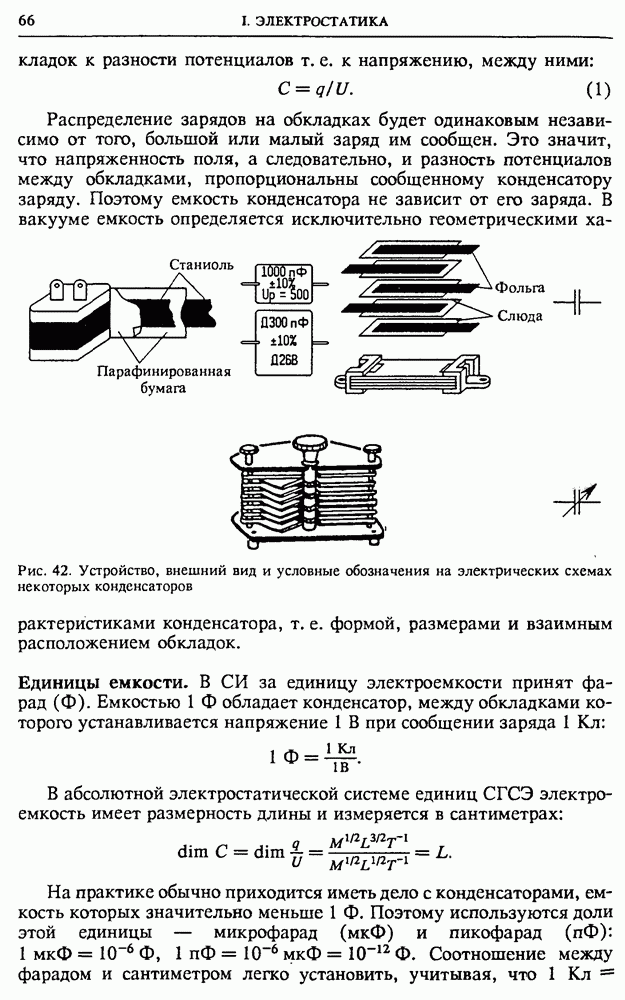
- § 8. Конденсаторы. Электроемкость
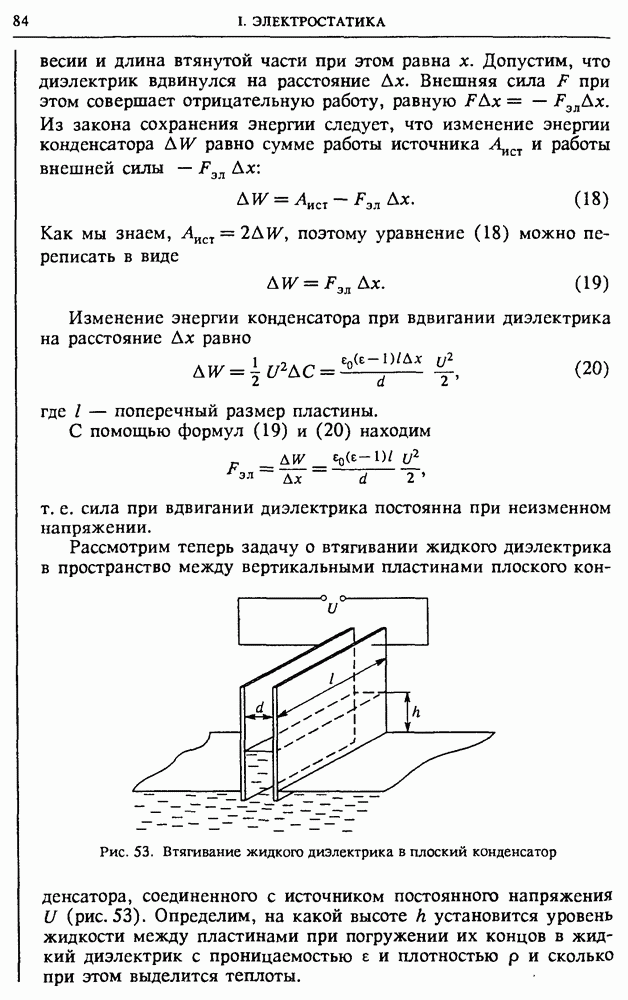
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
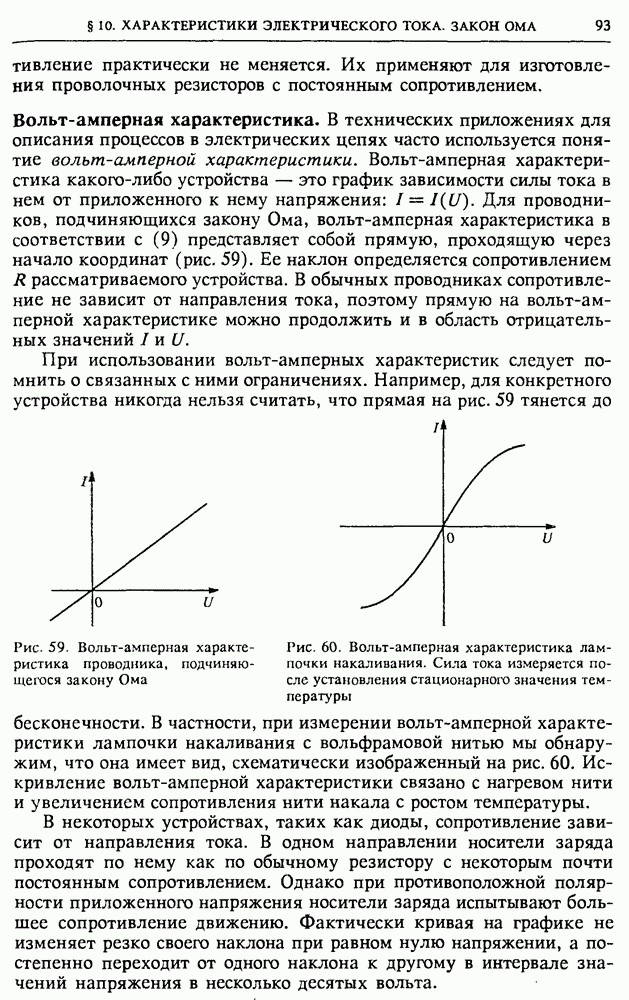
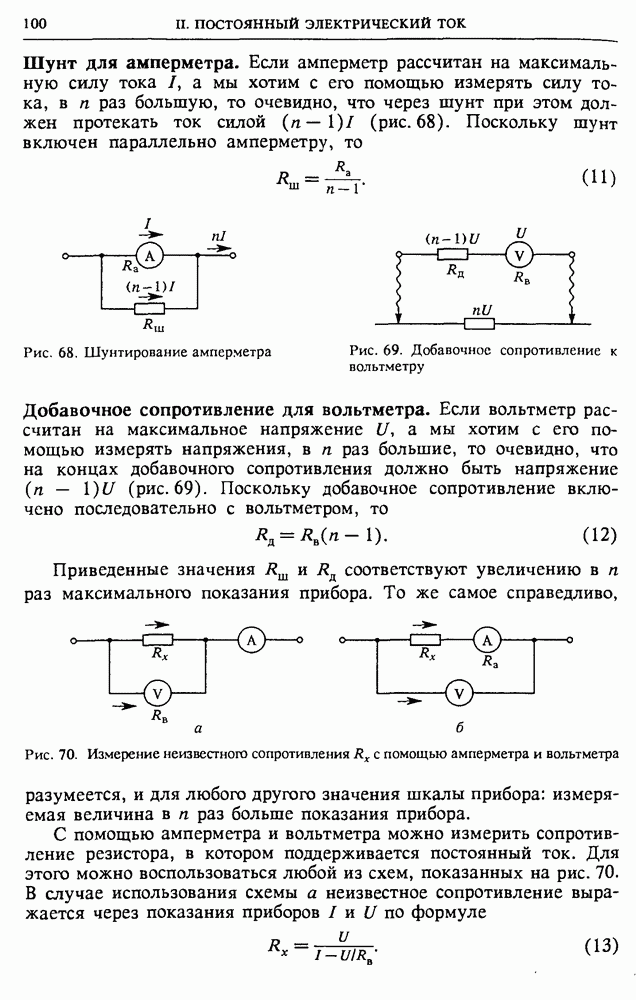
- § 10. Характеристики электрического тока. Закон Ома
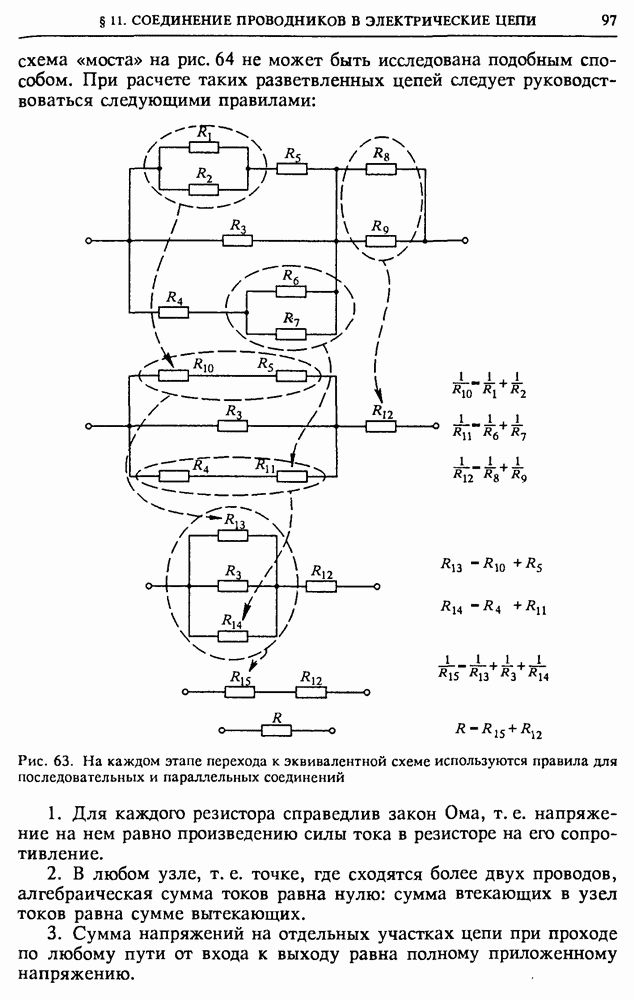
- § 11. Соединение проводников в электрические цепи
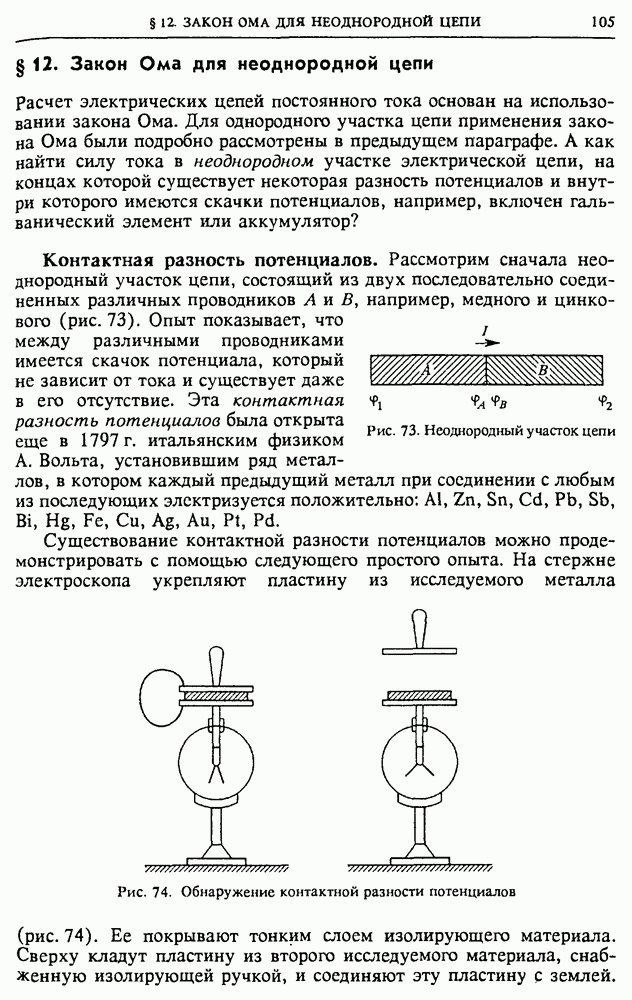
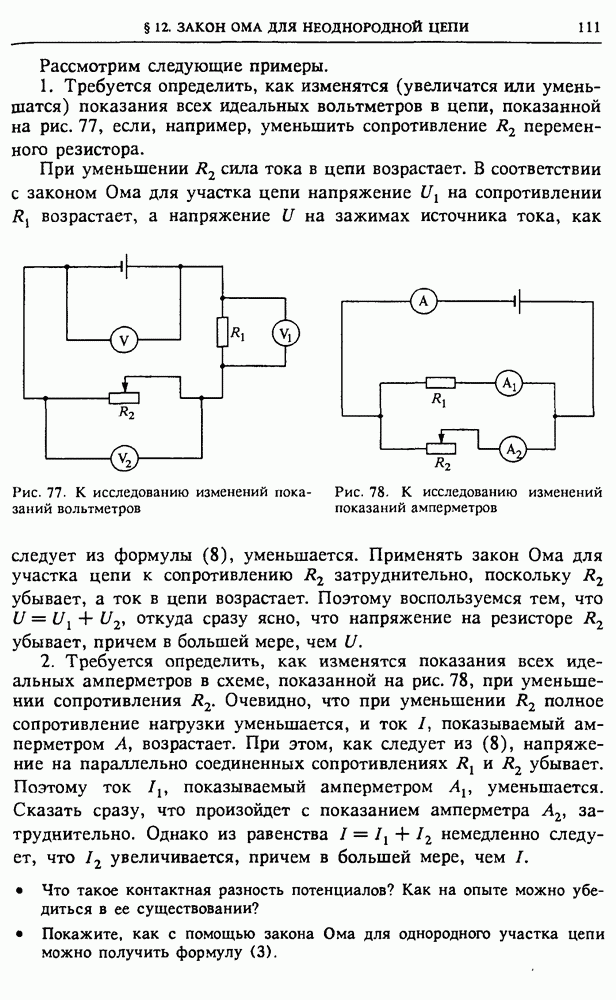
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
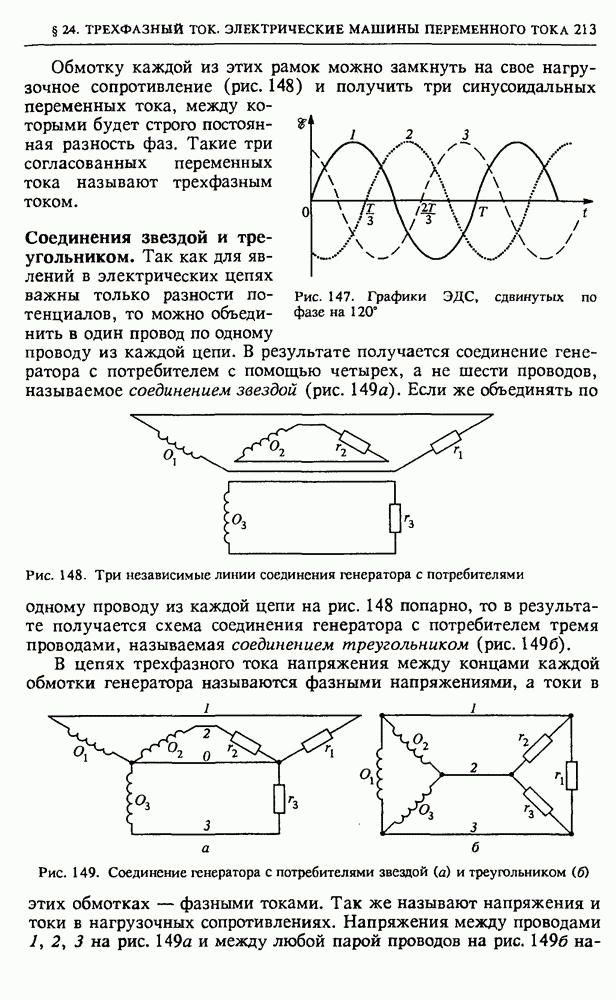
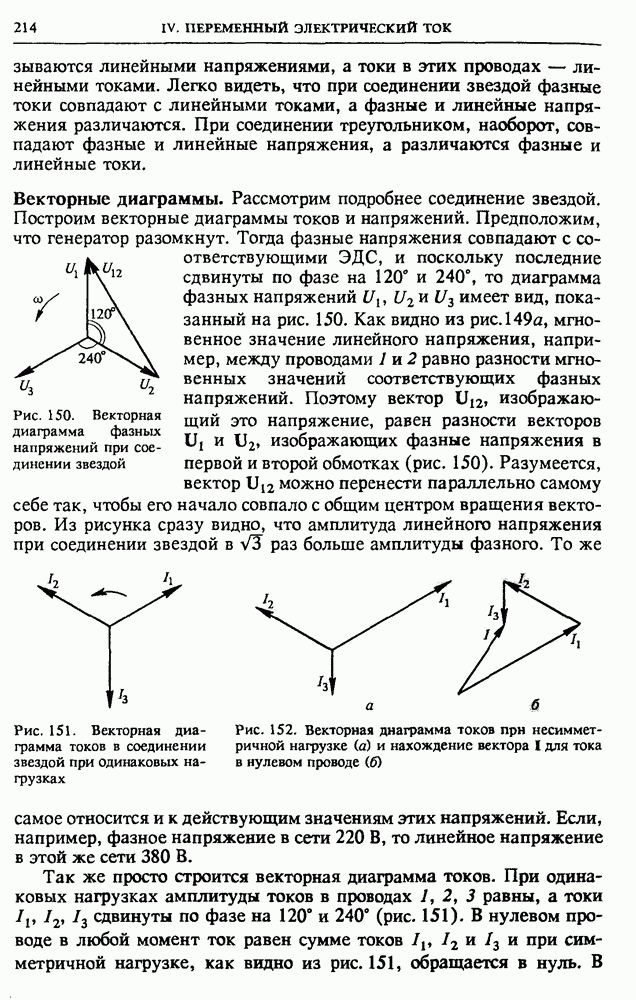
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
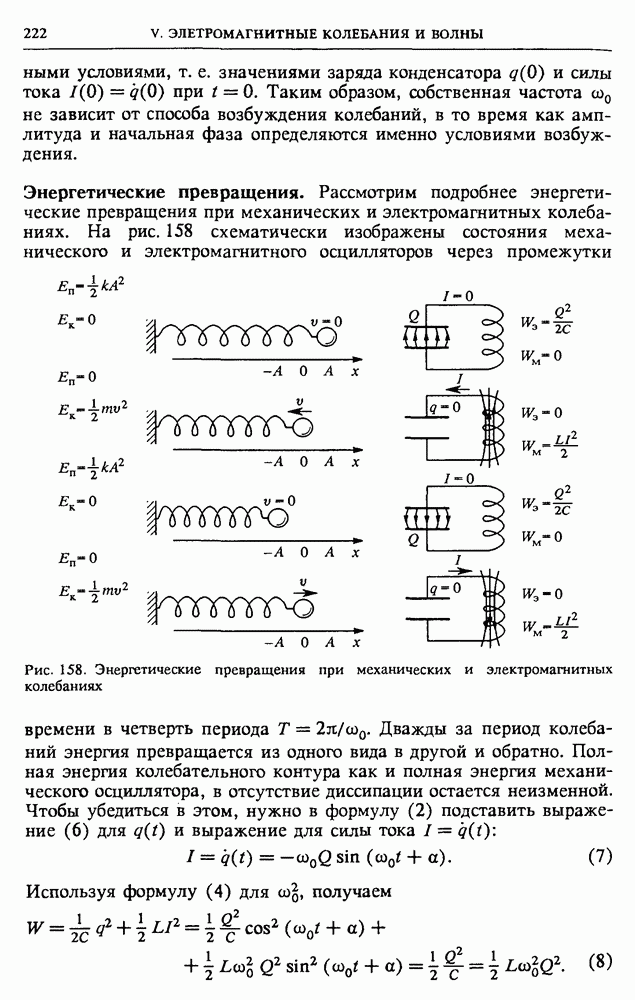
- § 25. Колебательный контур
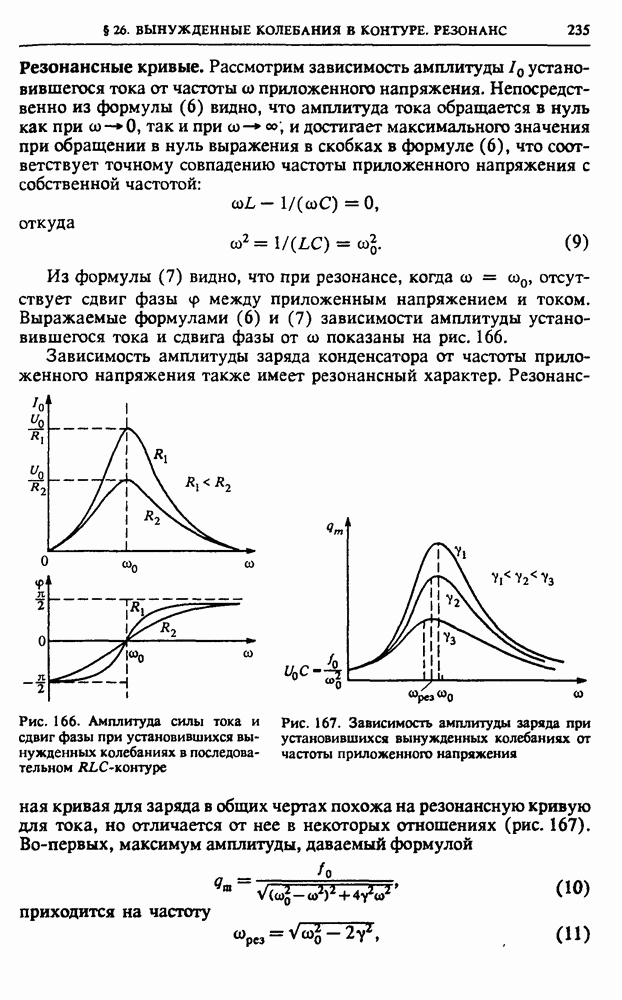
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
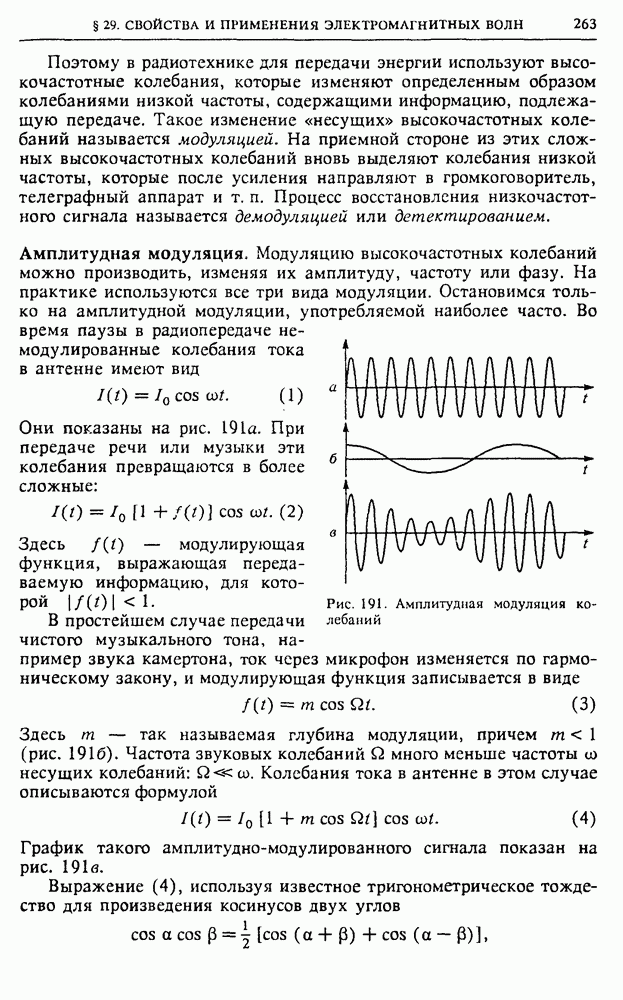
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
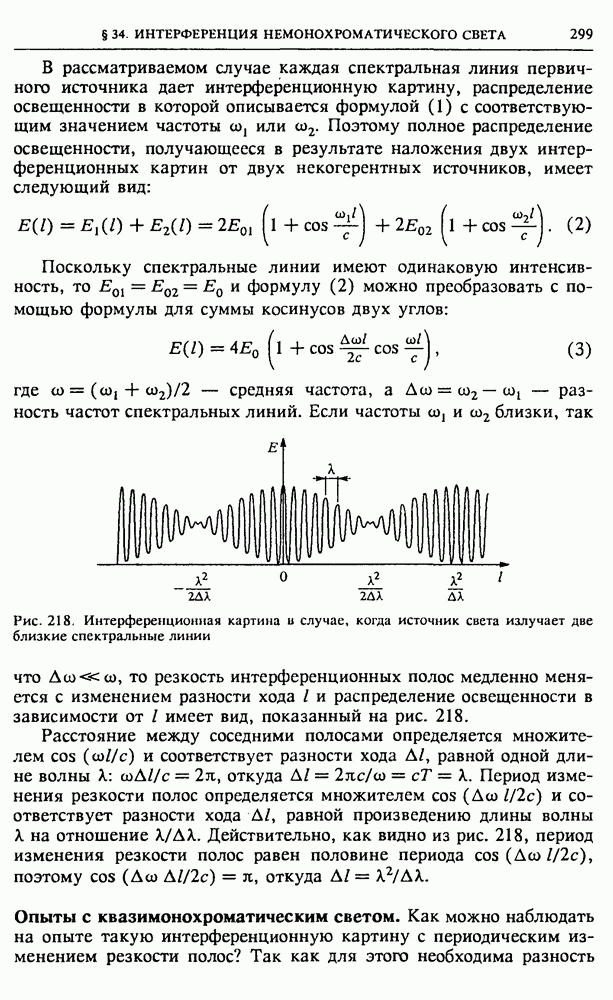
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение