| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. Основы теории электромагнитного поля
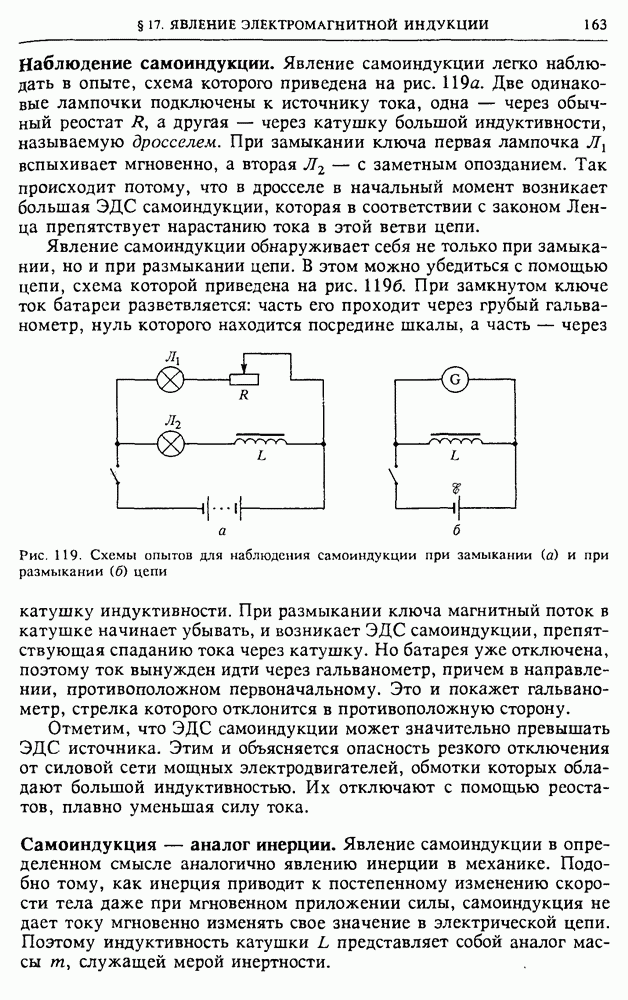
Изучая электромагнитную индукцию, мы видели, что при рассмотрении этого явления в определенной инерциальной системе отсчета возможны две различные причины возникновения индукционного тока. В лабораторной системе отсчета причина ЭДС — это либо появление вихревого электрического поля, либо действие силы Лоренца на движущиеся вместе с проводником электрические заряды со стороны магнитного поля. Однако при анализе возникновения ЭДС индукции за счет силы Лоренца в опыте с металлической рамкой, движущейся в магнитном поле (см. рис. 113), мы можем рассуждать и иначе.
Относительный характер электрического и магнитного полей.
Перейдем в систему отсчета, связанную с движущейся рамкой. В ней заряды неподвижны и, следовательно, со стороны магнитного
поля сила на них не действует. Строго говоря, при наличии тока заряды движутся вдоль проводника со скоростью дрейфа и (см. рис. 114), и в магнитном поле на них действует сила Лоренца. Однако она направлена поперек проводника и не может объяснить возникновение ЭДС.
Как же объяснить возникновение ЭДС индукции в этой системе отсчета? Единственное, что остается предположить, это наличие в этой системе электрического поля, направленного перпендикулярно магнитному вдоль стороны  рамки, которого не было в исходной системе отсчета. Действительно, в любой инерциальной системе отсчета в единицах СИ действующая на заряд сила определяется формулой (5) § 17:
рамки, которого не было в исходной системе отсчета. Действительно, в любой инерциальной системе отсчета в единицах СИ действующая на заряд сила определяется формулой (5) § 17:

Поскольку в системе отсчета, связанной с рамкой,  сила
сила  может быть обусловлена только электрическим полем Е, существующим в этой системе.
может быть обусловлена только электрическим полем Е, существующим в этой системе.
Электрическое и магнитное поля в разных системах отсчета. Итак, мы приходим к выводу об относительном характере электрического и магнитного полей. Согласно принципу относительности все инерциальные системы отсчета равноправны. Это справедливо не только для механических явлений, но и для явлений любой природы, в том числе электромагнитных.

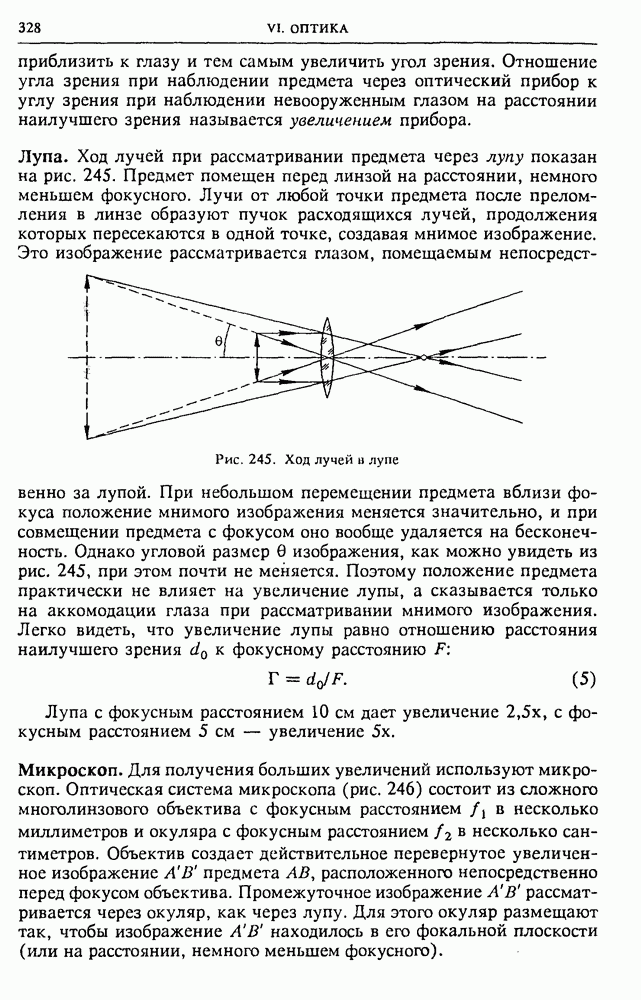
Рис. 125. К объяснению возникновения ЭДС индукции в разных системах отсчета
В обсуждаемом здесь опыте наблюдаемой величиной является ЭДС индукции в рамке, и она существует независимо от того, в какой инерциальной системе этот опыт рассматривается.
Как мы видели, в одной системе отсчета, где электрическое поле отсутствует, существование ЭДС объясняется силой Лоренца (рис. 125а), в то время как в другой, где рамка неподвижна, — только наличием электрического поля (рис. 1256). При малых скоростях  когда можно пренебречь изменением силы
когда можно пренебречь изменением силы  при переходе от одной системы отсчета к другой, из формулы (1) следует, что напряженность электрического поля Е в системе, где рамка
при переходе от одной системы отсчета к другой, из формулы (1) следует, что напряженность электрического поля Е в системе, где рамка
неподвижна, должна быть равна

Итак, движущийся магнит кроме магнитного создает и электрическое поле.
Обратим внимание на то, что относительный характер электрического и магнитного полей мы могли заметить и раньше. В самом деле, неподвижный заряд создает только электрическое поле. Однако заряд, неподвижный в какой-либо одной системе отсчета, относительно других систем отсчета движется. Такой движущийся заряд подобен электрическому току и потому создает магнитное поле. Таким образом, если в какой-либо системе отсчета есть только электрическое поле, то в любой другой системе будет еще и магнитное.
Получим формулу для индукции магнитного поля в этом случае, аналогичную формуле (2). Рассмотрим систему отсчета, движущуюся со скоростью  относительно заряда
относительно заряда  . В этой системе отсчета заряд движется со скоростью
. В этой системе отсчета заряд движется со скоростью  Создаваемое им магнитное поле, в соответствии с формулой (16) § 15, дается выражением
Создаваемое им магнитное поле, в соответствии с формулой (16) § 15, дается выражением

Но в этой же точке заряд  создает электрическое поле Е, равное
создает электрическое поле Е, равное

Сравнивая формулы (3) и (4), видим, что магнитное поле, создаваемое движущимся со скоростью —V зарядом, связано с электрическим полем Е, создаваемым этим же зарядом в той системе отсчета, где он неподвижен, соотношением

Эта формула, полученная для точечного заряда, справедлива и для поля, создаваемого любым распределением зарядов.
Таким образом, если в некоторой системе отсчета существует только электрическое поле Е, то в другой системе отсчета, движущейся со скоростью  относительно исходной, существует еще и магнитное поле В, которое вычисляется по формуле (5).
относительно исходной, существует еще и магнитное поле В, которое вычисляется по формуле (5).
Инварианты электромагнитного поля. Формулы (2) и (5) представляют собой частные случаи преобразования полей при переходе от одной инерциальной системы отсчета к другой. Они справедливы при малой относительной скорости систем отсчета ( ). В общем случае, когда в исходной системе отсчета есть и электрическое, и магнитное поле, нерелятивистские формулы преобразования в СИ имеют вид
). В общем случае, когда в исходной системе отсчета есть и электрическое, и магнитное поле, нерелятивистские формулы преобразования в СИ имеют вид

В дальнейшем мы увидим, что  где с — скорость света в вакууме.
где с — скорость света в вакууме.
Формулы преобразования электрического и магнитного полей при относительной скорости систем отсчета, сравнимой со скоростью света, более громоздки, чем (6). Однако всегда при переходе от одной инерциальной системы отсчета к другой существуют инвариантные, т. е. не меняющие своего значения, комбинации из векторов Е и В. Независимых комбинаций только две — это скалярное произведение этих векторов и их разность квадратов:

Формулы (7) и (8) позволяют сделать ряд важных выводов о свойствах электромагнитного поля. Если в какой-либо инерциальной системе отсчета электрическое и магнитное поля взаимно перпендикулярны, то, как видно из (7), они будут взаимно перпендикулярны и во всякой другой системе. Для таких взаимно ортогональных полей можно найти такую систему отсчета, в которой либо  либо
либо  смотря по тому, положителен или отрицателен инвариант (8).
смотря по тому, положителен или отрицателен инвариант (8).
Из относительного характера электрического и магнитного полей естественно вытекает, что при изучении электрических и магнитных явлений имеет смысл рассматривать эти поля совместно, как единое электромагнитное поле. При переходе от одной системы отсчета к другой электрическое поле в одной системе, как мы видели, выражается и через электрическое поле, и через магнитное поле в другой системе, и наоборот. Поэтому естественно ожидать, что между электрическими и магнитными явлениями существует определенная симметрия. Изменение магнитного поля порождает вихревое электрическое поле. Оказывается, что справедливо и обратное: изменяющееся во времени электрическое поле порождает магнитное поле.
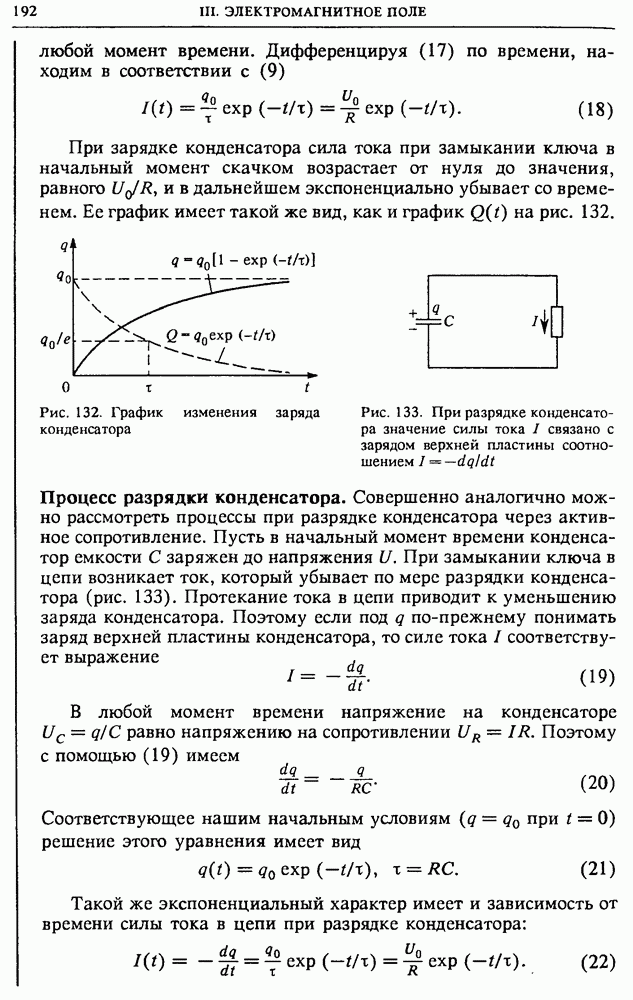
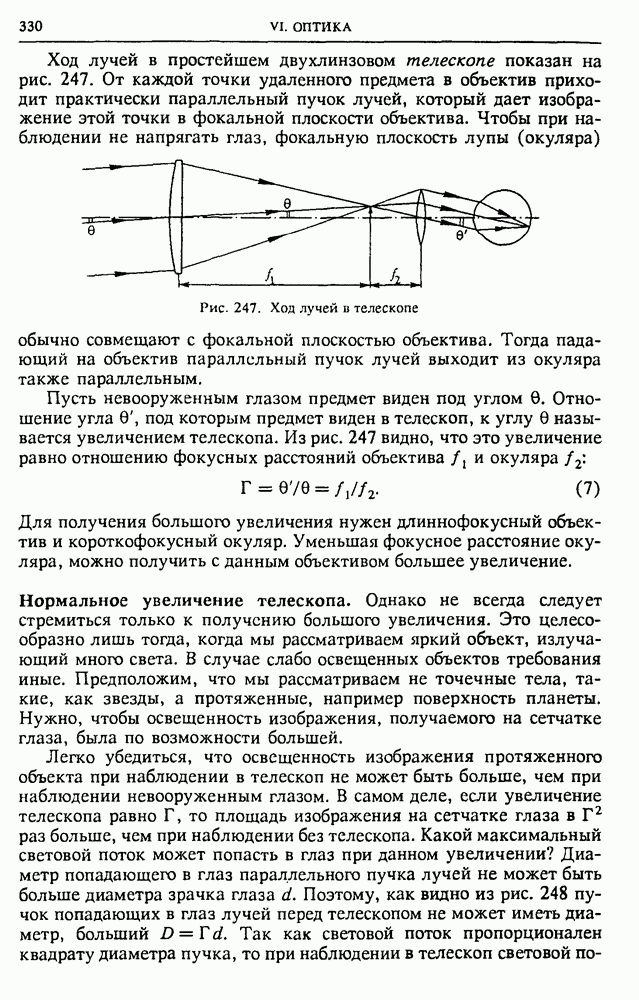
Изменяющееся электрическое поле как источник магнитного поля. К этому выводу можно прийти, анализируя уже известные нам экспериментальные факты и описывающие их физические законы. Рассмотрим участок электрической цепи, содержащий длинный прямолинейный провод и плоский конденсатор (рис. 126а). Будем считать, что в течение некоторого достаточно малого промежутка времени ток в этой цепи равен I. Этот ток связан с изменением заряда конденсатора соотношением 
Рассмотрим круговой контур I, охватывающий проводник, как показано на рис. 126а. Ток  создает магнитное поле, поэтому по теореме о циркуляции вектора индукции магнитного поля имеем
создает магнитное поле, поэтому по теореме о циркуляции вектора индукции магнитного поля имеем

В правой части (9) стоит заряд, пересекающий ограниченную контуром I поверхность  в единицу времени. Будем теперь растягивать поверхность, ограниченную контуром I, так, чтобы она, не пересекая провода с током, прошла в промежутке между пластинами конденсатора (S на рис. 126б). В этом случае никакие заряды не пересекают ограниченную контуром вытянутую поверхность, и в этом смысле ток I в (9) равен нулю. Но магнитное поле вокруг провода, в том месте, где расположен контур, исчезнуть не может, и левая часть (9) не изменяет своего значения при деформации поверхности. Мы приходим к противоречию: левая часть (9) отлична от нуля, а правая равна нулю. Значит, в формуле (9) чего-то не хватает. Естественно ожидать, что на самом деле в правой части этой формулы должен стоять еще один член, который равен нулю, если стягиваемая контуром поверхность пересекает провод.
в единицу времени. Будем теперь растягивать поверхность, ограниченную контуром I, так, чтобы она, не пересекая провода с током, прошла в промежутке между пластинами конденсатора (S на рис. 126б). В этом случае никакие заряды не пересекают ограниченную контуром вытянутую поверхность, и в этом смысле ток I в (9) равен нулю. Но магнитное поле вокруг провода, в том месте, где расположен контур, исчезнуть не может, и левая часть (9) не изменяет своего значения при деформации поверхности. Мы приходим к противоречию: левая часть (9) отлична от нуля, а правая равна нулю. Значит, в формуле (9) чего-то не хватает. Естественно ожидать, что на самом деле в правой части этой формулы должен стоять еще один член, который равен нулю, если стягиваемая контуром поверхность пересекает провод.

Рис. 126. Циркуляция вектора магнитной индукции не зависит от того, пересекает ли стягиваемая им поверхность провод с током (а) или проходит между обкладками конденсатора (б)
Как угадать вид этого члена? Так как левая часть формулы (9) при деформации поверхности не изменилась, то попробуем подставить в правую часть (9) вместо I равную ему скорость изменения заряда  на обкладках конденсатора и попытаемся интерпретировать эту величину так, чтобы она имела смысл и в той области, где отсутствуют движущиеся заряды. Поскольку заряд конденсатора
на обкладках конденсатора и попытаемся интерпретировать эту величину так, чтобы она имела смысл и в той области, где отсутствуют движущиеся заряды. Поскольку заряд конденсатора  равен произведению поверхностной плотности заряда а на площадь пластины
равен произведению поверхностной плотности заряда а на площадь пластины  то при неизменных размерах и форме конденсатора
то при неизменных размерах и форме конденсатора  Выражая поверхностную плотность заряда через напряженность электрического поля между пластинами
Выражая поверхностную плотность заряда через напряженность электрического поля между пластинами  перепишем (9) в виде
перепишем (9) в виде

В отличие от тока I, величина  не равна нулю в промежутке между обкладками конденсатора. Поскольку произведение
не равна нулю в промежутке между обкладками конденсатора. Поскольку произведение  представляет собой поток напряженности электрического поля Е через поверхность
представляет собой поток напряженности электрического поля Е через поверхность  ограниченную контуром, то в правой части (10) стоит величина, пропорциональная скорости изменения потока
ограниченную контуром, то в правой части (10) стоит величина, пропорциональная скорости изменения потока  напряженности электрического поля:
напряженности электрического поля:

Обобщение теоремы о циркуляции магнитного поля. Если теперь вместо (9) и (11) написать формулу

то она будет справедлива всегда, независимо от того, где проходит поверхность, ограниченная контуром I. Если поверхность пересекает провод, то второй член в правой части (12) практически равен нулю и мы возвращаемся к теореме о циркуляции магнитного поля (9). Если же поверхность проходит внутри конденсатора, то  первый член в правой части вклада не дает, но, как мы видели, положение спасает второе слагаемое.
первый член в правой части вклада не дает, но, как мы видели, положение спасает второе слагаемое.
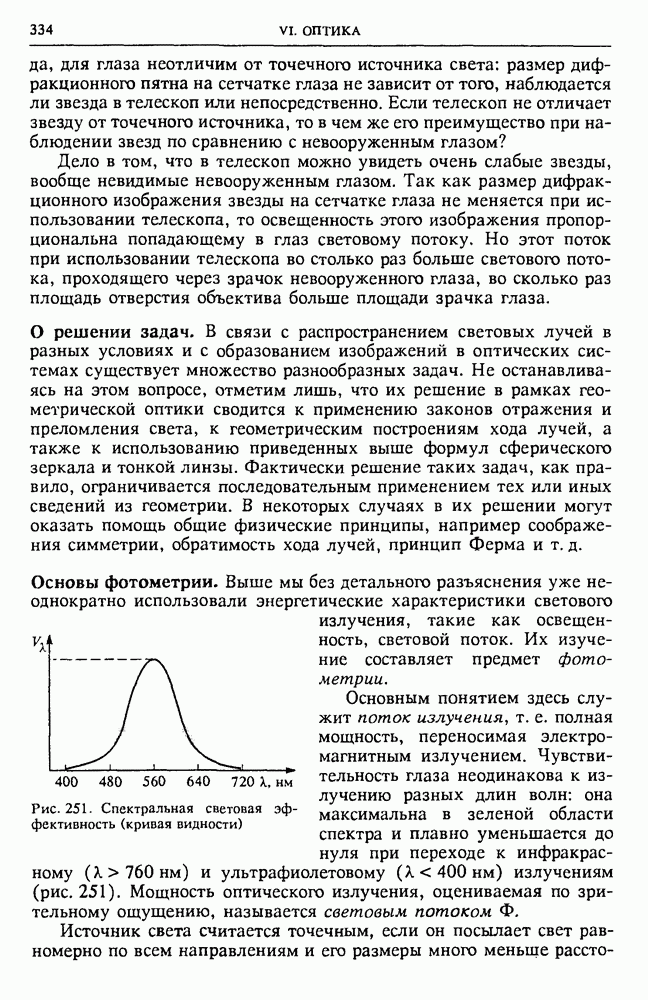
Возникает вопрос: является ли добавленное второе слагаемое в правой части (12) чисто формальным, необходимым только для того, чтобы формула была справедлива при любой поверхности, ограниченной данным контуром, или оно имеет физический смысл и соответствует тому, что магнитное поле возбуждается изменяющимся электрическим полем?

Рис. 127. Изменение электрического поля приводит к появлению магнитного поля
Ответ на этот вопрос можно получить, если рассмотреть несколько видоизмененный опыт (рис. 127), где контур I расположен целиком внутри большого конденсатора, расстояние между пластинами которого велико по сравнению с размерами контура. Опыт показывает, что внутри конденсатора есть магнитное поле; однако очевидно, что это поле не может создаваться далеко расположенными проводами с током  Значит, в этом случае магнитное поле возникает из-за изменения электрического поля. Циркуляция индукции этого магнитного поля по контуру определяется скоростью изменения потока напряженности электрического поля через поверхность, ограниченную этим контуром.
Значит, в этом случае магнитное поле возникает из-за изменения электрического поля. Циркуляция индукции этого магнитного поля по контуру определяется скоростью изменения потока напряженности электрического поля через поверхность, ограниченную этим контуром.
Ток смещения. Величина  получила название тока смещения, так как она, подобно току проводимости
получила название тока смещения, так как она, подобно току проводимости  является источником магнитного поля. Термин «смещение» обусловлен историческими причинами и связан с утратившей значение механической моделью электрического поля. Следует отметить, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Например, при наличии тока смещения не выделяется джоулева теплота.
является источником магнитного поля. Термин «смещение» обусловлен историческими причинами и связан с утратившей значение механической моделью электрического поля. Следует отметить, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Например, при наличии тока смещения не выделяется джоулева теплота.
Ток смещения был впервые предсказан Максвеллом на основе теоретического анализа известных к тому времени экспериментально установленных законов электромагнетизма. Максвелл показал,
что единая непротиворечивая картина электромагнитных явлений, согласующаяся с законом сохранения электрического заряда, может быть создана, только если предположить, что изменяющееся электрическое поле способно создавать магнитное поле. Из написанной им системы уравнений электромагнитного поля следуют как все экспериментальные законы электромагнетизма, так и существование тока смещения.
Уравнения Максвелла. Система уравнений Максвелла содержит четыре основных закона электромагнетизма. Первый закон — теорема Гаусса, связывающая поток напряженности электрического поля через замкнутую поверхность с полным зарядом внутри этой поверхности. В случае неподвижных зарядов теорема Гаусса дает иную математическую формулировку экспериментальному закону Кулона. Устанавливаемая теоремой Гаусса связь между потоком напряженности электрического поля через замкнутую поверхность и полным зарядом внутри поверхности справедлива при движении как зарядов, так и поверхности в целом или отдельных ее участков (т. е. при деформации поверхности).
Второй закон — теорема Гаусса для магнитного поля, согласно которой поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Эта теорема отражает вихревой характер магнитного поля и отсутствие в природе магнитных зарядов.
Третий закон — закон электромагнитной индукции Фарадея, согласно которому изменяющееся магнитное поле порождает вихревое электрическое поле.
Четвертый закон является обобщением закона Био—Савара— Лапласа. Магнитное поле может создаваться как движущимися электрическими зарядами, т. е. токами проводимости, так и изменяющимся электрическим полем, т. е. токами смещения.
Анализируя систему уравнений электромагнитного поля, Максвелл пришел к выводу, что эти уравнения допускают существование связанных между собой электрического и магнитного полей, распространяющихся в пространстве со скоростью света, — электромагнитных волн, которые позднее были экспериментально обнаружены Герцем.
Гауссова система единиц. При теоретическом описании электромагнитного поля наиболее простой и естественной является так называемая гауссова система единиц, которая для электрических величин совпадает с абсолютной электростатической системой СГСЭ. Единицы магнитных величин вводятся в гауссовой системе следующим образом.
Будем исходить из выражения для магнитной индукции поля, создаваемого бесконечным прямолинейным током:

Обнаружить магнитное поле можно по его действию на другой проводник с током. Если этот проводник расположить параллельно проводнику, создающему магнитное поле, то действующая на него сила согласно закону Ампера будет пропорциональна индукции магнитного поля В, силе тока в нем  и его длине
и его длине 

Напомним, что в единицах СИ коэффициент к в формуле (14) равен единице в соответствии с определением индукции магнитного поля В через момент сил, действующих на рамку с током. В формуле (13) или в законе Био—Савара—Лапласа, из которого она следует, коэффициент к записывается в виде  а его значение (или значение магнитной постоянной
а его значение (или значение магнитной постоянной  получается из определения ампера через силу взаимодействия двух параллельных токов.
получается из определения ампера через силу взаимодействия двух параллельных токов.
В гауссовой системе единиц коэффициенты  вводятся иначе.
вводятся иначе.
Коэффициент к в формуле (13) может быть выбран произвольно, так как единица индукции поля В еще не установлена. Но после того, как этот коэффициент к в (13) выбран (тем самым выбрана и единица индукции В), коэффициент к в формуле (14) уже не может выбираться произвольно, а должен определяться из эксперимента. Разумеется, можно поступить и наоборот: использовать уравнение (14) для введения единицы индукции поля, полагая  тогда коэффициент к в (13) будет определяться на опыте. В системе Гаусса поступают следующим образом. Выбирают коэффициент к в формуле (13) так, чтобы он равнялся коэффициенту к в формуле (14).
тогда коэффициент к в (13) будет определяться на опыте. В системе Гаусса поступают следующим образом. Выбирают коэффициент к в формуле (13) так, чтобы он равнялся коэффициенту к в формуле (14).
Электродинамическая постоянная. Если подставить в формулу (14) индукцию В из (13), то для силы взаимодействия двух параллельных проводников с токами I и  находящихся на расстоянии
находящихся на расстоянии  друг от друга, получим следующее выражение:
друг от друга, получим следующее выражение:

В гауссовой системе  Поскольку для всех величин, входящих в эту формулу, единицы уже выбраны, коэффициент
Поскольку для всех величин, входящих в эту формулу, единицы уже выбраны, коэффициент  как легко убедиться, имеет размерность
как легко убедиться, имеет размерность  т. е. обратную размерности квадрата скорости. Этот коэффициент должен определяться экспериментально по измерению силы взаимодействия двух параллельных проводников, находящихся на известном расстоянии, когда по ним протекают известные токи. Опыт показал, что числовое значение
т. е. обратную размерности квадрата скорости. Этот коэффициент должен определяться экспериментально по измерению силы взаимодействия двух параллельных проводников, находящихся на известном расстоянии, когда по ним протекают известные токи. Опыт показал, что числовое значение  равно
равно  где с — так называемая электродинамическая постоянная, равная скорости света в вакууме:
где с — так называемая электродинамическая постоянная, равная скорости света в вакууме:

В гауссовой системе единиц закон Био—Савара—Лапласа и закон Ампера записываются в виде

На основании последней формулы и устанавливается единица индукции магнитного поля — гаусс. Один гаусс — это индукция такого поля, которое действует на 1 см проводника с током в одну СГСЭ - единицу с силой, численно равной  дин, если проводник расположен перпендикулярно линиям индукции магнитного поля.
дин, если проводник расположен перпендикулярно линиям индукции магнитного поля.
Подчеркнем, что числовое значение магнитной постоянной  получается как прямое следствие определения ампера, а не устанавливается на опыте, в отличие от коэффициента
получается как прямое следствие определения ампера, а не устанавливается на опыте, в отличие от коэффициента  в гауссовой системе. Так получается потому, что в системе СИ число основных единиц больше, чем в гауссовой и единица силы тока является основной (выбранной произвольно), в то время как в гауссовой системе эта единица является производной.
в гауссовой системе. Так получается потому, что в системе СИ число основных единиц больше, чем в гауссовой и единица силы тока является основной (выбранной произвольно), в то время как в гауссовой системе эта единица является производной.
Основные формулы в гауссовой системе. Из второй формулы (16), выражающей закон Ампера, следует, что в гауссовой системе единиц выражение для силы Лоренца принимает вид:

Отсюда (как и из первой формулы  следует, что в гауссовой системе размерности напряженности электрического поля и индукции магнитного поля одинаковы. Это совпадение размерностей не случайно: как мы видели, при переходе из одной системы отсчета в другую происходит частичное взаимное превращение электрического и магнитного полей. Это свойство электромагнитного поля наиболее естественным образом выражается именно в гауссовой системе единиц, где превращающиеся друг в друга физические величины Е и В измеряются в единицах одинаковой размерности (хотя эти единицы и называются по-разному: единица напряженности электрического поля не имеет специального названия, а единица индукции магнитного поля называется гаусс).
следует, что в гауссовой системе размерности напряженности электрического поля и индукции магнитного поля одинаковы. Это совпадение размерностей не случайно: как мы видели, при переходе из одной системы отсчета в другую происходит частичное взаимное превращение электрического и магнитного полей. Это свойство электромагнитного поля наиболее естественным образом выражается именно в гауссовой системе единиц, где превращающиеся друг в друга физические величины Е и В измеряются в единицах одинаковой размерности (хотя эти единицы и называются по-разному: единица напряженности электрического поля не имеет специального названия, а единица индукции магнитного поля называется гаусс).
Отмеченное свойство проявляется в формулах преобразования полей при переходе из одной инерциальной системы отсчета в другую. Вместо (6) в гауссовой системе имеем

В этих формулах явно выступает одинаковая размерность слагаемых в правых частях.
В гауссовой системе единиц более симметричный вид принимают и выражения для инвариантов электромагнитного поля:

• Объясните кратко, почему при переходе из системы отсчета, где есть только электрическое поле, в другую систему, в последней будет еще и магнитное поле, и наоборот.
• Почему электрическое и магнитное поля, взаимно перпендикулярные в какой-либо системе отсчета, будут взаимно перпендикулярными и в любой другой системе отсчета?
• Как объяснить, что магнитное поле создается не только движущимися зарядами, но и изменяющимся со временем электрическим полем?
• В чем сходство и в чем различие между током проводимости и током смещения?
• Два электрона в вакууме отталкиваются, так как имеют одинаковые заряды. Когда они движутся параллельными курсами, между ними действует сила притяжения, как между параллельными токами. Существует ли такая скорость, при которой это притяжение превзойдет их кулоновское отталкивание?
• Какие экспериментальные законы электромагнитных явлений легли в основу системы уравнений Максвелла?
• Как вводятся коэффициенты в законах Ампера и Био—Савара—Лапласа в гауссовой системе единиц?
• Как определяется единица индукции магнитного поля в гауссовой системе единиц?
• Покажите, что в гауссовой системе единиц напряженность электрического поля и индукция магнитного поля имеют одинаковую размерность.
• Объясните, почему значение электрической постоянной  в гауссовой системе единиц устанавливается на опыте, а значение магнитной постоянной
в гауссовой системе единиц устанавливается на опыте, а значение магнитной постоянной  в СИ просто вычисляется. На основе чего оно вычисляется?
в СИ просто вычисляется. На основе чего оно вычисляется?
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
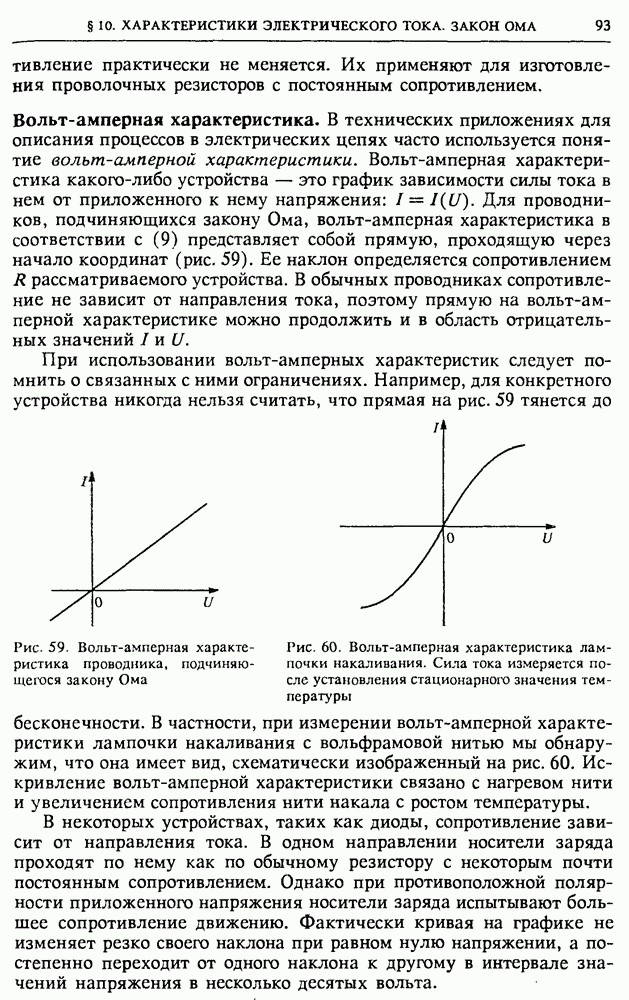
- § 10. Характеристики электрического тока. Закон Ома
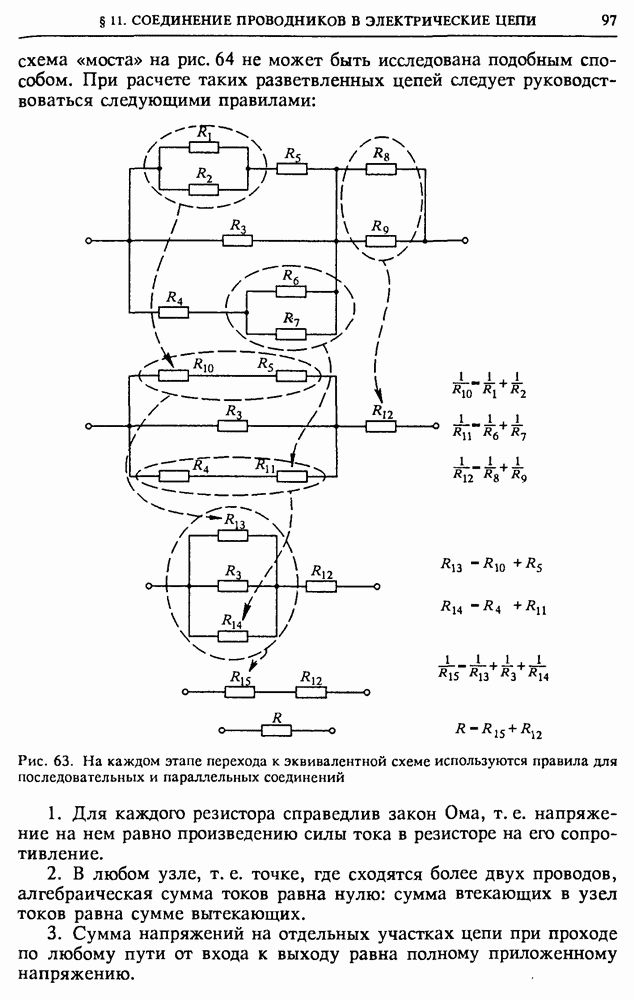
- § 11. Соединение проводников в электрические цепи
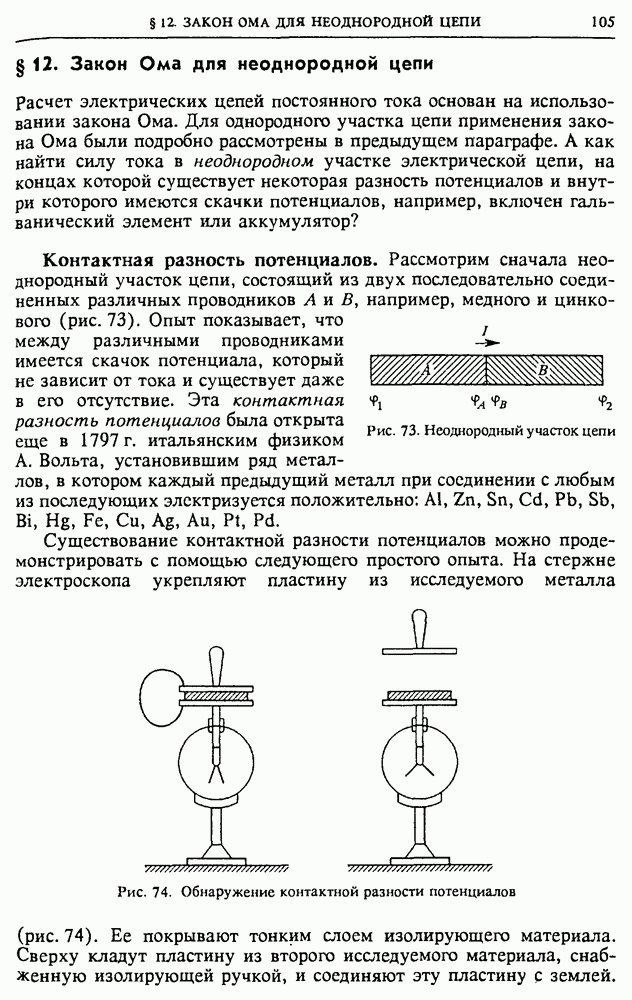
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение