§ 18. Электрические машины постоянного тока

Как уже отмечалось, принцип действия электродвигателей основан на использовании силы Ампера, действующей на проводник с током в магнитном поле. Однако при работе электродвигателя принципиальную роль играет явление самоиндукции в его обмотках.

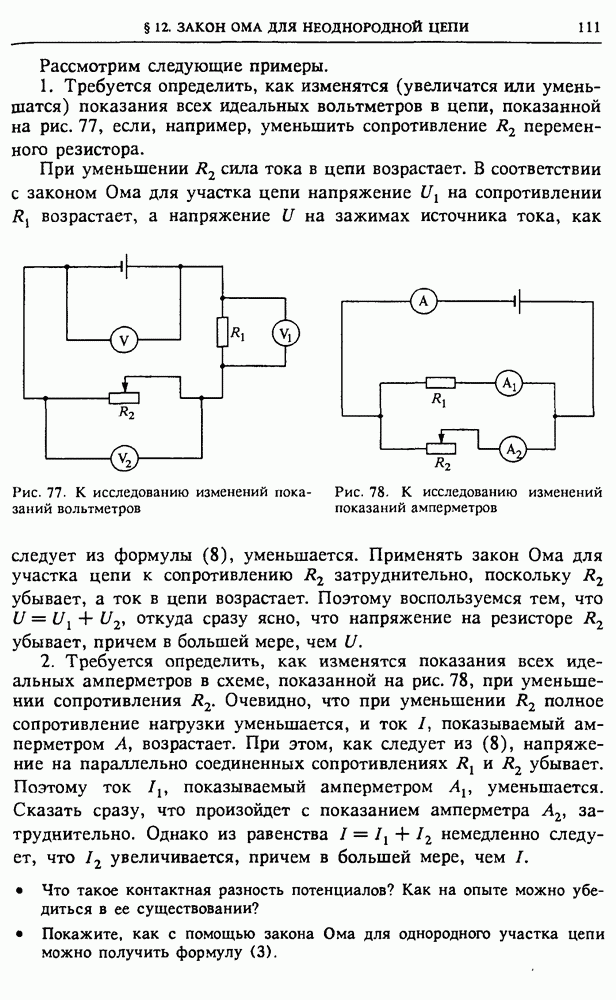
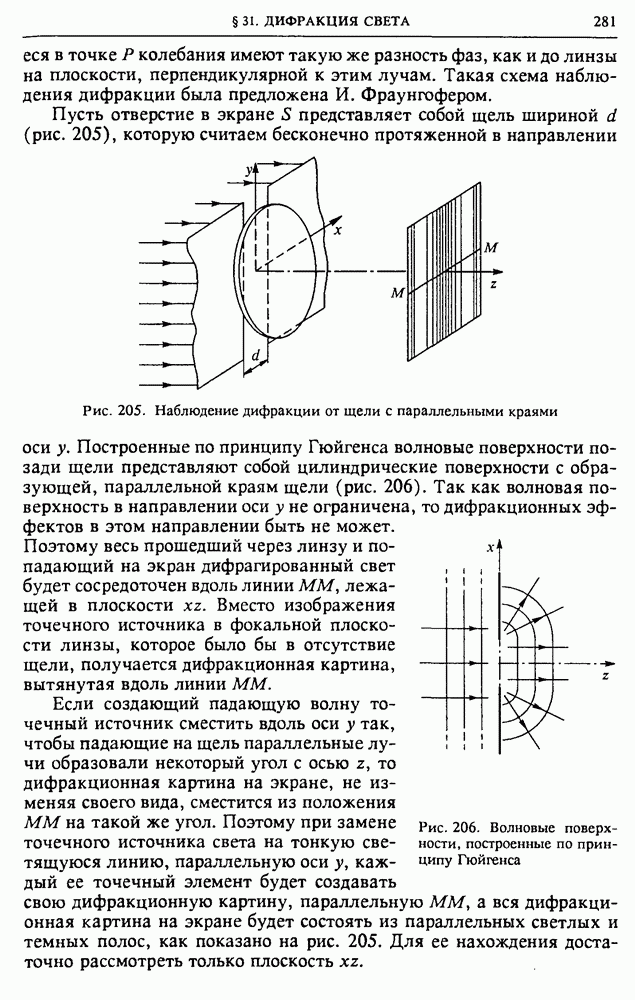
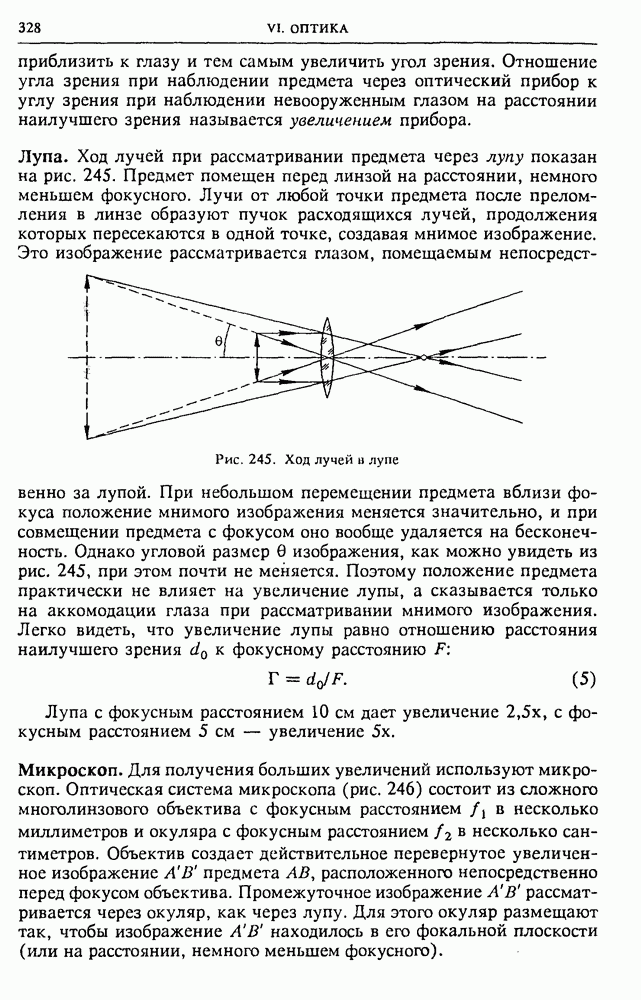
Модель электрической машины. Рассмотрим упрощенную линейную модель электрической машины (рис. 121): проводящий контур с включенным в него источником тока с ЭДС помещается в однородное магнитное поле. Подвижная часть контура — стержень — может без трения скользить по рельсам.

Обозначим через силу тока в контуре. На подвижную часть контура действует сила Ампера направленная, как показано на рисунке. Сила Ампера не зависит от того, покоится стержень или движется. Если мы хотим, чтобы стержень двигался

равномерно, необходимо приложить к нему внешнюю силу которая в любой момент уравновешивала бы силу Ампера.

Пусть за промежуток времени стержень переместился на расстояние в направлении действия силы Ампера. Напишем уравнение баланса энергии. За время источник совершил работу При этом во всех проводниках выделилась джоулева теплота где — полное сопротивление цепи. Кроме того, совершила работу сила Ампера:

Как совершение этой механической работы, так и выделение теплоты происходит за счет действия источника тока. На основании закона сохранения энергии совершенная источником работа равна сумме выделившейся теплоты и работы силы Ампера:

откуда, переходя к пределу для силы тока получаем

Сопоставляя это выражение с законом Ома для полной цепи, мы видим, что роль ЭДС играет величина, состоящая из двух слагаемых: из ЭДС источника тока и из величины Этот член представляет собой добавочную ЭДС (ЭДС индукции), обусловленную действием сторонних сил при движении участка

Рис. 121. К энергетическим превращениям при электромагнитной индукции

Обратим внимание на то, что приведенные рассуждения фактически представляют собой вывод закона электромагнитной индукции с помощью закона сохранения энергии.

Рассмотренный пример можно представить как упрощенную модель электродвигателя постоянного тока. Как видно из уравнения (2), энергия источника тока используется для совершения работы над внешними телами и частично рассеивается в виде джоулевой теплоты. Из формулы (3) видно, какую роль играет явление электромагнитной индукции в работе электродвигателя. Именно благодаря этому явлению не вся работа источника превращается в теплоту.

Теперь предположим, что стержень скользит в противоположном направлении, т. е. в направлении действия внешней силы. При этом работа силы Ампера отрицательна, так как Равная ей по модулю работа внешней силы положительна.

Джоулева теплота теперь выделяется как за счет работы источника тока, так и за счет работы внешней силы Закон сохранения энергии имеет вид

откуда, переходя к пределу получаем

В этом случае устройство работает как генератор. Даже если мы уберем источник тока в цепи все равно будет идти ток и выделяться теплота. Из уравнения (4) видно, что это будет происходить за счет работы внешней силы.

Обратим внимание на то, что на самом деле нет необходимости рассматривать эти случаи — электродвигатель и генератор по отдельности. Легко видеть, что уравнение баланса энергии (2) и уравнение закона Ома (3) охватывают оба случая, если только учитывать знак изменения магнитного потока Таким образом, одно и то же устройство может служить моделью и электродвигателя, и генератора. Его работа в любом режиме описывается одними и теми же уравнениями. В электрической машине направление преобразования энергии может быть изменено на обратное. Свойство обратимости присуще всем машинам постоянного тока и широко используется в технике.

Типы электрических машин. Конструктивно электрические машины постоянного тока могут быть выполнены по-разному. Основное различие заключается в способе создания магнитного поля. В простейших маломощных моторчиках используются постоянные магниты. В тех случаях, когда для этой дели используется электромагнит, его обмотка соединяется с обмоткой якоря либо параллельно (шун-товая машина), либо последовательно (сериесная машина). Возможны и комбинированные схемы соединения (компаунд-машины).

Каждая из таких машин имеет свои достоинства и недостатки. Для шунтовых двигателей характерно малое изменение скорости вращения якоря в широких пределах изменения механической нагрузки. Сериесные машины обеспечивают большой крутящий момент при трогании с места и потому находят широкое применение на транспорте. Скорость их вращения существенно меняется при изменении нагрузки.

Условия работы электродвигателя. Рассмотрим подробнее электродвигатель постоянного тока с независимым возбуждением, когда магнитное поле создается либо постоянным магнитом, либо обмотками, включенными параллельно якорю. Для простоты будем пренебрегать энергетическими потерями, связанными с созданием магнитного поля.

Пусть сопротивление обмотки якоря равно и двигатель включен в сеть с постоянным напряжением Пренебрегая трением в подшипниках, исследуем условия работы электродвигателя: найдем зависимость тока в цепи, полной потребляемой двигателем мощности и механической мощности, развиваемой двигателем, угловой скорости вращения якоря и коэффициента полезного действия от механической нагрузки, т. е. от момента внешних сил, действующих на якорь.

Предположим, что к якорю электродвигателя со стороны механической нагрузки приложен постоянный вращающий момент М. Будем рассматривать работу электродвигателя в стационарном режиме, когда угловая скорость вращения якоря не меняется со временем. Пусть в цепи якоря идет ток I. Воспользуемся законом сохранения энергии: потребляемую двигателем от сети мощность приравняем сумме механической мощности развиваемой двигателем, и джоулевой теплоты, выделяющейся в якоре в единицу времени:

Поскольку при вращении якоря в постоянном магнитном поле в его обмотке возникает ЭДС индукции, ток определяется законом Ома для неоднородного участка цепи:

где — абсолютная величина ЭДС самоиндукции.

Сравнивая эти формулы, легко увидеть, что

Это соотношение, разумеется, очевидно, если вспомнить, что ЭДС самоиндукции и представляет Собой работу сторонних сил.

Поскольку при независимом возбуждении магнитное поле статора постоянно, то скорость изменения магнитного потока и, следовательно, ЭДС индукции пропорциональна угловой скорости вращения якоря Поэтому равенство (8) можно переписать в виде

где — коэффициент пропорциональности, зависящий от индукции магнитного поля статора и от конструкции электродвигателя, т. е. от размеров и формы обмотки якоря. С другой стороны, развиваемая двигателем механическая мощность при равномерном вращении якоря равна произведению механического момента М на угловую скорость:

Из сравнения выражений (9) и (10) видим, что при установившемся вращении якоря ток в его обмотке пропорционален

приложенному механическому моменту:

Однако из соотношения (7) следует, что ток не может превышать значения

которое достигается при т. е. при неподвижном якоре. Это означает, что максимальный механический момент, который может развить двигатель, равен

Если момент внешних сил, действующих на якорь, будет превышать это значение, то якорь будет вращаться в противоположную сторону и двигатель будет работать как генератор.

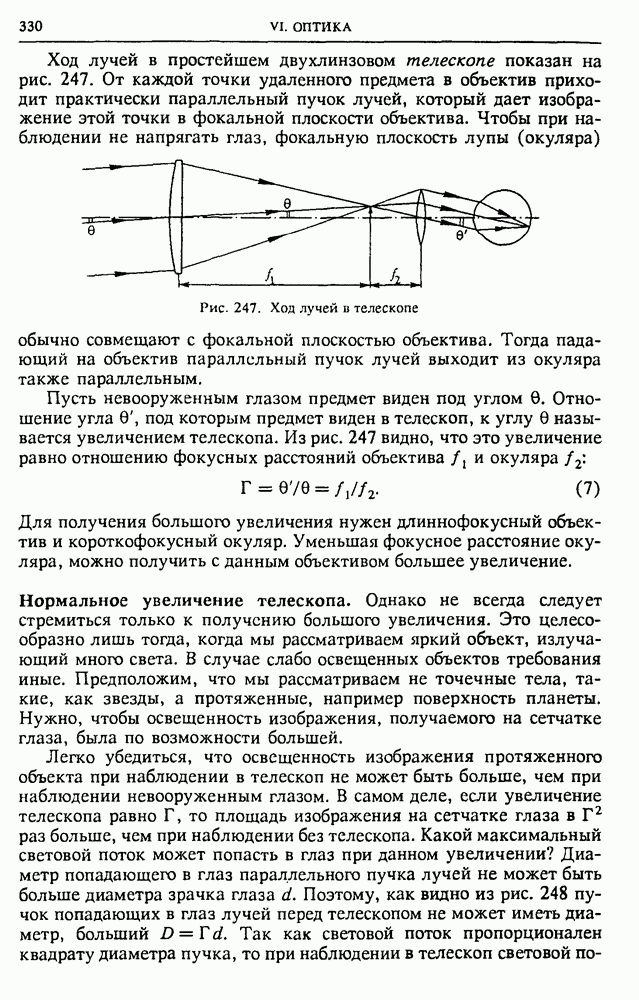
Максимальная мощность двигателя. Итак, из равенства (11) следует, что зависимость тока в якоре от приложенного механического момента линейная (рис. 122а), причем максимальные значения и Мтах даются формулами (12) и (13).

Полная мощность, потребляемая электродвигателем от сети, есть , а ее максимальное значение

Зависимость потребляемой мощности от М представлена на рис. 1226 прямой 1.

С помощью формул (6) и (11) выражение для механической мощности, развиваемой двигателем, можно представить в виде

Это уравнение параболы, ветви которой направлены вниз (кривая 2 на рис. 1226). Механическая мощность двигателя обращается в нуль при , т. е. при работе двигателя на холостом ходу, и при , когда якорь не вращается. Совсем нетрудно убедиться, что максимальное значение механической мощности двигателя достигается при и равно

КПД двигателя. Коэффициент полезного действия двигателя, определяемый как отношение механической мощности к полной мощности, потребляемой от сети, равен

Зависимость КПД от М представлена на рис. 122в. Для определения зависимости угловой скорости якоря от механической нагрузки вернемся к формуле (10). Подставляя в нее из (14), получаем График зависимости от М — также прямая (рис. 122г). При отсутствии внешней нагрузки, т. е. на холостом ходу, угловая скорость максимальна:

С помощью формулы (17) коэффициент пропорциональности к между ЭДС самоиндукции и угловой скоростью со, входящий в формулу для искомых величин, можно выразить через угловую скорость холостого хода которую легко измерить на опыте.

Приведенные на рисунке зависимости наглядно иллюстрируют условия работы электродвигателя. Стремление получить от данного электродвигателя возможно больший вращающий момент неизбежно приведет, как это видно из рис. 122б,в, к тому, что механическая мощность двигателя и его КПД будут крайне низкими, а угловая скорость якоря близка к нулю. Почти вся потребляемая при этом от сети энергия пойдет на нагревание обмотки якоря.

Рис. 122. Зависимость тока в обмотке якоря (а), полной и полезной мощности (б), КПД (в) и угловой скорости якоря (г) от момента внешних сил

Для получения максимальной полезной мощности от данного двигателя механическую нагрузку необходимо рассчитывать. Механический момент внешних сил должен быть равен половине максимального момента, который может развить данный электродвигатель. Этого можно добиться использованием редуктора.

Коэффициент полезного действия двигателя, работающего в таком режиме, равен 0,5.

Любую механическую мощность меньшую максимальной, можно получить при двух значениях момента внешних сил (рис. 1226).

Для получения высокого КПД при заданной полезной мощности следует, как видно из рис. 1226, выбирать меньшее значение момента внешних сил при этом бесполезный расход энергии на нагревание обмотки якоря будет меньше.

Задача

Якорь электродвигателя постоянного тока с независимым возбуждением потребляет от сети ток I. Чему равен КПД двигателя при работе в таком режиме, если при полном затормаживании якоря сила тока в нем возрастает до значения Потерями на трение пренебречь.

Решение. КПД электродвигателя — это отношение развиваемой им механической мощности к потребляемой якорем от сети электрической мощности Р: Потребляемая мощность равна, очевидно, где — напряжение сети. Механическая мощность в соответствии с (8) равна где самоиндукции, возникающая при вращении обмоток якоря в магнитном поле при заданном в условии режиме работы двигателя. Таким образом,

Отношение легко найти, если воспользоваться законом Ома для каждого из рассматриваемых случаев. При заторможенном якоре ЭДС индукции отсутствует и сила тока определяется соотношением

При вращающемся якоре сила тока в нем определяется законом Ома для неоднородного участка цепи:

Разделив почленно (20) на (19), выражаем отношение через отношение токов после чего с помощью (18) получаем

Этот результат можно, разумеется, получить и из приведенной в тексте формулы (16), если заметить, что в ней как следует из (11), равно силе тока в якоре при его вращении.

• Поясните описанную в тексте линейную модель электрической машины. В каком случае она соответствует электродвигателю и в каком — электрогенератору?

• Объясните возможность использования электродвигателя постоянного тока в качестве электрогенератора, основываясь на законе сохранения энергии.

• Используя аналогию между поступательным движением и вращением, покажите справедливость формулы для мощности, развиваемой механическим вращающим моментом М.

• Почему электродвигатель потребляет максимальный ток, когда его якорь заторможен? Почему при этом развиваемый данным двигателем крутящий момент будет наибольшим?

• Покажите, что максимальное значение механической мощности, развиваемой электродвигателем, равно четверти потребляемой им от сети мощности при заторможенном якоре. Чему равен КПД двигателя, когда он развивает максимальную механическую мощность?

• Нарисуйте электрические схемы включения обмоток шунтовых и сериесных электродвигателей и дайте качественное объяснение их особенностей, отмеченных в тексте.