§ 33. Протяженные источники света

Рассмотренные выше интерференционные и дифракционные явления волновой оптики относились к случаю монохроматического света, излучаемого точечным источником. Однако все реальные источники света имеют конечные размеры, а излучаемый ими свет, как мы уже обсуждали выше, никогда не является строго монохроматическим. Поэтому интересно выяснить, к каким изменениям в результатах приведет отказ от монохроматической идеализации и учет конечных размеров источников света. Для простоты и большей наглядности выясним роль каждого из этих факторов в отдельности.

Начнем с учета конечных размеров источника. Будем считать, что реальный протяженный источник состоит из большого числа точечных взаимно некогерентных элементов, излучающих свет определенной длины волны. В этом случае интенсивность в любой точке волнового поля равна сумме интенсивностей от каждого точечного источника.

Рассмотрим изменение интерференционной картины в опыте Юнга, обусловленное использованием протяженного источника света. Разумеется, речь идет не об увеличении размеров источника в направлении, параллельном щелям: при использовании такого линейного источника вид интерференционной картины, как мы видели, не меняется. Речь идет и не об увеличении размеров вторичных когерентных источников, т. е. ширины щелей при использовании

точечного первичного источника света, — этот случай уже был рассмотрен в конце предыдущего параграфа. Сейчас нас будет интересовать вид интерференционной картины при использовании первичного источника конечной ширины, а сами щели будем для простоты считать бесконечно узкими. Мы увидим, что с увеличением ширины источника резкость интерференционных полос уменьшается вплоть до их полного исчезновения. Это накладывает определенные условия на размеры источников света в направлении, соединяющем отверстия или щели, при их использовании в интерференционных экспериментах по схеме Юнга.

Явление уменьшения резкости интерференционных полос, с которым приходится бороться в лабораторных экспериментах, нашло совершенно неожиданное и очень эффективное применение в астрономии.

Роль дифракции в телескопе. Одной из важнейших астрономических задач является определение углового расстояния двойных звезд, т. е. того угла, под которым видны эти звезды с Земли. Если звезды находятся на очень маленьком угловом расстоянии 9 друг от друга, то даже с помощью самых совершенных телескопов эту задачу решить не удается, так как в фокальной плоскости объектива изображения этих звезд размыты вследствие явления дифракции и не могут быть разрешены. Согласно представлениям геометрической оптики параллельный пучок лучей, падающих на линзу объектива, должен собираться в одной точке фокальной плоскости. Поэтому изображение удаленной звезды, лучи от которой попадают в объектив практически параллельным пучком, должно получаться в виде точки.

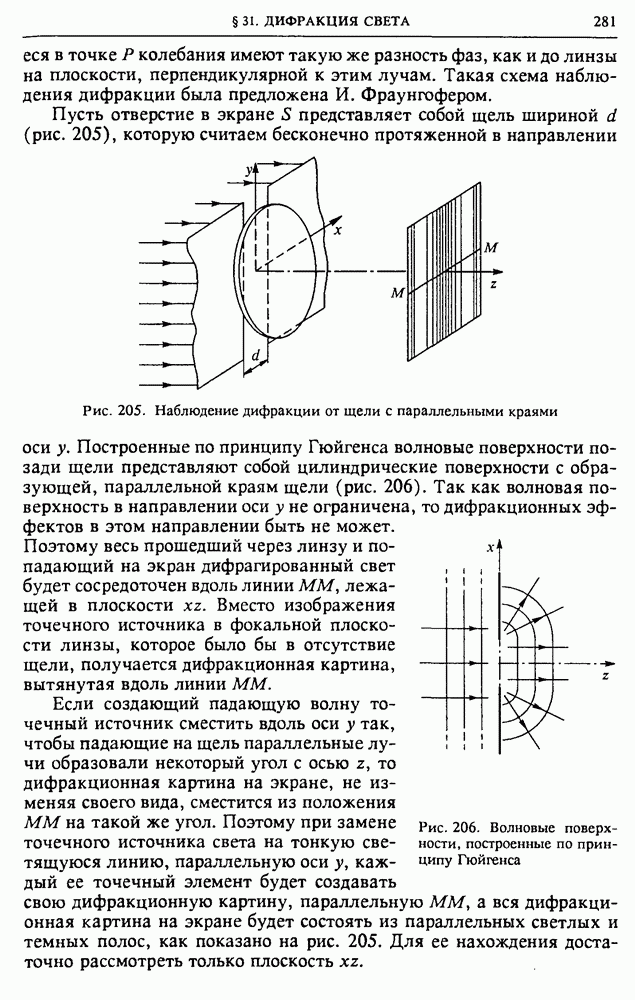
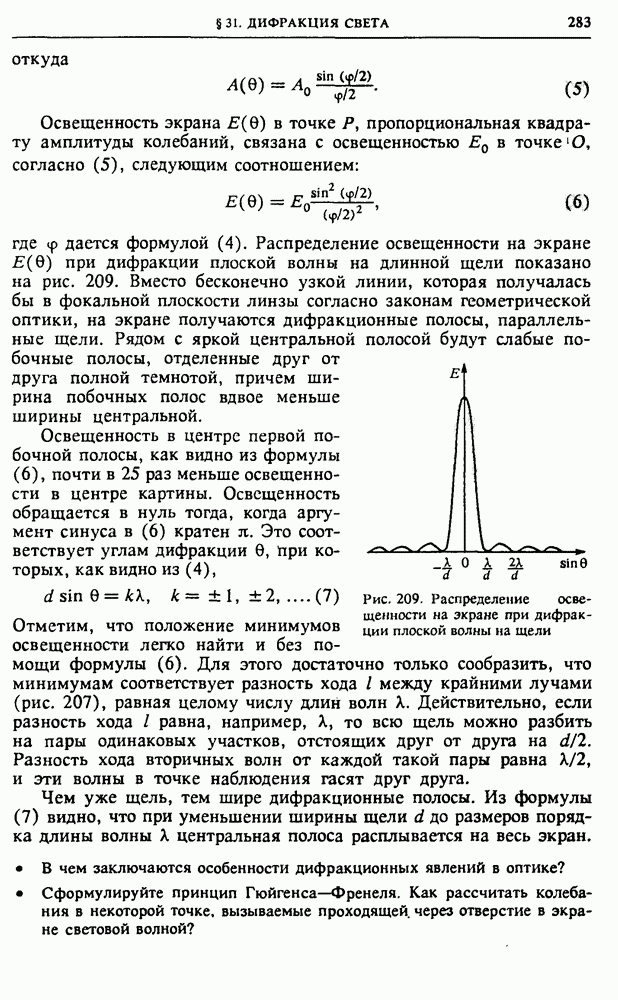
Выясним теперь, как на самом деле выглядит в фокальной плоскости объектива телескопа изображение звезды, которую из-за очень большого удаления можно считать точечным источником. Чтобы получить представление об этом, будем пока считать, что перед объективом телескопа помещена длинная щель шириной с параллельными прямыми краями. Поскольку приходящий от звезды свет можно рассматривать как плоскую волну, в фокальной плоскости объектива будет наблюдаться дифракционная картина от щели, которая была описана при рассмотрении дифракции в параллельных лучах. Распределение освещенности для этого случая было показано на рис. 209.

Освещенность экрана в первом боковом максимуме составляет, как было показано, менее освещенности в центре дифракционной картины. Это означает, что почти весь поток света, прошедший через щель, распространяется в интервале углов от — до где угол определяется формулой (7) § 31 при Поскольку мы рассматриваем щель, ширина которой много больше длины волны X, то можно заменить на и тогда

Изображение бесконечно удаленного точечного источника в фокальной плоскости линзы оказывается размытым в полоску, перпендикулярную краям щели. Длина а этой полоски ограничена размером центрального дифракционного максимума и поэтому равна

где — фокусное расстояние линзы.

Рассмотрение дифракции на круглом отверстии диаметром показывает, что изображение бесконечно удаленного источника размывается в круглое пятно, диаметр которого определяется той же формулой (2) с дополнительным числовым коэффициентом, близким к единице.

В телескопе роль круглого отверстия играет оправа объектива, и изображение звезды представляет собой создаваемую этой оправой дифракционную картину. Объективы большого диаметра могут давать изображение более высокого качества, так как (см. формулу уменьшается влияние дифракции.

Разрешение телескопа. Если в телескоп наблюдают две звезды, находящиеся на малом угловом расстоянии друг от друга, то дифракционные картины, создаваемые каждой звездой, налагаются одна на другую. Если при этом главные максимумы дифракционных картин сближаются на расстояние, меньшее радиуса центрального дифракционного пятна, то, согласно критерию Рэлея, измерить точно расстояние между ними, а тем самым и угловое расстояние между звездами, невозможно. Правда, современные методы обработки экспериментальных результатов позволяют разрешать дифракционные картины, для которых критерий Рэлея, строго говоря, не выполняется. Однако для оценки разрешающей способности телескопа это не принципиально.

Итак, минимальное угловое расстояние 9 между звездами, которое можно измерить с помощью телескопа, равно

По этой формуле легко оценить, что на телескопе-рефлекторе с диаметром зеркала в принципе можно измерять угловые размеры, не меньшие .

• Почему световые волны, испускаемые разными элементами поверхности протяженного источника, такого, как раскаленная нить лампочки, не создают интерференционной картины?

• Объясните, почему интерференционные полосы в опыте Юнга становятся менее отчетливыми по мере увеличения размеров первичного источника, освещающего щели.

• Какое применение в астроиомии нашло явление уменьшения резкости интерференционных полос при использовании первичного источника света конечных размеров?

• Какую роль играет дифракция света в формировании изображения в фокальной плоскости объектива телескопа? Какую форму имело бы изображение удаленной звезды, если бы она была, например, пятиконечной?

• Что происходит с наблюдаемым в телескопе изображением звезды при уменьшении диаметра отверстия объектива?

Звездный интерферометр. Для измерения еще меньших, угловых размеров используется звездный интерферометр Майкельсона, идею которого можно понять из рис. 216. Основными элементами интерферометра являются непрозрачный экран А с двумя отверстиями, расстояние между которыми можно изменять, собирающая линза расположенная непосредственно за экраном А, и экран В, находящийся в фокальной плоскости линзы, на котором наблюдаются интерференционные полосы.

Рис. 216. К объяснению принципа действия звездного интерферометра

Это есть одна из возможных реализаций опыта Юнга, отличающаяся от рассмотренной ранее тем, что интерференционные полосы наблюдаются не на удаленном экране, а в фокальной плоскости линзы, роль которой в звездном интерферометре выполняет объектив телескопа-рефлектора. При изменении расстояния между отверстиями резкость интерференционных полос изменяется, и по этим изменениям можно определить угловой размер двойной звезды 9.

Чтобы понять, почему меняется резкость полос, рассмотрим сначала интерференционную картину, создаваемую одним бесконечно удаленным точечным источником Если источник расположен на оптической оси (рис. 216а), то фазы вторичных источников совпадают и в некоторой точке Р на экране В будет находиться светлая или темная полоса в зависимости от того, будет ли разность хода лучей I равна четному или нечетному числу полуволн. Если источник смещен с оптической оси прибора на угол то создаваемая им интерференционная картина окажется сдвинутой, поскольку между вторичными источниками имеется разность фаз, обусловленная разностью хода лучей от

источника до отверстий в экране А (рис. 2166):

При наблюдении двойной звезды, которую можно рассматривать как два взаимно некогерентных точечных источника, на экране В будут налагаться одна на другую две независимые интерференционные картины, создаваемые каждой звездой, и освещенность в любой точке экрана будет равна сумме освещенностей от каждой интерференционной картины.

Как будет выглядеть эта суммарная интерференционная картина? Она будет отчетливой, если светлые полосы одной картины приходятся на светлые полосы другой, и исчезнет совсем, если светлые полосы одной совпадут с темными полосами другой. Полное исчезновение полос произойдет, конечно, только тогда, когда звезды имеют одинаковую яркость.

Теперь легко понять, почему меняется резкость полос при изменении расстояния между отверстиями на экране А. Если отверстия расположены очень близко друг к другу, то, как видно из формулы (4), фазы вторичных источников будут практически совпадать друг с другом как для одной, так и для другой звезды. Интерференционная картина будет отчетливой.

Если увеличить расстояние между отверстиями, то интерференционные картины от разных звезд будут смещаться относительно друг друга, и при некотором расстоянии светлые полосы одной картины совпадут с темными полосами другой — интерференционная картина исчезнет. Пусть в некоторой точке Р (рис. 216а) находится светлая полоса одной интерференционной картины и темная — другой. Это означает, что световые колебания от одной звезды приходят в точку Р в фазе, от другой — в противофазе. Поскольку разность хода лучей от вторичных источников до точки Р одинакова для обеих интерференционных картин, нетрудно сообразить, что наложение светлой полосы на темную имеет место при выполнении условия

где — любое целое число. С помощью формулы (4) условие полного исчезновения интерференционной картины (5) можно записать в виде

Итак, при увеличении расстояния между отверстиями первое исчезновение интерференционной картины происходит при

При дальнейшем увеличении интерференционные полосы появляются снова, затем снова исчезают и т. д.

Измерив расстояние между отверстиями интерферометра при котором впервые исчезает интерференционная картина, мы получаем возможность с помощью формулы (6) вычислить угловой размер двойной звезды. Как видно из этой формулы, чувствительность прибора тем больше, чем больше может быть сделано расстояние между щелями на объективе.

Оценим, какой минимальный угловой размер двойной звезды можно измерить с помощью интерферометра на базе шестиметрового телескопа: при он равен

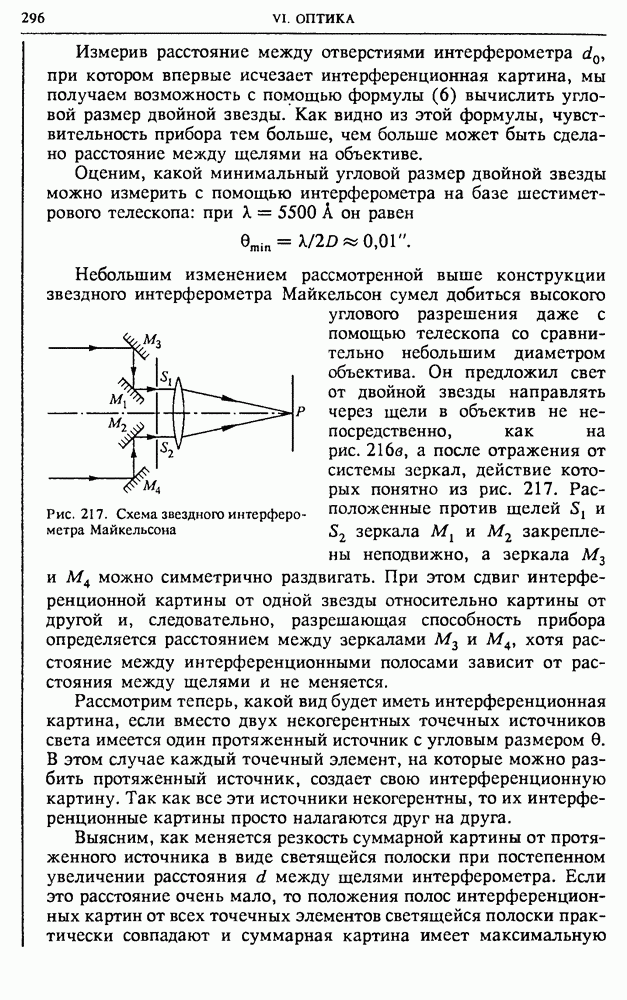
Рис. 217. Схема звездного интерферометра Майкельсона

Небольшим изменением рассмотренной выше конструкции звездного интерферометра Майкельсон сумел добиться высокого углового разрешения даже с помощью телескопа со сравнительно небольшим диаметром объектива. Он предложил свет от двойной звезды направлять через щели в объектив не непосредственно, как на рис. 216а, а после отражения от системы зеркал, действие которых понятно из рис. 217. Расположенные против щелей зеркала и закреплены неподвижно, а зеркала можно симметрично раздвигать. При этом сдвиг интерференционной картины от одной звезды относительно картины от другой и, следовательно, разрешающая способность прибора определяется расстоянием между зеркалами хотя расстояние между интерференционными полосами зависит от расстояния между щелями и не меняется.

Рассмотрим теперь, какой вид будет иметь интерференционная картина, если вместо двух некогерентных точечных источников света имеется один протяженный источник с угловым размером 9. В этом случае каждый точечный элемент, на которые можно разбить протяженный источник, создает свою интерференционную картину. Так как все эти источники некогерентны, то их интерференционные картины просто налагаются друг на друга.

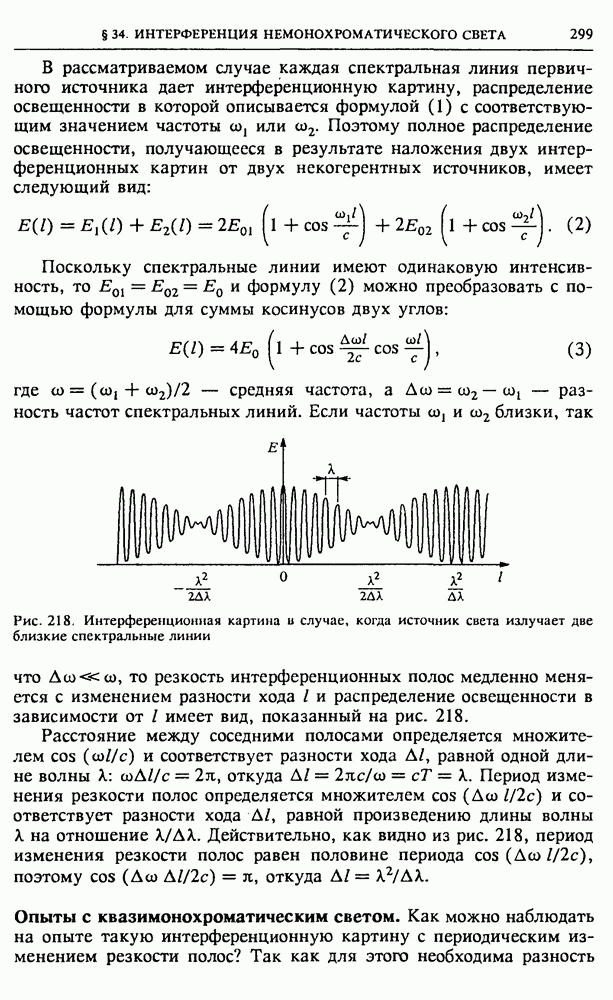
Выясним, как меняется резкость суммарной картины от протяженного источника в виде светящейся полоски при постепенном увеличении расстояния между щелями интерферометра. Если это расстояние очень мало, то положения полос интерференционных картин от всех точечных элементов светящейся полоски практически совпадают и суммарная картина имеет максимальную

резкость. По мере увеличения расстояния резкость картины уменьшается, и при некотором значении полосы пропадают.

Найти можно следующим образом. Мысленно разобьем равномерно светящуюся полоску на пары одинаковых элементов так, чтобы расстояние между элементами любой пары равнялось половине длины полоски. Угловое расстояние между элементами каждой пары, очевидно, равно 9/2. Если положение светлых полос интерференционной картины одного элемента пары совпадает с положением темных полос картины, создаваемой вторым элементом этой пары, то экран оказывается равномерно освещенным, так как условия совпадения одинаковы для всех пар элементов.

Из этих рассуждений следует, что условие исчезновения интерференционных полос от протяженного источника с угловым размером 9 дается той же формулой (6), что и от двух точечных источников, только в ней следует заменить 9 на 9/2:

В случае источника в виде равномерно светящегося диска условие исчезновения интерференционной картины будет отличаться от (7) лишь числовым множителем, близким к единице.

Звездный интерферометр Майкельсона позволяет определять не только угловое расстояние между компонентами двойных звезд, но и угловые диаметры не слишком удаленных одиночных звезд. Первой звездой, у которой Майкельсону удалось измерить угловой диаметр, была Бетельгейзе, относящаяся к так называемым красным гигантам. Он оказался равным Зная расстояние до Бетельгейзе, измеренное по параллаксу, можно было вычислить линейный диаметр звезды, оказавшийся равным примерно км, что превышает диаметр земной орбиты (3-108 км).

Формула (7) определяет допустимые размеры источника при проведении интерференционных опытов по схеме Юнга: угловой размер источника , видимый от щелей в экране, не должен превышать отношения длины волны X к расстоянию между щелями

• Объясните принцип действия звездного интерферометра Майкельсона. Как по наблюдаемой картине отличить двойную звезду от одиночной?

• Почему при увеличении расстояния между зеркалами звездного интерферометра интерференционные полосы от двойной звезды практически исчезают и появляются снова?

• Чем объясняется исчезновение интерференционных полос в звездном интерферометре при увеличении расстояния между зеркалами, если наблюдается одиночная, но очень большая звезда? Как из этих наблюдений можно оценить ее угловой размер?

• При какой максимальной ширине источника света в виде узкой полоски можно наблюдать интерференционные полосы в опыте Юнга, если расстояние между щелями мм, расстояние от источника до щелей а длина волны