| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 14. Работа и мощность постоянного тока
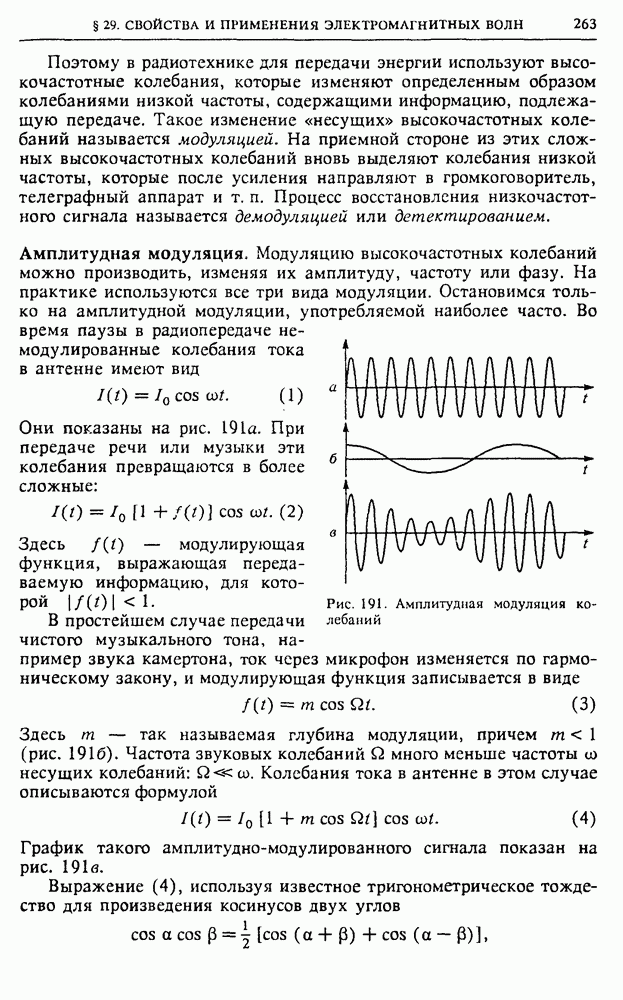
При прохождении тока, т. е. при упорядоченном движении носителей заряда в проводнике, действующее на них электрическое поле, определяемое приложенным к концам проводника напряжением, совершает работу. Эту работу обычно называют работой электрического тока.
Работа сил электрического поля при перемещении носителей заряда равна произведению переносимого заряда  на разность потенциалов
на разность потенциалов  между теми точками, где перемещается заряд:
между теми точками, где перемещается заряд:

При постоянном токе  — время, в течение которого переносится заряд
— время, в течение которого переносится заряд  Поэтому работа постоянного тока
Поэтому работа постоянного тока  за время
за время  на участке цепи, на концах которого поддерживается напряжение
на участке цепи, на концах которого поддерживается напряжение  определяется соотношением
определяется соотношением

Мощность Р электрического тока, определяемая работой, совершаемой за единицу времени, равна

Электрический ток, совершая работу, может раскалять нить электролампы, вращать якорь электродвигателя, плавить металлы, вызывать химические превращения, заряжать аккумулятор и т. д. Во всех этих случаях работа тока определяет меру превращения электрической энергии в другие формы — внутреннюю энергию теплового движения, механическую энергию и т. д.
Работа электрического тока измеряется в тех же единицах, что и механическая работа. Это  в системе СГСЭ и 1 Дж в
в системе СГСЭ и 1 Дж в 

Мощность измеряется в ваттах:  . Часто используются кратные единицы
. Часто используются кратные единицы  (киловатт)
(киловатт)  (мегаватт)
(мегаватт)  Вт. Для работы тока часто используется внесистемная единица
Вт. Для работы тока часто используется внесистемная единица  (киловатт-час) — работа, совершаемая за 1 час при развиваемой мощности
(киловатт-час) — работа, совершаемая за 1 час при развиваемой мощности 
Закон Джоуля-Ленца. Прохождение электрического тока через проводник, обладающий сопротивлением, всеща сопровождается выделением теплоты. Количество выделившейся за время  теплоты определяется законом Джоуля—Ленца:
теплоты определяется законом Джоуля—Ленца:

В случае однородного участка, коща  формулы (2) и (4) совпадают, т. е. количество выделяющейся теплоты равно работе тока, и работу тока можно выразить любым из эквивалентных способов:
формулы (2) и (4) совпадают, т. е. количество выделяющейся теплоты равно работе тока, и работу тока можно выразить любым из эквивалентных способов:

В однородном участке цепи, например в резисторе, работа тока сводится только к выделению теплоты.
В качестве примера рассмотрим какой-нибудь электронагревательный прибор, отдающий выделяющуюся теплоту в окружающую среду. Скорость теплопередачи, т. е. количества теплоты, отдаваемой нагретым элементом в единицу времени, пропорциональна разности температур  между нацзетым телом и окружающей средой:
между нацзетым телом и окружающей средой:

Коэффициент к зависит от свойств тела (площади поверхности, размеров и формы). Будем считать его значение известным. Выделяющуюся джоулеву теплоту можно подсчитать по любой из формул (5). Поскольку обычно нагревательный прибор включается в сеть с заданным напряжением, то удобно воспользоваться выражением

Сразу после включения выделяющаяся джоулева теплота превосходит отдаваемую окружающей среде, так как происходит нагревание самого прибора. В конце концов устанавливается такая его температура Т, при которой Р и  сравниваются наступает стационарное состояние, в котором разность температур
сравниваются наступает стационарное состояние, в котором разность температур  прибора и окружающей среды уже не меняется.
прибора и окружающей среды уже не меняется.
Если сопротивление нагреваемого током элемента не зависит от температуры, то, приравнивая значения Р и  немедленно получаем выражение для установившейся разности температур:
немедленно получаем выражение для установившейся разности температур:

Однако в действительности, как правило, сопротивление зависит от температуры. Для металлической проволоки эту зависимость можно считать линейной (см. § 10):

где с хорошей точностью под  можно понимать сопротивление при температуре
можно понимать сопротивление при температуре  окружающей среды. Если учитывать эту зависимость сопротивления от температуры, то, приравнивая Р и
окружающей среды. Если учитывать эту зависимость сопротивления от температуры, то, приравнивая Р и  приходим уже к квадратному уравнению для
приходим уже к квадратному уравнению для 

Имеющий физический смысл корень этого уравнения можно представить в следующем виде:

В условиях, когда  мало, т. е. превышение температуры нагревательного элемента прибора над окружающей средой невелико, второй
мало, т. е. превышение температуры нагревательного элемента прибора над окружающей средой невелико, второй
член в подкоренном выражении мал по сравнению с единицей и можно воспользоваться приближенной формулой  При этом получаем прежний результат
При этом получаем прежний результат 
В другом предельном случае больших  (как, например, у лампочки накаливания, температура нити которой составляет несколько тысяч градусов), можно, наоборот, в подкоренном выражении пренебречь единицей по сравнению со вторым членом. При этом для
(как, например, у лампочки накаливания, температура нити которой составляет несколько тысяч градусов), можно, наоборот, в подкоренном выражении пренебречь единицей по сравнению со вторым членом. При этом для  приближенно получаем
приближенно получаем

— разность температур теперь пропорциональна не квадрату, а первой степени приложенного напряжения.
В неоднородных участках цепи, где ток определяется формулой  выделяющаяся теплота не равна работе тока. Это означает, что протекание тока в таком участке сопровождается не только выделением теплоты, но и другими процессами, связанными с превращением энергии.
выделяющаяся теплота не равна работе тока. Это означает, что протекание тока в таком участке сопровождается не только выделением теплоты, но и другими процессами, связанными с превращением энергии.
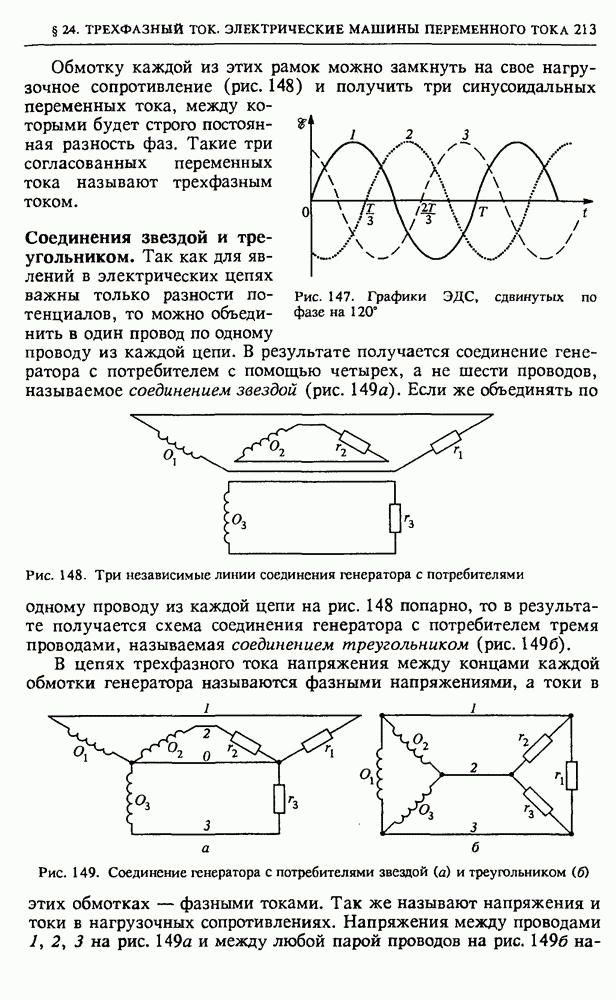
Зарядка аккумулятора. В качестве примера энергетических превращений в неоднородной цепи рассмотрим зарядку аккумулятора. Не вдаваясь в детали происходящих в аккумуляторе процессов, а только учитывая, что при зарядке все химические процессы внутри него идут «вспять», легко сообразить, что ток идет в направлении, противоположном току при разрядке, когда аккумулятор является источником питания для внешней цепи. Поэтому аккумулятор включается в цепь так, как показано на рис. 86, а ток в цепи идет в направлении, указанном стрелкой. Так как ЭДС аккумулятора (сумма скачков потенциала внутри него) понижает потенциал в цепи в направлении протекания тока, то, в соответствии с законом Ома для неоднородного участка, ток в цепи равен


Рис. 86. Схема включения аккумулятора на зарядку
В этой формуле  — внутреннее сопротивление аккумулятора, а сопротивление
— внутреннее сопротивление аккумулятора, а сопротивление  включено в цепь для регулировки зарядного тока. Легко видеть, что ток будет положительным и, следовательно, пойдет в указанном направлении только при условии, что подаваемое напряжение
включено в цепь для регулировки зарядного тока. Легко видеть, что ток будет положительным и, следовательно, пойдет в указанном направлении только при условии, что подаваемое напряжение  больше электродвижущей силы аккумулятора
больше электродвижущей силы аккумулятора  . Только при выполнении этого условия и можно зарядить аккумулятор.
. Только при выполнении этого условия и можно зарядить аккумулятор.
Работа, совершаемая зарядной станцией (т. е. внешним источником напряжения  в единицу времени, т. е. работа тока на всем рассматриваемом участке, равна
в единицу времени, т. е. работа тока на всем рассматриваемом участке, равна  На всех сопротивлениях,
На всех сопротивлениях,
включая внутреннее сопротивление аккумулятора, в единицу времени выделяется джоулева теплота, равная  . Кроме зарядки аккумулятора и выделения теплоты других энергетических превращений в рассматриваемой цепи не происходит. Поэтому на основании закона сохранения энергии можно утверждать, что
. Кроме зарядки аккумулятора и выделения теплоты других энергетических превращений в рассматриваемой цепи не происходит. Поэтому на основании закона сохранения энергии можно утверждать, что

где Рзар — мощность, идущая непосредственно на зарядку аккумулятора. Подставляя в (7) выражение для силы тока (6), получаем

Таким образом, при зарядке аккумулятор в единицу времени запасает энергию, равную 14. Разумеется, этого результата можно было ожидать из элементарных соображений: ведь процессы в аккумуляторе считаются обратимыми, а при разрядке аккумулятор развивает мощность 
Обратим внимание, что, считая известными выражения для полной работы тока, для джоулевой теплоты и для работы зарядки аккумулятора, можно с помощью закона сохранения энергии получить выражение (6) для тока в цепи. Для этого нужно просто подставить в  Это значит, что закон Ома для неоднородного участка можно получить как следствие закона сохранения энергии.
Это значит, что закон Ома для неоднородного участка можно получить как следствие закона сохранения энергии.
Работа источника тока. Источник тока — это устройство, поддерживающее разность потенциалов на концах подключенной к нему электрической цепи. Это происходит благодаря действию сторонних сил — сил неэлектростатической природы. Какие энергетические превращения при этом происходят?
Как мы видели, ЭДС  источника равна сумме напряжений во внешнем
источника равна сумме напряжений во внешнем  и внутреннем
и внутреннем  участках цепи:
участках цепи:

Домножим обе части этого равенства на заряд  проходящий по цепи за время
проходящий по цепи за время  В левой части получившегося равенства будет стоять сумма работ электрического тока во внешнем и во внутреннем участках цепи. Справа будет стоять произведение
В левой части получившегося равенства будет стоять сумма работ электрического тока во внешнем и во внутреннем участках цепи. Справа будет стоять произведение 
Электрический ток совершает работу за счет действия источника, т. е. сторонних сил. По закону сохранения энергии работа тока в цепи равна работе, совершаемой за это же время источником тока, т. е. работе действующих в нем сторонних сил.
Определение ЭДС. Итак, работа источника тока при перемещении по цепи заряда  равна
равна  Поэтому электродвижущей силе источника можно дать и такое определение: электродвижущей силой называется величина, равная отношению работы Лстор сторонних сил
Поэтому электродвижущей силе источника можно дать и такое определение: электродвижущей силой называется величина, равная отношению работы Лстор сторонних сил
при перемещении по цепи заряда  к этому заряду:
к этому заряду:

Поскольку работа источника тока равна  то развиваемая им мощность
то развиваемая им мощность

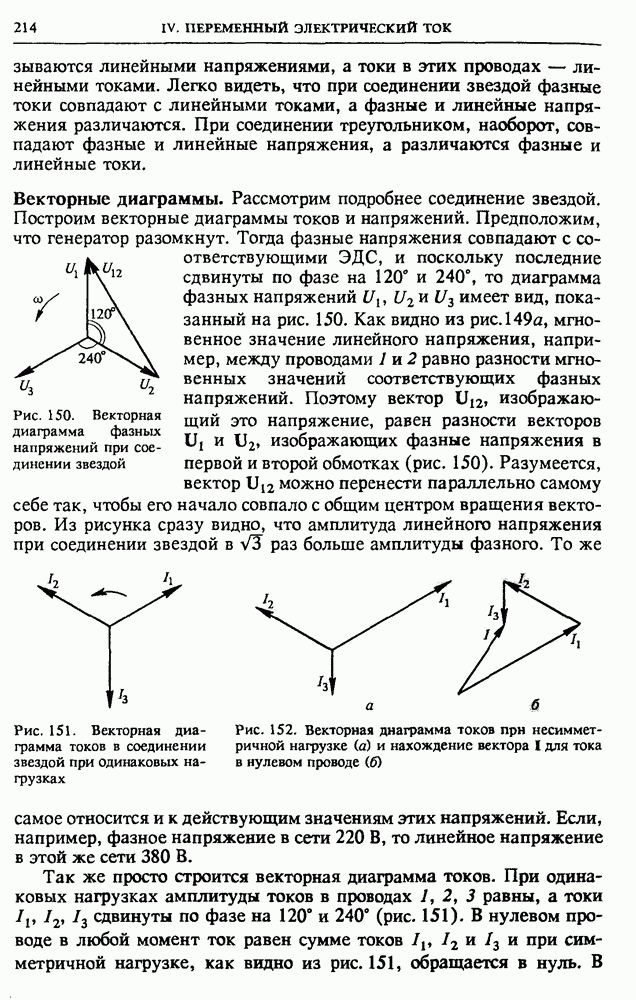
Мощность и КПД источника тока. Выясним, каким должно быть сопротивление нагрузки  для того, чтобы получить максимальную силу тока в цепи, максимальную полезную мощность, максимальный коэффициент полезного действия.
для того, чтобы получить максимальную силу тока в цепи, максимальную полезную мощность, максимальный коэффициент полезного действия.
Ток в цепи (рис. 87) определяется законом Ома:  Поэтому полная мощность Р, развиваемая источником тока, равна
Поэтому полная мощность Р, развиваемая источником тока, равна  . Полезная мощность
. Полезная мощность  т. е. мощность, выделяющаяся на нагрузке
т. е. мощность, выделяющаяся на нагрузке  дается соотношением
дается соотношением

Коэффициент полезного действия  источника в этой цепи, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки:
источника в этой цепи, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки:

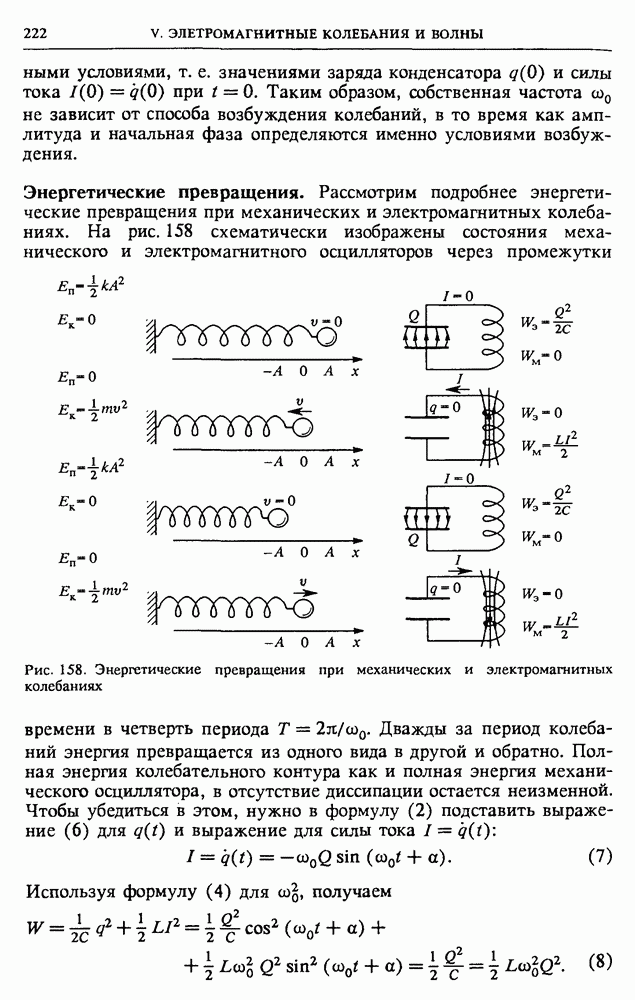
Исследуем полученные выражения. Полная мощность Р и ток в цепи I различаются постоянным множителем  поэтому их зависимость от сопротивления нагрузки
поэтому их зависимость от сопротивления нагрузки  одинакова (кривая 1 на рис. 88).
одинакова (кривая 1 на рис. 88).

Рис. 87. К исследованию условий работы источника тока

Рис. 88. Зависимость мощности и КПД источника тока от сопротивления нагрузки
Максимальным значение этих величин будет при  т. е. при коротком замыкании источника. Как видно из формул (12) и (13), при этом равны нулю полезная мощность
т. е. при коротком замыкании источника. Как видно из формул (12) и (13), при этом равны нулю полезная мощность  и коэффициент полезного действия
и коэффициент полезного действия  При
При  полная мощность и ток равны половине своего максимального значения, коэффициент полезного действия
полная мощность и ток равны половине своего максимального значения, коэффициент полезного действия  равен 0,5, а полезная мощность достигает своего максимального значения,
равен 0,5, а полезная мощность достигает своего максимального значения,
равного половине мощности Р при этой нагрузке. Для того чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность максимальна, преобразуем правую часть выражения (12) следующим образом:

Полезная мощность будет максимальной, когда знаменатель правой части выражения (14) минимален. Преобразуем знаменатель:

Функция (15) достигает минимума тогда, когда выражение в скобках равно нулю, т. е. при  Этот результат можно, разумеется, получить, приравнивая нулю производную по
Этот результат можно, разумеется, получить, приравнивая нулю производную по  знаменателя правой части выражения (14).
знаменателя правой части выражения (14).
При неограниченном увеличении сопротивления нагрузки  как полная, так и полезная мощность стремится к нулю (кривая 2), а коэффициент полезного действия — к единице (кривая 3).
как полная, так и полезная мощность стремится к нулю (кривая 2), а коэффициент полезного действия — к единице (кривая 3).
Из рис. 87 видно, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального КПД противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и КПД: почти вся совершаемая источником тока работа идет на выделение теплоты на внутреннем сопротивлении  Чтобы получить от данного источника тока максимальную полезную мощность, следует взять нагрузку с сопротивлением
Чтобы получить от данного источника тока максимальную полезную мощность, следует взять нагрузку с сопротивлением  равным внутреннему сопротивлению источника. Значение максимальной полезной мощности
равным внутреннему сопротивлению источника. Значение максимальной полезной мощности  но коэффициент полезного действия при этом равен всего лишь 0,5.
но коэффициент полезного действия при этом равен всего лишь 0,5.
Любую полезную мощность  меньшую максимальной, можно получить, как свидетельствует ход кривой 2 на рис. 88, при двух значениях
меньшую максимальной, можно получить, как свидетельствует ход кривой 2 на рис. 88, при двух значениях  сопротивления нагрузки. Практически для получения заданной полезной мощности следует выбирать нагрузку с большим сопротивлением
сопротивления нагрузки. Практически для получения заданной полезной мощности следует выбирать нагрузку с большим сопротивлением  так как КПД при этом выше. Для получения КПД, близкого к единице, следует брать нагрузку с сопротивлением, много большим внутреннего сопротивления источника тока, но при этом выделяющаяся мощность
так как КПД при этом выше. Для получения КПД, близкого к единице, следует брать нагрузку с сопротивлением, много большим внутреннего сопротивления источника тока, но при этом выделяющаяся мощность  .
.
• Работа каких сил имеется в виду, когда говорят о работе, совершаемой электрическим током?
• В каких случаях работа электрического тока  не равна выделяющейся в цепи джоулевой теплоте
не равна выделяющейся в цепи джоулевой теплоте 
• Для зарядки аккумулятора с ЭДС его включили в сеть с постоянным напряжением  Какая доля потребляемой от сети энергии запасается в аккумуляторе?
Какая доля потребляемой от сети энергии запасается в аккумуляторе?
• Каким образом работа сторонних сил связана с ЭДС источника тока? Аргументируйте свой ответ.
• Какой должна быть нагрузка, чтобы источник тока развивал максимальную полезную мощность? Каким при этом будет его КПД?
• Почему условия получения максимальной полезной мощности и максимального КПД от данного источника тока противоречат друг другу?
• Покажите, что два значения сопротивления нагрузки и  при которых в нагрузке выделяется одинаковая джоулева теплота, связаны соотношением
при которых в нагрузке выделяется одинаковая джоулева теплота, связаны соотношением  где
где  — внутреннее сопротивление источника тока.
— внутреннее сопротивление источника тока.
• Постройте графики зависимости мощности источника тока, полезной мощности и КПД от силы тока I в цепи.
Поле сторонних сил. Работа, совершаемая электрическим током при прохождении заряда по всей цепи, равна работе действующих в источнике сторонних сил. Поэтому ЭДС можно выразить через эти силы.
Введем новую величину Естор, которую назовем напряженностью поля сторонних сил. Это сила, действующая на единичный положительный заряд, обусловлена любыми причинами, кроме электростатического поля. Тогда полная сила, действующая на заряд, будет складываться из электростатической силы и сторонней силы:

Рассмотрим замкнутую цепь и рассчитаем полную работу, совершаемую всеми действующими на заряд силами при его перемещении по всей цепи. Работа электростатических сил на замкнутом контуре равна нулю, так как эти силы — потенциальные. Поэтому полная работа на замкнутом контуре равна работе только сторонних сил. Именно эта работа и определяет ЭДС источника тока.
Обратим внимание на кажущееся противоречие. Работа тока — это по определению работа сил электрического поля. В то же время, как мы видели, работа тока во всей цепи равна работе источника, т. е. работе сторонних сил. Но как мы только что выяснили, работа электростатического поля равна нулю. Как все это согласовать?
Дело в том, что, говоря о работе электрического тока, мы имели в виду работу электрических сил не на всем замкнутом пути, а только на тех участках цепи, где заряды движутся под действием электрических сил. Мы не включали работу электрических сил в местах скачков потенциала (где и действуют
сторонние силы), т. е. в местах, где электрическое поле направлено противоположно движению положительных зарядов. Именно в этих местах внутри источника тока движение зарядов против сил электрического поля обусловлено действием сторонних сил. Если учесть работу электрических сил и в этих местах, то полная их работа действительно будет равна нулю.
Здесь можно привести следующую механическую аналогию. Лыжник спускается с горы и, сделав круг, возвращается к ее подножию, а затем с помощью подъемника снова поднимается на вершину. Аналогом потенциального электростатического поля здесь является поле силы тяжести. Роль сторонних сил играют силы, поднимающие его наверх в подъемнике. Очевидно, что полная работа силы тяжести на всем замкнутом пути равна нулю. Однако в данном случае она не представляет интереса. Важна лишь та работа сил тяжести, что совершается при движении лыжника от вершины горы до ее основания. Эта работа как раз и равна работе «сторонних» сил, действующих на лыжника в подъемнике.
Работа и теплота в произвольной цепи. В неоднородном участке цепи, содержащем источник с ЭДС и внутренним сопротивлением  когда
когда  , для работы тока А, работы источника
, для работы тока А, работы источника  и выделяющейся теплоты
и выделяющейся теплоты  имеем
имеем

Выделяющаяся теплота равна сумме работы тока и работы источника:

Подчеркнем, что эти формулы справедливы во всех случаях, независимо от того, идет ли ток через источник в «естественном» направлении, когда он отдает энергию во внешнюю цепь, или в противоположном, как это бывает при зарядке аккумулятора, когда он потребляет энергию (в этом случае I и Ч имеют противоположные знаки и Лист  При этом теплота
При этом теплота  окажется во всех случаях положительной.
окажется во всех случаях положительной.
Как связаны между собой работа сторонних сил и работа сил электрического поля при переносе заряда вдоль всей замкнутой цепи?
Поясните аналогию между работой электрических и сторонних сил и работой силы тяжести и «подъемной» силы при катании лыжника на горе с подъемником.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
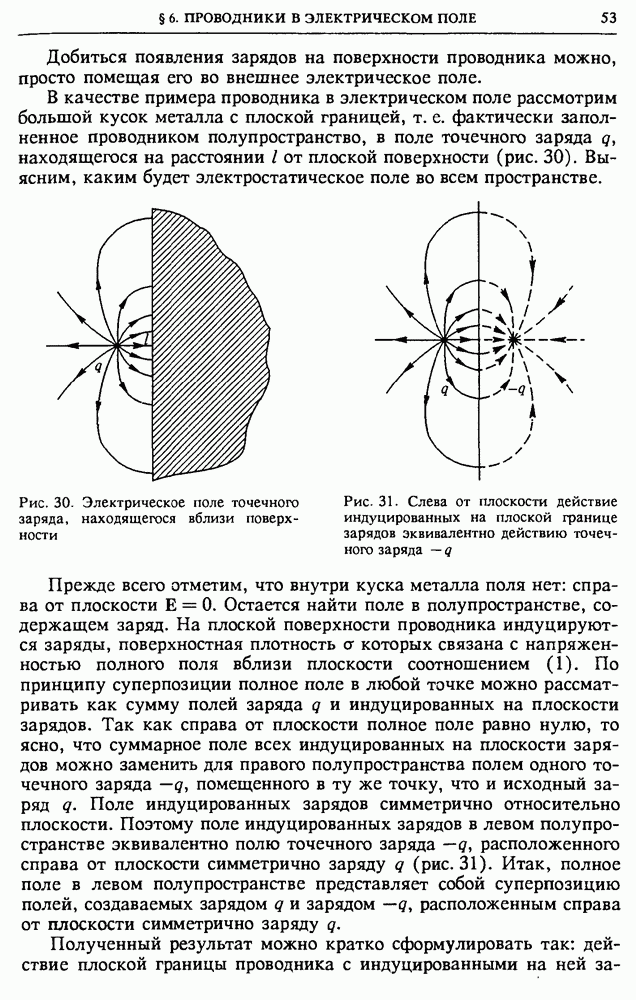
- § 6. Проводники в электрическом поле
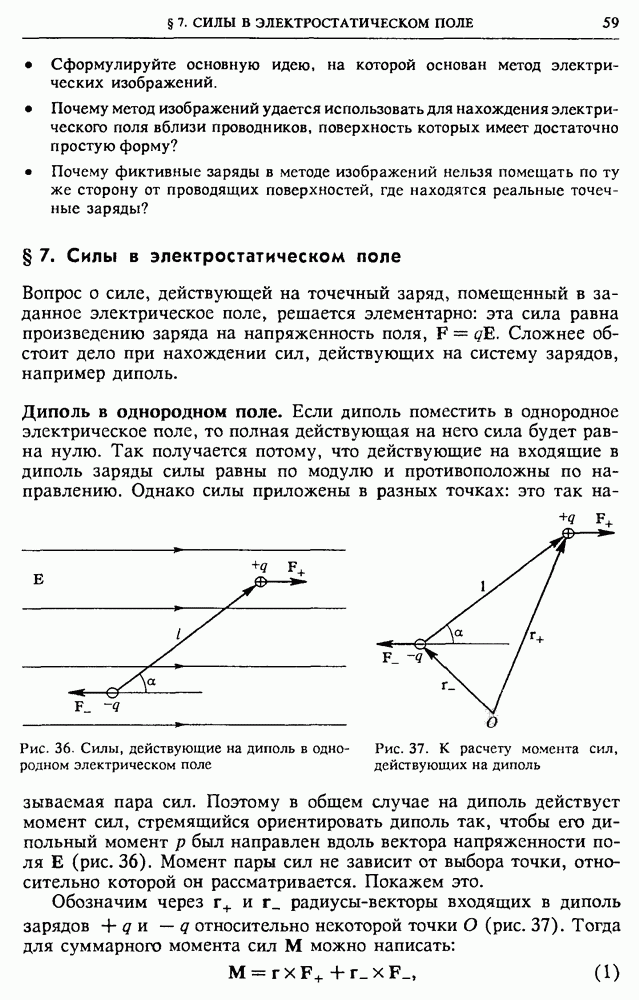
- § 7. Силы в электростатическом поле
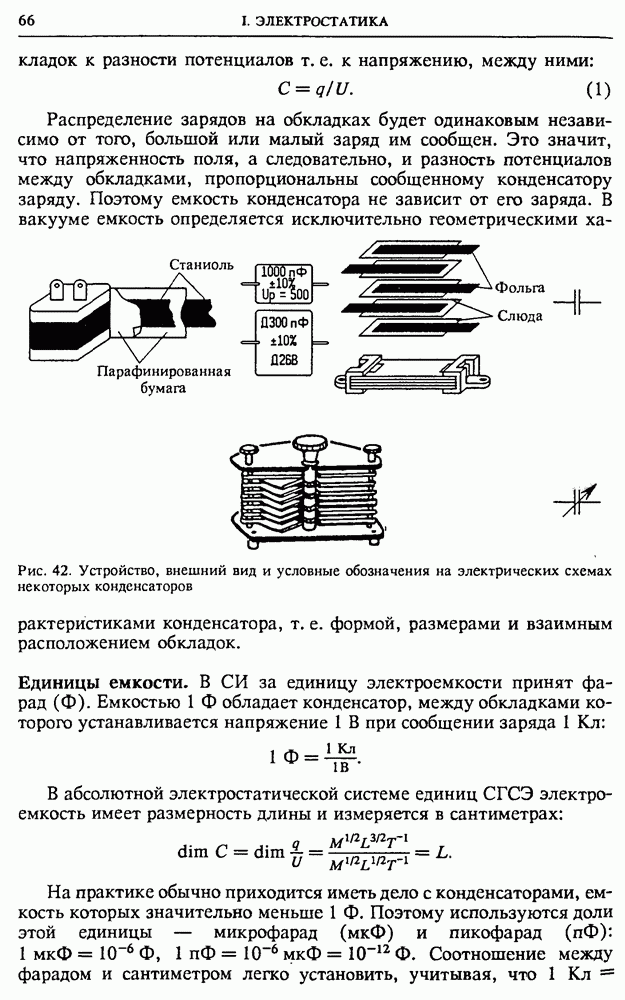
- § 8. Конденсаторы. Электроемкость
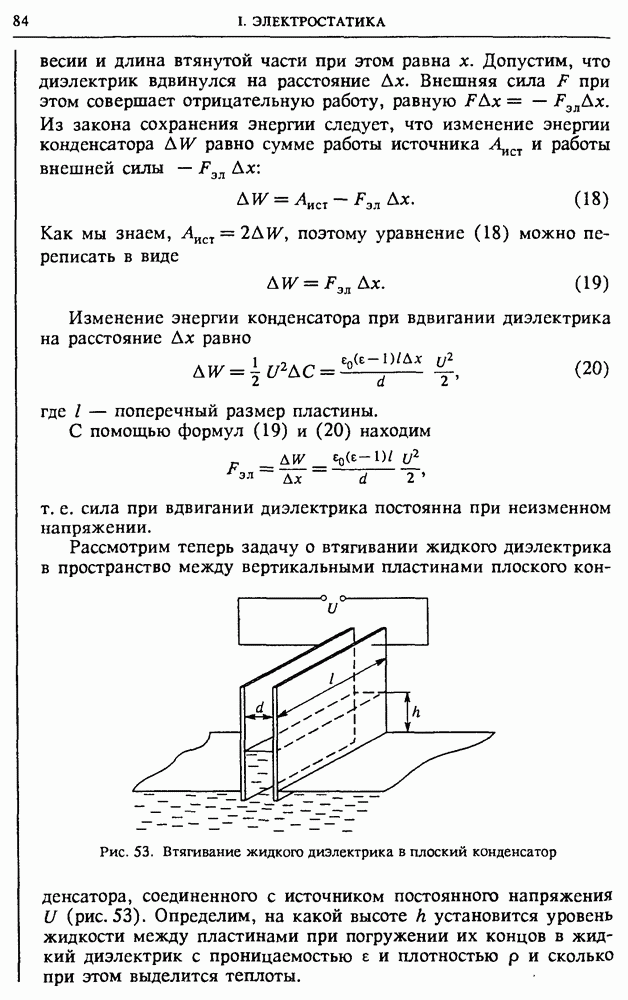
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
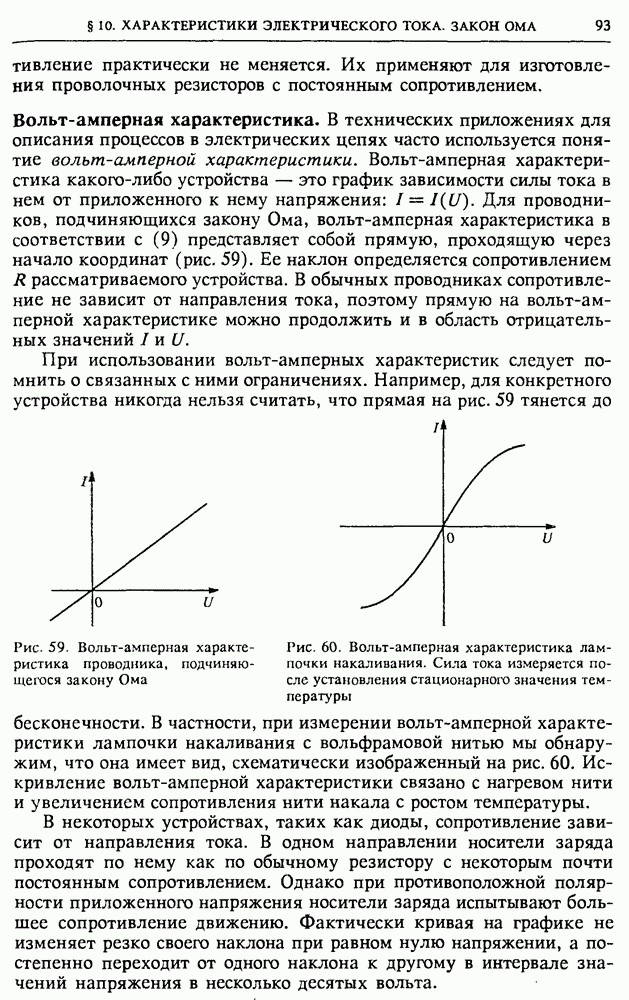
- § 10. Характеристики электрического тока. Закон Ома
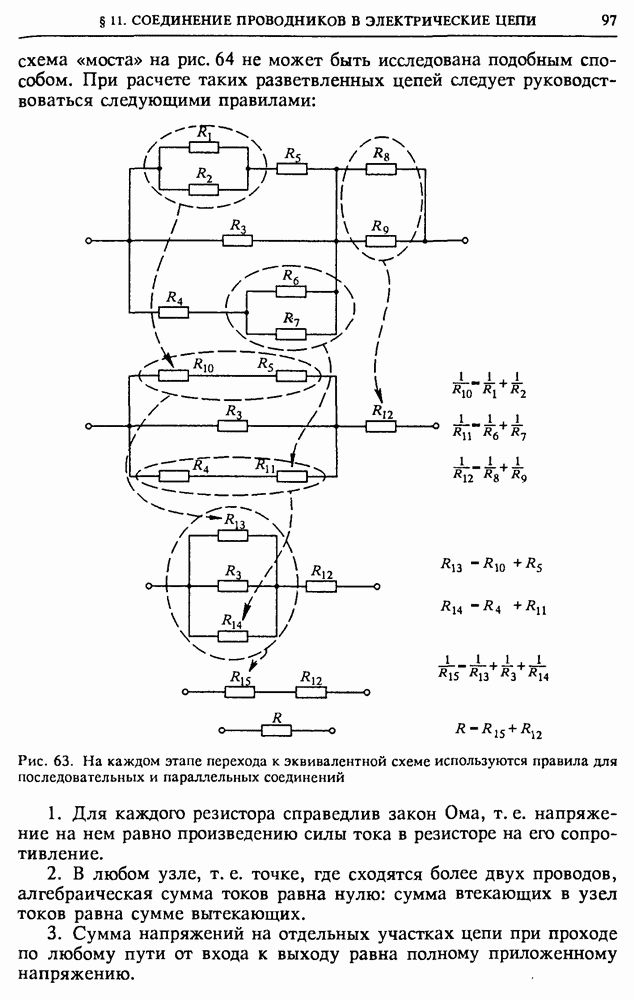
- § 11. Соединение проводников в электрические цепи
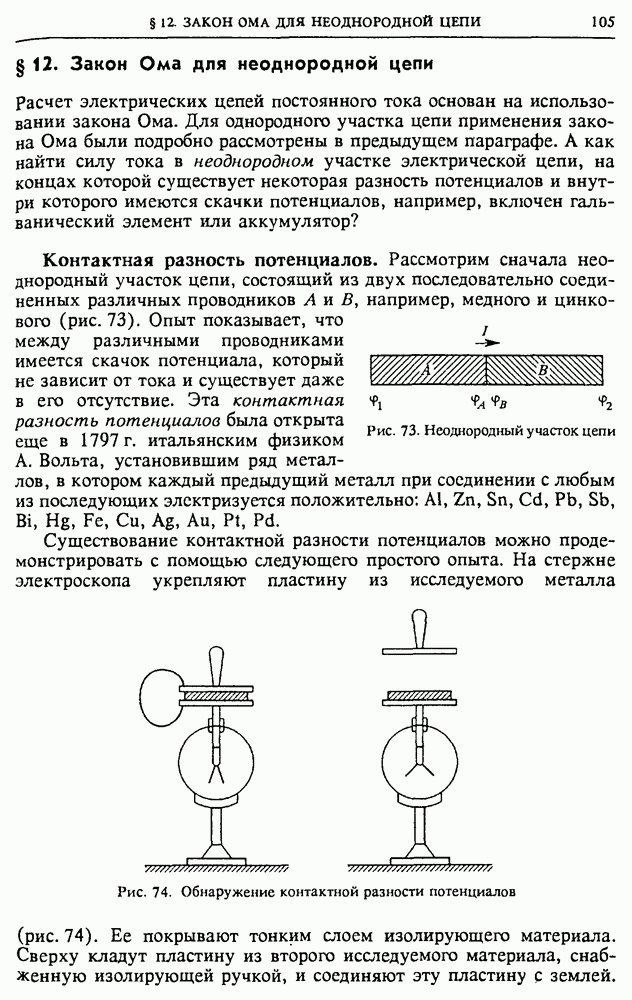
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
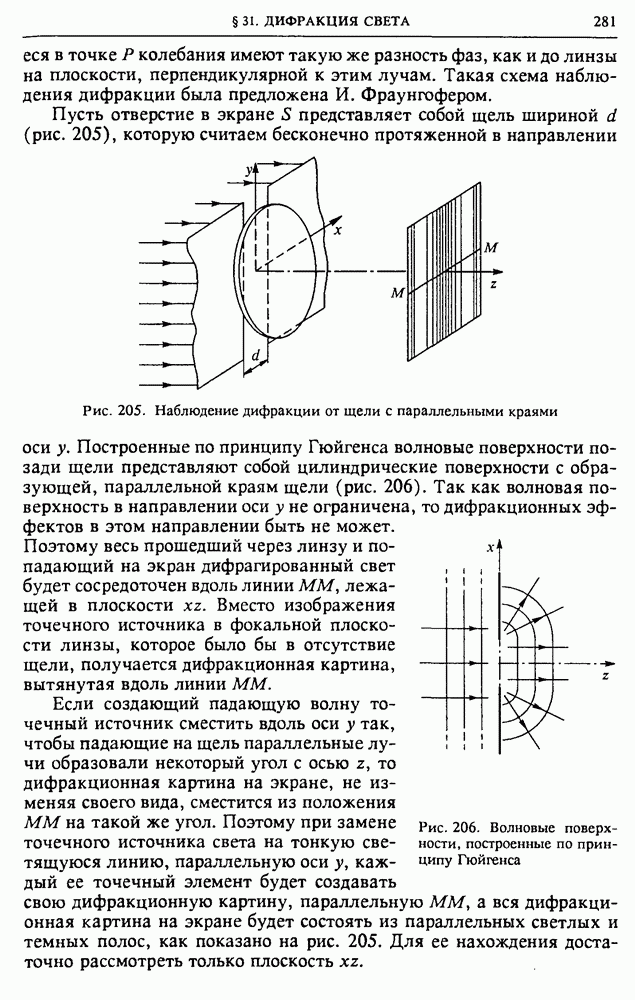
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение