| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 21. Квазистационарные явления в электрических цепях
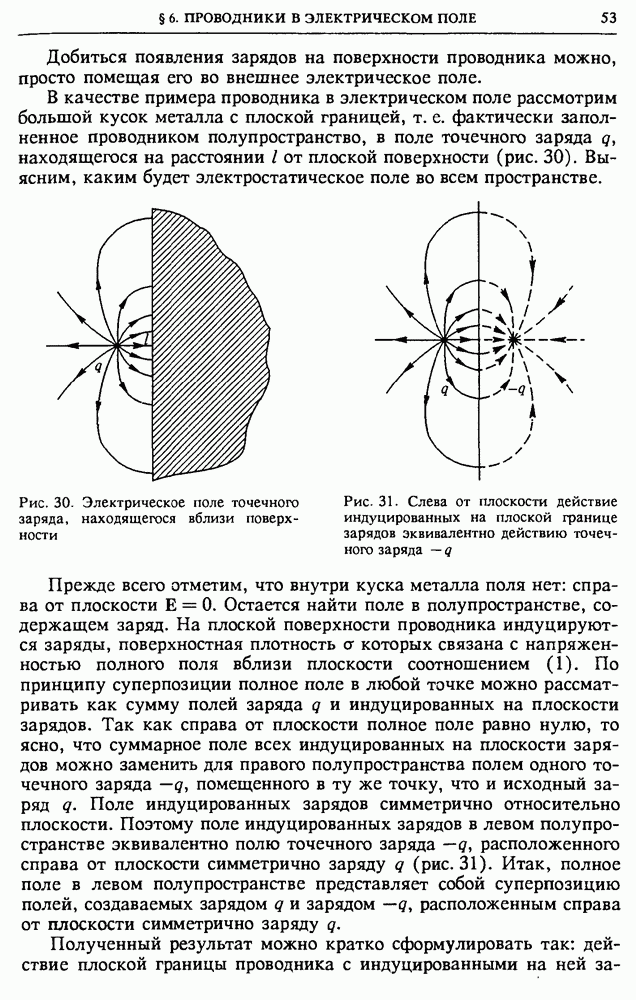
До сих пор при изучении электромагнитных явлений мы подробно исследовали случаи, соответствующие электрическому полю неподвижных зарядов и магнитному полю постоянных токов. Такие электрическое и магнитное поля существуют независимо и не связаны друг с другом. Тем не менее большинство установленных законов справедливы и для более общих случаев, когда происходят взаимные превращения электрического и магнитного полей.
Наиболее простые явления, связанные с изменяющимися электрическим или магнитным полями — это так называемые квазистационарные явления в электрических цепях, содержащих резисторы, конденсаторы и катушки индуктивности.
В действительности любой проводник обладает и сопротивлением, и емкостью, и индуктивностью. Но на практике различие, например, в индуктивности катушки и линейного проводника
настолько велико, что с хорошей точностью можно использовать модель цепи с сосредоточенными параметрами, т. е. считать, что каждый элемент цепи обладает только одной из этих трех характеристик.
Именно такие цепи широко используются в электротехнике, радиотелевизионной технике и микроэлектронике.
Условия квазистационарности. Будем называть явления в электрической цепи квазистационарными, если во всех ее последовательно соединенных участках силу тока в один и тот же момент времени можно считать одинаковой. В этом приближении пренебрегается конечностью скорости распространения электромагнитного поля вдоль проводов, образующих цепь. Например, при замыкании ключа ток появляется сразу, т. е. одновременно, в любом поперечном сечении, даже удаленном от источника, несмотря на то, что электроны из источника тока могут дойти до него спустя значительный промежуток времени.
Цепь с активным сопротивлением. Изучение квазистационарных явлений начнем с простейшего случая, когда изменяющееся со временем напряжение прикладывается к концам цепи, содержащей только резисторы, т. е. обычные сопротивления  Сила тока в цепи будет даваться таким же выражением, как при приложенном постоянном напряжении:
Сила тока в цепи будет даваться таким же выражением, как при приложенном постоянном напряжении:

Равенство (1) представляет собой закон Ома для цепи, содержащей только обычное сопротивление  называемое активным. При приложении к его концам переменного напряжения
называемое активным. При приложении к его концам переменного напряжения  ток в цепи изменяется по такому же закону, что и приложенное напряжение. Связывающий
ток в цепи изменяется по такому же закону, что и приложенное напряжение. Связывающий  постоянный множитель
постоянный множитель  — это то же самое сопротивление, что и для постоянного тока. Например, когда приложенное напряжение зависит от времени по гармоническому (синусоидальному) закону
— это то же самое сопротивление, что и для постоянного тока. Например, когда приложенное напряжение зависит от времени по гармоническому (синусоидальному) закону

сила тока в соответствии с (1) дается выражением

Ток в цепи изменяется в фазе с приложенным напряжением.
При прохождении тока, изменяющегося со временем, через активное сопротивление, происходит выделение теплоты в соответствии с законом Джоуля—Ленца. Это означает, что в резисторе происходит необратимое превращение (диссипация) электрической энергии во внутреннюю энергию.
В цепях, содержащих конденсаторы и катушки индуктивности, дело обстоит сложнее. В общем случае изменяющаяся со временем
сила тока не повторяет временной зависимости приложенного напряжения. Изучение этого вопроса начнем с частного случая, когда синусоидальное напряжение (2) прикладывается к цепи, содержащей только емкость С или только индуктивность 
Емкостное сопротивление. В цепи, содержащей только емкость С, силу тока проще всего найти, воспользовавшись тем, что в квазистационарном случае она определяется скоростью изменения заряда конденсатора:  Так как
Так как  а емкость конденсатора постоянна, то для силы тока получаем
а емкость конденсатора постоянна, то для силы тока получаем

Таким образом, ток в цепи имеет синусоидальный характер и опережает по фазе приложенное напряжение на 

Связи между амплитудными значениями подаваемого напряжения  и тока в цепи
и тока в цепи  можно, как видно из (4), придать вид закона Ома, если ввести понятие зависящего от частоты
можно, как видно из (4), придать вид закона Ома, если ввести понятие зависящего от частоты  емкостного сопротивления
емкостного сопротивления 

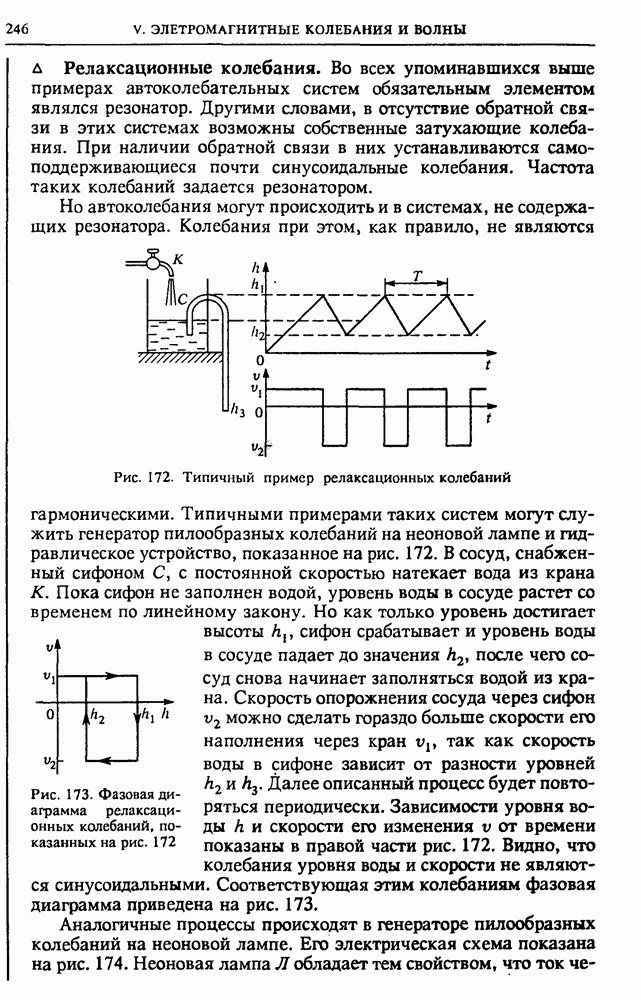
Полученный результат можно наглядно проиллюстрировать с помощью графиков зависимости напряжения и тока от времени (рис. 128). В те моменты времени, когда подаваемое напряжение достигает экстремальных значений, заряд на конденсаторе не меняется и, следовательно, ток в цепи обращается в нуль. В точках, где напряжение обращается в нуль, его значение меняется наиболее быстро и, следовательно, ток достигает экстремальных значений.

Рис. 128. Напряжение и ток в конденсаторе
Итак, физическая причина сдвига по фазе очевидна, величина сдвига равна  а направление сдвига (опережение или отставание по фазе) легко установить, рассматривая, например, первую четверть периода изменения напряжения: оно убывает, т. е. конденсатор разряжается, несмотря на то, что ток увеличивается по абсолютной величине. Это возможно, только если напряжение и ток имеют противоположные знаки, т. е. график тока действительно имеет вид, изображенный на рис. 128.
а направление сдвига (опережение или отставание по фазе) легко установить, рассматривая, например, первую четверть периода изменения напряжения: оно убывает, т. е. конденсатор разряжается, несмотря на то, что ток увеличивается по абсолютной величине. Это возможно, только если напряжение и ток имеют противоположные знаки, т. е. график тока действительно имеет вид, изображенный на рис. 128.
При прохождении электрического тока через конденсатор не происходит диссипации электрической энергии: при зарядке
конденсатора в нем накапливается энергия, а при разрядке эта энергия возвращается в электрическую цепь.
Индуктивное сопротивление. Случай, когда синусоидальное напряжение подается на индуктивность  проще всего проанализировать, сравнивая выражения
проще всего проанализировать, сравнивая выражения

Первая формула представляет собой выражение для тока в только что рассмотренной цепи, содержащей емкость С. Второе соотношение отражает тот факт, что поданное на индуктивность  синусоидальное напряжение
синусоидальное напряжение  в каждый момент времени компенсирует возникающую в катушке электродвижущую силу самоиндукции
в каждый момент времени компенсирует возникающую в катушке электродвижущую силу самоиндукции  Анализ первого из соотношений (6) привел к формуле (4). Следовательно, формула такого же типа будет получена при анализе второго из соотношений (6). Она получается из (4) заменой
Анализ первого из соотношений (6) привел к формуле (4). Следовательно, формула такого же типа будет получена при анализе второго из соотношений (6). Она получается из (4) заменой 

Из первого соотношения (6) следует, что ток  опережает напряжение
опережает напряжение  на
на  аналогично, из второго следует, что в такой цепи напряжение опережает ток на
аналогично, из второго следует, что в такой цепи напряжение опережает ток на  Задаваемой величиной является подаваемое напряжение
Задаваемой величиной является подаваемое напряжение  поэтому для тока
поэтому для тока  из (7) получаем
из (7) получаем


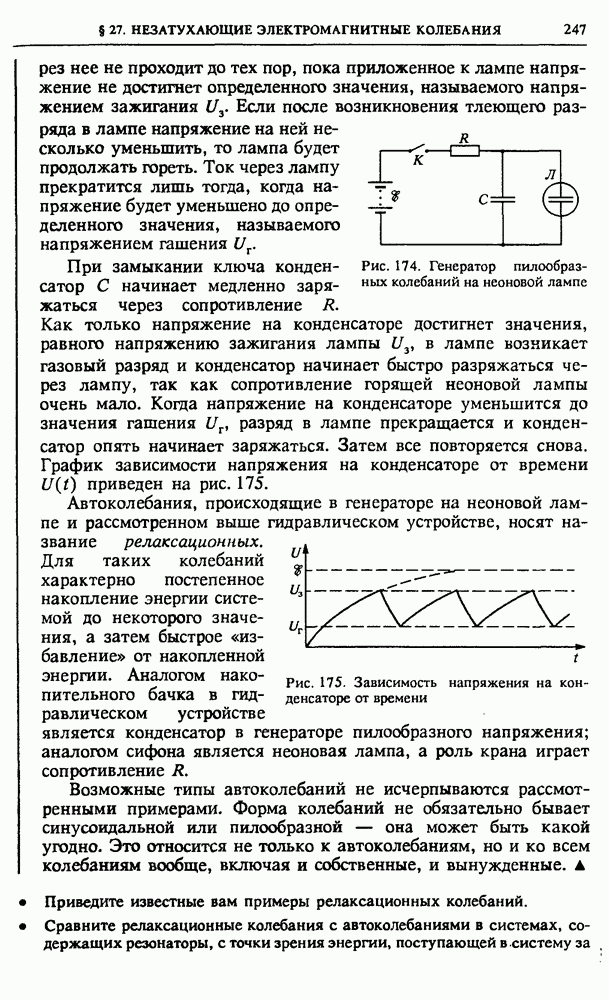
Рис. 129. Ток, ЭДС самоиндукции и напряжение на индуктивности
Как и раньше, связи между амплитудными значениями тока и напряжения можно придать вид закона Ома, если, воспользовавшись (7), ввести индуктивное сопротивление 

Полученный результат также можно проиллюстрировать с помощью графиков (рис. 129). На верхнем графике показана зависимость тока от времени. На втором графике изображена ЭДС самоиндукции. Положение экстремумов и сдвиг этого графика относительно графика тока легко определить с помощью закона электромагнитной индукции и закона Ленца: 
Действительно, ЭДС самоиндукции обращается в нуль в точках экстремума тока и достигает экстремальных значений в те
моменты, когда ток меняется наиболее быстро. В каждый момент полярность ЭДС самоиндукции должна быть такой, чтобы препятствовать изменению тока, — этим сразу устанавливается направление сдвига по фазе между током и ЭДС самоиндукции. И наконец, приложенное напряжение изменяется в противофазе с ЭДС самоиндукции (нижний график на рис. 129).
При прохождении электрического тока через катушку индуктивности не происходит диссипации энергии: при нарастании тока в катушке накапливается энергия магнитного поля, а при убывании тока эта энергия возвращается в электрическую цепь.
Фазовые сдвиги. Рассмотрение этих простейших цепей показывает, что, за исключением случая активного сопротивления  невозможно написать закон Ома для цепей переменного тока, определяющий мгновенное значение тока
невозможно написать закон Ома для цепей переменного тока, определяющий мгновенное значение тока  в виде отношения приложенного напряжения к сопротивлению соответствующего участка, вследствие того, что между током и напряжением существует сдвиг по фазе. Сдвиг по фазе между приложенным синусоидальным напряжением и силой тока характерен для цепей, содержащих емкостное или индуктивное сопротивление. Для них используется общее название — реактивное сопротивление. Как мы видели, закон Ома справедлив только для амплитудных значений тока и напряжения.
в виде отношения приложенного напряжения к сопротивлению соответствующего участка, вследствие того, что между током и напряжением существует сдвиг по фазе. Сдвиг по фазе между приложенным синусоидальным напряжением и силой тока характерен для цепей, содержащих емкостное или индуктивное сопротивление. Для них используется общее название — реактивное сопротивление. Как мы видели, закон Ома справедлив только для амплитудных значений тока и напряжения.
Подчеркнем, что введенные выше понятия емкостного и индуктивного сопротивлений имеют смысл только для синусоидального приложенного напряжения. Сами их определения содержат циклическую частоту  этого напряжения. Ясно, что эти понятия неприменимы в случаях, когда конденсатор или катушка индуктивности подключаются к источнику постоянного напряжения или напряжения, изменяющегося со временем по какому-либо иному (несинусоидальному) закону.
этого напряжения. Ясно, что эти понятия неприменимы в случаях, когда конденсатор или катушка индуктивности подключаются к источнику постоянного напряжения или напряжения, изменяющегося со временем по какому-либо иному (несинусоидальному) закону.
• В каких случаях явления в электрических цепях называются квазистационарными?
• Как связаны между собой сила тока и изменяющееся приложенное напряжениие в цепи, содержащей только обычное (активное) сопротивление R?
• Как связаны между собой сила тока и приложенное напряжение в цепи, содержащей только емкость С или только индуктивность  Можно ли этой связи придать вид закона Ома? Применимы ли соответствующие соотношения при несинусоидальном приложенном напряжении?
Можно ли этой связи придать вид закона Ома? Применимы ли соответствующие соотношения при несинусоидальном приложенном напряжении?
• Объясните физическую причину возникновения сдвига по фазе между приложенным синусоидальным напряжением и силой тока в цепях, содержащих емкость и индуктивность.
• Что такое реактивное сопротивление? В каких случаях имеют смысл понятия индуктивного и емкостного сопротивлений?
Процесс зарядки конденсатора. Рассмотрим процесс зарядки конденсатора при подключении его к источнику постоянного напряжения  При замыкании ключа К в цепи скачком возникает ток и конденсатор начинает заряжаться.
При замыкании ключа К в цепи скачком возникает ток и конденсатор начинает заряжаться.

Рис. 130. Конденсатор С заряжается от источника постоянного напряжения  через резистор
через резистор 

Рис. 131. При таком выборе направления тока его значение I связано с зарядом верхней пластины  соотношением
соотношением 
По мере увеличения напряжения на конденсаторе сила тока в цепи убывает. Процесс зарядки конденсатора будет происходить до тех пор, пока напряжение на конденсаторе не станет равным напряжению источника  После накопления на пластинах конденсатора необходимого для этого заряда
После накопления на пластинах конденсатора необходимого для этого заряда  ток в цепи прекратится, т. е. переходные процессы закончатся.
ток в цепи прекратится, т. е. переходные процессы закончатся.
Обозначим заряд верхней на рис. 130 пластины конденсатора через д. Скорость изменения этого заряда  определяет силу тока
определяет силу тока  в цепи:
в цепи:

Знак в правой части формулы (9) соответствует такому выбору направления тока, которое указано на рис. 131: положительное значение силы тока в (9) соответствует возрастанию заряда верхней пластины конденсатора, т. е. положительному значению производной 
В рассматриваемой последовательной цепи сумма напряжений на активном сопротивлении  и конденсаторе
и конденсаторе  равна приложенному напряжению
равна приложенному напряжению  Так как напряжение на сопротивлении
Так как напряжение на сопротивлении  равно произведению силы тока I на сопротивление
равно произведению силы тока I на сопротивление  то
то

Подставляя сюда значение силы тока I из (9) и учитывая, что напряжение  на конденсаторе в квазистационарных условиях в любой момент равно
на конденсаторе в квазистационарных условиях в любой момент равно  получаем
получаем

Это дифференциальное уравнение для функции  определяет зависимость заряда конденсатора от времени, если добавить
определяет зависимость заряда конденсатора от времени, если добавить
к нему начальное условие  при
при  выражающее отсутствие заряда в начальный момент. Уравнение (11) удобно переписать в несколько ином виде, учитывая, что приложенное напряжение
выражающее отсутствие заряда в начальный момент. Уравнение (11) удобно переписать в несколько ином виде, учитывая, что приложенное напряжение  равно отношению окончательного заряда конденсатора
равно отношению окончательного заряда конденсатора  к его емкости С:
к его емкости С:  Тогда вместо (11) получим
Тогда вместо (11) получим

Это уравнение легко привести к хорошо известному виду, если вместо заряда пластины  ввести другую неизвестную величину
ввести другую неизвестную величину  характеризующую, насколько заряд пластины
характеризующую, насколько заряд пластины  в данный момент отличается от окончательного заряда
в данный момент отличается от окончательного заряда 

Дифференциальное уравнение процесса. Из определения (13) следует, что  Поэтому уравнение (12) после замены (13) принимает вид
Поэтому уравнение (12) после замены (13) принимает вид

Экспоненциальная зависимость q(t). Уравнение (14) означает, что скорость изменения недостающего заряда  пропорциональна самому
пропорциональна самому  Решением такого уравнения является экспоненциальная функция
Решением такого уравнения является экспоненциальная функция

Постоянная А определяется с помощью начальных условий. В начальный момент конденсатор не заряжен  Поэтому недостающий заряд
Поэтому недостающий заряд  при
при  равен
равен  Таким образом, постоянная А в (15) равна окончательному заряду конденсатора
Таким образом, постоянная А в (15) равна окончательному заряду конденсатора 
График зависимости  показан штриховой линией на рис. 132. Из формулы (15) видно, что произведение RC равно промежутку времени
показан штриховой линией на рис. 132. Из формулы (15) видно, что произведение RC равно промежутку времени  в течение которого значение
в течение которого значение  уменьшается в
уменьшается в 

Зависимость заряда конденсатора  от времени для рассматриваемого процесса получается из формулы (13) после подстановки в нее выражения для
от времени для рассматриваемого процесса получается из формулы (13) после подстановки в нее выражения для  из (15)
из (15)

График  показанный на рис. 132, можно построить как разность между постоянным значением окончательного заряда
показанный на рис. 132, можно построить как разность между постоянным значением окончательного заряда  и графиком зависимости
и графиком зависимости 
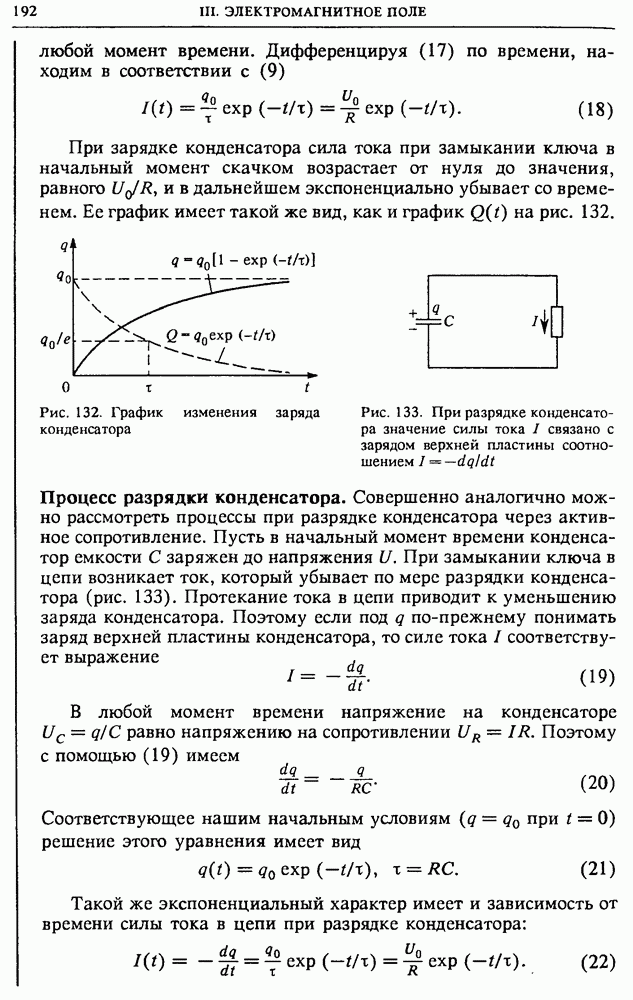
Найденная зависимость заряда конденсатора от времени (17) позволяет найти силу тока в цепи при зарядке конденсатора в
любой момент времени. Дифференцируя (17) по времени, находим в соответствии с (9)

При зарядке конденсатора сила тока при замыкании ключа в начальный момент скачком возрастает от нуля до значения, равного  и в дальнейшем экспоненциально убывает со временем. Ее график имеет такой же вид, как и график
и в дальнейшем экспоненциально убывает со временем. Ее график имеет такой же вид, как и график  на рис. 132.
на рис. 132.

Рис. 132. График изменения заряда конденсатора

Рис. 133. При разрядке конденсатора значение силы тока I связано с зарядом верхней пластины соотношением 
Процесс разрядки конденсатора. Совершенно аналогично можно рассмотреть процессы при разрядке конденсатора через активное сопротивление. Пусть в начальный момент времени конденсатор емкости С заряжен до напряжения  При замыкании ключа в цепи возникает ток, который убывает по мере разрядки конденсатора (рис. 133). Протекание тока в цепи приводит к уменьшению заряда конденсатора. Поэтому если под
При замыкании ключа в цепи возникает ток, который убывает по мере разрядки конденсатора (рис. 133). Протекание тока в цепи приводит к уменьшению заряда конденсатора. Поэтому если под  по-прежнему понимать заряд верхней пластины конденсатора, то силе тока I соответствует выражение
по-прежнему понимать заряд верхней пластины конденсатора, то силе тока I соответствует выражение 

В любой момент времени напряжение на конденсаторе  равно напряжению на сопротивлении
равно напряжению на сопротивлении  Поэтому с помощью (19) имеем
Поэтому с помощью (19) имеем

Соответствующее нашим начальным условиям  при
при  решение этого уравнения имеет вид
решение этого уравнения имеет вид

Такой же экспоненциальный характер имеет и зависимость от времени силы тока в цепи при разрядке конденсатора:

Как видно из полученных соотношений (17) и (21) (или (18) и (22)), и процесс зарядки конденсатора, и процесс разрядки, строго говоря, продолжаются бесконечно долго. Поэтому для характеристики длительности таких процессов вводят время  в течение которого сила тока I изменяется в
в течение которого сила тока I изменяется в  раза. Для электрической цепи, содержащей конденсатор и сопротивление, таким параметром является величина
раза. Для электрической цепи, содержащей конденсатор и сопротивление, таким параметром является величина

В любой реальной системе переходный процесс продолжается в течение конечного промежутка времени, так как говорить о таком процессе имеет смысл только до тех пор, пока рассматриваемая величина не уменьшится до значения, соответствующего уровню тепловых флуктуаций в системе.
Использованное при рассмотрении процессов зарядки и разрядки конденсатора условие квазистационарности связано с возможностью пренебречь временем распространения электромагнитного поля вдоль цепи по сравнению с  . Если длину цепи обозначить через
. Если длину цепи обозначить через  то условие квазистационарности принимает вид
то условие квазистационарности принимает вид


Рис. 134. К расчету силы тока в цепи при замыкании ключа К
Ток в цепи с индуктивностью. Аналогично можно рассмотреть процесс установления тока в цепи, содержащей резистор  и катушку индуктивности
и катушку индуктивности  (рис. 134). При замыкании ключа К в цепи возникает ток, быстрому нарастанию которого препятствует ЭДС самоиндукции, возникающая в катушке индуктивности. Ток нарастает до тех пор, пока не достигнет постоянного значения
(рис. 134). При замыкании ключа К в цепи возникает ток, быстрому нарастанию которого препятствует ЭДС самоиндукции, возникающая в катушке индуктивности. Ток нарастает до тех пор, пока не достигнет постоянного значения 
Выражение для силы тока  в каждый момент можно записать, используя закон Ома для неоднородного участка цепи:
в каждый момент можно записать, используя закон Ома для неоднородного участка цепи:

Поскольку ЭДС самоиндукции  выражается соотношением
выражается соотношением  то равенство (25) можно записать в виде
то равенство (25) можно записать в виде

Равенство (26) можно было написать и сразу, учитывая, что напряжение  на концах последовательной цепи равно сумме напряжений на отдельных ее элементах, а напряжение на индуктивности в каждый момент времени компенсирует возникающую в катушке ЭДС самоиндукции.
на концах последовательной цепи равно сумме напряжений на отдельных ее элементах, а напряжение на индуктивности в каждый момент времени компенсирует возникающую в катушке ЭДС самоиндукции.
Соотношение (26) представляет собой дифференциальное уравнение для силы тока  Оно совершенно аналогично
Оно совершенно аналогично
уравнению (11) для заряда  поэтому и решать его можно таким же способом. Представим
поэтому и решать его можно таким же способом. Представим  как
как  и перепишем (26) в виде
и перепишем (26) в виде

Это уравнение аналогично (12). Учитывая начальное условие  при
при  можно записать решение уравнения (27) в виде, подобном (17):
можно записать решение уравнения (27) в виде, подобном (17):

где характерное время  установления тока в цепи, содержащей сопротивление и индуктивность, дается соотношением
установления тока в цепи, содержащей сопротивление и индуктивность, дается соотношением

Для процессов в цепях с индуктивностью характерны те же моменты, которые отмечались выше для цепей с емкостью. В частности, условие квазистационарности в цепи длиной  имеет вид
имеет вид

• Найдите время, по прошествии которого на пластинах разряжающегося конденсатора останется только одна тысячная часть первоначального заряда, если  .
.
• При выполнении какого условия процесс зарядки (или разрядки) конденсатора можно считать квазистационарным?
• Почему реальный процесс зарядки конденсатора имеет конечную длительность, хотя определенная выражением (18) сила зарядного тока обращается в нуль только при 
Какую роль играют начальные условия при решении дифференциальных уравнений, описывающих квазистационарные процессы в цепях, содержащих конденсаторы или индуктивности?
• Из чего следует исходить при формулировке начальных условий к дифференциальным уравнениям, т. е. при задании значений изменяющихся со временем величин при  в конкретных электрических цепях?
в конкретных электрических цепях?
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
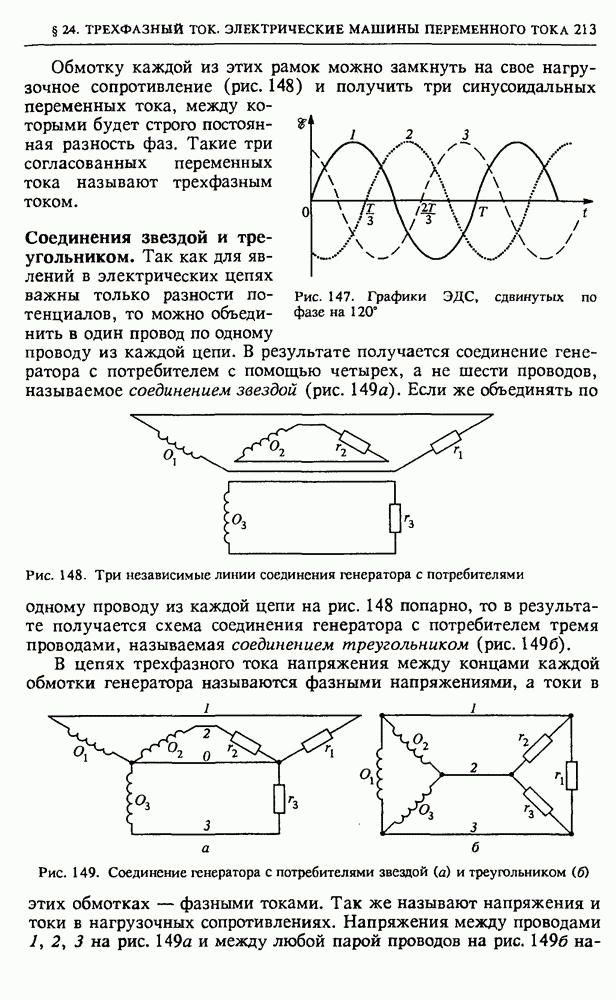
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
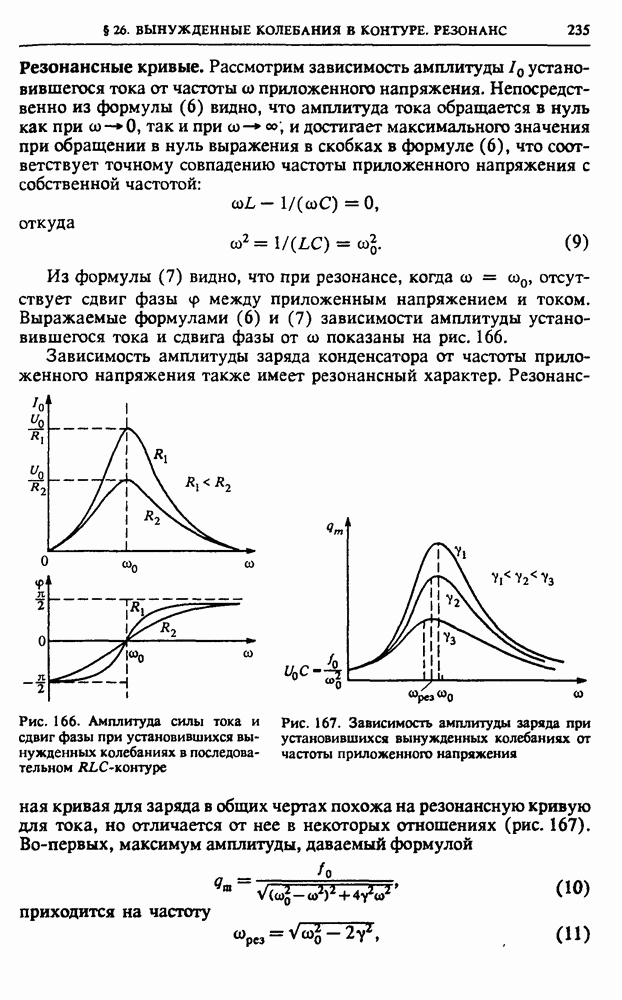
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение