| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 19. Энергия магнитного поля
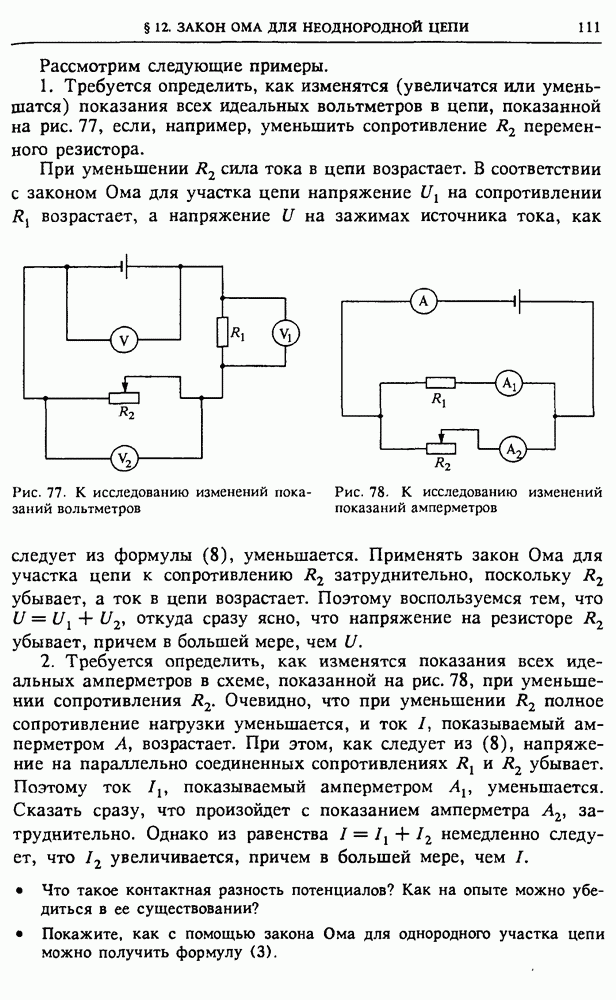
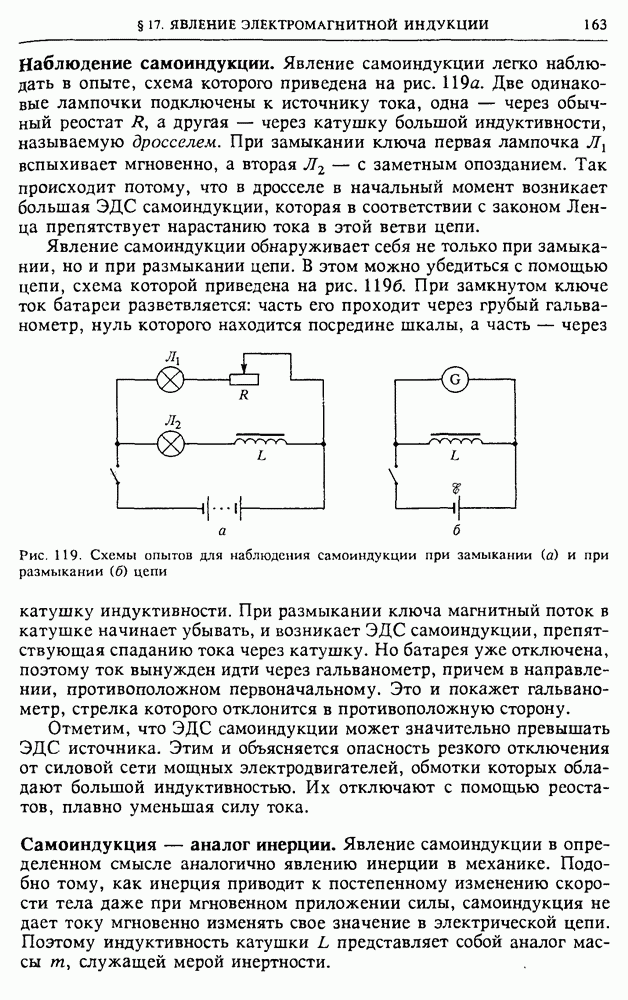
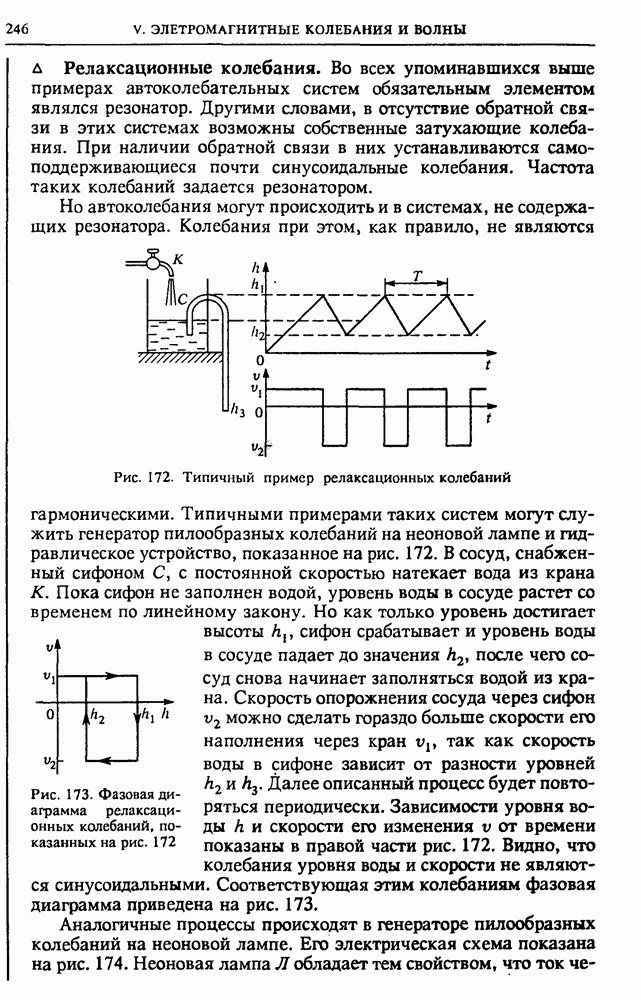
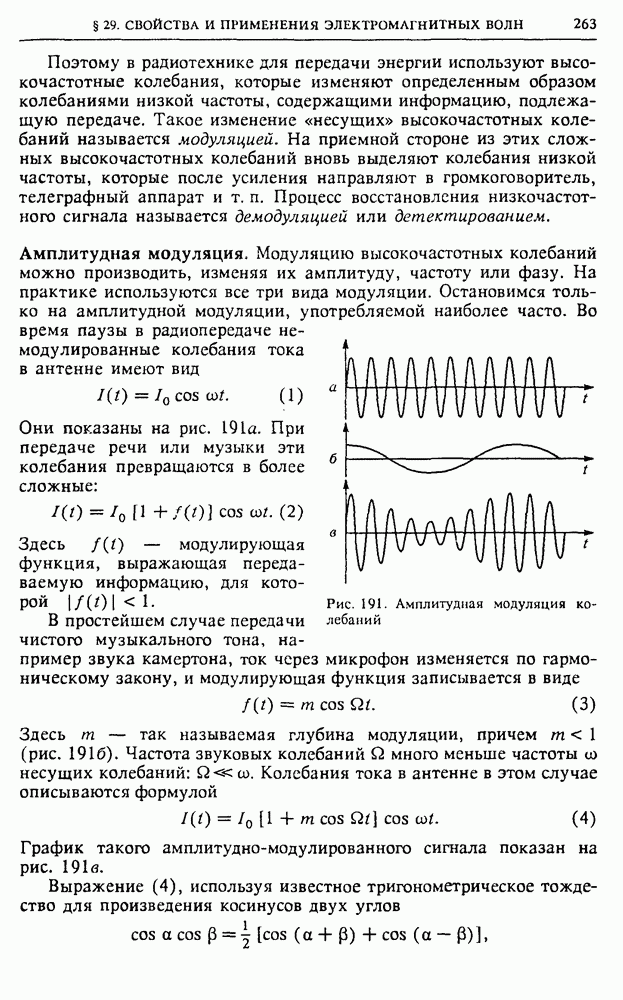
Магнитное поле обладает энергией. Проще всего в этом убедиться, рассматривая процесс спадания тока в катушке при отсоединении ее от источника тока в схеме на рис. 123а.
Опыт по обнаружению энергии магнитного поля. До размыкания ключа в катушке идет некоторый ток  и этот ток создает магнитное поле. При размыкании ключа остается последовательная цепь из катушки и резистора
и этот ток создает магнитное поле. При размыкании ключа остается последовательная цепь из катушки и резистора  (рис. 1236). Ток в катушке благодаря самоиндукции спадает постепенно, и при этом на сопротивлении
(рис. 1236). Ток в катушке благодаря самоиндукции спадает постепенно, и при этом на сопротивлении  продолжает выделяться джоулева теплота.
продолжает выделяться джоулева теплота.
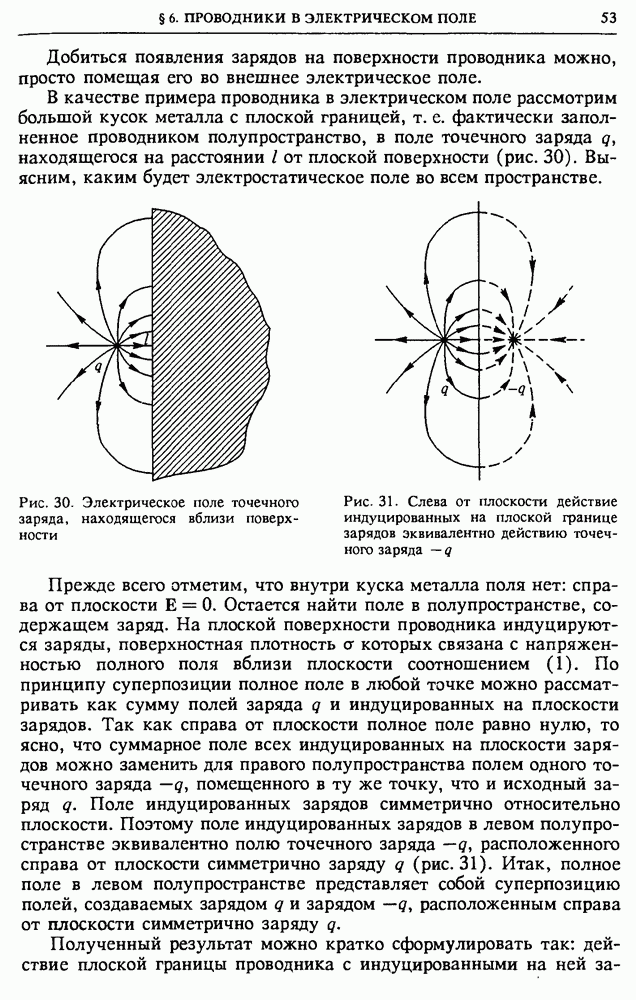
За счет каких запасов энергии выделяется теплота — ведь источник питания уже отключен? Здесь убывает ток и создаваемое им магнитное поле; значит, мы можем говорить об энергии тока или об энергии создаваемого им магнитного поля.

Рис. 123. Электрическая цепь для изучения магнитной энергии тока
По аналогии с электростатикой, где можно говорить об энергии зарядов или об энергии создаваемого ими поля, естественно ожидать, что в случае постоянного тока допустимы оба представления: энергию можно рассматривать либо как энергию тока, либо как энергию создаваемого им магнитного поля. Но мы уже видели, что, хотя не бывает электрического заряда без создаваемого им поля, электрическое поле без заряда — вихревое поле — может существовать и оно обладает энергией. Поэтому вопрос о локализации электрической энергии решается в пользу поля. Как мы увидим немного позже, точно так же обстоит дело и с магнитной энергией.
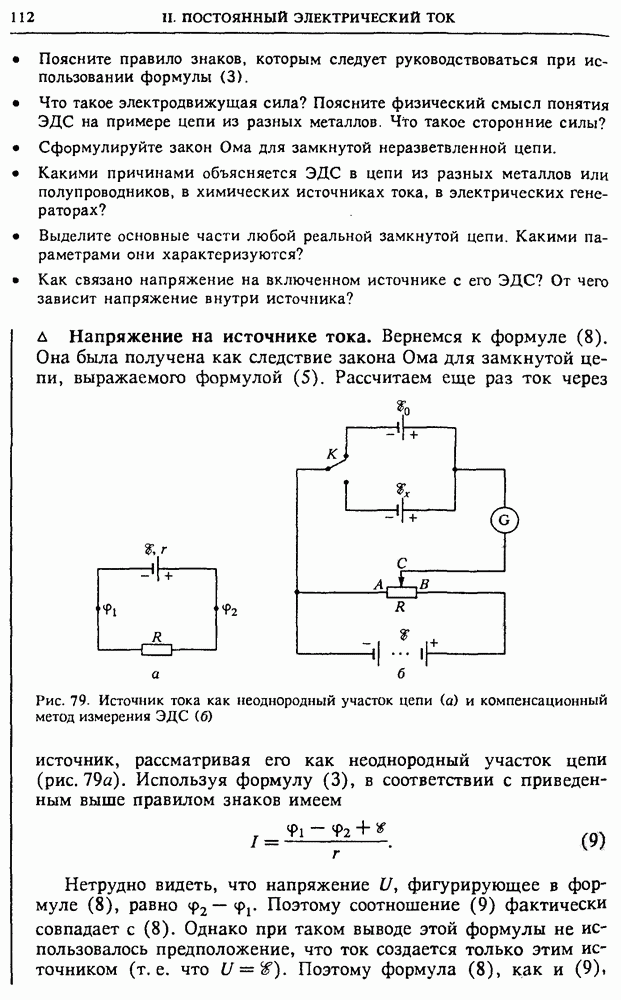
Расчет энергии магнитного поля. Подсчитаем энергию магнитного поля. Из закона сохранения энергии очевидно, что в рассматриваемом нами опыте (рис. 123б) вся энергия магнитного поля в конце концов выделится в виде джоулевой теплоты на сопротивлении  За время
За время  на сопротивлении
на сопротивлении  выделяется количество теплоты
выделяется количество теплоты  По закону Ома ток
По закону Ома ток  равен
равен

С учетом этого равенства выражение для  можно записать в виде
можно записать в виде

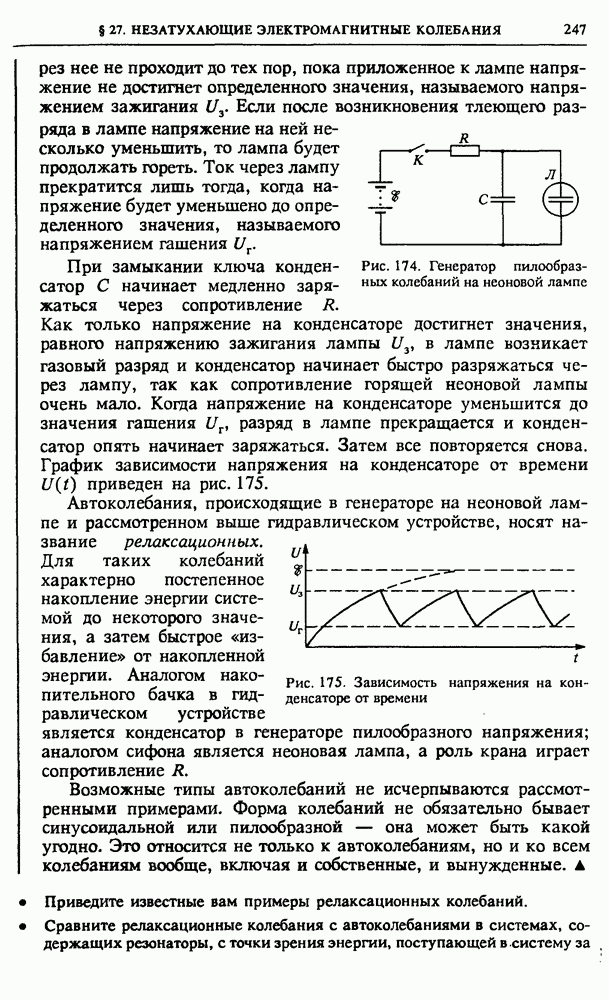
Выделяющаяся теплота  разумеется, положительна, так как ток убывает и, следовательно,
разумеется, положительна, так как ток убывает и, следовательно,  Изобразив на графике зависимость магнитного потока
Изобразив на графике зависимость магнитного потока  от тока
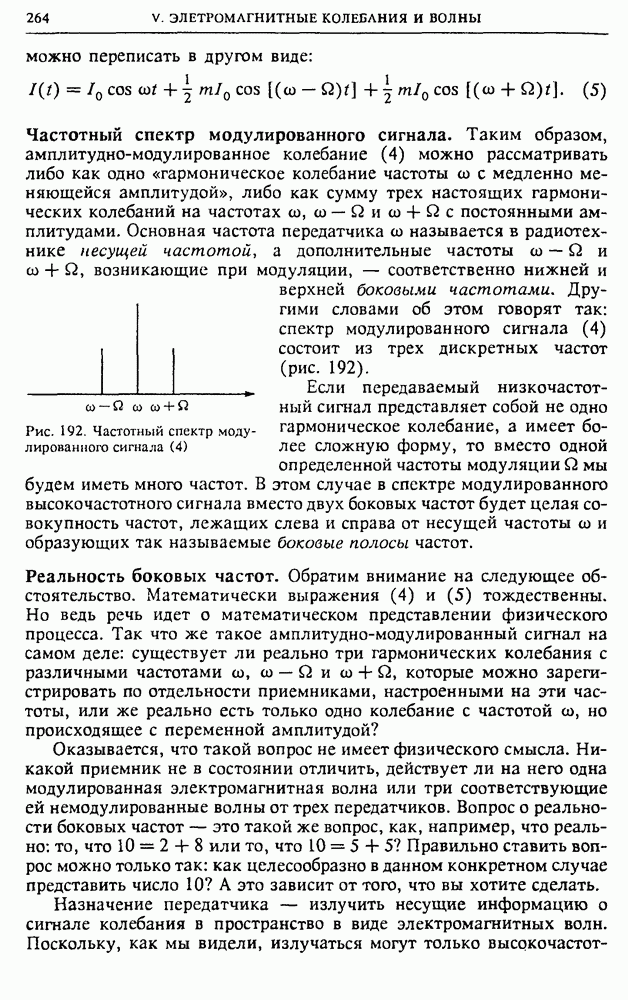
от тока  (рис. 124), легко сообразить, что полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью заштрихованного треугольника
(рис. 124), легко сообразить, что полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью заштрихованного треугольника  Таким образом, выражение для энергии магнитного поля
Таким образом, выражение для энергии магнитного поля  создаваемого током
создаваемого током  в катушке с индуктивностью
в катушке с индуктивностью  имеет вид
имеет вид


Рис. 124. К вычислению энергии магнитного поля
Объемная плотность энергии магнитного поля. Как и в электростатике, можно ввести понятие объемной плотности энергии магнитного поля. Рассматривая однородное магнитное поле внутри длинного соленоида, подставим во вторую из формул (3) выражение (10) § 17 для индуктивности длинного соленоида, а ток  выразим через индукцию магнитного поля с помощью формулы (8) § 17. В результате получим
выразим через индукцию магнитного поля с помощью формулы (8) § 17. В результате получим

откуда объемная плотность энергии магнитного поля  равна
равна

Вернемся к опыту, схема которого показана на рис. 123, и повторим его, вдвинув предварительно в катушку железный сердечник. Установившееся значение силы тока в катушке будет таким же, так как сердечник не сказывается на полном сопротивлении цепи постоянного тока. Но при размыкании ключа мы обнаружим, что теперь в резисторе  выделится гораздо большее количество теплоты, чем в отсутствие сердечника. Это означает, что в катушке с сердечником запас энергии магнитного поля при том же токе в ней стал гораздо больше. Глядя на формулу (3), выражающую энергию магнитного поля через силу тока I, убеждаемся, что благодаря железному сердечнику возрастает индуктивность
выделится гораздо большее количество теплоты, чем в отсутствие сердечника. Это означает, что в катушке с сердечником запас энергии магнитного поля при том же токе в ней стал гораздо больше. Глядя на формулу (3), выражающую энергию магнитного поля через силу тока I, убеждаемся, что благодаря железному сердечнику возрастает индуктивность  катушки и создаваемый ею магнитный поток Ф.
катушки и создаваемый ею магнитный поток Ф.
Магнитная проницаемость вещества. Опыт показывает, что индуктивность всякого контура зависит от свойств среды, в которой он находится. Будем считать, что окружающая среда однородна и
заполняет все пространство, где имеется магнитное поле. Для длинной катушки это практически означает, что сердечник заполняет все пространство внутри ее обмотки. Тем более это справедливо и для замкнутой тороидальной катушки.
Обозначим через  индуктивность катушки в вакууме, а через
индуктивность катушки в вакууме, а через  — ее индуктивность с сердечником. Безразмерное отношение
— ее индуктивность с сердечником. Безразмерное отношение

называют относительной магнитной проницаемостью (или просто магнитной проницаемостью) вещества, из которого сделан сердечник.
Магнитная проницаемость зависит от рода (химического состава) вещества и от его состояния, например от температуры. Она показывает, во сколько раз увеличивается  или уменьшается
или уменьшается  магнитная индукция в веществе по сравнению с ее значением в вакууме при тех же значениях токов, создающих магнитное поле.
магнитная индукция в веществе по сравнению с ее значением в вакууме при тех же значениях токов, создающих магнитное поле.
Вещества с  (железо, кобальт, никель, некоторые сплавы) называются ферромагнетиками. Магнитное поле в них усиливается во много раз. Для каждого ферромагнетика существует характерная температура, точка Кюри, выше которой он превращается в парамагнетик. Парамагнетиками называют вещества с
(железо, кобальт, никель, некоторые сплавы) называются ферромагнетиками. Магнитное поле в них усиливается во много раз. Для каждого ферромагнетика существует характерная температура, точка Кюри, выше которой он превращается в парамагнетик. Парамагнетиками называют вещества с  (алюминий, платина, кислород). Вещества с
(алюминий, платина, кислород). Вещества с  в которых магнитное поле ослабляется, называются диамагнетиками (медь, серебро, висмут). В неоднородном магнитном поле парамагнетик втягивается в область сильного поля, а диамагнетик — выталкивается из нее. В сверхпроводники магнитное поле вообще не проникает (эффект Мейсснера).
в которых магнитное поле ослабляется, называются диамагнетиками (медь, серебро, висмут). В неоднородном магнитном поле парамагнетик втягивается в область сильного поля, а диамагнетик — выталкивается из нее. В сверхпроводники магнитное поле вообще не проникает (эффект Мейсснера).
О природе магнитных свойств вещества. Магнитные свойства вещества обусловлены тем, что при помещении его во внешнее магнитное поле происходит намагничивание — каждый малый его элемент приобретает магнитный момент, т. е. становится магнитным диполем, подобным маленькому замкнутому контуру с током.
Диамагнетизм вещества представляет собой индукционный эффект, обусловленный индуцированными магнитным полем орбитальными токами в атомах или молекулах. Диамагнетизм — общее свойство всех веществ, но наиболее он проявляется в тех веществах, где атомы или молекулы не обладают собственным магнитным моментом. Парамагнетизм и ферромагнетизм, как правило, связаны с наличием у электронов собственных, не связанных с их орбитальным движением магнитных моментов. В кристаллах ферромагнитных веществ оказывается энергетически выгодной параллельная ориентация магнитных моментов электронов, и образуются макроскопические намагниченные области протяженностью  — так называемые домены. В разных доменах магнитное поле ориентировано по-разному, но при наложении внешнего магнитного поля происходит
— так называемые домены. В разных доменах магнитное поле ориентировано по-разному, но при наложении внешнего магнитного поля происходит
упорядочение полей отдельных доменов. У некоторых ферромагнитных веществ упорядоченная ориентация магнитных моментов доменов сохраняется и после выключения внешнего магнитного поля — получаются постоянные магниты.
Отмеченными тремя типами магнетиков не исчерпывается все многообразие магнитных свойств вещества. Среди магнитоупорядоченных веществ, кроме ферромагнетиков, различают еще, например, антиферромагнетики, ферримагнетики, для которых характерны более сложные закономерности магнитной структуры.
Микроскопическая теория, правильно объясняющая строение и магнитные свойства вещества, может быть развита только на основе квантовых представлений.
Магнитоупорядоченные вещества находят все более и более широкое применение в науке и технике, начиная от всем известных радио- и электротехнических устройств до современной микроэлектроники и вычислительной техники.
• Покажите из энергетических соображений, что при замыкании цепи ток в катушке индуктивности нарастает постепенно. От чего зависит скорость его нарастания?
• Какой вывод о зависимости магнитной энергии от индуктивности катушки можно сделать из формулы (3): эта энергия пропорциональна или обратно пропорциональна индуктивности?
• Объясните, почему наличие железного сердечника не приводит к изменению установившегося значения силы тока в катушке в опыте, схема которого показана на рис. 123.
• Приведите аргументы, подтверждающие квадратичную зависимость объемной плотности магнитной энергии от индукции поля.
• Дайте качественное объяснение различию в характере поведения диамагнетиков и парамагнетиков в неоднородном магнитном поле.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
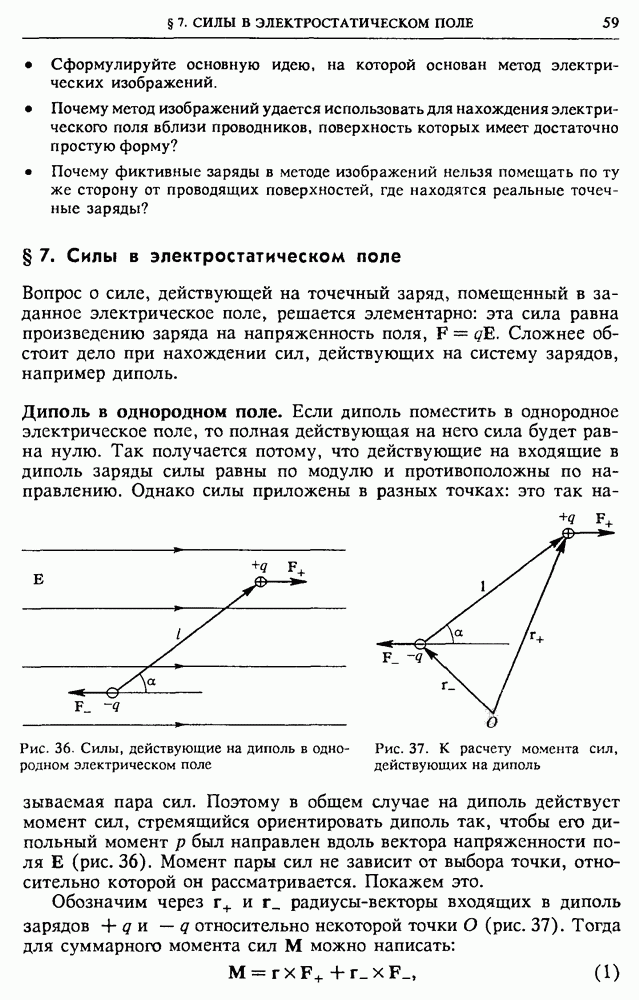
- § 7. Силы в электростатическом поле
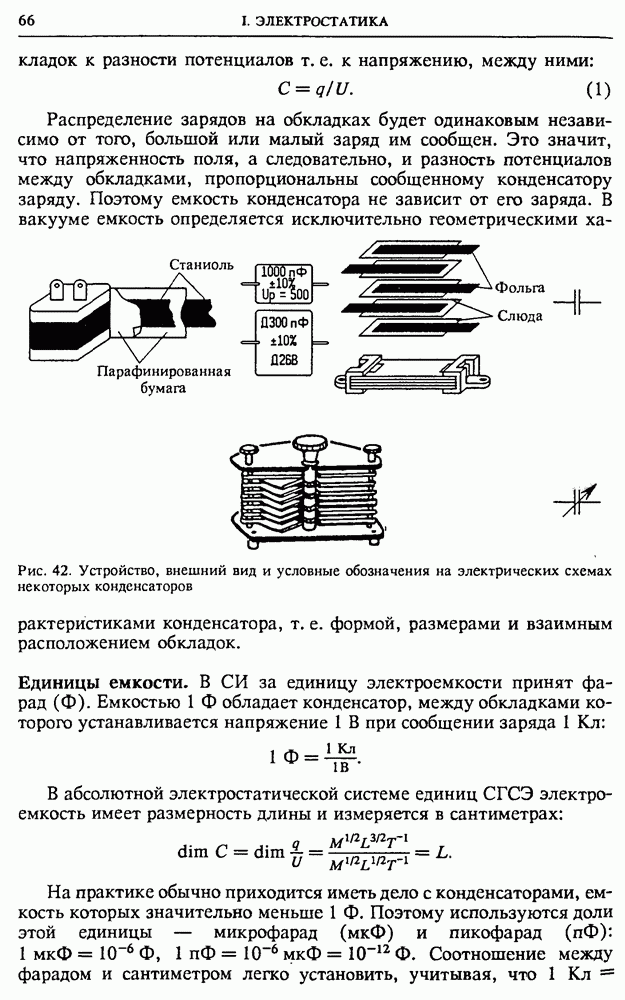
- § 8. Конденсаторы. Электроемкость
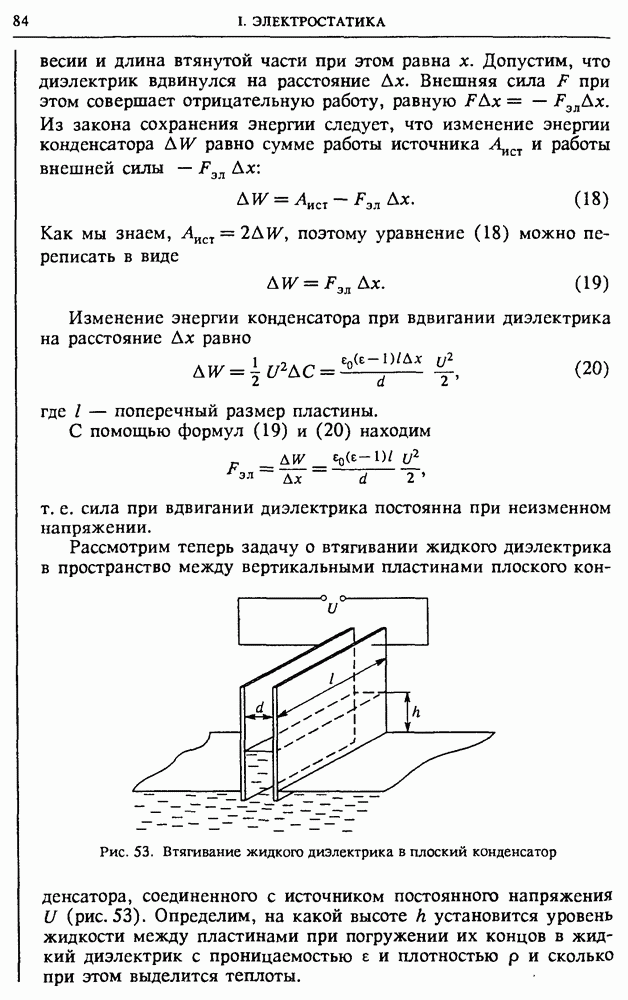
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
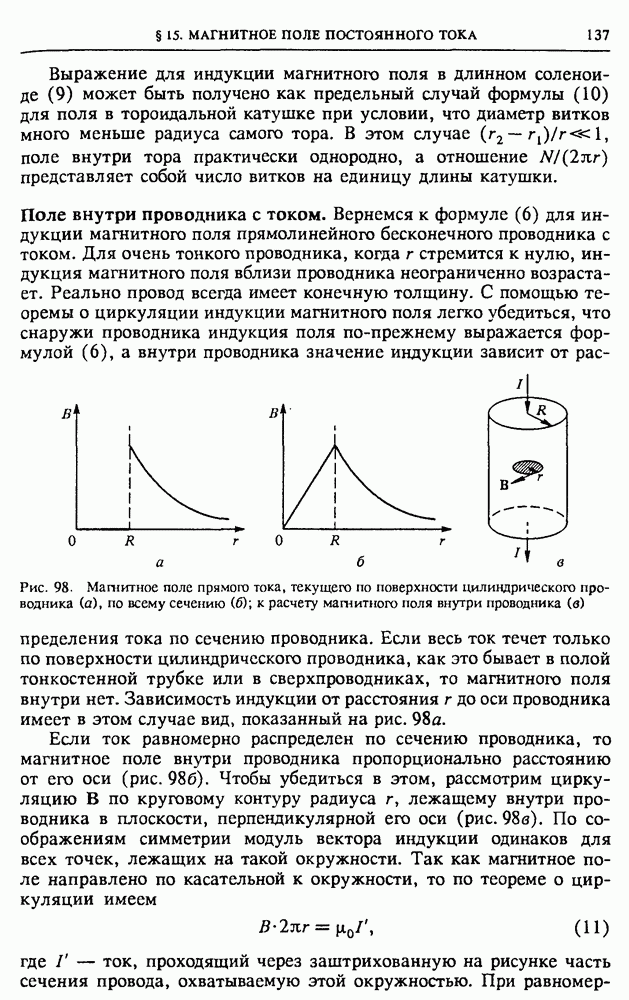
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
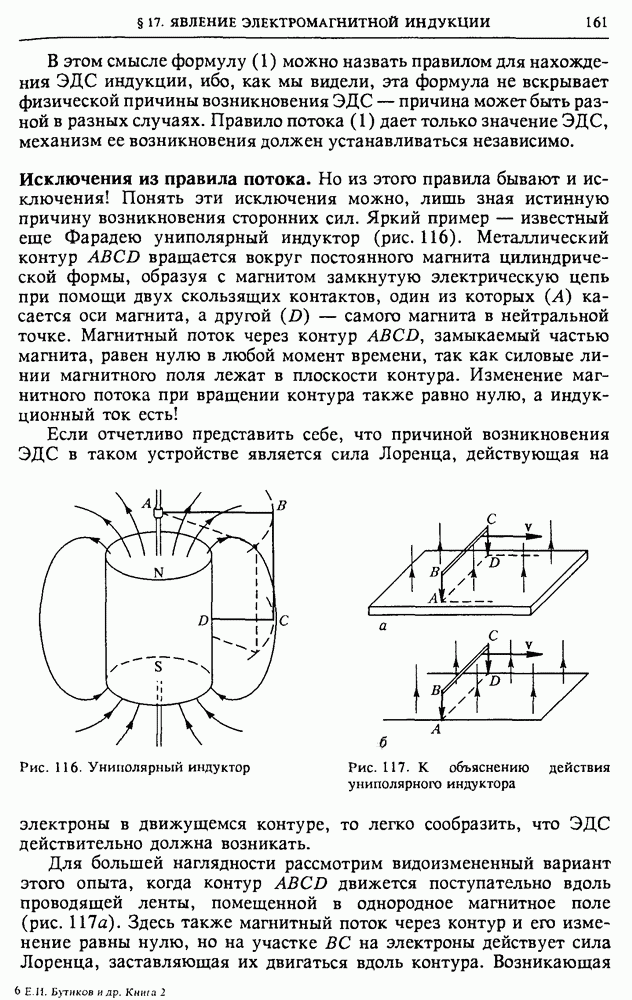
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение