| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Электрическое поле. Напряженность поля
Наряду с законом Кулона возможно и другое описание взаимодействия электрических зарядов.
Дальнодействие и близкодействие. Закон Кулона, подобно закону всемирного тяготения, трактует взаимодействие зарядов как «действие на расстоянии», или «дальнодействие». Действительно, кулоновская сила зависит лишь от величины зарядов и от расстояния между ними. Кулон был убежден, что промежуточная среда, т. е. «пустота» между зарядами, никакого участия во взаимодействии не принимает.
Такая точка зрения, несомненно, была навеяна впечатляющими успехами ньютоновской теории тяготения, блестяще подтверждавшейся астрономическими наблюдениями. Однако еще сам Ньютон писал: «Непонятно, каким образом неодушевленная косная материя, без посредства чего-либо иного, что нематериально, могла бы действовать на другое тело без взаимного прикосновения». Тем не менее концепция дальнодействия, основанная на представлении о мгновенном действии одного тела на другое на расстоянии без участия какой-либо промежуточной среды, еще долго доминировала в научном мировоззрении.
Идея поля как материальной среды, посредством которой осуществляется любое взаимодействие пространственно удаленных тел, была введена в физику в 30-е годы XIX века великим английским естествоиспытателем М. Фарадеем, который считал, что «материя присутствует везде, и нет промежуточного пространства, не занятого
ею». Фарадей развил последовательную концепцию электромагнитного поля, основанную на идее конечной скорости распространения взаимодействия. Законченная теория электромагнитного поля, облеченная в строгую математическую форму, была впоследствии развита другим великим английским физиком Дж. Максвеллом.
По современным представлениям электрические заряды наделяют окружающее их пространство особыми физическими свойствами — создают электрическое поле. Основным свойством поля является то, что на находящуюся в этом поле заряженную частицу действует некоторая сила, т. е. взаимодействие электрических зарядов осуществляется посредством создаваемых ими полей. Поле, создаваемое неподвижными зарядами, не изменяется со временем и называется электростатическим. Для изучения поля необходимо найти его физические характеристики. Рассматривают две такие характеристики — силовую и энергетическую.
Напряженность электрического поля. Для экспериментального изучения электрического поля в него нужно поместить пробный заряд. Практически это будет какое-то заряженное тело, которое, во-первых, должно иметь достаточно малые размеры, чтобы можно было судить о свойствах поля в определенной точке пространства, и, во-вторых, его электрический заряд должен быть достаточно малым, чтобы можно было пренебречь влиянием этого заряда на распределение зарядов, создающих изучаемое поле.
На пробный заряд, помещенный в электрическое поле, действует сила, которая зависит как от поля, так и от самого пробного заряда. Эта сила тем больше, чем больше пробный заряд. Измеряя силы, действующие на разные пробные заряды, помещенные в одну и ту же точку, можно убедиться, что отношение силы к пробному заряду уже не зависит от величины заряда. Значит, это отношение характеризует само поле. Силовой характеристикой электрического поля является напряженность Е — векторная величина, равная в каждой точке отношению силы  действующей на пробный заряд
действующей на пробный заряд  помещенный в эту точку, к заряду
помещенный в эту точку, к заряду 

Другими словами, напряженность поля Е измеряется силой, действующей на единичный положительный пробный заряд. В общем случае напряженность поля разная в разных точках. Поле, в котором напряженность во всех точках одинакова как по модулю, так и по направлению, называется однородным.
Зная напряженность электрического поля, можно найти силу, действующую на любой заряд  помещенный в данную точку. В соответствии с (1) выражение для этой силы имеет вид
помещенный в данную точку. В соответствии с (1) выражение для этой силы имеет вид

Как же найти напряженность поля в какой-либо точке?
Напряженность электрического поля, создаваемого точечным зарядом, можно рассчитать с помощью закона Кулона. Будем рассматривать точечный заряд  как источник электрического поля. Этот заряд действует на расположенный на расстоянии
как источник электрического поля. Этот заряд действует на расположенный на расстоянии  от него пробный заряд
от него пробный заряд  с силой, модуль которой равен
с силой, модуль которой равен

Поэтому в соответствии с (1), разделив это выражение на  получаем модуль Е напряженности поля в точке, где расположен пробный заряд, т. е. на расстоянии
получаем модуль Е напряженности поля в точке, где расположен пробный заряд, т. е. на расстоянии  от заряда
от заряда 

Таким образом, напряженность поля точечного заряда убывает с расстоянием обратно пропорционально квадрату расстояния или, как говорят, по закону обратных квадратов. Такое поле называют кулоновским. При приближении к создающему поле точечному заряду напряженность поля точечного заряда неограниченно возрастает: из (4) следует, что  при
при 
Коэффициент к в формуле (4) зависит от выбора системы единиц. В СГСЭ к = 1, а в СИ  . Соответственно формула (4) записывается в одном из двух видов:
. Соответственно формула (4) записывается в одном из двух видов:

Единица напряженности в СГСЭ специального названия не имеет, а в СИ она называется «вольт на метр» 
Вследствие изотропности пространства, т. е. эквивалентности всех направлений, электрическое поле уединенного точечного заряда сферически-симметрично. Это обстоятельство проявляется в формуле (4) в том, что модуль напряженности поля зависит только от расстояния  до заряда, создающего поле. Вектор напряженности Е имеет радиальное направление: он направлен от создающего поле заряда
до заряда, создающего поле. Вектор напряженности Е имеет радиальное направление: он направлен от создающего поле заряда  если это положительный заряд (рис. 6а, а), и к создающему поле заряду
если это положительный заряд (рис. 6а, а), и к создающему поле заряду  если этот заряд отрицательный (рис. 6б).
если этот заряд отрицательный (рис. 6б).
Выражение для напряженности поля точечного заряда можно записать в векторном виде. Начало координат удобно поместить в точку, где находится заряд, создающий поле. Тогда напряженность поля в любой точке, характеризуемой радиусом-вектором  дается выражением
дается выражением

В этом можно убедиться, сопоставив определение (1) вектора напряженности поля с формулой (2) § 1, либо отталкиваясь

Рис. 6. Напряженность Е поля, создаваемого зарядом  и сила
и сила  действующая на пробный заряд
действующая на пробный заряд 
непосредственно от формулы (4) и учитывая сформулированные выше соображения о направлении вектора Е.
Принцип суперпозиции. Как найти напряженность электрического поля, создаваемого произвольным распределением зарядов?
Опыт показывает, что электрические поля удовлетворяют принципу суперпозиции. Напряженность поля, создаваемого несколькими зарядами, равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

Принцип суперпозиции фактически означает, что присутствие других электрических зарядов никак не сказывается на поле, создаваемом данным зарядом. Такое свойство, когда отдельные источники действуют независимо и их действия просто складываются, присуще так называемым линейным системам, и само такое свойство физических систем называется линейностью. Происхождение этого названия связано с тем, что такие системы описываются линейными уравнениями (уравнениями первой степени).
Подчеркнем, что справедливость принципа суперпозиции для электрического поля не является логической необходимостью или чем-то само собой разумеющимся. Этот принцип представляет собой обобщение опытных фактов.
Принцип суперпозиции позволяет рассчитать напряженность поля, создаваемого любым распределением неподвижных электрических зарядов. В случае нескольких точечных зарядов рецепт расчета результирующей напряженности очевиден. Любой неточечный заряд можно мысленно разбить на такие малые части, чтобы каждую из них можно было рассматривать как точечный заряд. Напряженность электрического поля в произвольной точке находится как
векторная сумма напряженностей, создаваемых этими «точечными» зарядами. Соответствующие расчеты значительно упрощаются в тех случаях, коща в распределении создающих поле зарядов имеется определенная симметрия.
Линии напряженности. Наглядное графическое изображение электрических полей дают линии напряженности или силовые линии.

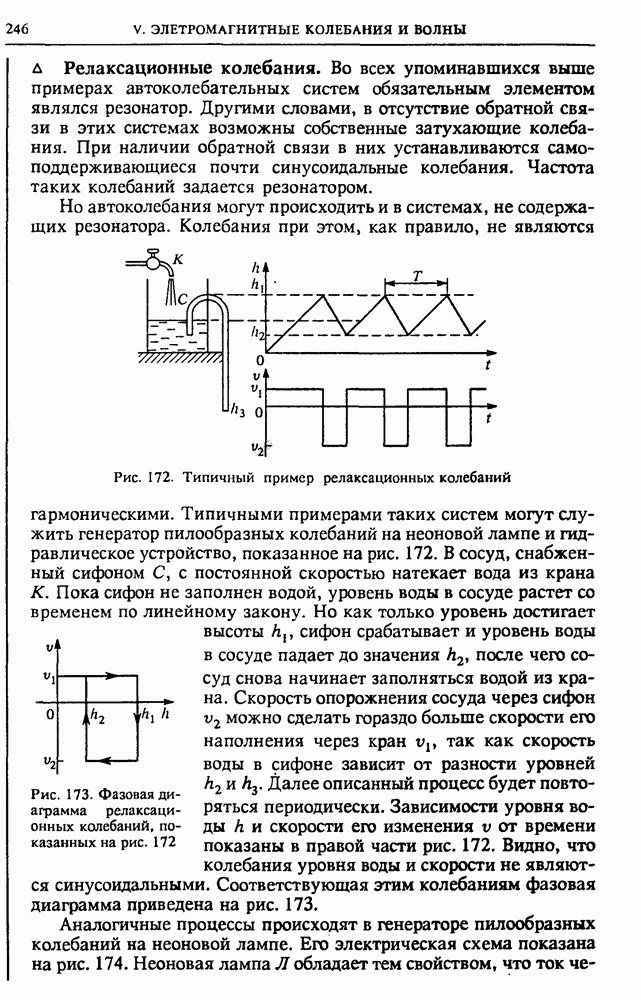
Рис. 7. Линии напряженности поля положительного и отрицательного точечных зарядов
Эти линии электрического поля проводятся таким образом, чтобы в каждой точке касательная к линии совпадала по направлению с вектором напряженности в этой точке. Иначе говоря, в любом месте вектор напряженности направлен по касательной к силовой линии, проходящей через эту точку. Силовым линиям приписывают направление: они выходят из положительных зарядов или приходят из бесконечности. Они либо оканчиваются на отрицательных зарядах, либо уходят в бесконечность. На рисунках это направление указывают стрелками на силовой линии.
Силовую линию можно провести через любую точку электрического поля.
Линии проводят гуще в тех местах, где напряженность поля больше, и реже там, где она меньше. Таким образом, густота силовых линий дает представление о модуле напряженности.

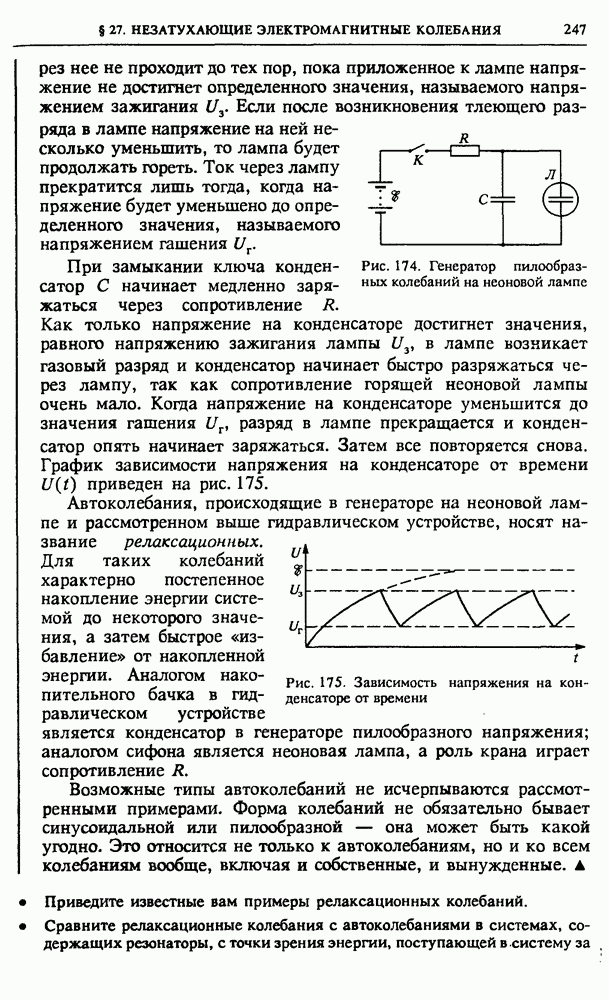
Рис. 8. Линии напряженности поля разноименных одинаковых зарядов
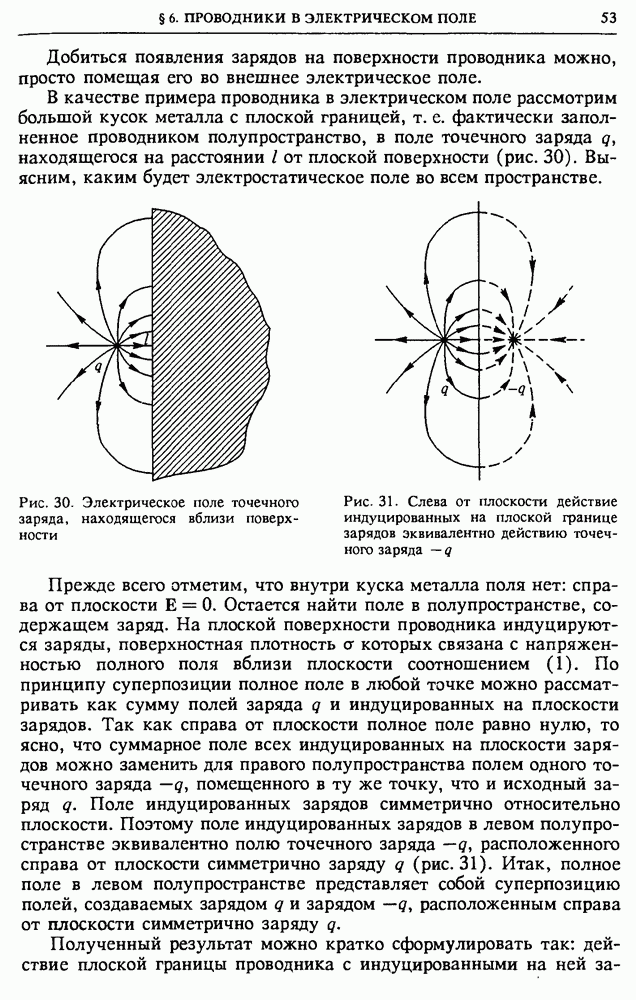
На рис. 7 показаны силовые линии поля уединенного положительного и отрицательного точечных зарядов. Из симметрии очевидно, что это радиальные прямые, распределенные с одинаковой густотой по всем направлениям.
Более сложный вид имеет картина линий поля, создаваемого двумя зарядами противоположных знаков. Такое поле, очевидно,
обладает осевой симметрией: вся картина остается неизменной при повороте на любой угол вокруг оси, проходящей через заряды. Когда модули зарядов одинаковы, картина линий также симметрична относительно плоскости, проходящей перпендикулярно соединяющему их отрезку через его середину (рис. 8). В этом случае силовые линии выходят из положительного заряда и все они оканчиваются на отрицательном, хотя на рис. 8 нельзя показать, как замыкаются уходящие далеко от зарядов линии.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- I. ЭЛЕКТРОСТАТИКА
- § 1. Электрический заряд. Закон Кулона
- § 2. Электрическое поле. Напряженность поля
- § 3. Теорема Гаусса
- § 4. Потенциал электростатического поля. Энергия системы зарядов
- § 5. Расчет электрических полей
- § 6. Проводники в электрическом поле
- § 7. Силы в электростатическом поле
- § 8. Конденсаторы. Электроемкость
- § 9. Энергия электрического поля
- II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 10. Характеристики электрического тока. Закон Ома
- § 11. Соединение проводников в электрические цепи
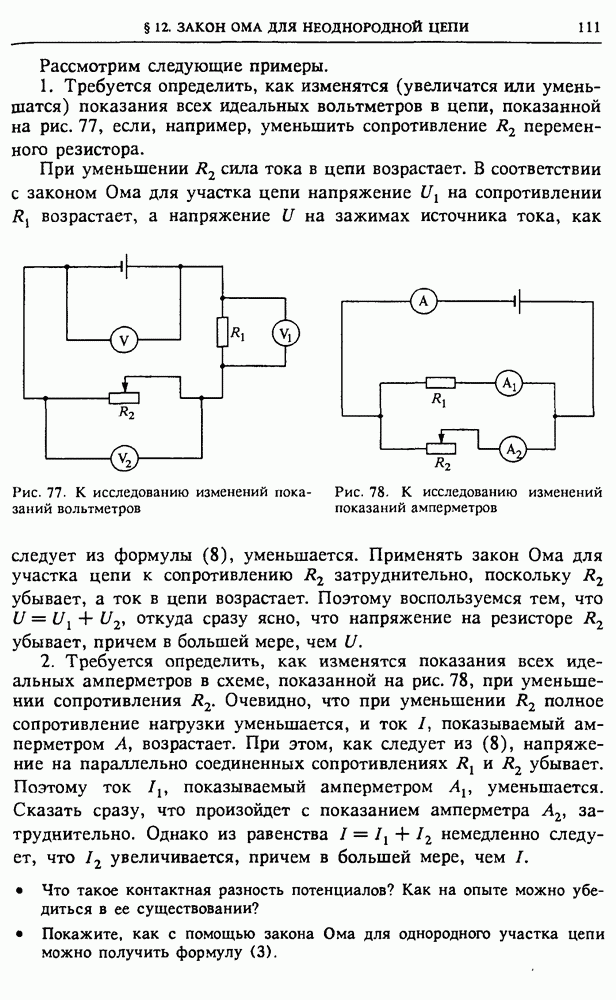
- § 12. Закон Ома для неоднородной цепи
- § 13. Расчет цепей постоянного тока
- § 14. Работа и мощность постоянного тока
- § 15. Магнитное поле постоянного тока
- § 16. Действие магнитного поля на движущиеся заряды
- III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 17. Явление электромагнитной индукции
- § 18. Электрические машины постоянного тока
- § 19. Энергия магнитного поля
- § 20. Основы теории электромагнитного поля
- § 21. Квазистационарные явления в электрических цепях
- IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 22. Цепи переменного тока. Закон Ома
- § 23. Работа и мощность переменного тока. Передача электроэнергии
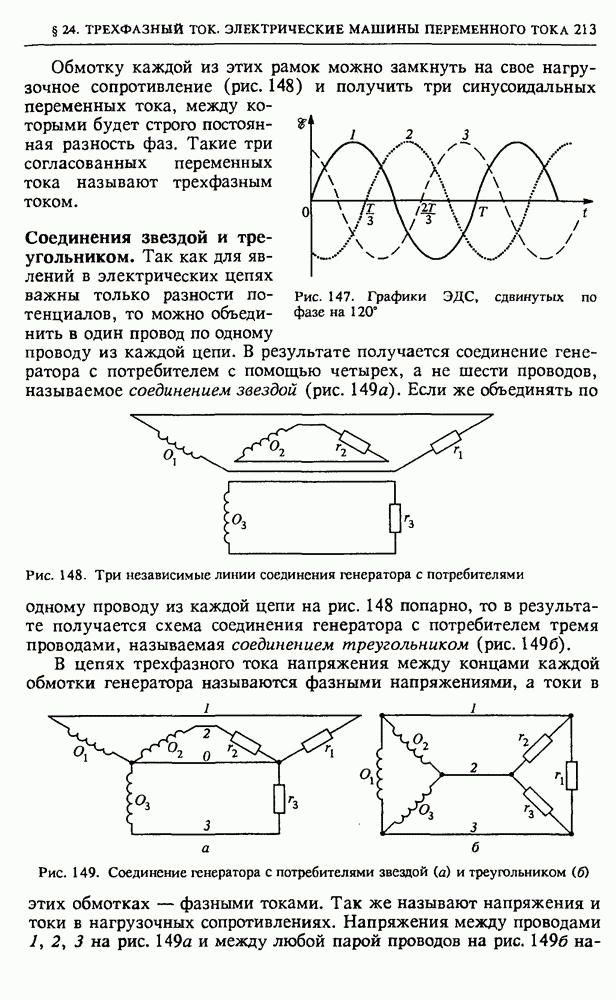
- § 24. Трехфазный ток. Электрические машины переменного тока
- V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 25. Колебательный контур
- § 26. Вынужденные колебания в контуре. Резонанс
- § 27. Незатухающие электромагнитные колебания
- § 28. Электромагнитные волны
- § 29. Свойства и применения электромагнитных волн
- VI. ОПТИКА
- § 30. Свет как электромагнитные волны. Интерференция
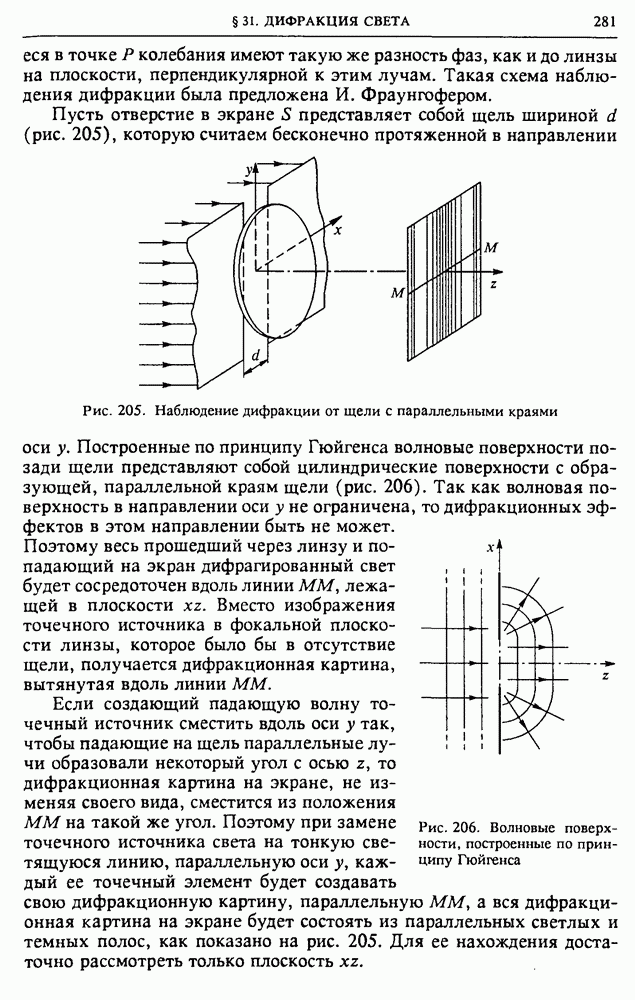
- § 31. Дифракция света
- § 32. Спектральные приборы. Дифракционная решетка
- § 33. Протяженные источники света
- § 34. Интерференция немонохроматического света
- § 35. Физические принципы голографии
- § 36. Геометрическая оптика
- § 37. Оптические приборы, формирующие изображение