| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
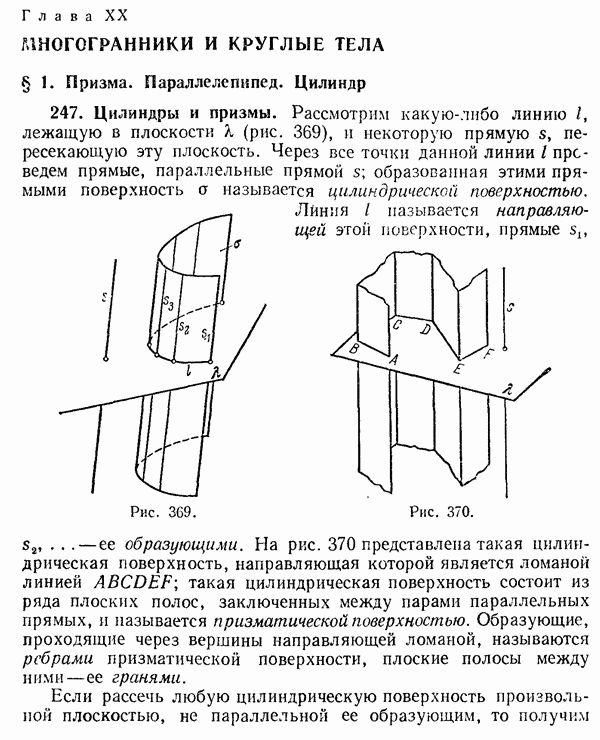
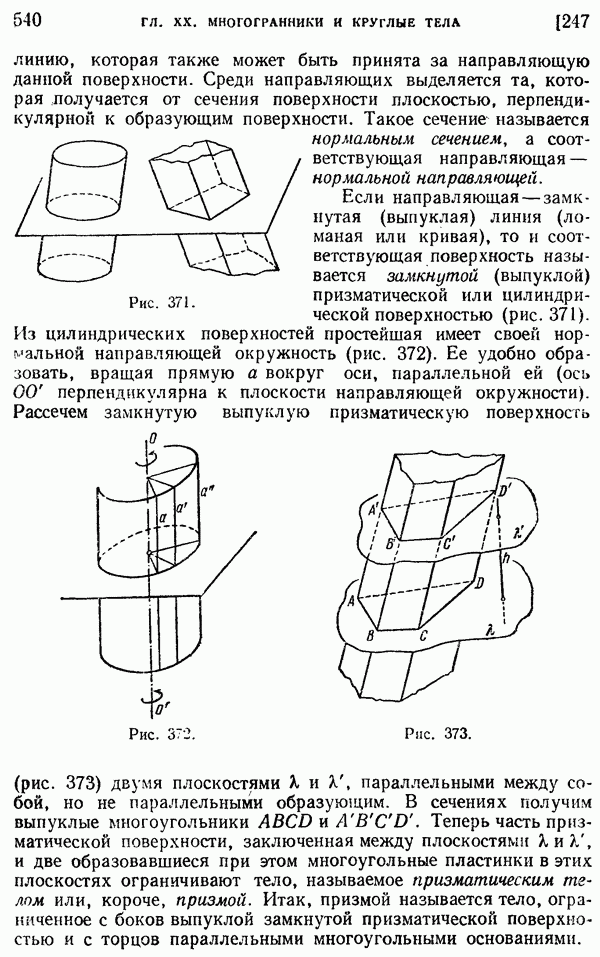
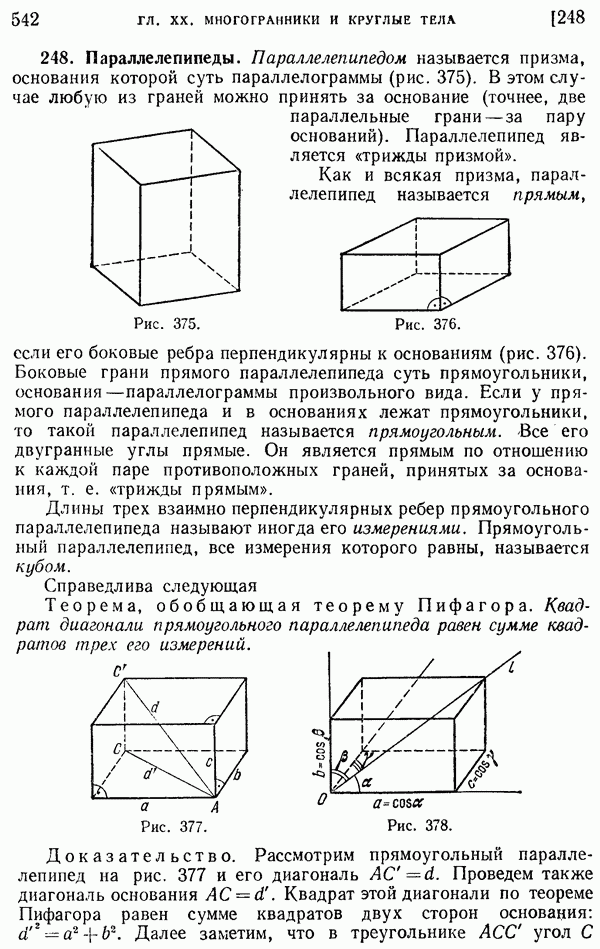
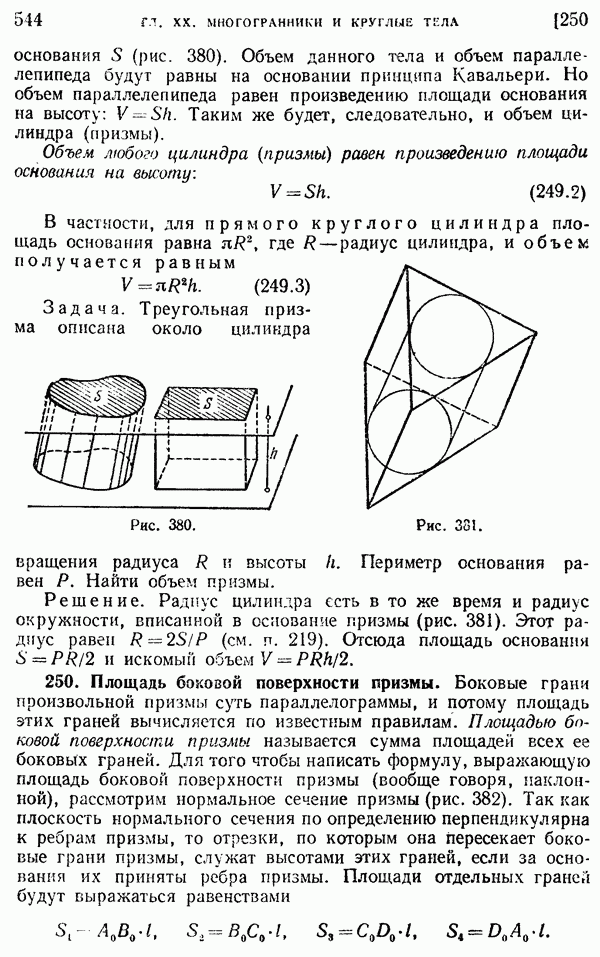
§ 2. Длина окружности. Площадь круга и его частей
229. Длина окружности.
Наглядное представление о длине кривой линии, в частности окружности, как о длине нити, навернутой на эту линию, а затем распрямленной, не позволяет математически обоснованно вычислить длину кривой. Следующее определение длины окружности позволяет вычислить эту длину и принципиально близко к общему определению длины кривой, которое рассматривается в курсах высшей математики.
Определение. Длиной окружности называется общий предел, к которому стремятся периметры вписанных и описанных правильных многоугольников при неограниченном удвоении числа их сторон.
Это значит, что в окружность вписываются (и вокруг нее описываются) правильные многоугольники, например шестиугольник (начинаем с него, как с простейшего), а затем двенадцатиугольник, двадцатичетырехугольник и т. д.
Как доказывается, периметры вписанных и описанных многоугольников стремятся при этом к одному и тому же пределу; этот предел принимается по определению за длину окружности. Можно было бы в определении говорить не об удвоении, а об утроении, упятерении или об увеличении числа сторон на единицу; но удвоение удобнее тем, что при этом рассуждения значительно упрощаются. Можно доказать, что, вообще, периметр правильного многоугольника при неограниченном увеличении числа его сторон стремится к тому же пределу — длине окружности, в которую многоугольник вписан (вокруг которой он описан). Более того, важно лишь, что длины сторон многоугольника стремятся к нулю; при соблюдении этого условия можно даже допустить и произвольные, не обязательно правильные многоугольники (центр окружности должен лежать внутри многоугольников).
Для оправдания данного выше определения длины окружности нам предстоит доказать три утверждения: 1°. Периметры вписанных многоугольников при неограниченном удвоении числа их сторон стремятся к определенному пределу Р. 2°. Периметры описанных многоугольников при том же условии также имеют определенный предел  . Оба указанных предела равны:
. Оба указанных предела равны:  .
.
1°. Периметры вписанных многоугольников при неограниченном удвоении числа их сторон стремятся к определенному пределу:
Действительно, при удвоении числа сторон периметр возрастает:  . В то же время величина этого периметра остается ограниченной; она заведомо не превышает периметра шестиугольника, описанного вокруг данной окружности. По признаку существования предела монотонно возрастающей, ограниченной сверху последовательности (п. 84) предел периметров вписанных многоугольников существует:
. В то же время величина этого периметра остается ограниченной; она заведомо не превышает периметра шестиугольника, описанного вокруг данной окружности. По признаку существования предела монотонно возрастающей, ограниченной сверху последовательности (п. 84) предел периметров вписанных многоугольников существует:

2°. Периметры описанных многоугольников при неограниченном удвоении числа их сторон стремятся к определенному пределу.
Действительно, периметр при этих условиях убывает, но ограничен снизу (подробности оставляем читателю). Полагаем 
3°. Пределы периметров вписанных и описанных многоугольников равны: 
Заметим сначала, что сторона вписанного правильного  -угольника стремится к нулю при увеличении числа его сторон. В самом деле, периметр ограничен, число же сторон стремится к бесконечности; длина одной стороны
-угольника стремится к нулю при увеличении числа его сторон. В самом деле, периметр ограничен, число же сторон стремится к бесконечности; длина одной стороны  будет бесконечно малой величиной при
будет бесконечно малой величиной при 
Далее, апофема вписанного многоугольника при тех же условиях имеет своим пределом радиус окружности. Это видно из неравенства, связывающего радиус, апофему и сторону (см. рис. 314):  .
.
Отсюда  и так как
и так как  , то и
, то и  .
.
Вспомним теперь, что периметры двух правильных  -угольников относятся, как их апофемы. Имеем для вписанного и описанного
-угольников относятся, как их апофемы. Имеем для вписанного и описанного  и при
и при  (например, при неограниченном удвоении числа сторон)
(например, при неограниченном удвоении числа сторон)

По теореме о пределе частного  отсюда получим
отсюда получим

т. е. оба предела, как и требовалось доказать, совпадают. Теперь получается
Основная теорема о длине окружности. Отношение длины окружности к ее диаметру есть постоянная величина, не зависящая от диаметра.
Действительно, имеем

Из этого равенства видно, что отношение длины окружности к ее диаметру, выраженное в виде предела  , не зависит от самого диаметра; оно обозначается яиравно
, не зависит от самого диаметра; оно обозначается яиравно  поэтому мы и пишем быражение для длины окружности в виде
поэтому мы и пишем быражение для длины окружности в виде

Зная длину окружности, нетрудно вычислить длины любых дуг окружности. Пусть требуется, например, определить длину  дуги окружности радиуса R, отвечающей центральному углу
дуги окружности радиуса R, отвечающей центральному углу  радиан). Так как равным центральным углам отвечают равные дуги, то всякая дуга составляет такую долю от полной окружности, какую ее центральный угол
радиан). Так как равным центральным углам отвечают равные дуги, то всякая дуга составляет такую долю от полной окружности, какую ее центральный угол  радиан) составляет от полного угла
радиан) составляет от полного угла  радиан). Отсюда получается пропорция
радиан). Отсюда получается пропорция  и для угла, выраженного в градусной (радианной) мере, имеем соответственно
и для угла, выраженного в градусной (радианной) мере, имеем соответственно

Последняя формула проще:
Длина дуги окружности равна произведению ее радиуса на центральный угол, выраженный в радианах.
В этом проявляется одно из преимуществ радианной меры перед градусной.
Задача 1. Найти длину, дуги в одну секунду на экваторе земного шара.
Решение. Примем экваториальный радиус земного шара за 6300 км. Тогда имеем

Задача 2. Найти длину окружности, вписанной в равнобедренный прямоугольный треугольник с гипотенузой, равной с.
Решение. Имеем для периметра треугольника выражение

Площадь треугольника равна  Но для радиуса вписанной окружности известно соотношение
Но для радиуса вписанной окружности известно соотношение  Отсюда
Отсюда  искомая длина равна
искомая длина равна 
Задача 3. Найти длину дуги окружности радиуса R, отсекаемой от нее прямой, проходящей на расстоянии d от центра окружности 
Решение. Для косинуса половины центрального угла находим

Задача 4. Найти периметр луночки, образованной дугами двух равных окружностей радиуса R, расположенных так, что каждая из них проходит через центр второй.

Рис. 320.
Решение. Имеем по рис.  т. е. треугольник
т. е. треугольник  равносторонний. Поэтому центральный угол МОМ содержит 120°. Каждая из дуг, ограничивающих луночку, составляет одну треть полной окружности, а весь периметр равен
равносторонний. Поэтому центральный угол МОМ содержит 120°. Каждая из дуг, ограничивающих луночку, составляет одну треть полной окружности, а весь периметр равен

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
- 2. Простые и составные числа. Признаки делимости.
- 3. Наибольший общий делитель и наименьшее общее кратное.
- 4. Целые числа. Рациональные числа.
- 5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
- 6. Иррациональные числа. Действительные числа.
- 7. Действия с приближенными числами.
- 8. Числовая ось. Координаты точки на плоскости.
- § 2. Степени и корни
- 9. Степени с натуральными показателями.
- 10. Степени с целыми показателями.
- 11. Корни.
- 12. Степени с рациональными показателями. Степени с действительными показателями.
- 13. Алгоритм извлечения квадратного корня.
- § 3. Комплексные числа
- 14. Основные понятия и определения.
- 15. Рациональные действия с комплексными числами.
- 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
- 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
- 18. Извлечение корня из комплексного числа.
- Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
- 19. Алгебраические выражения. Одночлены и многочлены.
- 20. Формулы сокращенного умножения.
- 21. Бином Ньютона.
- 22. Разложение многочлена на множители.
- 23. Дробные алгебраические выражения.
- § 2. Иррациональные алгебраические выражения
- 24. Радикалы из алгебраических выражений.
- 25. Освобождение от иррациональности в знаменателе дроби.
- Глава III. ЛОГАРИФМЫ
- 26. Определение и свойства логарифмов.
- 27. Логарифмы по различным основаниям. Модуль перехода.
- § 2. Десятичные логарифмы
- 28. Характеристика и мантисса десятичного логарифма.
- 29. Применение десятичных логарифмов к вычислениям.
- Глава IV. ФУНКЦИИ И ГРАФИКИ
- 30. Величина. Числовые множества.
- 31. Определение функции.
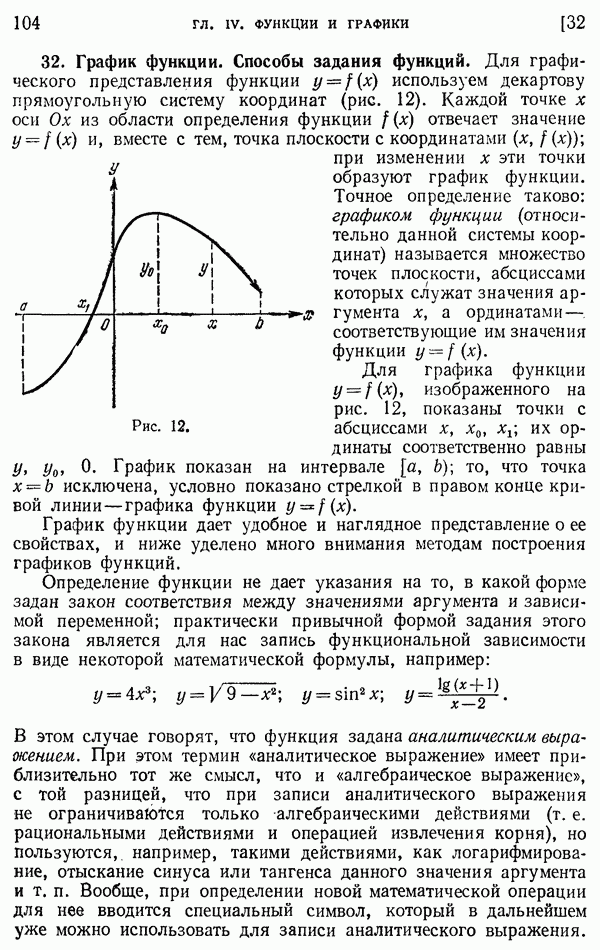
- 32. График функции. Способы задания функций.
- 33. Элементарное исследование поведения функции.
- 34. Сложная функция.
- 35. Обратная функция.
- 36. Функции нескольких переменных.
- § 2. Элементарные функции
- 37. Обзор элементарных функций.
- 38. Линейная функция.
- 39. Квадратичная функция у=ах^2.
- 40. Степенная функция у = х^n.
- 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
- 42. Показательная функция.
- 43. Логарифмическая функция.
- § 3. Преобразование графиков
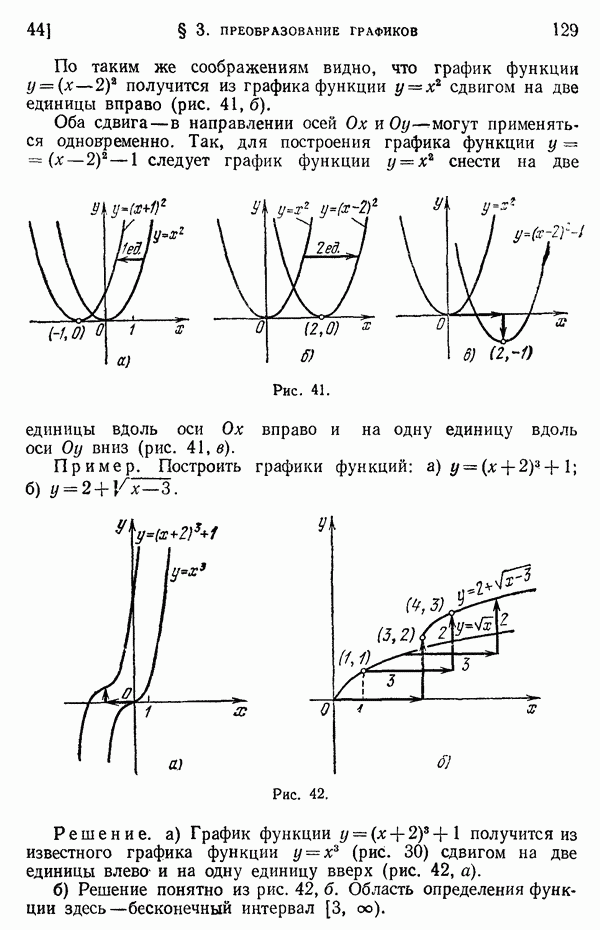
- 44. Параллельный сдвиг графика.
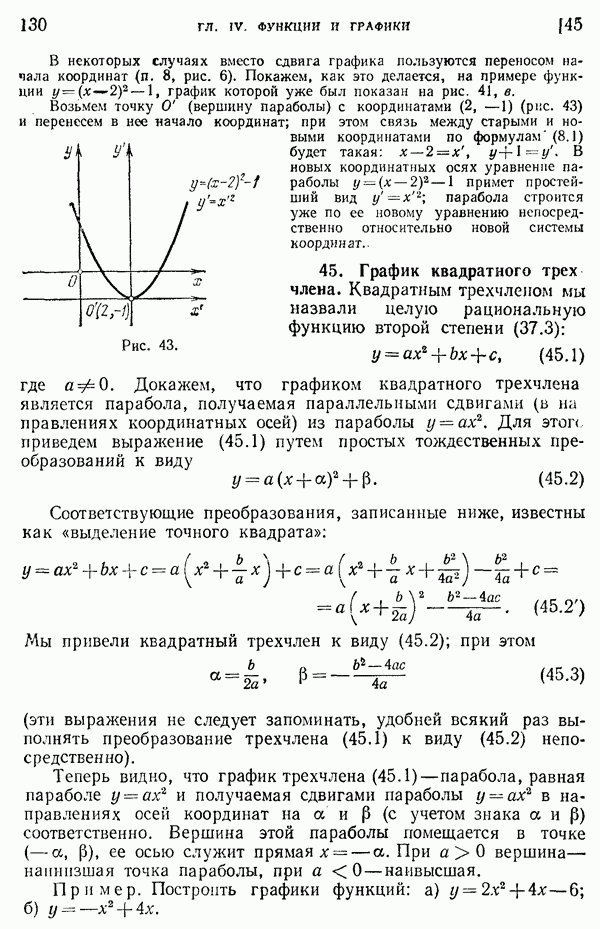
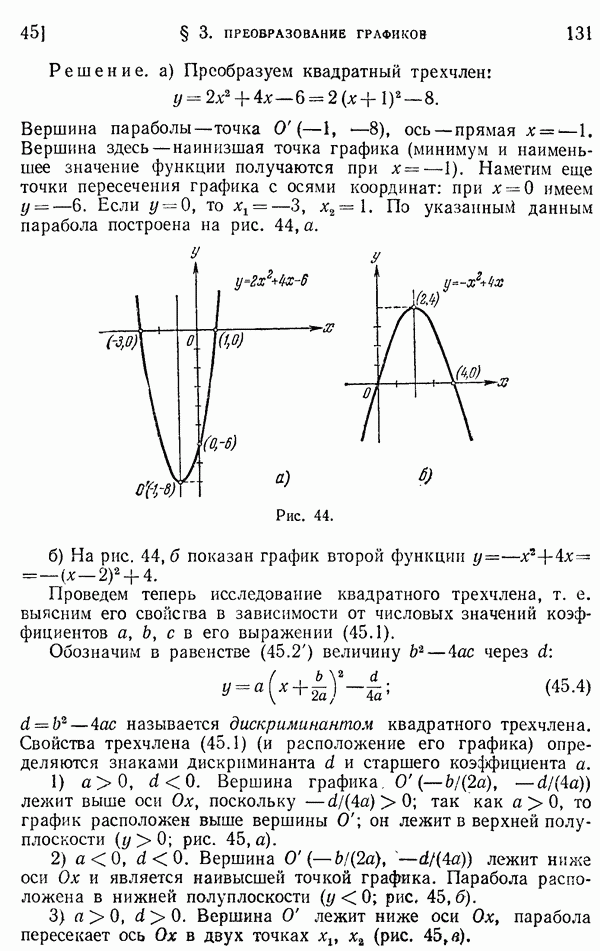
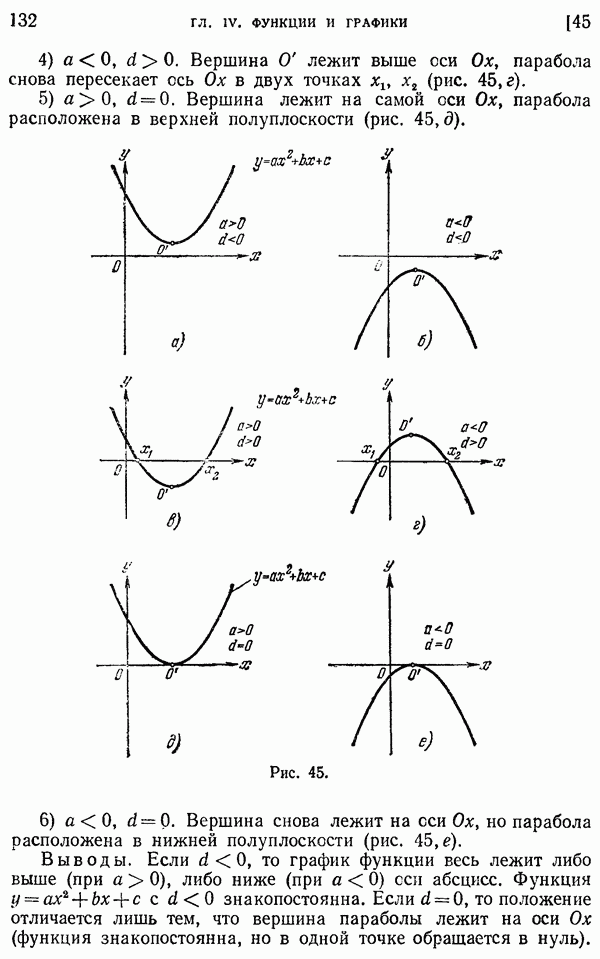
- 45. График квадратного трех члена.
- 46. График дробно-линейной функции.
- 47. Преобразование симметрии. Сжатие и растяжение графика.
- 48. Построение графиков функций.
- 49. Сложение графиков.
- § 4. Некоторые сведения о рациональных функциях
- 50. Целые и дробные рациональные функции. Деление многочленов.
- 51. Схема Горнера. Теорема Безу.
- 52. Нули многочлена. Разложение многочлена на множители.
- Глава V. УРАВНЕНИЯ
- 53. Уравнение. Корни уравнения.
- 54. Равносильные уравнения.
- 55. Системы уравнений.
- 56. Графическое решение уравнений.
- §. 2. Алгебраические уравнения с одной неизвестной
- 57. Число и кратность корней.
- 58. Уравнения первой степени (линейные уравнения).
- 59. Уравнения второй степени (квадратные уравнения).
- 60. Формулы Виета. Разложение квадратного трехчлена на множители.
- 61. Исследование квадратного уравнения.
- 62. Уравнения высших степеней. Целые корни.
- 63. Двучленные уравнения.
- 64. Уравнения, сводящиеся к квадратным.
- 65. Возвратные уравнения.
- § 3. Системы алгебраических уравнений
- 66. Линейные системы.
- 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
- 68. Системы, состоящие из уравнения второй степени и линейного уравнения.
- 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
- § 4. Иррациональные, показательные и логарифмические уравнения
- 70. Иррациональные уравнения.
- 71. Показательные уравнения.
- 72. Логарифмические уравнения.
- 73. Разные уравнения. Системы уравнений.
- Глава VI. НЕРАВЕНСТВА
- 74. Свойства неравенств. Действия над неравенствами.
- 75. Алгебраические неравенства.
- § 2. Решение неравенств
- 76. Множество решений неравенства. Равносильные неравенства.
- 77. Графическое решение неравенств.
- 79. Квадратные неравенства.
- 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
- 81. Иррациональные, показательные и логарифмические неравенства.
- 82. Неравенства с двумя неизвестными.
- Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
- 83. Числовая последовательность.
- 84. Предел числовой последовательности.
- 85. Бесконечно малые. Правила предельного перехода.
- § 2. Арифметическая прогрессия
- 86. Арифметическая прогрессия. Формула общего члена.
- 87. Свойства арифметической прогрессии.
- 88. Формула для суммы n членов арифметической прогрессии.
- § 3. Геометрическая прогрессия
- 89. Геометрическая прогрессия. Формула общего члена.
- 90. Свойства геометрической прогрессии.
- 91. Формулы для суммы n членов геометрической прогрессии.
- 92. Бесконечно убывающая геометрическая прогрессия.
- Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
- 93. Вектор, проекция вектора.
- 94. Положительные углы и дуги, меньшие 360°.
- 95. Углы и дуги, большие 360°.
- 96. Отрицательные углы. Сложение и вычитание углов.
- § 2. Тригонометрические функции произвольного угла
- 97. Определение основных тригонометрических функций.
- 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
- § 3. Соотношения между тригонометрическими функциями одного и того же угла
- 99. Основные тригонометрические тождества.
- 100. Вычисление значений тригонометрических функций по значению одной из них.
- 101. Значения тригонометрических функций некоторых углов.
- § 4. Четность, нечетность и периодичность тригонометрических функций
- 102. Четность и нечетность.
- 103. Понятие периодической функции.
- 104. Периодичность тригонометрических функций.
- § 5. Формулы приведения
- 105. Зависимость между тригонометрическими функциями дополнительных углов.
- 106. Формулы приведения.
- Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
- § 1. Тригонометрические функции числового аргумента
- 108. Области определения и области изменения значений тригонометрических функций.
- 109. Некоторые неравенства и их следствия.
- § 2. Графики тригонометрических функций
- 110. Первоначальные сведения о таблицах тригонометрических функций.
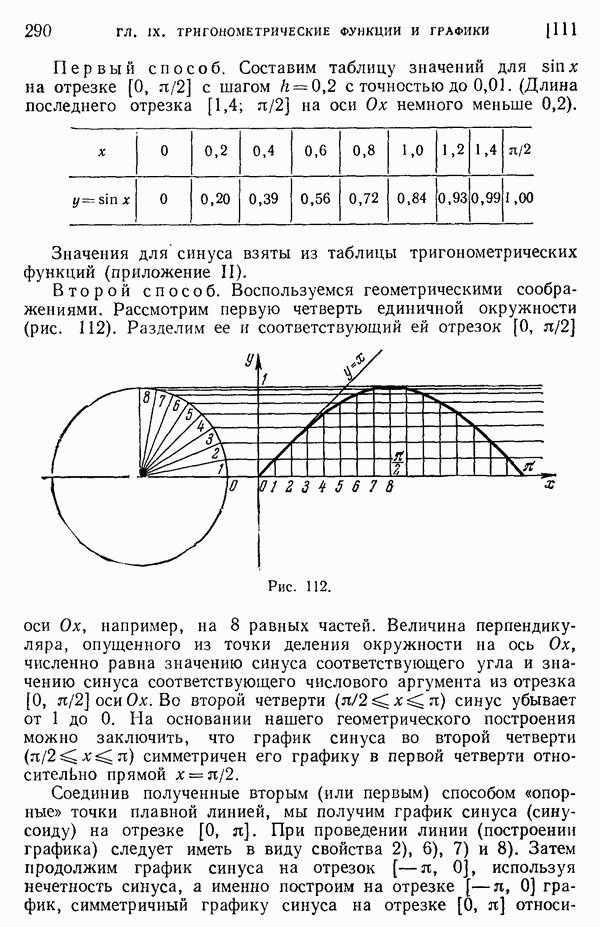
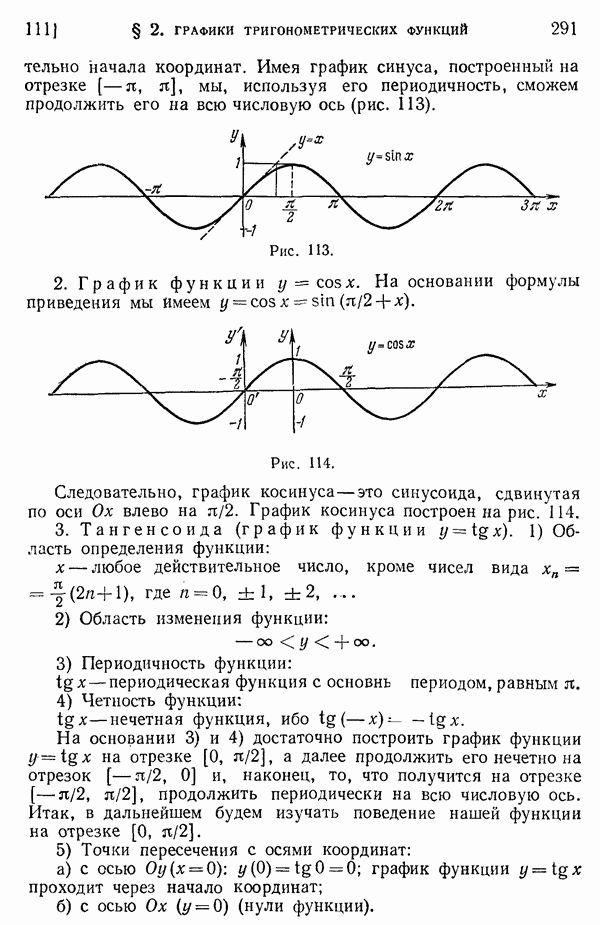
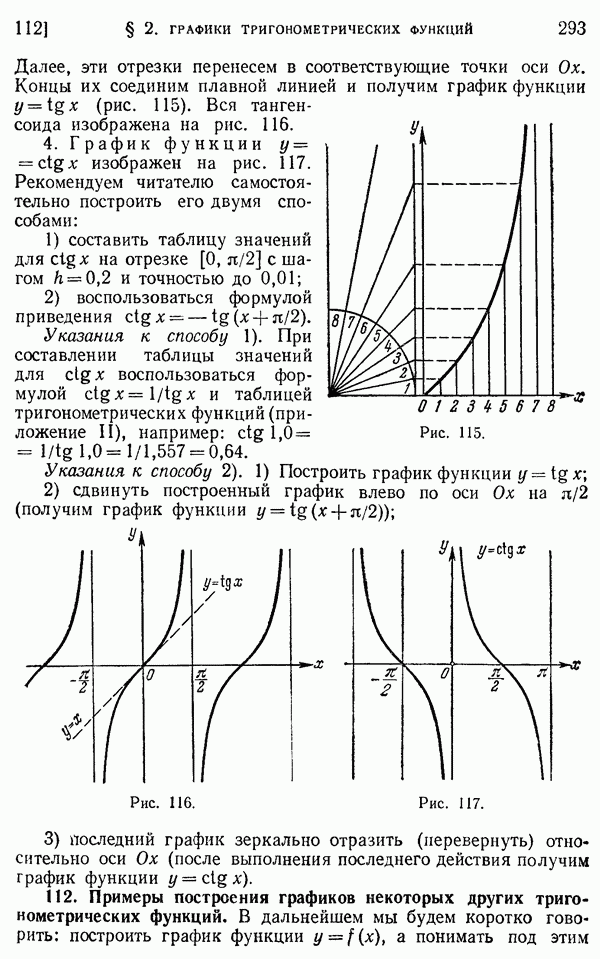
- 111. Основные графики.
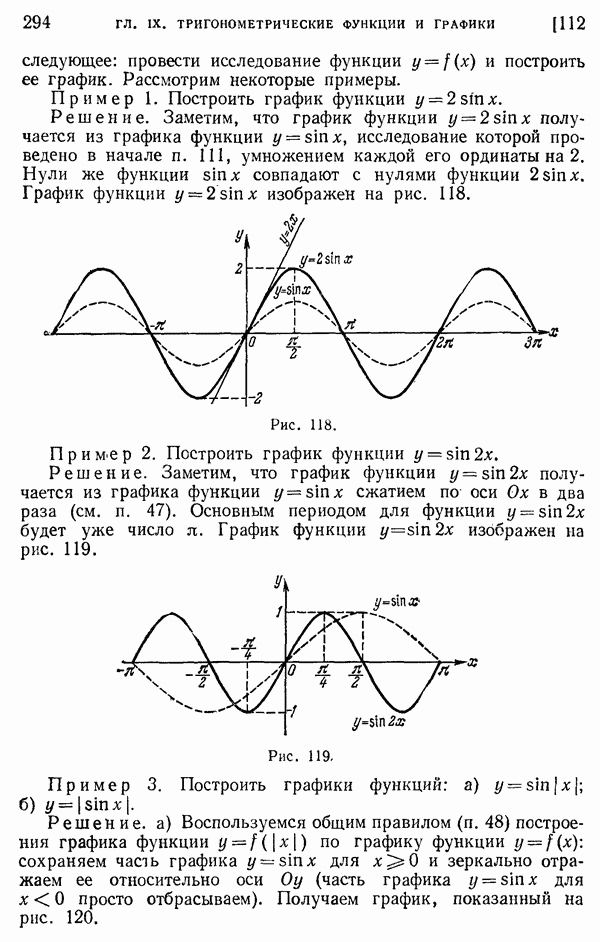
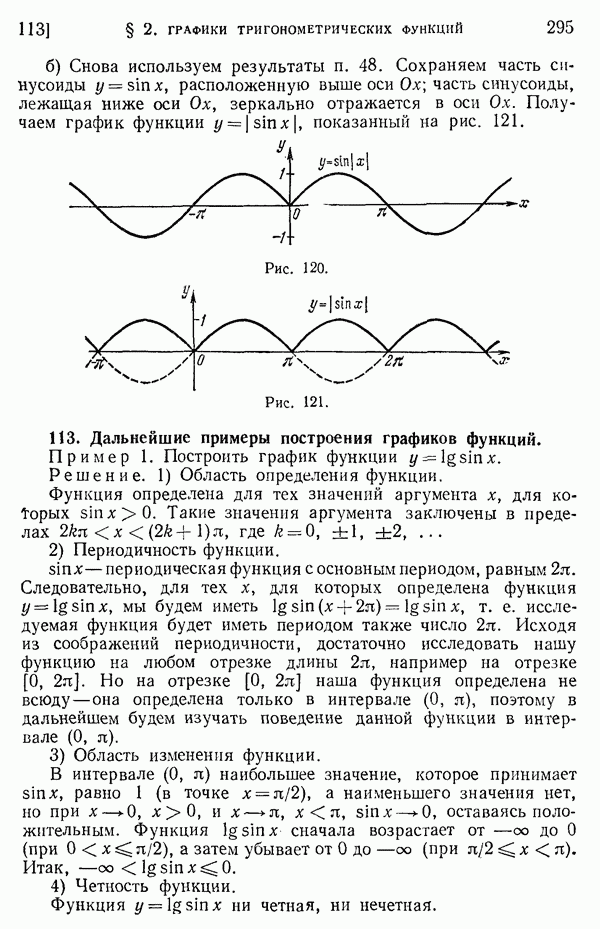
- 112. Примеры построения графиков некоторых других тригонометрических функций.
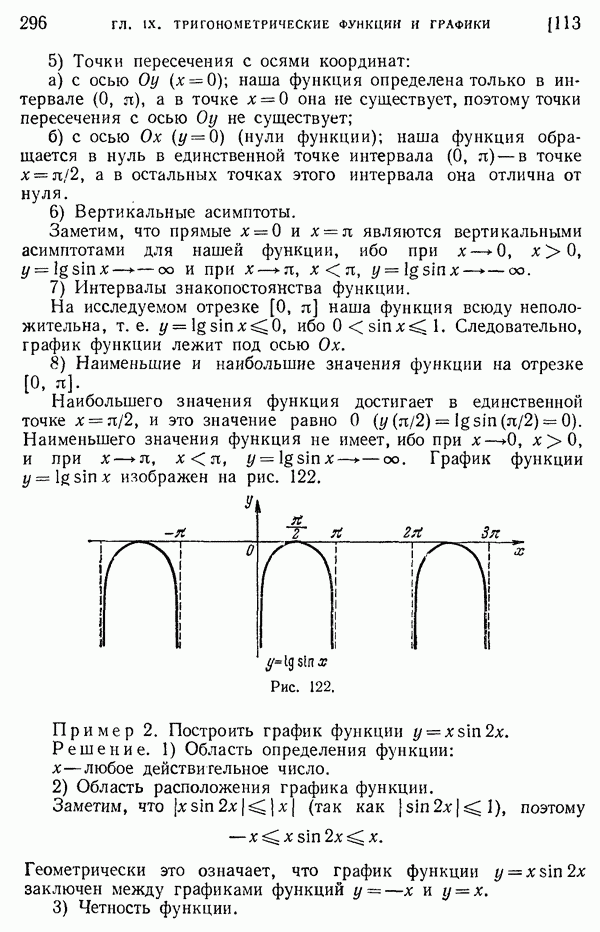
- 113. Дальнейшие примеры построения графиков функций.
- Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
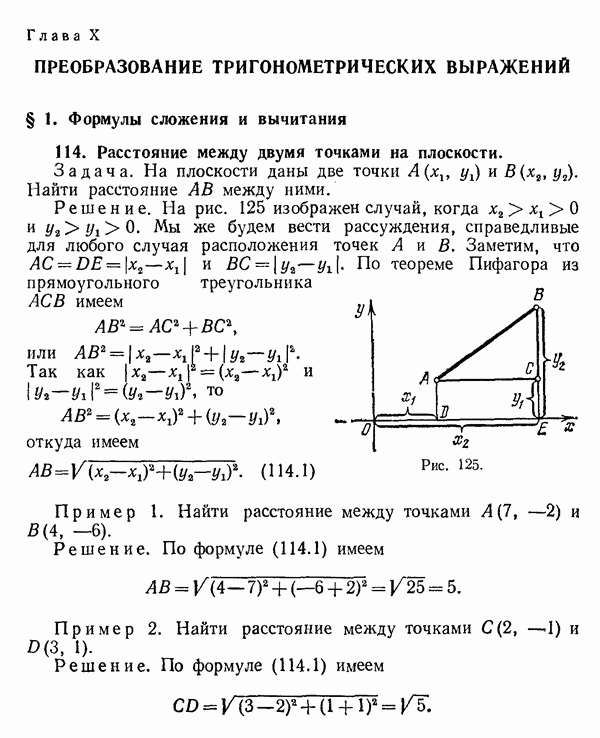
- 114. Расстояние между двумя точками на плоскости.
- 115. Косинус суммы и разности двух аргументов.
- 116. Синус суммы и разности двух аргументов.
- 117. Тангенс суммы и разности двух аргументов.
- 118. О формулах сложения для нескольких аргументов.
- § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
- 119. Тригонометрические функции двойного аргумента.
- 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
- 121. Тригонометрические функции половинного аргумента.
- 122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
- § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
- § 4. Преобразование в произведение сумм вида
- § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
- 127. Преобразование в произведение выражения a•sina + b•cosa.
- 128. Преобразование в произведение выражений a•sina+b и a•cosa+b
- 129. Преобразование в произведение выражения a•tga+b.
- Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
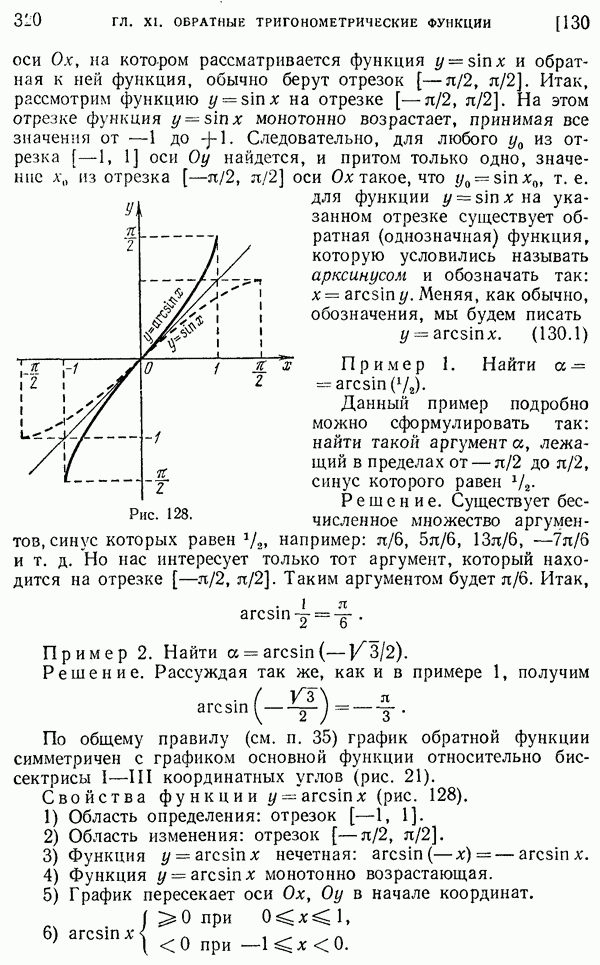
- 130. Функция у = arcsin x (арксинус).
- 131. Функция y = arccos x (арккосинус).
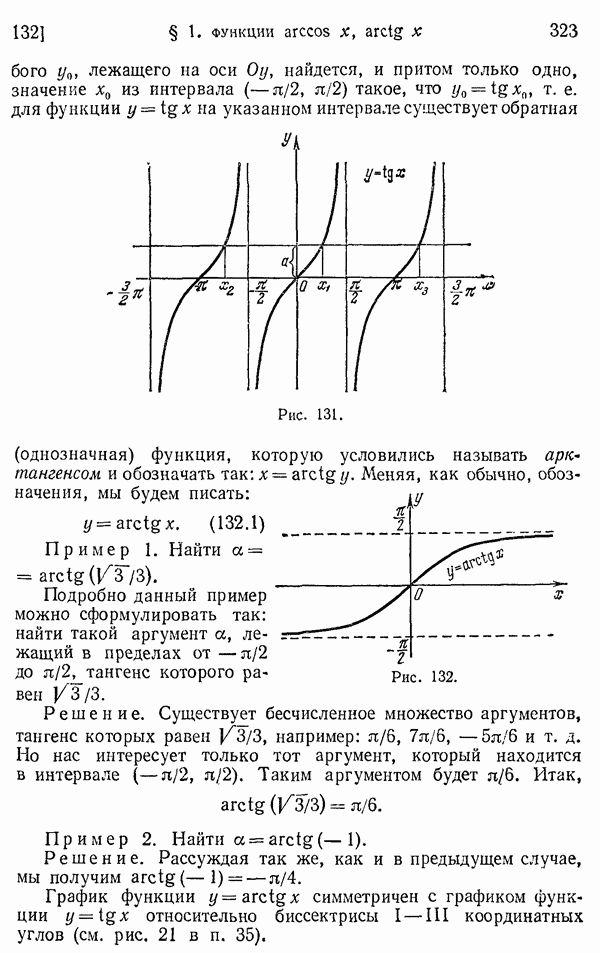
- 132. Функция y = arctg x (арктангенс).
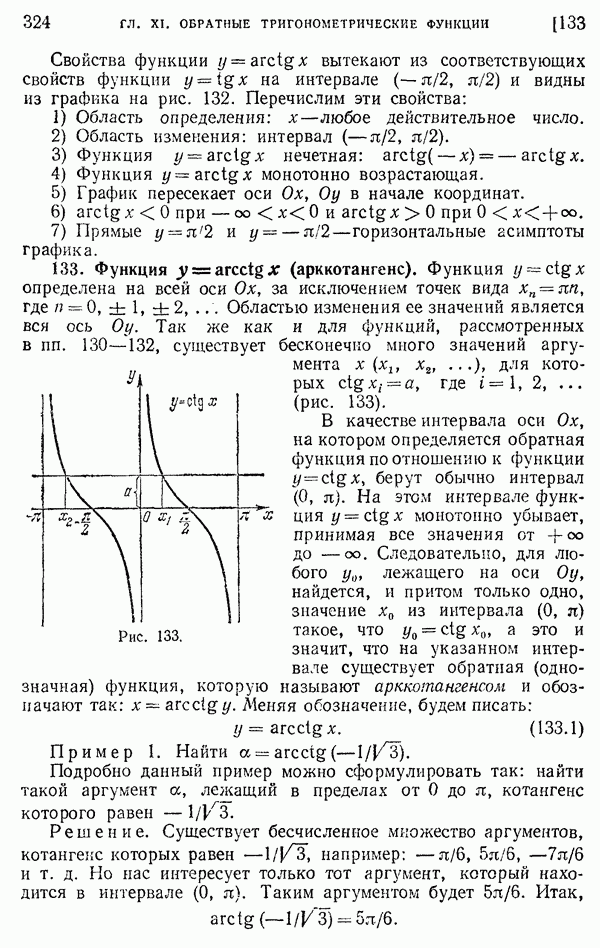
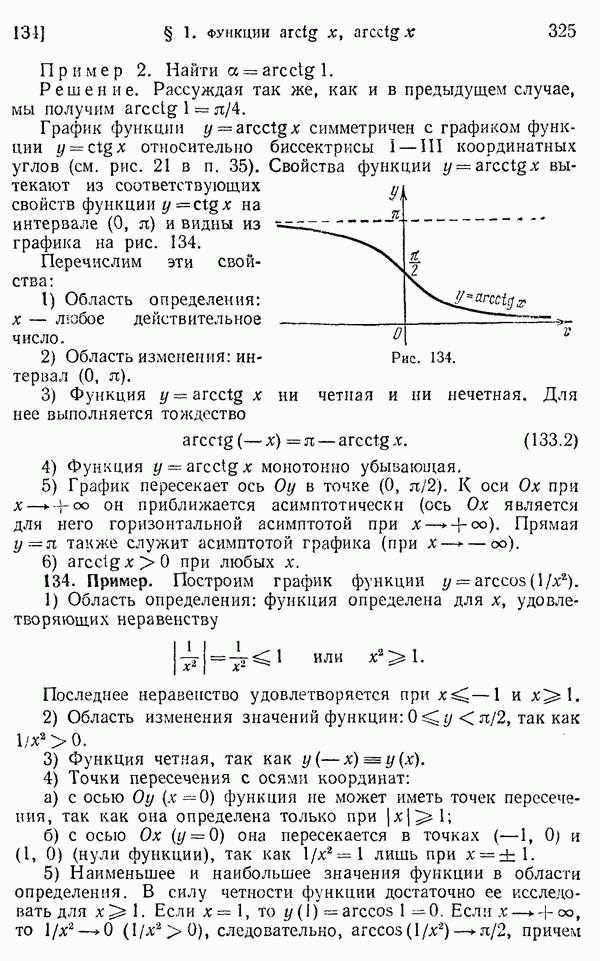
- 133. Функция y = arcctg x (арккотангенс).
- 134. Пример.
- § 2. Операции над обратными тригонометрическими функциями
- 135. Тригонометрические операции.
- 136. Операции сложения (вычитания).
- § 3. Обратные тригонометрические операции над тригонометрическими функциями
- 137. Функция у = arcsin (sin x).
- 138. Функция y = arctg (tg x).
- Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
- 139. Уравнение sin х = а.
- 140. Уравнение cos х = a.
- 141. Уравнение tg x = a.
- 142. Уравнение ctg x = a.
- 143. Некоторые дополнения.
- § 2. Способ приведения к одной функции одного и того же аргумента
- 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
- 146. Способ разложения на множители.
- 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
- § 3. Некоторые частные приемы решения тригонометрических уравнений и систем
- 148. Введение вспомогательного аргумента.
- 149. Преобразование произведения в сумму или разность.
- 150. Переход к функциям удвоенного аргумента.
- 151. Решение уравнения типа…
- 152. Применение подстановок sinx ± соsx = y.
- § 4. Решение тригонометрических неравенств
- 154. Простейшие тригонометрические неравенства.
- 155. Примеры тригонометрических неравенств, сводящихся к простейшим.
- Часть вторая. ГЕОМЕТРИЯ
- 156. Точка. Прямая. Луч. Отрезок.
- 157. Плоскость. Фигуры и тела.
- 160. Равенство фигур. Движение.
- 161. Равенство тел.
- § 2. Измерение геометрических величин
- 162. Сложение отрезков. Длина отрезка.
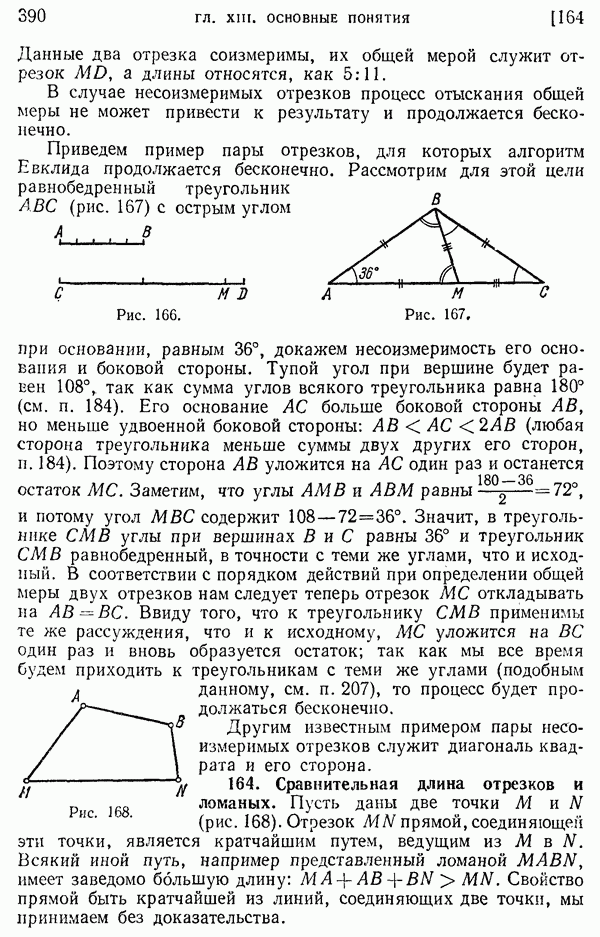
- 163. Общая мера двух отрезков.
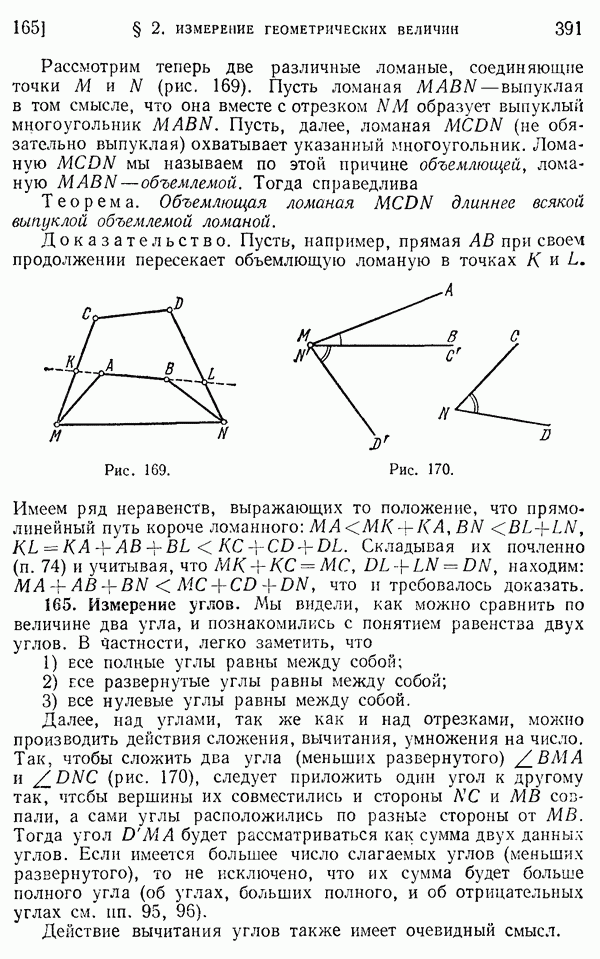
- 164. Сравнительная длина отрезков и ломаных.
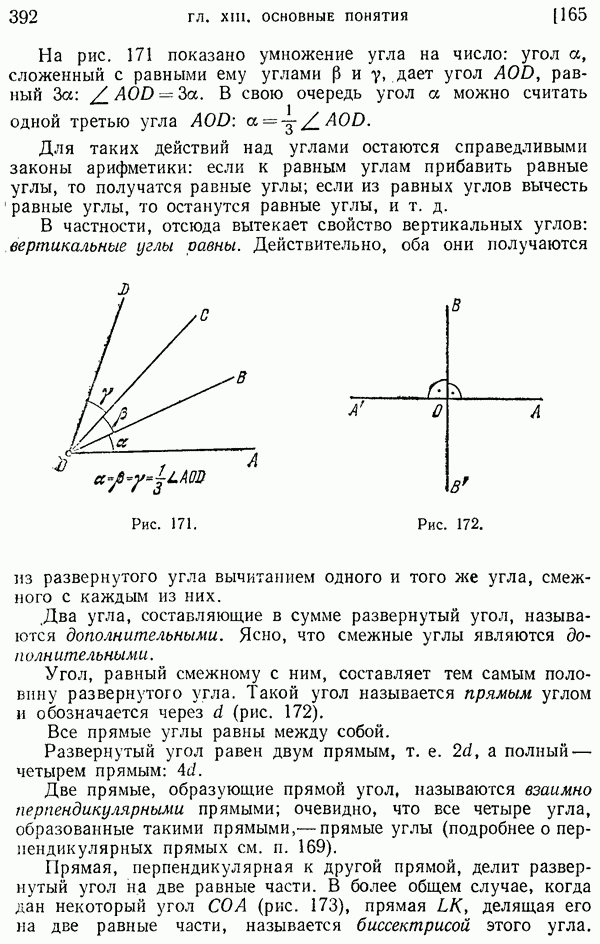
- 165. Измерение углов.
- 166. Радианная мера угла.
- 167. Измерение площадей.
- 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
- Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
- 169. Перпендикуляр и наклонные.
- 170. Свойство перпендикуляра, проведенного к отрезку в его середине.
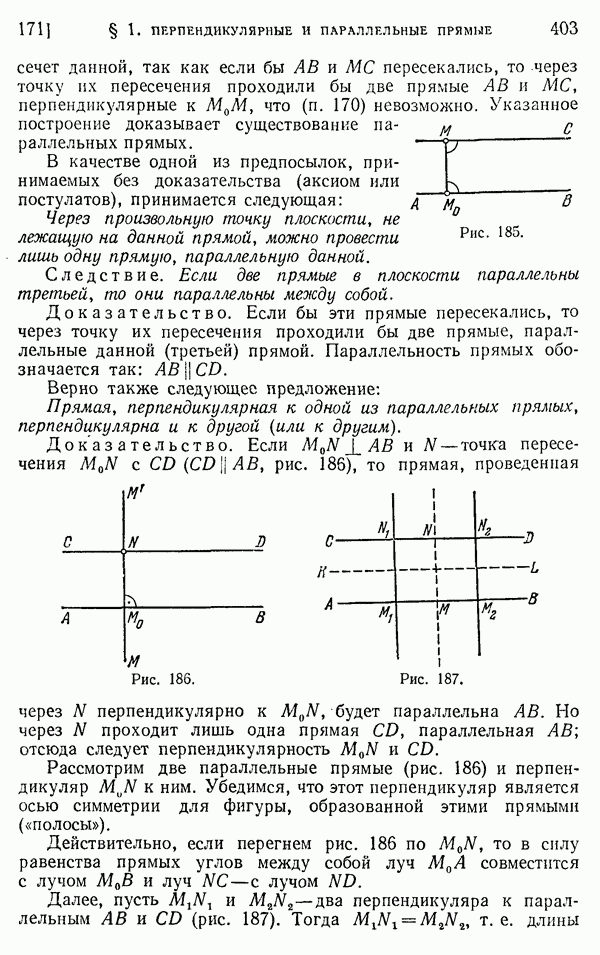
- 171. Параллельные прямые.
- 172. Углы, образованные двумя параллельными прямыми и секущей.
- 173. Углы с параллельными или перпендикулярными сторонами.
- § 2. Геометрические места точек. Окружность
- 174. Геометрическое место точек.
- 175. Свойство биссектрисы угла.
- 176. Окружность.
- 177. Взаимное расположение прямой и окружности. Касательная и секущая.
- 178. Хорда и диаметр. Сектор и сегмент.
- 179. Взаимное расположение двух окружностей.
- § 3. Основные задачи на построение
- 181. Деление отрезка пополам. Построение перпендикуляров.
- 182. Построение углов.
- 183. Другие задачи на построение.
- Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
- 184. Стороны и углы треугольника.
- 185. Биссектрисы треугольника. Вписанная окружность.
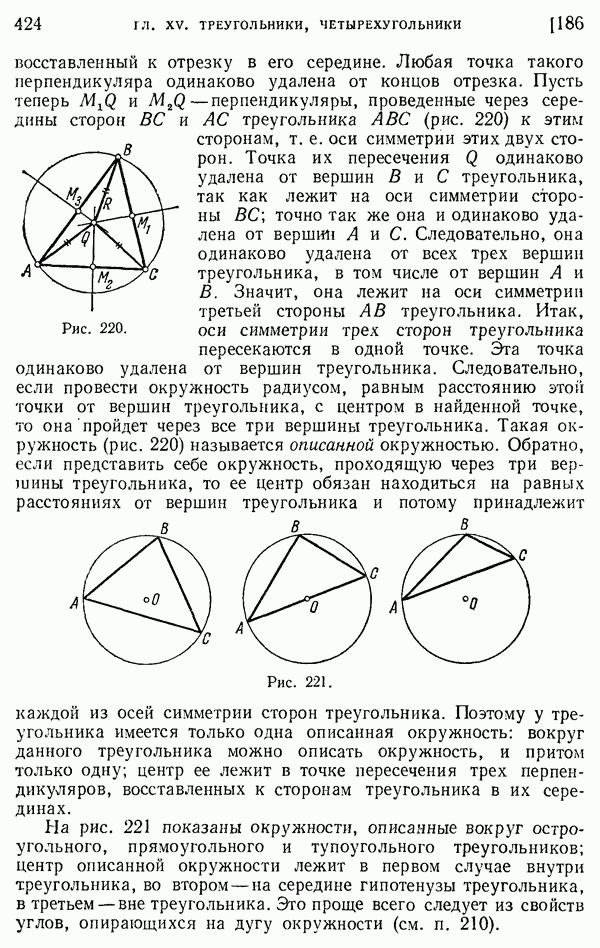
- 186. Оси симметрии сторон треугольника. Описанная окружность.
- 187. Медианы и выcоты треугольника.
- 188. Равенство треугольников.
- 189. Построение треугольников.
- 190. Равнобедренные треугольники.
- 191. Прямоугольные треугольники.
- § 2. Параллелограммы
- 192. Четырехугольники.
- 193. Параллелограмм и его свойства.
- 194. Прямоугольник.
- § 3. Трапеция
- 196. Трапеция.
- 197. Средняя линия треугольника.
- 198. Средняя линия трапеции.
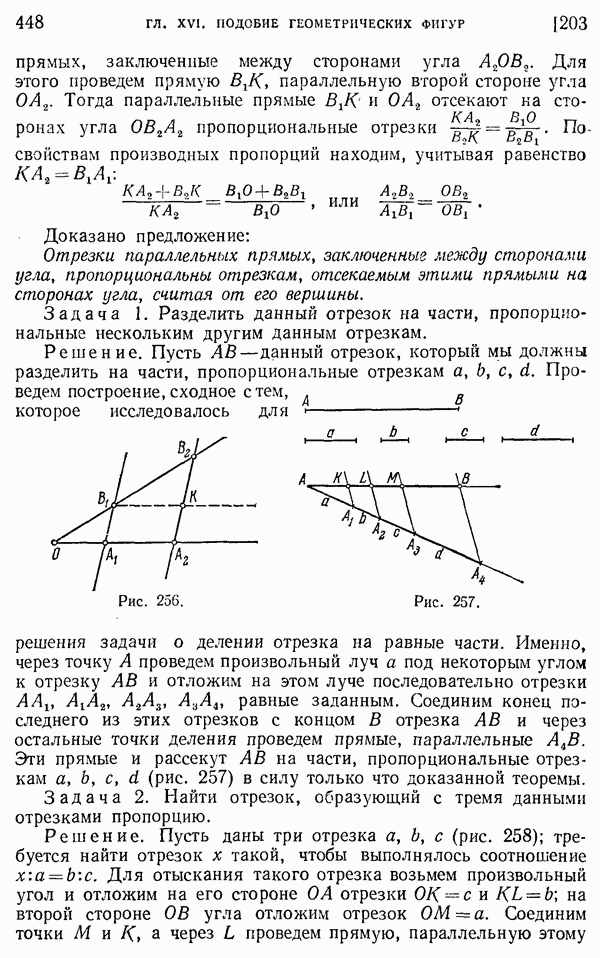
- 199. Деление отрезка на равные части.
- § 4. Площади треугольников и четырехугольников
- 200. Площадь параллелограмма.
- 201. Площадь треугольника.
- 202. Площадь трапеции.
- Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
- 203. Пропорциональные отрезки.
- 204. Свойства биссектрис внутреннего и внешнего углов треугольника.
- § 2. Подобное преобразование фигур (гомотетия)
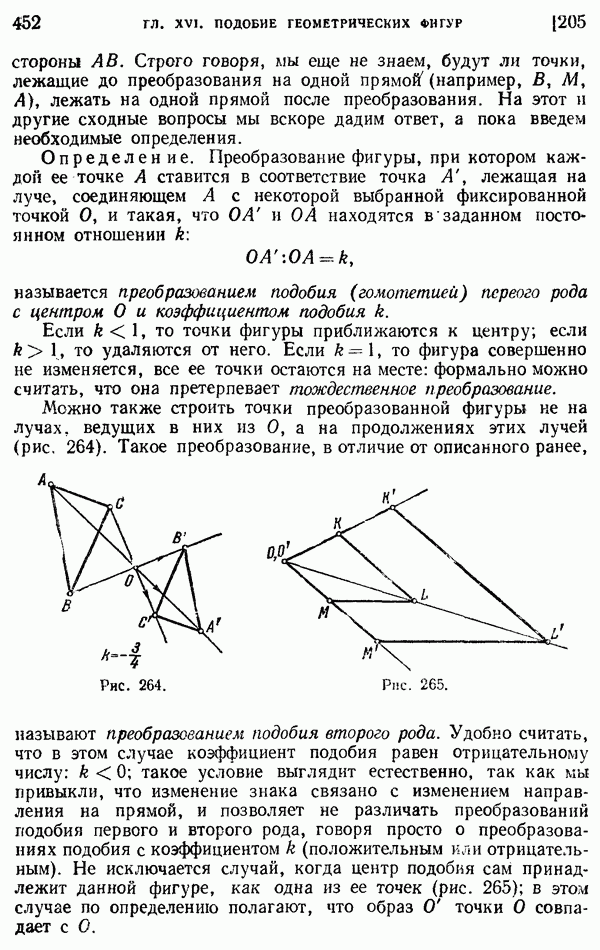
- 205. Определение гомотетичных фигур.
- 206. Свойства преобразования подобия.
- § 3. Общее подобное соответствие фигур
- 207. Подобные фигуры.
- 208. Периметры и площади подобных треугольников.
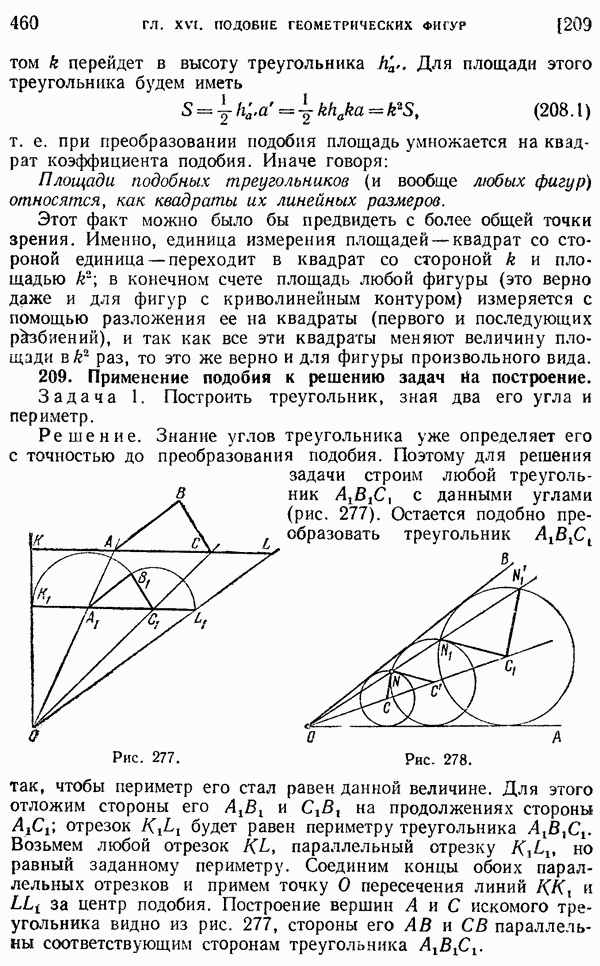
- 209. Применение подобия к решению задач на построение.
- Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
- 210. Углы с вершиной на окружности.
- 211. Углы с вершиной внутри и вне круга.
- 212. Угол, под которым виден данный отрезок.
- 213. Четырехугольники, вписанные в окружность.
- 214. Пропорциональные отрезки в круге.
- 215. Задачи на построение.
- § 2. Метрические соотношения в треугольнике
- 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора.
- 218. Теорема синусов. Формула Герона.
- 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
- 218. Теорема синусов. Формула Герона.
- 219. Радиусы вписанной и описанной окружностей.
- § 3. Решение треугольников
- 220. Таблицы функций.
- 221. Решение треугольников. Сводка основных формул.
- 222. Решение прямоугольных треугольников.
- 223. Решение косоугольных треугольников.
- Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
- 224. Выпуклые многоугольники.
- 225. Правильные многоугольники.
- 226. Соотношения между стороной, радиусом и апофемой.
- 227. Периметр и площадь правильного n-угольника.
- 228. Удвоение числа сторон правильного многоугольника.
- § 2. Длина окружности. Площадь круга и его частей
- 229. Длина окружности.
- 230. Площадь круга и его частей.
- Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
- 231. Взаимное расположение двух прямых в пространстве.
- 232. Взаимное расположение прямой линии и плоскости.
- 233. Взаимное расположение двух плоскостей.
- 234. Свойства параллельных прямых и плоскостей.
- 235. Построения в стереометрии.
- § 2. Перпендикулярность прямых и плоскостей
- 236. Перпендикуляр к плоскости.
- 237. Перпендикуляр и наклонные.
- 238. Угол между прямой и плоскостью.
- 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
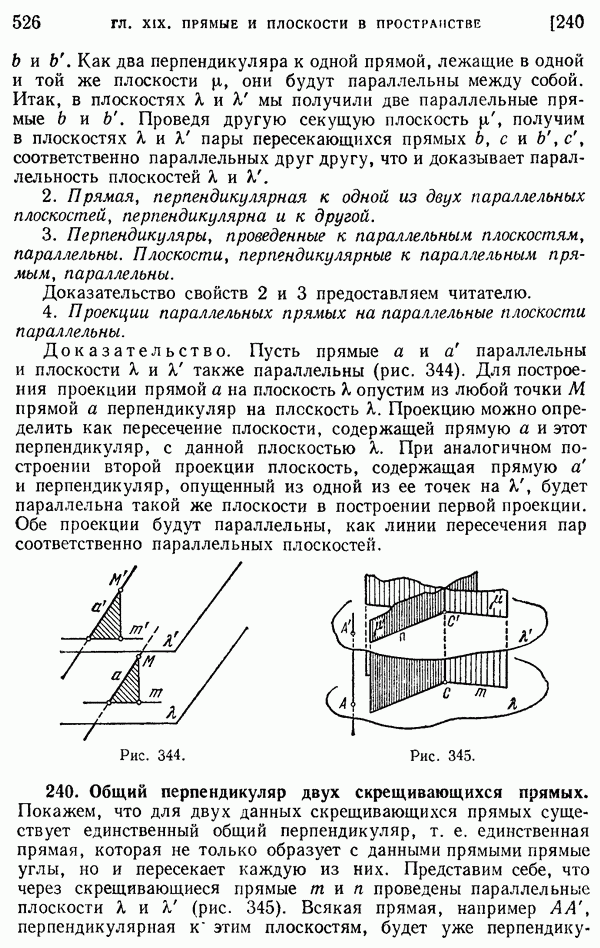
- 240. Общий перпендикуляр двух скрещивающихся прямых.
- § 3. Двугранные и многогранные углы
- 241. Двугранный угол.
- 242. Взаимно перпендикулярные плоскости.
- 243. Трехгранные углы.
- 244. Многогранные углы.
- § 4. Многогранники
- 245. Многогранники.
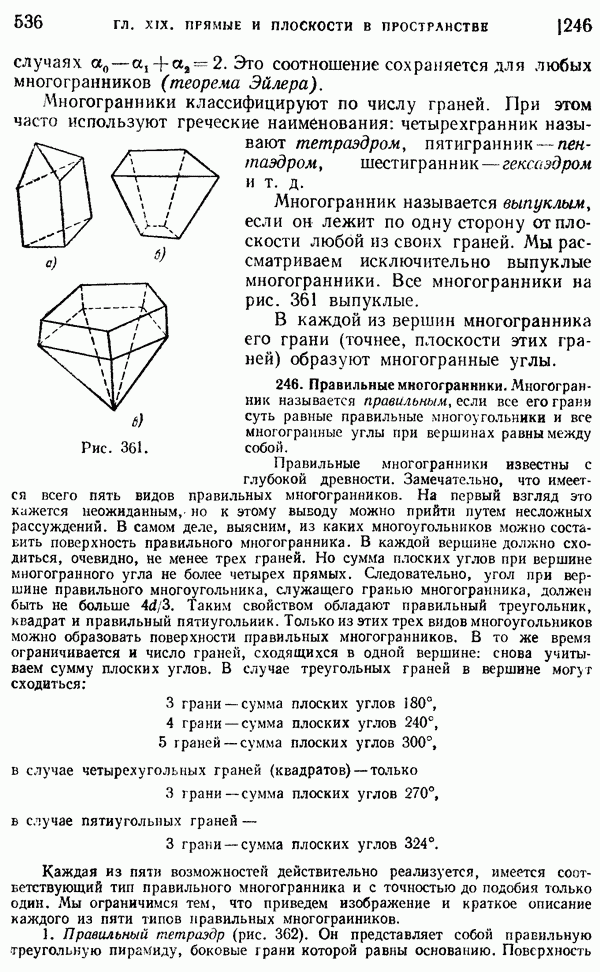
- 246. Правильные многогранники.
- Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
- 247. Цилиндры и призмы.
- 248. Параллелепипеды.
- 249. Объемы призм и цилиндров.
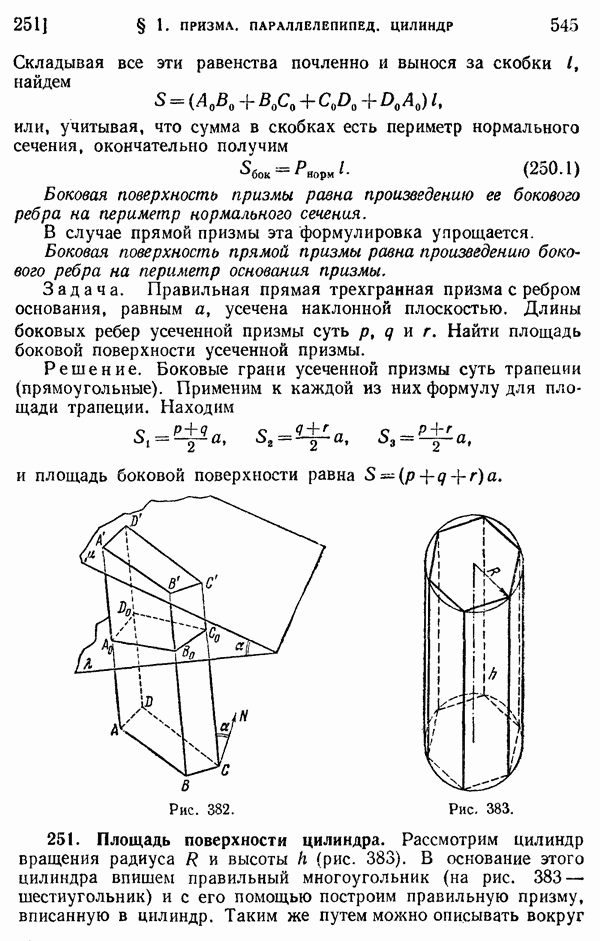
- 250. Площадь боковой поверхности призмы.
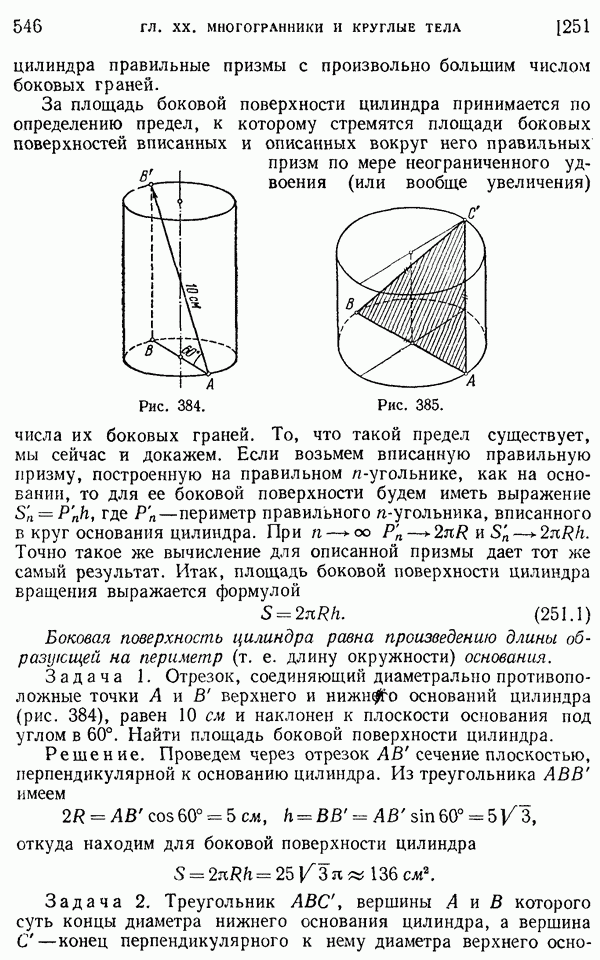
- 251. Площадь поверхности цилиндра.
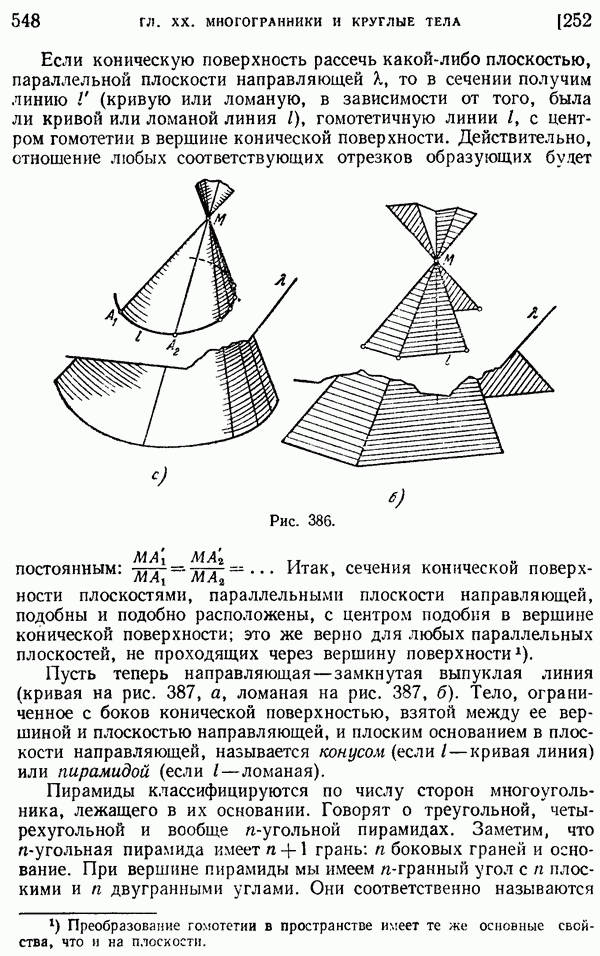
- § 2. Пирамида. Конус
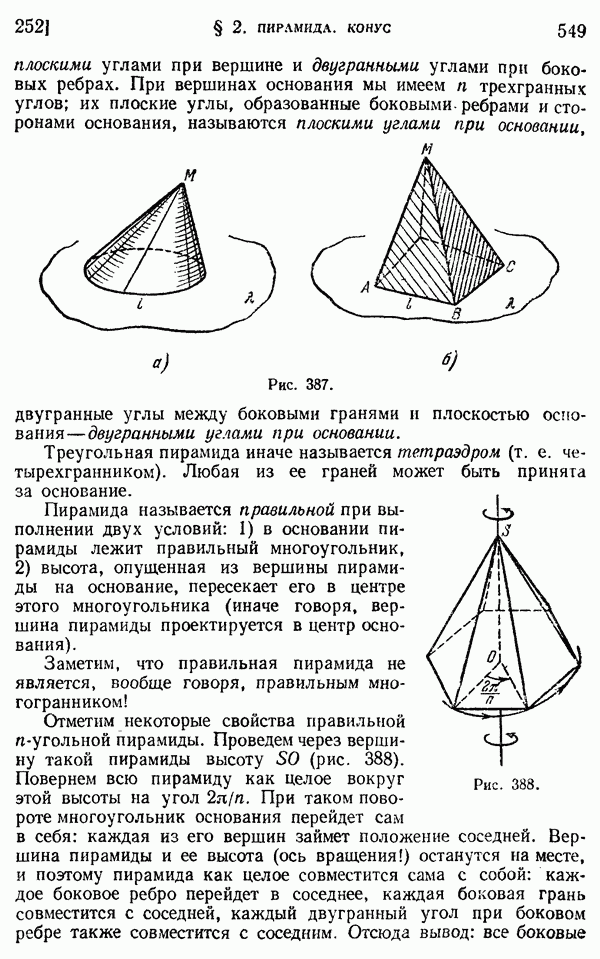
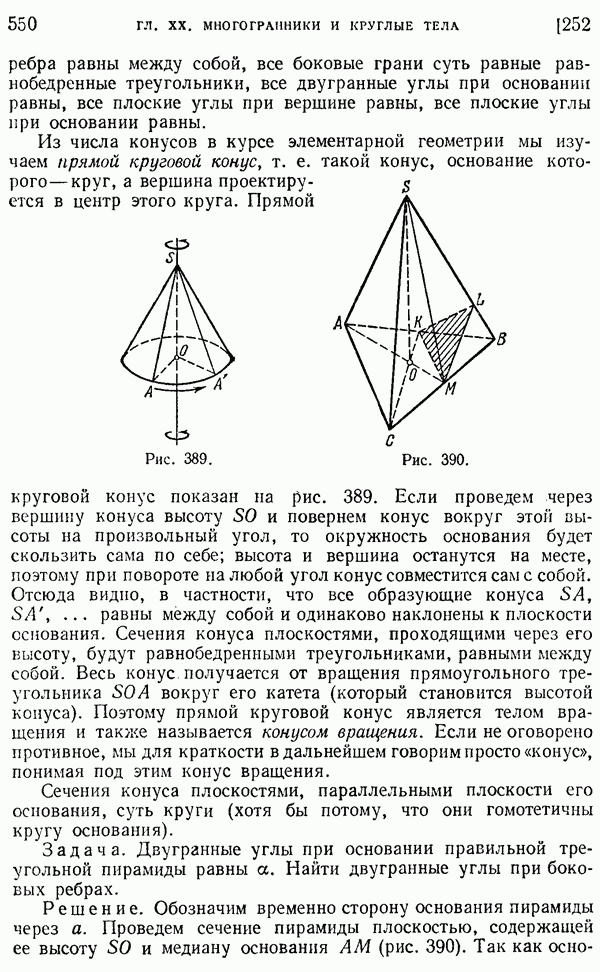
- 252. Свойства пирамиды и конуса.
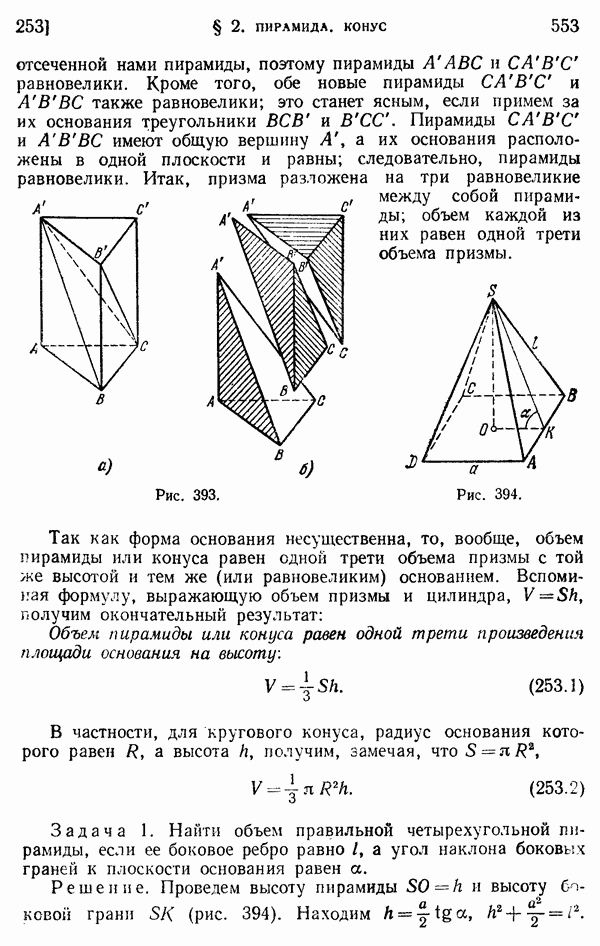
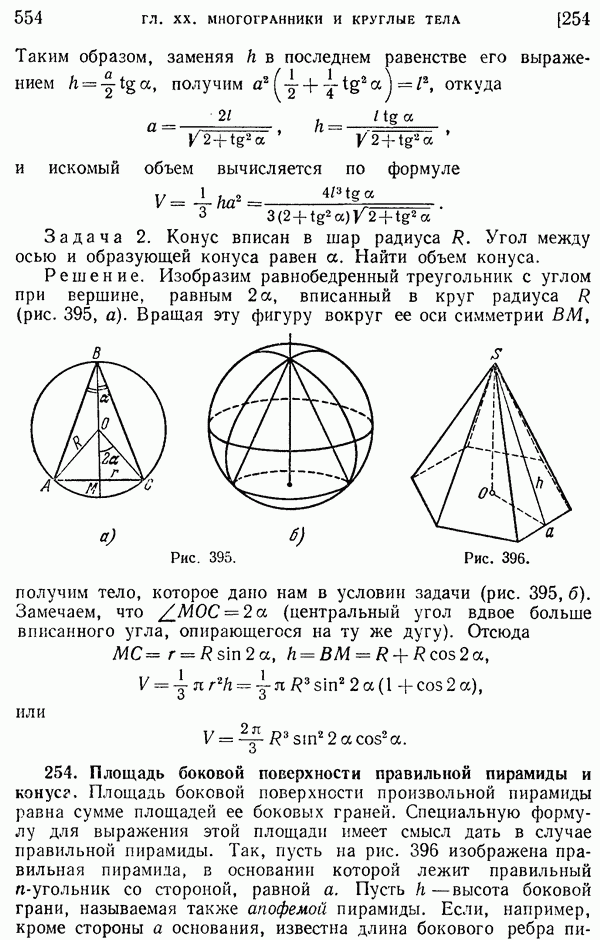
- 253. Объем пирамиды и конуса.
- 254. Площадь боковой поверхности правильной пирамиды и конуса.
- 255. Усеченный конус и усеченная пирамида.
- § 3. Шаровая поверхность. Шар
- 256. Шар и шаровая поверхность.
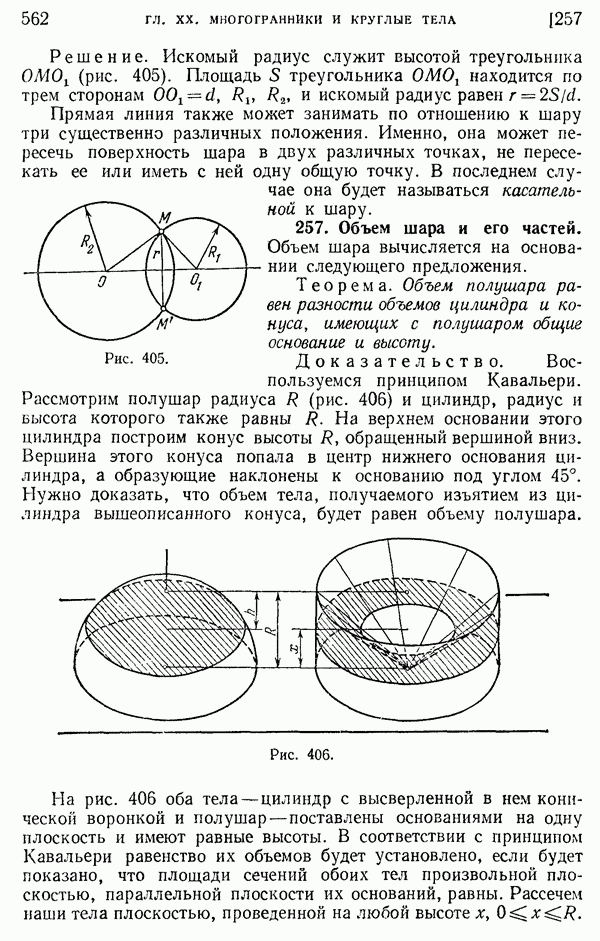
- 257. Объем шара и его частей.
- 258. Площадь поверхности шара и ее частей.
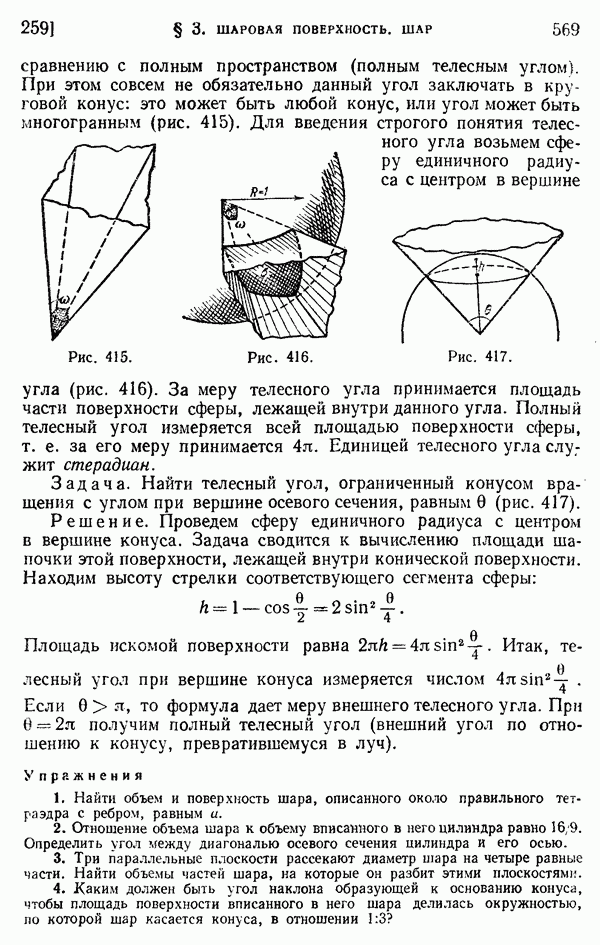
- 259. Понятие телесного угла.
- Ответы к упражнениям
- Приложения