| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
В п. 2.2 мы показали, как световые лучи захватываются и направляются по зигзагообразной траектории вдоль оптического волокна со ступенчатым профилем показателя преломления за счет полного внутреннего отражения на границе раздела сердцевина—оболочка. Такая модель распространения света является, однако, весьма приблизительной, хотя и удовлетворительной с практической точки зрения в тех случаях, когда радиус сердцевины превосходит длину волны распространяющегося излучения. Для волокон с малыми радиусами сердцевины  мкм), т. е. в тех случаях, когда К становится сравнима с а, лучевое приближение уже не дает нужной точности и приходится прибегать с электромагнитному анализу, основанному на уравнениях Максвелла. Как было уже показано в п. 2.4, степень применимости лучевой модели для анализа процессов в конкретном волокне оценивается с помощью параметра V [см. уравнение (2.6) ]. Обычно, чтобы описать процесс распространения излучения в волокнах, имеющих V с 10, приходится привлекать аппарат волновой оптики.
мкм), т. е. в тех случаях, когда К становится сравнима с а, лучевое приближение уже не дает нужной точности и приходится прибегать с электромагнитному анализу, основанному на уравнениях Максвелла. Как было уже показано в п. 2.4, степень применимости лучевой модели для анализа процессов в конкретном волокне оценивается с помощью параметра V [см. уравнение (2.6) ]. Обычно, чтобы описать процесс распространения излучения в волокнах, имеющих V с 10, приходится привлекать аппарат волновой оптики.
Таким образом, для полного описания распространения излучения в оптических волокнах мы используем электромагнитный модовый анализ, подобный описанному в п. 2.3 для планарных волноводов. Однако вследствие цилиндрической геометрии оптических волокон целесообразно получить соотношения, эквивалентные уравнениям (2.24)-(2.26) и (2.27)-(2.29), в цилиндрических координатах, связывающие компоненты  для электрического и магнитного полей распространяющейся волны. Вычисления проводятся аналогично, однако теперь мы имеем дело с цилиндрическими координатами. Так, для получения мод волновода обычно рассматривают плоскую волну, описываемую волновым уравнением (2.17). Мы предполагаем, что
для электрического и магнитного полей распространяющейся волны. Вычисления проводятся аналогично, однако теперь мы имеем дело с цилиндрическими координатами. Так, для получения мод волновода обычно рассматривают плоскую волну, описываемую волновым уравнением (2.17). Мы предполагаем, что
компоненты электрического Е и магнитного Н полей выражаются через формулы (2.19) и (2.20):

где  При записи этих уравнений предполагалось, что волна распространяется в положительном направлении оси
При записи этих уравнений предполагалось, что волна распространяется в положительном направлении оси  Проделывая то же преобразование, что и в п. 2.3, можно разложить уравнения Максвелла для ротора (2.8) и (2.9) на шесть уравнений для компонентов в цилиндрических координатах, учитывая, что ротор в данном случае записывается как
Проделывая то же преобразование, что и в п. 2.3, можно разложить уравнения Максвелла для ротора (2.8) и (2.9) на шесть уравнений для компонентов в цилиндрических координатах, учитывая, что ротор в данном случае записывается как

где  — единичные векторы (орты) координатных осей; А — произвольный вектор. Используя эту систему из шести уравнений, после ряда алгебраических преобразований можно выразить поперечные компоненты
— единичные векторы (орты) координатных осей; А — произвольный вектор. Используя эту систему из шести уравнений, после ряда алгебраических преобразований можно выразить поперечные компоненты  векторов Е и Н через продольные компоненты
векторов Е и Н через продольные компоненты  в Следующем виде:
в Следующем виде:

где  — поперечный компонент волнового вектора к плоской волны в волноводе с показателем преломления
— поперечный компонент волнового вектора к плоской волны в волноводе с показателем преломления 

В цилиндрических координатах компоненты поля Е (так же, как и Н) соотносятся с соответствующими декартовыми координатами следующим образом:

Из уравнений (2.101) вытекает, что  -компонент поля будет удовлетворять скалярной форме волнового уравнения, а именно уравнения (2.17), но без члена
-компонент поля будет удовлетворять скалярной форме волнового уравнения, а именно уравнения (2.17), но без члена  Более того, так как компоненты
Более того, так как компоненты  полей могут быть выражены через
полей могут быть выражены через  [см. уравнения
[см. уравнения
2.99)], то решение скалярного волнового уравнения для  будет достаточным для получения всех компонентов векторов Е и Н электромагнитного поля. В цилиндрических координатах скалярное волновое уравнение выглядит так:
будет достаточным для получения всех компонентов векторов Е и Н электромагнитного поля. В цилиндрических координатах скалярное волновое уравнение выглядит так:

Для того чтобы применить метод разделения переменных (см. п. 2.3) в решении уравнения (2.102), можно записать

Подставив уравнение (2.103) в уравнение (2.102), получим

где I должно быть целым числом для обеспечения периодичности поля по  . Таким образом уравнение (2.102) принимает вид
. Таким образом уравнение (2.102) принимает вид

Уравнение (2.105) является известной формой дифференциального уравнения Бесселя второго порядка, имеющего два независимых решения в виде любых двух различных цилиндрических функций. Действительный выбор этих функций определяется ограничениями, положенными геометрией волновода на пространственное распределение полей. Для того чтобы получить моды, соответствующие определенной волноводной геометрии, надо решить уравнение (2.105) для поля  и соответствующей постоянной распространения (3.
и соответствующей постоянной распространения (3.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
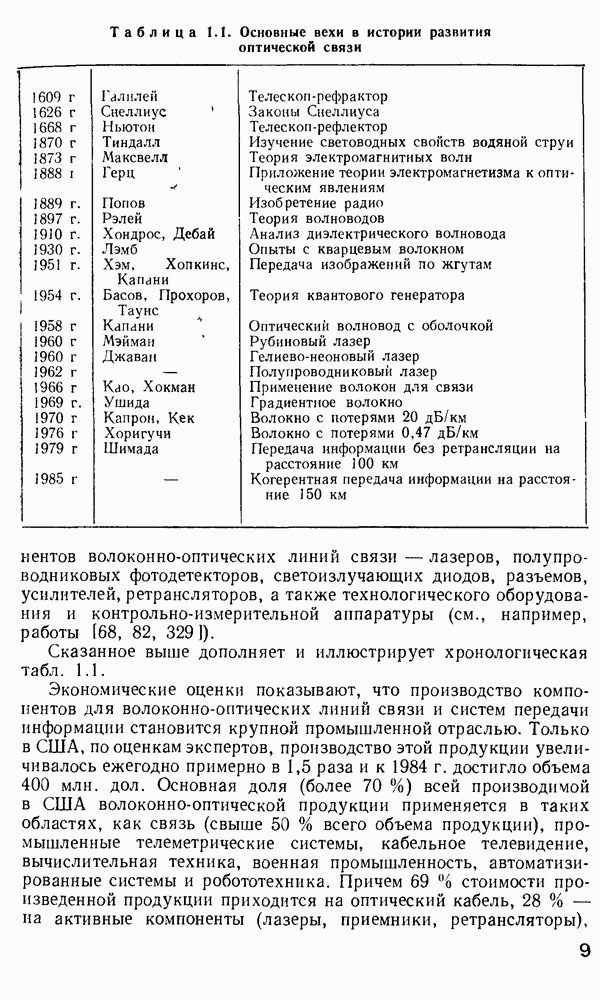
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
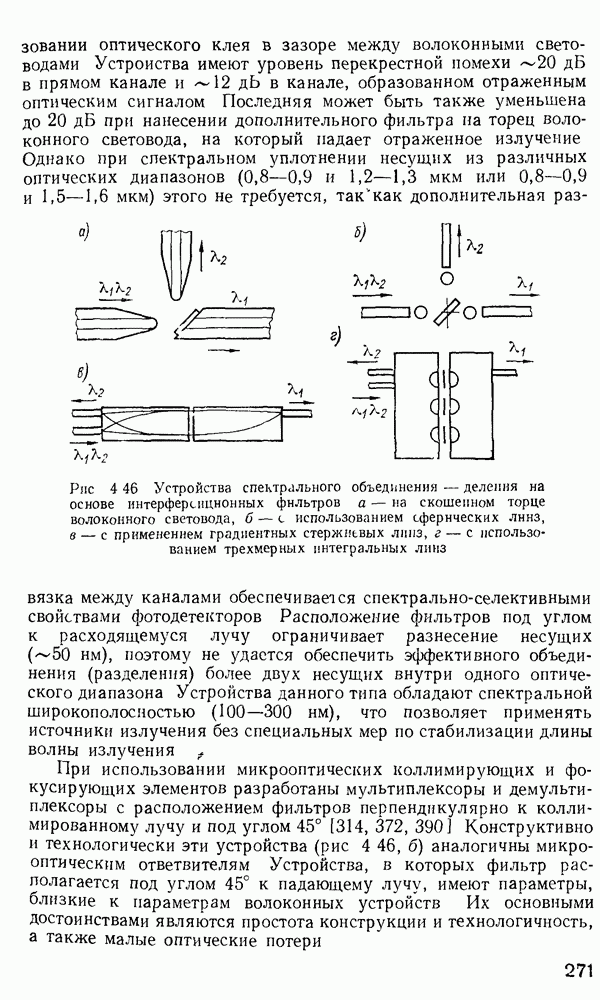
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
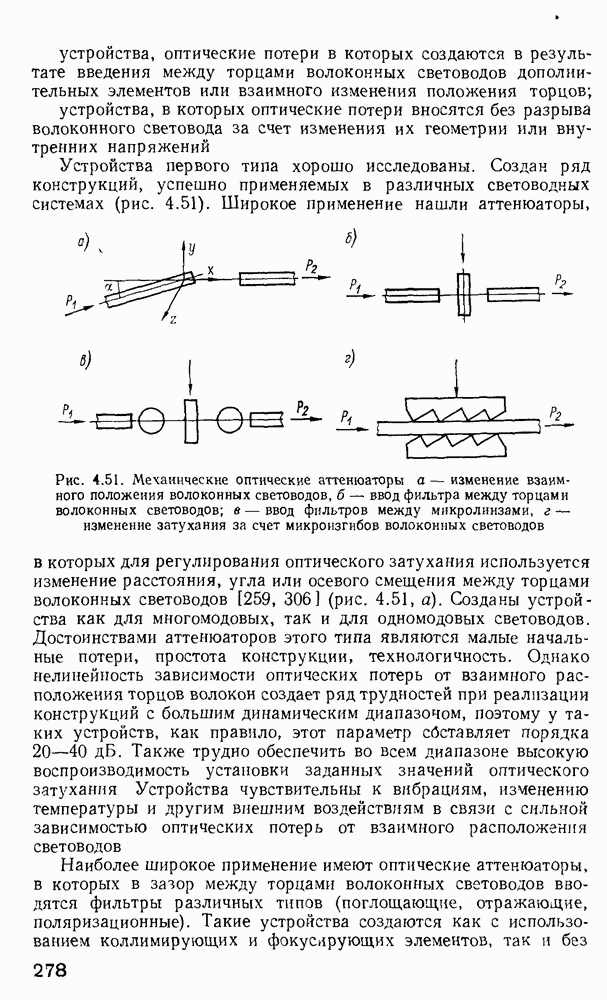
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
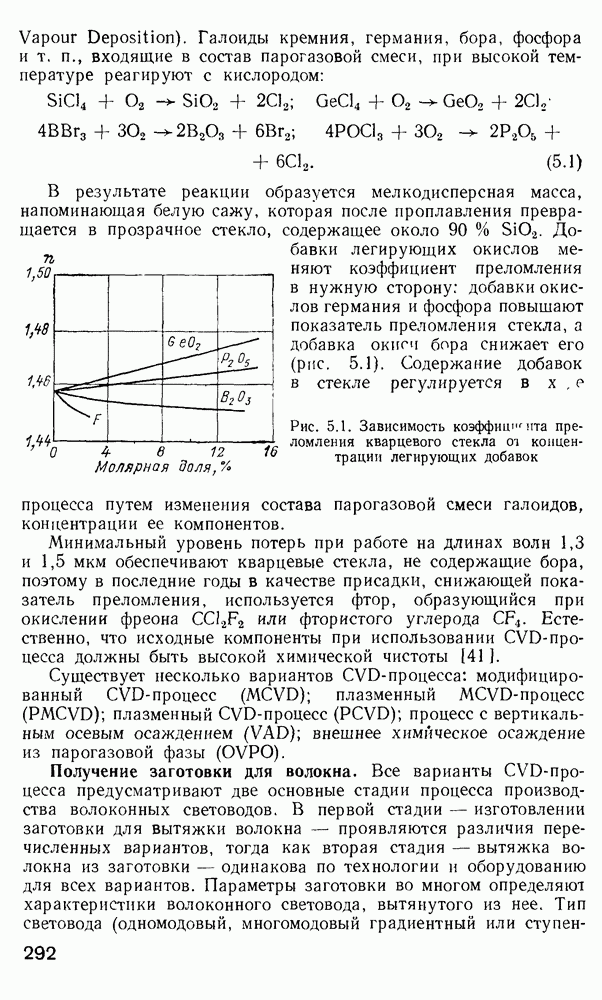
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ