| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
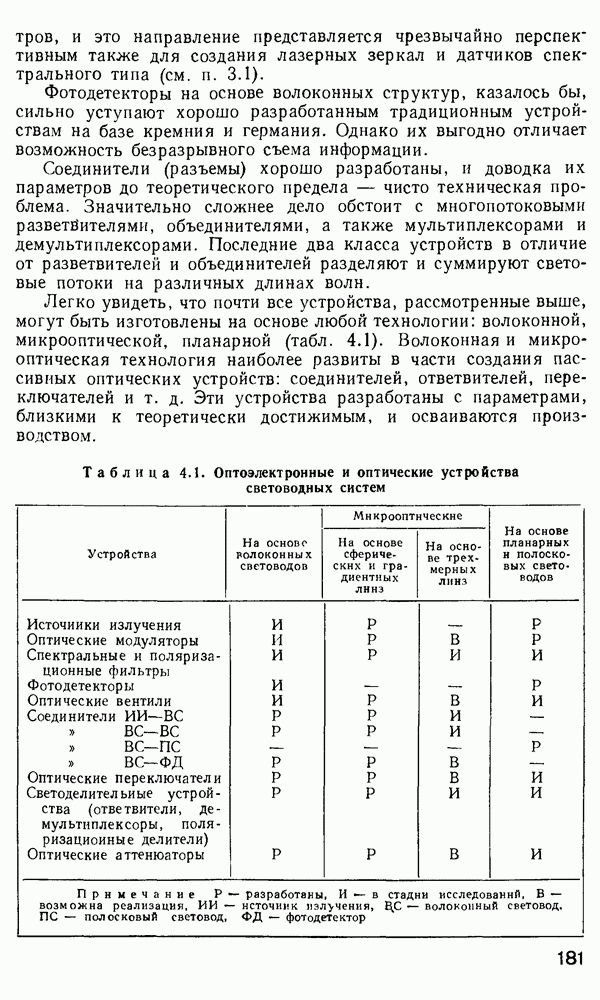
Распространение импульса в оптических волокнах.
Предположим, что на вход волокна попадает неограниченный во времени гармонический сигнал с частотой 

где  — амплитуда сигнала. Если
— амплитуда сигнала. Если  — обобщенный индекс моды, включающий в себя введенные ранее индексы
— обобщенный индекс моды, включающий в себя введенные ранее индексы  представляет ссбой поперечное, распределение, характерное для поля одной из мод, постоянная распространения которой
представляет ссбой поперечное, распределение, характерное для поля одной из мод, постоянная распространения которой  тогда входной сигнал можно представить в виде суперпозиции мод волокна. На произвольном расстоянии
тогда входной сигнал можно представить в виде суперпозиции мод волокна. На произвольном расстоянии  от входного торца поле в волокне описывается как
от входного торца поле в волокне описывается как 

где  — амплитуда поля
— амплитуда поля  моды,
моды,  — эффективность возбуждения этой моды.
— эффективность возбуждения этой моды.
Если падающая на торец волокна волна промодулирована сигнальным импульсом  (напршйер, гауссовым импульсом), тогда с учетом формулы (2.179) поле на входе записывается как
(напршйер, гауссовым импульсом), тогда с учетом формулы (2.179) поле на входе записывается как

Здесь

где Т — полуширина импульса по уровню  . Представим
. Представим  в виде Фурье-спектра
в виде Фурье-спектра 

В свою очередь, спектр сигнала  выражается как
выражается как

т. е. спектром гауссовой формы. На практике  (например, для импульсов
(например, для импульсов  ), и соответствующий Фурье-спектр
), и соответствующий Фурье-спектр  есть очень узкий пик на частоте
есть очень узкий пик на частоте  [78, 387]. Далее
[78, 387]. Далее  — обычно очень медленно изменяющиеся функции переменной
— обычно очень медленно изменяющиеся функции переменной  ю С учетом всего сказанного, исходя из формул (2.180) и (2.182), можно выразить
ю С учетом всего сказанного, исходя из формул (2.180) и (2.182), можно выразить  в виде суперпозиции мод следующим образом:
в виде суперпозиции мод следующим образом:

где

Теперь используем тот факт, что  есть острый пик вблизи
есть острый пик вблизи  и разложим
и разложим  в ряд вблизи
в ряд вблизи  Удерживая члены второго порядка малости, получаем из (2.184)
Удерживая члены второго порядка малости, получаем из (2.184)

где 
Используя стандартный интеграл

получаем

Учитывая, что в качестве приемника используется обычно квадратичный детектор, подсчитаем интенсивность импульса, которая пропорциональна После прохождения расстояния  вдоль волокна временное распределение интенсивности
вдоль волокна временное распределение интенсивности  моды выражается как
моды выражается как


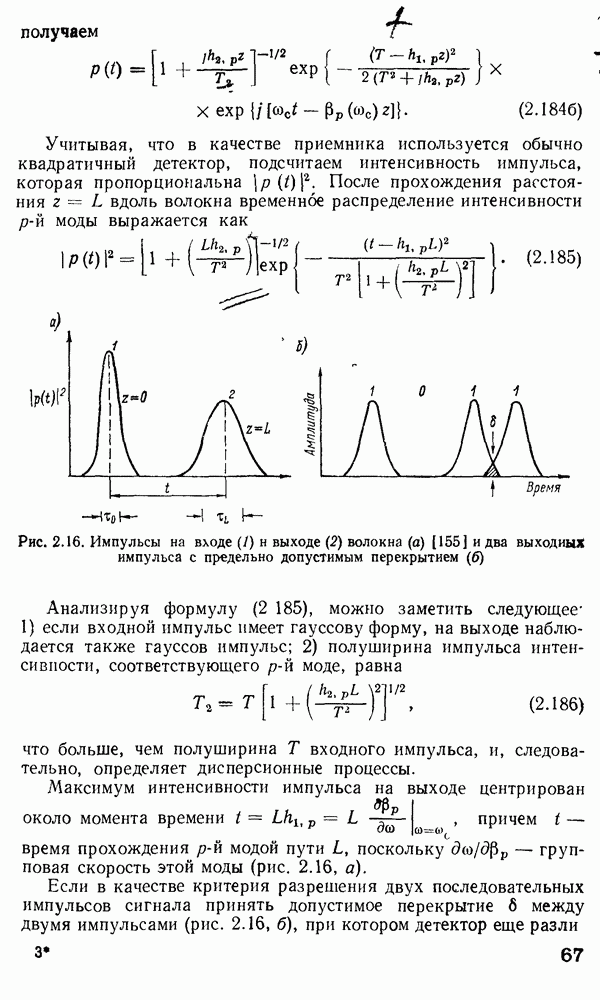
Рис. 2.16. Импульсы на входе (1) и выходе (2) волокна (а) [155] и два выходных импульса с предельно допустимым перекрытием (б)
Анализируя формулу (2 185), можно заметить  если входной импульс имеет гауссову форму, на выходе наблюдается также гауссов импульс; 2) полуширина импульса интенсивности, соответствующего
если входной импульс имеет гауссову форму, на выходе наблюдается также гауссов импульс; 2) полуширина импульса интенсивности, соответствующего  моде, равна
моде, равна

что больше, чем полуширина Т входного импульса, и, следовательно, определяет дисперсионные процессы.
Максимум интенсивности импульса на выходе центрирован около момента времени  причем
причем  — время прохождения
— время прохождения  модой пути
модой пути  поскольку
поскольку  групповая скорость этой моды (рис. 2.16, а).
групповая скорость этой моды (рис. 2.16, а).
Если в качестве критерия разрешения двух последовательных импульсов сигнала принять допустимое перекрытие  между двумя импульсами (рис. 2.16, б), при котором детектор еще
между двумя импульсами (рис. 2.16, б), при котором детектор еще
различает их как два независимых импульса, то можио потребовать, чтобы

где  — полуширина выходного импульса. Поэтому
— полуширина выходного импульса. Поэтому

Соответственно максимальная скорость передачи [152]

в волокне, в котором распространяется только одна мода.
В соответствии с выражением (2.185), задающим форму импульса  моды и время его прихода, в типичном многомодовом волокне импульс на выходе можно представить как пакет импульсов отдельных мод
моды и время его прихода, в типичном многомодовом волокне импульс на выходе можно представить как пакет импульсов отдельных мод

Из всего сказанного выше следуют два вывода: 1) Задержка каждой моды на выходе определяется как  а следовательно, межмодовая дисперсия зависит от разницы времен прихода разных мод; 2) для гауссова входного импульса на выходе уширение импульса в одной моде пропорционально величине
а следовательно, межмодовая дисперсия зависит от разницы времен прихода разных мод; 2) для гауссова входного импульса на выходе уширение импульса в одной моде пропорционально величине  которая прямо связана с параметром
которая прямо связана с параметром 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
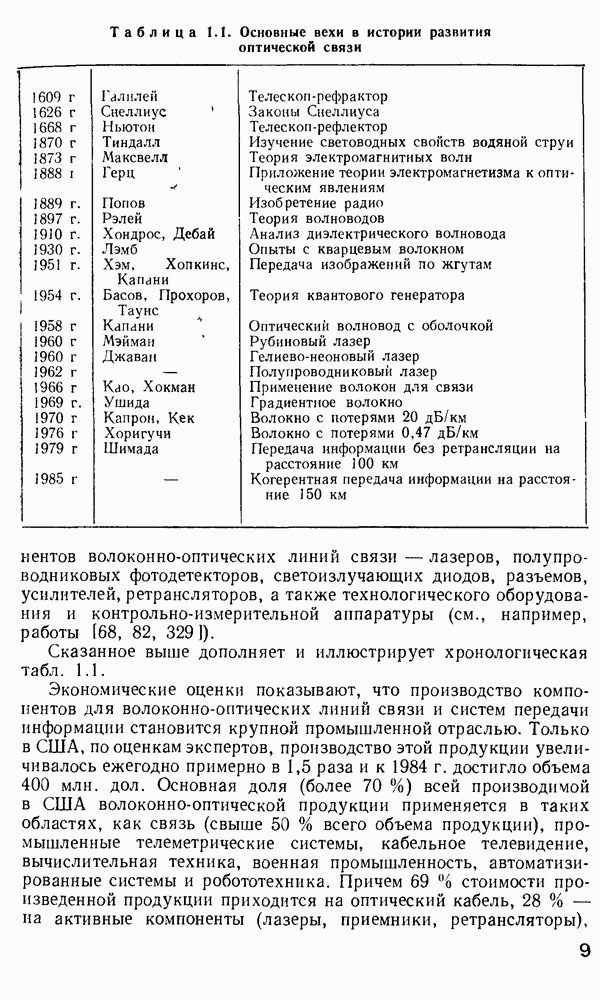
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
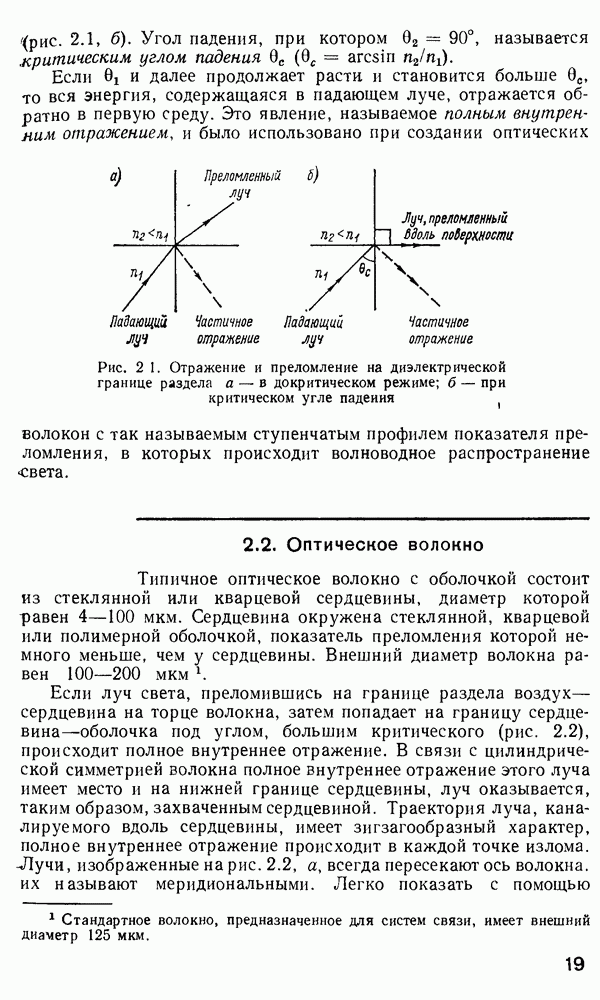
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
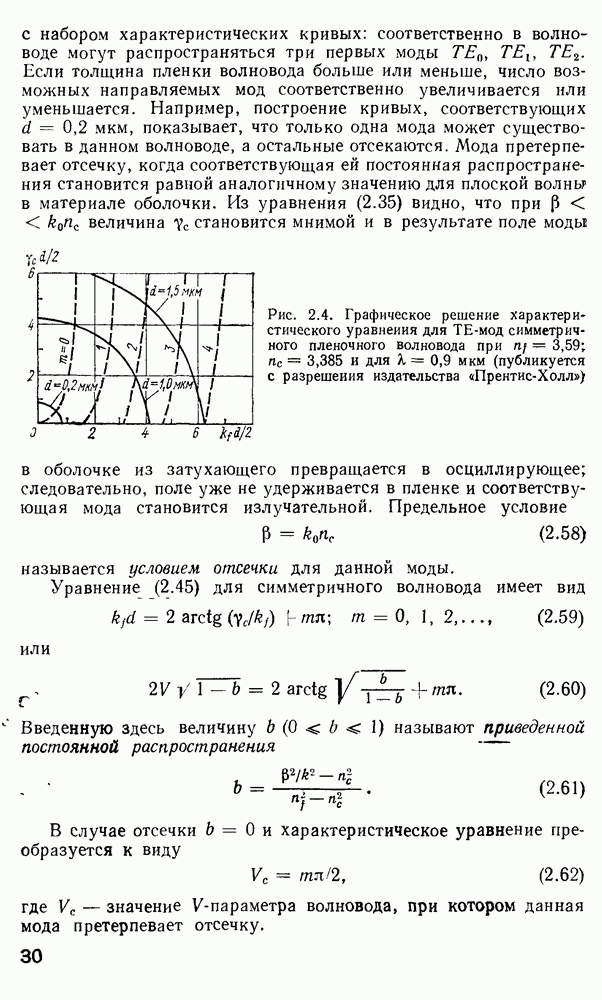
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
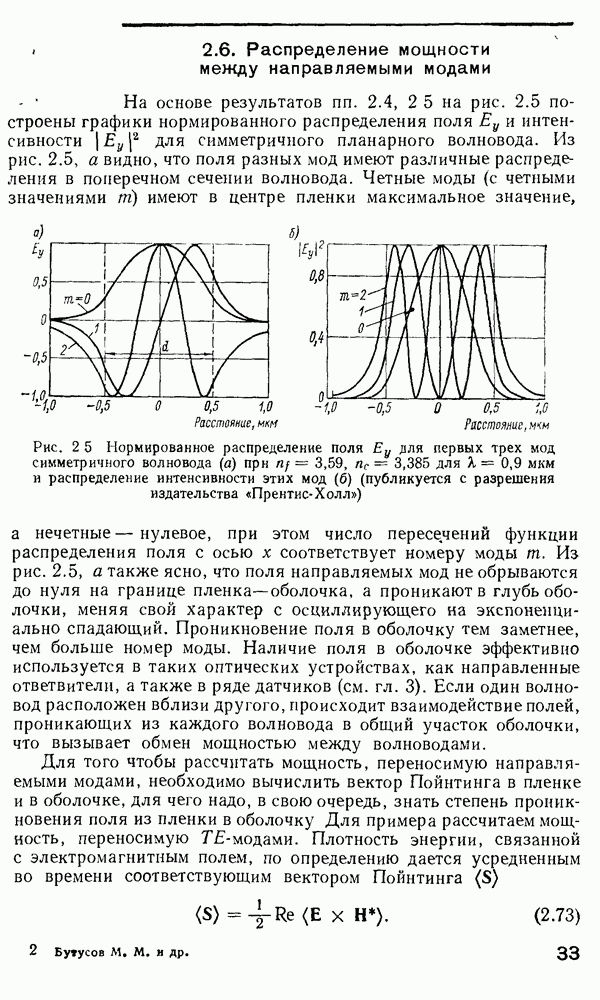
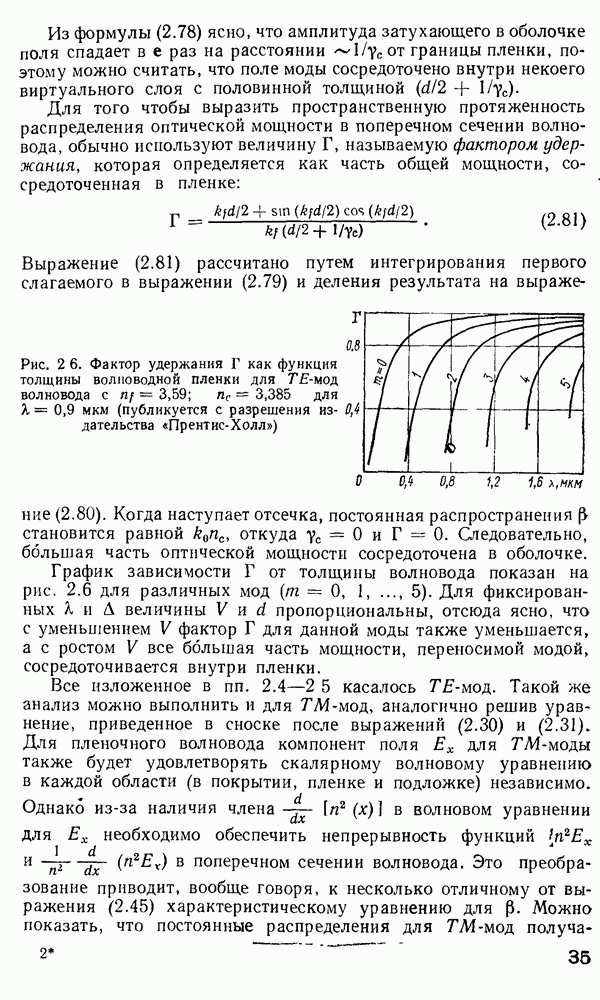
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
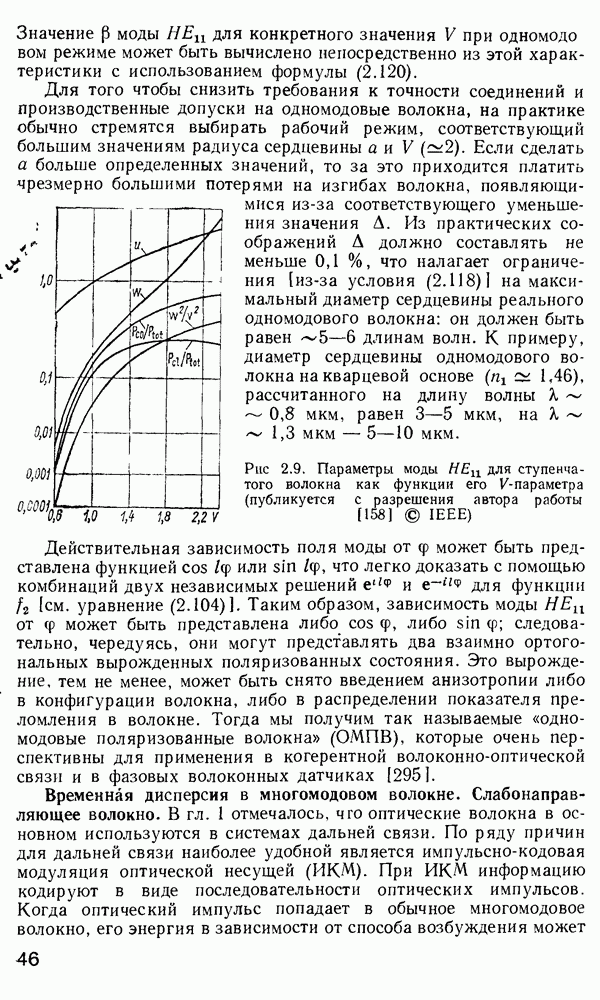
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
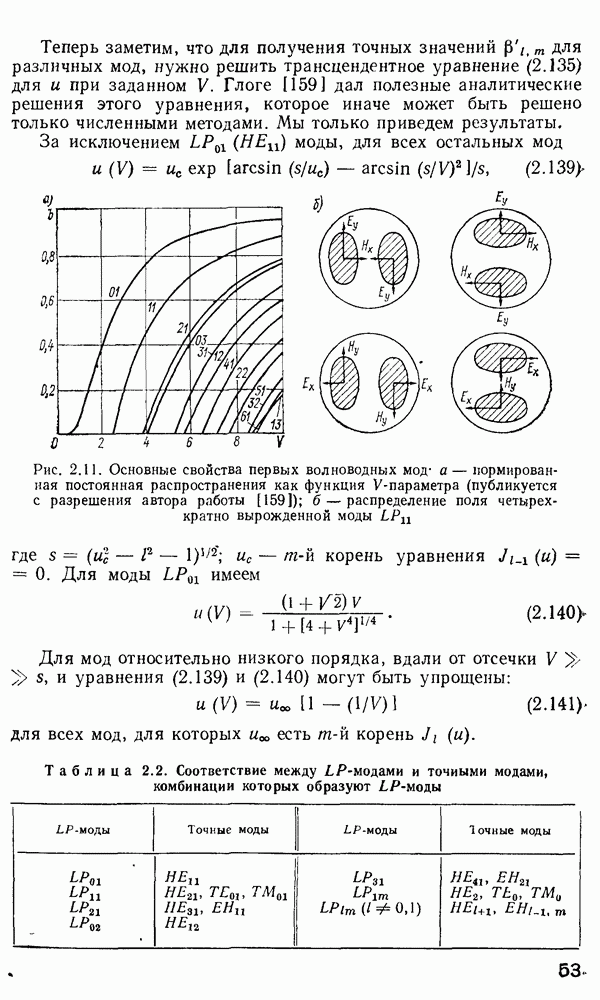
- Линейно-поляризованные моды в слабонаправляющих волокнах.
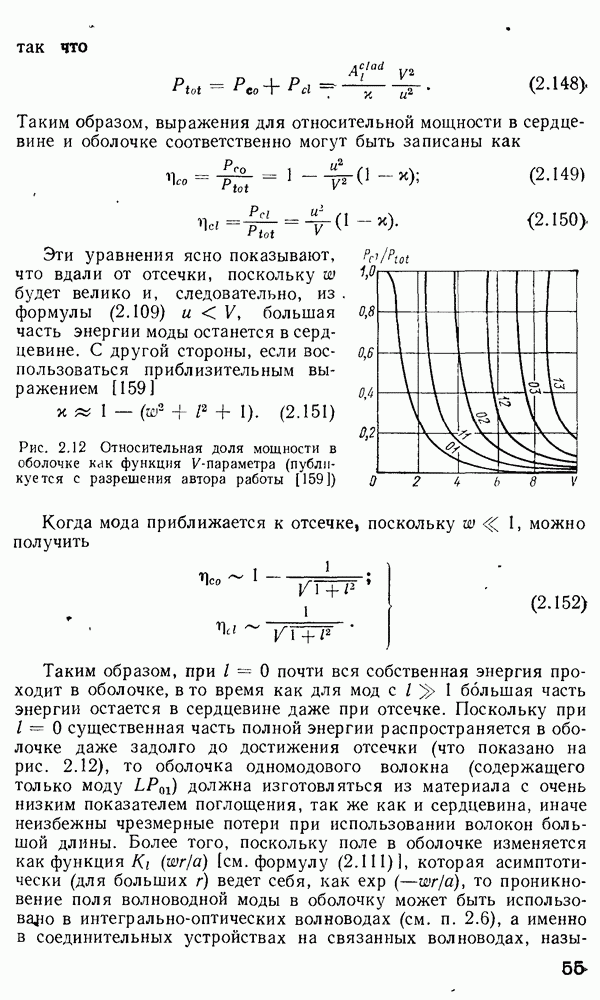
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
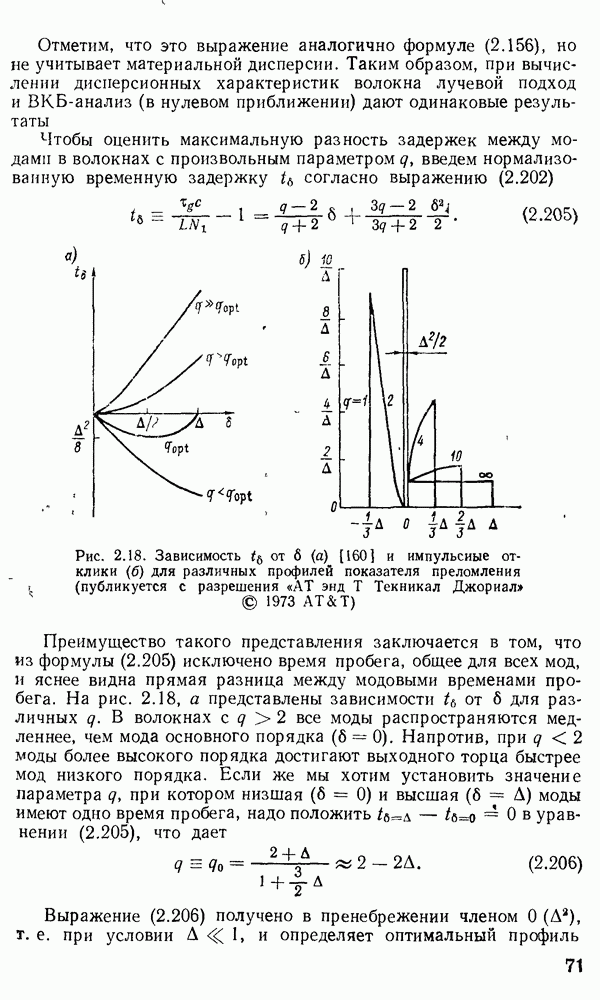
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
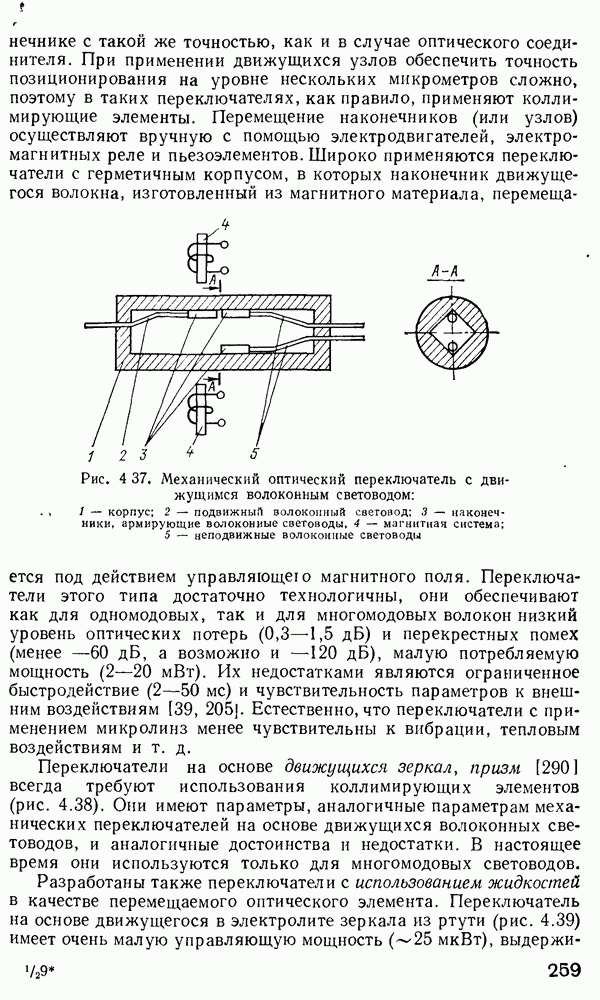
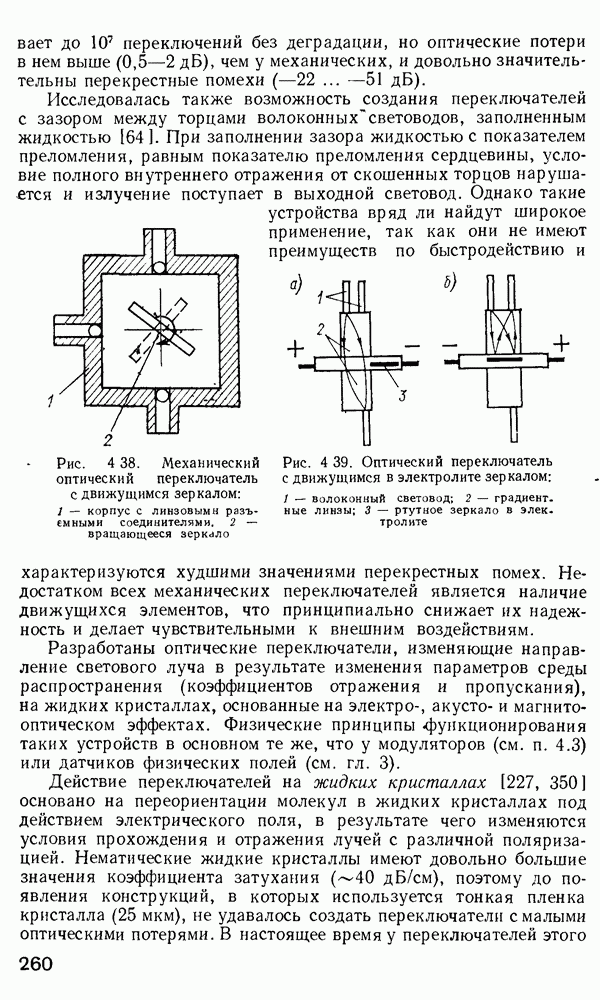
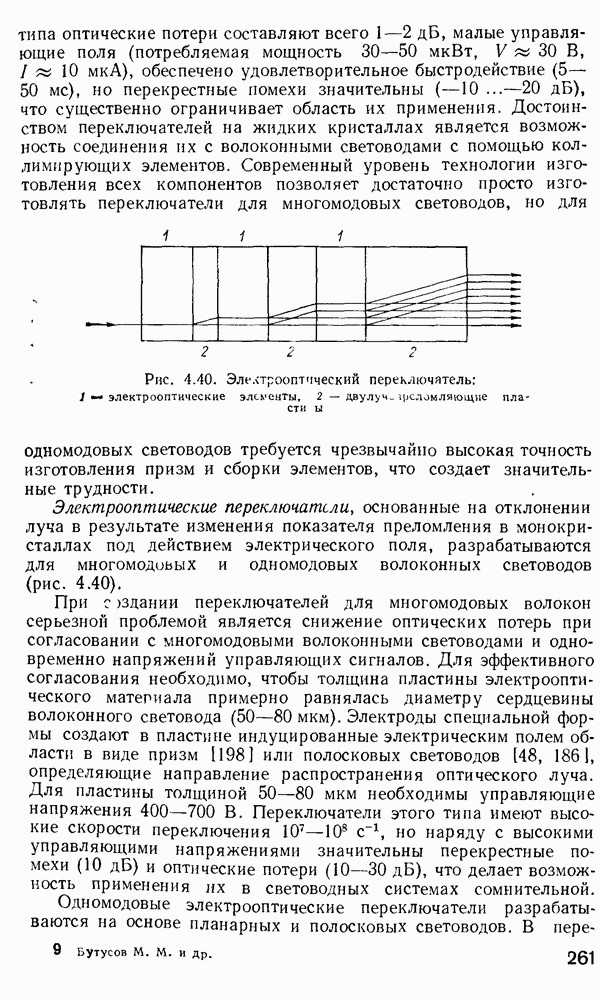
- 4.7. Волоконно-оптические переключатели
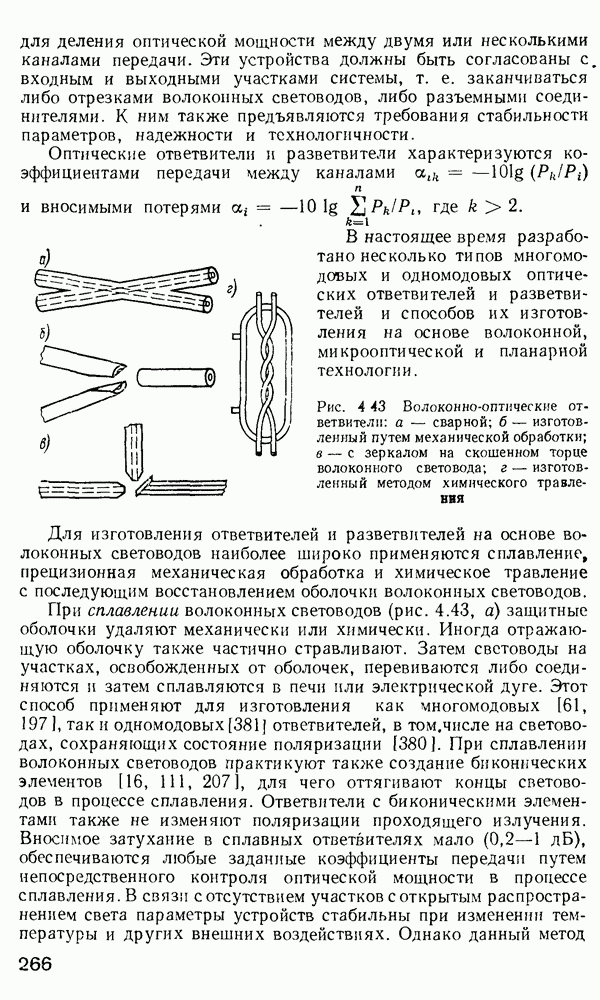
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
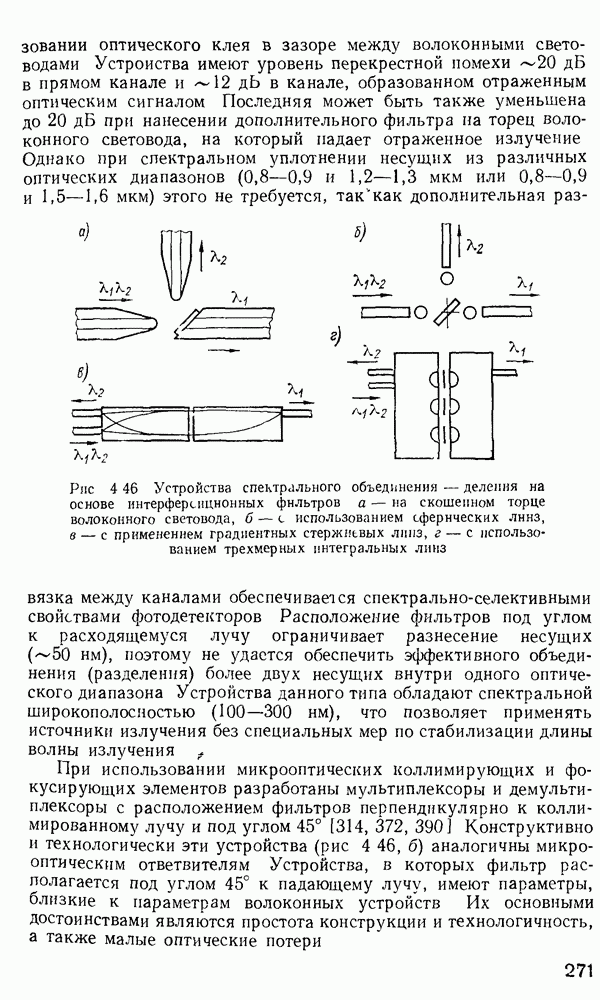
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
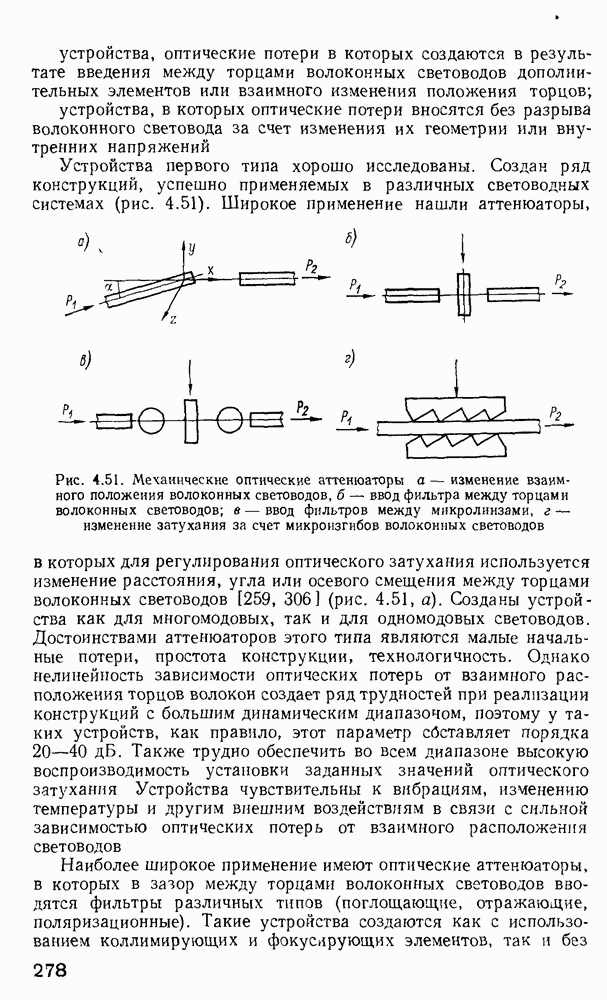
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
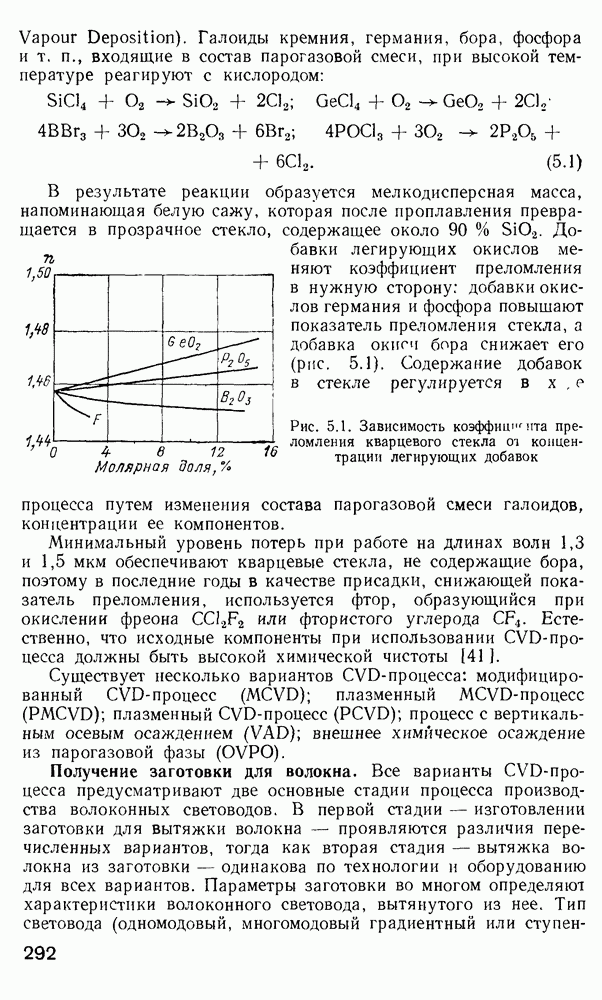
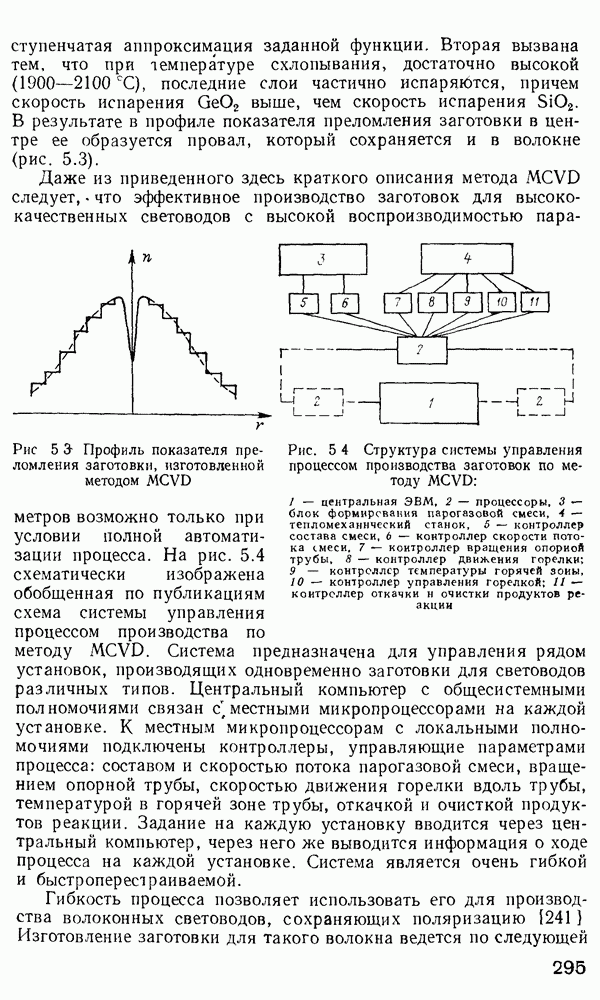
- Получение заготовки для волокна.
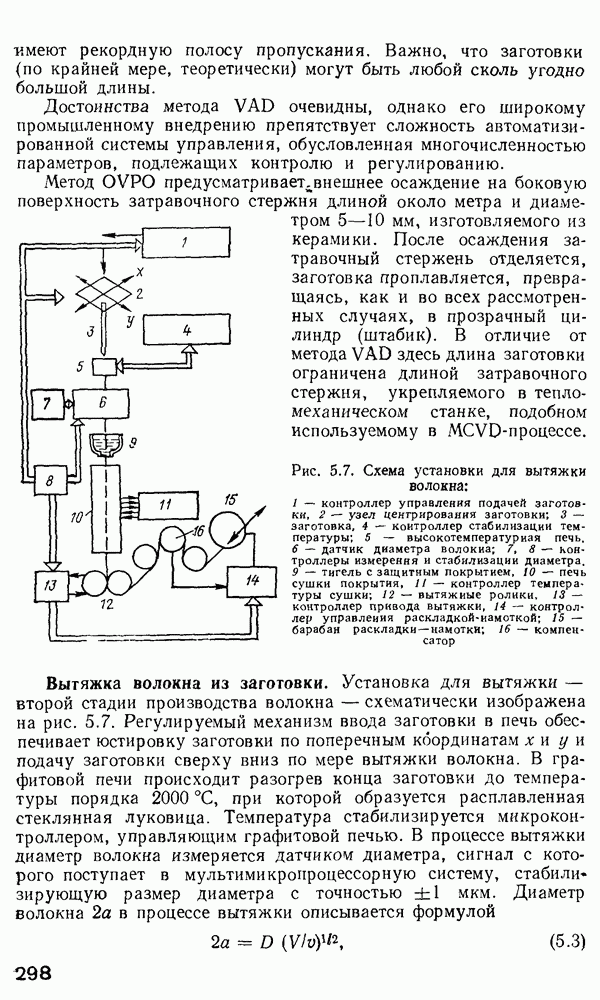
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
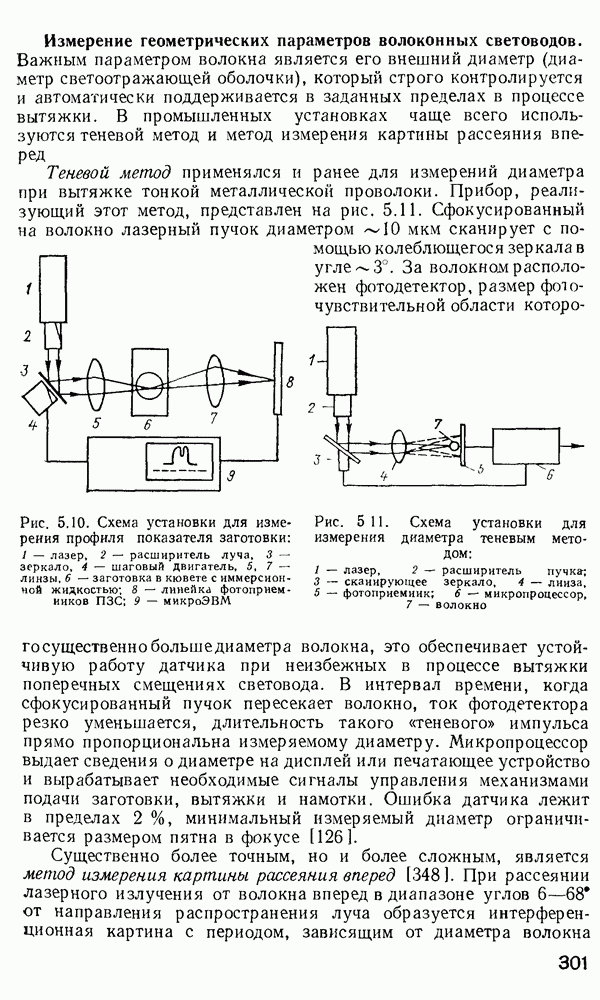
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ