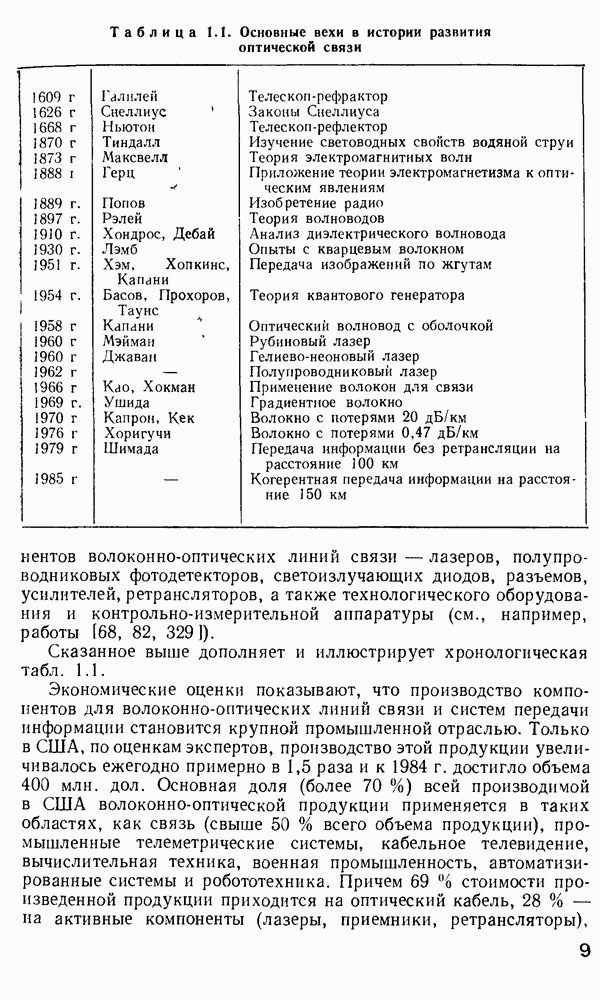
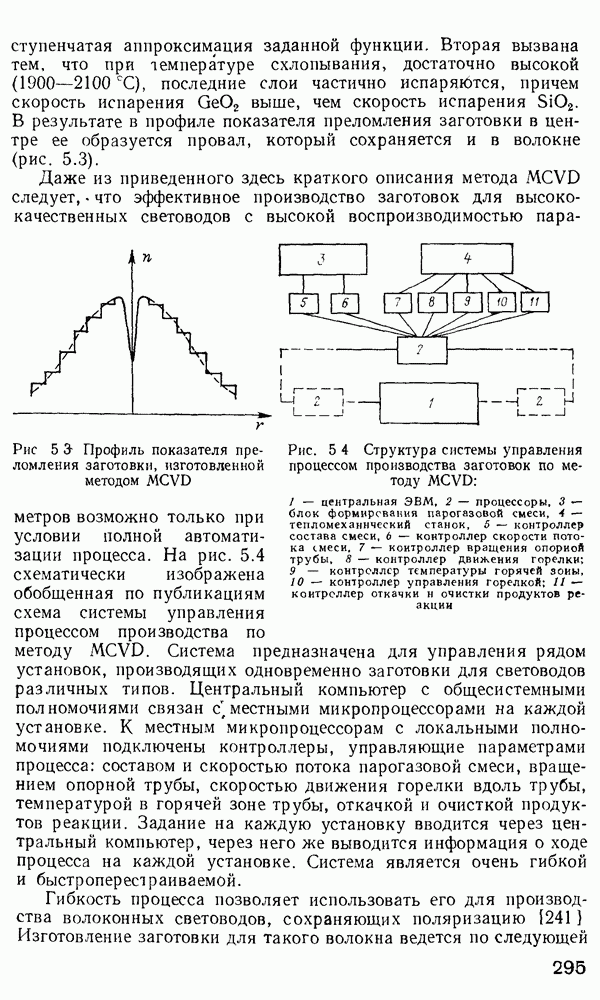
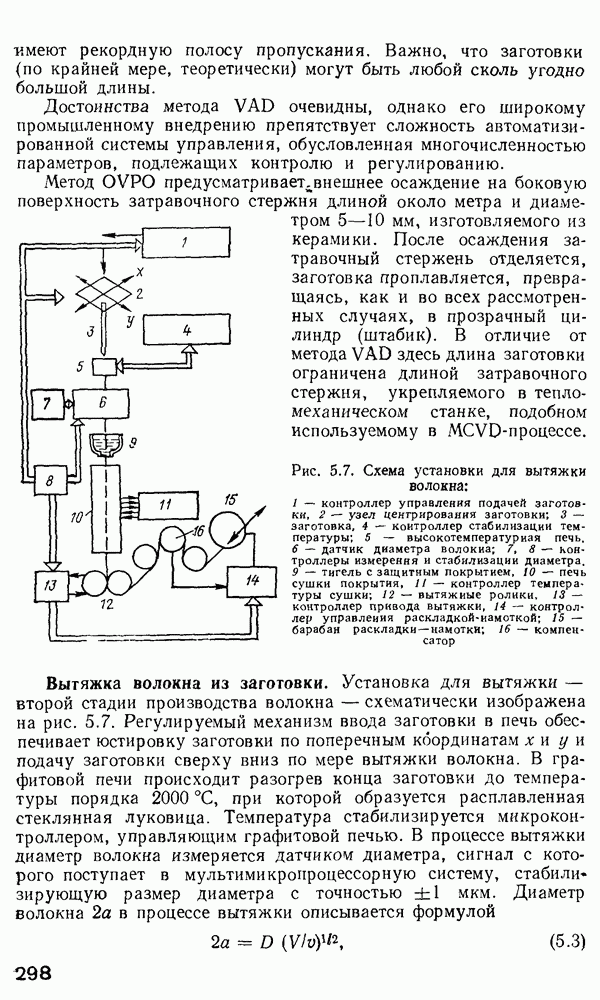
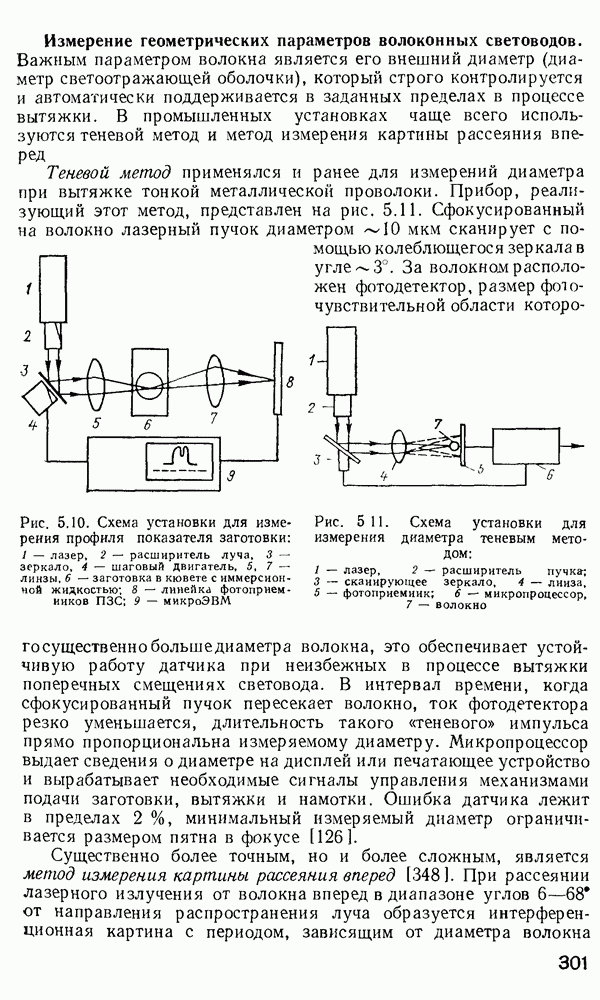
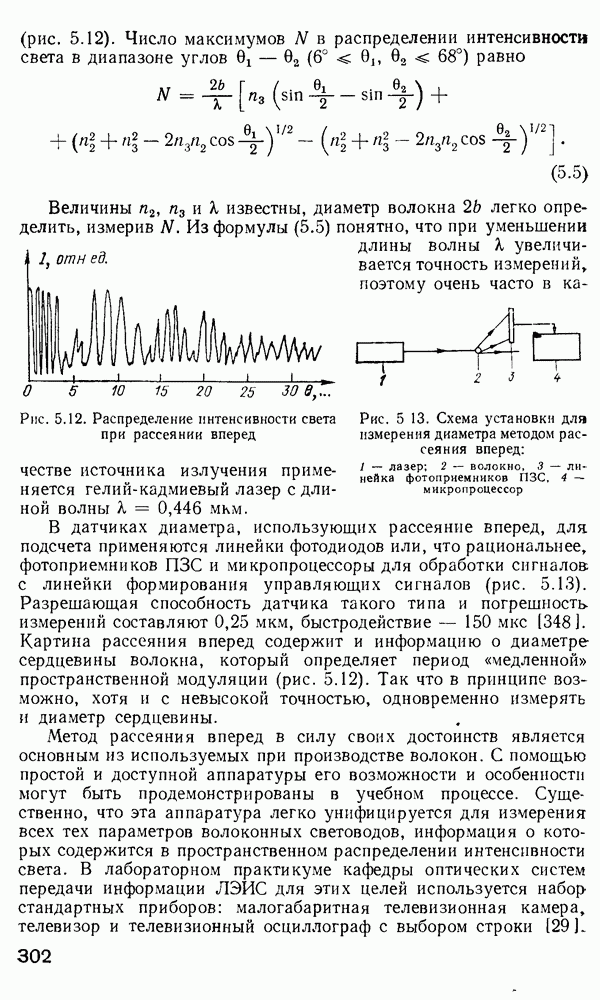
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
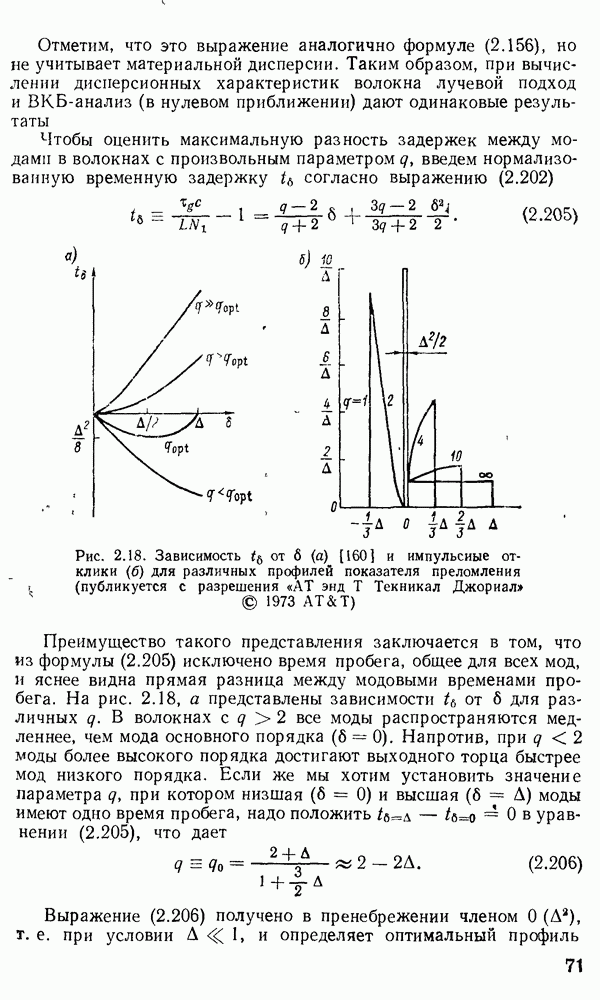
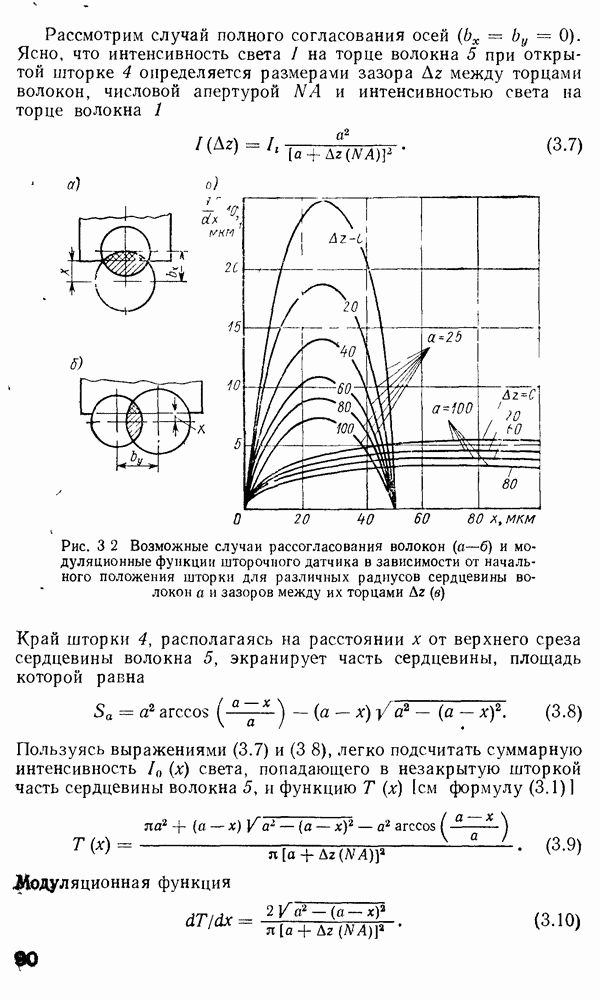
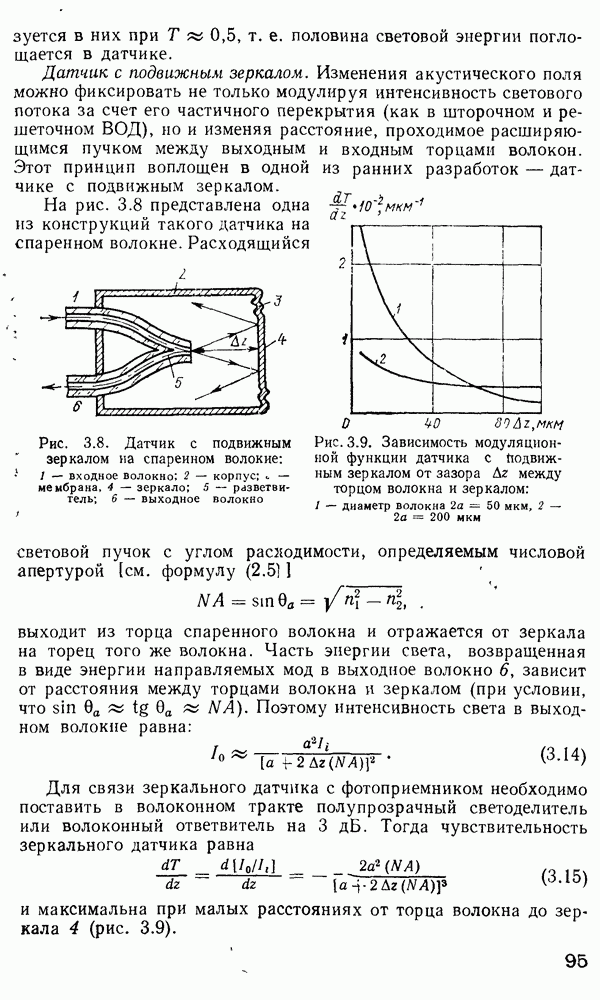
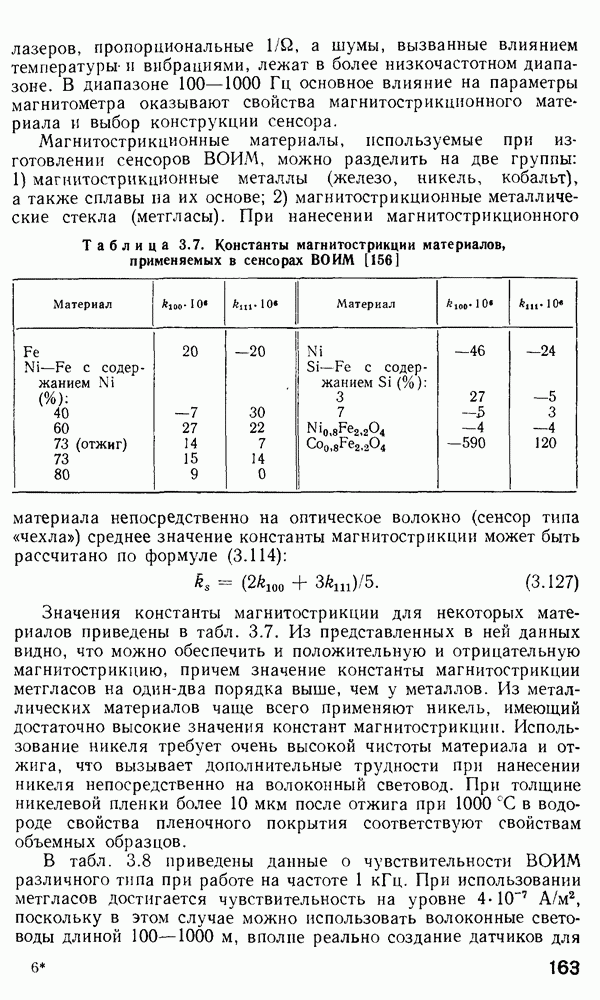
Решение уравнения (2.157) методом ВКБ.
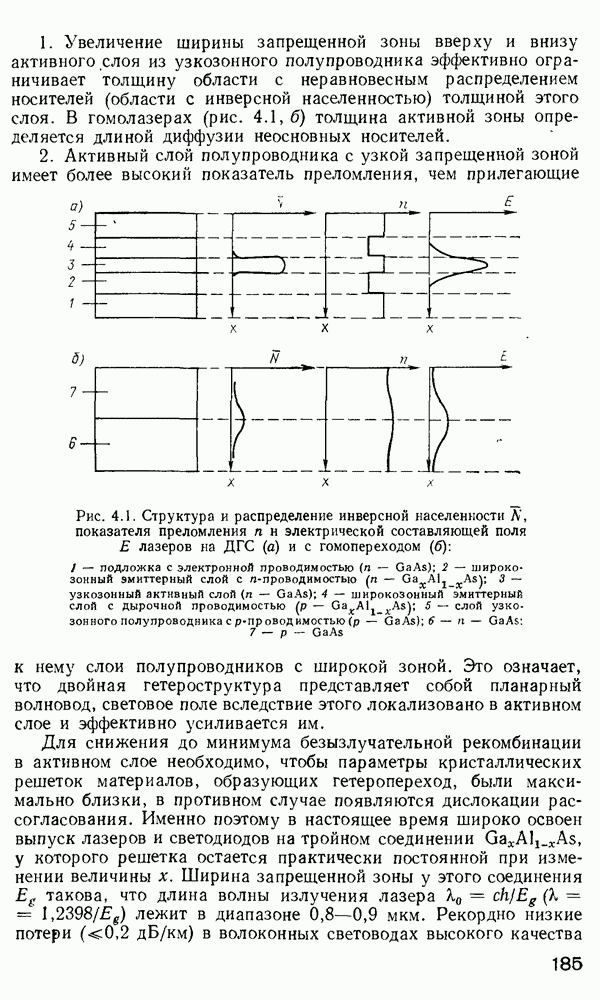
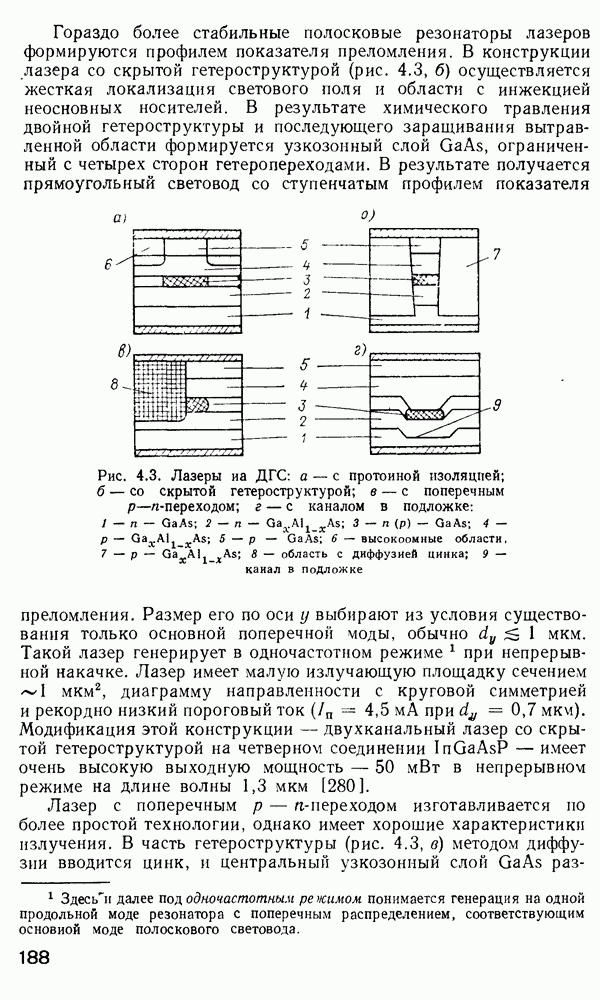
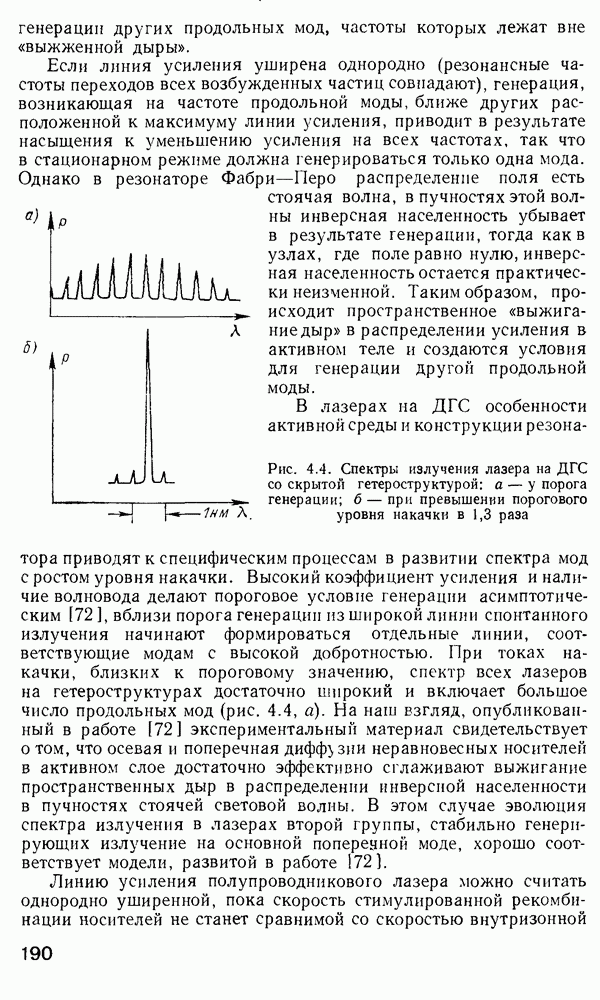
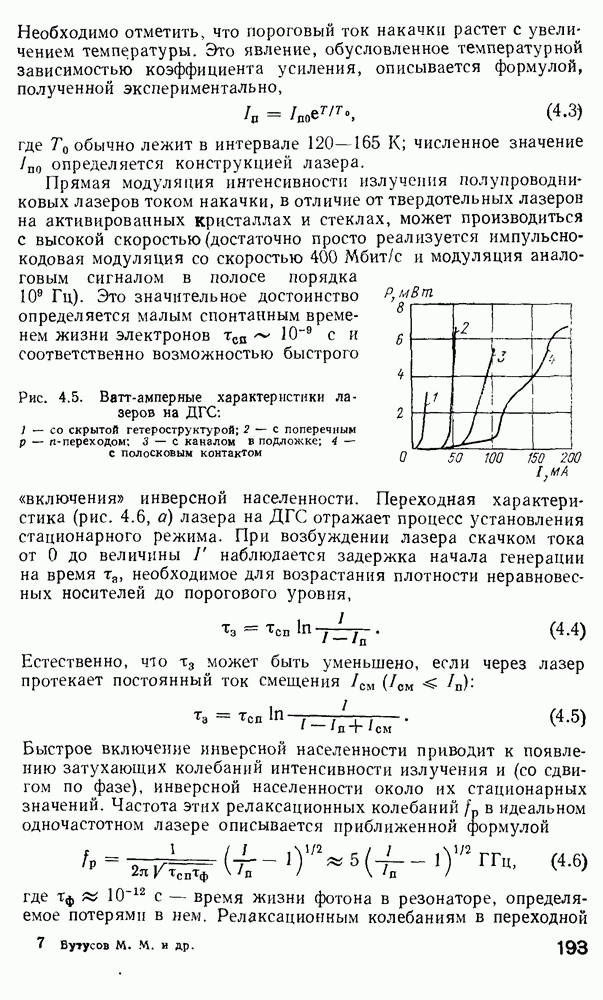
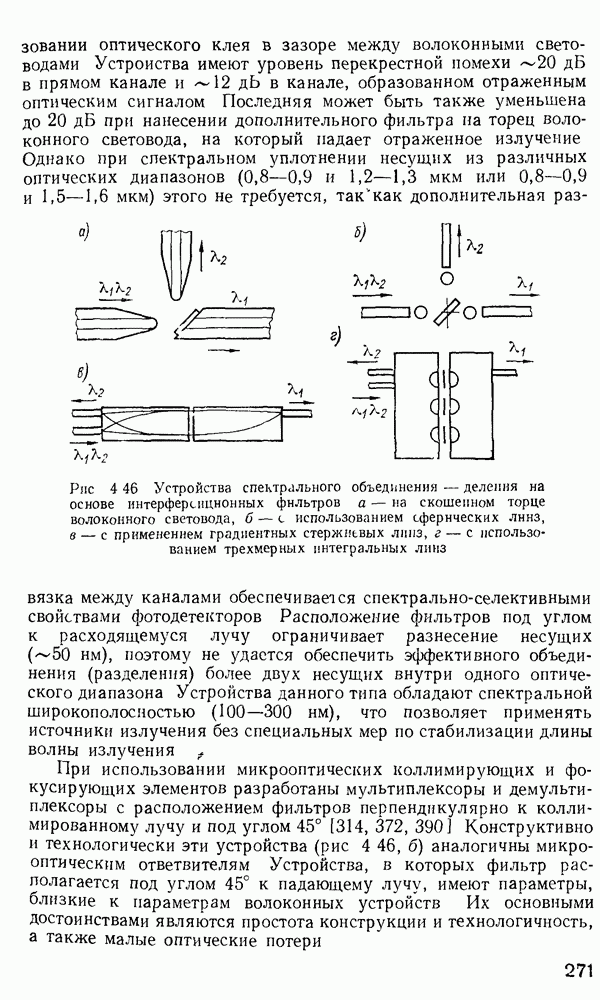
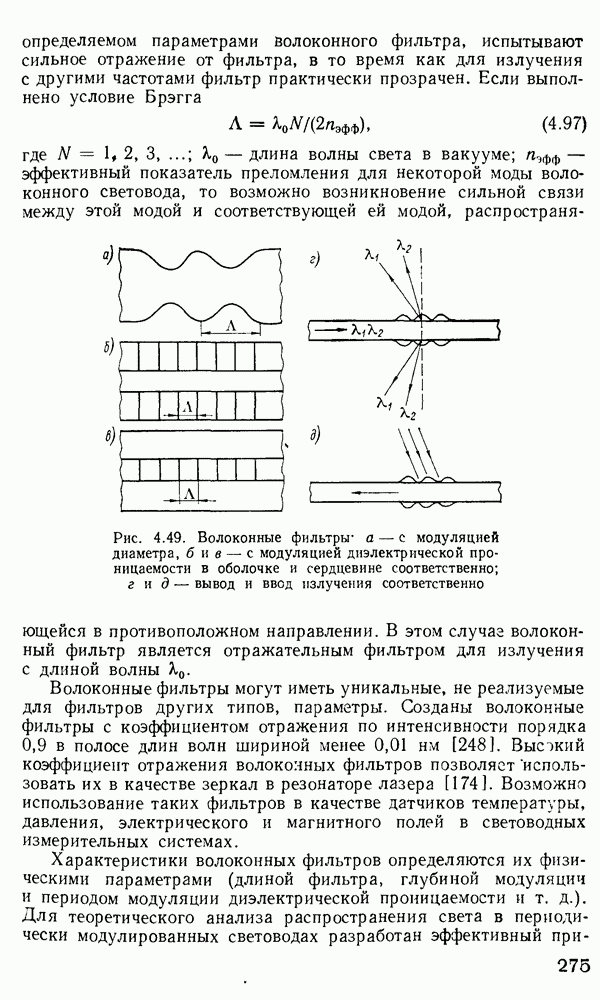
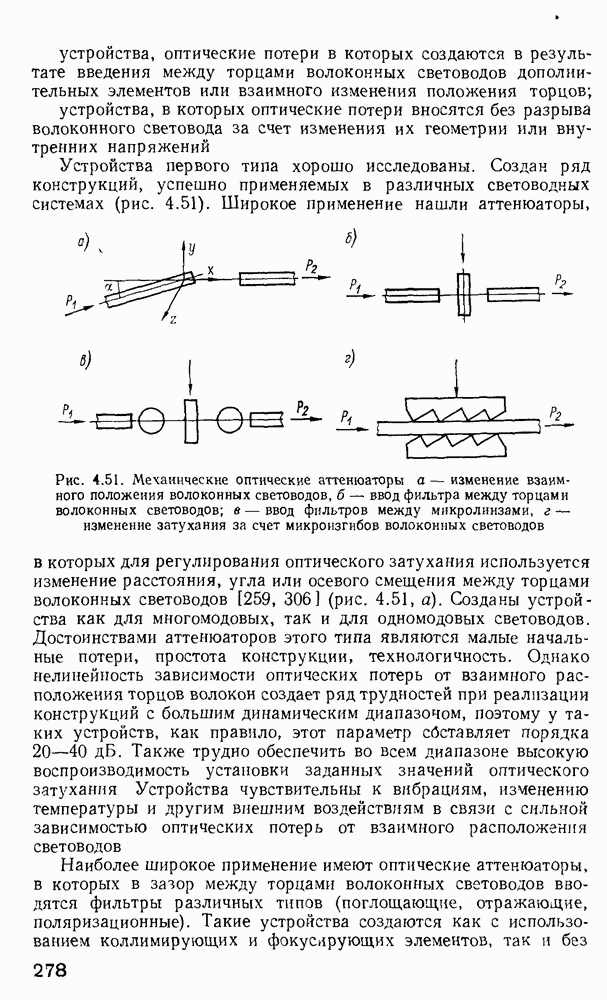
Для изучения особенностей распространения излучения в градиентных волокнах с произвольным значением  при решении уравнения (2.157) применяется метод ВКБ [160, 170]. Этот метод применяется в квантовой механике для получения собственных значений энергии частиц, движущихся в потенциальной яме. Распространение света в неоднородной среде в определенном смысле аналогично распространению квантовой частицы в потенциальной яме. Для тога чтобы теория ВКБ была применима в оптике, должно выполняться следующее условие:
при решении уравнения (2.157) применяется метод ВКБ [160, 170]. Этот метод применяется в квантовой механике для получения собственных значений энергии частиц, движущихся в потенциальной яме. Распространение света в неоднородной среде в определенном смысле аналогично распространению квантовой частицы в потенциальной яме. Для тога чтобы теория ВКБ была применима в оптике, должно выполняться следующее условие:

что равносильно утверждению, что показатель преломления медленно меняется при изменении радиальной координаты на величину порядка длины волны света. Итак, в предположении, что условие (2.162) выполняется, что верно для многомодовых слабонаправляющих волокон, можно применить результаты ВКБ-анализа для преобразования уравнения (2.157) в форму одномерного волнового уравнения. Вводя обозначение

мы преобразуем уравнение (2.157) к виду

Используя обозначение

переписываем уравнение (2.164):

С помощью квантово-механической аналогии можно показать, что для связанных мод должно выполняться соотношение

где  является радиальным номером моды, а пределы интегрирования
является радиальным номером моды, а пределы интегрирования  могут быть найдены решением уравнения
могут быть найдены решением уравнения
 Радиусы
Радиусы  для которых
для которых  равно нулю, называются каустиками, или точками поворота. Для связанных мод
равно нулю, называются каустиками, или точками поворота. Для связанных мод  является действительной величиной в интервале между
является действительной величиной в интервале между  что ведет к существованию осциллирующих полей в этой области. В то же время за пределами каустик
что ведет к существованию осциллирующих полей в этой области. В то же время за пределами каустик  мнимая величина, и поля имеют экспоненциально спадающий вид.
мнимая величина, и поля имеют экспоненциально спадающий вид.
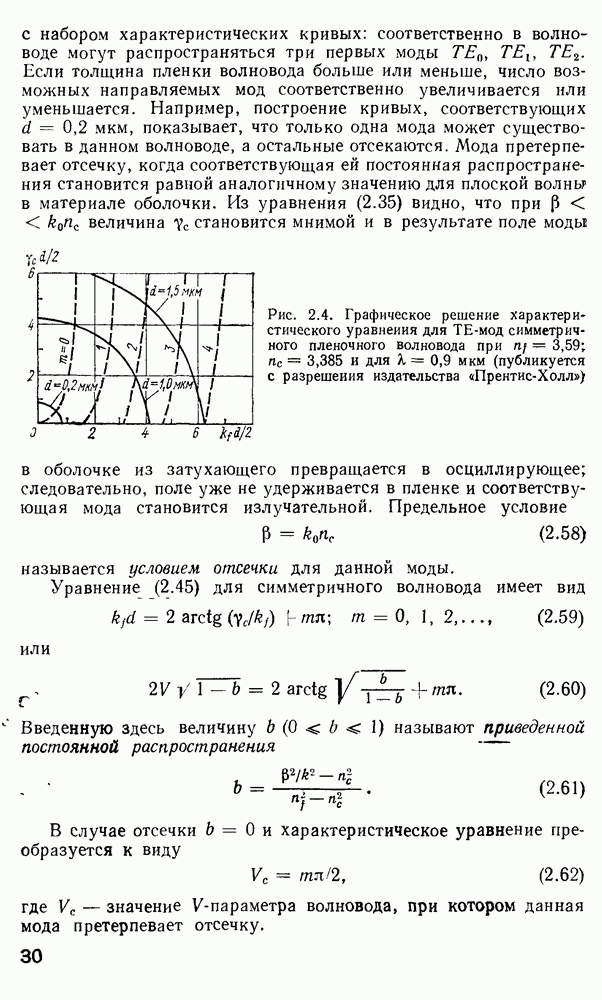
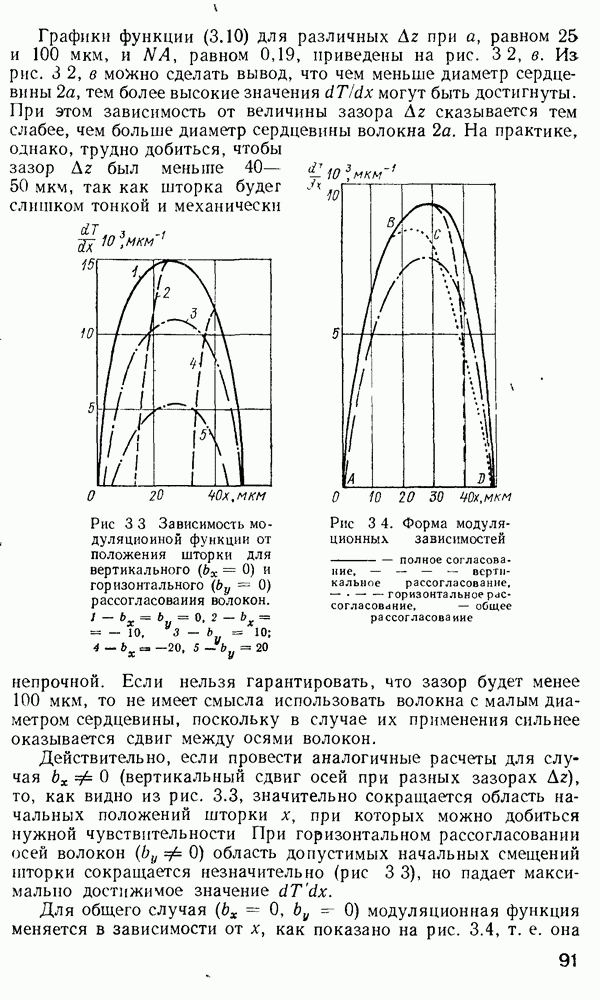
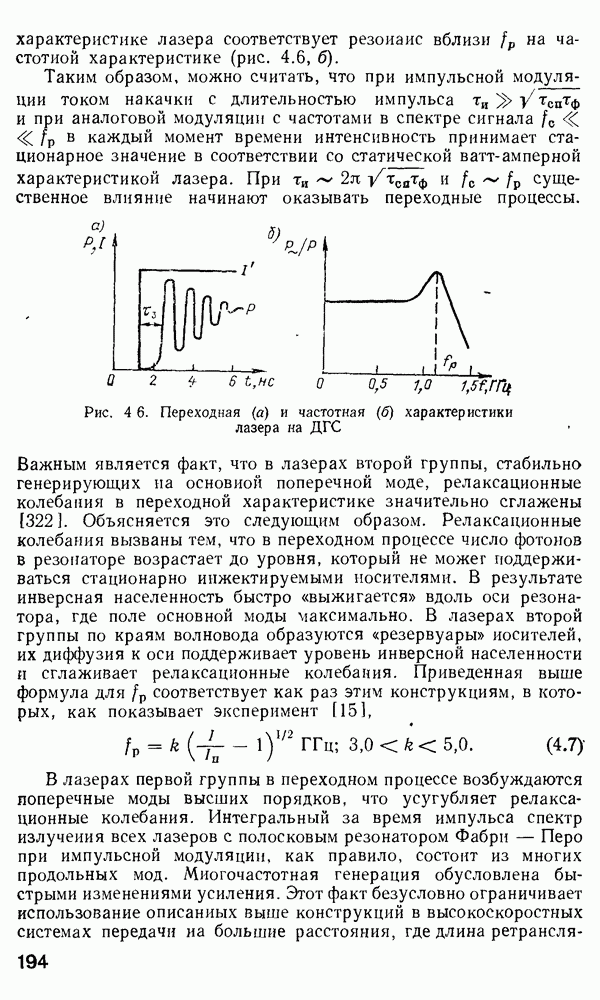
Эти свойства функций, полученных в результате решения по методу  становятся яснее после изучения графической формы компонентов
становятся яснее после изучения графической формы компонентов  (рис. 2.14).
(рис. 2.14).

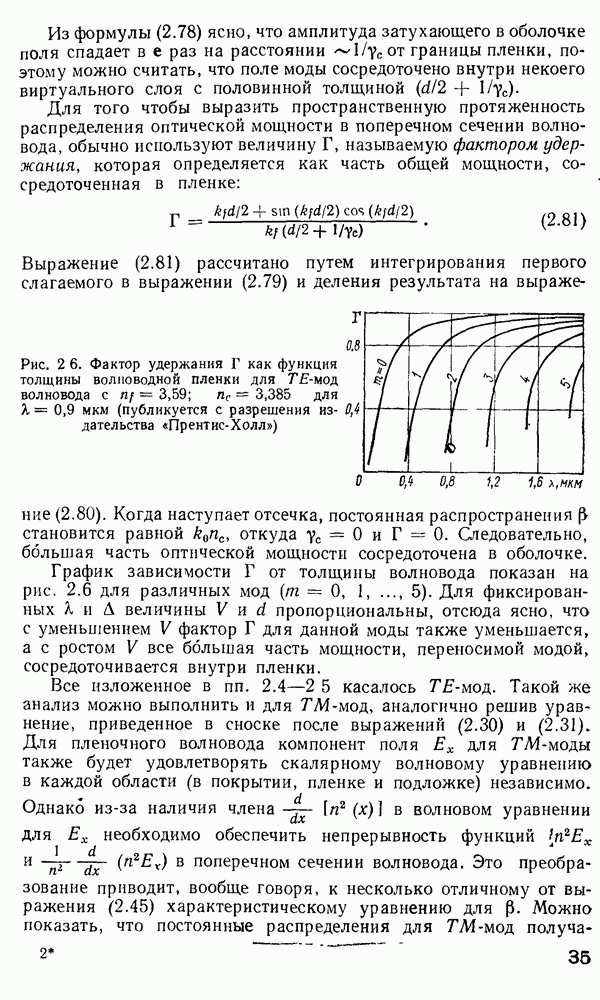
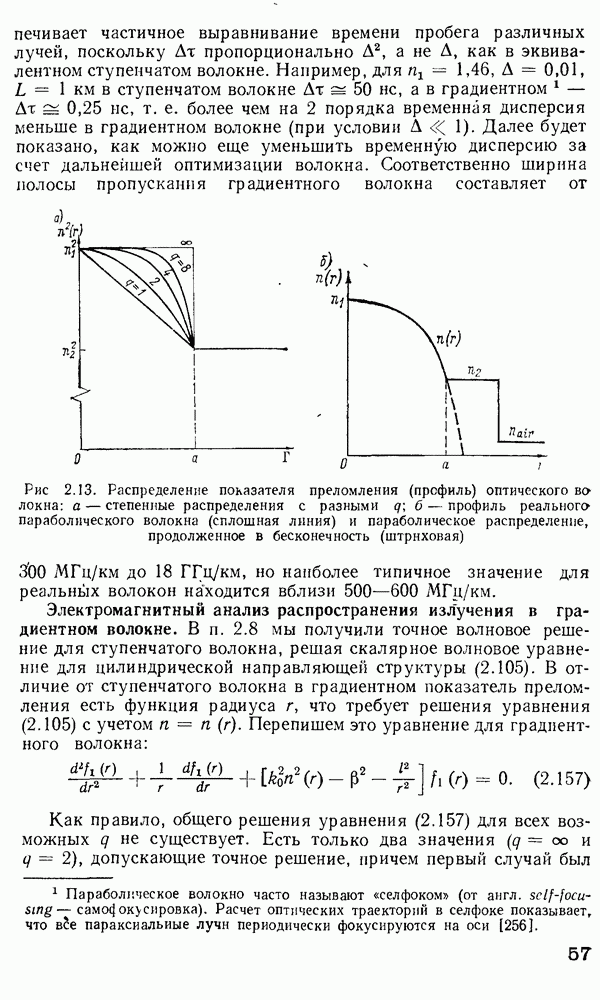
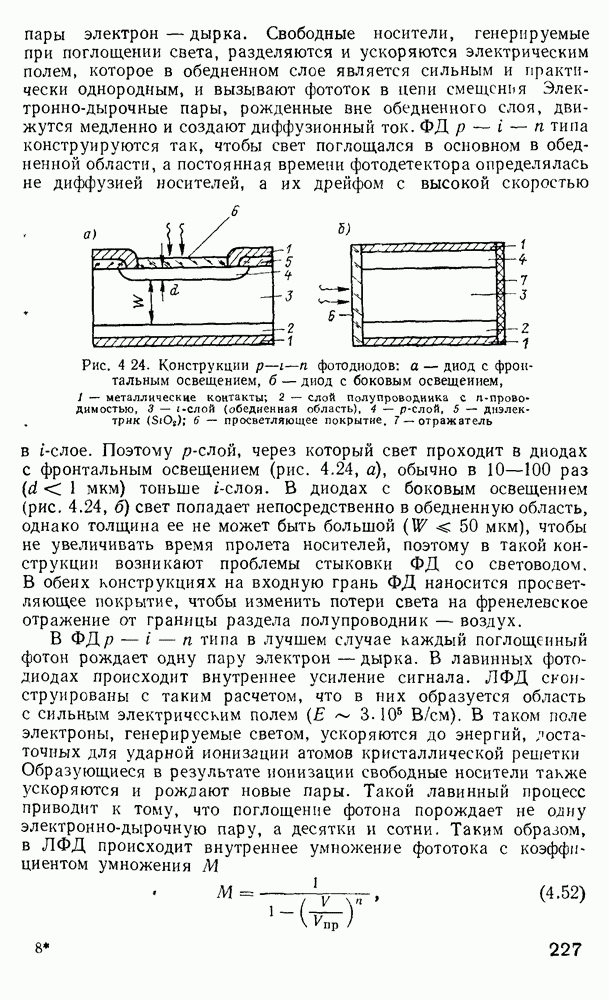
Рис. 2.14. Графическое представление решения по методу  и лучевое представление мод утечки
и лучевое представление мод утечки  [97]: 1 — преломленный луч; 2 — туннелирующее излучение; 3 — направляемый луч
[97]: 1 — преломленный луч; 2 — туннелирующее излучение; 3 — направляемый луч
Из рис. 2.14, а видно, что две кривые  пересекаются в точках поворота
пересекаются в точках поворота  где
где  области В, имеющей форму кольца, ограниченного радиусами
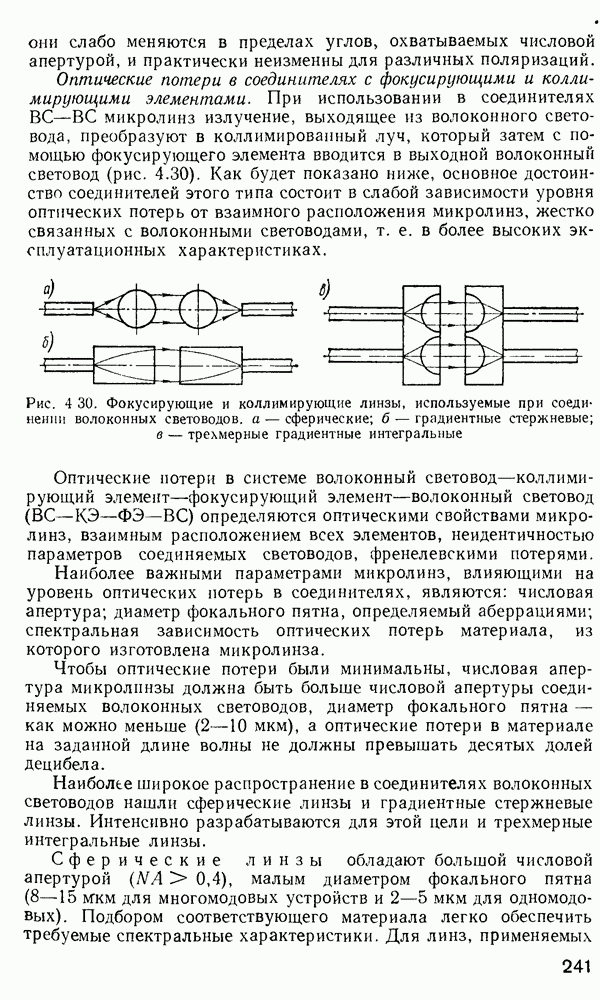
области В, имеющей форму кольца, ограниченного радиусами  поле моды имеет осциллирующую
поле моды имеет осциллирующую  так как
так как  действительно в этой области, в то время как в областях
действительно в этой области, в то время как в областях  поле спадает экспоненциально, так как
поле спадает экспоненциально, так как  мнимое. Условия распространения моды для данного распределения
мнимое. Условия распространения моды для данного распределения  зависят от
зависят от  Для данного значения (3, если I нарастает, область В становится все уже до тех пор, пока обе каустики не сомкнутся в одну. Если
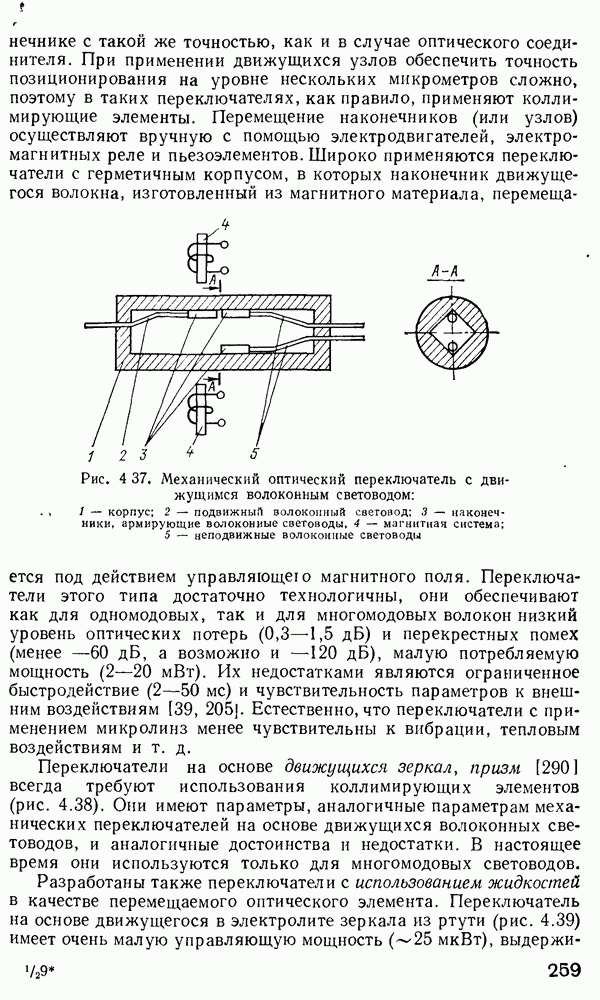
Для данного значения (3, если I нарастает, область В становится все уже до тех пор, пока обе каустики не сомкнутся в одну. Если  нарастает дальше, для всех последующих I не существует решений в виде связанных мод. С другой стороны, для фиксированных
нарастает дальше, для всех последующих I не существует решений в виде связанных мод. С другой стороны, для фиксированных  у мод, далеких от отсечки,
у мод, далеких от отсечки,  весьма близка к
весьма близка к  и область В узка по сравнению с модами, которые близки к отсечке. Если же
и область В узка по сравнению с модами, которые близки к отсечке. Если же  то
то  больше не становится отрицательной для больших
больше не становится отрицательной для больших
 что может привести к ситуации, когда возникает третья каустика для
что может привести к ситуации, когда возникает третья каустика для  расположенного в области оболочки (рис. 2.14, б). В этом случае наблюдается новое явление.
расположенного в области оболочки (рис. 2.14, б). В этом случае наблюдается новое явление.
Наличие каустик при  приводит к наличию дискретных значений
приводит к наличию дискретных значений  [получающихся при решении уравнения (2.167)]. Наличие третьей каустики при
[получающихся при решении уравнения (2.167)]. Наличие третьей каустики при  приводит к тому, что в области
приводит к тому, что в области  поле моды экспоненциально спадает по радиусу, а в области
поле моды экспоненциально спадает по радиусу, а в области  вновь возникает осциллирующая зависимость. Строго говоря, такое решение также описывает волноводную моду. Фактически, когда такие моды возбуждены в сердцевине волокна, они вначале распространяются, как связанные моды, вдоль волокна, но постепенно их энергия вытекает в оболочку. Длина волокна, на которой отмечается значительная утечка энергии таких мод в оболочку, зависит от величин
вновь возникает осциллирующая зависимость. Строго говоря, такое решение также описывает волноводную моду. Фактически, когда такие моды возбуждены в сердцевине волокна, они вначале распространяются, как связанные моды, вдоль волокна, но постепенно их энергия вытекает в оболочку. Длина волокна, на которой отмечается значительная утечка энергии таких мод в оболочку, зависит от величин 
Если  очень близки друг к другу, энергия соответствующей моды очень быстро выводится из сердцевины в оболочку. Если же
очень близки друг к другу, энергия соответствующей моды очень быстро выводится из сердцевины в оболочку. Если же  разделяет достаточный зазор, мода может распространяться на большие расстояния (километры) вдоль волокна, прежде чем утечка энергии в оболочку станет существенной. Наилучший метод аналитического рассмотрения мод утечки основан на применении набора лучей, как это показано на рис. 2.14, в. Каждый раз, как луч приближается к каустике
разделяет достаточный зазор, мода может распространяться на большие расстояния (километры) вдоль волокна, прежде чем утечка энергии в оболочку станет существенной. Наилучший метод аналитического рассмотрения мод утечки основан на применении набора лучей, как это показано на рис. 2.14, в. Каждый раз, как луч приближается к каустике  часть энергии этого луча выводится в оболочку. Такие лучи в волокнах называются туннельными, или лучами утечки [97, 345]. Хотя изучение туннельных лучей весьма интересно, на практике общая доля лучей утечки в энергии, переносимой по волокну, ничтожна на малых расстояниях, измеряемых метрами, причем она зависит от условий ввода. Например, лучи утечки могут образовываться на местах сварки волокон и, следовательно, могут влиять на результаты измерения потерь в волоконных линиях.
часть энергии этого луча выводится в оболочку. Такие лучи в волокнах называются туннельными, или лучами утечки [97, 345]. Хотя изучение туннельных лучей весьма интересно, на практике общая доля лучей утечки в энергии, переносимой по волокну, ничтожна на малых расстояниях, измеряемых метрами, причем она зависит от условий ввода. Например, лучи утечки могут образовываться на местах сварки волокон и, следовательно, могут влиять на результаты измерения потерь в волоконных линиях.
Для мод, характеризующихся  имеется только одна точка поворота, а лучи, образующие такие моды, проходят через ось волокна и называются меридиональными.
имеется только одна точка поворота, а лучи, образующие такие моды, проходят через ось волокна и называются меридиональными.
Возвращаемся теперь к решению уравнения (2.167), которое должно дать нам постоянные распространения (3 различных мод. Для параболического профиля мы находим, подставляя выражение (2.154) с  в уравнение (2.167), что
в уравнение (2.167), что

Здесь мы пренебрегли  по сравнению с
по сравнению с  что оправдано по отношению ко всем модам, кроме тех, которые имеют очень малые азимутальные номера. Переходя от переменной
что оправдано по отношению ко всем модам, кроме тех, которые имеют очень малые азимутальные номера. Переходя от переменной  к переменной
к переменной  и используя таблицу стандартных интегралов [90], из уравнения (2.168) можно получить [256]
и используя таблицу стандартных интегралов [90], из уравнения (2.168) можно получить [256]

что идентично уравнению (2.158). Этот результат наглядно демонстрирует достоинства метода ВКБ.
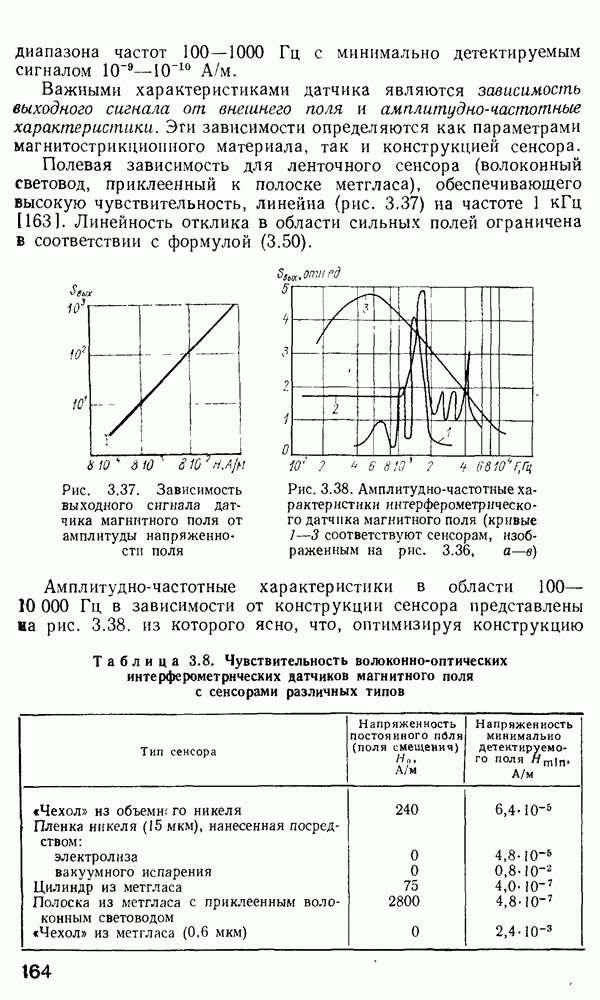
Если стремиться получить более общие сведения о модовой структуре и не обращать особого внимания на индивидуальные свойства мод с низкими индексами, то можно пренебречь в выражении (2.167) слагаемыми 1 и 1/4 и переписать это уравнение в приближенной форме

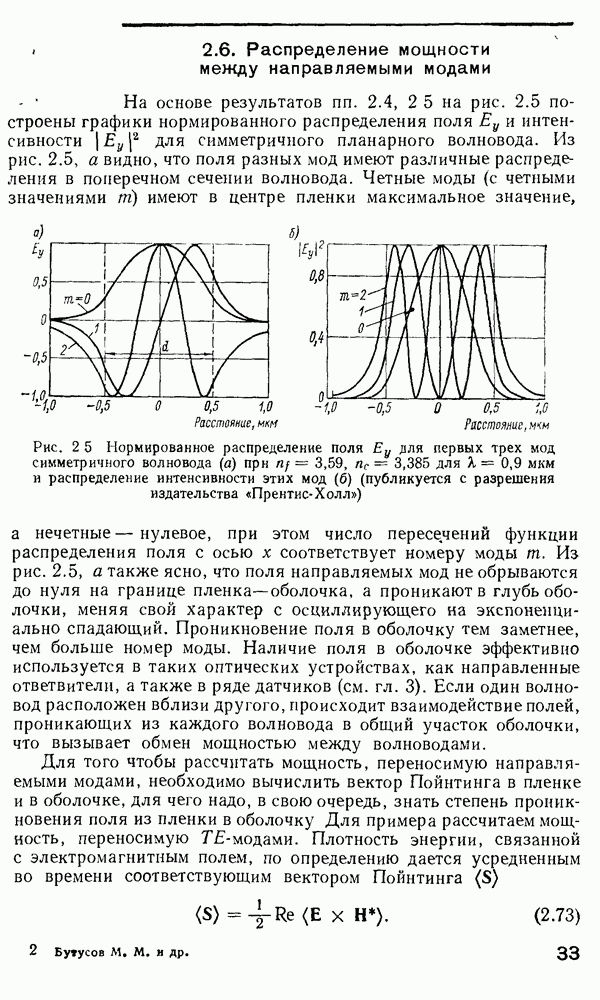
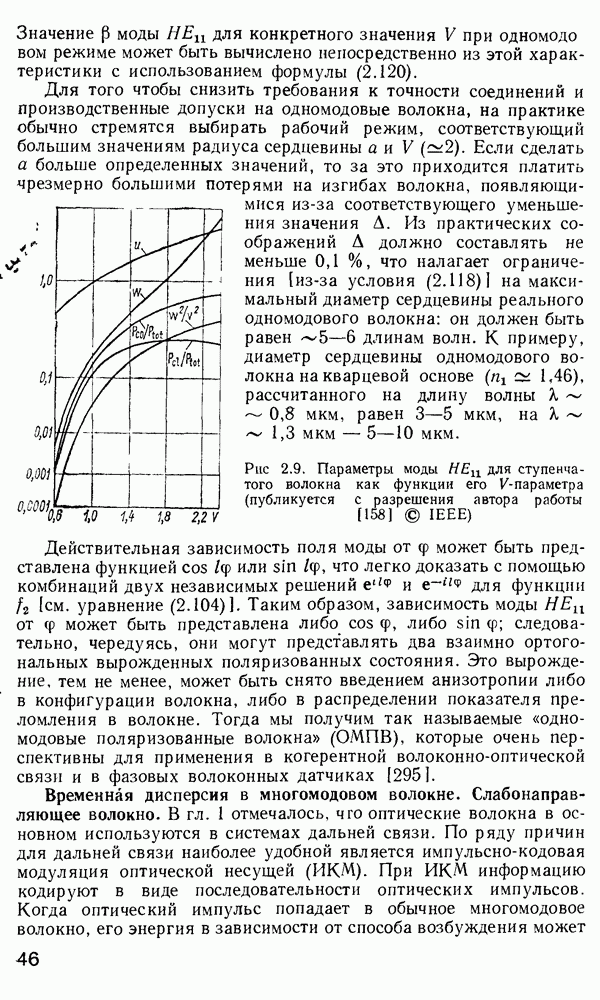
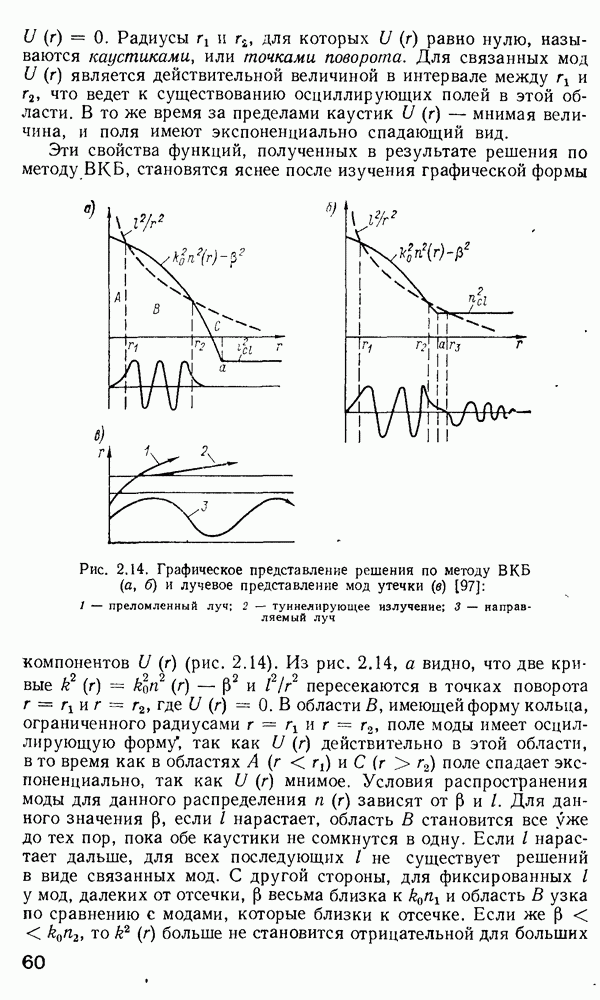
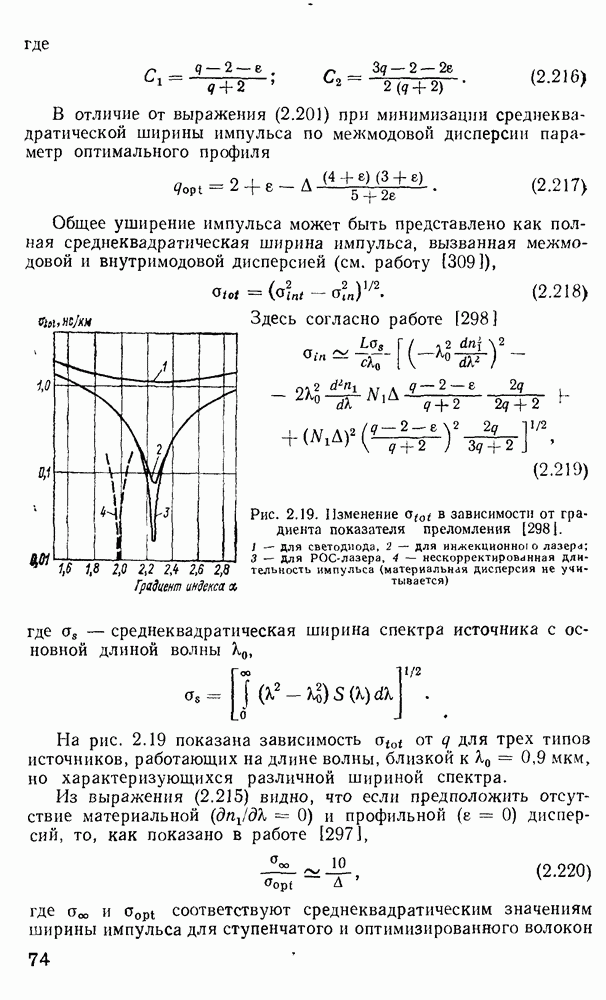
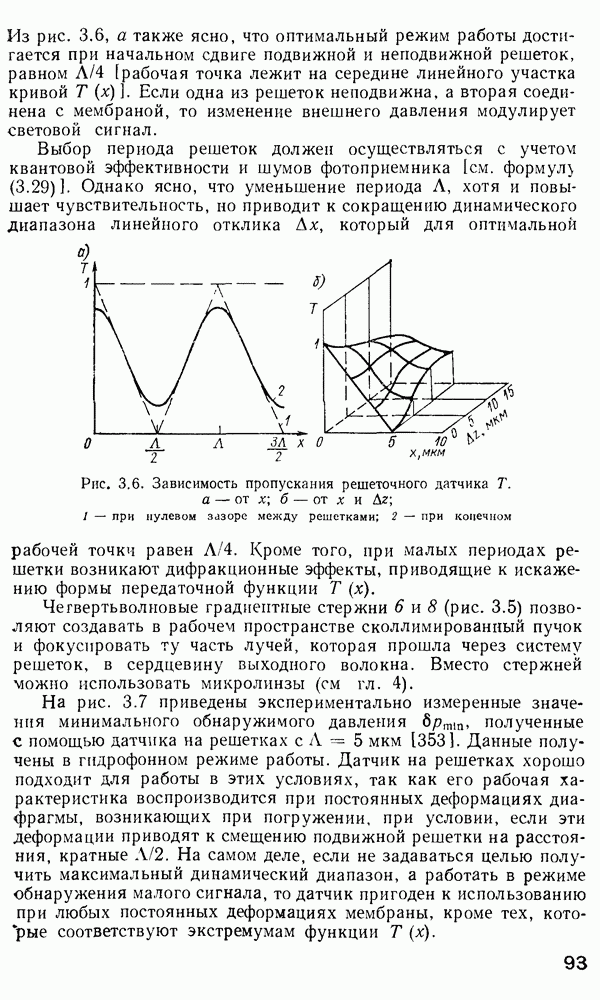
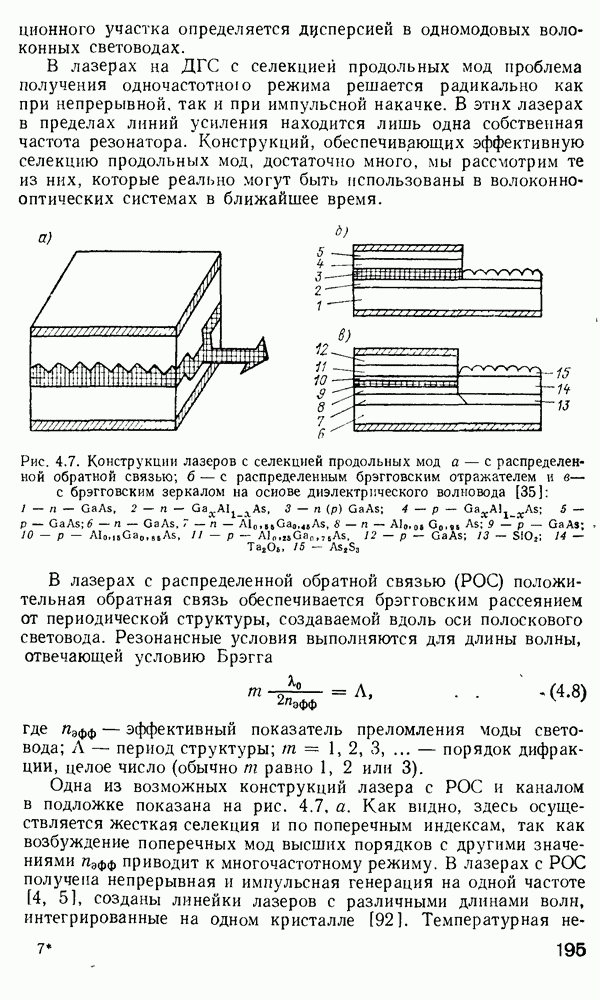
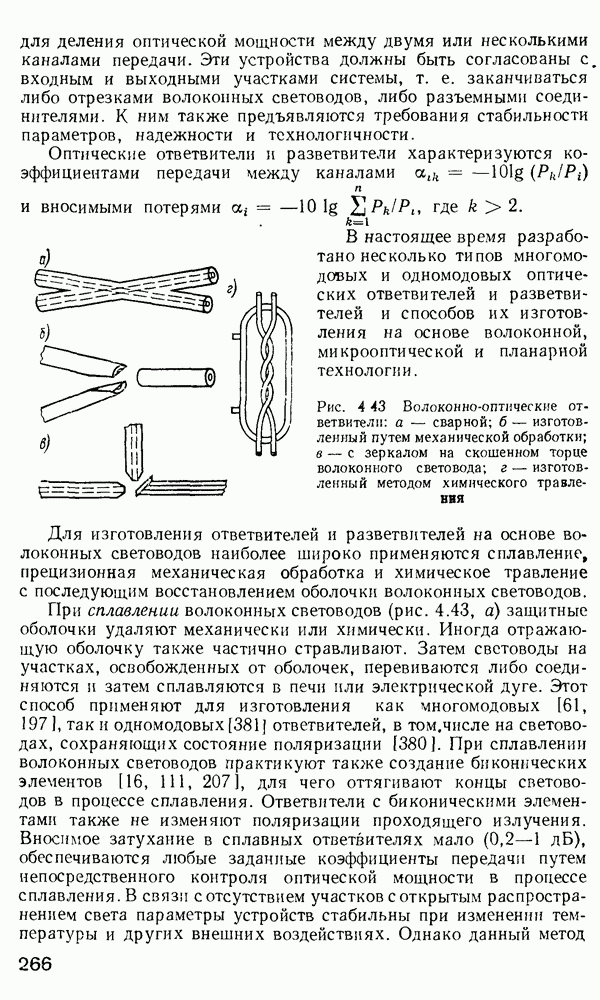
По-видимому, выражение (2.170) является достаточно точным характеристическим уравнением для многомодового градиентного волокна. Каждая мода может быть представлена отдельной точкой на модовой диаграмме (рис. 2.15). Для подсчета полного числа мод нужно принять во внимание, что каждая мода с конкретными индексами  может существовать в двух ортогонально-поляризованных состояниях, а каждое такое состояние может иметь азимутальный множитель: либо
может существовать в двух ортогонально-поляризованных состояниях, а каждое такое состояние может иметь азимутальный множитель: либо  либо
либо 

Рис. 2.15. Модовая диаграмма для волноводных мод
Поэтому на самом деле каждой точке на модовой диаграмме соответствуют четыре различных моды, что должно при расчете числа мод учитываться как четырехкратное вырождение всех мод (за исключением имеющих  которые двукратно вырождены). Ошибка, вносимая модами с
которые двукратно вырождены). Ошибка, вносимая модами с  в расчет, невелика, так как число этих мод незначительно. Все моды, представленные точками, лежащими на кривой
в расчет, невелика, так как число этих мод незначительно. Все моды, представленные точками, лежащими на кривой  имеют одинаковую постоянную распространения. Поэтому если
имеют одинаковую постоянную распространения. Поэтому если  есть число мод с постоянной распространения большей, чем Р, величина М может быть сопоставлена с площадью под кривой
есть число мод с постоянной распространения большей, чем Р, величина М может быть сопоставлена с площадью под кривой  на модовой диаграмме и, следовательно, рассчитывается как
на модовой диаграмме и, следовательно, рассчитывается как 

Изменив порядок интегрирования в формуле (2.171а), мы сначала выполним интегрирование по  а затем по
а затем по  и получим, что
и получим, что

где  можно найти из выражения
можно найти из выражения

а для определенного  величина
величина  вычисляется из
вычисляется из

Следовательно,

а для волокон со степенным профилем [см. формулу (2.154)]

Таково число мод с постоянной распространения, большей Р. Из рис. 2.15 ясно, что штриховая кривая  отделяет истинно волноводные моды от мод утечки и радиационных мод и что площадь под кривой
отделяет истинно волноводные моды от мод утечки и радиационных мод и что площадь под кривой  определяет полное число направляемых мод. Обозначим это число буквой
определяет полное число направляемых мод. Обозначим это число буквой  для волокна со ступенчатым профилем
для волокна со ступенчатым профилем

Сопоставив выражения (2.1736) и (2.174), получим

Для  можно показать, что уравнения (2.168) и (2.175) идентичны. Введя в полученные формулы
можно показать, что уравнения (2.168) и (2.175) идентичны. Введя в полученные формулы  -параметр волокна [см. формулу (2.6)], имеем
-параметр волокна [см. формулу (2.6)], имеем

Для ступенчатого волокна  , следовательно,
, следовательно,

а для параболического градиентного волокна с 

Итак, при заданном V общее число направляемых мод в ступенчатом волокне вдвое больше, чем в эквивалентном параболическом. Например, если для типичного многомодового волокна  то в ступенчатом волокне будет распространяться 1250 мод, а в параболическом — 625.
то в ступенчатом волокне будет распространяться 1250 мод, а в параболическом — 625.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
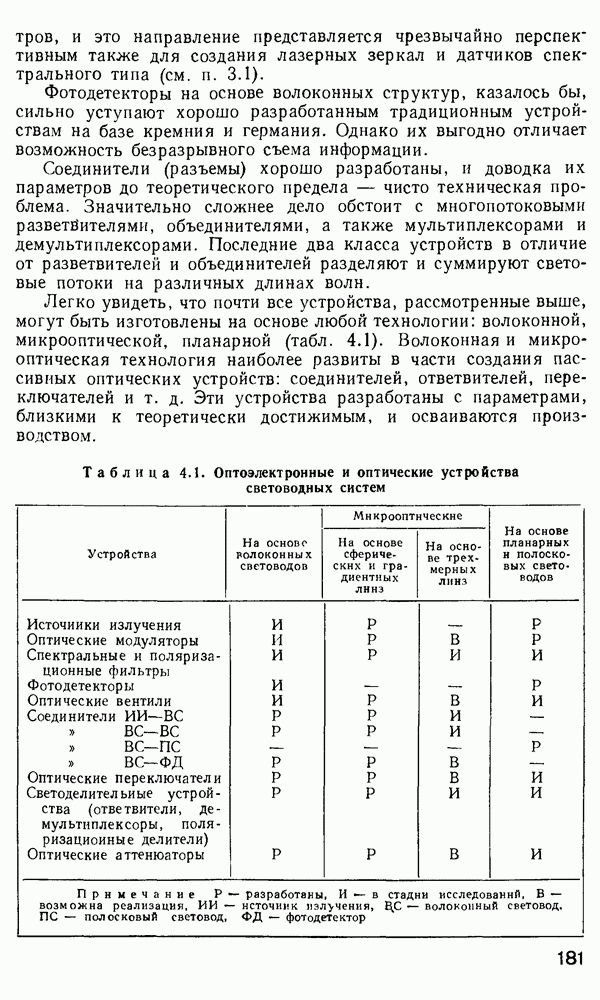
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
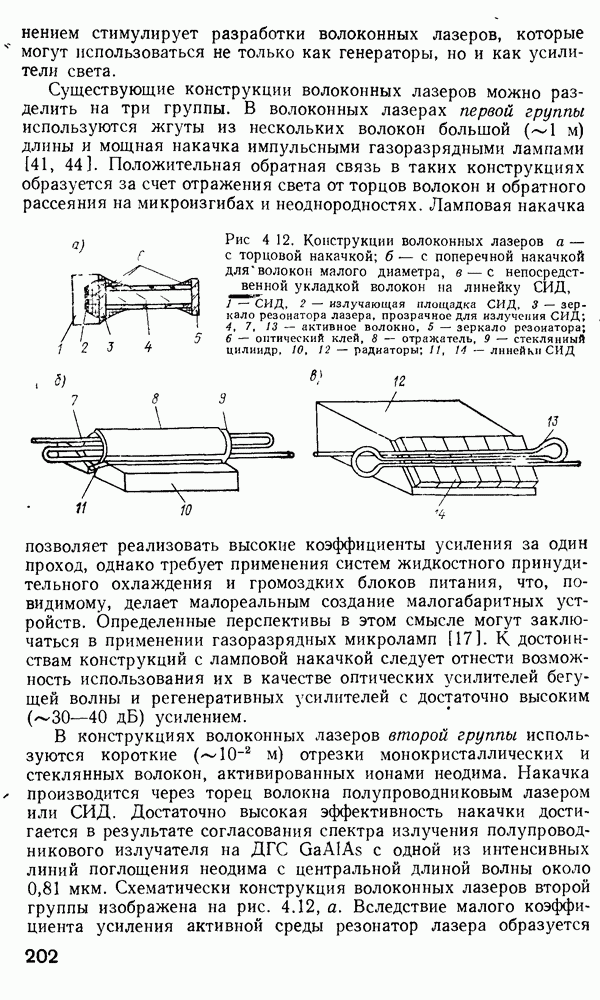
- Волоконные лазеры.
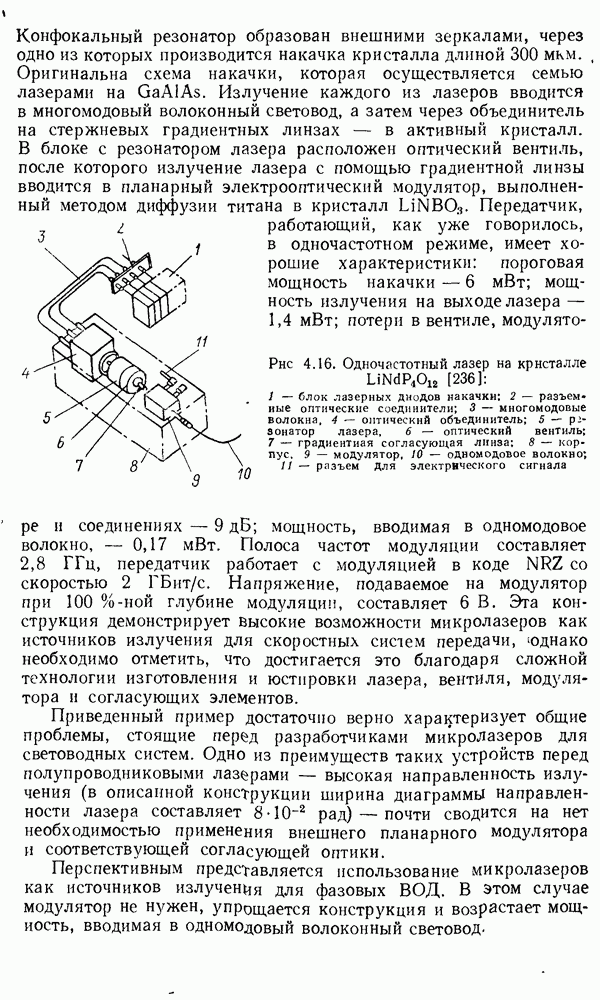
- Объемные микролазеры.
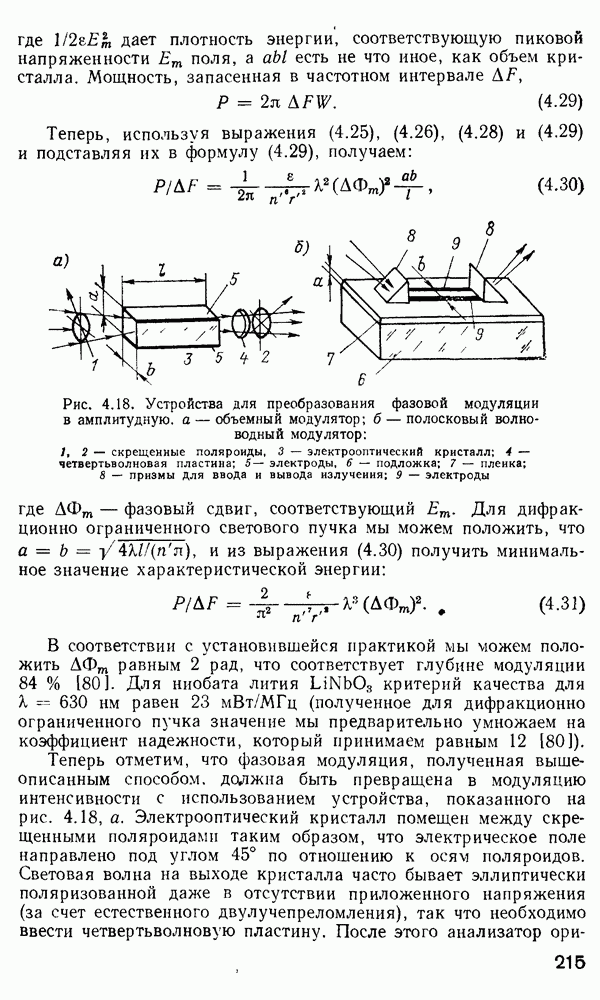
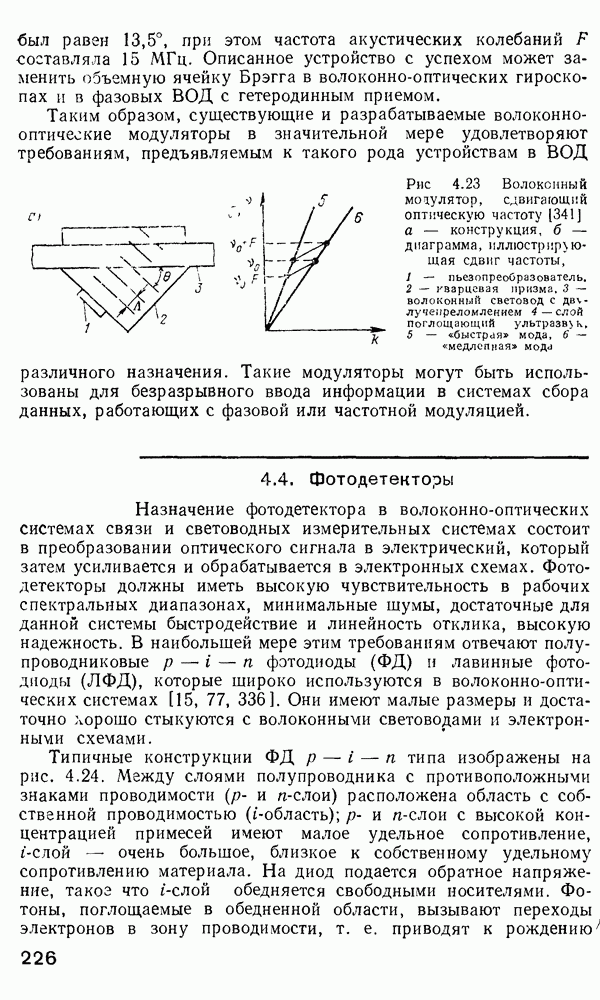
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ