| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
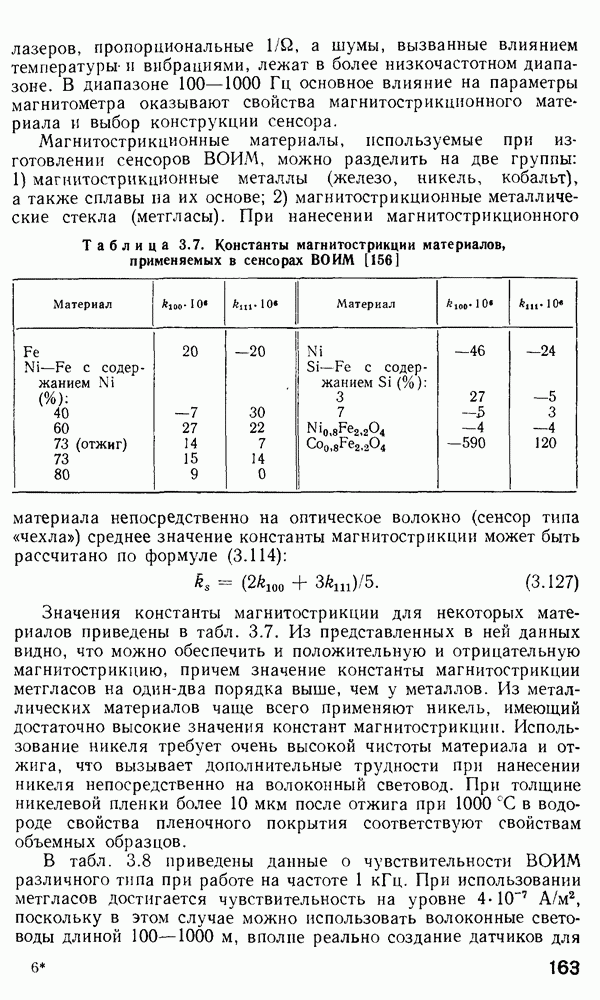
2.7. Прямоугольные волноводы
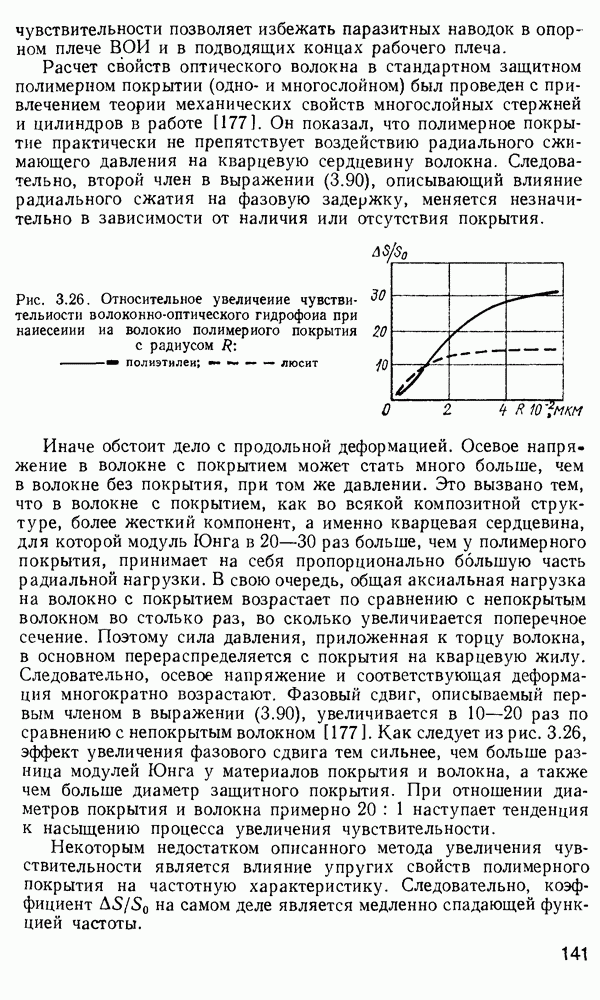
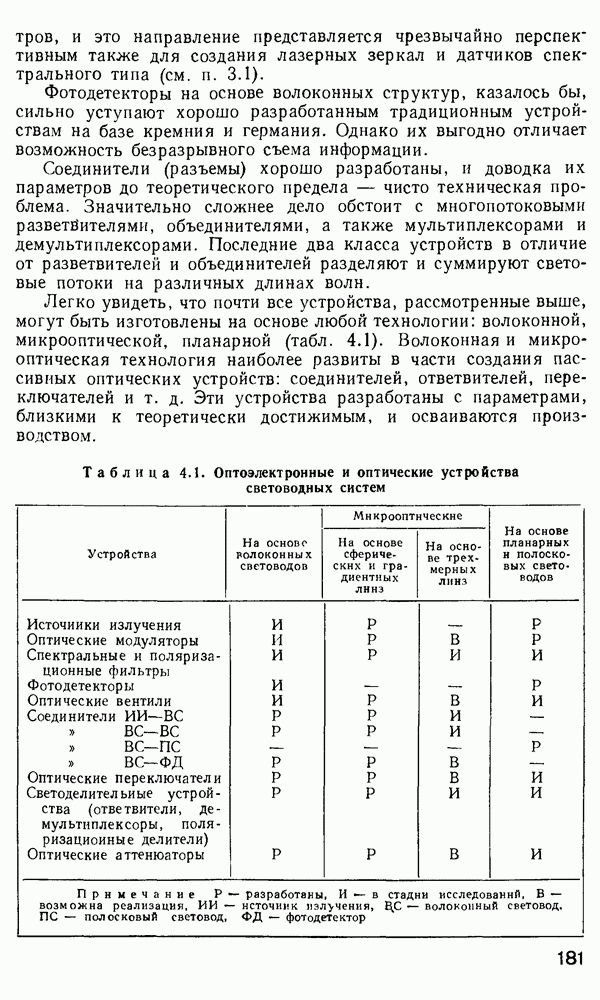
Как уже сообщалось выше, планарные волноводы, помимо того, что служат упрощенной теоретической моделью волноводных явлений в более сложных структурах, оказываются практически полезными в интегральной оптике, так как позволяют удерживать энергию света в тонком слое.

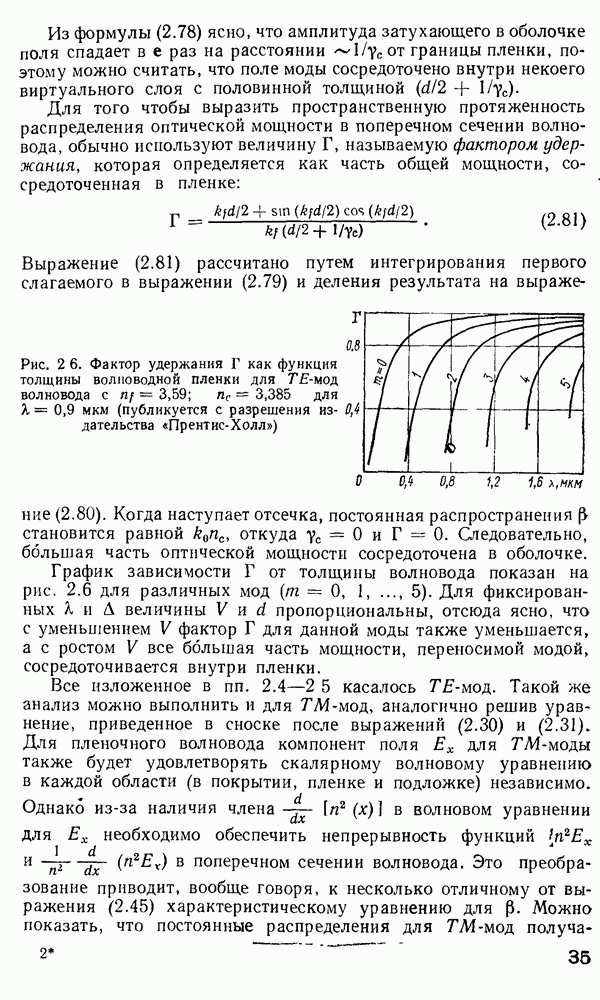
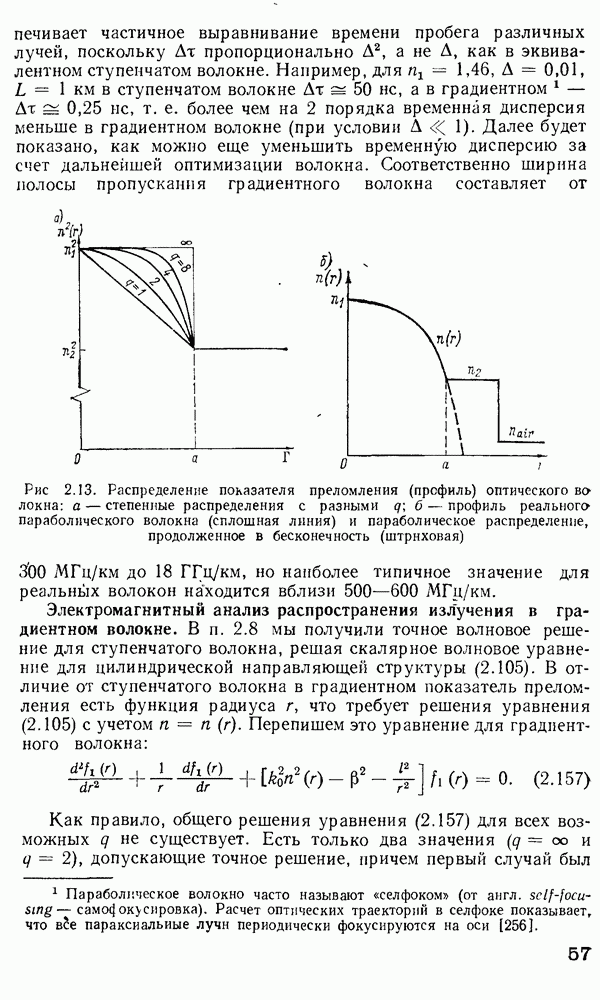
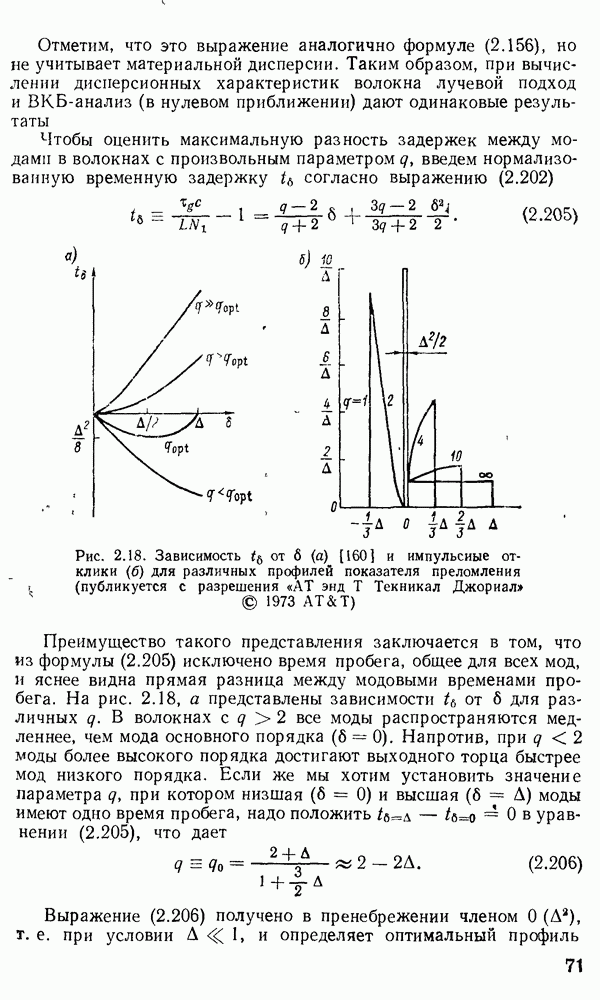
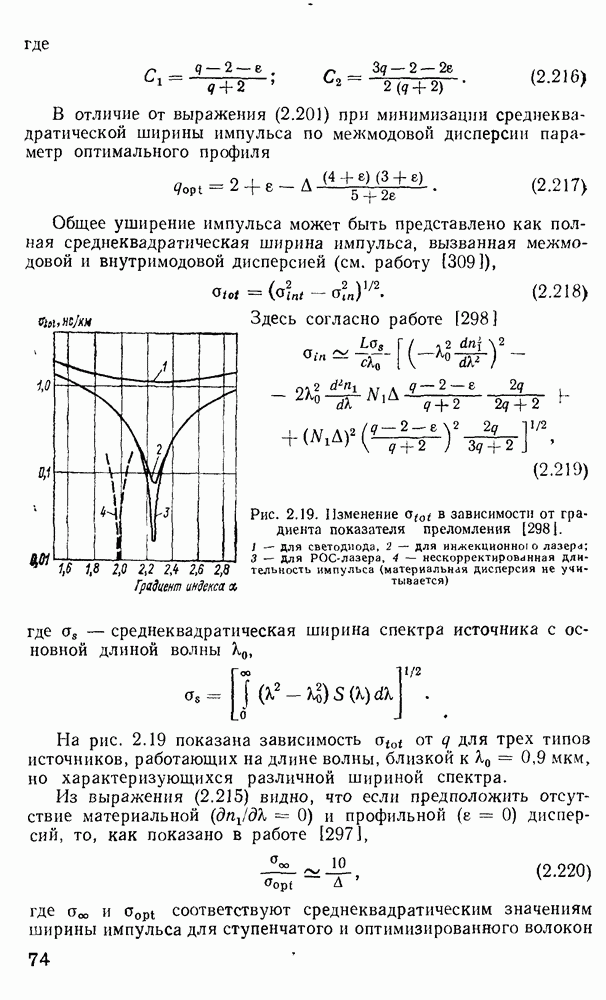
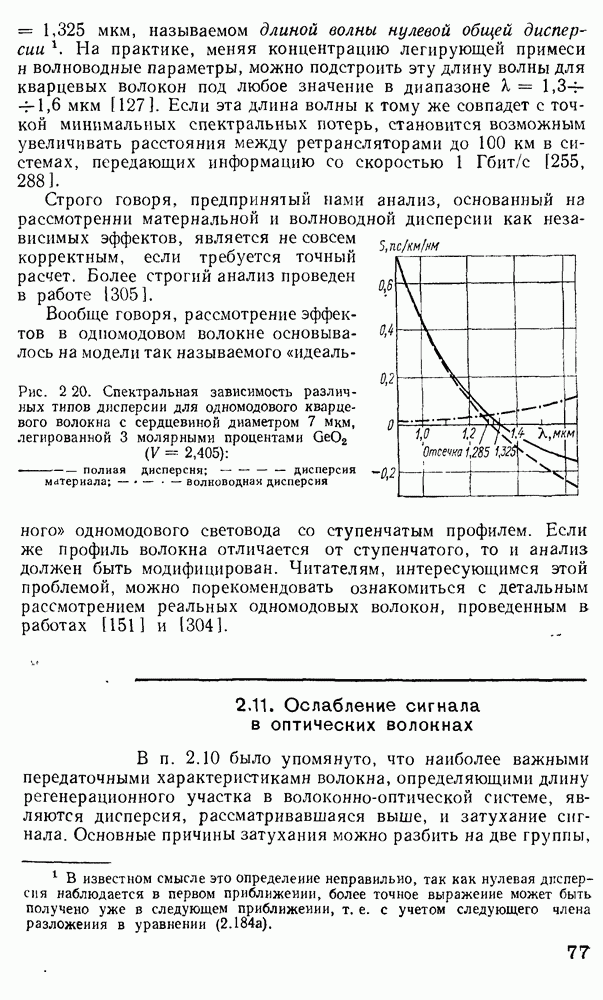
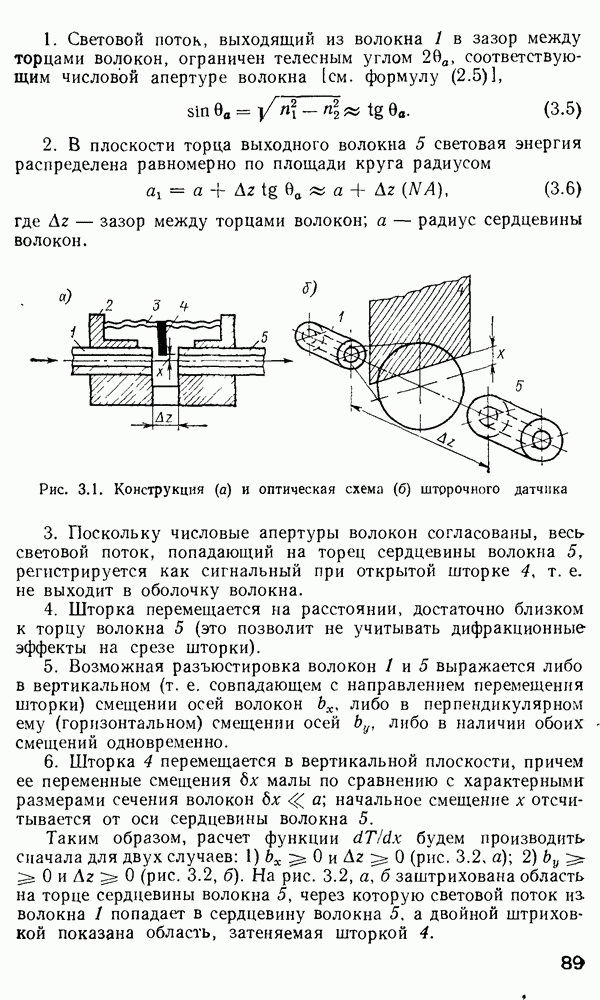
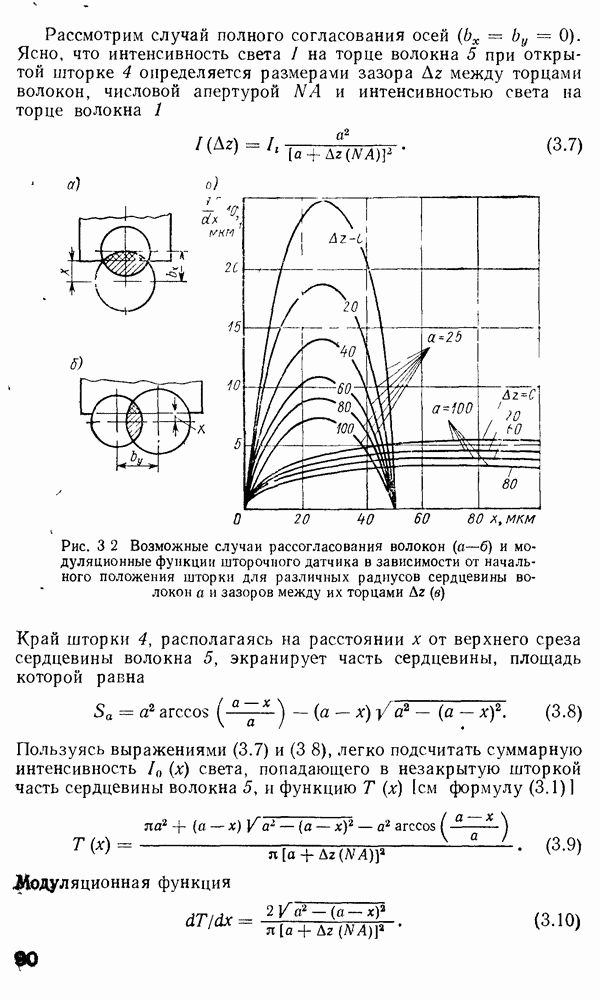
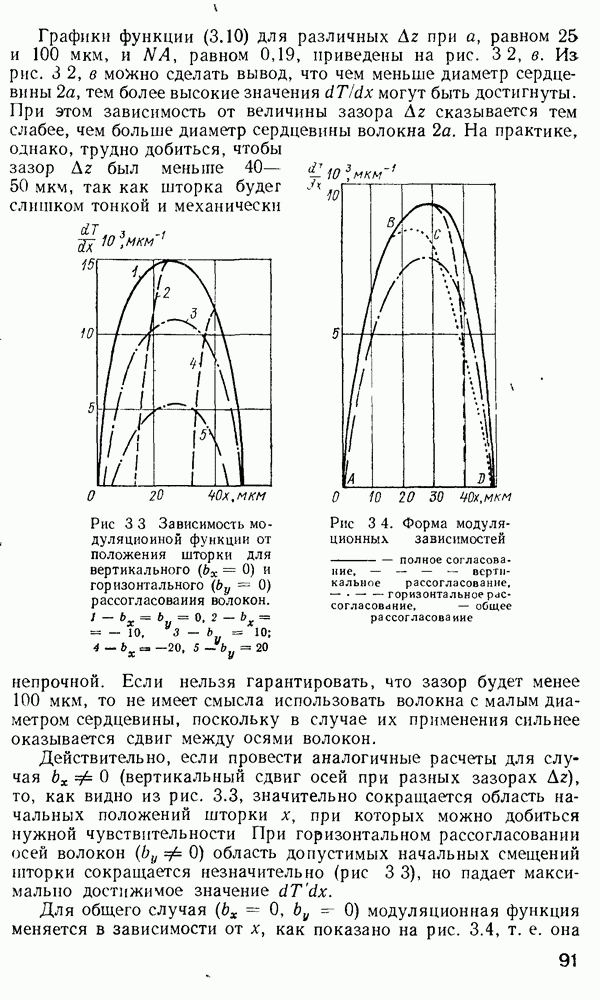
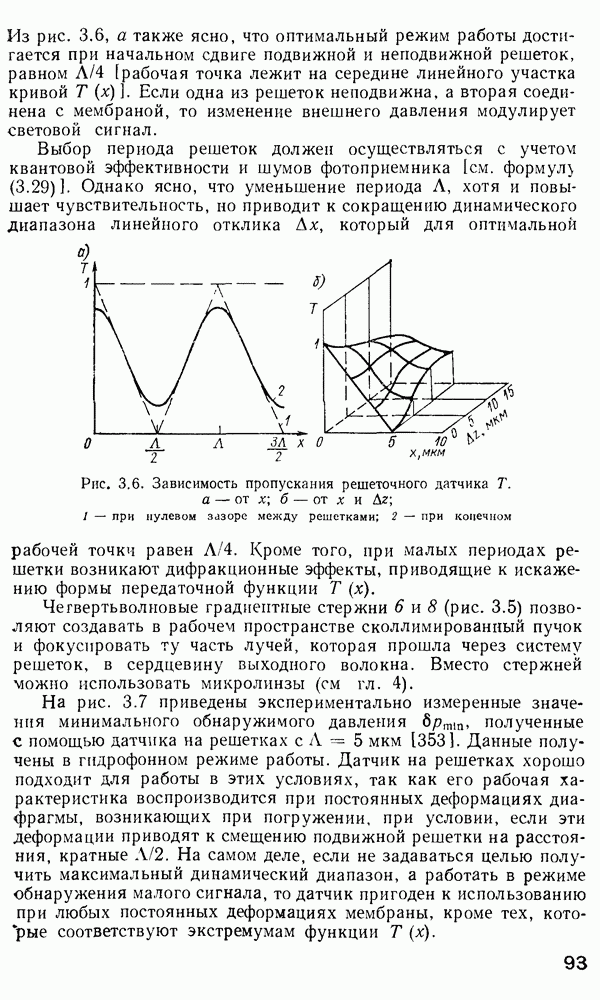
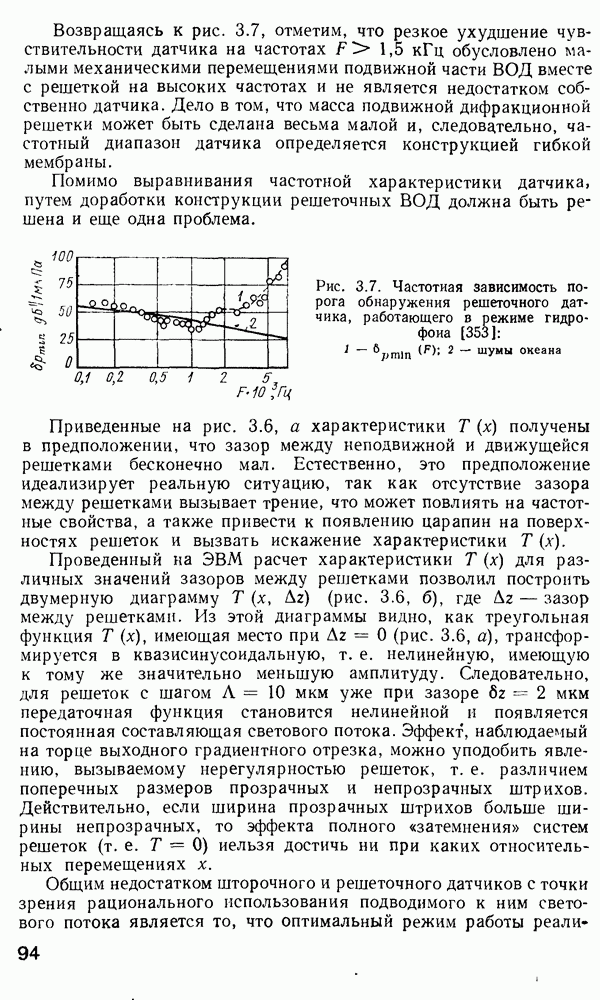
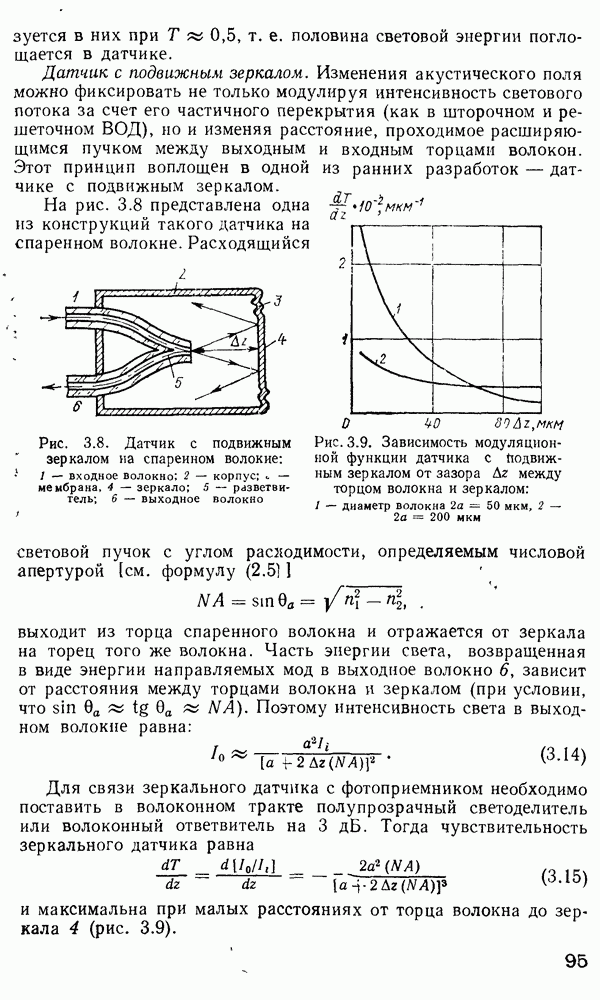
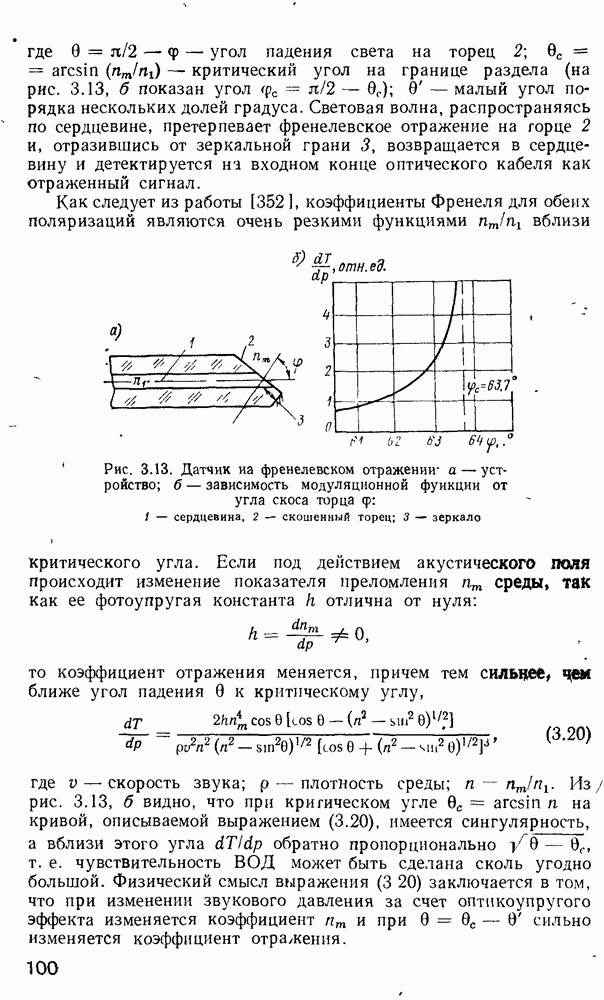
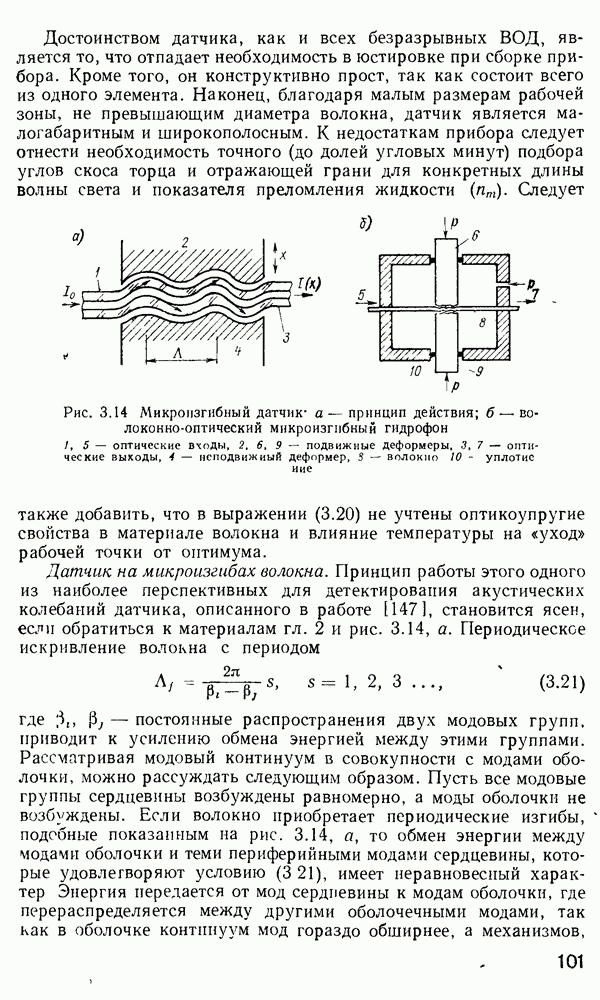
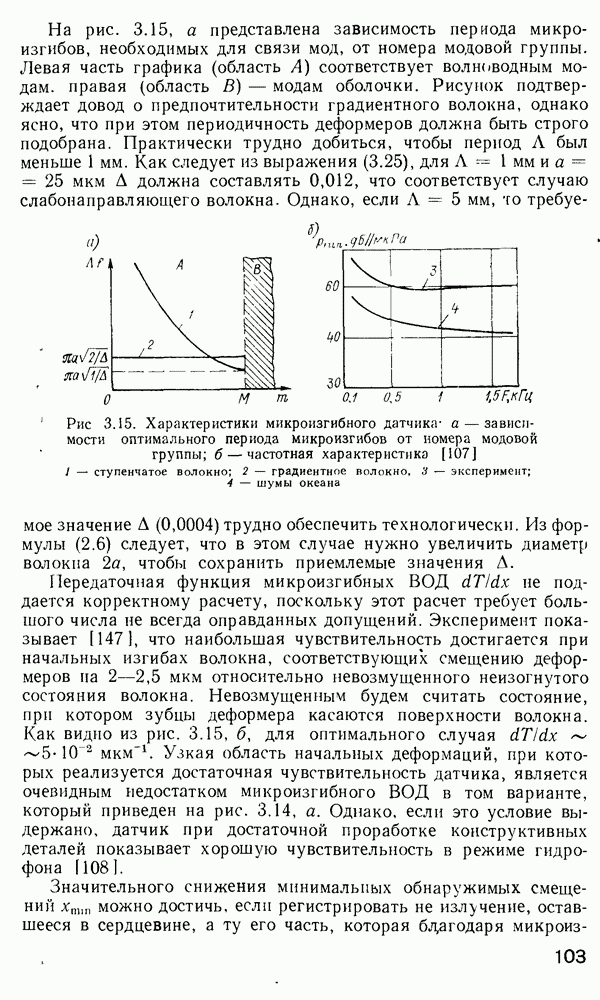
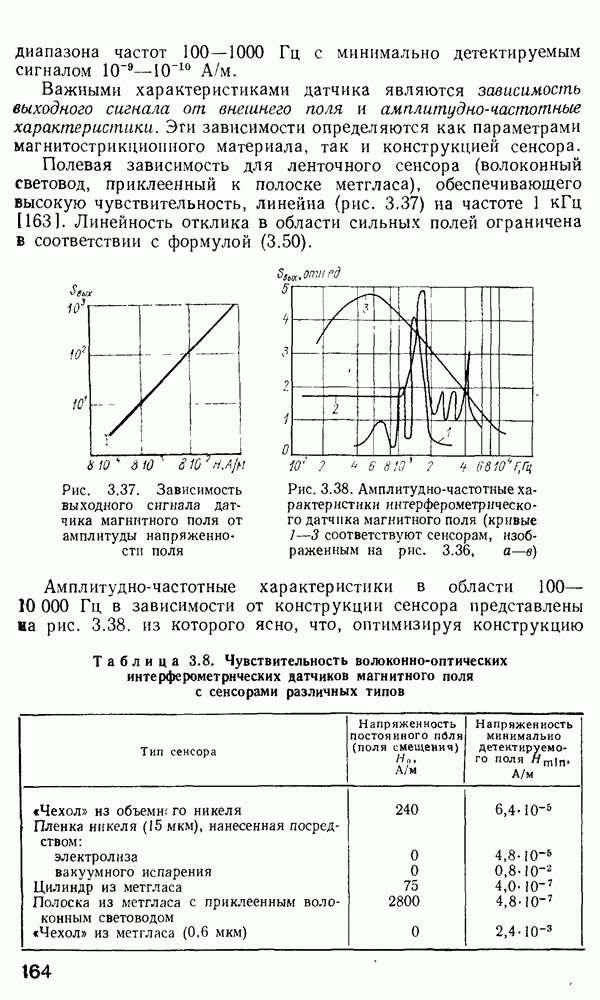
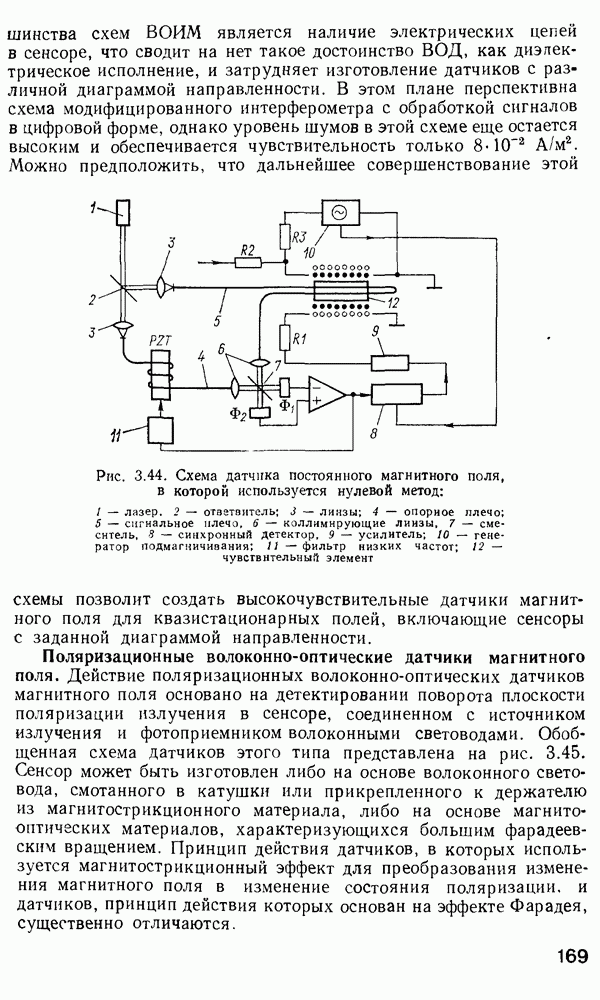
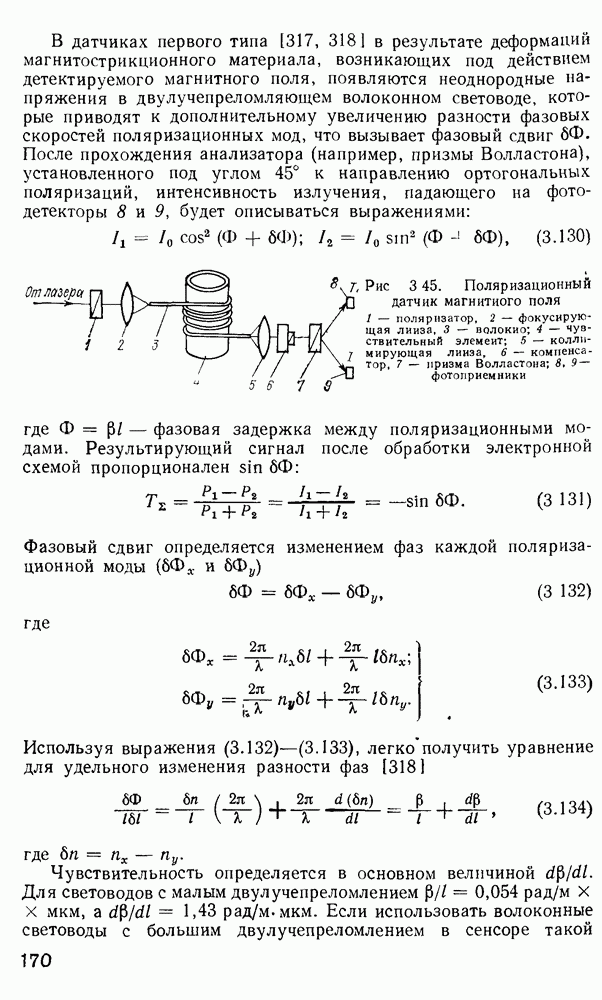
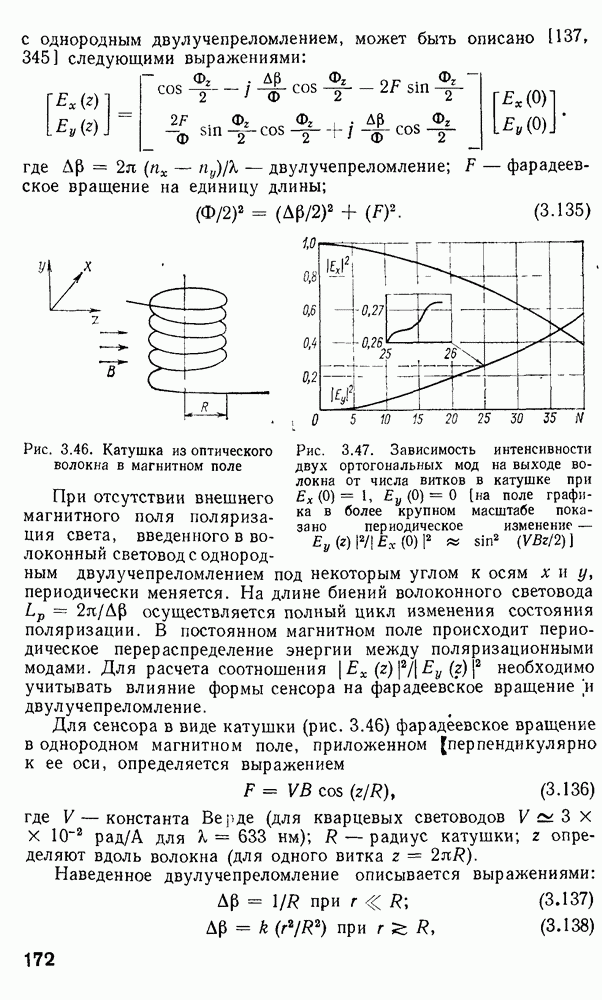
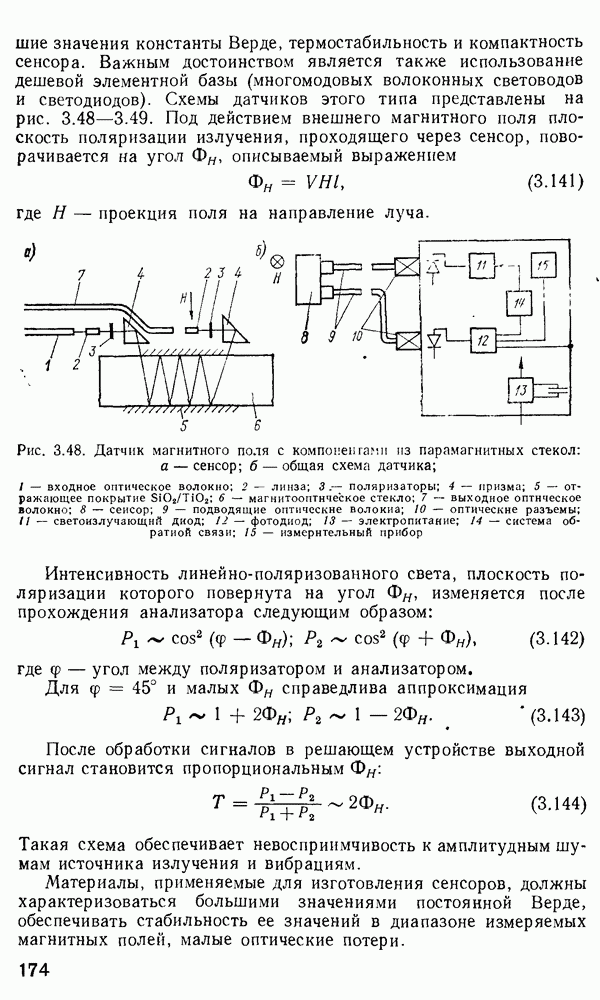
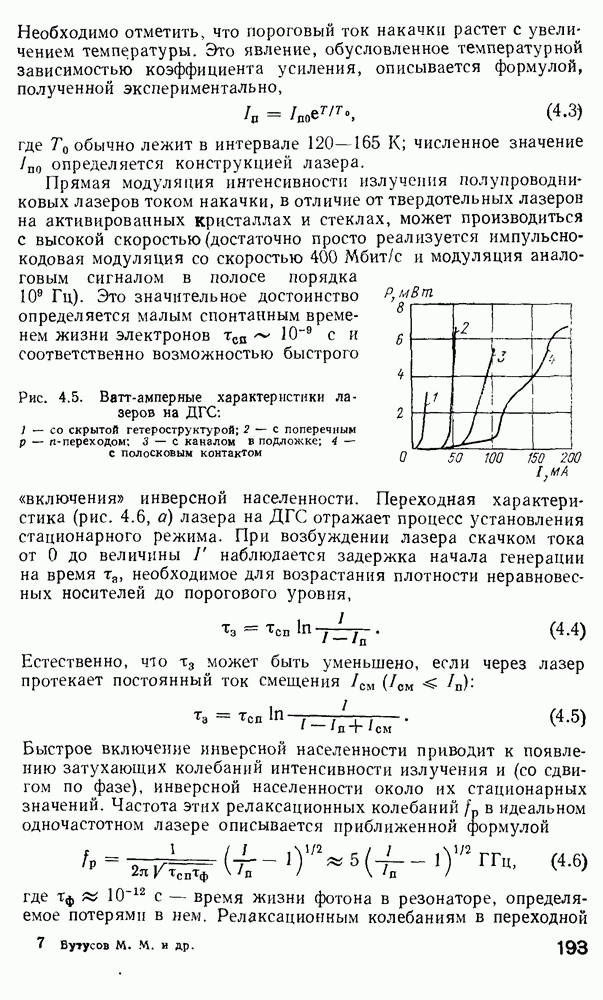
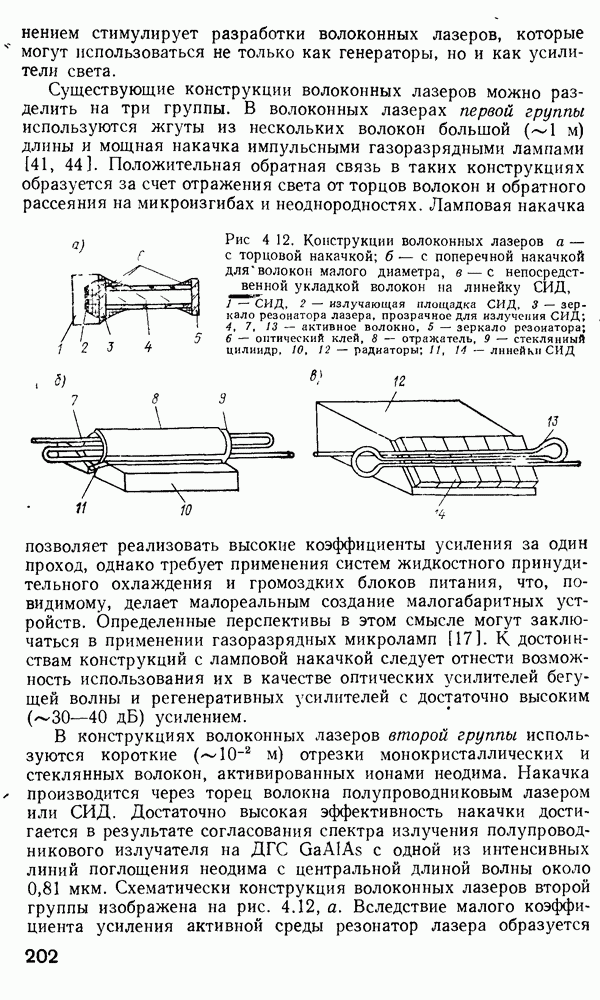
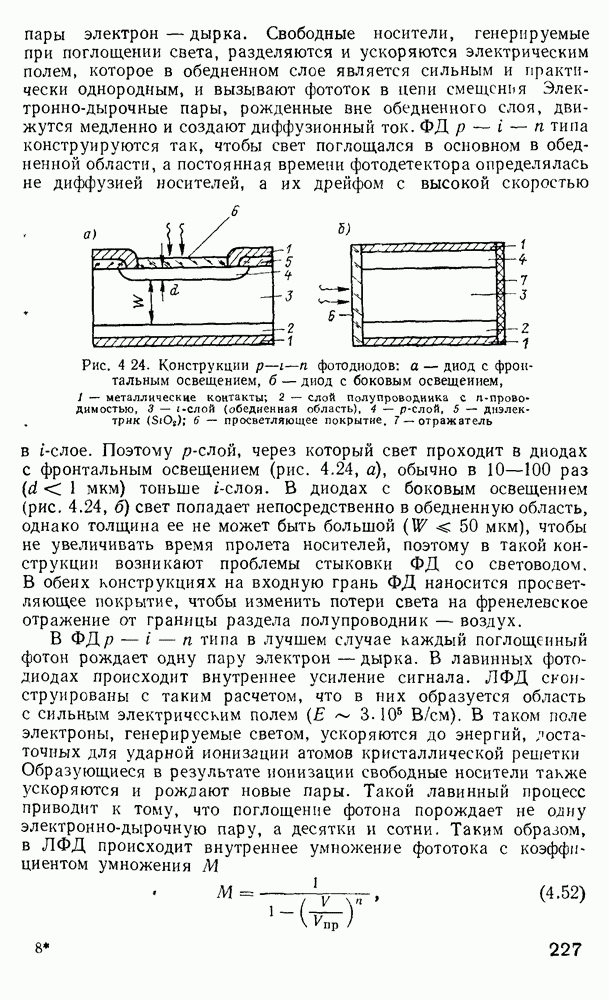
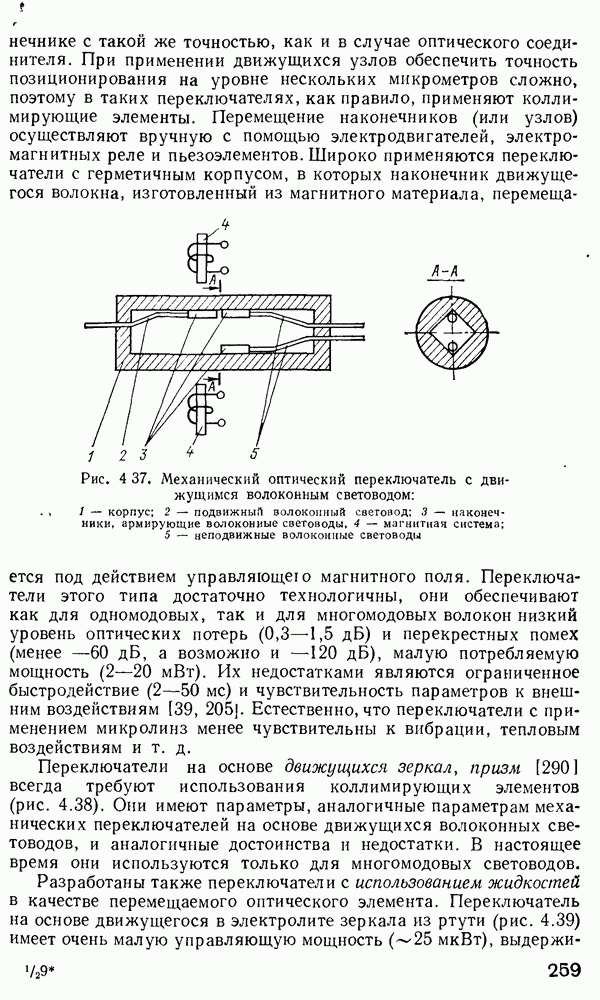
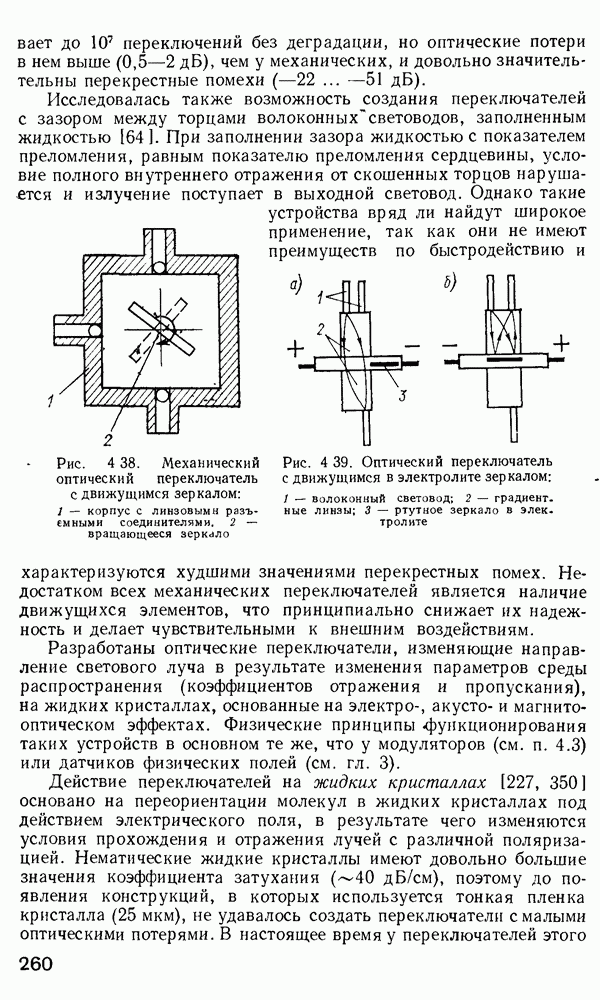
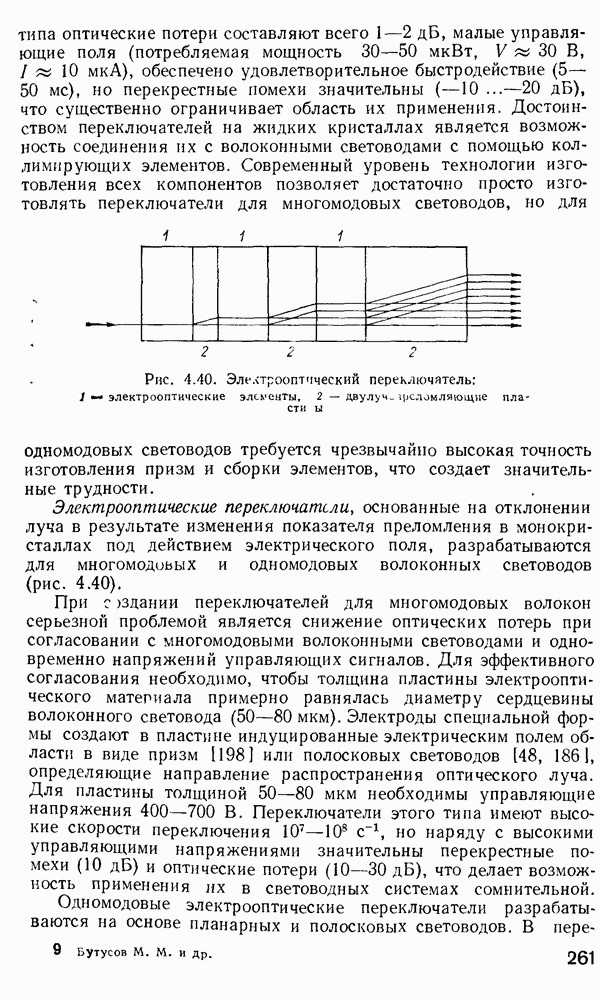
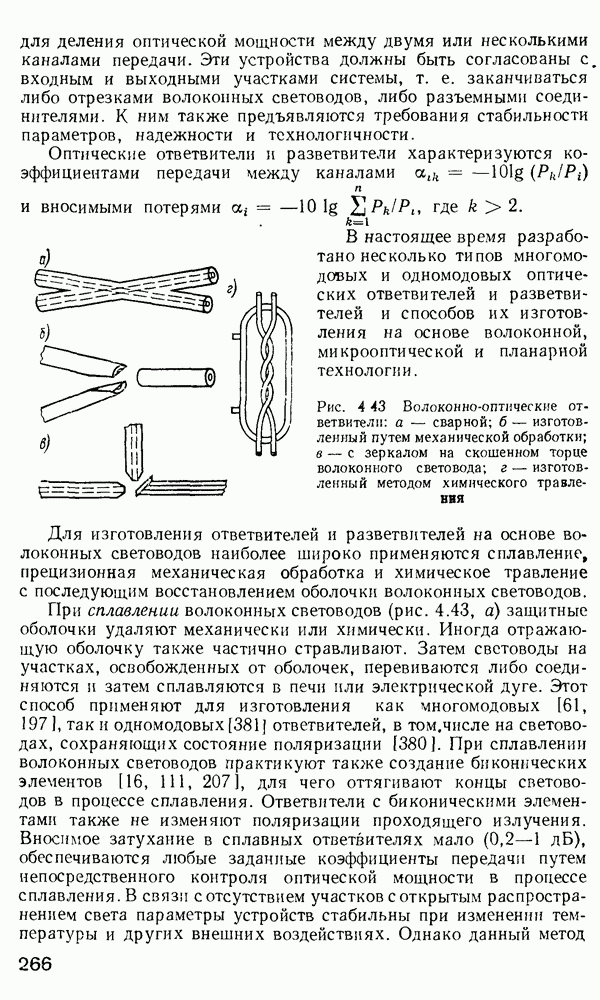
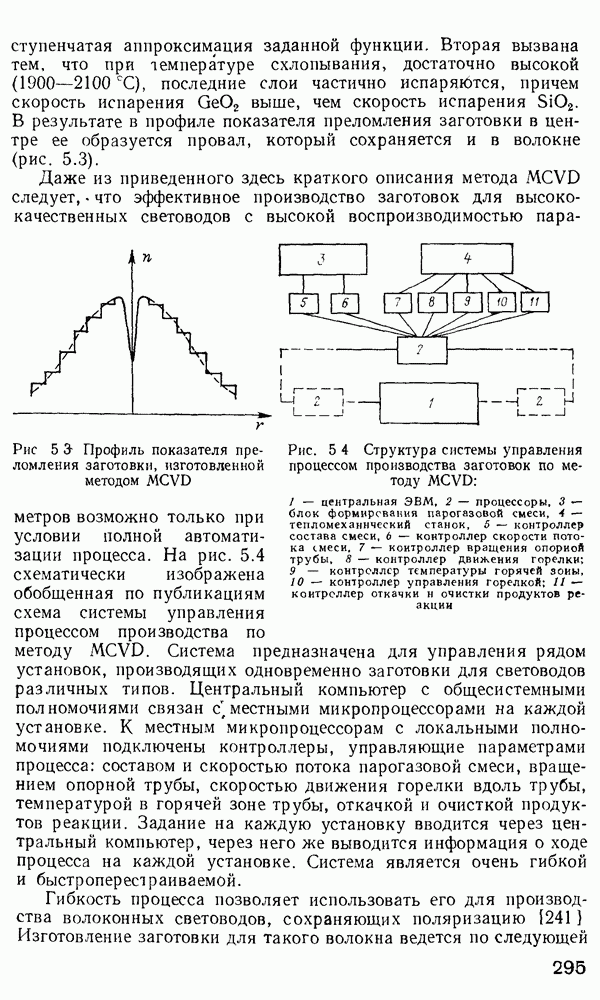
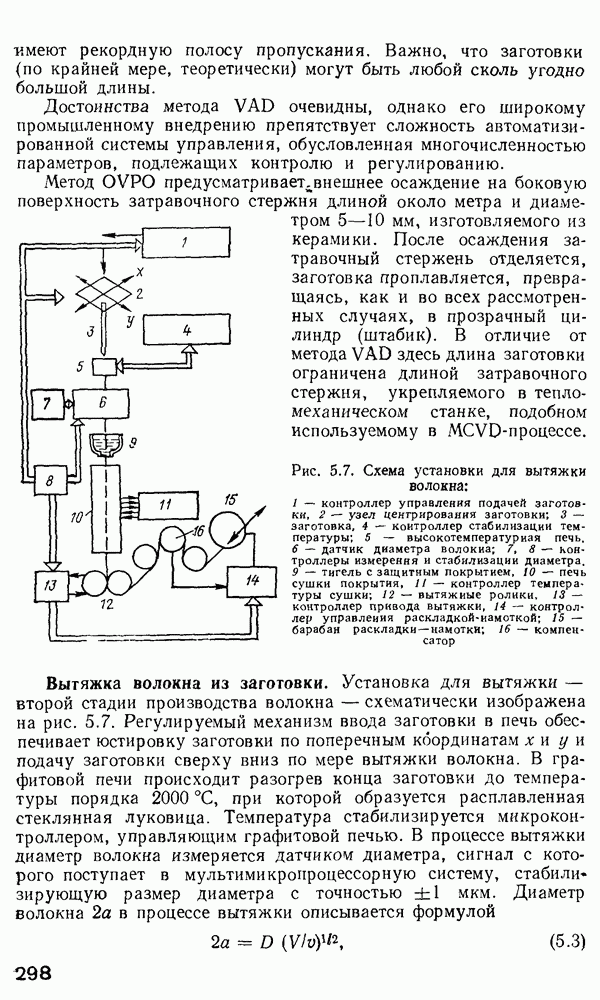
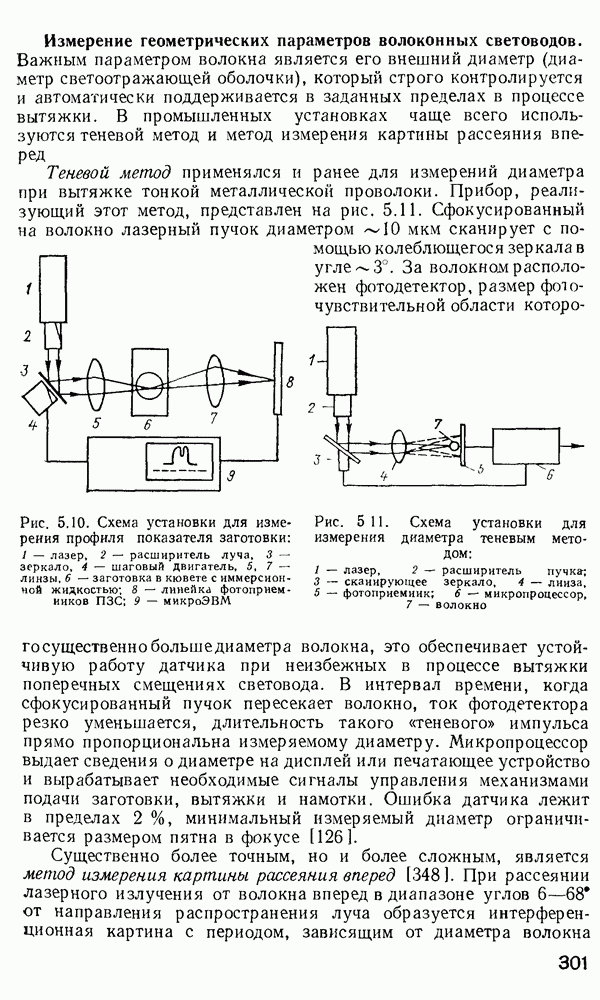
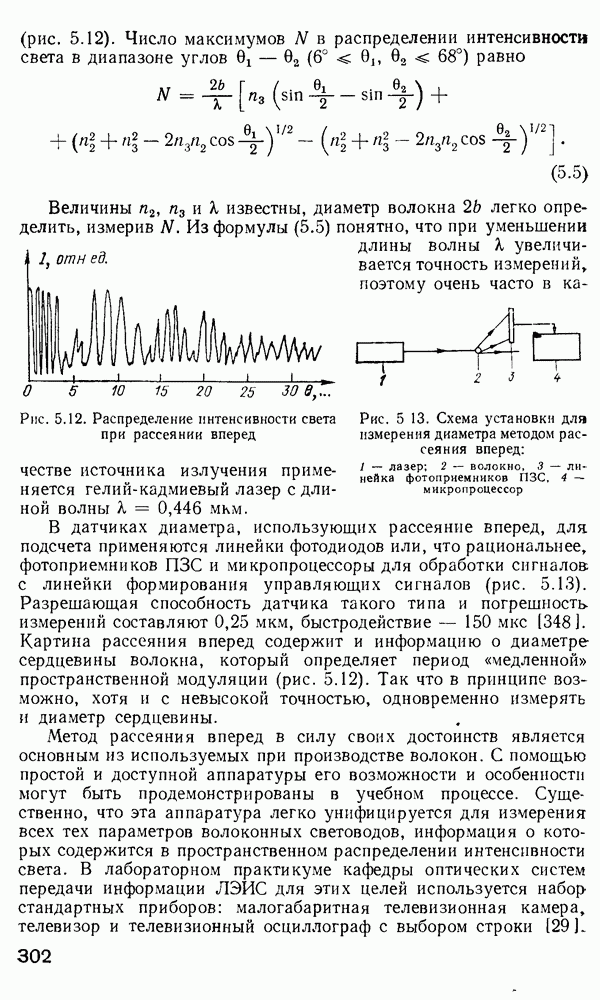
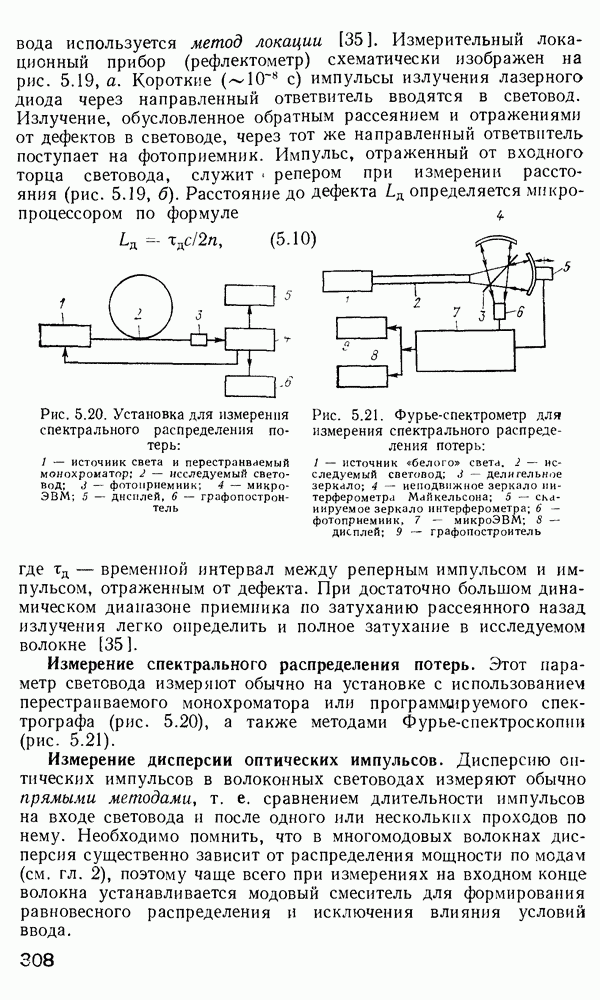
Рис. 2 7 Полосковый волновод прямоугольного сечення: а - гипотетический, б — реальный, получаемый методом возмущений из гипотетического
Однако в большинстве интегрально-оптических устройств требуется направлять энергию вдоль одной координаты и удерживать ее в двух перпендикулярных направлениях, что осуществляется с помощью полоскового волновода прямоугольного сечения (рис. 2.7).
Действительно, пленочные структуры, рассматривавшиеся ранее, обеспечивали удержание энергии вдоль оси х, но не накладывали каких-либо ограничений на распространение в плоскости  Прямоугольный же волновод — это структура, в которой свет не распространяется как вдоль оси х, так и вдоль оси у. Он состоит из волноводной области с более высоким показателем преломления окруженной оболочкой с показателем
Прямоугольный же волновод — это структура, в которой свет не распространяется как вдоль оси х, так и вдоль оси у. Он состоит из волноводной области с более высоким показателем преломления окруженной оболочкой с показателем  Поскольку в прямоугольном волноводе в отличие от планарного показатель преломления
Поскольку в прямоугольном волноводе в отличие от планарного показатель преломления  может быть функцией двух координат, получить формулы для распределения поля и постоянных распространения оказывается делом очень непростым и требующим обычно обширных численных расчетов [161, 253]. Совсем недавно было получено точное аналитическое решение волноводных свойств гипотетического прямоугольного волновода (рис. 2.7, а).
может быть функцией двух координат, получить формулы для распределения поля и постоянных распространения оказывается делом очень непростым и требующим обычно обширных численных расчетов [161, 253]. Совсем недавно было получено точное аналитическое решение волноводных свойств гипотетического прямоугольного волновода (рис. 2.7, а).
Используя это решение, можно получить моды реального волновода, применив теорию возмущений первого порядка [238] Распределение показателя преломления гипотетического волновода (рис 2 7, а)

где

Скалярное волновое уравнение (2.18) для этого случая записывают в виде

где  Если
Если  описывается с помощью выражений (2.82)-(2.84), то уравнение (2.85) решается методом разделения переменных, т. е.
описывается с помощью выражений (2.82)-(2.84), то уравнение (2.85) решается методом разделения переменных, т. е.  что дает раздельные решения для функций
что дает раздельные решения для функций 

где  Чтобы решить уравнение (2.86), введем новую переменную
Чтобы решить уравнение (2.86), введем новую переменную  При этом для областей
При этом для областей  уравнение (2.86) приобретает вид
уравнение (2.86) приобретает вид

где

Поскольку функция  симметрична относительно
симметрична относительно  является либо симметричной, либо антисимметричной функцией
является либо симметричной, либо антисимметричной функцией  Для симметричной функции решение уравнений (2.88) таково:
Для симметричной функции решение уравнений (2.88) таково:

Параметр  содержащий постоянную распространения определяется характеристическим уравнением
содержащий постоянную распространения определяется характеристическим уравнением

которое получается на основании непрерывности X и ее производных при  Для антисимметричной моды характеристическое уравнение имеет вид
Для антисимметричной моды характеристическое уравнение имеет вид

Аналогичным образом можно получить решение для поля и характеристические уравнения той части скалярного уравнения, которая зависит от у. В частности, характеристические уравнения соответственно для симметричной и антисимметричной функции  даются в форме
даются в форме

где

Опираясь на полученные результаты, легко вывести аналитические выражения для распределения модовых полей различных мод в зависимости от того, являются они симметричными либо антисимметричными вдоль х и у. Приведенная постоянная распределения имеет вид

Теперь для того чтобы получить постоянную распределения для реального волновода, показанного на рис.  используем тот факт, что реальное распределение показателя преломления может быть получено из изображенного на рис. 2.7, а гипотетического распределения с помощью возмущения функции показателя преломления в углах гипотетического волновода. Возмущение имеет, очевидно, порядок
используем тот факт, что реальное распределение показателя преломления может быть получено из изображенного на рис. 2.7, а гипотетического распределения с помощью возмущения функции показателя преломления в углах гипотетического волновода. Возмущение имеет, очевидно, порядок  а поскольку на практике
а поскольку на практике  это возмущение является малым.
это возмущение является малым.
Следовательно, зная степень возмущения и используя теорию возмущений первого порядка, можно найти приведенную постоянную распространения для волновода, подобного изображенному на рис. 2.7, б,

где согласно [238]

где  для симметричных и антисимметричных мод по х и у соответственно.
для симметричных и антисимметричных мод по х и у соответственно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
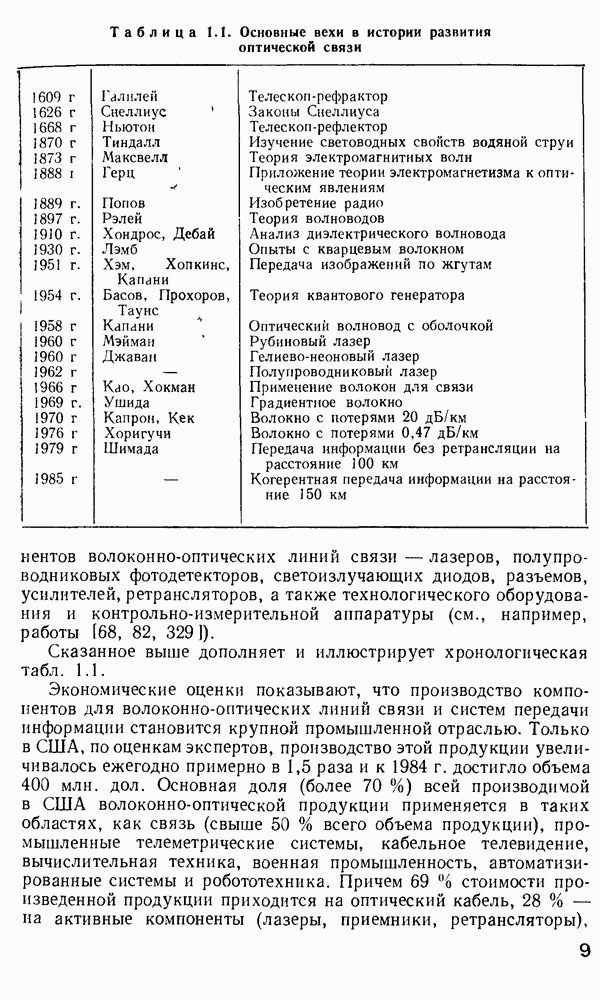
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
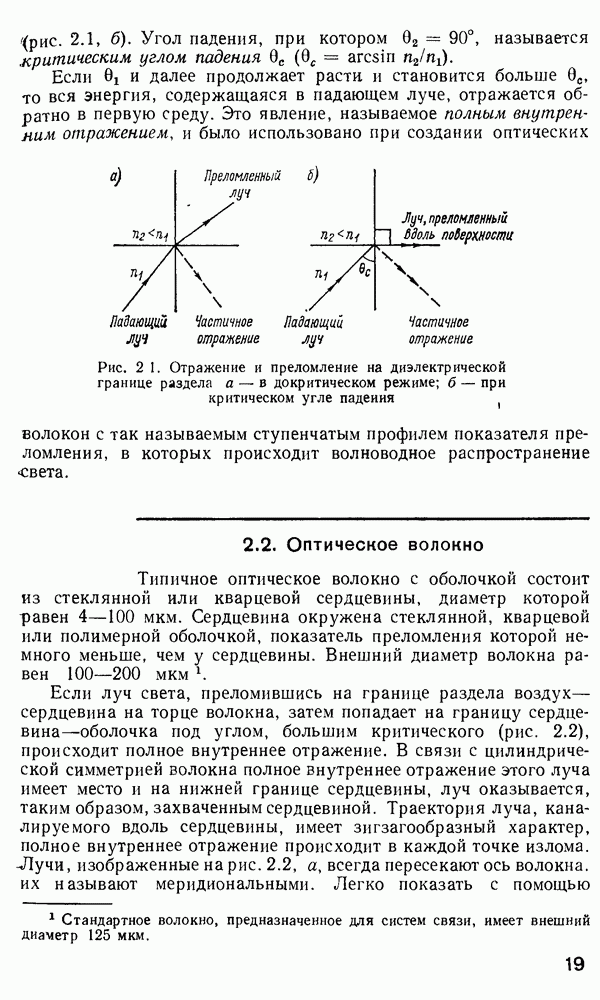
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
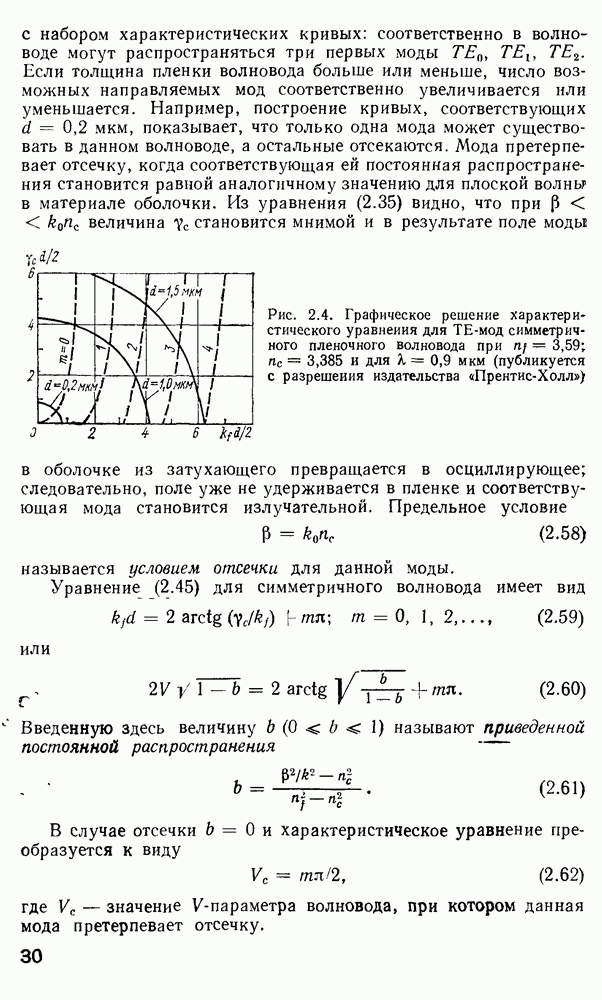
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
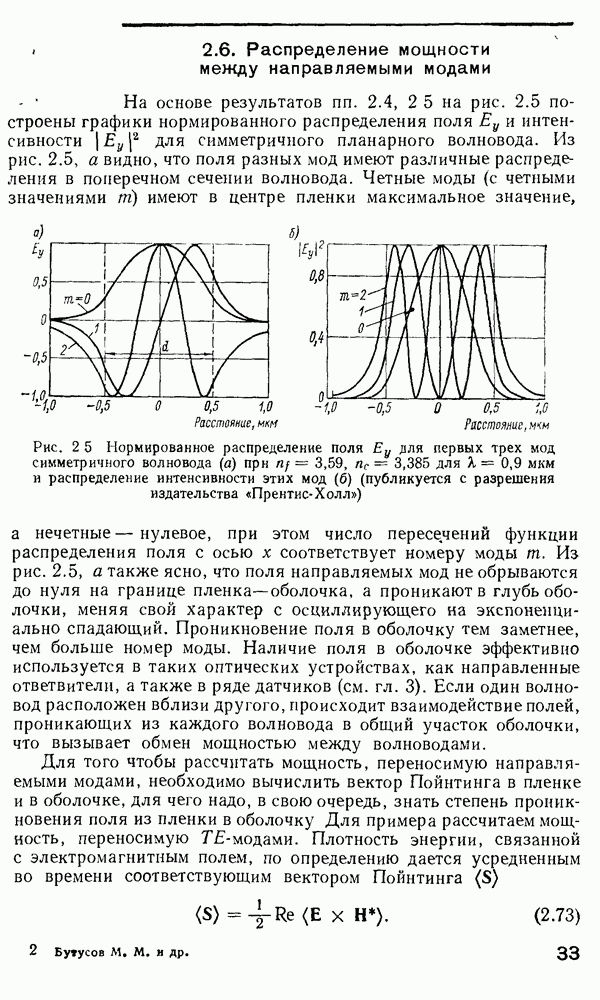
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
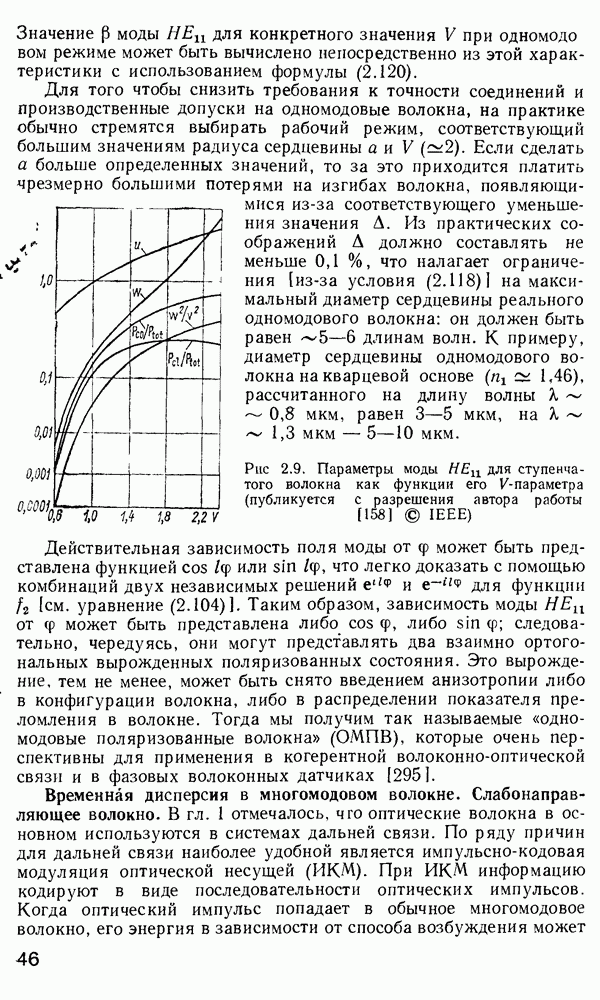
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
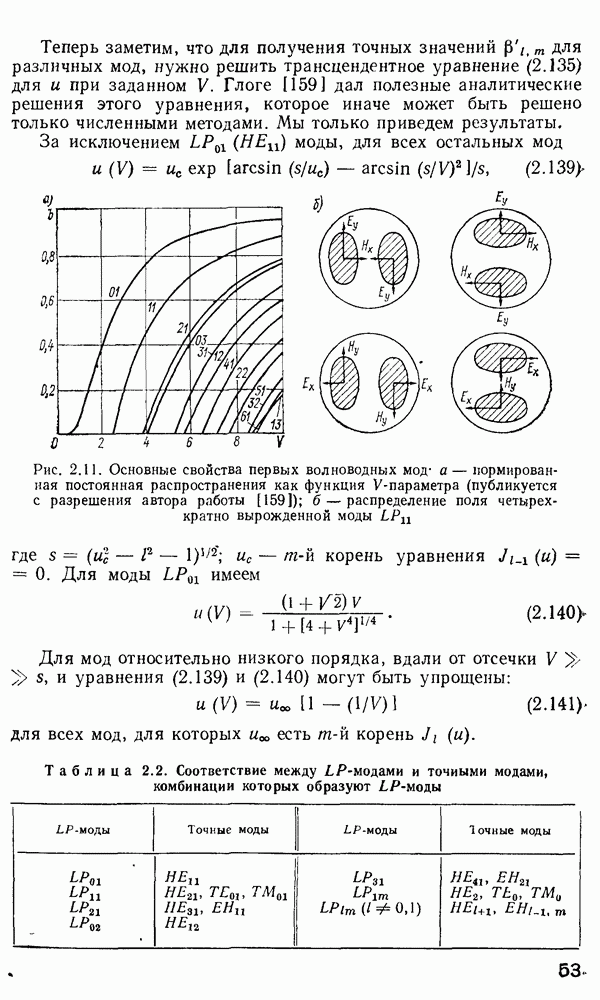
- Линейно-поляризованные моды в слабонаправляющих волокнах.
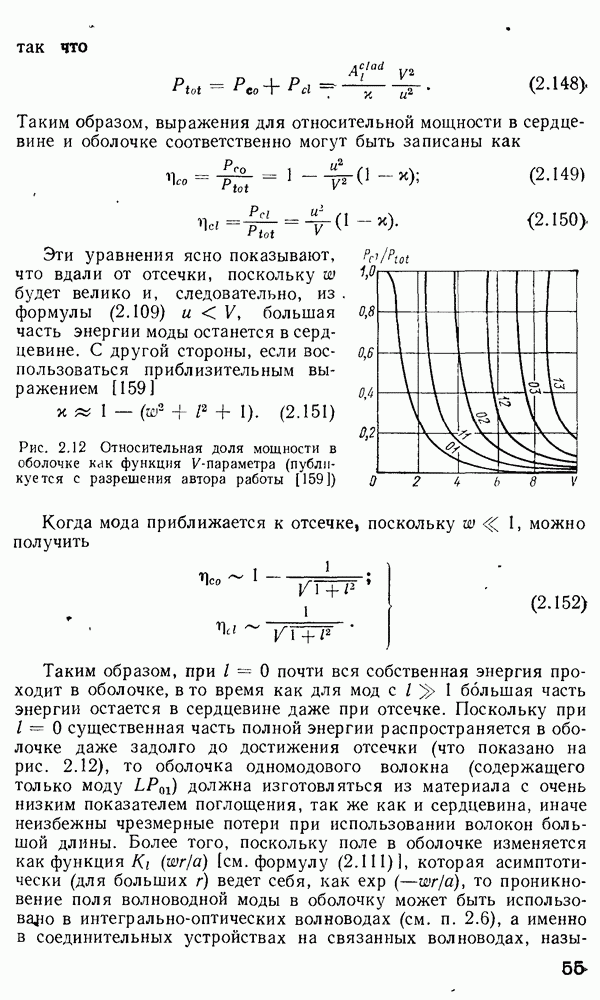
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
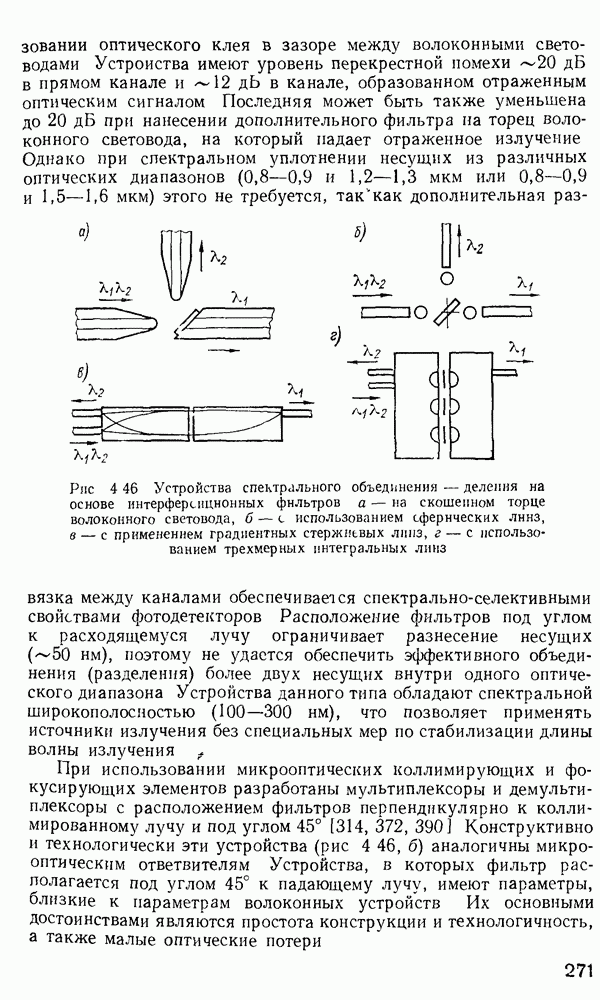
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
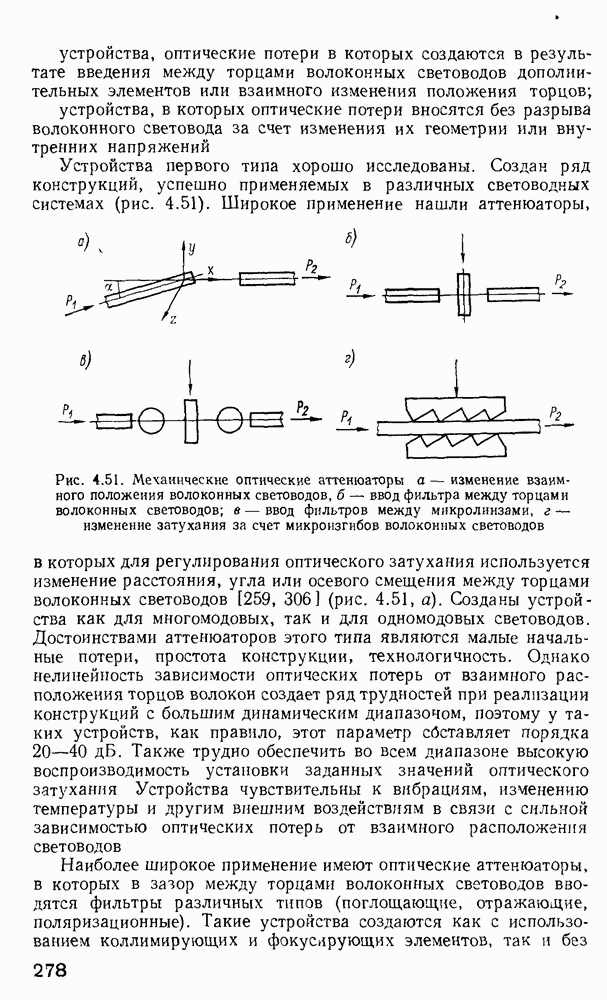
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
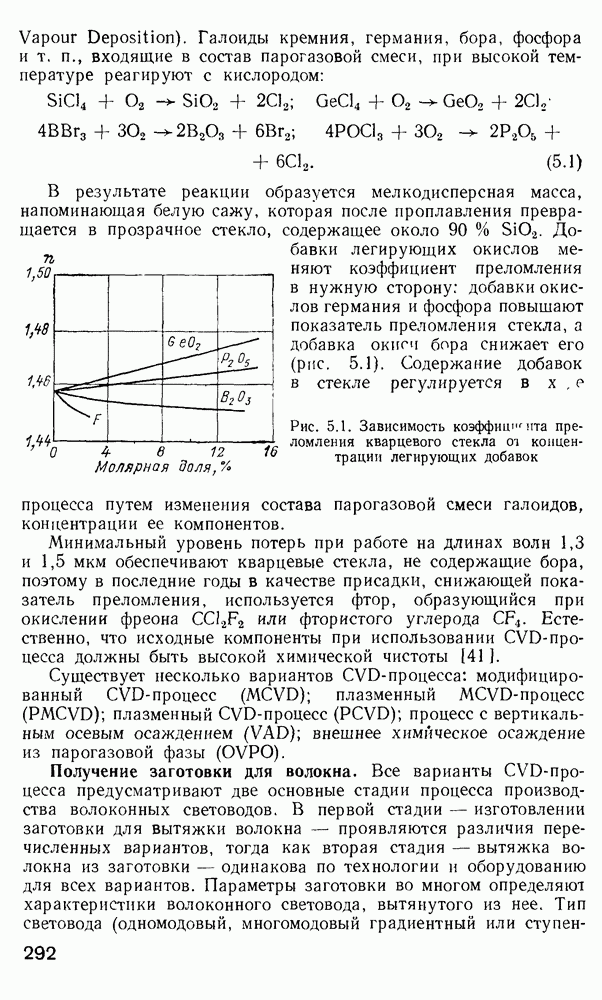
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ