| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
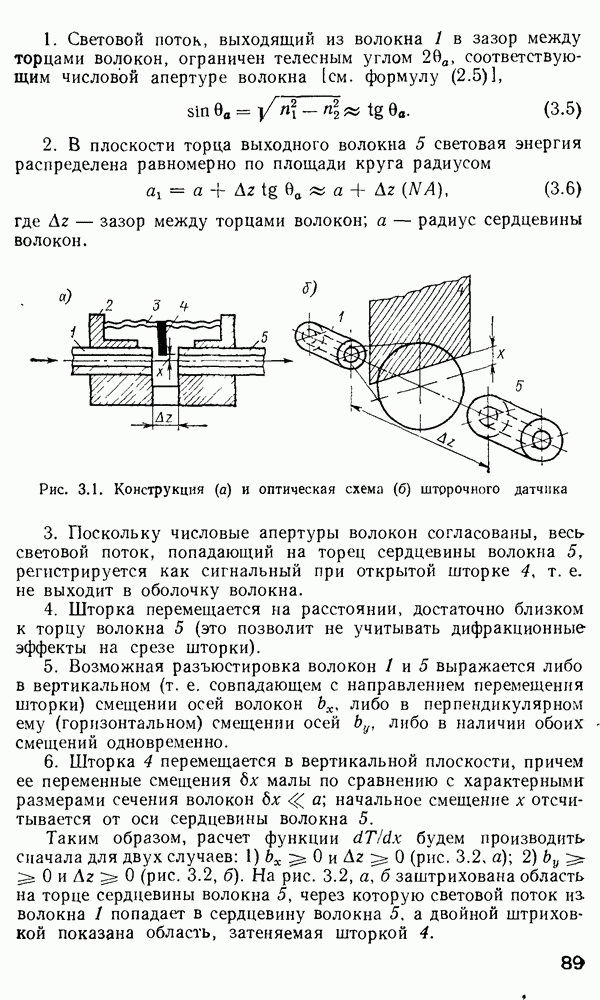
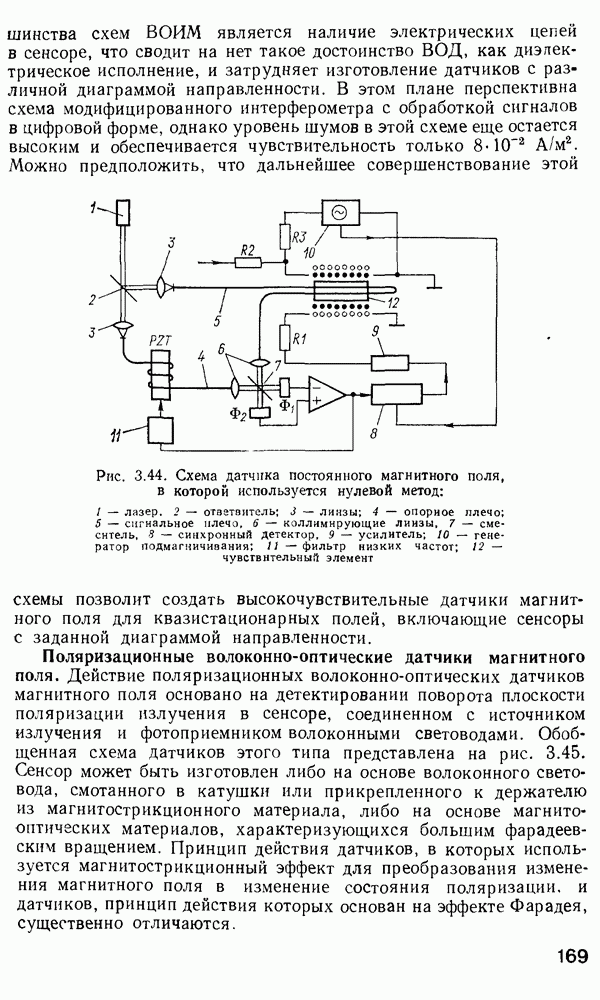
Применение метода ВКБ для многомодовых градиентных волокон.
Выше мы определили, что время прохождения модой пути  по волокну
по волокну  что можно переписать как
что можно переписать как

где  — длина волны излучения в свободном пространстве;
— длина волны излучения в свободном пространстве;  — волновое число в свободном пространстве; с — скорость света;
— волновое число в свободном пространстве; с — скорость света;  — называют групповым показателем,
— называют групповым показателем,

мы привели одну из многочисленных форм характеристического уравнения для постоянной распространения Р в приближении ВКБ [см. формулу (2.175)] С помощью уравнения (2.176) для
выражение (2.175) можно переписать в виде

Введя параметр

где

перепишем уравнение (2.191):

Поскольку  с
с  очевидно, что
очевидно, что

Теперь из формул (2.189) и (2.191) получим

или

Поэтому

Здесь

где  называют параметром профильной дисперсии, которая определяется как
называют параметром профильной дисперсии, которая определяется как 
Разлагая правую часть выражения (2 196) в ряд и удерживая члены порядка  получаем
получаем

Используя формулу (2.189), выводим выражение для групповой задержки

Иногда также используется другая форма выражения (2 199), получаемая путем подстановки выражения для  [см формулу (2.192)]
[см формулу (2.192)]

Из формулу  вытекает, что для
вытекает, что для

разница между задержками различных мод исчезает в первом приближении по параметру  так как всем модам требуется одинаковое время
так как всем модам требуется одинаковое время  чтобы достичь выходного торца волокна Из формулы (2 201) можно сделать очевидный вывод, что
чтобы достичь выходного торца волокна Из формулы (2 201) можно сделать очевидный вывод, что  определяется степенью изменения
определяется степенью изменения  в зависимости от
в зависимости от  т. е. от профильной дисперсии, которую мы упоминали выше.
т. е. от профильной дисперсии, которую мы упоминали выше.
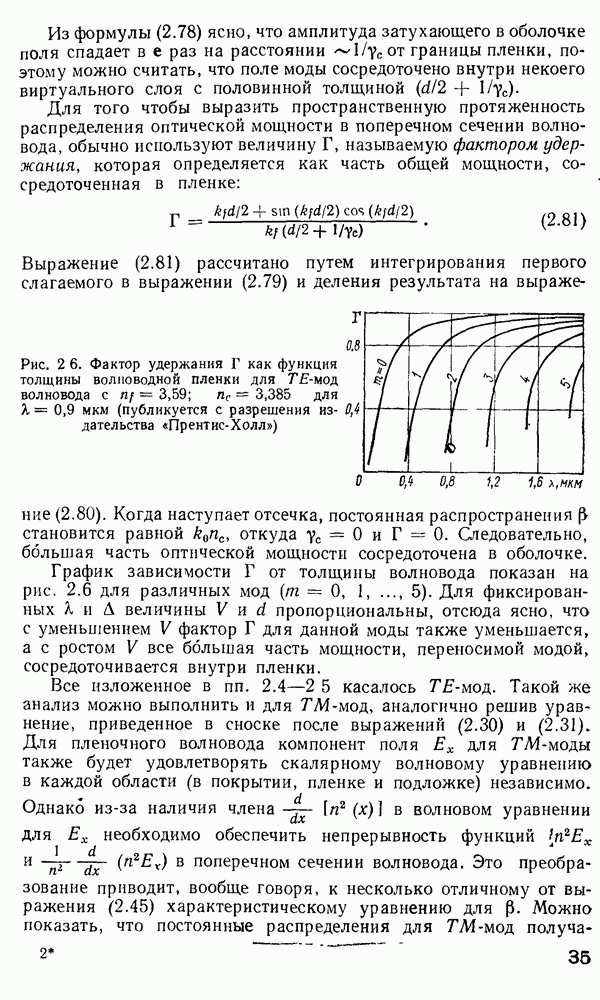
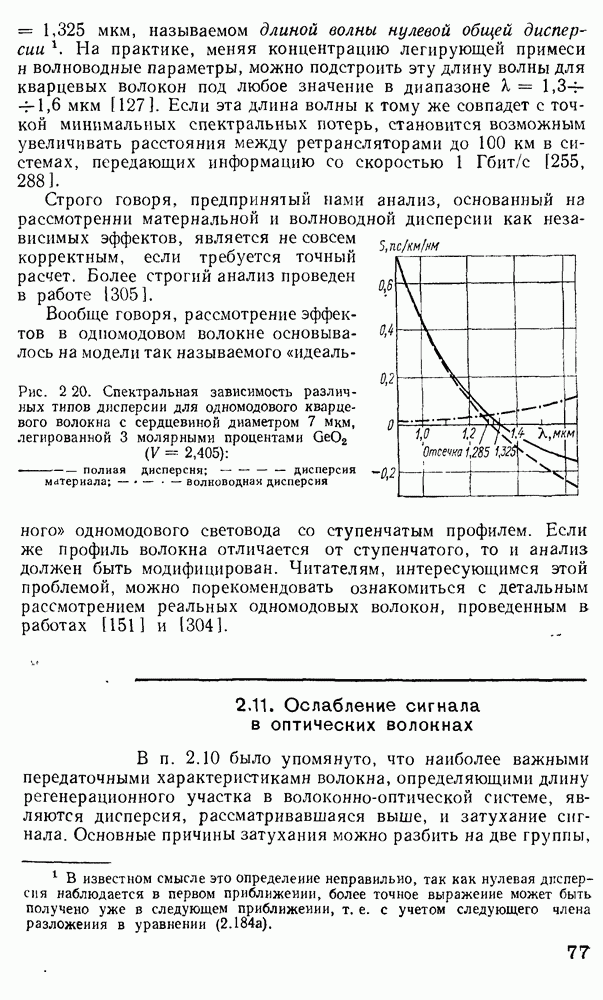
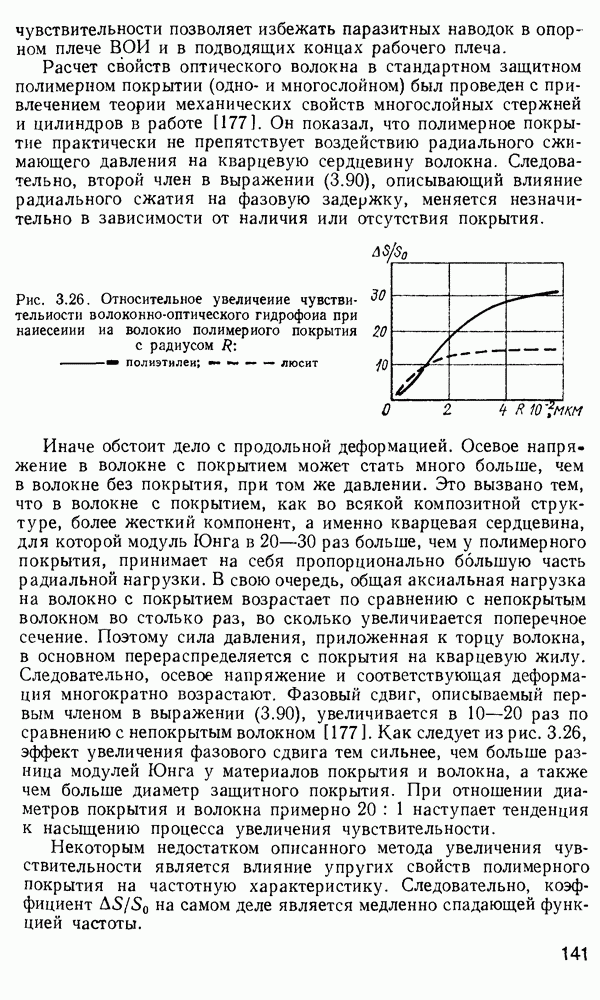
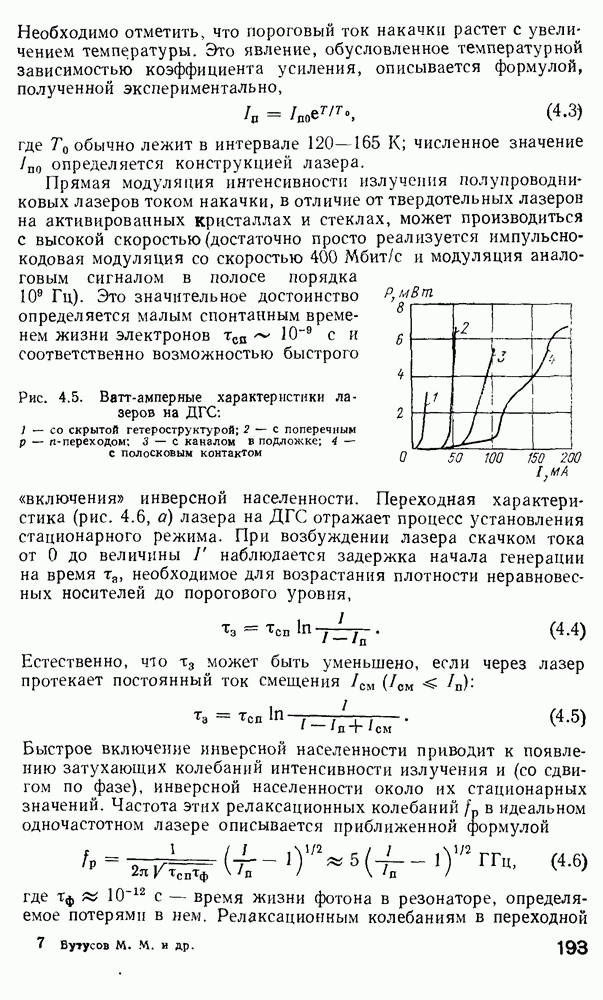
На рис. 2.17 представлена зависимость  от длины волны для различных материалов, используемых при легировании сердцевины волокон. Очевидно, чтобы сделать зависимость
от длины волны для различных материалов, используемых при легировании сердцевины волокон. Очевидно, чтобы сделать зависимость  менее чувствительной к вариациям
менее чувствительной к вариациям  , надо использовать тройные соединения
, надо использовать тройные соединения  для изготовления сердцевины. Это решение сулит значительный выигрыш в том случае, когда волокно предназначено для передачи широкополосных сигналов на нескольких длинах волн оптической несущей.
для изготовления сердцевины. Это решение сулит значительный выигрыш в том случае, когда волокно предназначено для передачи широкополосных сигналов на нескольких длинах волн оптической несущей.

Рис. 2.17. Зависимости  от длины волны для различных материалов, используемых при легировании сердцевины [120]
от длины волны для различных материалов, используемых при легировании сердцевины [120]
Если пренебречь профильной дисперсией, т. е. принять, что  то из уравнения (2.199) получим, удерживая квадратичные члены [46],
то из уравнения (2.199) получим, удерживая квадратичные члены [46],

Если  не слишком близко к 2, то линейный член в уравнении (2.202) доминирует и можно получить разницу времен прохода по волокну «быстрейшей» (соответствующей
не слишком близко к 2, то линейный член в уравнении (2.202) доминирует и можно получить разницу времен прохода по волокну «быстрейшей» (соответствующей  и «самой медленной»
и «самой медленной»  мод
мод

В ступенчатом волокне  и
и

Если пренебречь материальной дисперсией, это выражение сводится к уравнению (2.123), полученному в лучевом приближении. С другой стороны, в параболическом волокне, т. е. для 

Отметим, что это выражение аналогично формуле (2.156), но не учитывает материальной дисперсии. Таким образом, при вычислении дисперсионных характеристик волокна лучевой подход и ВКБ-анализ (в нулевом приближении) дают одинаковые результаты
Чтобы оценить максимальную разность задержек между модами в волокнах с произвольным параметром  введем нормализованную временную задержку
введем нормализованную временную задержку  согласно выражению (2.202)
согласно выражению (2.202)


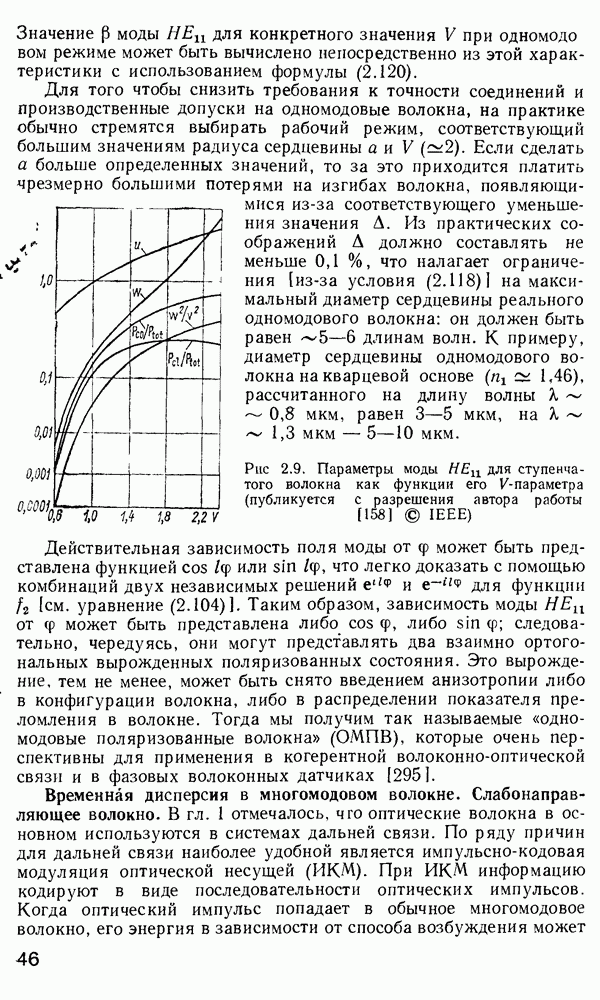
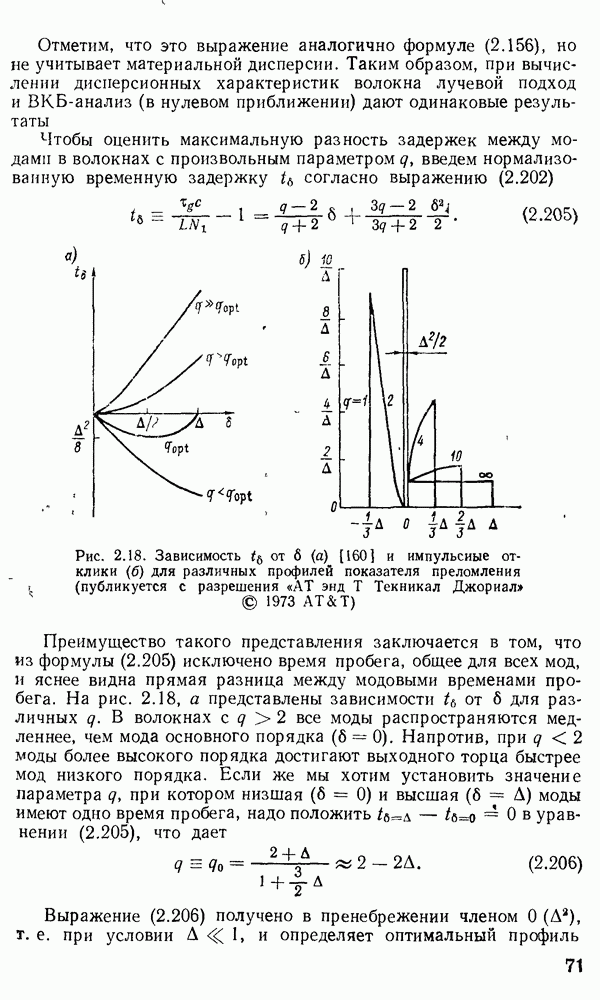
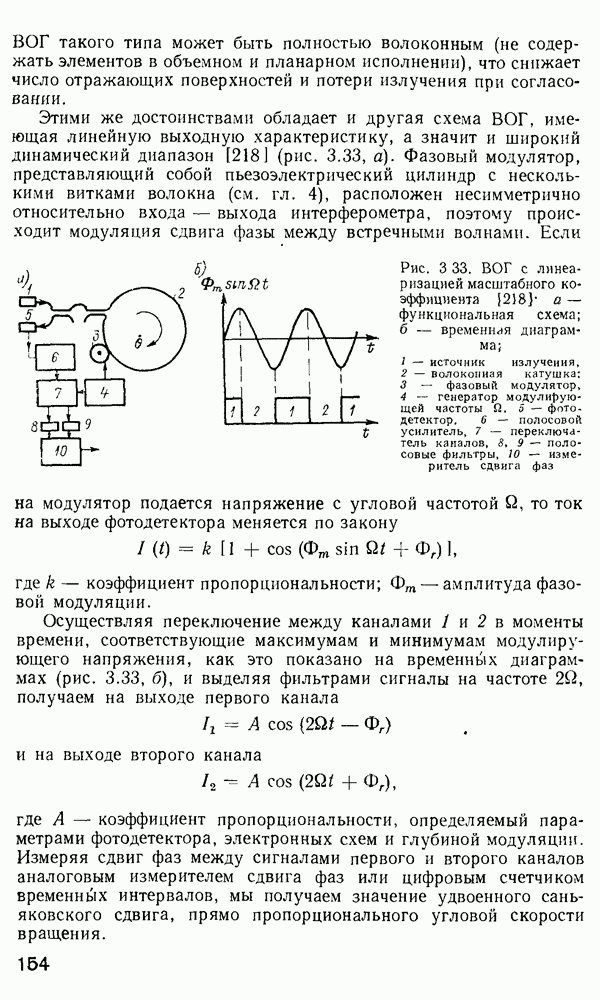
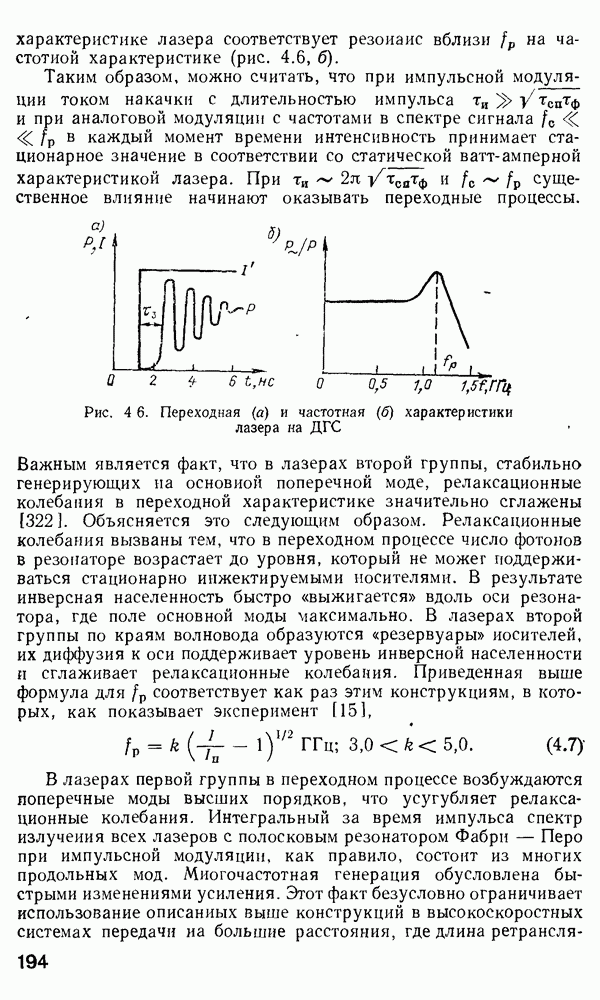
Рис. 2.18. Зависимость от  (а) [160} и импульсные отклики (б) для различных профилей показателя преломления
(а) [160} и импульсные отклики (б) для различных профилей показателя преломления  (публикуется с разрешения
(публикуется с разрешения  Текникал Джориал»
Текникал Джориал» 
Преимущество такого представления заключается в том, что из формулы (2.205) исключено время пробега, общее для всех мод, и яснее видна прямая разница между модовыми временами пробега. На рис. 2.18, а представлены зависимости  от
от  для различных
для различных  . В волокнах с
. В волокнах с  все моды распространяются медленнее, чем мода основного порядка
все моды распространяются медленнее, чем мода основного порядка  Напротив, при
Напротив, при  моды более высокого порядка достигают выходного торца быстрее мод низкого порядка. Если же мы хотим установить значение параметра
моды более высокого порядка достигают выходного торца быстрее мод низкого порядка. Если же мы хотим установить значение параметра  при котором низшая
при котором низшая  и высшая
и высшая  моды имеют одно время пробега, надо положить
моды имеют одно время пробега, надо положить  в уравнении (2.205), что дает
в уравнении (2.205), что дает

Выражение (2.206) получено в пренебрежении членом  т. е. при условии
т. е. при условии  и определяет оптимальный профиль
и определяет оптимальный профиль
без учета профилей дисперсии [160]. Из рис. 2.18, а видно, что в волокне с  высшая и низшая моды приходят в одно время, а все остальные моды несколько «быстрее», т. е. наиболее «быстрая» мода не соответствует
высшая и низшая моды приходят в одно время, а все остальные моды несколько «быстрее», т. е. наиболее «быстрая» мода не соответствует  Если обозначить значение
Если обозначить значение  соответствующее наиболее «быстрой» моде в волокне с
соответствующее наиболее «быстрой» моде в волокне с  через
через  то из уравнения
то из уравнения  получим, что
получим, что

Последнее равенство в выражении (2.207) соблюдается при условии пренебрежения членами порядка  Итак,
Итак,  является мерой дисперсии в волокне с
является мерой дисперсии в волокне с  и выражается как
и выражается как

следовательно,

что в четыре раза меньше, чем для волокна с  , т. е. параболического [см. выражение (2.204а)]. Это значит, что волокно, характеризующееся
, т. е. параболического [см. выражение (2.204а)]. Это значит, что волокно, характеризующееся  позволяет передавать в четыре раза больше информации, чем параболическое.
позволяет передавать в четыре раза больше информации, чем параболическое.
Все изложенные выше соображения относительно дисперсии сводились к подсчету времен пробега для различных мод. Для системного анализа также важно получить такие характеристики, как импульсный отклик и среднеквадратическая ширина импульса. Первая характеристика дает форму выходного импульса, а вторая полезна, когда точная форма импульса не может быть аппроксимирована известными аналитическими функциями. Не вдаваясь в детали, приведем основные положения анализа, выполненного в работах [160, 298].
Положим, что количество энергии, полученное на выходном торце в момент времени  пропорционально
пропорционально  т. е. числу мод с постоянными распространения большими, чем
т. е. числу мод с постоянными распространения большими, чем  [см. формулу (2.173а)]. В малый интервал времени
[см. формулу (2.173а)]. В малый интервал времени  это число мод будет соответственно равно
это число мод будет соответственно равно  Импульсный отклик для многомодового волокна
Импульсный отклик для многомодового волокна

При выводе этоготвыражения проведено нормирование сигнала на единицу введением коэффициента  Из уравнения) (2.200) и из определения
Из уравнения) (2.200) и из определения  получаем, что
получаем, что

а из выражения (2.205) имеем:

Итак,

На рис. 2.18, б показаны формы импульсного отклика для различных профилей волокна. Поскольку  меняется от 0 до
меняется от 0 до

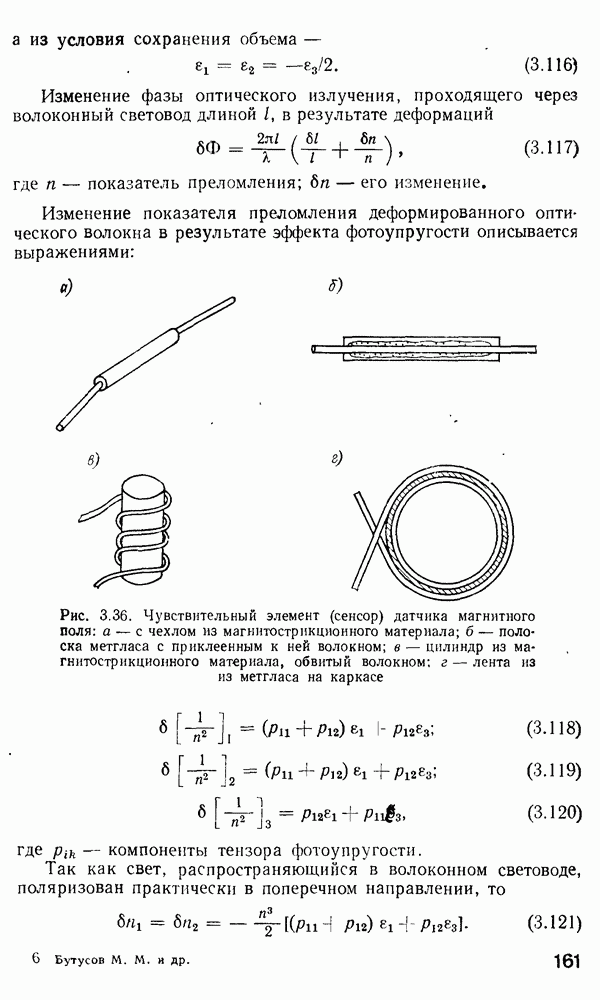
Уравнение (2.212) определяет ширину импульсного отклика для градиентного одномодового волокна (в отсутствие профильной дисперсии, т. е. 
Рис. 2.18, б ясно показывает, что малое изменение параметра  вблизи
вблизи  приводит к очень большим уширениям импульсного отклика. Например, изменение значения
приводит к очень большим уширениям импульсного отклика. Например, изменение значения  от 2 до 1 или до 4 делает импульсный отклик волокна всего в три раза уже, чем для ступенчатого волокна. Среднеквадратическая ширина импульса
от 2 до 1 или до 4 делает импульсный отклик волокна всего в три раза уже, чем для ступенчатого волокна. Среднеквадратическая ширина импульса  произвольной формы
произвольной формы

где

представляет полную энергию импульса, а

определяет среднее время прихода импульса. Можно показать, опираясь на данные работы [298], что

где

В отличие от выражения (2.201) при минимизации среднеквадратической ширины импульса по межмодовой дисперсии параметр оптимального профиля

Общее уширение импульса может быть представлено как полная среднеквадратическая ширина импульса, вызванная межмодовой и внутримодовой дисперсией (см. работу [309]),


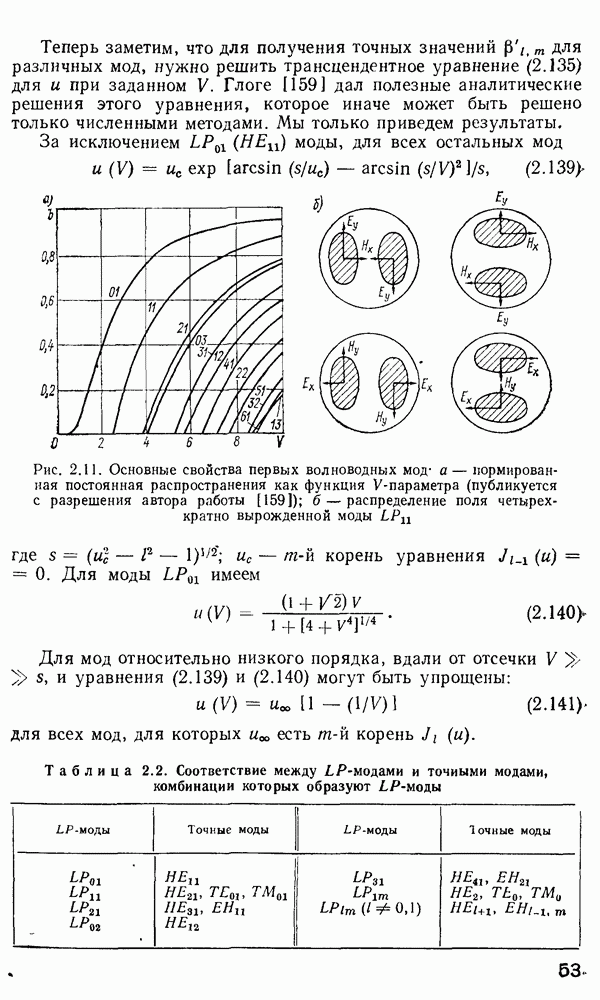
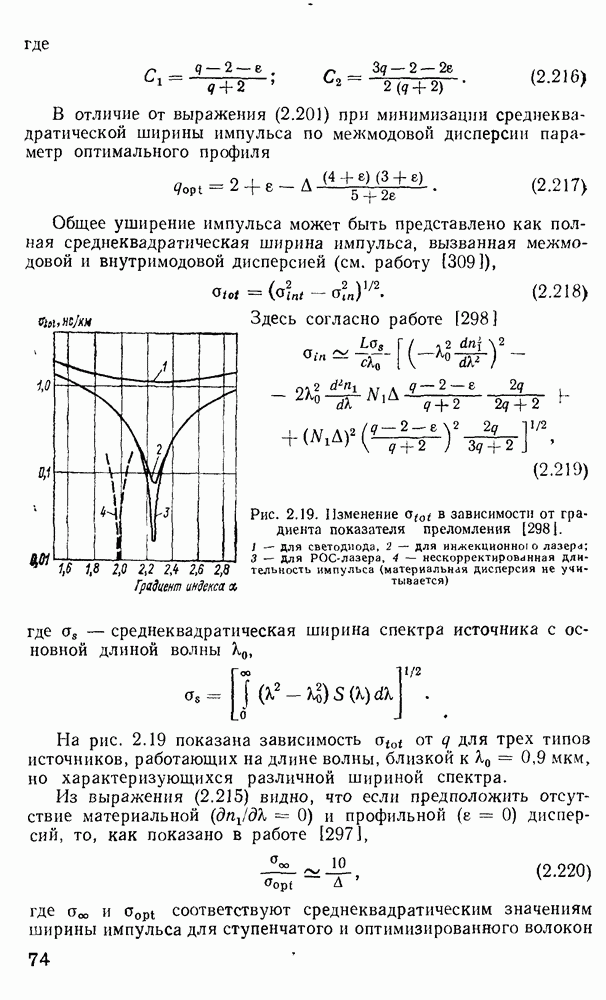
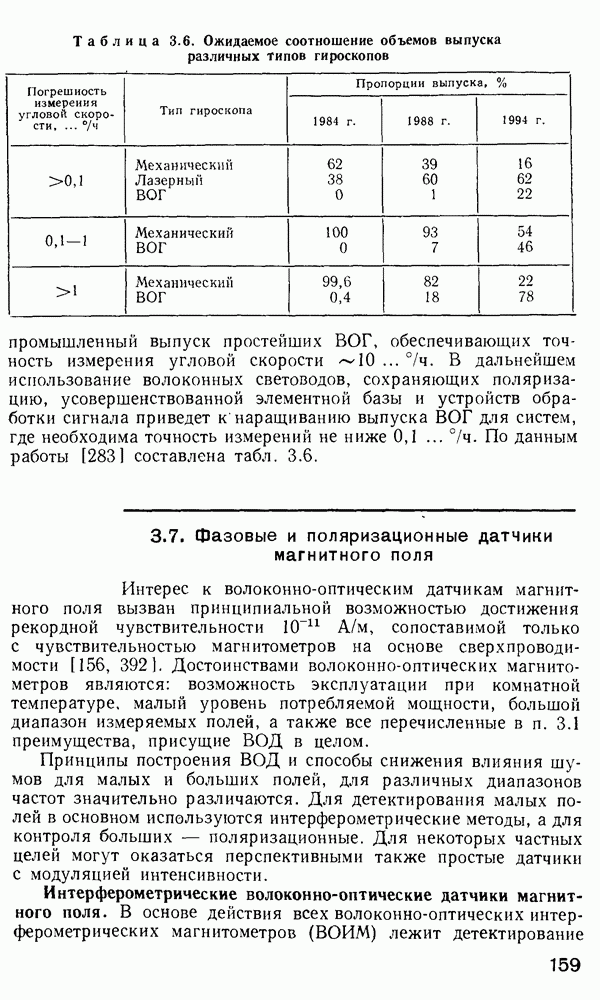
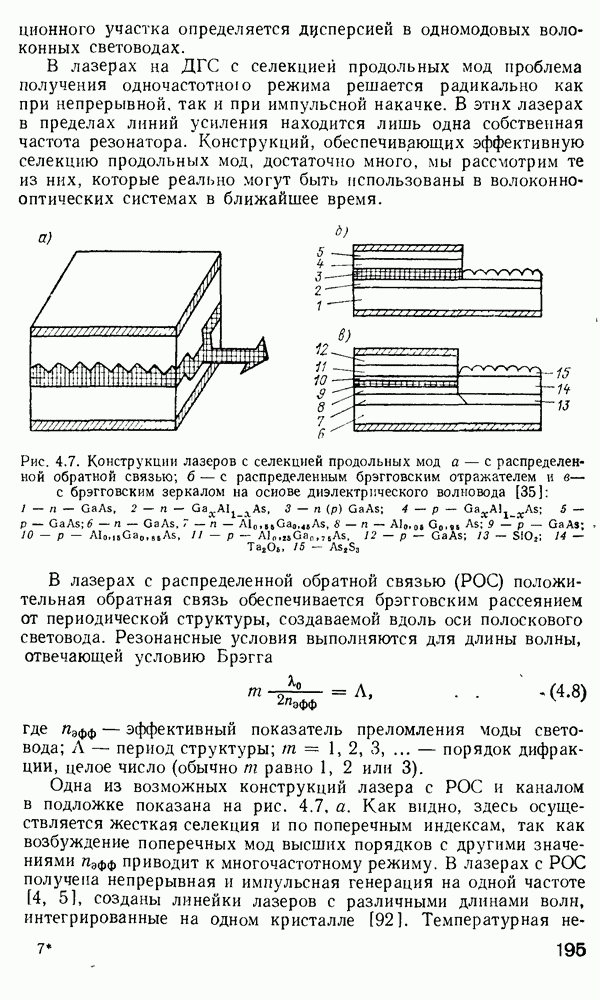
Рис. 2.19. Изменение  в зависимости от градиента показателя преломления [2981. 1 — Для светодиода, 2 — для инжекционног о лазера; 3 — Для РОС-лазера, 4 — нескорректировежная длительностъ импульса (материальная дисперсия не учитывается)
в зависимости от градиента показателя преломления [2981. 1 — Для светодиода, 2 — для инжекционног о лазера; 3 — Для РОС-лазера, 4 — нескорректировежная длительностъ импульса (материальная дисперсия не учитывается)
Здесь согласно работе [298]

где  — среднеквадратическая ширина спектра источника с основной длиной волны
— среднеквадратическая ширина спектра источника с основной длиной волны 

На рис. 2.19 показана зависимость  от
от  для трех типоз источников, работающих на длине волны, близкой к
для трех типоз источников, работающих на длине волны, близкой к  мкм, но характеризующихся различной шириной спектра.
мкм, но характеризующихся различной шириной спектра.
Из выражения (2.215) видно, что если предположить отсутствие материальной (дпдк  и профильной
и профильной  дисперсий, то, как показано в работе [297],
дисперсий, то, как показано в работе [297],

где  и
и  соответствуют среднеквадратическим значениям ширины импульса для ступенчатого и оптимизированного волокон
соответствуют среднеквадратическим значениям ширины импульса для ступенчатого и оптимизированного волокон
соответственно. Обычно, если  уширение импульса в ступенчатом волокне составляет
уширение импульса в ступенчатом волокне составляет  а в оптимизированном — менее чем
а в оптимизированном — менее чем 
Здесь следует отметить, что в связи с технологическими ограничениями редко удается достичь оптимальной формы профиля. Более того, даже если оптимум достигнут, малое возмущение параметра  немедленно ведет к сильной дисперсии [217, 297]. Например, хорошо известно, что на оси волокон, полученных по методу MCVD, обычно имеется провал в профиле показателя преломления, что вызвано испарением легирующих примесей при схлопывании заготовки. Используя теорию возмущений, 1217], можно показать, что для типичного параболического волокна с
немедленно ведет к сильной дисперсии [217, 297]. Например, хорошо известно, что на оси волокон, полученных по методу MCVD, обычно имеется провал в профиле показателя преломления, что вызвано испарением легирующих примесей при схлопывании заготовки. Используя теорию возмущений, 1217], можно показать, что для типичного параболического волокна с  импульсный отклик увеличивается с
импульсный отклик увеличивается с  (в отсутствие провала) до
(в отсутствие провала) до  при
при  провале на кривой рефракционного профиля, имеющего форму гауссовой кривой с полушириной
провале на кривой рефракционного профиля, имеющего форму гауссовой кривой с полушириной  , где а — радиус сердцевины.
, где а — радиус сердцевины.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
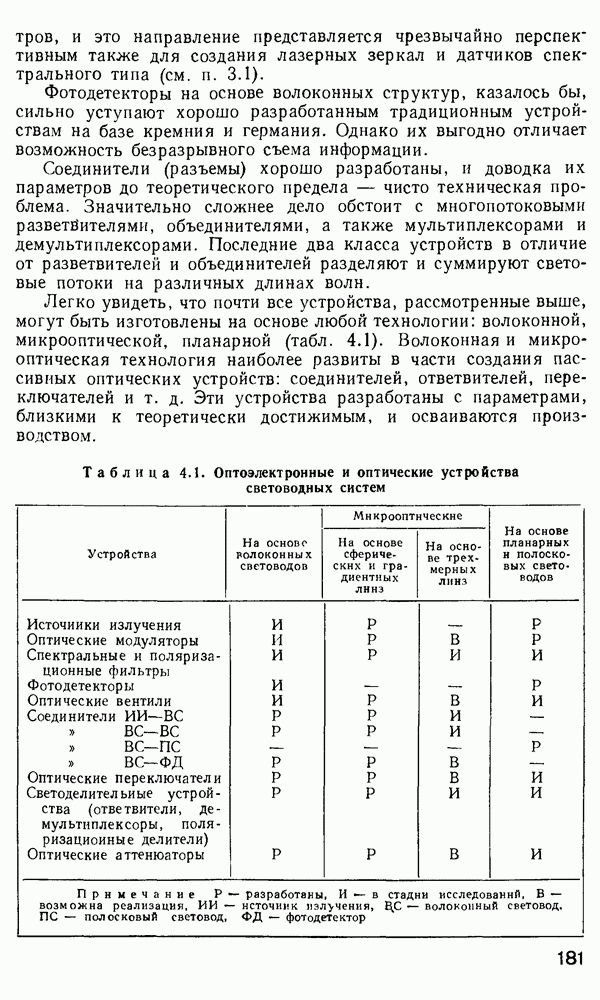
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
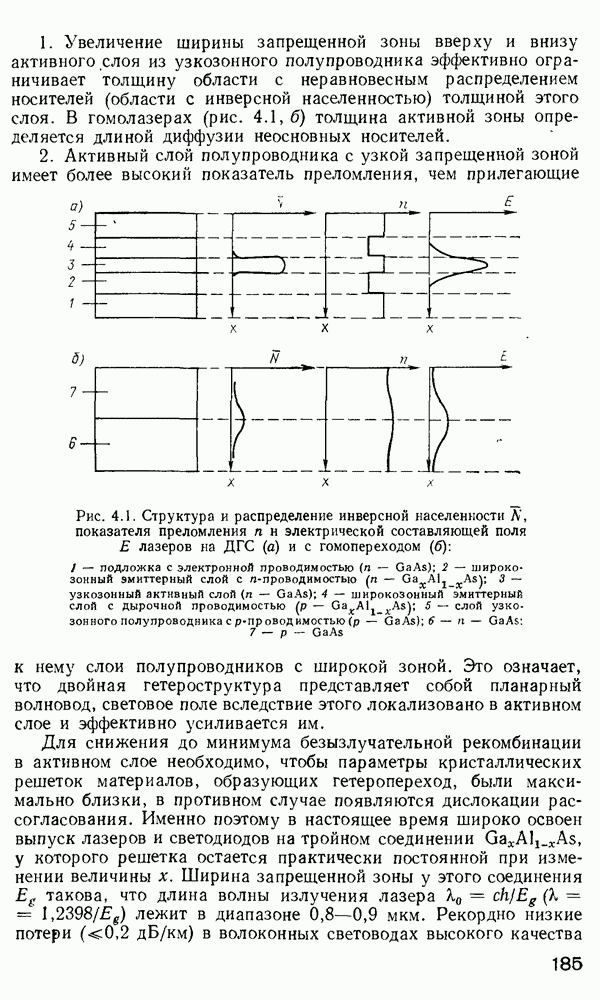
- Полупроводниковые источники излучения.
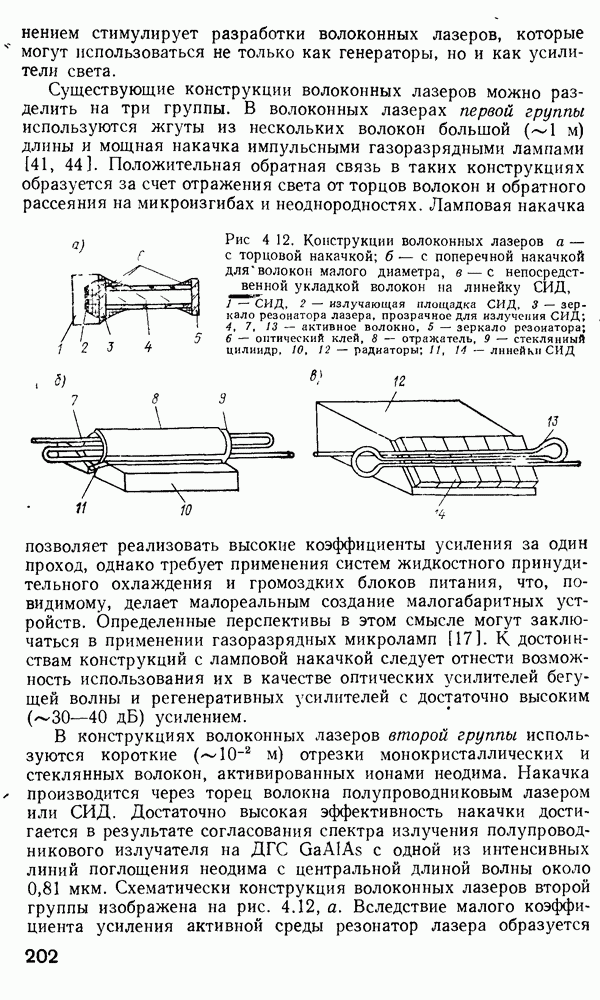
- Волоконные лазеры.
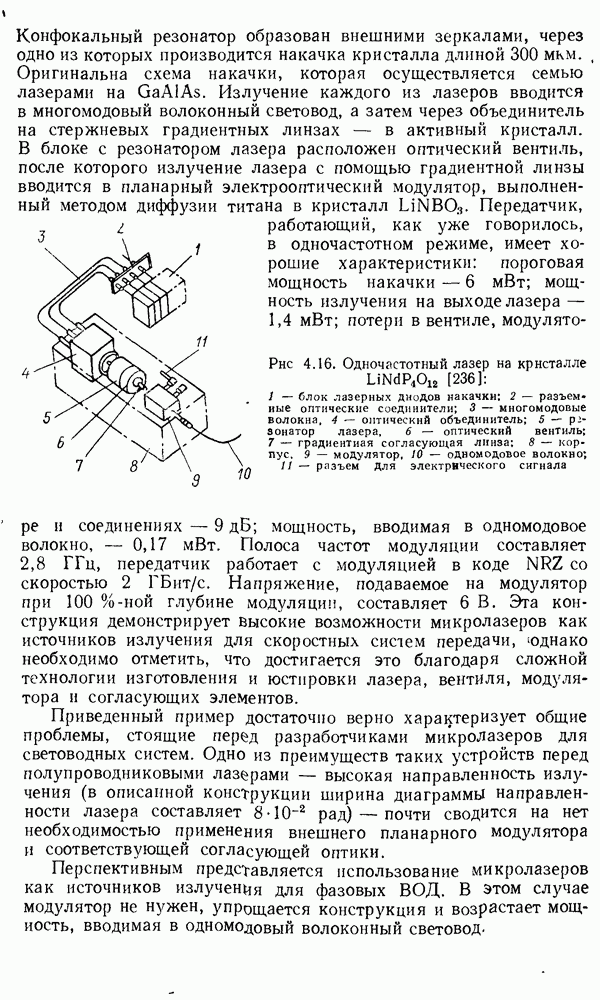
- Объемные микролазеры.
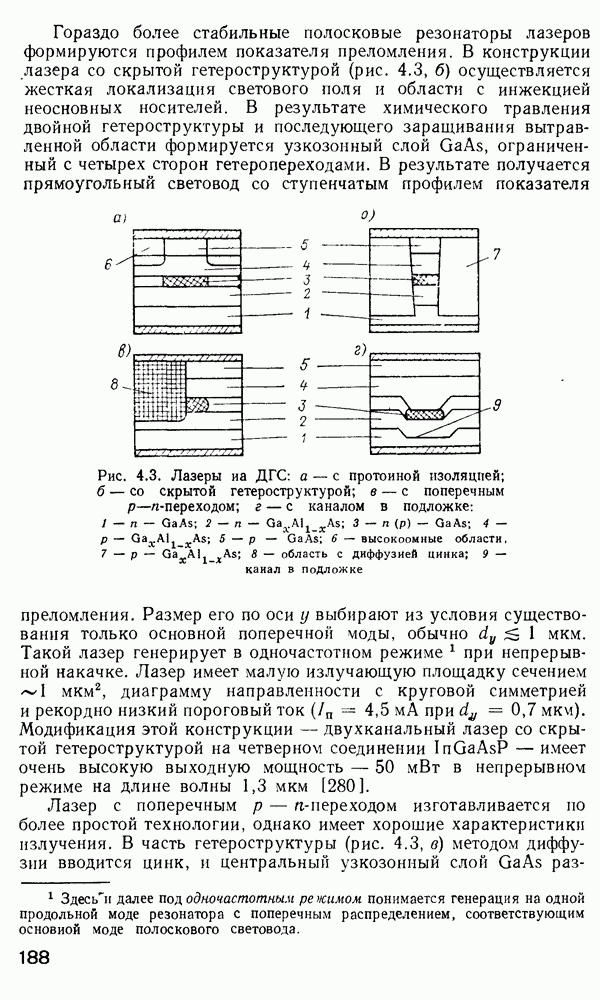
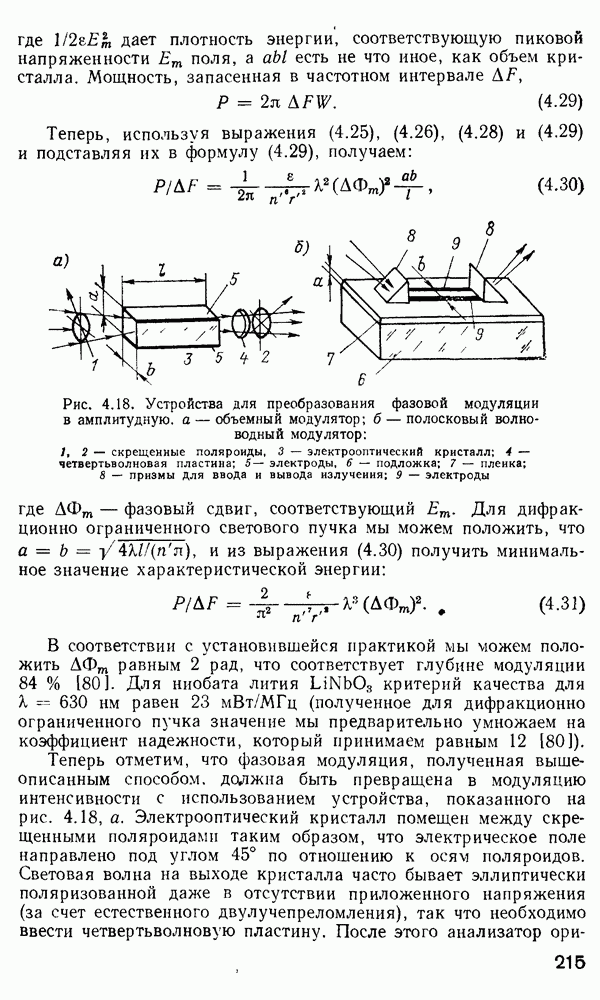
- 4.3. Оптические модуляторы
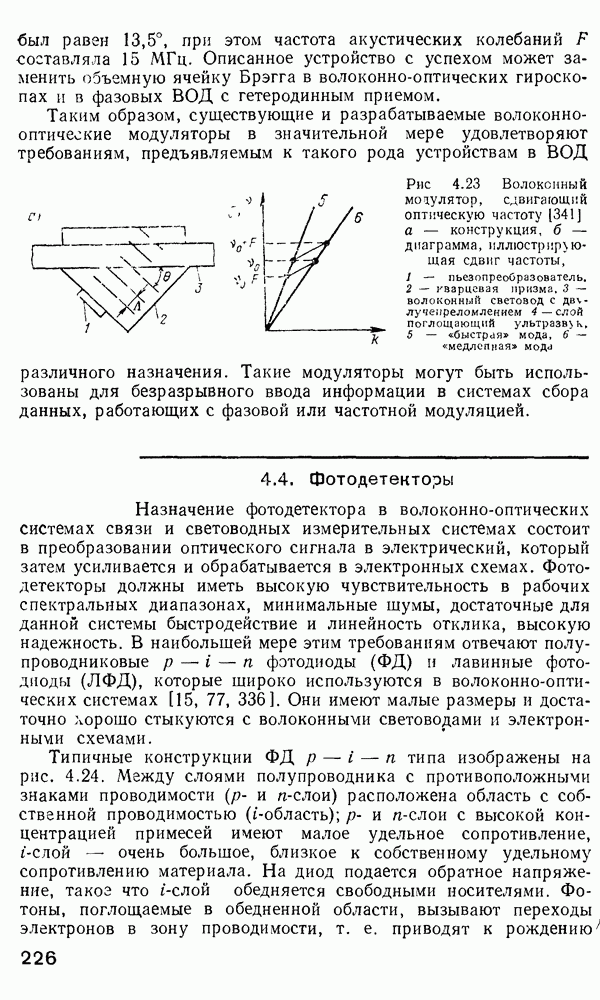
- 4.4. Фотодетекторы
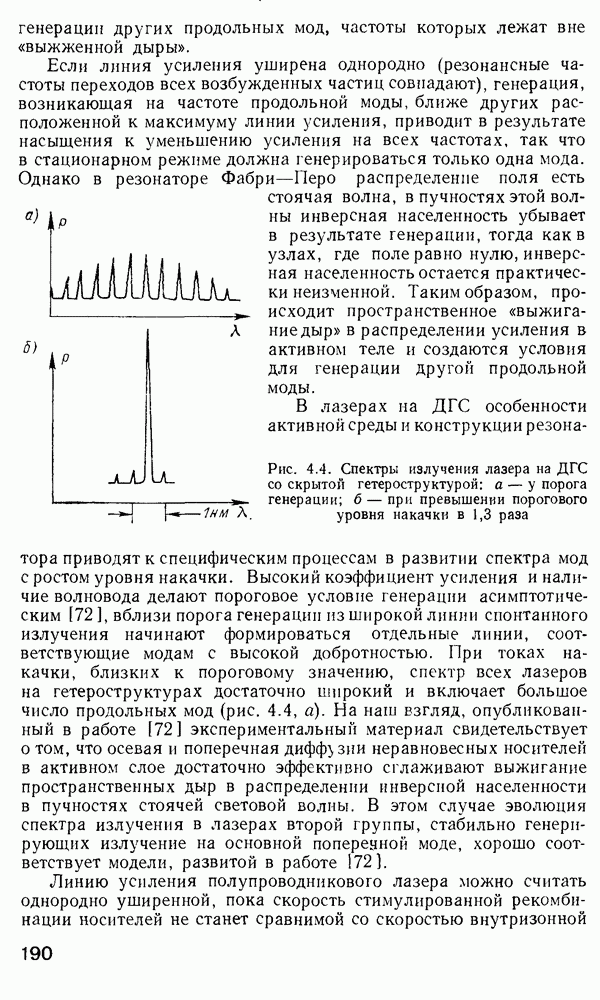
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
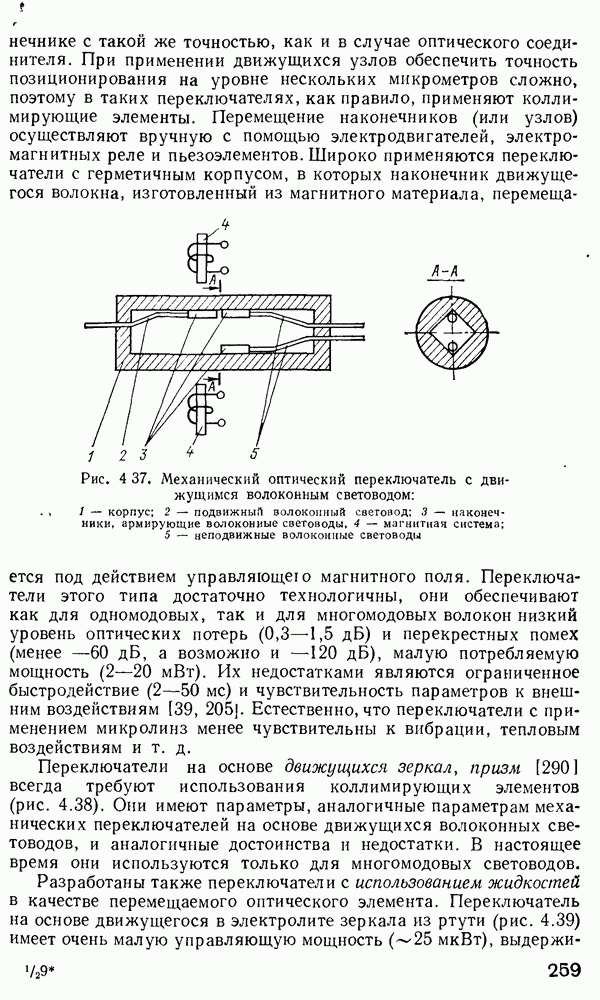
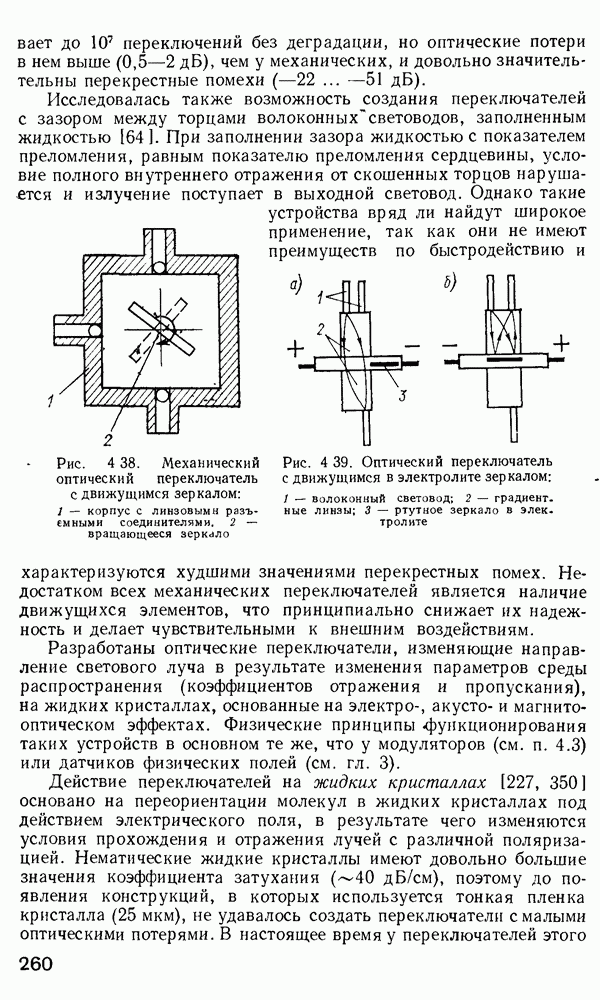
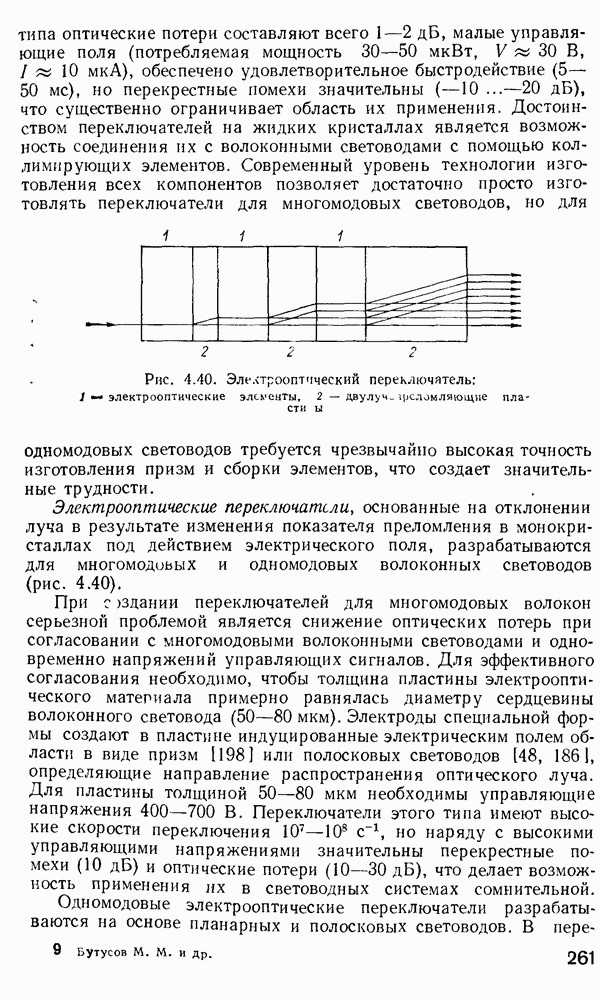
- 4.7. Волоконно-оптические переключатели
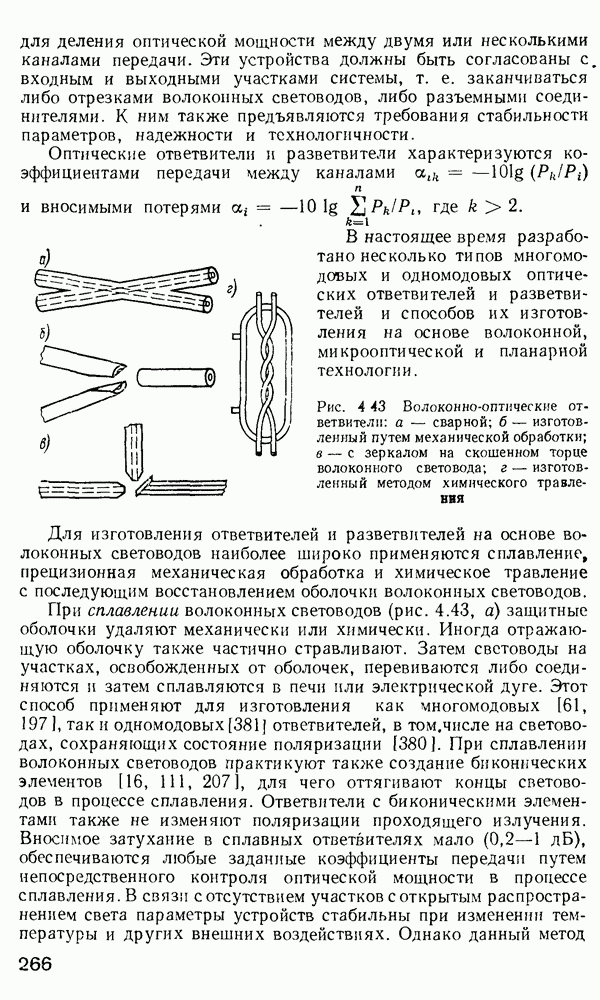
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
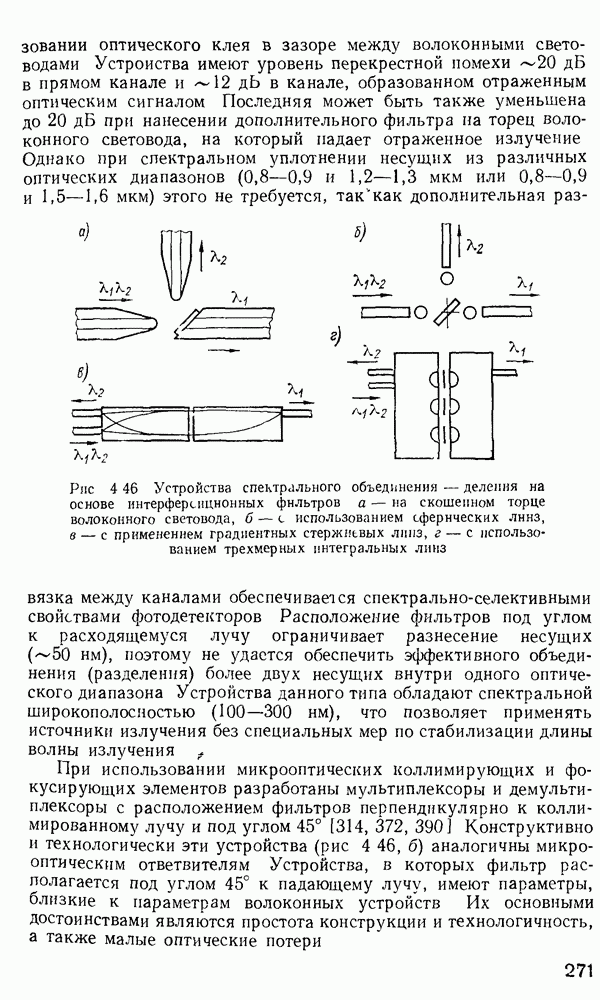
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
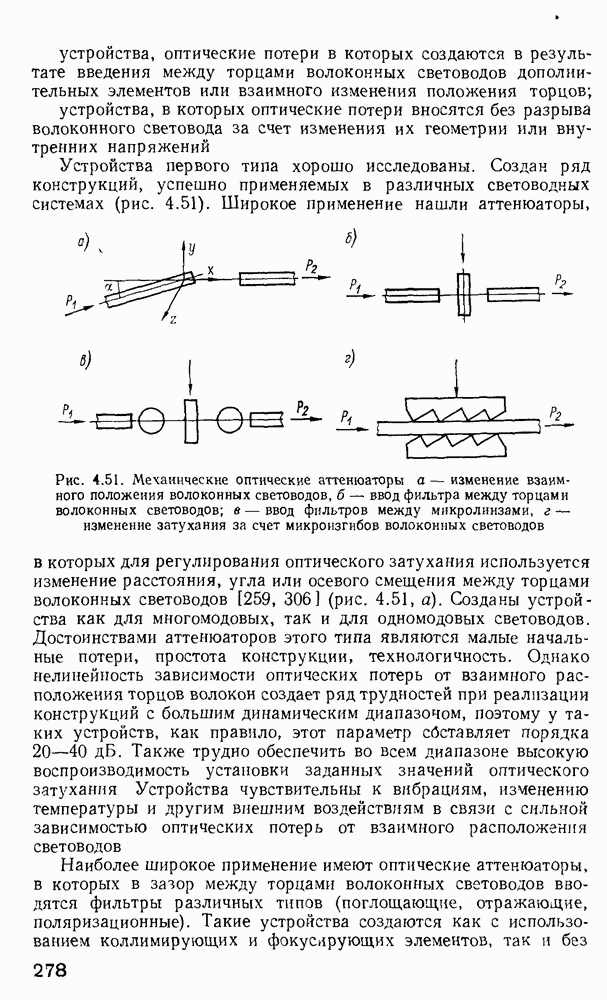
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
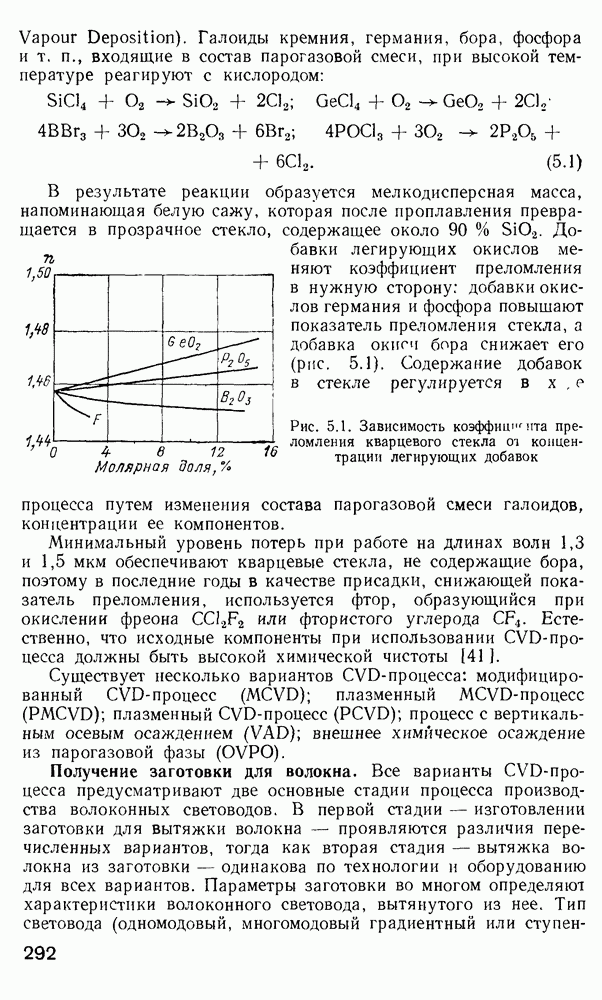
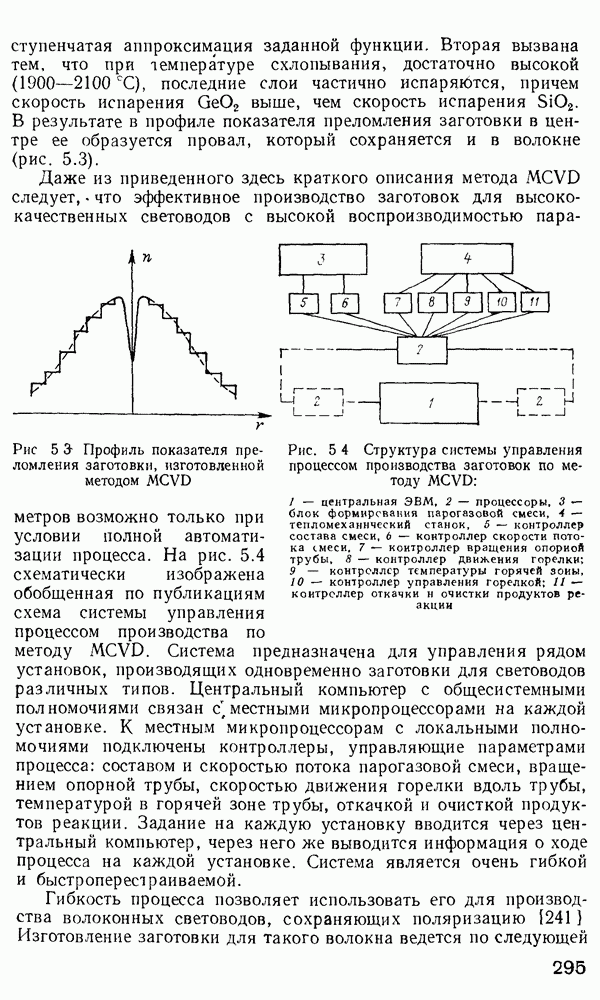
- Получение заготовки для волокна.
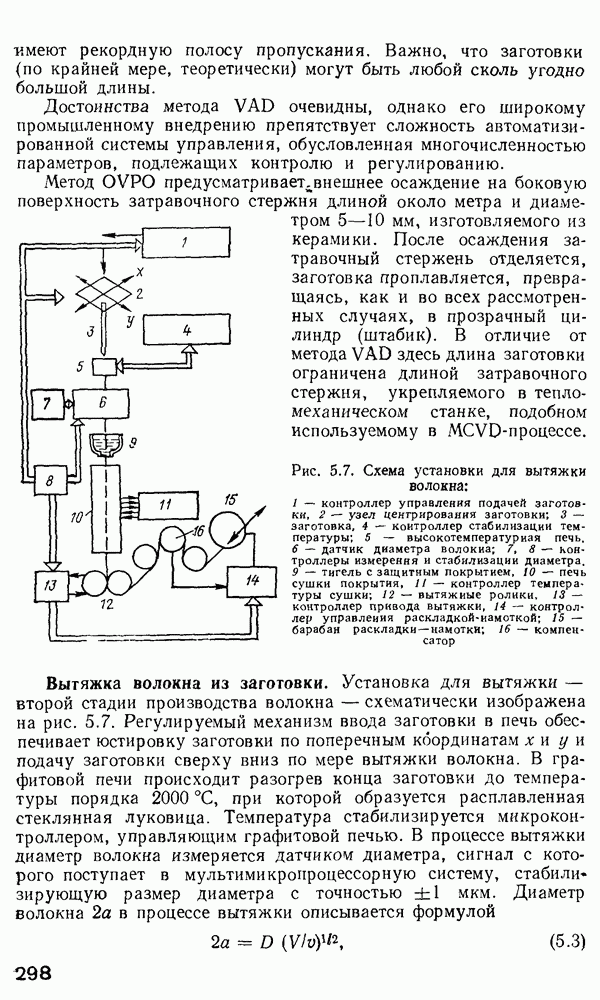
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
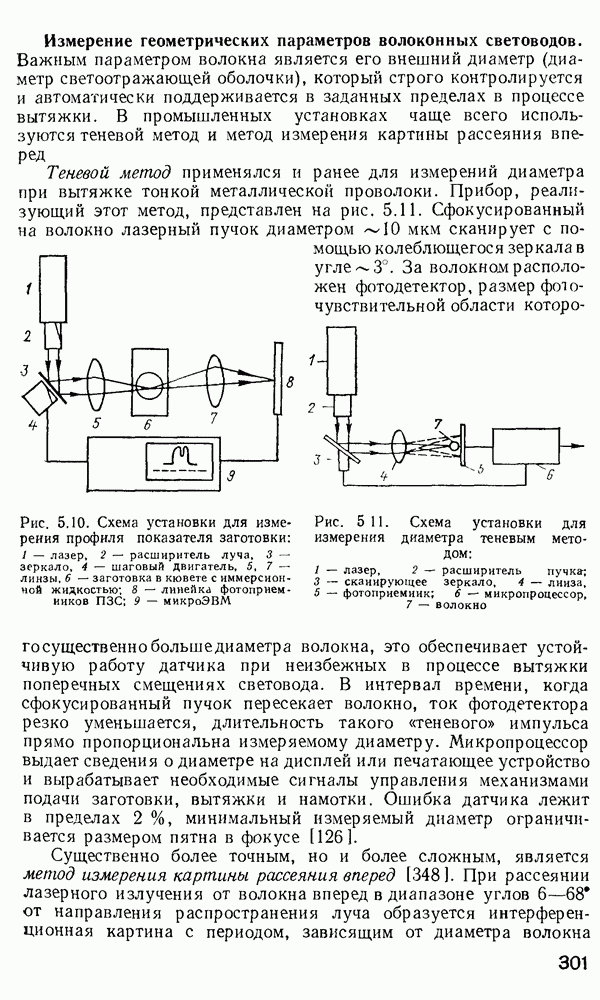
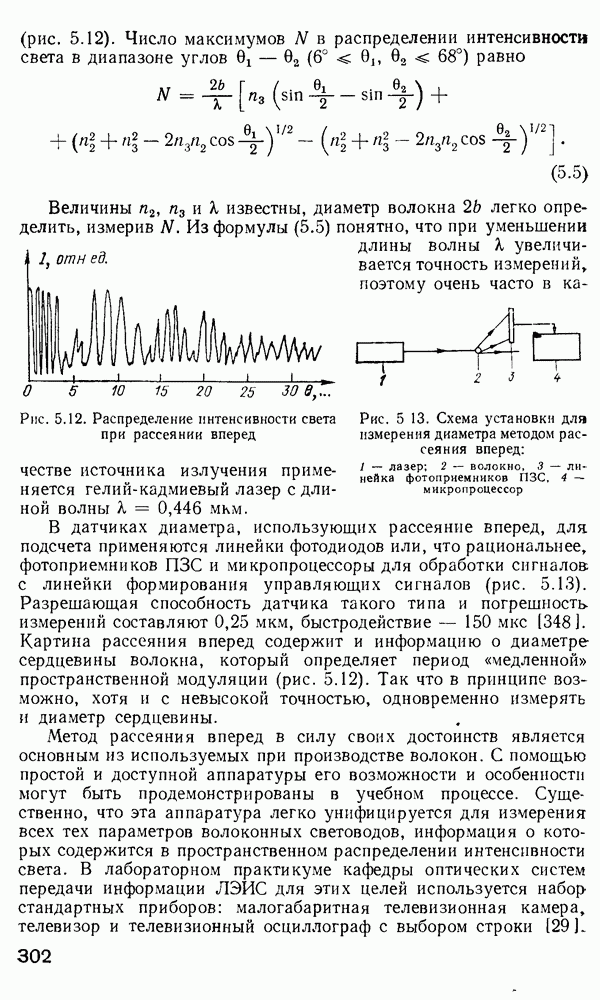
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ