| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Линейно-поляризованные моды в слабонаправляющих волокнах.
Не нарушая общности, можно предположить, что преобладающий поперечный компонент электрического поля в слабонаправляющем волокне радиуса а направлен вдоль оси у, а компонент  много меньше, чем
много меньше, чем  Покажем, что допущение
Покажем, что допущение  не приводит к противоречию до тех пор, пока
не приводит к противоречию до тех пор, пока  Из выводов, сделанных в
Из выводов, сделанных в  с очевидностью вытекает, что, как и компонент
с очевидностью вытекает, что, как и компонент  компонент
компонент  также удовлетворяет скалярному волновому уравнению (2.102). Следовательно, можно утверждать [сравните формулы (2.111) и (2.112)], что
также удовлетворяет скалярному волновому уравнению (2.102). Следовательно, можно утверждать [сравните формулы (2.111) и (2.112)], что  в сердцевине и оболочке соответственно будет задаваться а виде:
в сердцевине и оболочке соответственно будет задаваться а виде:

Здесь предполагается, что  непрерывно при
непрерывно при  хотя, строго говоря,
хотя, строго говоря,  не непрерывна для всех
не непрерывна для всех  На самом деле также требуется, чтобы были непрерывны
На самом деле также требуется, чтобы были непрерывны  на границе раздела сердцевина — оболочка. Однако допущенная ошибка ничтожна до тех пор, пока условие
на границе раздела сердцевина — оболочка. Однако допущенная ошибка ничтожна до тех пор, пока условие  удовлетворяется [76, 159]. Если предположить, что
удовлетворяется [76, 159]. Если предположить, что  то
то  , следовательно, из уравнений Максвелла
, следовательно, из уравнений Максвелла  можно получить
можно получить

Опять-таки, поскольку  , волны эффективнее распространяются под малыми углами к оси волокна, наконец, поскольку поперечное электрическое поле считается полностью направленным вдоль оси у, можно с уверенностью считать, что мода образована поперечно-поляризованной вдоль оси у плоской волной, распространяющейся вдоль направления оси
, волны эффективнее распространяются под малыми углами к оси волокна, наконец, поскольку поперечное электрическое поле считается полностью направленным вдоль оси у, можно с уверенностью считать, что мода образована поперечно-поляризованной вдоль оси у плоской волной, распространяющейся вдоль направления оси  в почти бесконечно протяженной среде, имеющей показатель преломления
в почти бесконечно протяженной среде, имеющей показатель преломления  Тогда
Тогда  -компонент в уравнении (2.8) для почти плоской волны будет
-компонент в уравнении (2.8) для почти плоской волны будет

где индексы 1 и 2 относятся к сердцевине и оболочке соответст венно,  импеданс плоской волны в свободном пространстве.
импеданс плоской волны в свободном пространстве.
Использовав следующие стандартные соотношения:

получим, что

Из уравнений (2.125)-(2.127) можно получить

Сравнивая уравнения (2.125) и (2.131), можно обнаружить, что в сердцевине 

так как для малой разницы между  Таким образом, поскольку
Таким образом, поскольку  продольный компонент поля
продольный компонент поля  Подобные заключения могут быть сделаны и для поля в оболочке. Наличие порядков
Подобные заключения могут быть сделаны и для поля в оболочке. Наличие порядков  может служить подтверждением того, что эти моды были сформированы в результате суперпозиции собственных мод. Из непрерывности тангенциального (к границе раздела) компонента
может служить подтверждением того, что эти моды были сформированы в результате суперпозиции собственных мод. Из непрерывности тангенциального (к границе раздела) компонента  при
при
 а после предположения, что
а после предположения, что  гц, и с использованием ранее выведенных соотношений можно получить, что:
гц, и с использованием ранее выведенных соотношений можно получить, что:

Отсюда получаем следующее характеристическое уравнение для вычисления значений постоянной распространения  для различных мод:
для различных мод:

которое идентично уравнению (2.124). Непрерывность  при
при  приведет к такому же характеристическому уравнению. Таким образом, наше предварительное допущение о том, что в слабонаправляющем волокне моды линейно поляризованы, ведет к такому же характеристическому уравнению, как и то, которое было получено после применения условия
приведет к такому же характеристическому уравнению. Таким образом, наше предварительное допущение о том, что в слабонаправляющем волокне моды линейно поляризованы, ведет к такому же характеристическому уравнению, как и то, которое было получено после применения условия  к точному характеристическому уравнению (2.113). Этим самым еще раз подтверждается допущение о том, что предположение
к точному характеристическому уравнению (2.113). Этим самым еще раз подтверждается допущение о том, что предположение  не ведет к каким-либо противоречиям при
не ведет к каким-либо противоречиям при  .
.
Если теперь мы проанализируем уравнение (2.135) в пределе  для того, чтобы получить частоты отсечки различных мод, то найдем, что для низшей разрешенной моды
для того, чтобы получить частоты отсечки различных мод, то найдем, что для низшей разрешенной моды  частота от сечки соответствует первому корню уравнения
частота от сечки соответствует первому корню уравнения

в то время как для следующей моды частота отсечки  задается первым корнем уравнения
задается первым корнем уравнения

Для нулей функций  соответственно имеющих место при
соответственно имеющих место при  значения
значения  для
для  равны
равны  Литеры
Литеры  обозначают, что моды линейно поляризованы (от англ. linear polarization) Индекс I соответствует
обозначают, что моды линейно поляризованы (от англ. linear polarization) Индекс I соответствует  порядку функции Бесселя, он определяет условие отсечки для соответствующего номера моды, а также азимутальную периодичность, т. е. число периодов функций
порядку функции Бесселя, он определяет условие отсечки для соответствующего номера моды, а также азимутальную периодичность, т. е. число периодов функций  или
или  уложившихся на окружности. Из этого определения для обозначения
уложившихся на окружности. Из этого определения для обозначения  -моды можно также наглядно представить распределение поля для отдельных мод, потому что физически I представляет собой число пучностей в угловом распределении, уложившихся вдоль полукруга, в то время как
-моды можно также наглядно представить распределение поля для отдельных мод, потому что физически I представляет собой число пучностей в угловом распределении, уложившихся вдоль полукруга, в то время как  есть число пучностей в радиальном распределении. Это ясно показано на рис. 2.10,
есть число пучностей в радиальном распределении. Это ясно показано на рис. 2.10,
где поперечные распределения интенсивностей для двух  -мод относительно высокого порядка изображены схематично так, как они выглядят на фотографии х.
-мод относительно высокого порядка изображены схематично так, как они выглядят на фотографии х.
Здесь следует отметить, что в волноводе большой протяженности чрезвычайно трудно поддерживать распространение отдельной моды относительно высокого порядка. Это происходит потому, что любое малое возмущение в волокне способствует перекачке энергии из данной моды в другие волноводные воды, в связи с чем возникает суперпозиция различных мод и на выходе волокна в результате нет четко определенной и регулярной картины. Только если волокно изготовлено таким образом, что рабочее значение У-параметра лежит в диапазоне, соответствующем фундаментальной моде 
2,4048, есть возможность поддерживать распространение отдельной моды по волноводу.

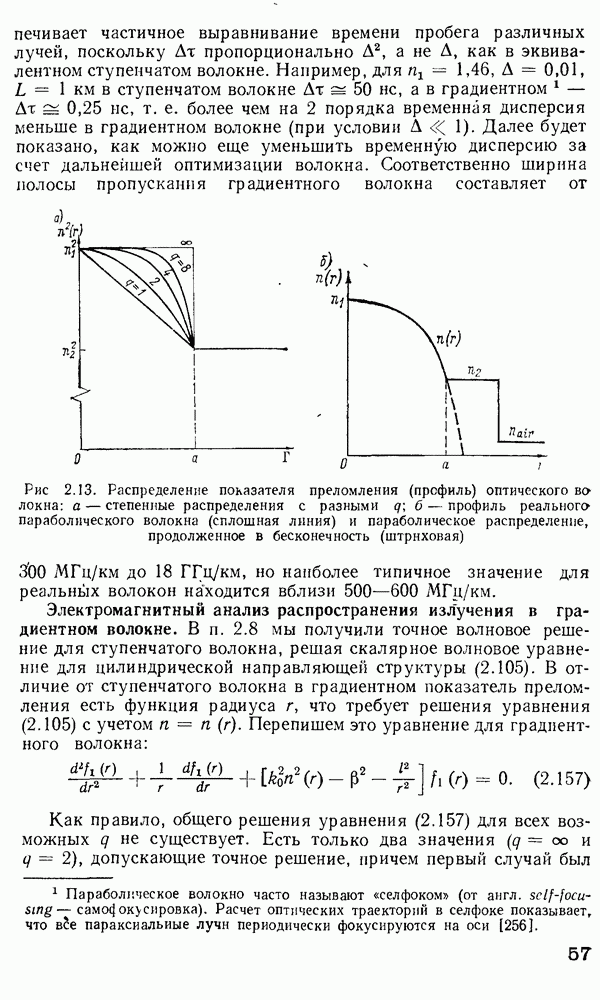
Рис. 2.10. Схематическое представление картин распределения интенсивности для мод 
Вид нормированной постоянной распространения  в зависимости от V показан на рис. 2.11, а, где
в зависимости от V показан на рис. 2.11, а, где

так что для волноводных мод [см. соотношение (2.110)] лежит между 0 и 1. Каждая кривая на графике соответствует одной из  мод. Значение
мод. Значение  для отсечки различных
для отсечки различных  -мод может быть найдено непосредственно по графику; оно соответствует точке пересечения каждой кривой с осью V. Как уже отмечалось выше, при каждая
-мод может быть найдено непосредственно по графику; оно соответствует точке пересечения каждой кривой с осью V. Как уже отмечалось выше, при каждая  -мода в действительности состоит из линейной комбинации
-мода в действительности состоит из линейной комбинации  мод, каждая из которых также может быть представлена в азимутальной зависимости
мод, каждая из которых также может быть представлена в азимутальной зависимости  или
или  Однако поскольку каждая
Однако поскольку каждая  -мода может быть поляризована либо по оси х, либо по оси у, а каждое из этих направлений поляризации имеет азимутальную зависимость вида либо
-мода может быть поляризована либо по оси х, либо по оси у, а каждое из этих направлений поляризации имеет азимутальную зависимость вида либо  либо
либо  то можно сказать, что каждая
то можно сказать, что каждая  -мода четырежды вырождена, т. е. каждому обозначению
-мода четырежды вырождена, т. е. каждому обозначению  соответствуют на самом деле четыре дискретных модовых распределения (рис. 2.11, б). Исключение представляет мода
соответствуют на самом деле четыре дискретных модовых распределения (рис. 2.11, б). Исключение представляет мода  которая только дважды вырождена. Таким образом, в системе обозначений мод по типу
которая только дважды вырождена. Таким образом, в системе обозначений мод по типу  четыре распределения для каждой
четыре распределения для каждой  -моды соответствуют четырем видам комбинаций
-моды соответствуют четырем видам комбинаций  и ЕН-мод. Комбинации точных мод, образующих различные
и ЕН-мод. Комбинации точных мод, образующих различные  -моды, показаны в табл. 2.2.
-моды, показаны в табл. 2.2.
Теперь заметим, что для получения точных значений  для различных мод, нужно решить трансцендентное уравнение (2.135) для и при заданном V. Глоге [159] дал полезные аналитические решения этого уравнения, которое иначе может быть решено только численными методами. Мы только приведем результаты.
для различных мод, нужно решить трансцендентное уравнение (2.135) для и при заданном V. Глоге [159] дал полезные аналитические решения этого уравнения, которое иначе может быть решено только численными методами. Мы только приведем результаты.
За исключением  (НЕ) моды, для всех остальных мод
(НЕ) моды, для всех остальных мод

где  корень уравнения
корень уравнения 

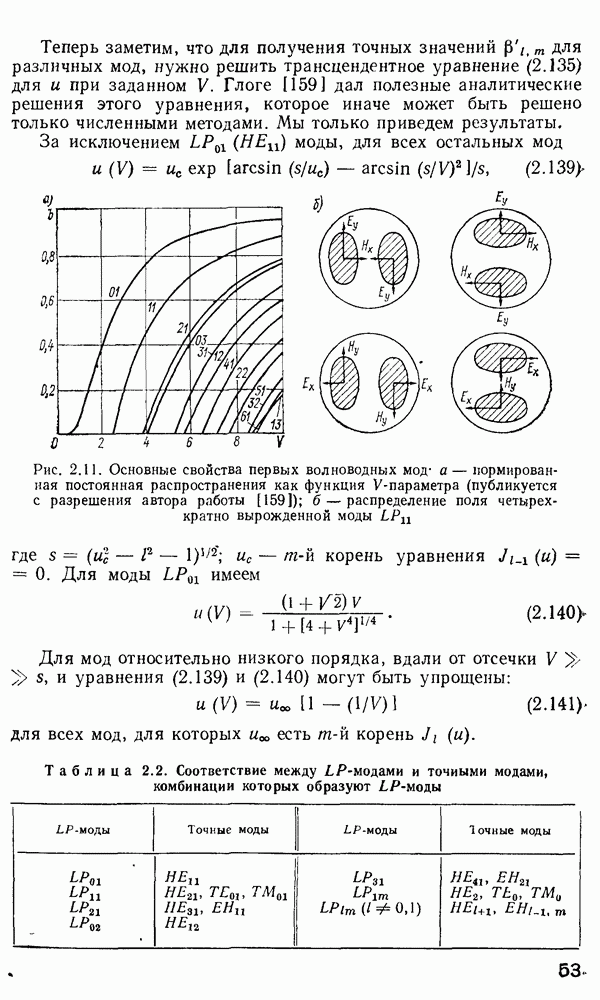
Рис. 2.11. Основные свойства первых волноводных мод: а — нормированная постоянная распространения как функция  -параметра (публикуется с разрешения автора работы [159]); б — распределение поля четырехкратно вырожденной моды
-параметра (публикуется с разрешения автора работы [159]); б — распределение поля четырехкратно вырожденной моды 
Для моды  имеем
имеем

Для мод относительно низкого порядка, вдали от отсечки  и уравнения (2.139) и (2.140) могут быть упрощены:
и уравнения (2.139) и (2.140) могут быть упрощены:

для всех мод, для которых есть  корень
корень  .
.
Таблица 2.2. Соответствие между Z-P-модами и точными модами, комбинации которых образуют  -моды
-моды

Очевидно, что с практической точки зрения теория слабонаправляющих волокон, созданная Снайдером [343] и Глоге [159], вполне подходит для изучения эффектов распространения лучей в оптических волноводах, что подтверждает проведенное выше сопоставление ее положений с точной модовой теорией.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
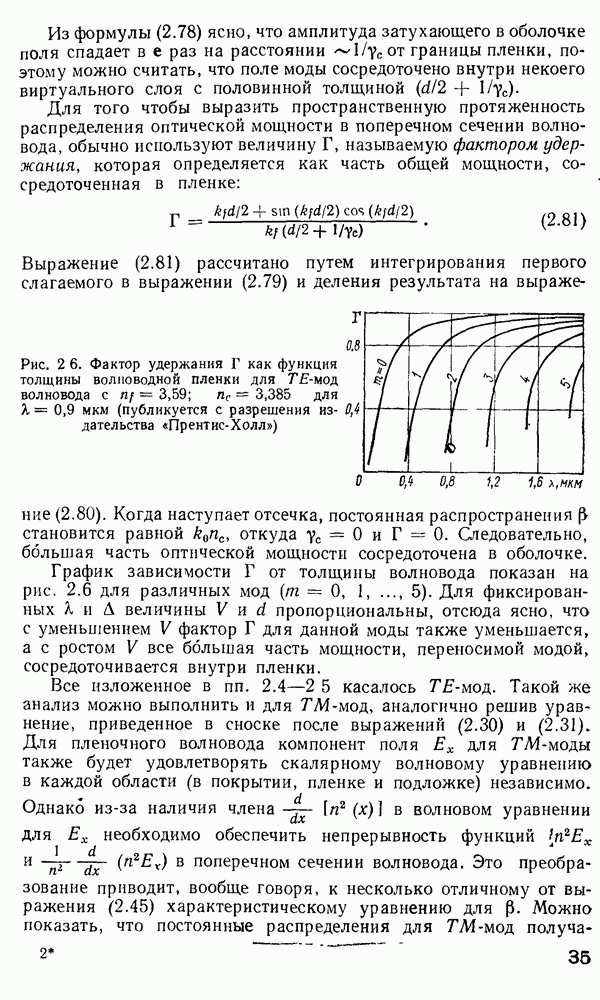
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
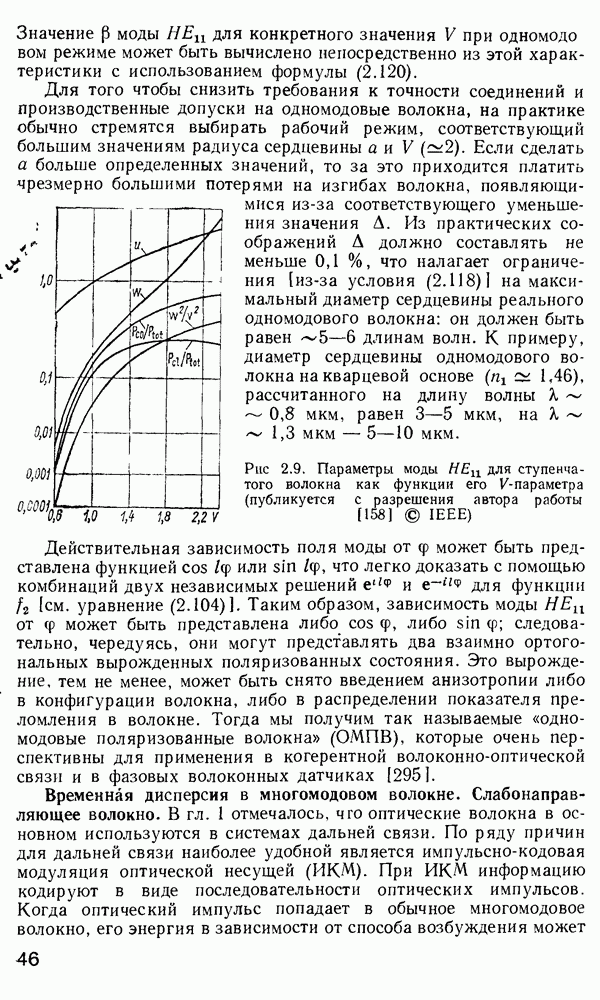
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
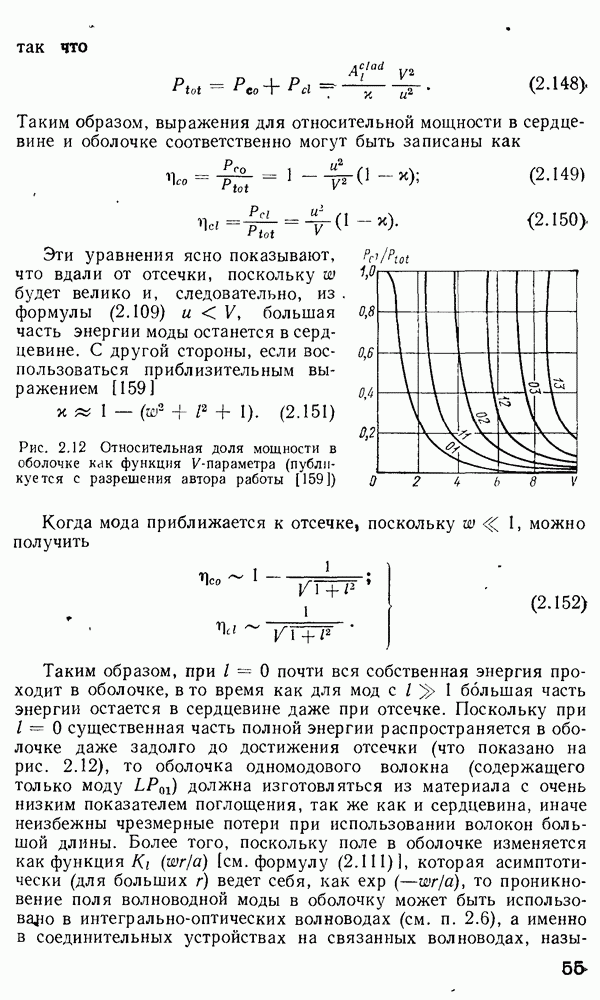
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
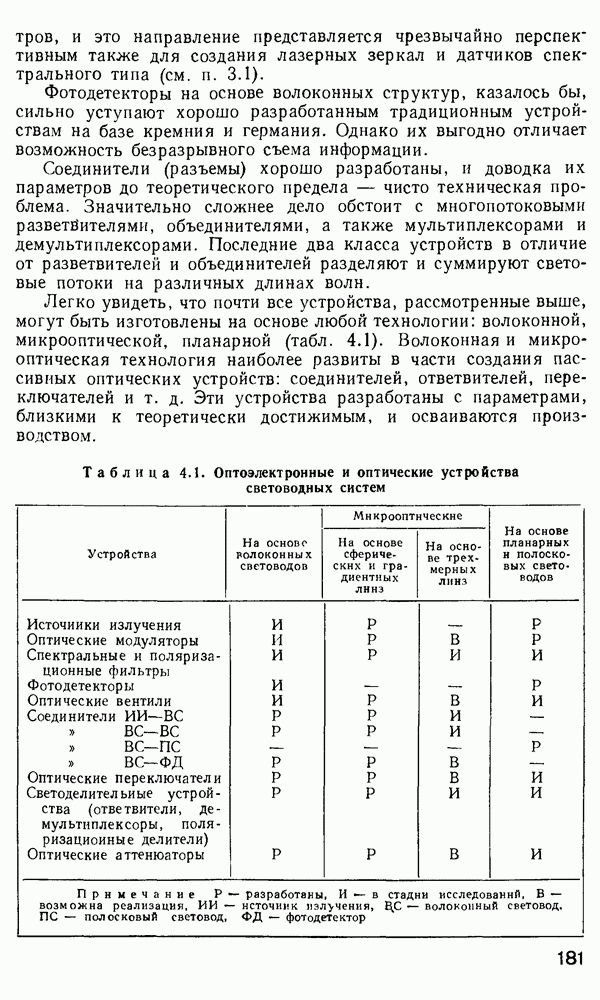
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
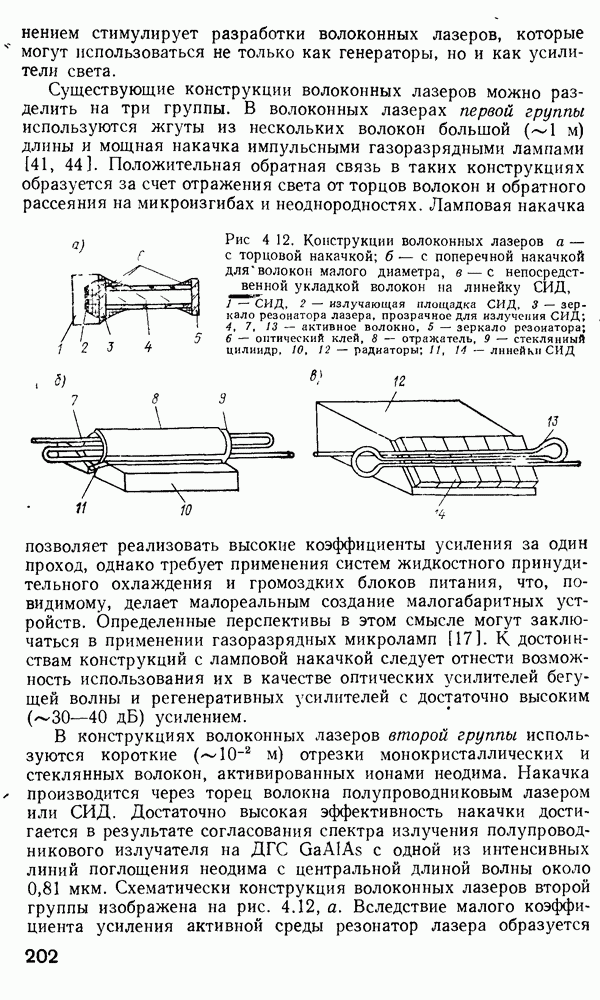
- Волоконные лазеры.
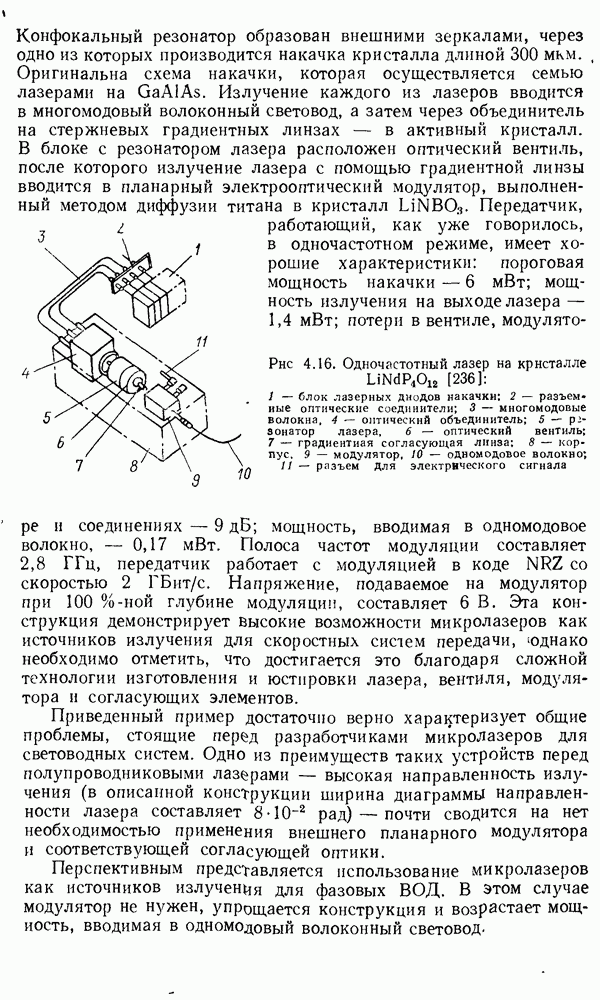
- Объемные микролазеры.
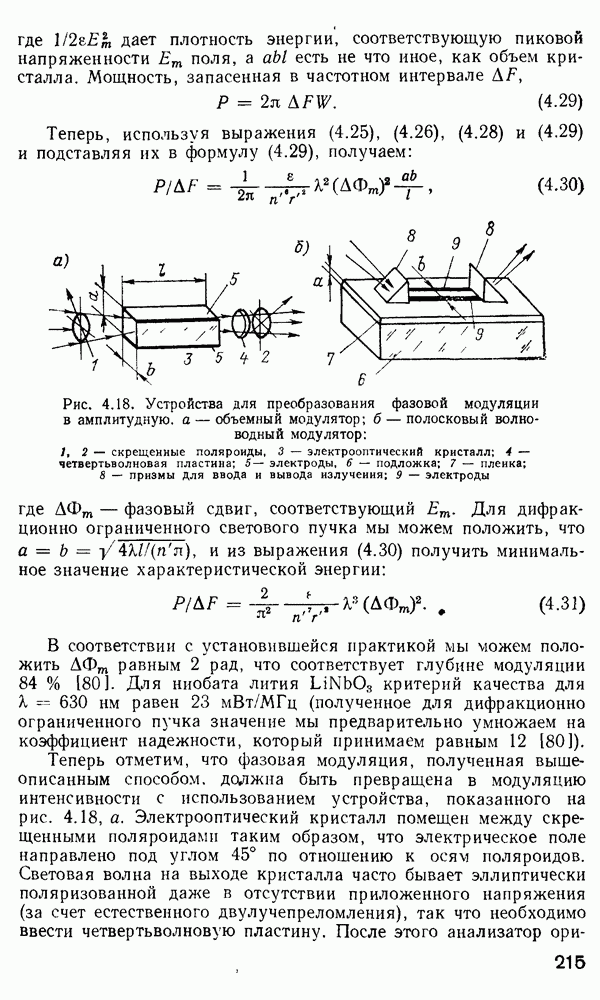
- 4.3. Оптические модуляторы
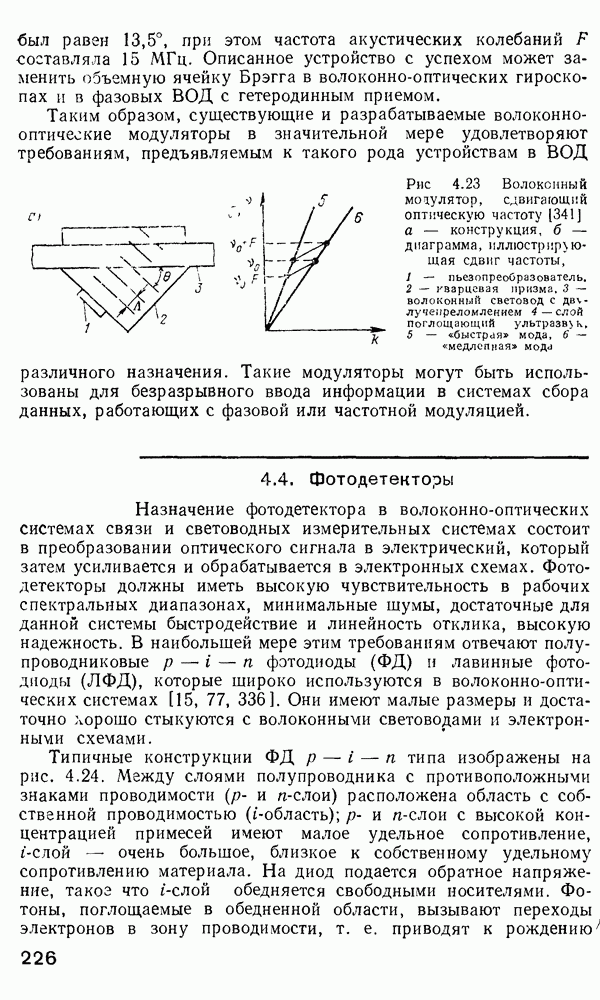
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
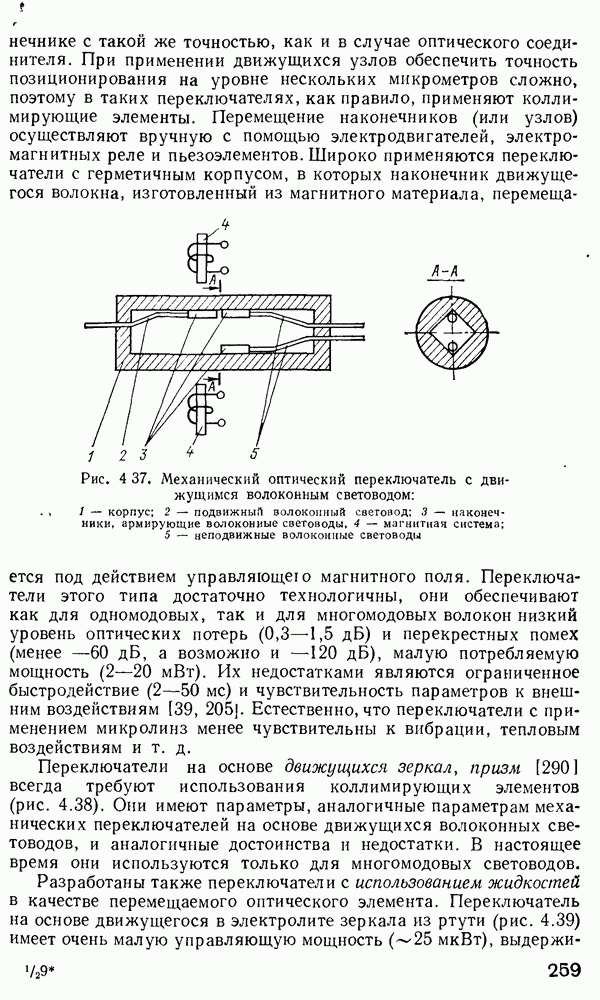
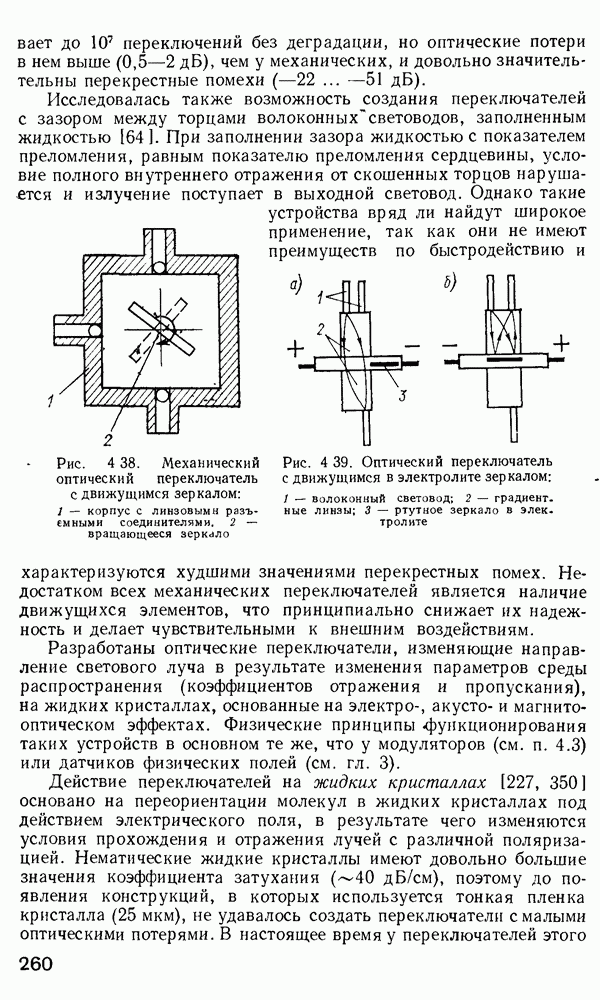
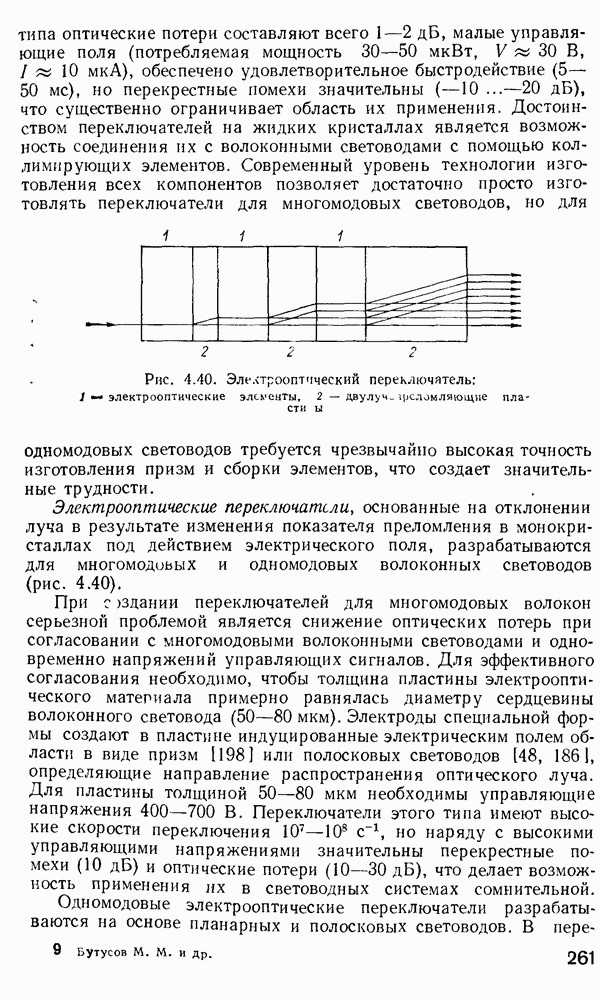
- 4.7. Волоконно-оптические переключатели
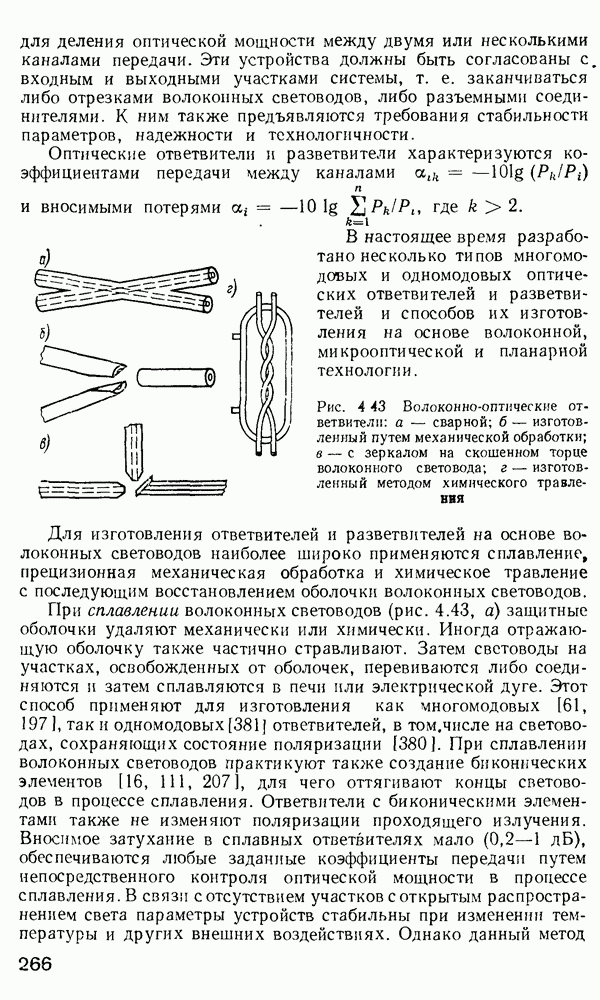
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
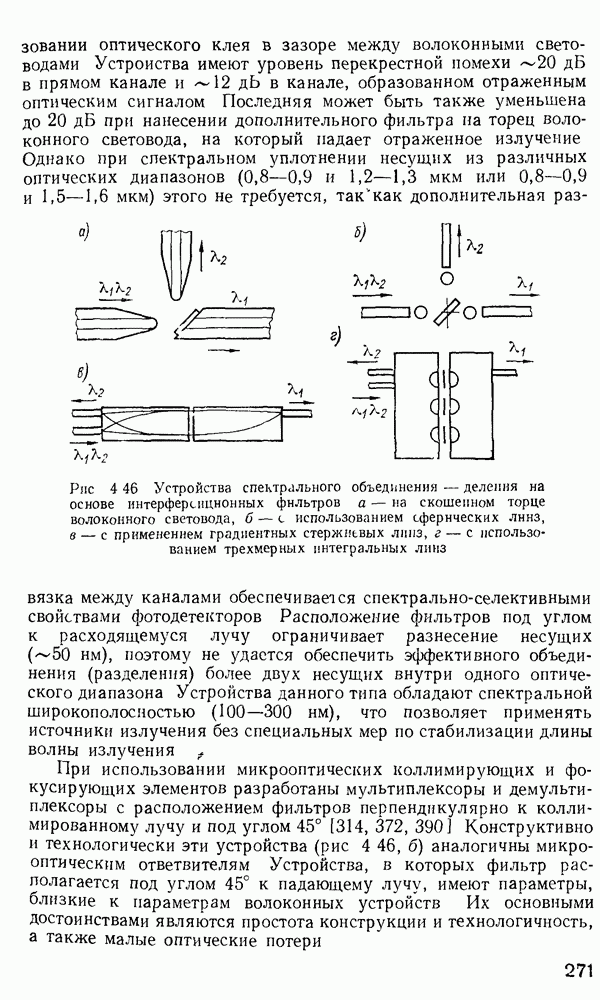
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
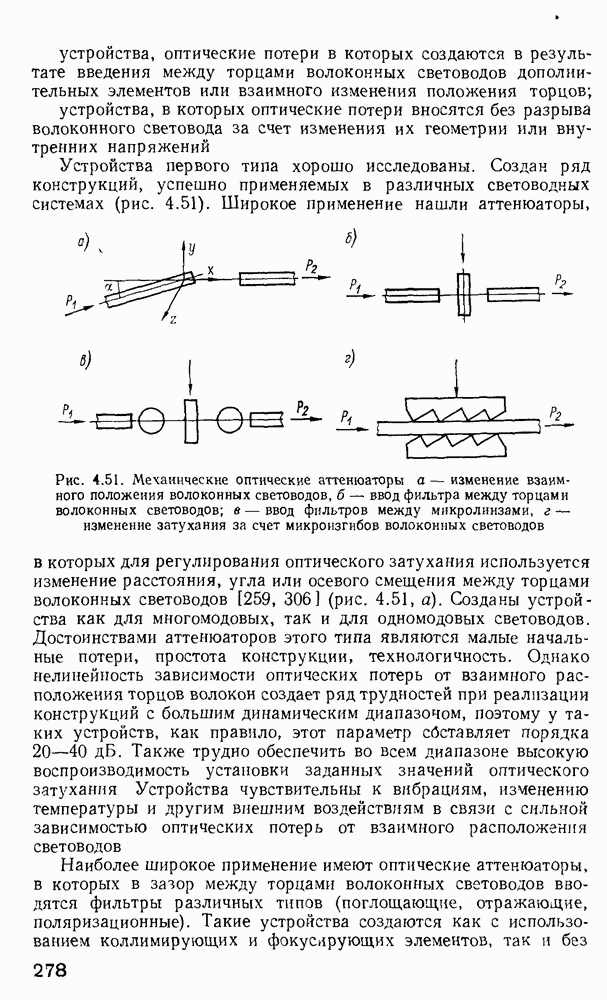
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
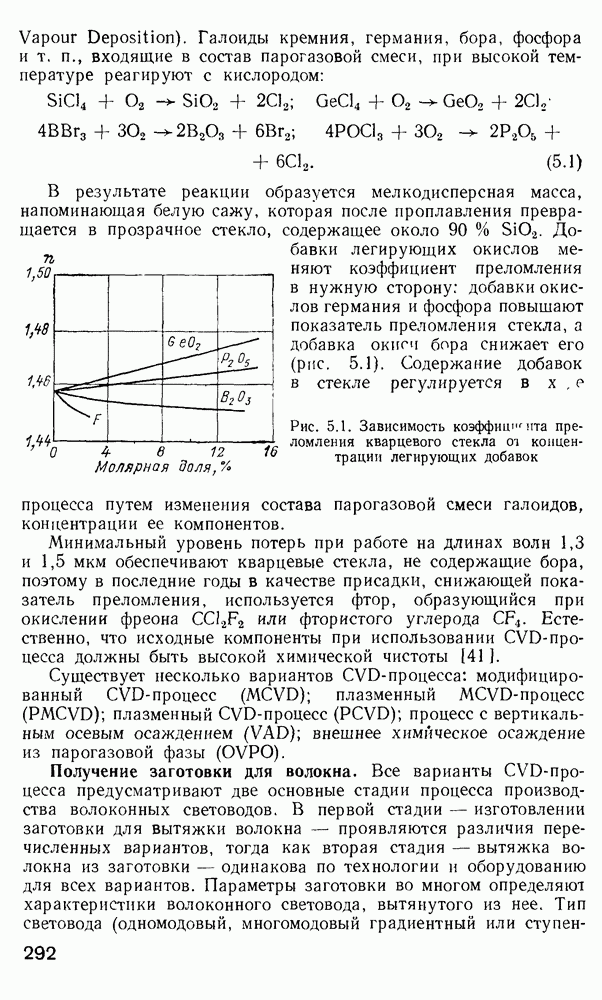
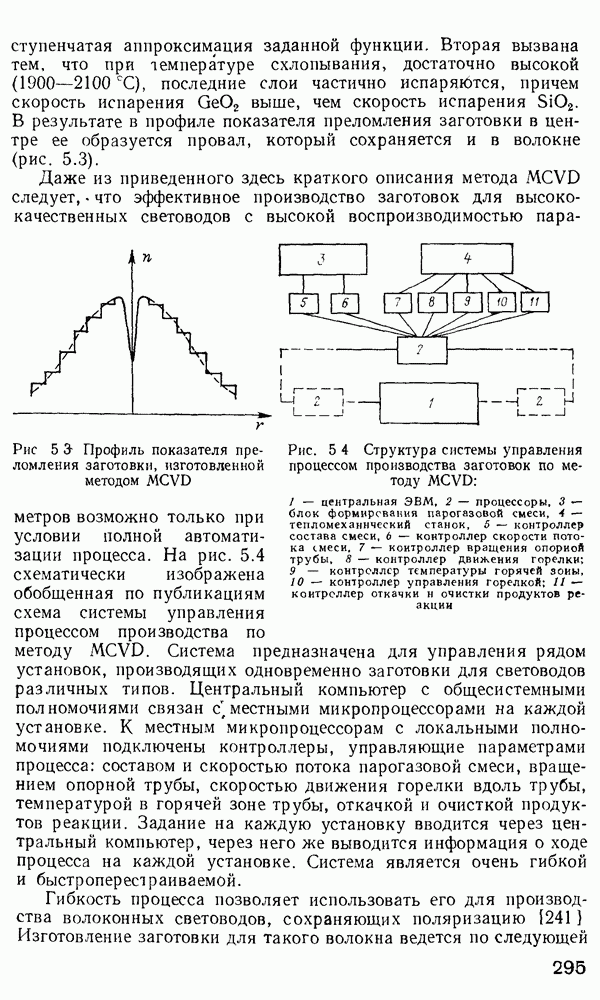
- Получение заготовки для волокна.
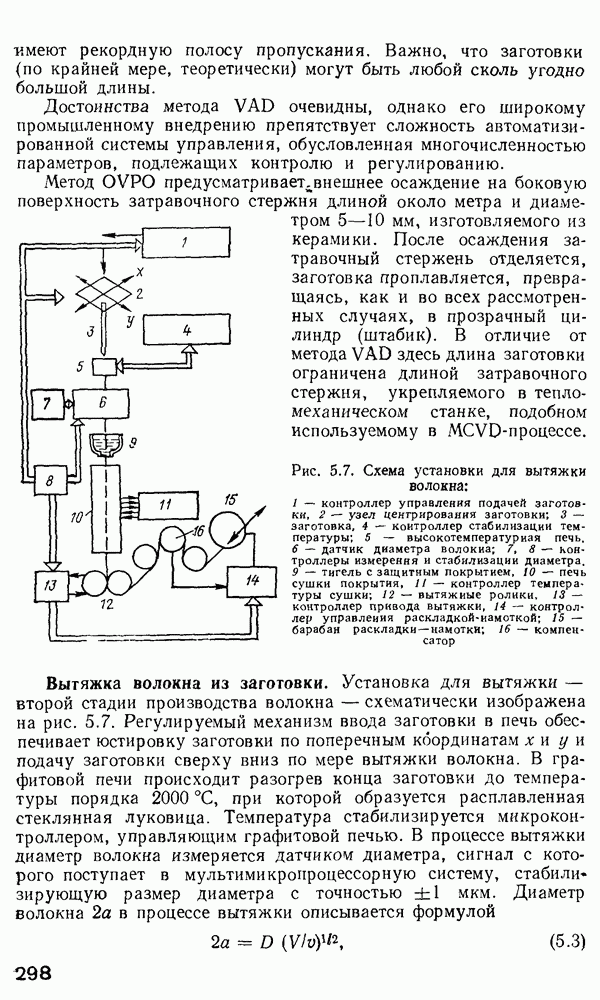
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
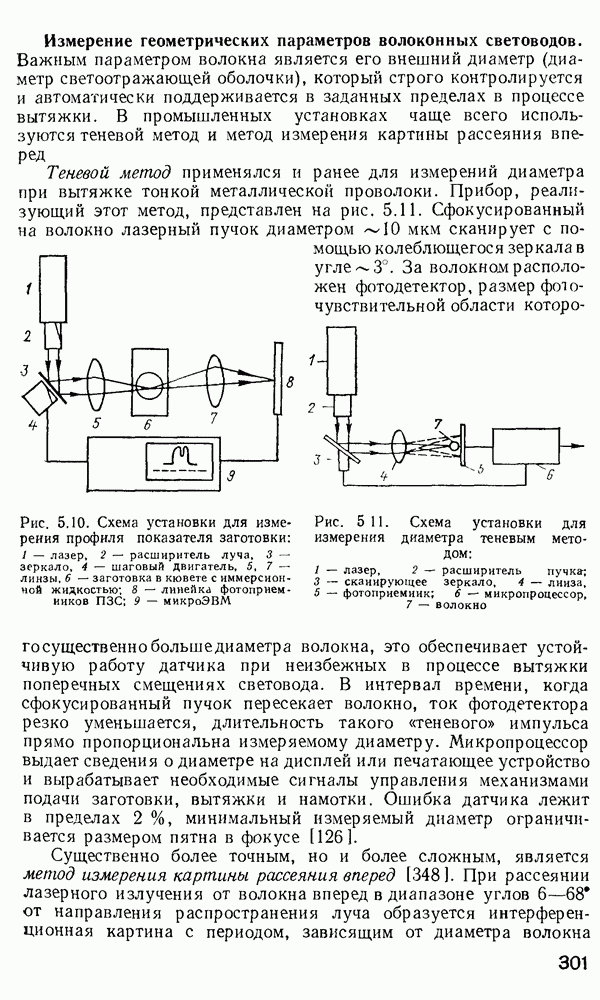
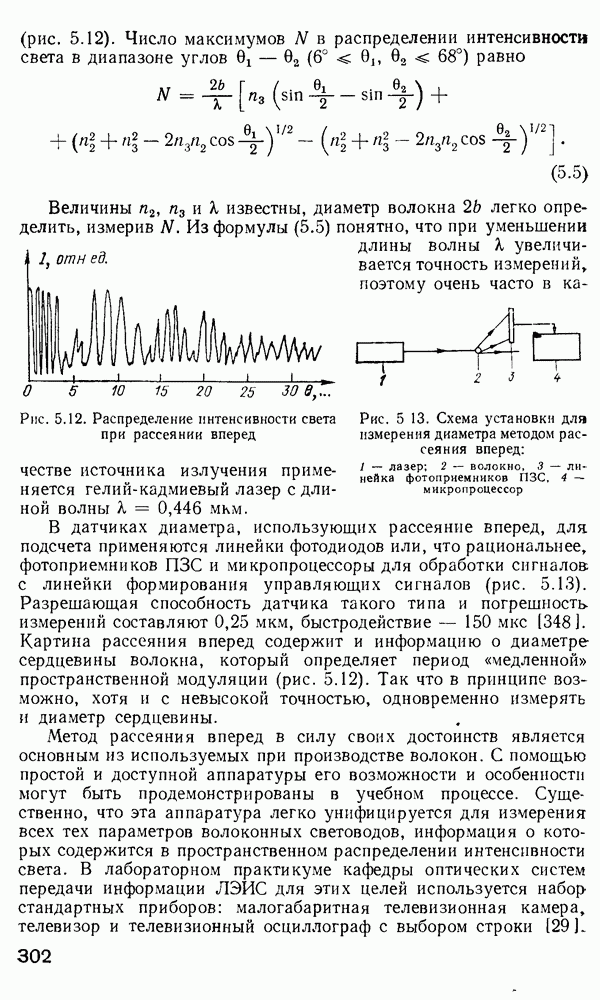
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ