| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
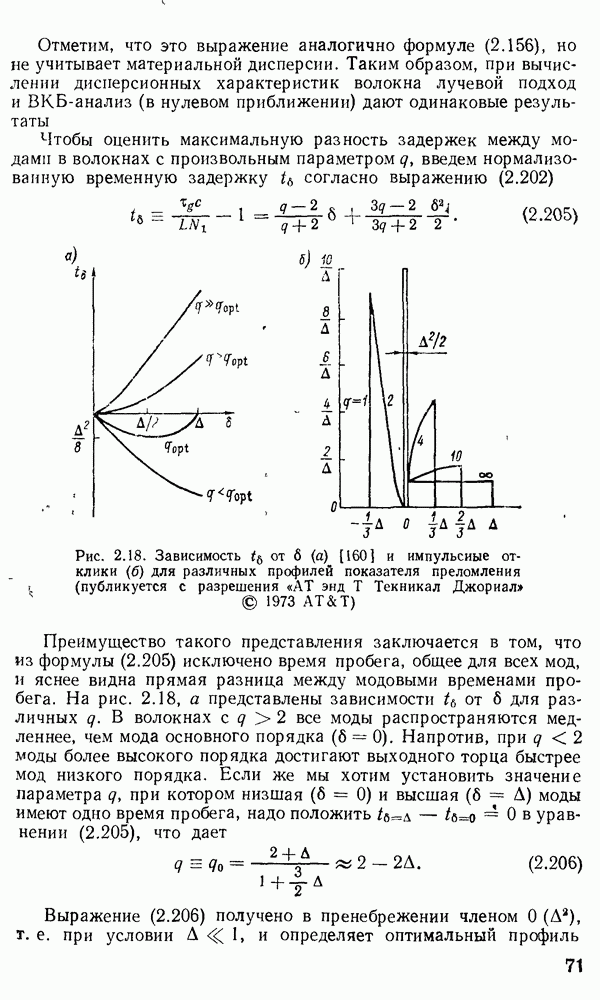
Решение уравнения (2.105) для волокна со ступенчатым профилем.
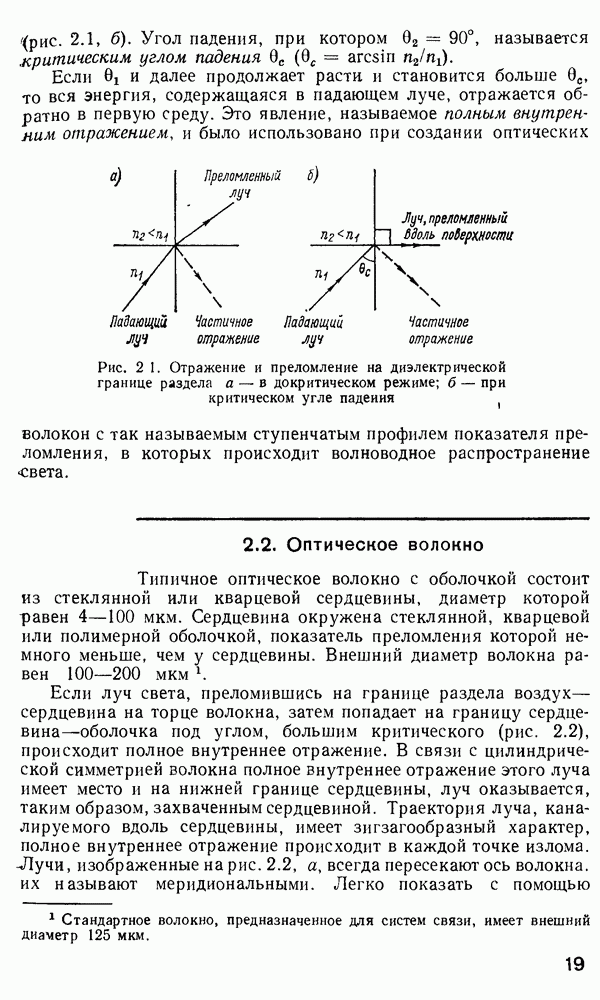
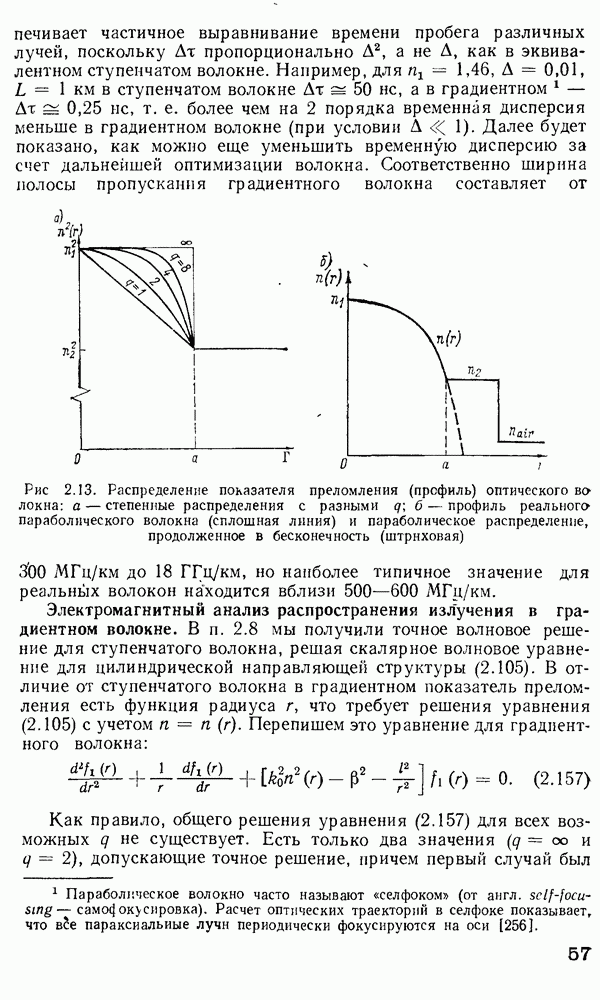
Первыми среди использованных были оптические волноводы с постоянным показателем преломления сердцевины (диаметром 2а), окруженной покрытием с постоянным показателем преломления  (см. рис. 2.2). Таким образом для сердцевины и покрытия уравнение (2.105) может быть переписано соответственно в
(см. рис. 2.2). Таким образом для сердцевины и покрытия уравнение (2.105) может быть переписано соответственно в  де
де

и

где параметры

были выбраны по тем же критериям, что и параметры  [см. уравнения (2.35)-(2.37)]. Параметры и и до можно
[см. уравнения (2.35)-(2.37)]. Параметры и и до можно
связать с приведенной частотой или параметром V волновода [см. формулу (2.6)]

Далее будет показано, что для физически реальных решении, а именно для направляемых мод волоконного световода, и и  должны быть положительными. Это подразумевает, что значения Р для направляемых мод должны лежать в пределах
должны быть положительными. Это подразумевает, что значения Р для направляемых мод должны лежать в пределах

Решения уравнения (2.106) есть функции Бесселя первого рода  порядка
порядка  и второго рода
и второго рода  тогда как решения уравнения (2.107) есть модифицированные функции Бесселя первого и второго рода
тогда как решения уравнения (2.107) есть модифицированные функции Бесселя первого и второго рода  где
где  Однако для того чтобы корректно выбрать цилиндрические функции для правильного представления направляемых мод, мы примем во внимание с учетом ассимптотической природы этих функций [78], что
Однако для того чтобы корректно выбрать цилиндрические функции для правильного представления направляемых мод, мы примем во внимание с учетом ассимптотической природы этих функций [78], что  ведут себя как стоячие волны с уменьшающейся амплитудой (для больших действительных значений их аргумента). С другой стороны,
ведут себя как стоячие волны с уменьшающейся амплитудой (для больших действительных значений их аргумента). С другой стороны,  есть монотонно спадающая функция от
есть монотонно спадающая функция от  есть монотонно возрастающая функция от х. Далее при
есть монотонно возрастающая функция от х. Далее при  функция
функция  ограничена, в то время как
ограничена, в то время как  — расходится. В то же время при
— расходится. В то же время при  . Следовательно, для ограниченных решений
. Следовательно, для ограниченных решений  должны быть отвергнуты и можно записать решеиия уравнений (2.106) и (2.107) для правильного представления волноводных мод волокна со ступенчатым профилем показателя преломления следующим образом:
должны быть отвергнуты и можно записать решеиия уравнений (2.106) и (2.107) для правильного представления волноводных мод волокна со ступенчатым профилем показателя преломления следующим образом:

где использована непрерывность  при
при  Поперечные компоненты поля
Поперечные компоненты поля  могут быть легко выражены с помощью уравнения (2.99) через
могут быть легко выражены с помощью уравнения (2.99) через  Полное поперечное поле
Полное поперечное поле

что может быть использовано для образования распределений поля различных мод. Когда определенное волокно содержит большое число мод, полная картина распределения поля будет сложной композицией всех этих мод, в связи с чем образуется своеобразная спекл-структура. Интерференционная спекл-структура наблюдается на выходе многомодового волокна, освещенного когерентным излучением от гелиево-неонового лазера.
Граничные условия, налагаемые геометрией волновода, требуют непрерывности  так же как других тангенциальных компонентов
так же как других тангенциальных компонентов  при
при  Эти условия непрерывности приведут к системе четырех уравнений для неизвестных постоянных А, В, С, D Для нетривиальных решений соответствующий определитель (образованный из коэффициентов А, В, С, D), должен быть равен нулю, и в результате длительных, хотя и простых, алгебраических преобразований, можно получить следующее трансцендентное уравнение для постоянной распространения [78 1:
Эти условия непрерывности приведут к системе четырех уравнений для неизвестных постоянных А, В, С, D Для нетривиальных решений соответствующий определитель (образованный из коэффициентов А, В, С, D), должен быть равен нулю, и в результате длительных, хотя и простых, алгебраических преобразований, можно получить следующее трансцендентное уравнение для постоянной распространения [78 1:

где штрихи означают дифференцирование функции по ее аргументу. Это уравнение, хотя математически более сложно, по существу эквивалентно характеристическому уравнению, полученному в п. 2.3 для планарного оптического волновода. Таким образом, по аналогии с уравнением (2.45) решения уравнения (2.113) для Р в пределах области, ограниченной условием (2.110), будут определять распространяющуюся волноводную моду в волокне со ступенчатым профилем показателя преломления Однако в цилиндрическом волоконно-оптическом волноводе, вообще говоря, все шесть компонентов полей  конечны, в отличие от планарного волновода, где или
конечны, в отличие от планарного волновода, где или  или
или  (для чистых
(для чистых  ТТИ-мод соответственно). В связи с отличием от нуля компонентов
ТТИ-мод соответственно). В связи с отличием от нуля компонентов  моды в волоконном волноводе называют гибридным и и обозначают как
моды в волоконном волноводе называют гибридным и и обозначают как  и ЕН-моды. Тем не менее, для специального случая радиально симметричных
и ЕН-моды. Тем не менее, для специального случая радиально симметричных  мод, когда правая часть в уравнении (2.113) исчезает, можно получить
мод, когда правая часть в уравнении (2.113) исчезает, можно получить

либо

Можно показать, что уравнение (2.114) соответствует  -моде а уравнение (2.115) —
-моде а уравнение (2.115) —  -моде.
-моде.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
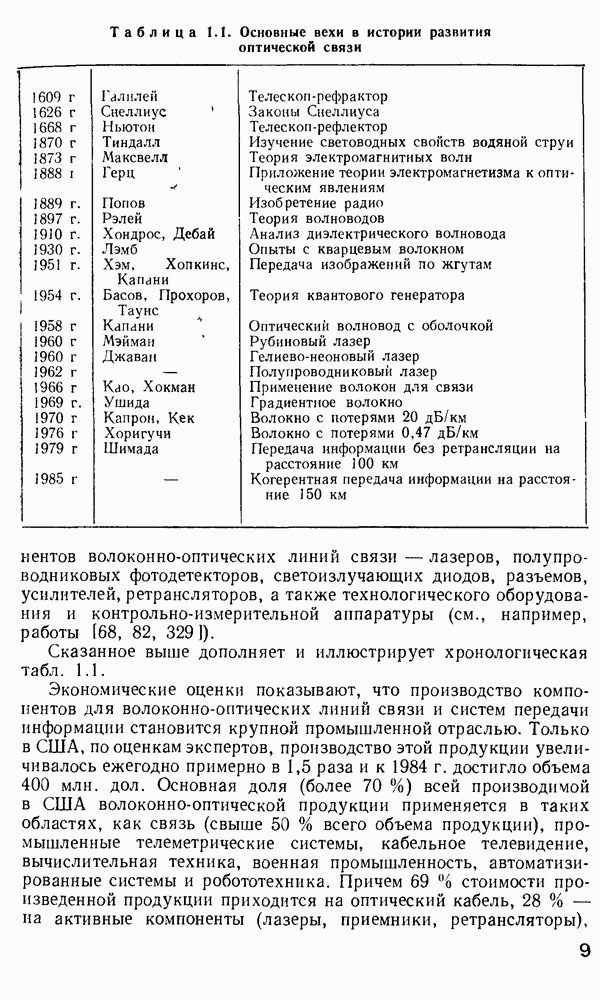
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
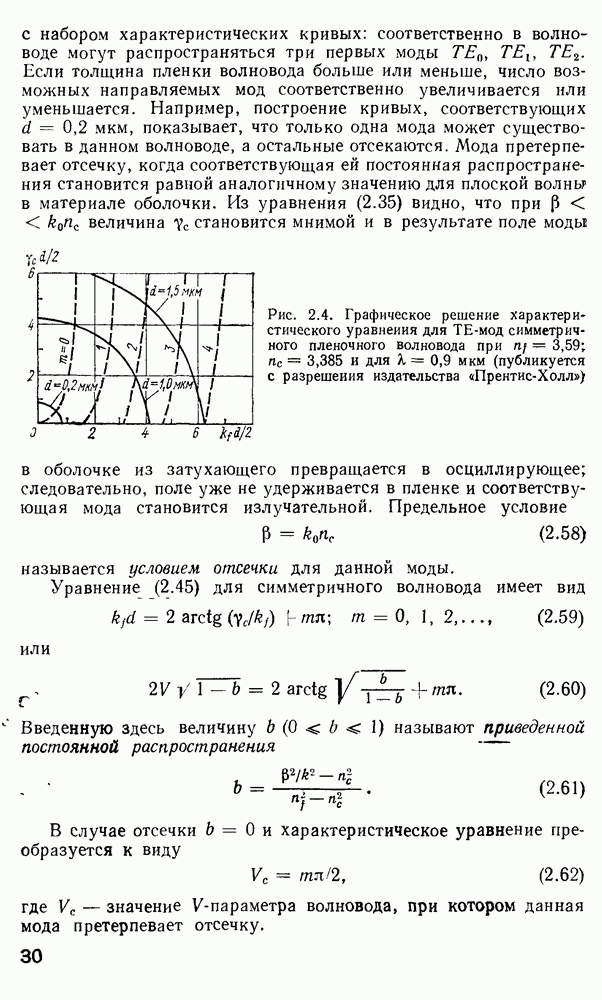
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
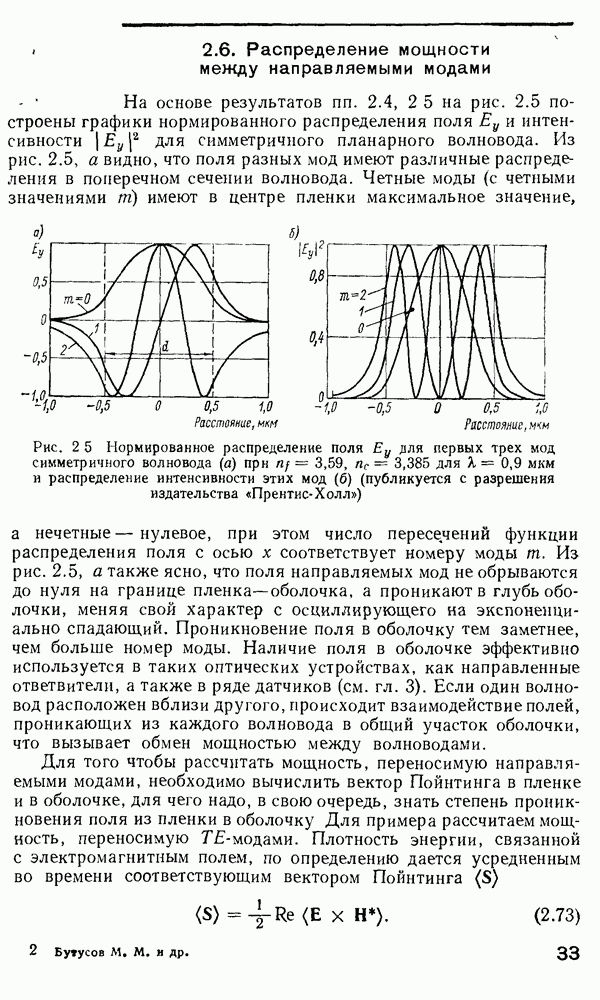
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
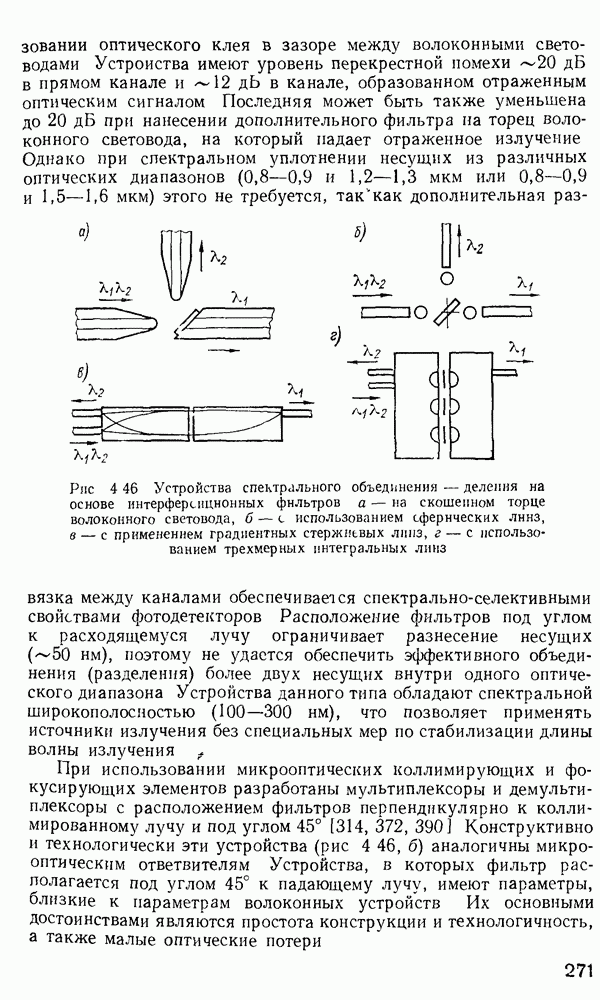
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
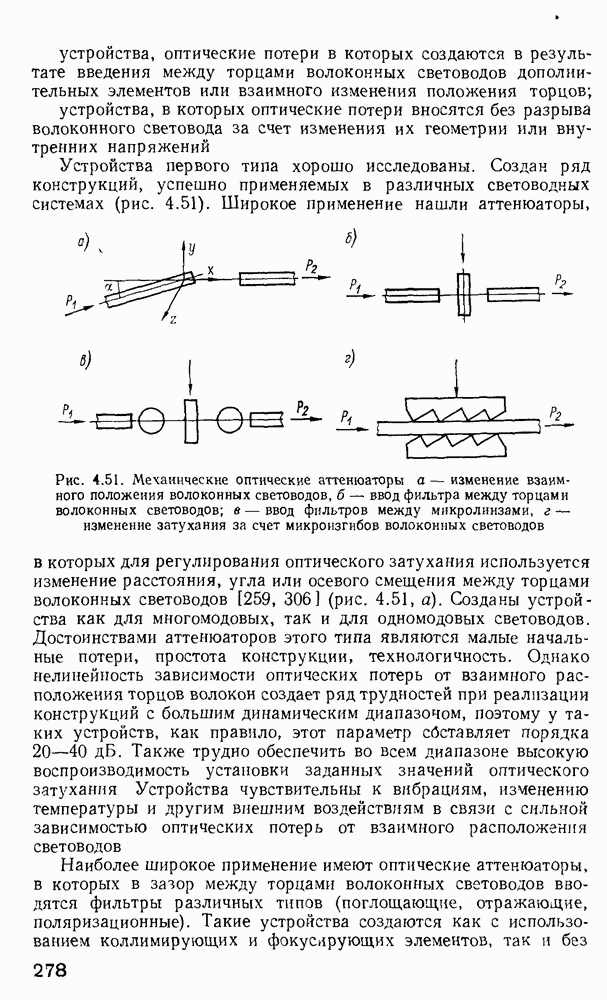
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
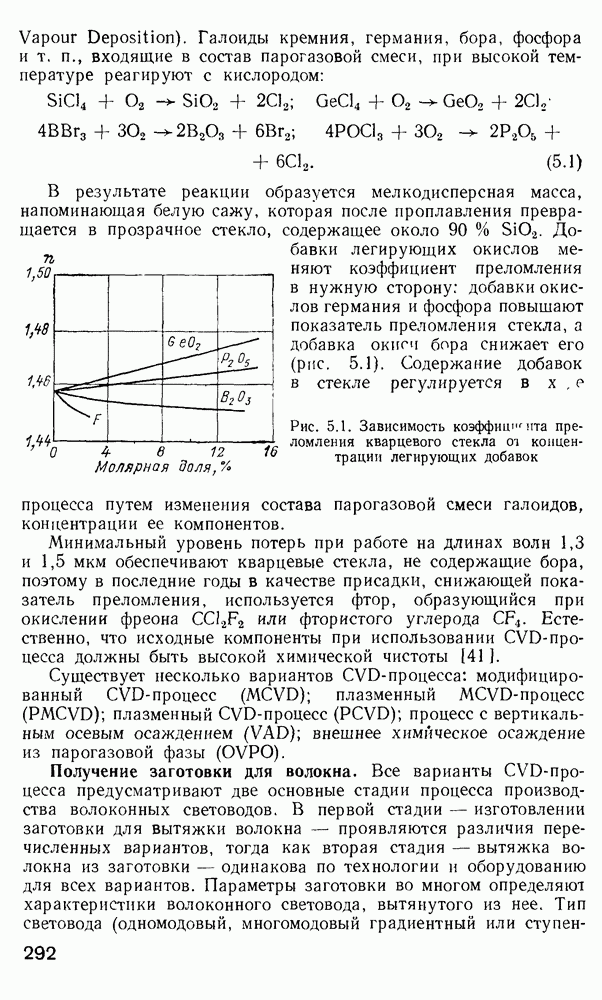
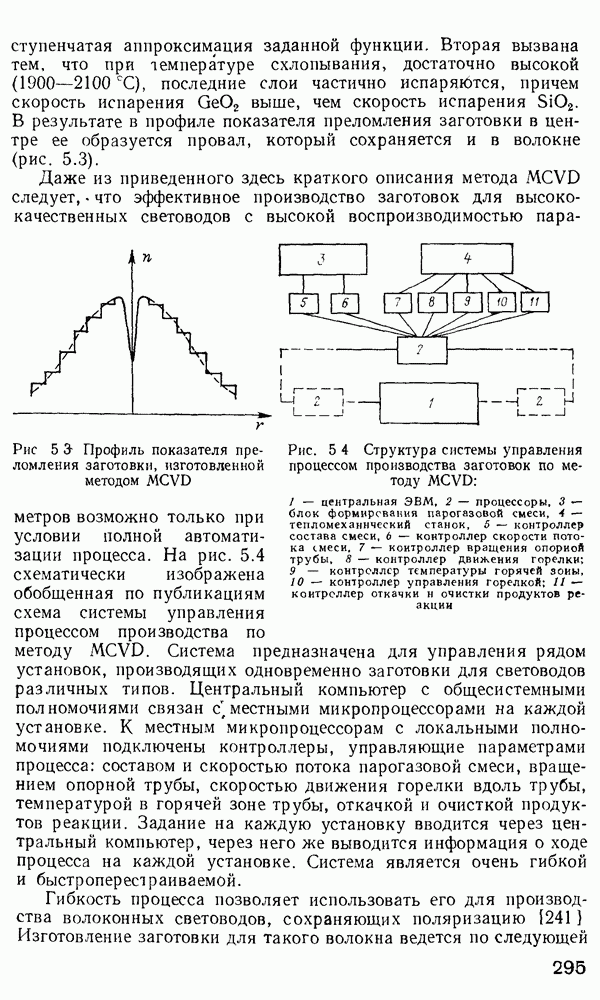
- Получение заготовки для волокна.
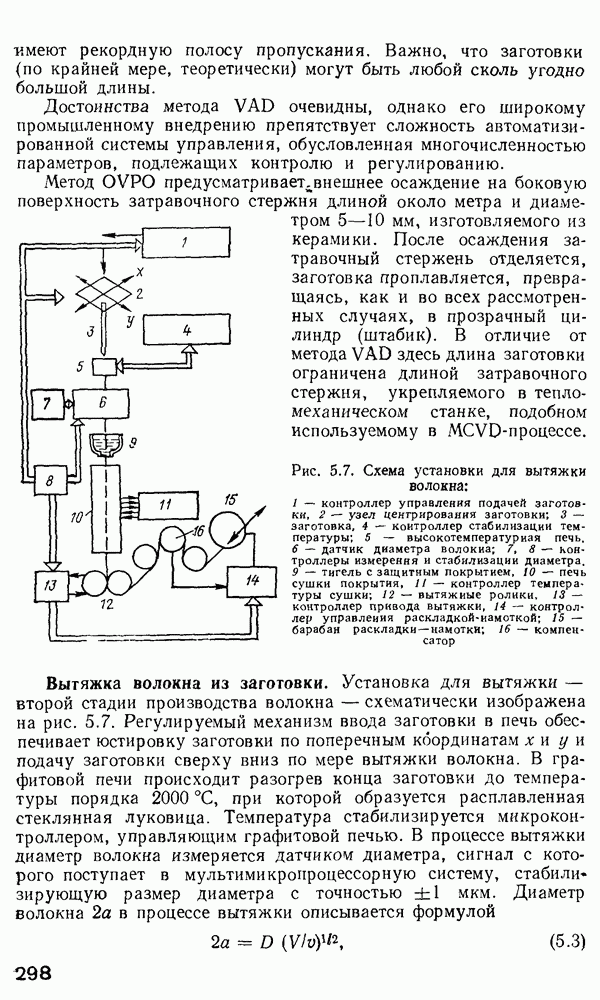
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
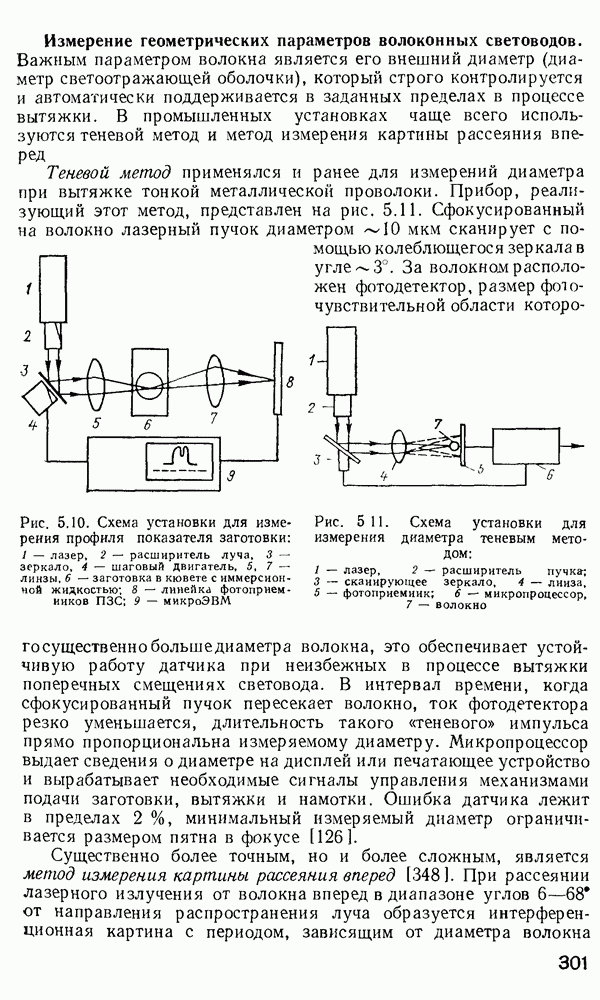
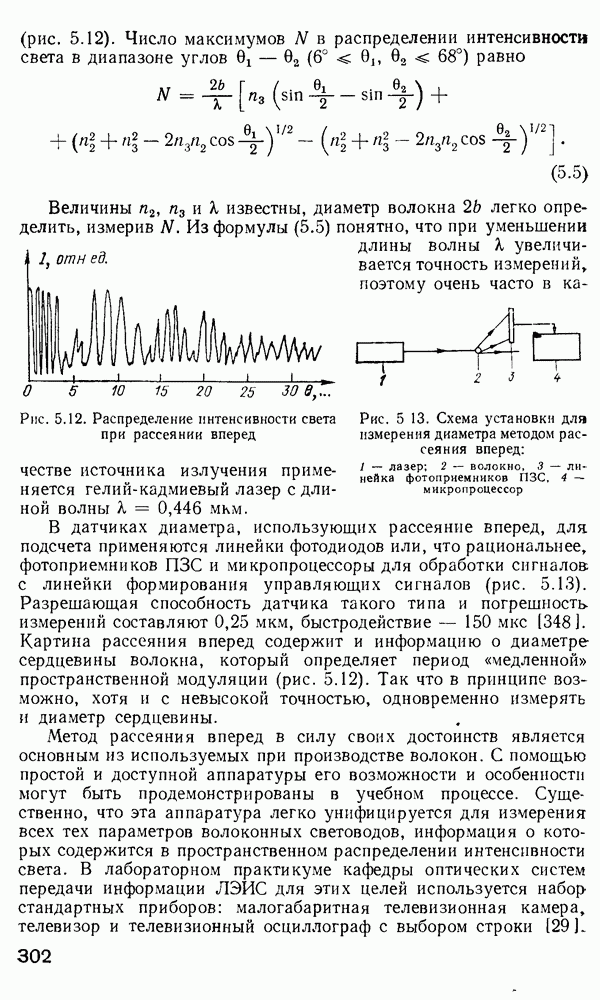
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ