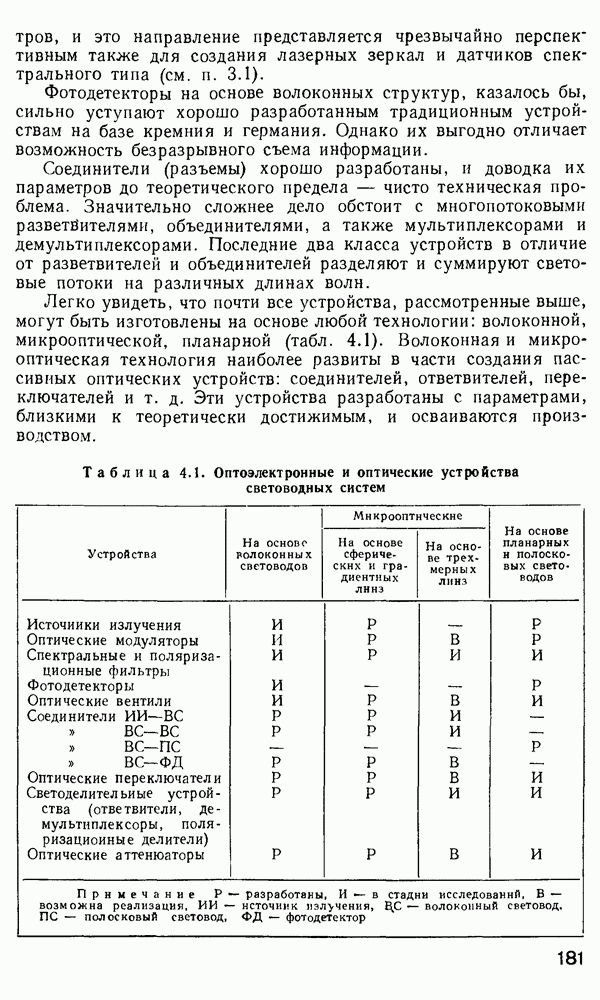
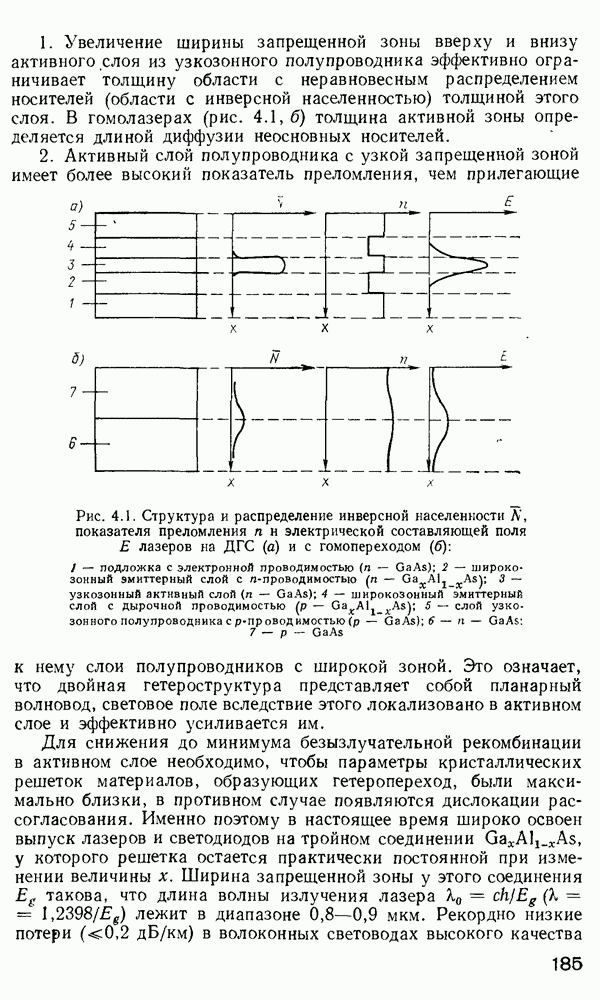
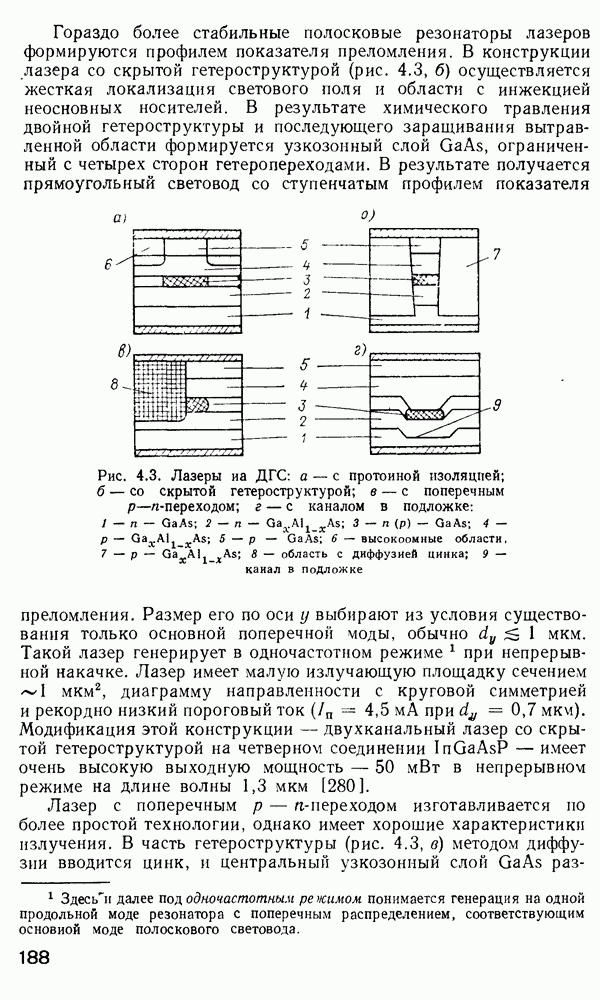
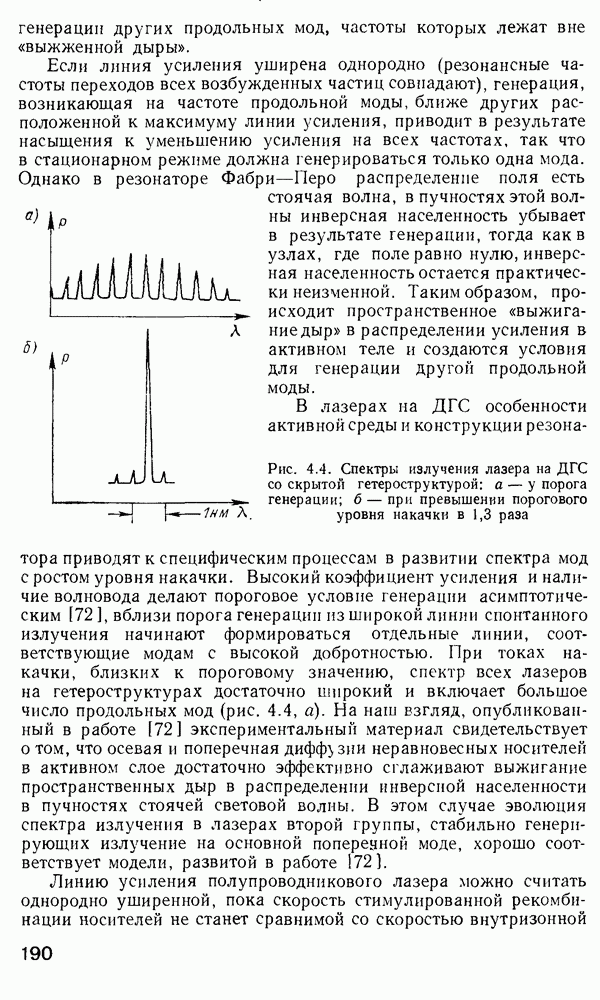
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
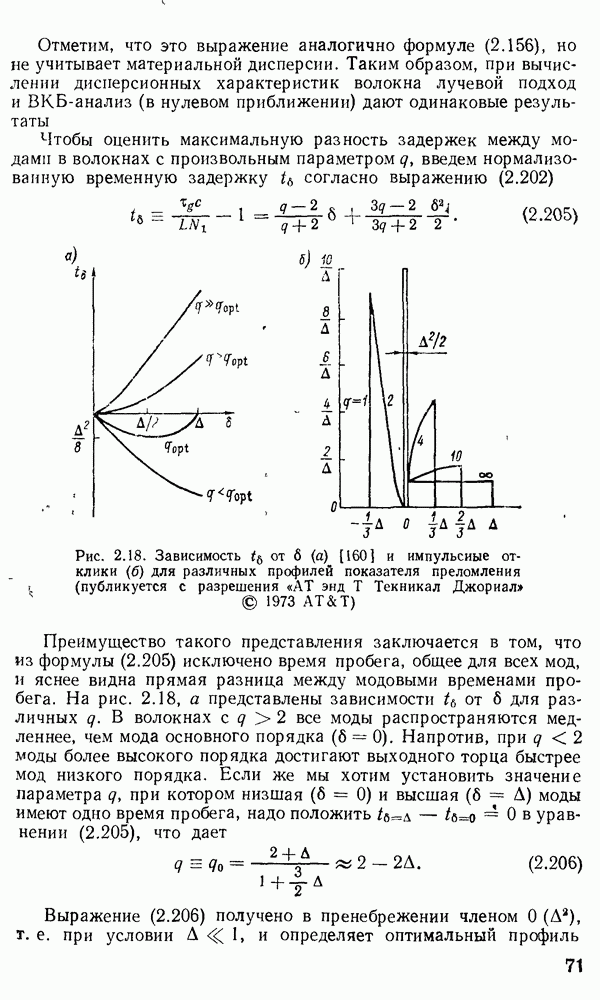
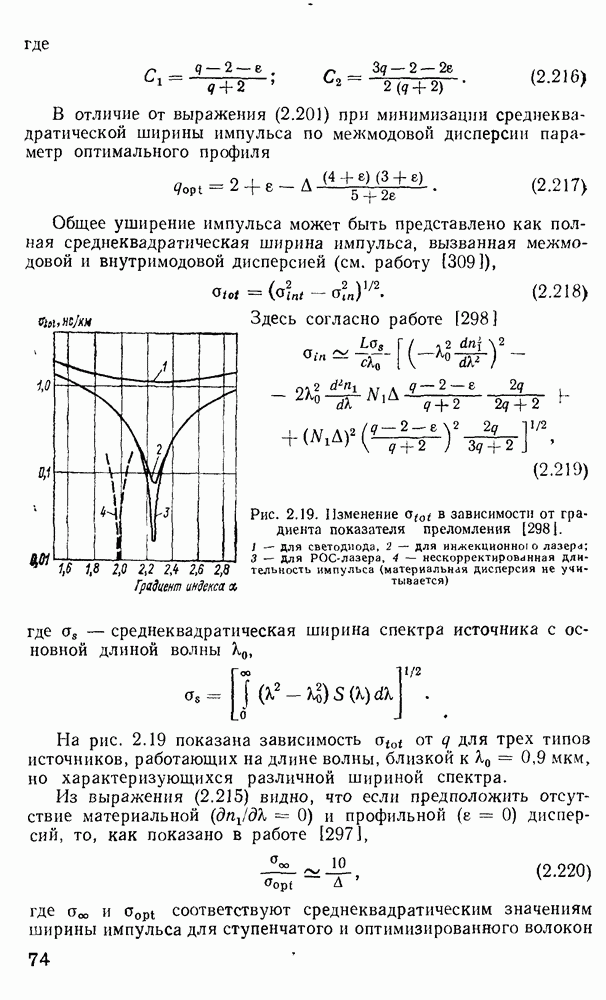
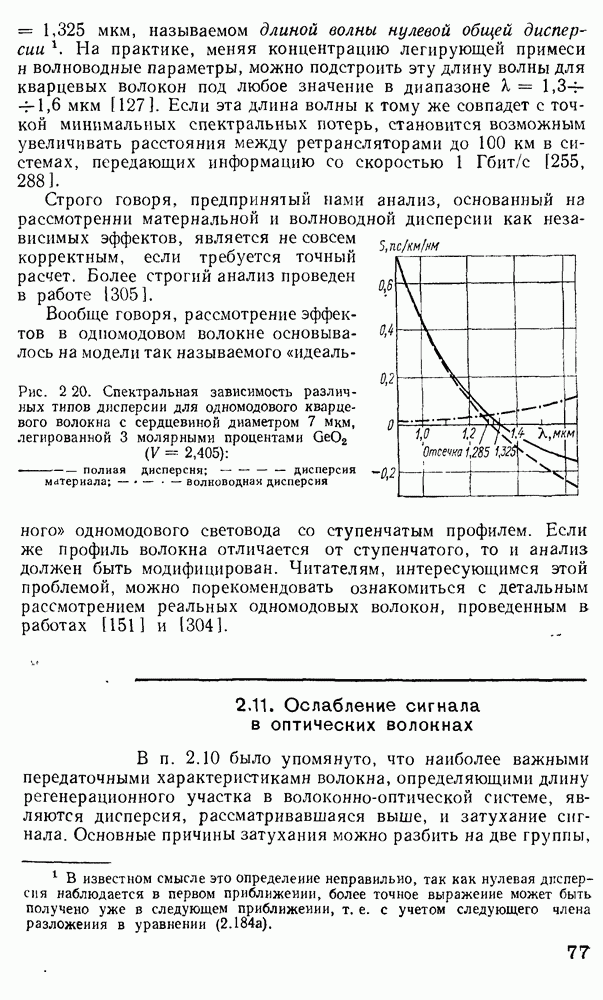
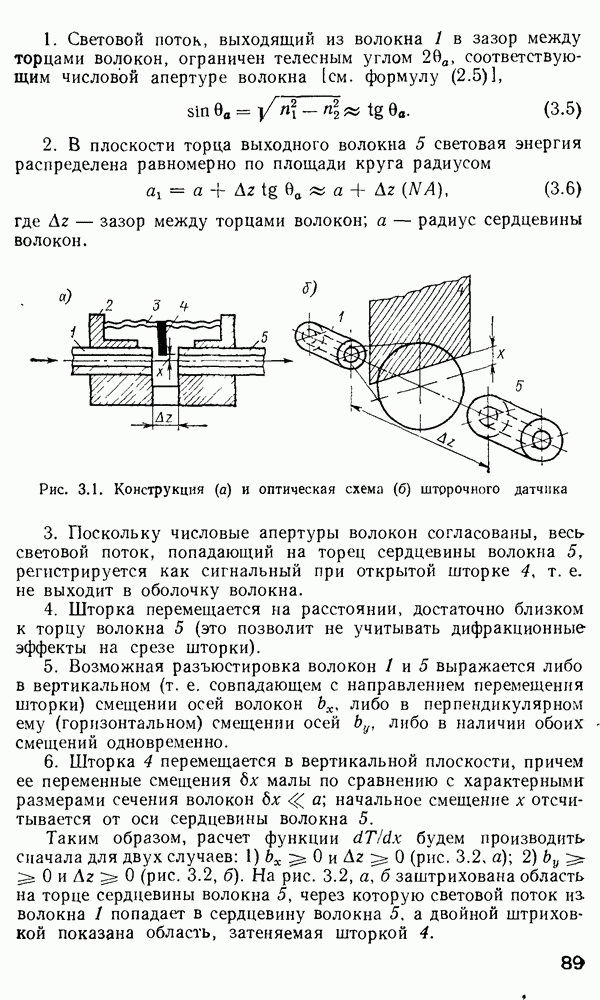
4.3. Оптические модуляторы
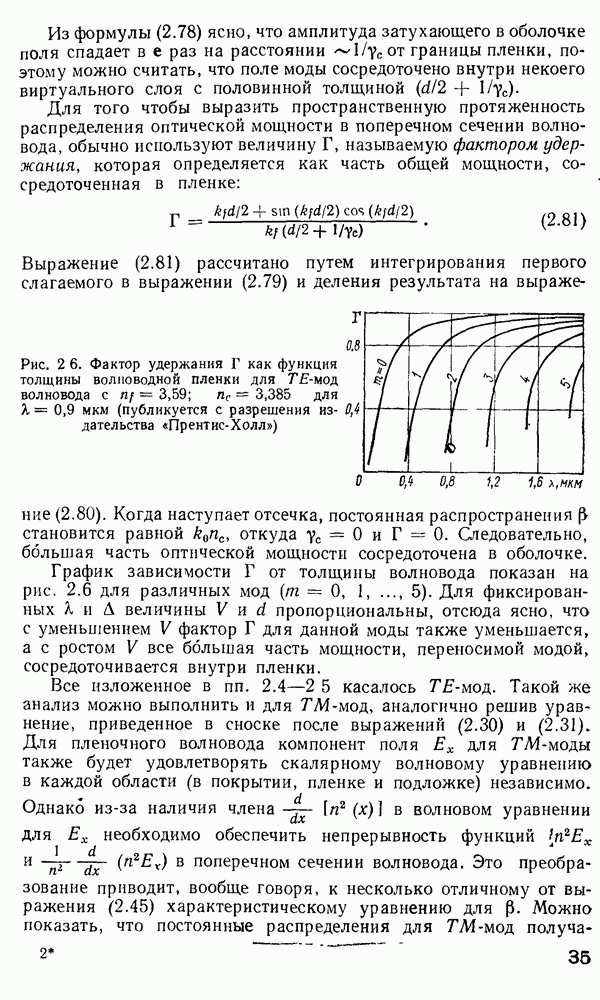
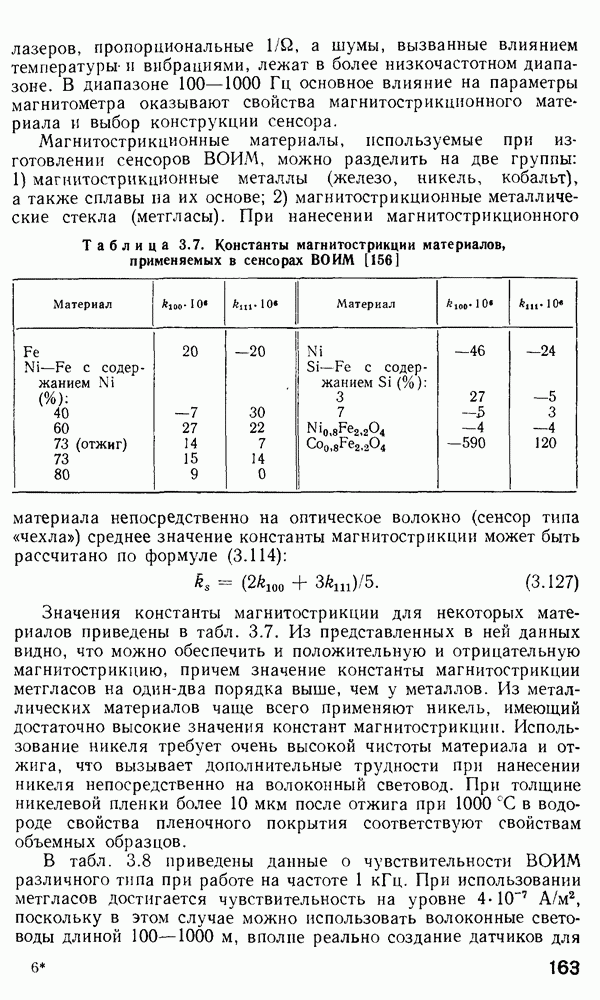
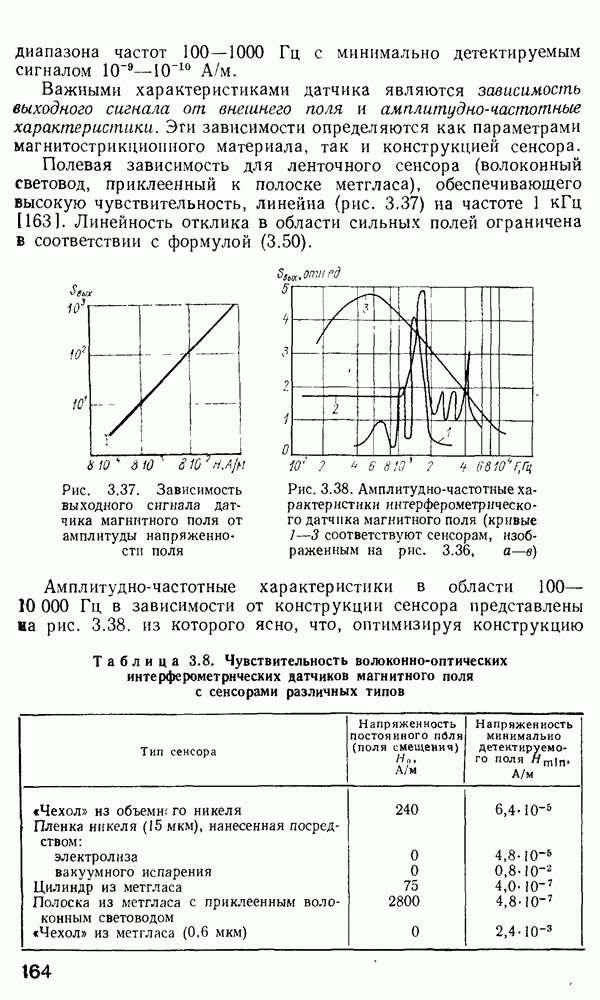
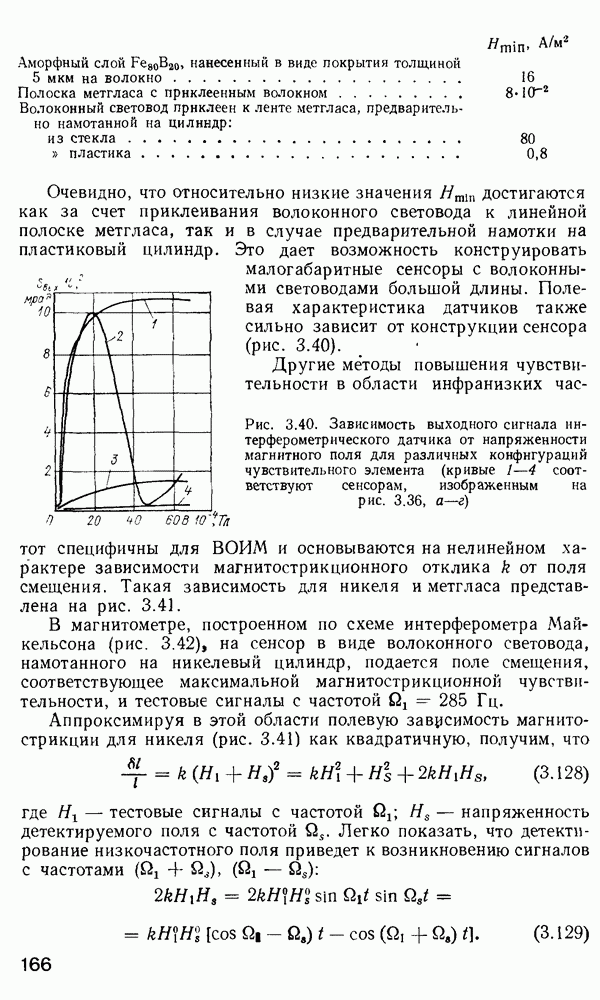
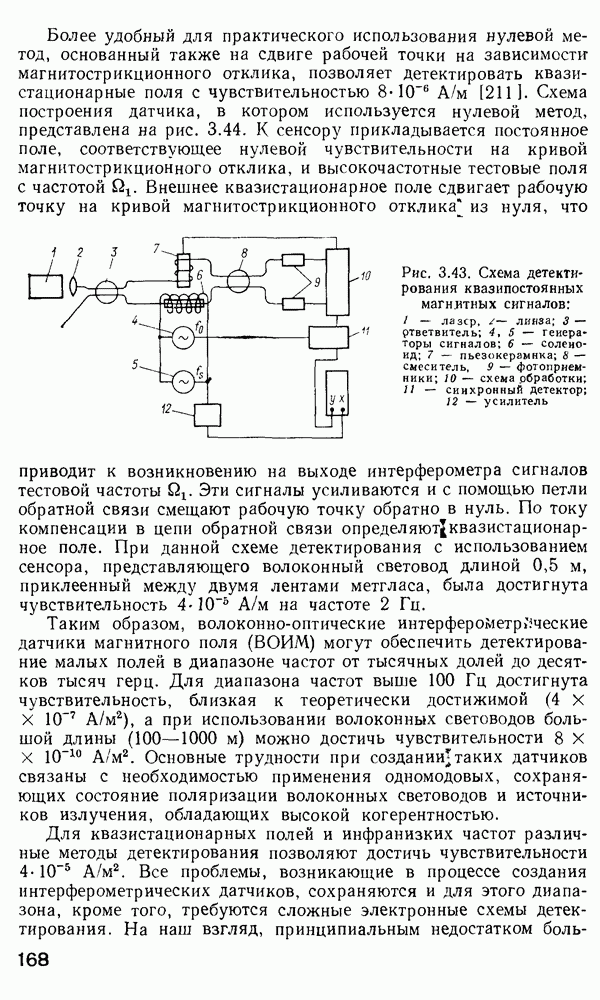
Оптические модуляторы предназначены для ввода информации в световую волну, путем изменения во времени одного из ее параметров — амплитуды (интенсивности), частоты, фазы или состояния поляризации. Действие оптических переключателей, рассмотренных в п. 4.7, зачастую основано на тех же физических принципах, что и модуляторов, однако их функция заключается в перераспределении оптической мощности между волоконными световодами.
По принципу действия оптические модуляторы обычно разделяют на три класса: электрооптические модуляторы на эффекте Поккельса; акустооптические модуляторы, в которых параметры световой волны изменяются в результате дифракции света на ультразвуковых волнах; магнитооптические модуляторы на эффекте Фарадея. Кроме того, известны модуляторы света на эффектах Керра, Франца — Келдыша, пьезоэлектрическом эффекте и т. п.
В принципе, большинство названных устройств может быть выполнено в любом исполнении: объемном, планарном или волоконном; исключение составляют модуляторы на основе моно-кристаллических сред, их волоконное исполнение представляется достаточно проблематичным, так как требует выращивания монокристаллов в виде волокон. Широкое развитие получили модуляторы в планарном (интегрально-оптическом) исполнении, это связано с рядом их значительных преимуществ перед объемными устройствами. Планарные и полосковые модуляторы незаменимы в устройствах обработки информации, однако целесообразность использования их, как, впрочем, и объемных устройств такого рода, в волоконно-оптических системах, на наш взгляд, отнюдь не очевидна.
Прямая модуляция полупроводниковых источников излучения позволяет эффективно вводить информацию в световой сигнал практически во всех необходимых случаях, в то время как о целесообразности ввода информации путем модуляции излучения, распространяющегося в оптическом тракте, за счет включения планарного устройства (например, в сетях сбора данных) далеко не бесспорен, поскольку неизбежны потери при соединении волоконных и полосковых световодов. Определенные возможности в этом направлении открывают рассмотренные в настоящем разделе волоконные модуляторы, которые сейчас не вышли еще из стадии исследований. Основные области применения интегрально-оптических и объемных модуляторов в интересующих нас системах связаны с созданием скоростных переключателей, конструкции которых рассмотрены в п. 4.7. Тем не менее, настоящая книга, по мнению авторов, была бы не полной, если бы в ней не были рассмотрены принципы построения объемных и планарных модуляторов. Читателя, интересующегося деталями и
конкретными решениями, мы адресуем к многочисленным книгам, посвященным модуляторам [34, 54, 63, 80, 181, 256, 329].
Электрооптический эффект Поккельса представляет собой изменение показателя преломления в анизотропных средах (кристаллах) под действием электрического поля. В таких средах векторы электрического поля Е и индукции  в общем случае не параллельны, их проекции связаны уравнениями
в общем случае не параллельны, их проекции связаны уравнениями

Девять величин являются константами среды и образуют тензор диэлектрической проницаемости. Можно показать, что закон сохранения энергии выполняется, если [104]

т. е. тензор  — симметричный.
— симметричный.

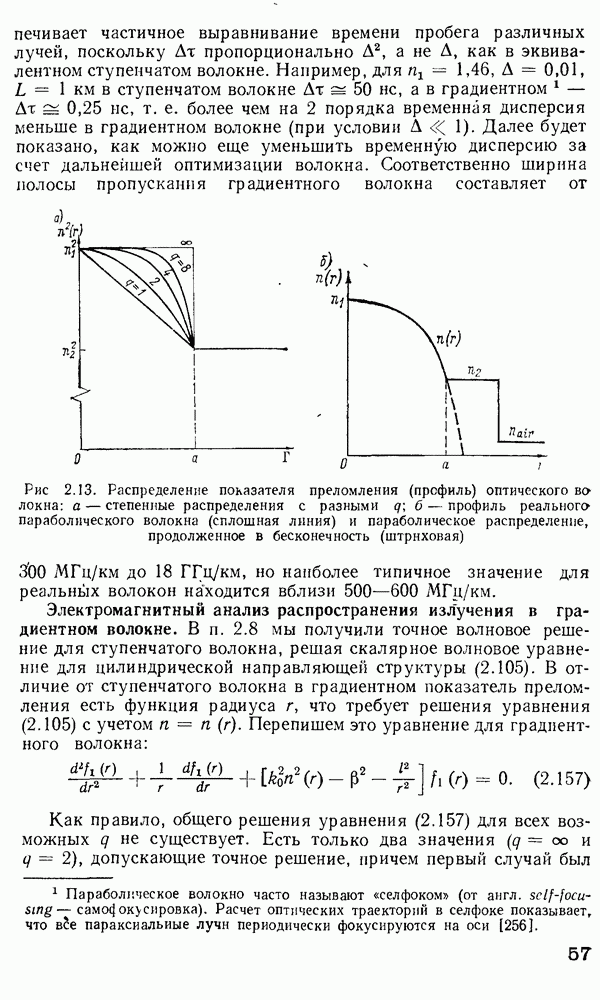
Рис. 4.17. Эллипсоид показателей преломления в кристалле
Уравнение (4.20) есть уравнение эллипсоида, которое можно привести к канонической форме выбором системы координат и нормировкой  к единице. В этом случае мы получаем уравнение эллипсоида Френеля
к единице. В этом случае мы получаем уравнение эллипсоида Френеля

где второй индекс при  опущен за ненадобностью. Так как главные оси эллипсоида Френеля являются одновременно и главными осями тензорного эллипсоида, дающего значения Е через компоненты
опущен за ненадобностью. Так как главные оси эллипсоида Френеля являются одновременно и главными осями тензорного эллипсоида, дающего значения Е через компоненты  [т. е. обратного в этом смысле тензору (4.19)], можно найти эллипсоид, соответствующий этому обратному тензору. Выражая его через показатели преломления, получаем эллипсоид показателей преломления, или индикатрису (рис. 4.17),
[т. е. обратного в этом смысле тензору (4.19)], можно найти эллипсоид, соответствующий этому обратному тензору. Выражая его через показатели преломления, получаем эллипсоид показателей преломления, или индикатрису (рис. 4.17),

Длины полуосей этого эллипсоида равны главным значениям показателя преломления кристалла. На практике большинство электрооптических кристаллов являются одноосными в том смысле, что они имеют только одну главную ось (обычно это ось  которую также называют осью с, или главной осью). Диэлектрическая проницаемость вдоль этой оси равна
которую также называют осью с, или главной осью). Диэлектрическая проницаемость вдоль этой оси равна  , а в перпендикулярных направлениях
, а в перпендикулярных направлениях  не зависит от выбора осей
не зависит от выбора осей  Такие одноосные кристаллы имеют два главных значения показателя
Такие одноосные кристаллы имеют два главных значения показателя
преломления  Значения показателей преломления в остальных направлениях могут быть найдены с помощью следующей процедур
Значения показателей преломления в остальных направлениях могут быть найдены с помощью следующей процедур 
Плоскость, содержащая вектор к (волновой вектор падающей волны), и ось z образуют главную плоскость эллипсоида (плоскость симметрии — на рис. 4.17 она заштрихована). Следовательно, эллиптическое сечение, перпендикулярное к вектору к, одновременно перпендикулярно и к главной плоскости. Таким образом, главные оси этого эллипса перпендикулярны друг к  и параллельны главной плоскости. Поэтому, если мы разложим электрический вектор на два компонента вдоль осей эллипса (а электрический вектор нормален к волновому и, следовательно, лежит в плоскости эллипса), тогда один из компонентов всегда нормален к главной плоскости, а другой параллелен ей. Другими словами, в волне можно выделить две составляющие поляризации: одна соответствует колебаниям электрического поля перпендикулярно к главной плоскости (обыкновенная волна), другая — колебаниям вектора Е параллельно этой плоскости (необыкновенная волна). Для любого углового направления 0 волнового вектора к колебания обыкновенной волны направлены вдоль главной оси эллипсоида показателей преломления (ось у на рис. 4.17), что соответствует обыкновенному показателю преломления
и параллельны главной плоскости. Поэтому, если мы разложим электрический вектор на два компонента вдоль осей эллипса (а электрический вектор нормален к волновому и, следовательно, лежит в плоскости эллипса), тогда один из компонентов всегда нормален к главной плоскости, а другой параллелен ей. Другими словами, в волне можно выделить две составляющие поляризации: одна соответствует колебаниям электрического поля перпендикулярно к главной плоскости (обыкновенная волна), другая — колебаниям вектора Е параллельно этой плоскости (необыкновенная волна). Для любого углового направления 0 волнового вектора к колебания обыкновенной волны направлены вдоль главной оси эллипсоида показателей преломления (ось у на рис. 4.17), что соответствует обыкновенному показателю преломления  Другая ось эллипса меняется с изменением угла
Другая ось эллипса меняется с изменением угла  но ее значение всегда заключено между
но ее значение всегда заключено между  Это значение обычно именуется необыкновенным показателем преломления пе.
Это значение обычно именуется необыкновенным показателем преломления пе.
Итак, при распространении вдоль оси  кристалла обе волны движутся с одинаковыми скоростями
кристалла обе волны движутся с одинаковыми скоростями  Говорят, что в этом случае двулучепреломление отсутствует. С другой стороны, при распространении в направлении нормали к оси
Говорят, что в этом случае двулучепреломление отсутствует. С другой стороны, при распространении в направлении нормали к оси  двулучепреломление будет максимальныметак как векторы электрического поля будут направлены по осям у (или
двулучепреломление будет максимальныметак как векторы электрического поля будут направлены по осям у (или  Двулучепреломление считается отрицательным, если
Двулучепреломление считается отрицательным, если  и положительным, если
и положительным, если 
С нашей точки зрения, наиболее знаменательным фактом является то, что действие электрического поля или механического напряжения может вызвать деформацию эллипсоида показателей преломления и тем самым увеличить или вызвать двулучепреломление. Такие процессы являются прямым следствием деформаций кристаллической решетки, которые возникают из-за пьезоэффекта и электрической поляризации в одном случае и из-за прямых механических нагрузок в другом. В общем случае главные оси тензоров не совпадают, и в нашей координатной системе уравнение эллипсоида показателей преломления принимает следующий вид:

Изменения, вызванные электрическим полем, могут быть представлены в виде следующих изменений шести членов типа 

где  — приложенное электрическое поле,
— приложенное электрическое поле,  коэффициенты электрооптической матрицы (их всего 18). Для практически используемых материалов в результате симметрии число коэффициентов значительно уменьшается. Из формулы (4.24) можно сделать вывод, что мы рассматриваем эффект, который прямо пропорционален электрическому полю. Очевидно, что довольно трудно подсчитать, насколько изменяется показатель преломления в общем случае, а поэтому желательно провести некоторые упрощения. С практической точки зрения целесообразно предположить, что направление распространения света перпендикулярно к главной оси. Тогда изменения показателя преломления могут быть выражены следующим образом:
коэффициенты электрооптической матрицы (их всего 18). Для практически используемых материалов в результате симметрии число коэффициентов значительно уменьшается. Из формулы (4.24) можно сделать вывод, что мы рассматриваем эффект, который прямо пропорционален электрическому полю. Очевидно, что довольно трудно подсчитать, насколько изменяется показатель преломления в общем случае, а поэтому желательно провести некоторые упрощения. С практической точки зрения целесообразно предположить, что направление распространения света перпендикулярно к главной оси. Тогда изменения показателя преломления могут быть выражены следующим образом:

где  — линейная комбинация главных показателей преломления;
— линейная комбинация главных показателей преломления;  — линейная сумма электраоптических коэффициентов; Е — соответствующий компонент приложенного электрического поля [80].
— линейная сумма электраоптических коэффициентов; Е — соответствующий компонент приложенного электрического поля [80].
Если значение  подсчитано, то фазовый сдвиг световой волны после прохождения ею расстояния
подсчитано, то фазовый сдвиг световой волны после прохождения ею расстояния 

Пользуясь формулами (4.25) и (4.26), можно оценить то напряжение, которое нужно приложить поперек кристалла длиной  для того, чтобы получить результирующий фазовый сдвиг
для того, чтобы получить результирующий фазовый сдвиг  . Это напряжение, известное под названием полуволнового напряжения,
. Это напряжение, известное под названием полуволнового напряжения,

Полуволновое напряжение меняется в диапазоне от 0,2 до  для различных электрических материалов.
для различных электрических материалов.
Другая оценочная характеристика модуляторов — критерий качества или характеристическая энергия — связана с использованием электрооптических модуляторов в высокочастотном диапазоне и определяется как отношение управляющей мощности к рабочему диапазону частот. Для нахождения этой характеристики вспомним, что энергия, запасенная в электрооптическом модуляторе,

где  дает плотность энергии, соответствующую пиковой напряженности
дает плотность энергии, соответствующую пиковой напряженности  поля,
поля,  есть не что иное, как объем кристалла. Мощность, запасенная в частотном интервале
есть не что иное, как объем кристалла. Мощность, запасенная в частотном интервале 

Теперь, используя выражения (4.25), (4.26), (4.28) и (4.29) и подставляя их в формулу (4.29), получаем:

где  — фазовый сдвиг, соответствующий
— фазовый сдвиг, соответствующий  .
.

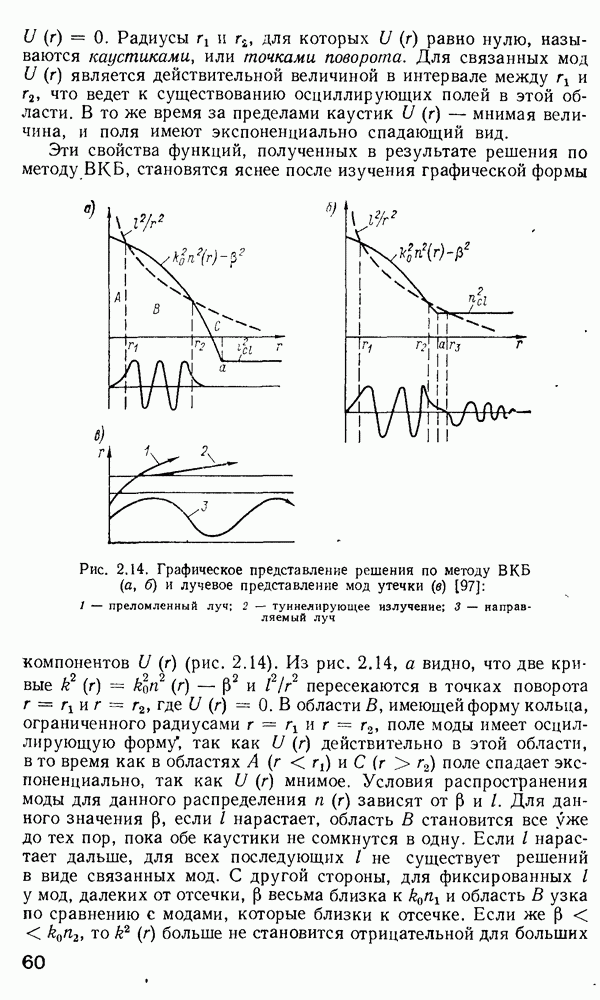
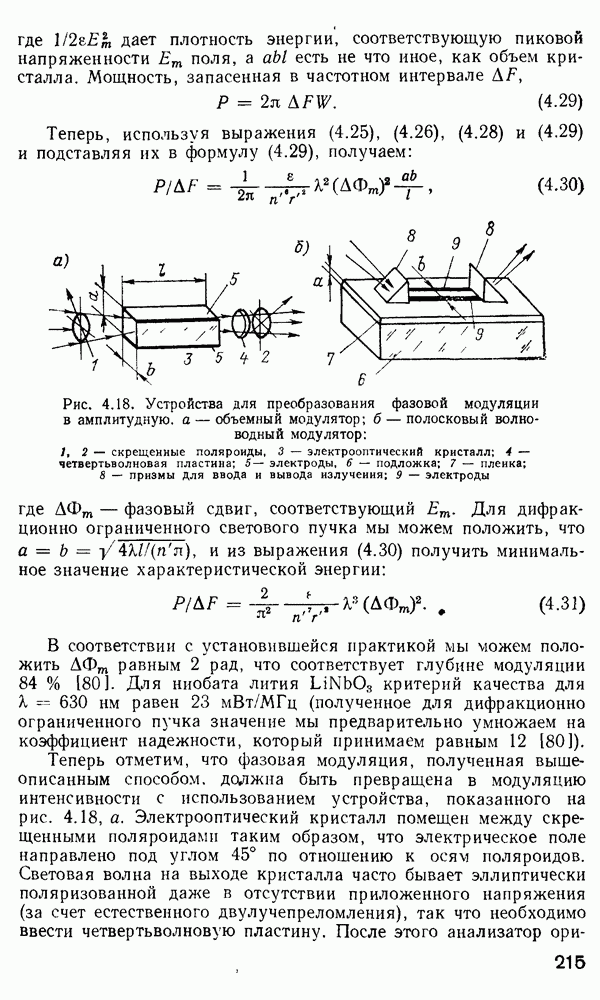
Рис. 4.18. Устройства для преобразования фазовой модуляции в амплитудную, а — объемный модулятор;  — полосковый волноводный модулятор: 1,2 — скрещенные поляроиды, 3 — электрооптический кристалл; 4 — четвертьволновая пластина; 5— электроды,
— полосковый волноводный модулятор: 1,2 — скрещенные поляроиды, 3 — электрооптический кристалл; 4 — четвертьволновая пластина; 5— электроды,  — подложка; 7 — пленка; 8 — призмы Для ввода и вывода излучения; 9 — электроды
— подложка; 7 — пленка; 8 — призмы Для ввода и вывода излучения; 9 — электроды
Для дифракционно ограниченного светового пучка мы можем положить, что  и из выражения (4.30) получить минимальное значение характеристической энергии:
и из выражения (4.30) получить минимальное значение характеристической энергии:

В соответствии с установившейся практикой мы можем положить  равным 2 рад, что соответствует глубине модуляции
равным 2 рад, что соответствует глубине модуляции  Для ниобата лития
Для ниобата лития  критерий качества для
критерий качества для  нм равен
нм равен  (полученное для дифракционно ограниченного пучка значение мы предварительно умножаем на коэффициент надежности, который принимаем равным 12 [80]).
(полученное для дифракционно ограниченного пучка значение мы предварительно умножаем на коэффициент надежности, который принимаем равным 12 [80]).
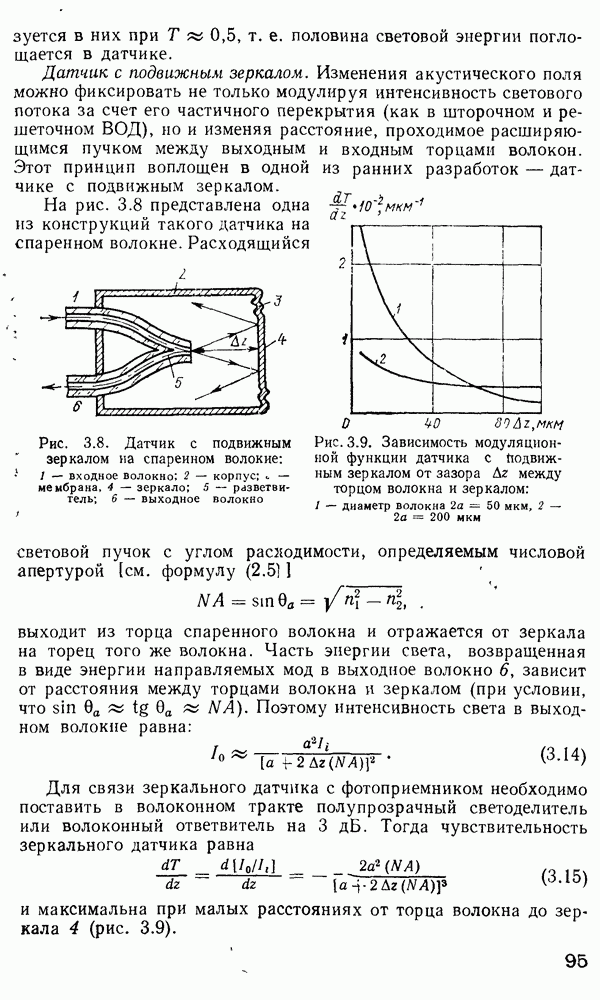
Теперь отметим, что фазовая модуляция, полученная вышеописанным способом, должна быть превращена в модуляцию интенсивности с использованием устройства, показанного на рис. 4.18, а. Электрооптический кристалл помещен между скрещенными поляроидами таким образом, что электрическое поле направлено под углом 45° по отношению к осям поляроидов. Световая волна на выходе кристалла часто бывает эллиптически поляризованной даже в отсутствии приложенного напряжения (за счет естественного двулучепреломления), так что необходимо ввести четвертьволновую пластину. После этого анализатор
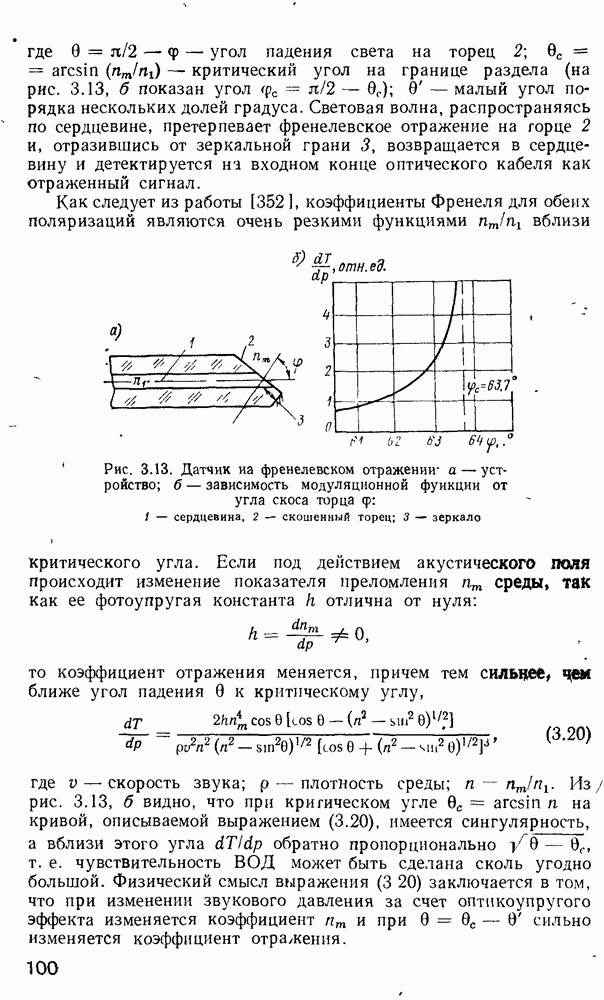
Когда  осуществляется дифракция Брэгга, а значит наблюдается только один порядок дифракции (кроме нулевого), как показано на рис. 4.19, б. Более того, в случае
осуществляется дифракция Брэгга, а значит наблюдается только один порядок дифракции (кроме нулевого), как показано на рис. 4.19, б. Более того, в случае  этот тип дифракции очень эффективен, что подтверждается формулами для интенсивностей дифрагированного излучения, отнесенного к интенсивности падающего излучения,
этот тип дифракции очень эффективен, что подтверждается формулами для интенсивностей дифрагированного излучения, отнесенного к интенсивности падающего излучения,

Очевидно, что мощность падающего излучения может быть полностью «перекачана» в дифрагированный пучок, в то время как в режиме Рамана — Ната максимальная дифракционная эффективность равна « в одном порядке. Важно помнить, что частота дифрагированного излучения сдвинута относительно частоты нулевого порядка (и падающего пучка) на
в одном порядке. Важно помнить, что частота дифрагированного излучения сдвинута относительно частоты нулевого порядка (и падающего пучка) на  где
где  — частота звуковой волны. Это наблюдение одинаково правомерно по отношению к обоим режимам дифракции. Частотный сдвиг в режиме дифракции Брэгга используется в датчиках акустических колебаний, волоконно-оптических гироскопах (см. пп. 3.3 и 3.6).
— частота звуковой волны. Это наблюдение одинаково правомерно по отношению к обоим режимам дифракции. Частотный сдвиг в режиме дифракции Брэгга используется в датчиках акустических колебаний, волоконно-оптических гироскопах (см. пп. 3.3 и 3.6).
Частотная характеристика брэгговского модулятора определяется, в частности, тем фактом, что угол Брэгга, а значит и дифракционная эффективность, зависят от длины волны  . Но наиболее неблагоприятным обстоятельством является то, что акустические волны распространяются относительно медленно, и требуется время
. Но наиболее неблагоприятным обстоятельством является то, что акустические волны распространяются относительно медленно, и требуется время  для прохождения через поперечное сечение светового пучка. Поэтому, если модулирующий сигнал меняется быстро, то происходит смазывание информации, переносимой на световой сигнал. Характеристическая энергия акусто-оптического модулятора может быть оценена в предположении, что частота не превышает предела
для прохождения через поперечное сечение светового пучка. Поэтому, если модулирующий сигнал меняется быстро, то происходит смазывание информации, переносимой на световой сигнал. Характеристическая энергия акусто-оптического модулятора может быть оценена в предположении, что частота не превышает предела  а также что акустическая мощность, как это следует из формул (4.34) и (4.26),
а также что акустическая мощность, как это следует из формул (4.34) и (4.26),

Итак, характеристическая энергия

Для дифракционно ограниченных пучков оптимальный режим работы достигается, когда диаметры светового и звукового пучков одинаковы. Тогда можно считать, что (см. работу [329])

Подставляя этот результат в формулу (4.38), получаем:

Далее, потребовав, чтобы диаметр акустического излучателя  оптимальную величину, т. е.
оптимальную величину, т. е.  мы окончательно получим, что
мы окончательно получим, что

Необходимо отметшь, что характеристические энергии объемных акустооптнческих модуляторов значительно ниже, чем электрооптических аналогов. Однако это преимущество часто сводится на нет теми практическими трудностями, которые возникают, например, на стадии электромеханического преобразования электрического сигнала в акустический на больших уровнях мощности и высоких частотах.
Возвращаясь к вопросу о ширине полосы акустооптнческих модуляторов, заметим, что так же, как и в случае электрооптических устройств, ширина полосы может быть расширена при переходе к тонкопленочным модуляторам. Схема такого прибора показана на рис. 4.19, в. Свет вводится с помощью призмы в планарный световод, расположенный на подложке.. Поверхностные акустические волны генерируются преобразователем. Важной чертой устройства является то, что поверхностный слой толщиной Л одновременно служит и как оптический волновод и как акустический, что повышает эффективность взаимодействия. Характеристическая энергия такого устройства может быть ориентировочно подсчитана по формуле (4.40), если разделить правую часть на величину Эта величина, называемая фактором перекрытия, учитывает тот факт, что неоднородная акустическая волна взаимодействует с неоднородной оптической волной [80]. Когда достигнута полная идентичность распределений акустического и оптического полей, то фактор перекрытия равен единице, а во всех остальных случаях он может быть только меньше [80]. На практике была достигнута характеристическая энергия 
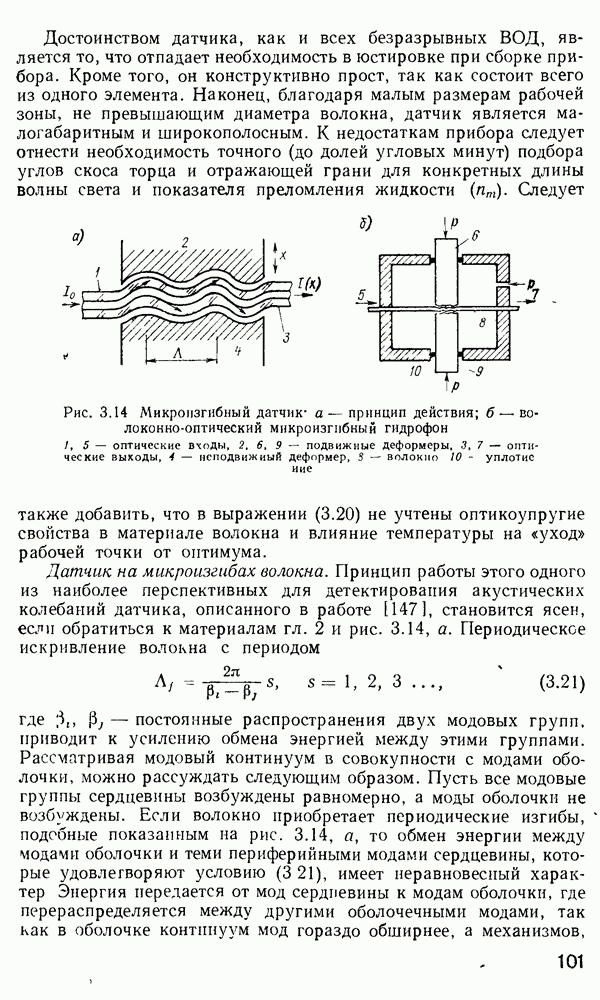
Наша следующая цель — анализ магнитооптических модуляторов на основе эффекта Фарадея. Эффект Фарадея можно упрощенно описать как вращение плоскости поляризации линейно-поляризованного света, происходящее под действием приложенного магнитного поля. Обычно магнитное поле используется для изменения направления или численного значения характеристик внутреннего поля магнитооптического материала. На практике объемный модулятор, подобный показанному на рис. 4.20, а, состоит из цилиндрического образца магнитооптического материала (например, железоиттриевого граната), который помещен в соленоид. Если вдоль цилиндрического образца проходит линейно-поляризованное световое излучение, то поляризация, а после прохождения анализатора — и интенсивность световой волны, окажутся функциями приложенного магнитного поля.
В гиромагнитной среде, в которой имеется поперечное магнитное поле, достигшее насыщения, намагничивание, которое создается продольным магнитным полем [129],

где  — напряженность начального магнитного поля;
— напряженность начального магнитного поля;  — напряженность продольного магнитного поля, прикладываемого к образцу;
— напряженность продольного магнитного поля, прикладываемого к образцу;  — магнитная восприимчивость;
— магнитная восприимчивость;  — намагниченность в состоянии насыщения.
— намагниченность в состоянии насыщения.

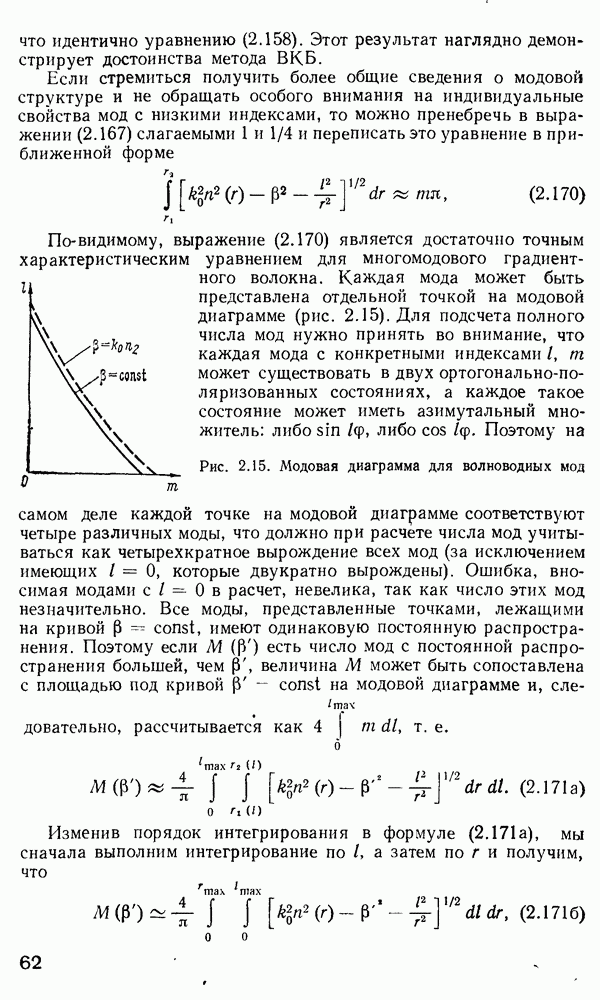
Рис. 4.20. Объемный (а) и планарный (5) магнитооптические модуляторы: 1 — магнитооптический образец; 2 — соленоид; 3 — поляроид; 4 — подложка; 5 — пленка; 6 — электроды типа «серпантин»; 7 — призмы ввода и вывода излучения
Угол фарадеевского вращения теперь может быть выражен как

где  угол вращения на единицу длины образца, соответствующий насыщенной намагниченности;
угол вращения на единицу длины образца, соответствующий насыщенной намагниченности;  — длина образца [129]. Используя формулы (4.42) и (4.43), можно оценить магнитную энергию, запасенную в катушке, используя формулу, аналогичную выражению (4.28),
— длина образца [129]. Используя формулы (4.42) и (4.43), можно оценить магнитную энергию, запасенную в катушке, используя формулу, аналогичную выражению (4.28),

где  — магнитная восприимчивость свободного пространства, а множитель в середине представляет собой объем цилиндрического стержня. Выражение для характеристической энергии может быть нолучено с привлечением формулы (4.29):
— магнитная восприимчивость свободного пространства, а множитель в середине представляет собой объем цилиндрического стержня. Выражение для характеристической энергии может быть нолучено с привлечением формулы (4.29):

Если теперь мы положим, что  а площадь поперечника ячейки приравняем к площади сечения дифракционно-ограниченного пучка
а площадь поперечника ячейки приравняем к площади сечения дифракционно-ограниченного пучка  то получим:
то получим:

В формулах (2.39) и  измеряется в тесла, а
измеряется в тесла, а  в радианах на метр.
в радианах на метр.
Можно сделать вывод, что минимальная характеристическая энергия пропорциональна  в то время как из выражений (4.31) и (4.41) следует, что она пропорциональна
в то время как из выражений (4.31) и (4.41) следует, что она пропорциональна 
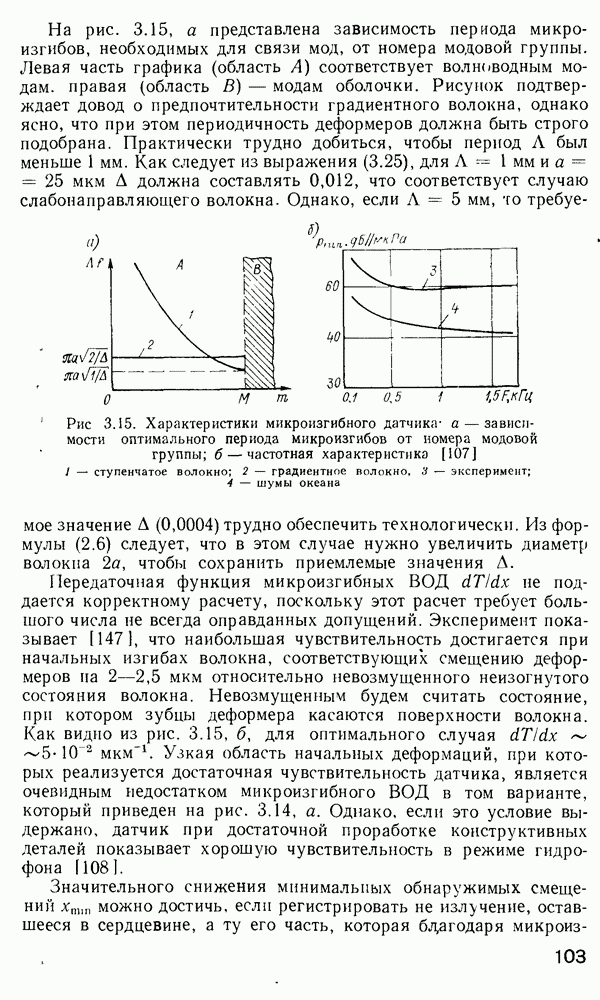
Тонкопленочный вариант магнитооптического модулятора показан на рис. 4.20, б. Направление намагниченности выбрано под некоторым углом  по отношению к вектору распространения света. Магнитное поле создается структурой типа «серпантин», имеющей период
по отношению к вектору распространения света. Магнитное поле создается структурой типа «серпантин», имеющей период  Этот период выбран таким образом, чтобы соответствующая пространственная частота
Этот период выбран таким образом, чтобы соответствующая пространственная частота

где  — соответственно постоянные распространения двух соседних
— соответственно постоянные распространения двух соседних  и ТМ-мод. В результате вектор магнитного поля в направлении распространения света имеет компонент, меняющийся с периодичностью
и ТМ-мод. В результате вектор магнитного поля в направлении распространения света имеет компонент, меняющийся с периодичностью  что обеспечивает сильный эффект преобразования мод
что обеспечивает сильный эффект преобразования мод  Так как рутил имеет сильное двулучепреломление,
Так как рутил имеет сильное двулучепреломление,  и
и  -моды распространяются под разными углами (например,
-моды распространяются под разными углами (например,  и
и  -моды разделены углом около 20°). Поэтому любая модуляция тока намагничения приводит к изменениям мощности, переносимой данной модой.
-моды разделены углом около 20°). Поэтому любая модуляция тока намагничения приводит к изменениям мощности, переносимой данной модой.
Можно оценить характеристическую энергию такого модулятора, если заменить площадь поперечного сечения  на
на  а также предположить, что а не зависит от
а также предположить, что а не зависит от  в то время как для
в то время как для  сохраняется требование дифракционной ограниченности, т. е.
сохраняется требование дифракционной ограниченности, т. е.  Тогда получается следующий результат:
Тогда получается следующий результат:

На практике, как следует из работы [80], были получены значения порядка  что не является сколько-нибудь значительным шагом вперед по сравнению с объемными устройствами.
что не является сколько-нибудь значительным шагом вперед по сравнению с объемными устройствами.
Наиболее серьезной проблемой при создании магнитооптических модуляторов является то, что у большинства пригодных для использования материалов коэффициент поглощения весьма велик в диапазоне видимого и ближнего инфракрасного излучения. Однако на длинах волн 1,3 мкм и 1,55 мкм, которые перспективны для систем оптической связи, эти ограничения мечее серьезны. Следовательно, в ряде случаев применение этих приборов может оказаться достаточно эффективным.
Рассмотрим ряд других эффектов, которые также представляют интерес с точки зрения модуляции света.
В общем случае изменение эллипсоида индексов под действием внешнего электрического поля является более сложным, чем это описывается формулой эффекта Поккельса [34]. Мы можем учесть
этот факт, если запишем формулу для показателя преломления в виде ряда

или

где Е — напряженность приложенного электрического поля;  напряженность внутреннего электрического ноля кристалла (которая, например, приводит к собственному двулучепреломлению);
напряженность внутреннего электрического ноля кристалла (которая, например, приводит к собственному двулучепреломлению);  — константы. Для некоторых типов центросимметричных кристаллов, таких как
— константы. Для некоторых типов центросимметричных кристаллов, таких как  изменение показателя преломления хорошо описывается именно членом второго порядка относительно поля. Это явление носит название эффекта Керра и может быть использовано для бинарной модуляции сигналов (в режиме «да» — «нет»),
изменение показателя преломления хорошо описывается именно членом второго порядка относительно поля. Это явление носит название эффекта Керра и может быть использовано для бинарной модуляции сигналов (в режиме «да» — «нет»),
У некоторых типов оптических керамик (чаще всего  с добавками
с добавками  так называемой ЦТСЛ-керамики) анизотропия электрооптических свойств обусловлена существованием доменных областей с выраженными ссгнетоэлектрическими свойствами. В кристаллах, где границы доменов, как правило, хорошо определены, внешнее поле может быть использовано для ориентации доменов. В керамиках влияние электрического поля сказывается также на размерах и числе доменов, что приводит к большему разнообразию электрооптических свойств керамик по сравнению с кристаллами. Поэтому в некоторых видах ЦТСЛ-керамик электрооптический эффект (по типу зависимости от электрического поля, а не из-за сходства физической природы) также может быть классифицирован как эффект Керра [250].
так называемой ЦТСЛ-керамики) анизотропия электрооптических свойств обусловлена существованием доменных областей с выраженными ссгнетоэлектрическими свойствами. В кристаллах, где границы доменов, как правило, хорошо определены, внешнее поле может быть использовано для ориентации доменов. В керамиках влияние электрического поля сказывается также на размерах и числе доменов, что приводит к большему разнообразию электрооптических свойств керамик по сравнению с кристаллами. Поэтому в некоторых видах ЦТСЛ-керамик электрооптический эффект (по типу зависимости от электрического поля, а не из-за сходства физической природы) также может быть классифицирован как эффект Керра [250].
У крупнозернистых керамик (с размером зерен порядка 10 мкм) наблюдается эффект динамического рассеяния, который редко встречается в твердых телах, его чаще связывают с жидкими кристаллами. Под действием внешнего поля в такой керамике возникают значительные изменения размеров и ориентации сегнетоэлектрических доменов. Благодаря сильному двулучепреломлению и большому показателю преломления каждого домена усиливается процесс рассеяния на стенках доменов, особенно когда размеры домена достигают размеров зерен, т. е. сравнимых с длиной волны света.
За исключением динамического рассеяния, все ранее рассмотренные процессы основаны на эффекте фазовой модуляции. Конечно, гораздо удобнее было бы иметь модулятор, позволяющий непосредственно влиять на интенсивность проходящего света, чтобы упростить оптическую схему устройства, исключив из нее поляризатор, анализатор и т. д. С этой точки зрения весьма интересен эффект Франца — Келдыша, который наблюдается в некоторых полупроводниках —  Эффект
Эффект
заключается в том, что при приложении электрического поля достаточной напряженности возникает сдвиг края полосы поглощения материала, Поэтому можно использовать внешнее электрическое поле в качестве фактора, влияющего на поглощение, а стало быть, и на интенсивность проходящего света.
В некоторых материалах (чаще всего в сегнетоэлектриках) из-за неизбежно происходящего на границе твердого тела резкого скачка потенциала, возникают так называемые поверхностные слои, или слои Кенцига [7], которые имеют показатель преломления, отличный от показателя преломления в массе материала вне этих слоев. Скачок потенциала наблюдается на глубинах, определяемых параметром экранирования, т. е. способностью твердого тела к перестройке внутреннего распределения объемного заряда. Наличие слоев Кенцига и упомянутая разность показателей преломления позволяет надеяться, что слои могут быть использованы в качестве маломодовых световодов, модовым составом которых можно было бы управлять с помощью внешнего электрического поля.
Волоконно-оптические модуляторы открывают новые возможности построения волоконных систем передачи, особенно локальных сетей, позволяя осуществлять многократный безразрывный ввод информации в световой сигнал, становится возможным создание датчиков, интегрированных на волокне, которые как ясно из гл. 3, имеют улучшенные характеристики и более технологичны.
Хотя в принципе считается, что модулятор любого типа может быть изготовлен целиком в волоконном исполнении, на деле это далеко не так. Все рассмотренные выше электрооптическне эффекты играют существенную роль только в некоторых материалах, стекла, из которых изготавливают обычные волоконные световоды, к ним не относятся. Определенные возможности связаны с монокристаллическими волокнами [115], однако какие-либо конкретные прогнозы по поводу создания устройств на их основе преждевременны.
Модуляция состояния поляризации световой волны, распространяющейся в волокне, под действием магнитного поля в результате эффекта Фарадея, используется в датчиках магнитного поля и электрического тока (см. п. 3.7). Аналогичным образом могут быть построены и волоконно-оптические модуляторы, однако поскольку кварцевые стекла характеризуются низким значением постоянной Верде, эти устройства слишком громоздки. Таким образом, и здесь необходимы волоконные световоды, изготовленные из специальных материалов с высоким значением постоянной Верде.
В существующих конструкциях волоконных модуляторов используются фотоупругий эффект и взаимодействие мод световода с акустическими волнами. Первая конструкция фазового модулятора на многомодовом или одномодовом волокне была предложена
в 1974 г. [134], схематически она изображена на рис. 4.21, а. Модулятор представляет собой катушку из нескольких витков волокна, намотанных на пьезоэлектрический полый цилиндр. Под действием электрического напряжения, приложенного к контактам, нанесенным на внутреннюю и внешнюю поверхности цилиндра, его диаметр меняется, происходит модуляция фазы световой волны за счет удлинения волокна и фотоупругого эффекта (изменения показателя преломления). Набег фазы  для моды с номером
для моды с номером  определяется выражением
определяется выражением

где  — эффективный показатель преломления моды с номером
— эффективный показатель преломления моды с номером  — число витков; V — электрическое напряжение, приложенное к пьезокерамике;
— число витков; V — электрическое напряжение, приложенное к пьезокерамике;  — пьезоэлектрический коэффициент в направлении приложенного напряжения;
— пьезоэлектрический коэффициент в направлении приложенного напряжения;  — компоненты тензора фотоупругости;
— компоненты тензора фотоупругости;  — коэффициент Пуассона.
— коэффициент Пуассона.

Рис. 4.21. Волоконные фазовые модуляторы: а — на пьезоэлектрическом цилиндре [134]; б — с осесимметричным возбуждением [193]; 1 — пьезоэлектрический цилиндр; 2,3 — волоконные световоды; 4 — пьезоэлектрический полуцилиндр
Для кварцевых световодов  Из-за различия
Из-за различия  фазовые набеги для различных мод различны, однако максимальный относительный разброс составляет
фазовые набеги для различных мод различны, однако максимальный относительный разброс составляет  т. е. обычно не превышает
т. е. обычно не превышает  . При использовании реально существующих волокон характеристики модулятора таковы, что
. При использовании реально существующих волокон характеристики модулятора таковы, что  рад/В виток. Этого вполне достаточно для использования волоконных модуляторов такой конструкции в фазовых ВОД. Рабочая полоса частот определяется размерами пьезоэлектрического цилиндра, верхняя граничная частота не превышает обычно 104—106 Гц. Существенным недостатком описанной конструкции является то, что в процессе модуляции появляется двулучепреломление в волоконном световоде, вызванное его деформацией.
рад/В виток. Этого вполне достаточно для использования волоконных модуляторов такой конструкции в фазовых ВОД. Рабочая полоса частот определяется размерами пьезоэлектрического цилиндра, верхняя граничная частота не превышает обычно 104—106 Гц. Существенным недостатком описанной конструкции является то, что в процессе модуляции появляется двулучепреломление в волоконном световоде, вызванное его деформацией.
Этого недостатка лишена конструкция, изображенная на рис. 4.21, б. Пьезопреобразователь, выполненный из двух полуцилиндров, индуцирует акустическое поле, сфокусированное на оси световода, так что напряжения, возникающие в волокне, осесимметричны и двулучепреломление отсутствует [219]. Близка к описанной выше конструкция волоконно-оптического фазового модулятора, представленная на рис. 4.22, а. Участок волоконного
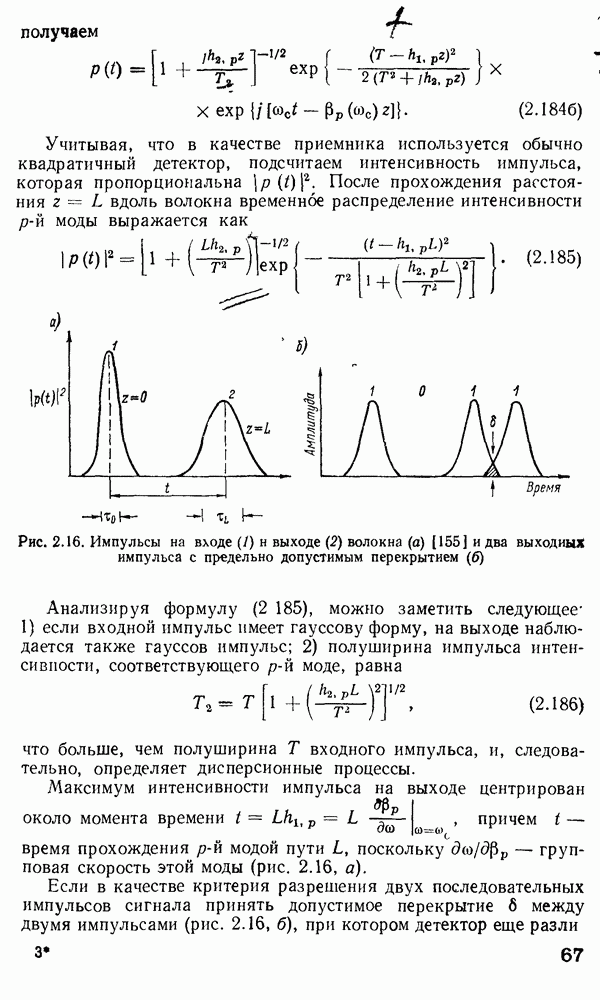
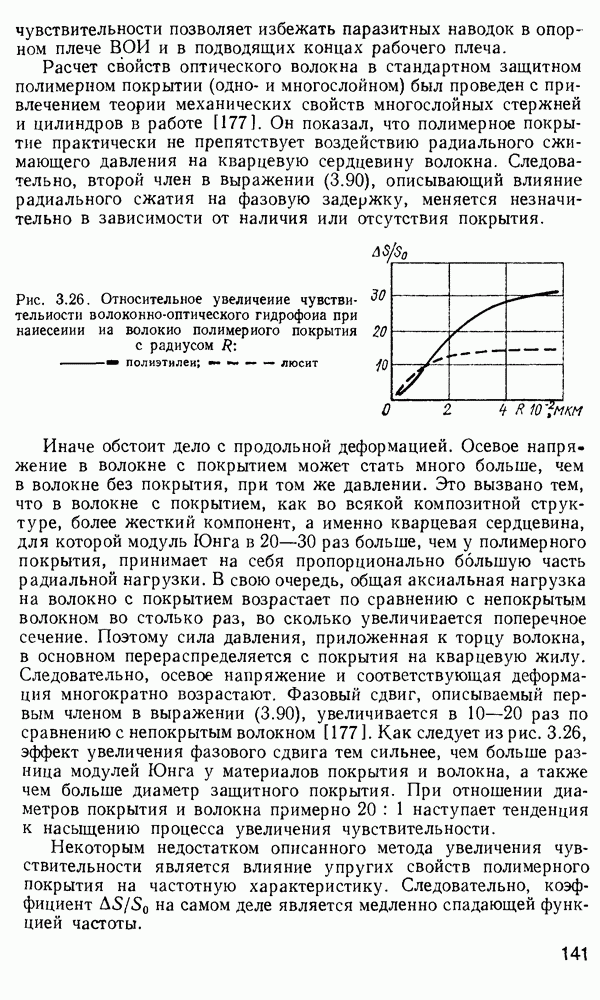
световода покрыт оболочкой из радиально-поляризованного пьезоактивного полимера. Модулятор достаточно эффективно работает в полосе частот  МГц, его частотная характеристика изображена на рис. 4.22, б [193]. Характеристика имеет явно выраженные резонансные пики, соответствующие продольному резонансу, радиальным резонансам полимерной оболочки и самого волокна.
МГц, его частотная характеристика изображена на рис. 4.22, б [193]. Характеристика имеет явно выраженные резонансные пики, соответствующие продольному резонансу, радиальным резонансам полимерной оболочки и самого волокна.
Интересным представляется волоконно-оптическое устройство, по своим функциям аналогичное акустооптической ячейке Брэгга, сдвигающей световую частоту. Конструкция такого модулятора изображена на рис. 4.23, а [341].

Рис. 4.22. Волоконный фазовый модулятор с пьезоактивным полимером [193]: а — конструкция;  — частотная характеристика; 1 — волокно; 2 — металлическое покрытие; 3 — оболочка из пьезоактивного полимера, 4 — аксиальный (продольный) резонанс; 5 — радиальный резонанс полимерной оболочки; 6 — радиальный резонанс волокна
— частотная характеристика; 1 — волокно; 2 — металлическое покрытие; 3 — оболочка из пьезоактивного полимера, 4 — аксиальный (продольный) резонанс; 5 — радиальный резонанс полимерной оболочки; 6 — радиальный резонанс волокна
В одномодовом волокне с двулучепреломлением (световод, сохраняющий поляризацию) возбуждается ультразвуковая волна так, что угол между фронтом волны и осью волокна составляет величину 0, такую что

где  — длина акустической волны;
— длина акустической волны;  — длина биений между модами с ортогональными состояниями поляризации. Условие (4.51) означает, что период изменений показателя преломления вдоль оси световода, обусловленный акустическим воздействием, совпадает с длиной биений. В результате взаимодействия световой волны с движущейся структурой с периодом
— длина биений между модами с ортогональными состояниями поляризации. Условие (4.51) означает, что период изменений показателя преломления вдоль оси световода, обусловленный акустическим воздействием, совпадает с длиной биений. В результате взаимодействия световой волны с движущейся структурой с периодом  происходит эффективное преобразование мод. Если в световоде распространяется «быстрая» мода, поляризованная вдоль малой оси эллипса показателя преломления двулучепреломляющего волокна, она преобразуется в ортогонально-поляризованную «медленную» моду, при этом происходит сдвиг световой частоты
происходит эффективное преобразование мод. Если в световоде распространяется «быстрая» мода, поляризованная вдоль малой оси эллипса показателя преломления двулучепреломляющего волокна, она преобразуется в ортогонально-поляризованную «медленную» моду, при этом происходит сдвиг световой частоты  она увеличивается на величину
она увеличивается на величину  — частоту акустических колебаний (рис. 4.23, б). Если же возбуждена была «медленная» мода, то ее преобразование сопровождается уменьшением частоты на величину
— частоту акустических колебаний (рис. 4.23, б). Если же возбуждена была «медленная» мода, то ее преобразование сопровождается уменьшением частоты на величину  В работе
В работе  такое устройство было реализовано на волоконном световоде с длиной биений
такое устройство было реализовано на волоконном световоде с длиной биений  мм на длине волны 0,63 мкм, угол
мм на длине волны 0,63 мкм, угол 
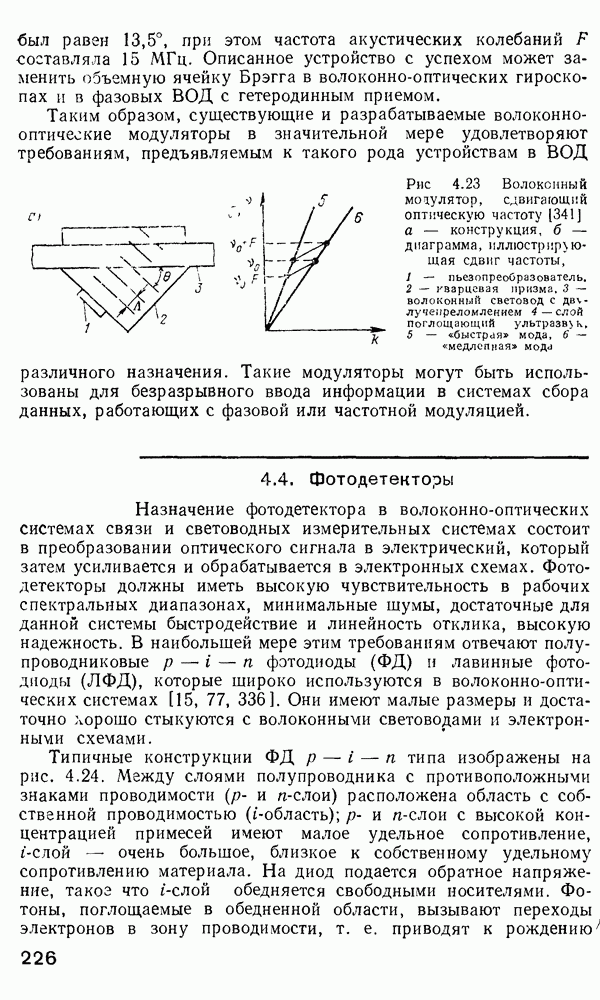
был равен 13,5°, при этом частота акустических колебаний  составляла 15 МГц. Описанное устройство с успехом может заменить объемную ячейку Брэгга в волоконно-оптических гироскопах и в фазовых ВОД с гетеродинным приемом.
составляла 15 МГц. Описанное устройство с успехом может заменить объемную ячейку Брэгга в волоконно-оптических гироскопах и в фазовых ВОД с гетеродинным приемом.
Таким образом, существующие и разрабатываемые волоконно-оптические модуляторы в значительной мере удовлетворяют требованиям, предъявляемым к такого рода устройствам в ВОД различного назначения.

Рис. 4.23 Волоконный модулятор, сдвигающий оптическую частоту [341] а — конструкция, б — диаграмма, иллюстрирующая сдвиг частоты, 1 — пьезопреобразователь. 2 — кварцевая призма, 3 — волоконный световод с двулучепреломлением 4 - слой поглощающий ультразвук, 5 — «быстрая» мода, 6 — «медленная» мода
Такие модуляторы могут быть использованы для безразрывного ввода информации в системах сбора данных, работающих с фазовой или частотной модуляцией.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
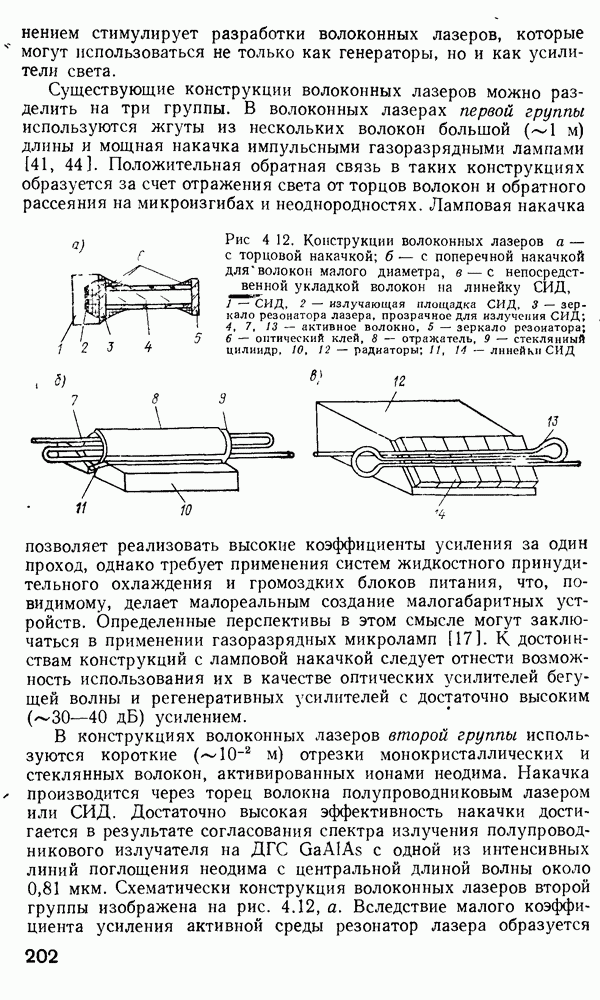
- Волоконные лазеры.
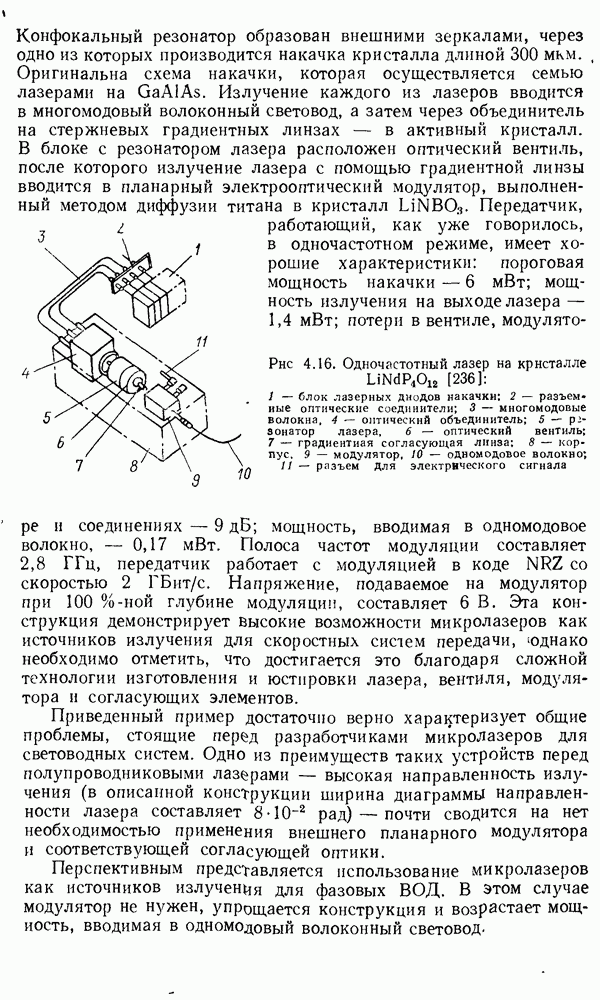
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
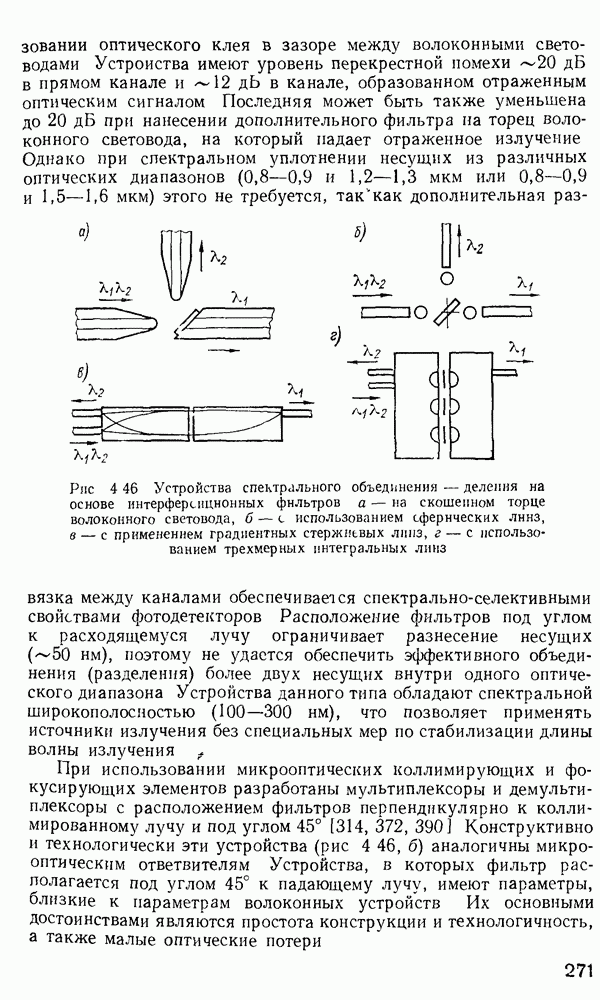
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
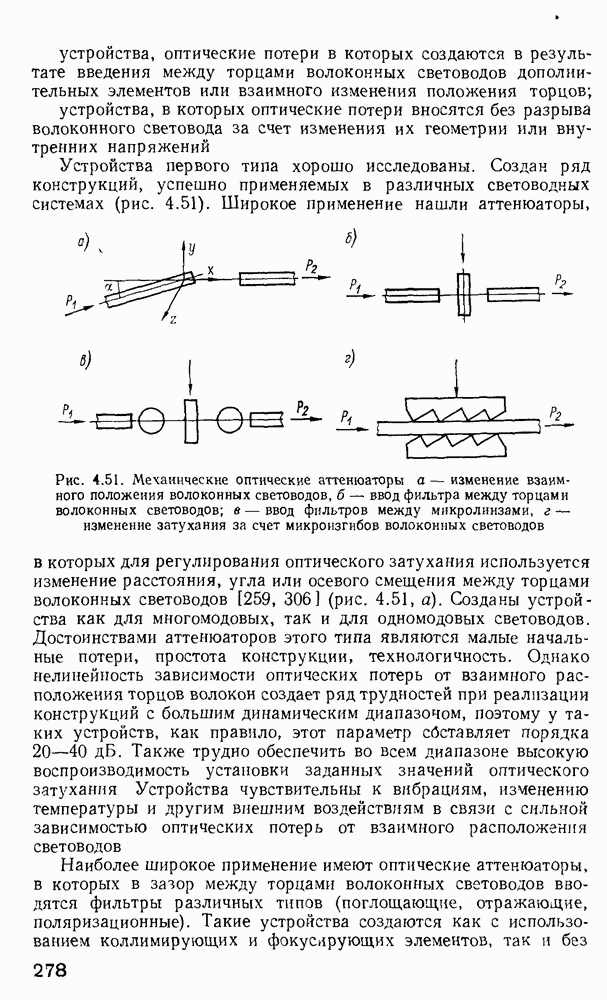
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
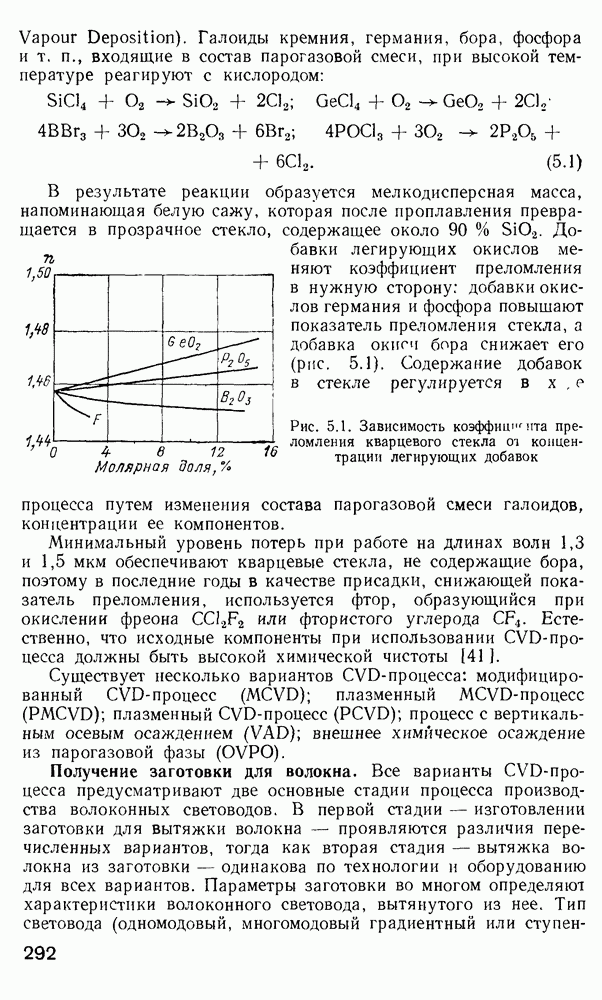
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ