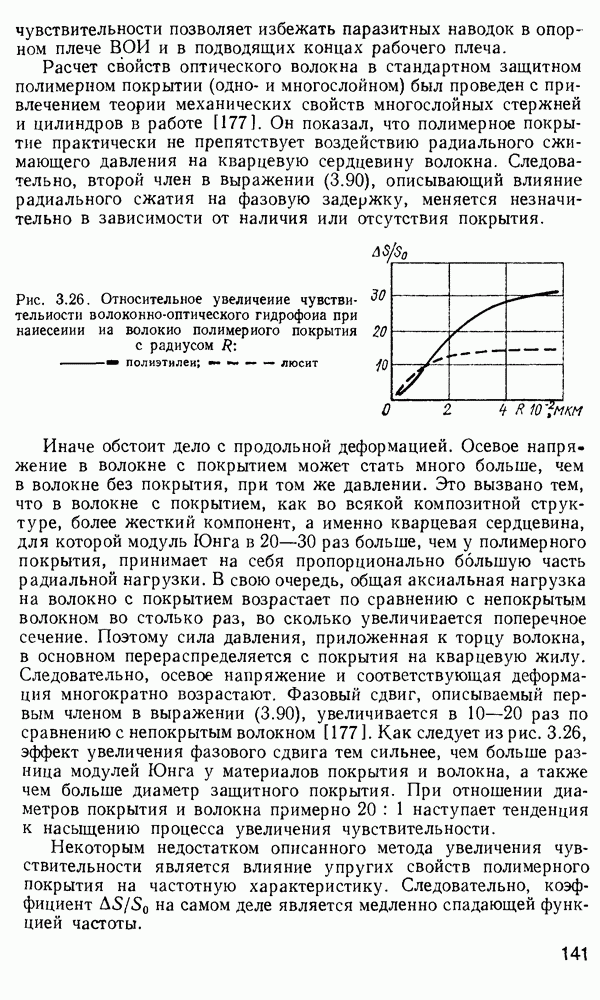
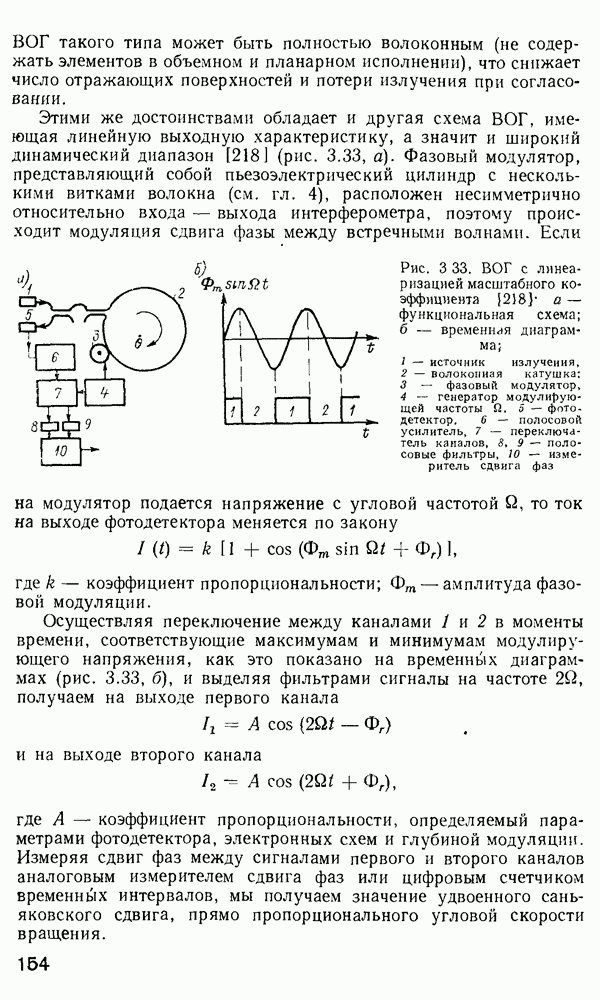
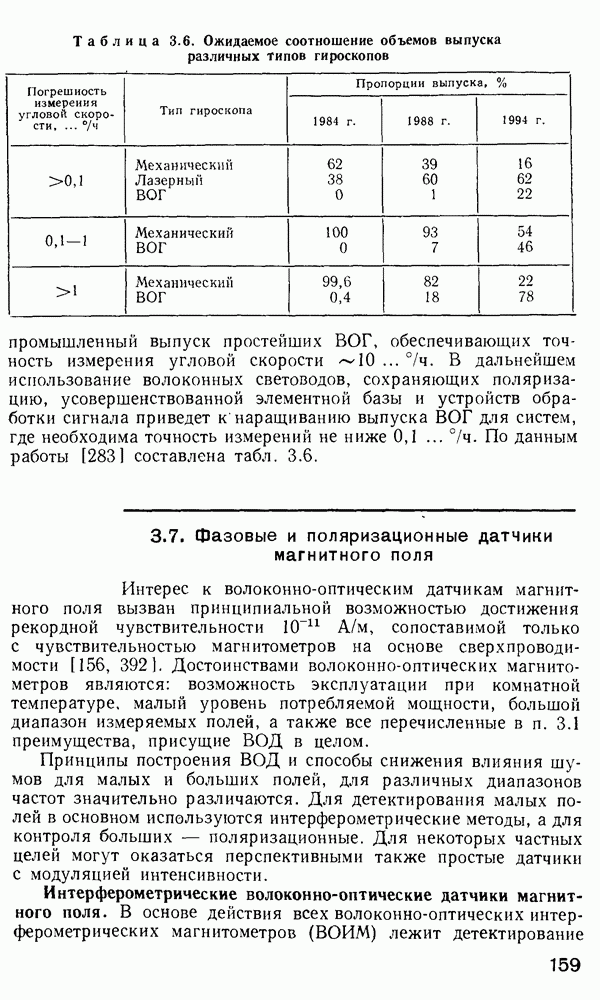
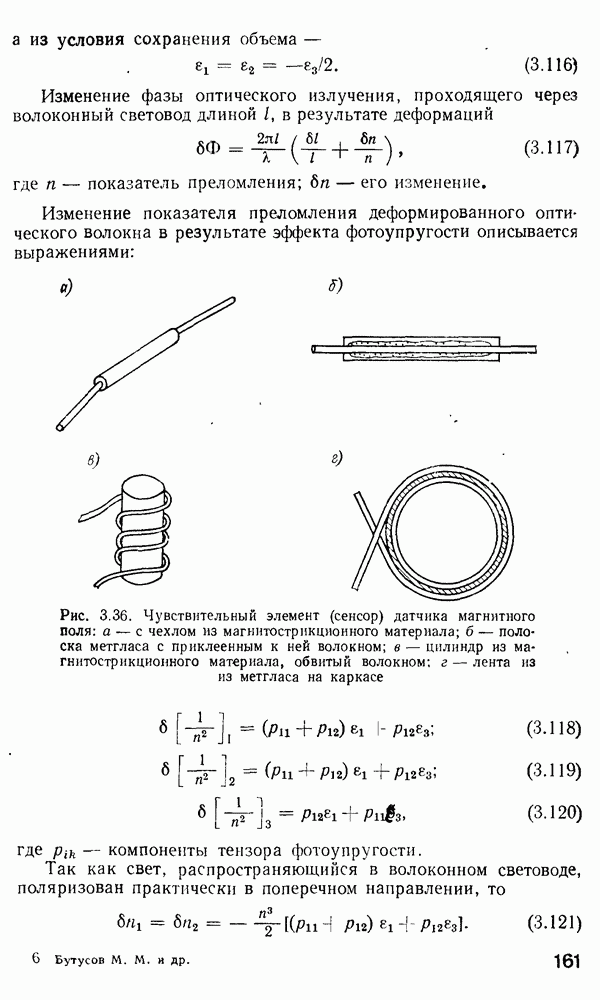
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
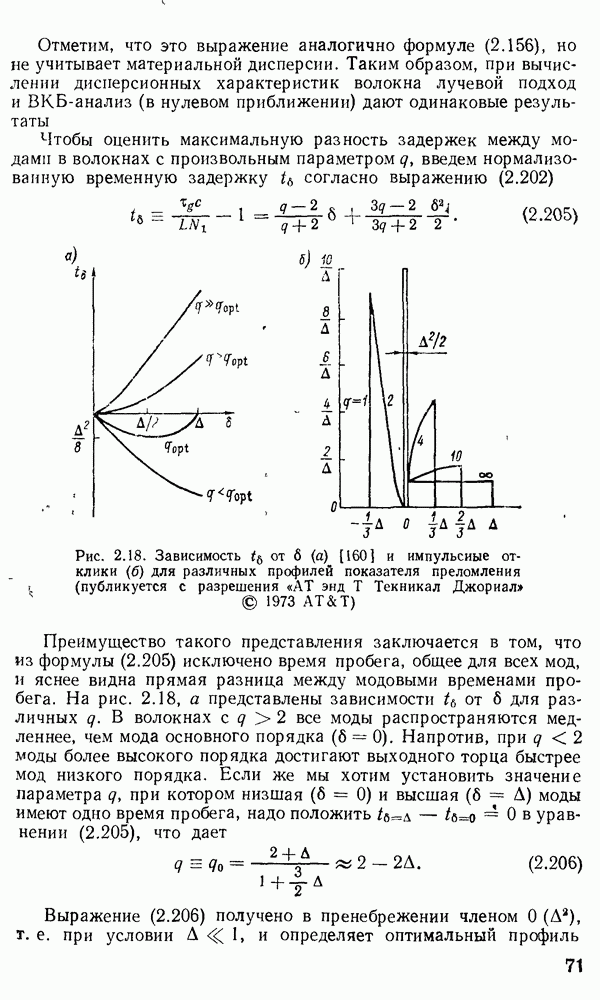
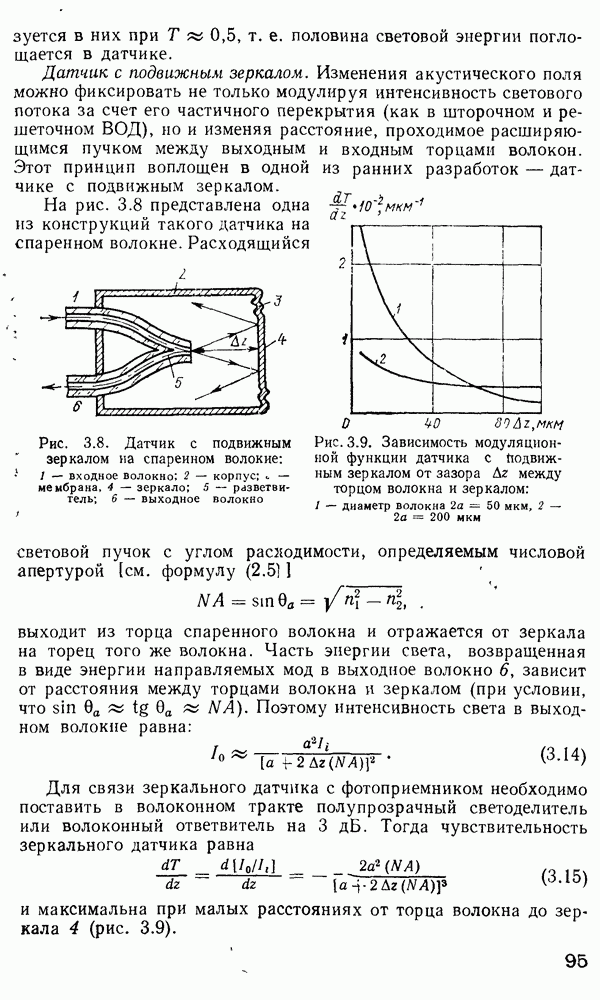
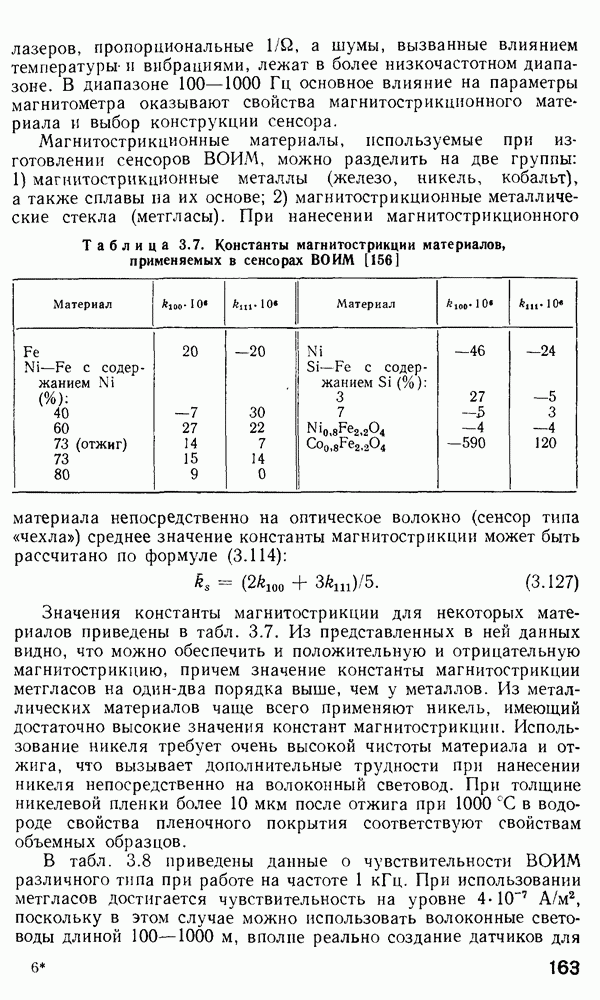
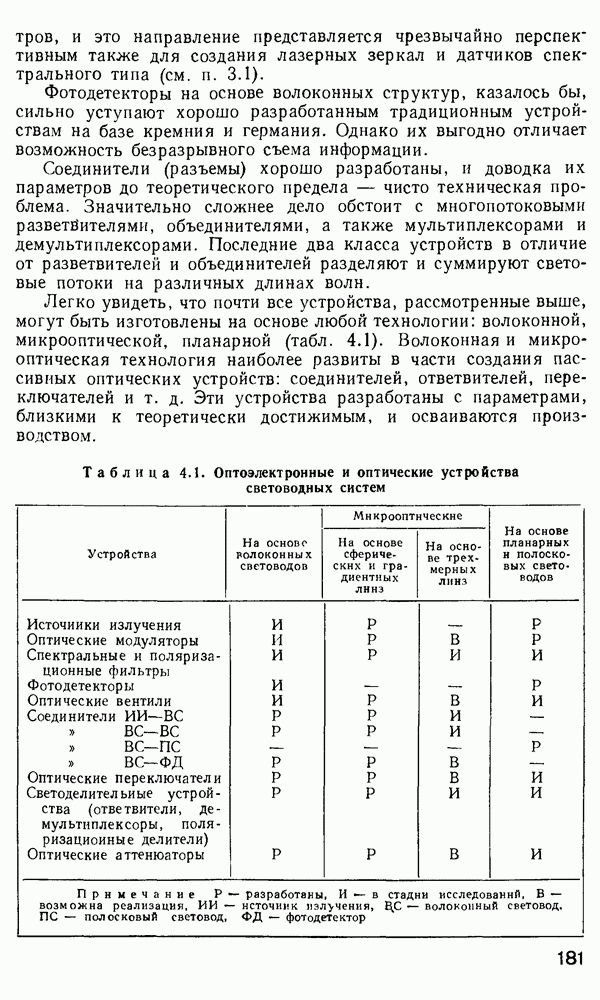
Безразрывные акустические ВОД с модуляцией интенсивности.
Обязательным компонентом описанных выше ВОД ФВ является пара оптических волокон, между которыми происходит обмен энергией, причем степень энергообмена модулируется акустическим полем. Серьезной проблемой при серийном производстве таких датчиков является необходимость точной взаимной юстировки волокон. Безразрывные ВОД свободны от этого недостатка. Датчик на френелевском отражении. Этот датчик, описанный в работе [311], состоит из одного одномодового волокна со скошенным торцом (рис. 3.13, а). Торец 2 сполирован под таким углом  что при определенном показателе преломления
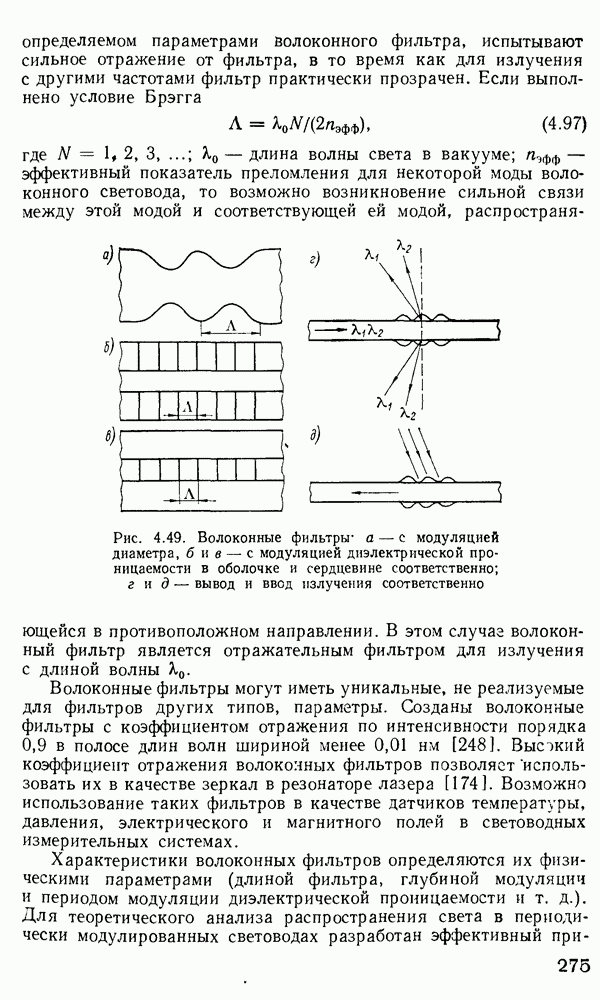
что при определенном показателе преломления  среды, окружающей датчик, выполняется соотношение
среды, окружающей датчик, выполняется соотношение

где  угол падения света на торец
угол падения света на торец  критический угол на границе раздела (на рис.
критический угол на границе раздела (на рис.  показан угол
показан угол  малый угол порядка нескольких долей градуса. Световая волна, распространяясь по сердцевине, претерпевает френелевское отражение на торце 2 и, отразившись от зеркальной грани 3, возвращается в сердцевину и детектируется на входном конце оптического кабеля как отраженный сигнал.
малый угол порядка нескольких долей градуса. Световая волна, распространяясь по сердцевине, претерпевает френелевское отражение на торце 2 и, отразившись от зеркальной грани 3, возвращается в сердцевину и детектируется на входном конце оптического кабеля как отраженный сигнал.
Как следует из работы  коэффициенты Френеля для обеих поляризаций являются очень резкими функциями
коэффициенты Френеля для обеих поляризаций являются очень резкими функциями  вблизи критического угла.
вблизи критического угла.

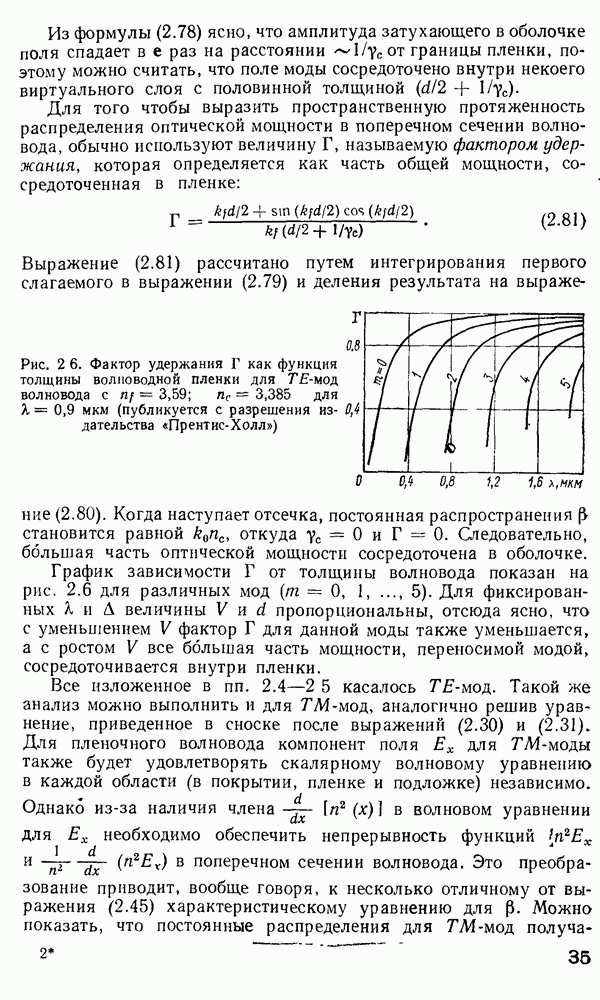
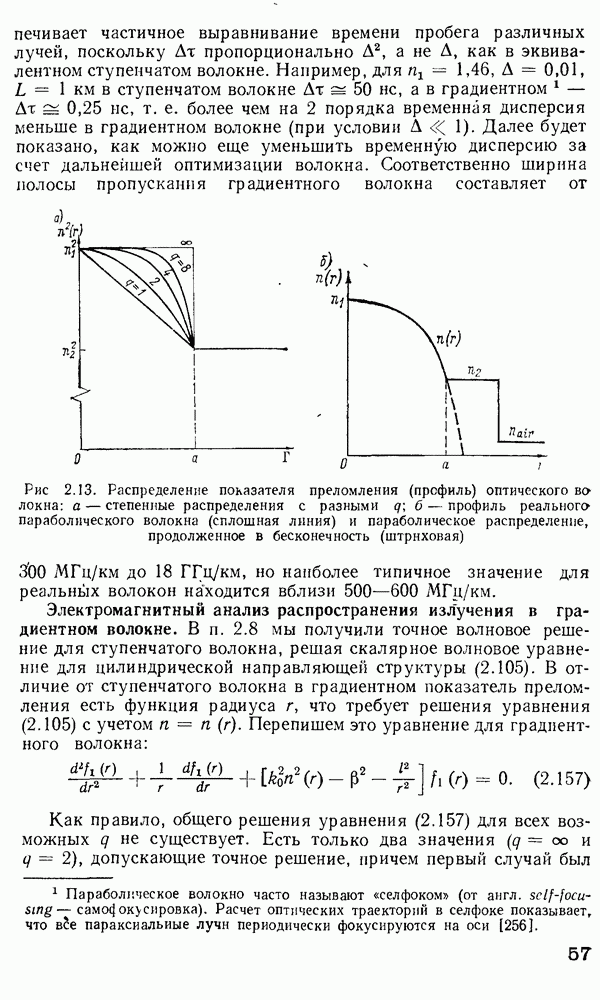
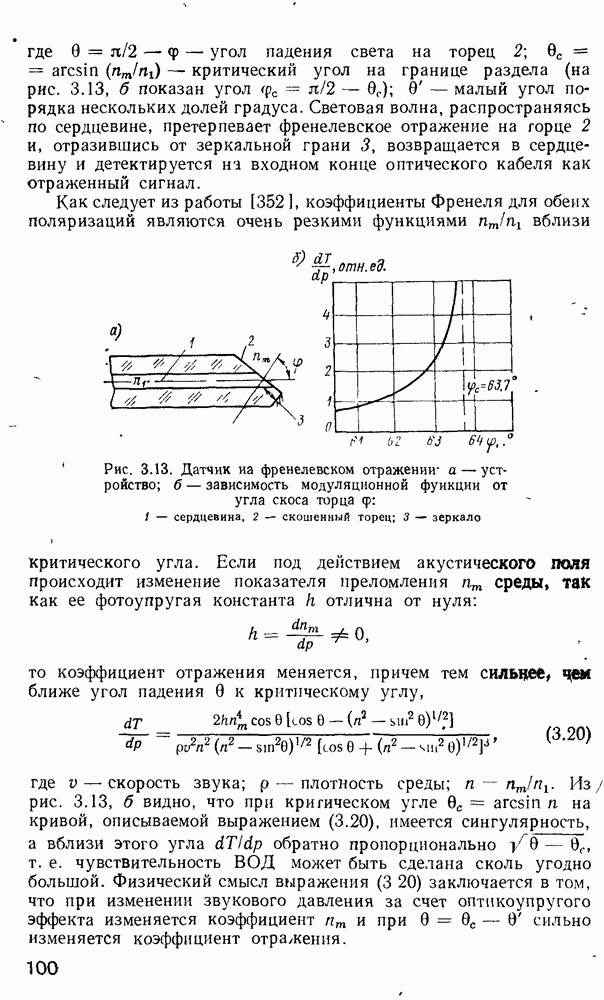
Рис. 3.13. Датчик на френелевском отражении: а — устройство; б — зависимость модуляционной функции от угла скоса торца  : 1 — сердцевина, 2 — скошенный торец; 3 — зеркало
: 1 — сердцевина, 2 — скошенный торец; 3 — зеркало
Если под действием акустического поля происходит изменение показателя преломления  среды, так как ее фотоупругая константа
среды, так как ее фотоупругая константа  отлична от нуля;
отлична от нуля;

то коэффициент отражения меняется, причем тем сильнее, чем ближе угол падения 0 к критическому углу,

где  — скорость звука;
— скорость звука;  — плотность среды;
— плотность среды;  Из
Из  рис. 3.13, б видно, что при критическом угле
рис. 3.13, б видно, что при критическом угле  на кривой, описываемой выражением (3.20), имеется сингулярность, а вблизи этого угла
на кривой, описываемой выражением (3.20), имеется сингулярность, а вблизи этого угла  обратно пропорционально
обратно пропорционально  т. е. чувствительность ВОД может быть сделана сколь угодно большой. Физический смысл выражения (3 20) заключается в том, что при изменении звукового давления за счет оптикоупругого эффекта изменяется коэффициент
т. е. чувствительность ВОД может быть сделана сколь угодно большой. Физический смысл выражения (3 20) заключается в том, что при изменении звукового давления за счет оптикоупругого эффекта изменяется коэффициент  и при
и при  сильно изменяется коэффициент отражения.
сильно изменяется коэффициент отражения.
Достоинством датчика, как и всех безразрывных ВОД, является то, что отпадает необходимость в юстировке при сборке прибора. Кроме того, он конструктивно прост, так как состоит всего из одного элемента. Наконец, благодаря малым размерам рабочей зоны, не превышающим диаметра волокна, датчик является малогабаритным и широкополосным. К недостаткам прибора следует отнести необходимость точного (до долей угловых минут) подбора углов скоса торца и отражающей грани для конкретных длины волны света и показателя преломления жидкости 

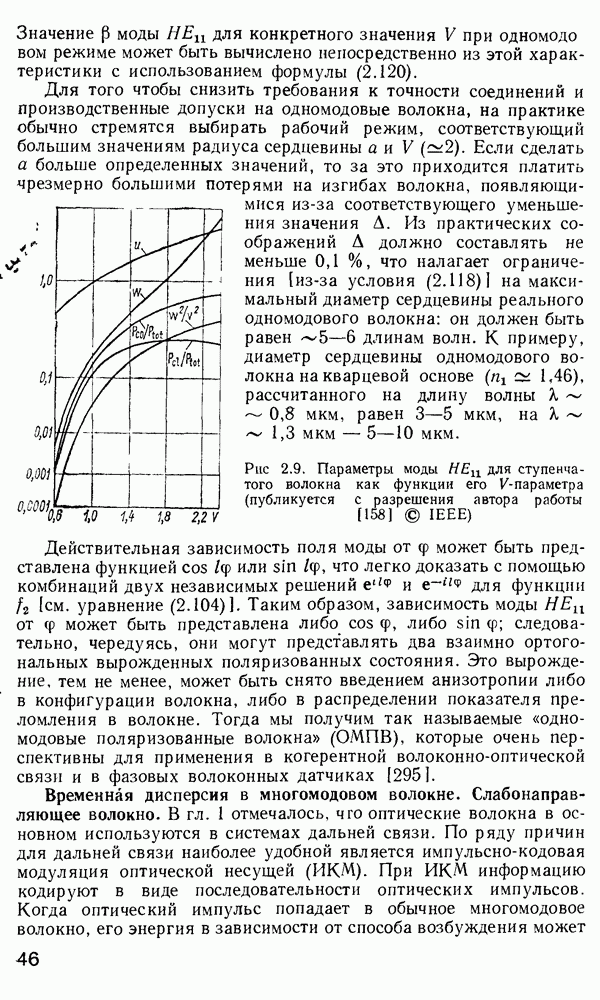
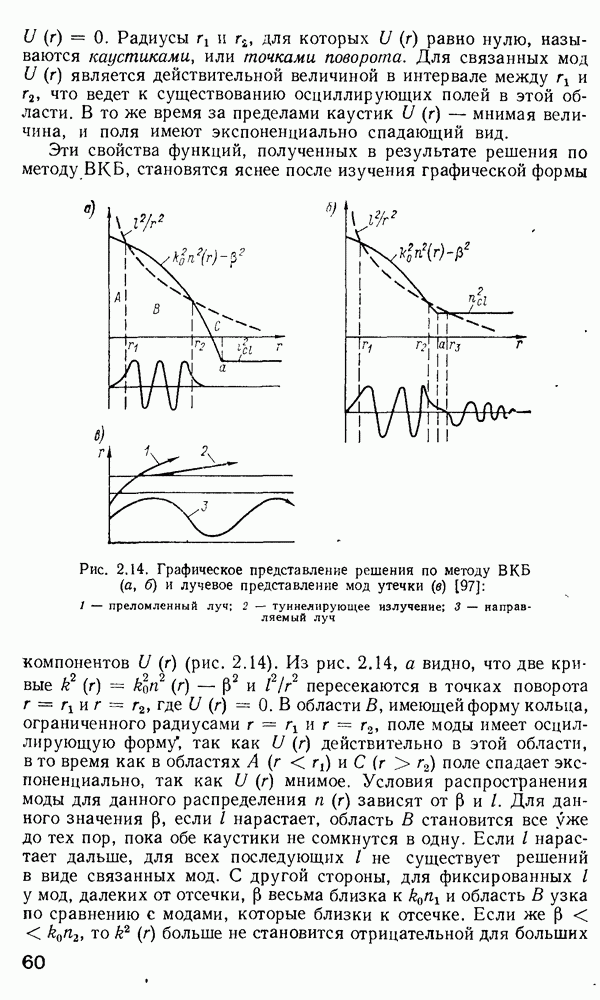
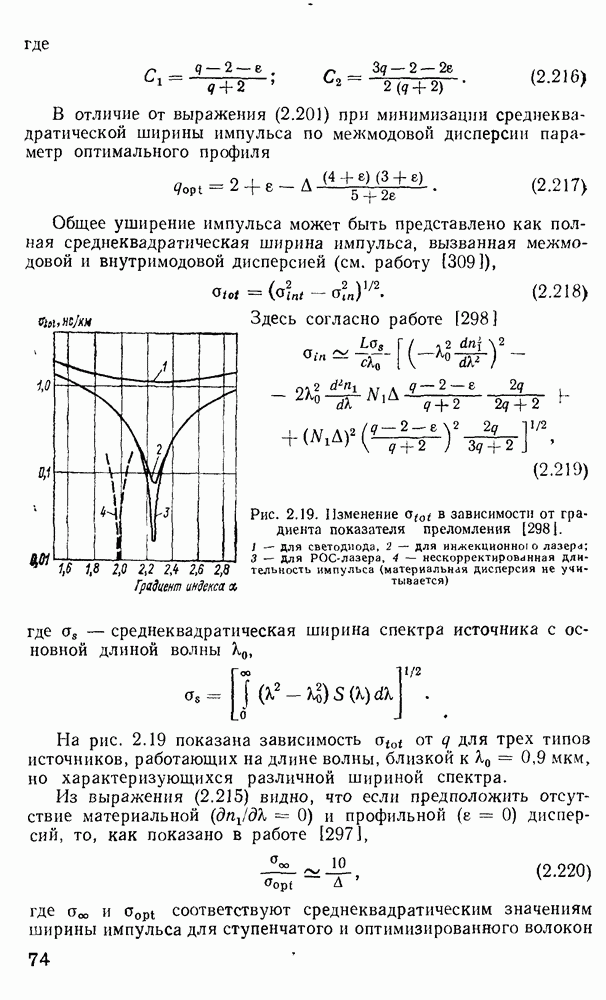
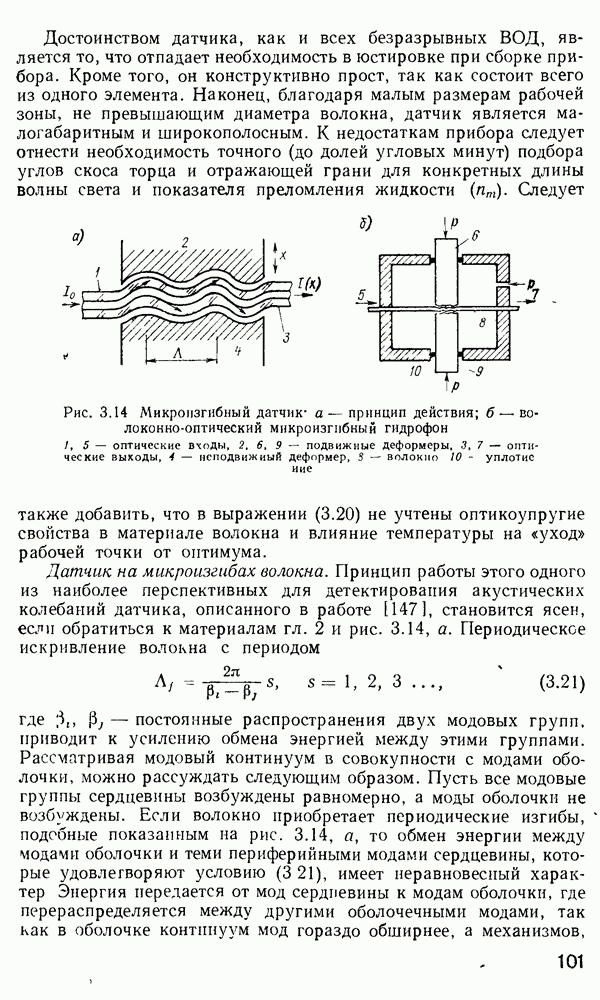
Рис. 3.14 Микроизгибный датчик: а — принцип действия; б — волоконно-оптический мнкроизгнбный гидрофон 1,5 — оптические входы, 2, 6, 9 — подвижные деформеры, 3,7 — оптические выходы, 4 — неподвижный деформер, 5 волокно 10 - уплотнение
Следует также добавить, что в выражении (3.20) не учтены оптикоупругие свойства в материале волокна и влияние температуры на «уход» рабочей точки от оптимума.
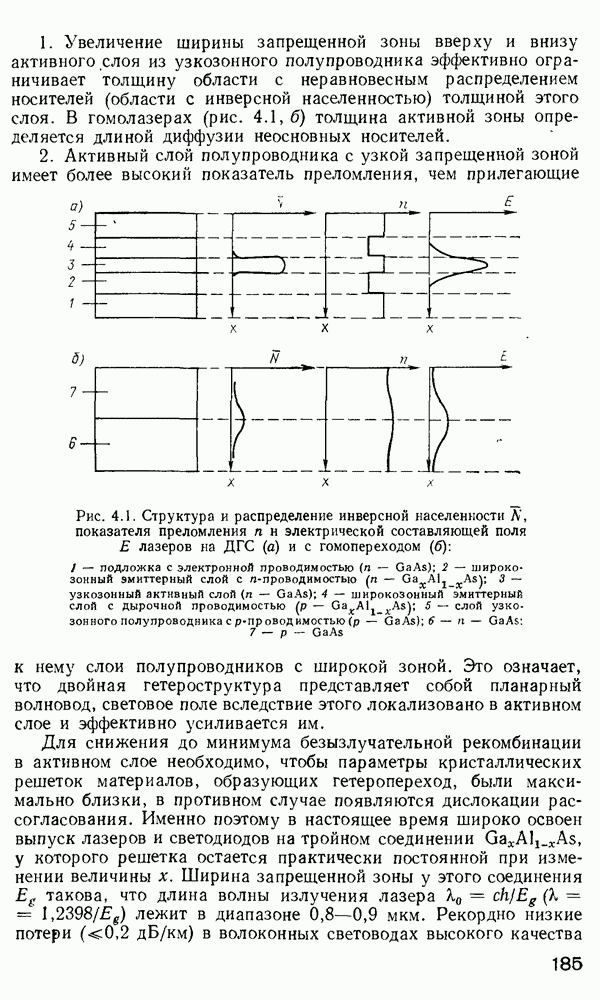
Датчик на микроизгибах волокна. Принцип работы этого одного из наиболее перспективных для детектирования акустических колебаний датчика, описанного в работе [147], становится ясен, если обратиться к материалам гл. 2 и рис. 3.14, а. Периодическое искривление волокна с периодом

где Р — постоянные распространения двух модовых групп, приводит к усилению обмена энергией между этими группами. Рассматривая модовый континуум в совокупности с модами оболочки, можно рассуждать следующим образом. Пусть все модовые группы сердцевины возбуждены равномерно, а моды оболочки не возбуждены. Если волокно приобретает периодические изгибы, подобные показанным на рис. 3.14, а, то обмен энергии между модами оболочки и теми периферийными модами сердцевины, которые удовлетворяют условию (3 21), имеет неравновесный характер Энергия передается от мод сердцевины к модам оболочки, где перераспределяется между другими оболочечными модами, так как в оболочке континуум мод гораздо обширнее, а механизмов,
способствующих перераспределению энергии, (релеевское рассеяние и др.) больше. Таким образом, «слой» периферийных мод сердцевины, удовлетворяющих условию (3.21), теряет энергию.
С другой стороны, если соотношение (3.21) справедливо для этих мод и каких-либо модовых групп из числа более фундаментальных (т. е. имеющих наименьшие индексы  ), то эти последние в свою очередь передают энергию периферийным модам сердцевины, от которых она выводится далее в оболочку. Таким образом, периодические искривления волокна способствуют эффективному выводу энергии из сердцевины в оболочку. Обратный процесс также возможен, но он менее эффективен 1.
), то эти последние в свою очередь передают энергию периферийным модам сердцевины, от которых она выводится далее в оболочку. Таким образом, периодические искривления волокна способствуют эффективному выводу энергии из сердцевины в оболочку. Обратный процесс также возможен, но он менее эффективен 1.
Рассмотрим, какой тип волокон наиболее пригоден для создания микроизгибных ВОД.
Эффективность связи между двумя модами, имеющими распределение поля в поперечном сечении  определяется степенью перекрытия этих полей в той области волокна, где присутствует возмущение
определяется степенью перекрытия этих полей в той области волокна, где присутствует возмущение  вызывающее связь мод,
вызывающее связь мод,

Поле в основном сосредоточено в сердцевине, поле  — в оболочке волокна. Отсюда ясно, что в микроизгибных ВОД предпочтительно применять волокна с малым
— в оболочке волокна. Отсюда ясно, что в микроизгибных ВОД предпочтительно применять волокна с малым  (слабонаправляющие), так как поля волноводных мод в таких волокнах в большей степени простираются в оболочку, нежели в волокнах с большими значениями
(слабонаправляющие), так как поля волноводных мод в таких волокнах в большей степени простираются в оболочку, нежели в волокнах с большими значениями  [см. выражение (2.6)], и интеграл перекрытия (3.22) больше. Далее, как следует из приведенных выше рассуждений, для более эффективной связи мод желательно, чтобы соотношение (3.22) выполнялось для большого числа модовых групп. В волокнах со ступенчатым профилем разница постоянных распространения групп зависит от номера моды
[см. выражение (2.6)], и интеграл перекрытия (3.22) больше. Далее, как следует из приведенных выше рассуждений, для более эффективной связи мод желательно, чтобы соотношение (3.22) выполнялось для большого числа модовых групп. В волокнах со ступенчатым профилем разница постоянных распространения групп зависит от номера моды 

при  . В градиентных волокнах
. В градиентных волокнах

Следовательно, градиентные волокна предпочтительнее, чем ступенчатые, при условии, что их параметры подобраны в соответствии с микроизгибами датчика

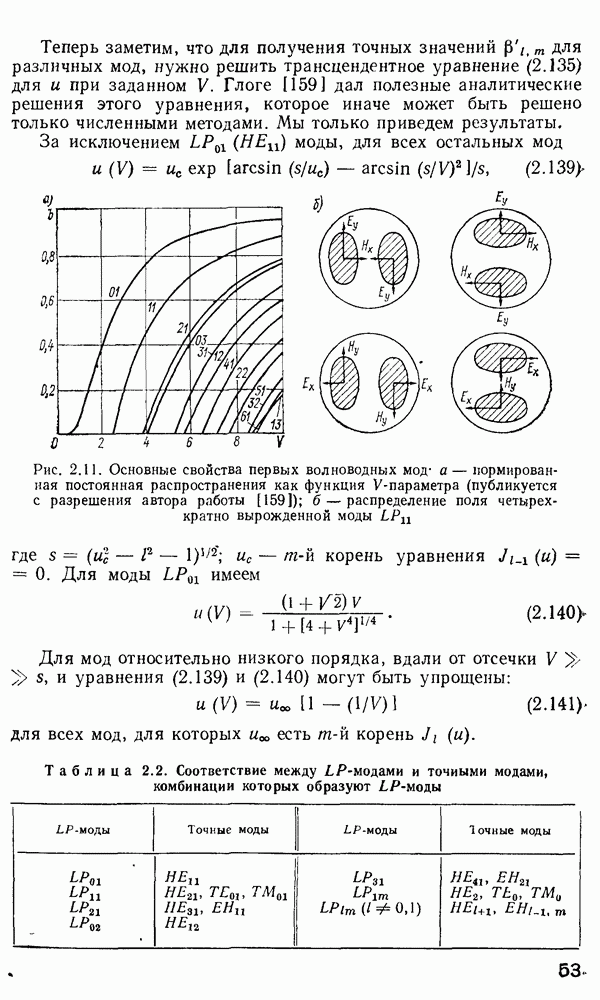
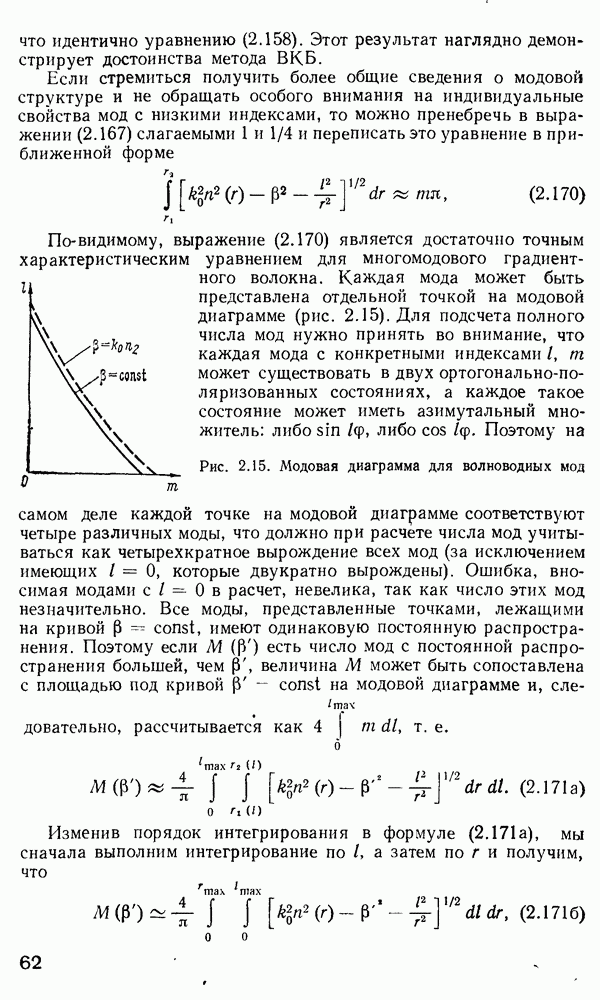
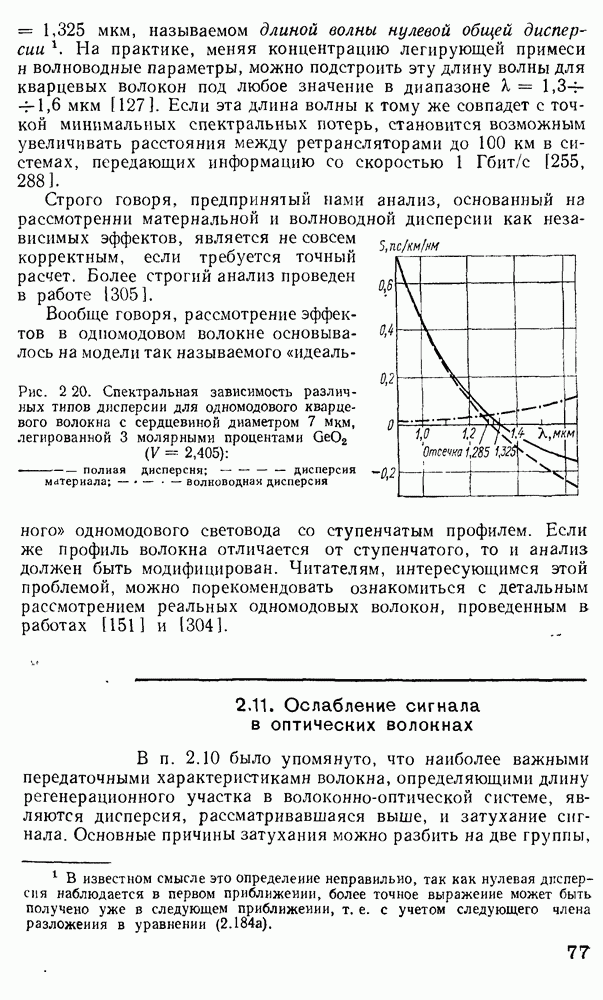
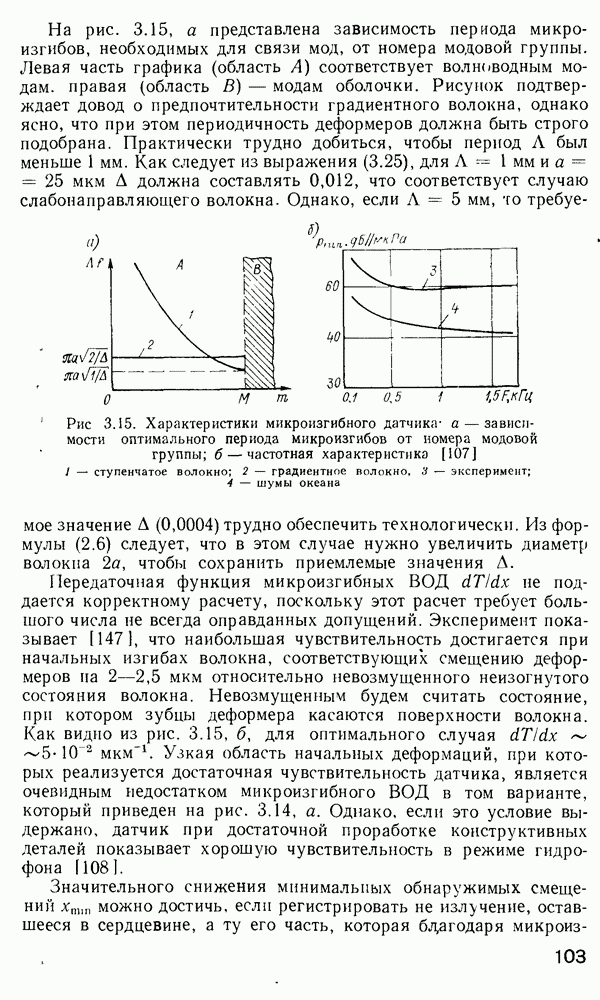
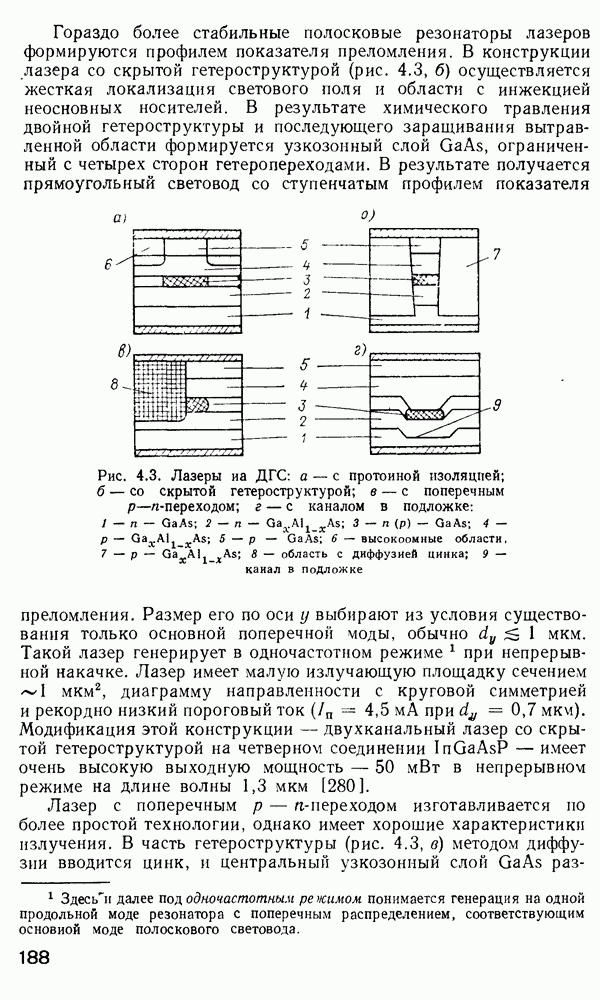
На рис. 3.15, а представлена зависимость периода микроизгибов, необходимых для связи мод, от номера модовой группы. Левая часть графика (область А) соответствует волноводным модам. правая (область В) — модам оболочки. Рисунок подтверждает довод о предпочтительности градиентного волокна, однако ясно, что при этом периодичность деформеров должна быть строго подобрана. Практически трудно добиться, чтобы период Л был меньше 1 мм. Как следует из выражения (3.25), для  мм и
мм и  мкм А должна составлять 0,012, что соответствует случаю слабонаправляющего волокна. Однако, если
мкм А должна составлять 0,012, что соответствует случаю слабонаправляющего волокна. Однако, если  мм, то требуемое значение А (0,0004) трудно обеспечить технологически.
мм, то требуемое значение А (0,0004) трудно обеспечить технологически.

Рис. 3.15. Характеристики микроизгибного датчика: а — зависимости оптимального периода микроизгибов от номера модовой группы;  — частотная характеристика [107] 1 — ступенчатое волокно; 2 — градиентное волокно, 3 — эксперимент; 4 — шумы океана
— частотная характеристика [107] 1 — ступенчатое волокно; 2 — градиентное волокно, 3 — эксперимент; 4 — шумы океана
Из формулы (2.6) следует, что в этом случае нужно увеличить диаметр волокна 2а, чтобы сохранить приемлемые значения А.
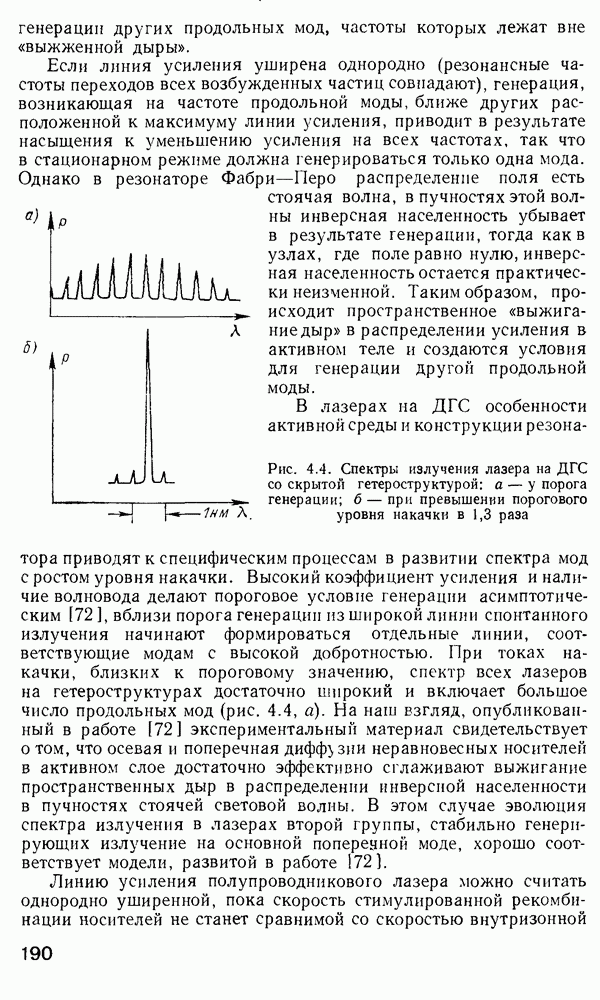
Передаточная функция микроизгибных ВОД  не поддается корректному расчету, поскольку этот расчет требует большого числа не всегда оправданных допущений. Эксперимент показывает [147], что наибольшая чувствительность достигается при начальных изгибах волокна, соответствующих смещению деформеров на
не поддается корректному расчету, поскольку этот расчет требует большого числа не всегда оправданных допущений. Эксперимент показывает [147], что наибольшая чувствительность достигается при начальных изгибах волокна, соответствующих смещению деформеров на  мкм относительно невозмущенного неизогнутого состояния волокна. Невозмущенным будем считать состояние, при котором зубцы деформера касаются поверхности волокна. Как видно из рис. 3.15, б, для оптимального случая
мкм относительно невозмущенного неизогнутого состояния волокна. Невозмущенным будем считать состояние, при котором зубцы деформера касаются поверхности волокна. Как видно из рис. 3.15, б, для оптимального случая  Узкая область начальных деформаций, при которых реализуется достаточная чувствительность датчика, является очевидным недостатком микроизгибного ВОД в том варианте, который приведен на рис. 3.14, а. Однако, если это условие выдержано, датчик при достаточной проработке конструктивных деталей показывает хорошую чувствительность в режиме гидрофона [108].
Узкая область начальных деформаций, при которых реализуется достаточная чувствительность датчика, является очевидным недостатком микроизгибного ВОД в том варианте, который приведен на рис. 3.14, а. Однако, если это условие выдержано, датчик при достаточной проработке конструктивных деталей показывает хорошую чувствительность в режиме гидрофона [108].
Значительного снижения минимальных обнаружимых смещений  можно достичь, если регистрировать не излучение, оставшееся в сердцевине, а ту его часть, которая благодаря
можно достичь, если регистрировать не излучение, оставшееся в сердцевине, а ту его часть, которая благодаря
микроизгибам выходит в оболочку. Малые изменения интенсивности легче регистрировать на фоне незначительной постоянной составляющей, как при использовании известного метода «темного поля» в классической оптике. Одна из разновидностей микроизгибного ВОД такого типа (рис. 3.14, б) позволяет измерять блщщ  мкм [133, 247], т. е. обнаружительная способность данного ВОД значительно выше, чем для такого же датчика обычной конструкции.
мкм [133, 247], т. е. обнаружительная способность данного ВОД значительно выше, чем для такого же датчика обычной конструкции.
Большое значение имеют гибкость, упругость и прочность волокна, используемого в микроизгибном ВОД. Расчеты [247] показывают, что поскольку модуль Юнга для стекол практически постоянен (лишь добавки  уменьшают Е на 20-40 %), то добиться большей податливости волокна можно за счет уменьшения его диаметра. Однако из выражения (3.25) следует, что при этом возникает необходимость уменьшения периода микроизгибов
уменьшают Е на 20-40 %), то добиться большей податливости волокна можно за счет уменьшения его диаметра. Однако из выражения (3.25) следует, что при этом возникает необходимость уменьшения периода микроизгибов  что затруднительно. Выбор профиля зубцов деформера представляет также проблему: волокно испытывает более резкие искривления на острых зубцах, однако при этом могут возникнуть избыточные напряжения, приводящие к разрушению волокна.
что затруднительно. Выбор профиля зубцов деформера представляет также проблему: волокно испытывает более резкие искривления на острых зубцах, однако при этом могут возникнуть избыточные напряжения, приводящие к разрушению волокна.

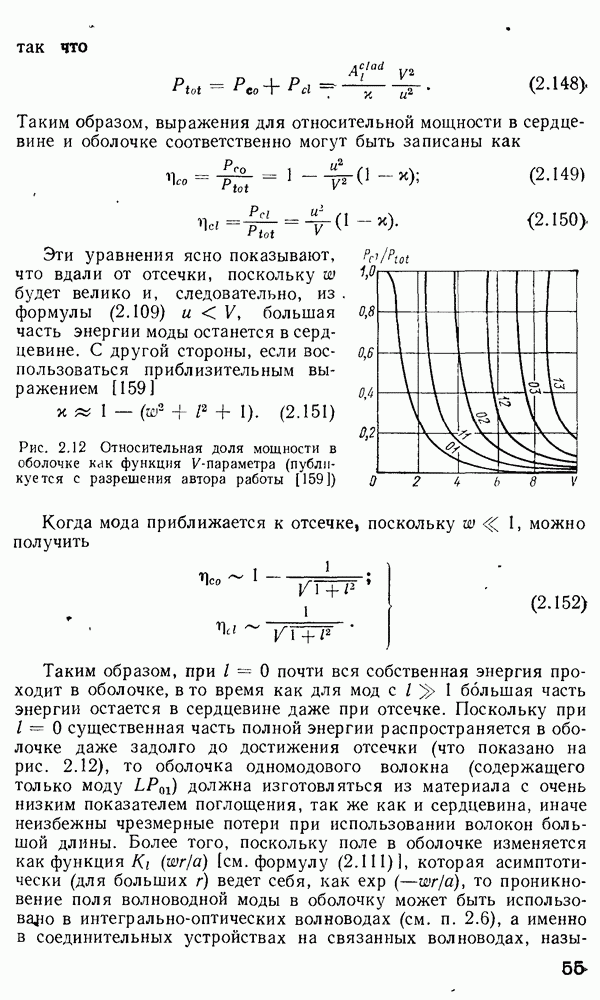
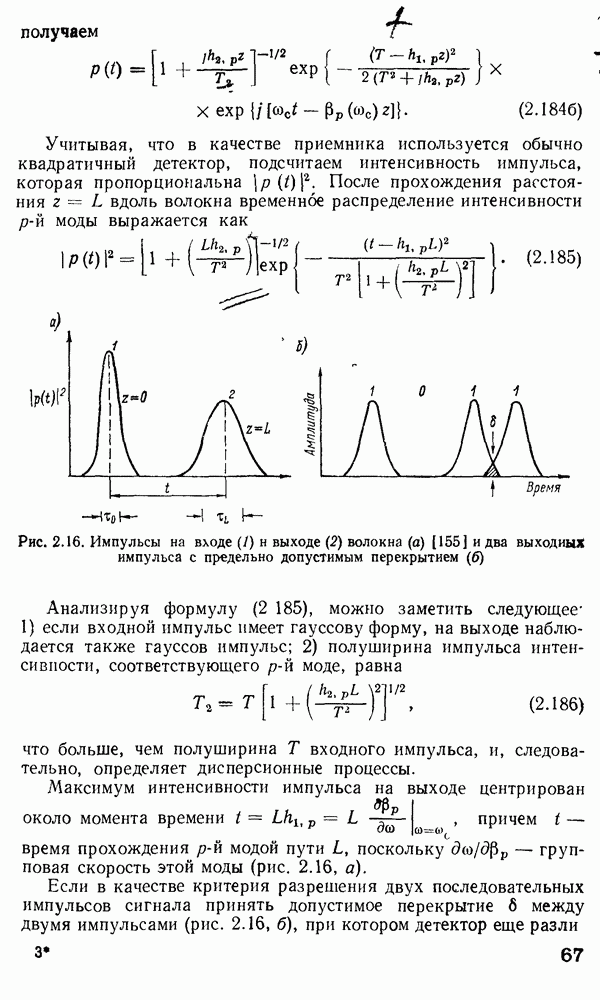
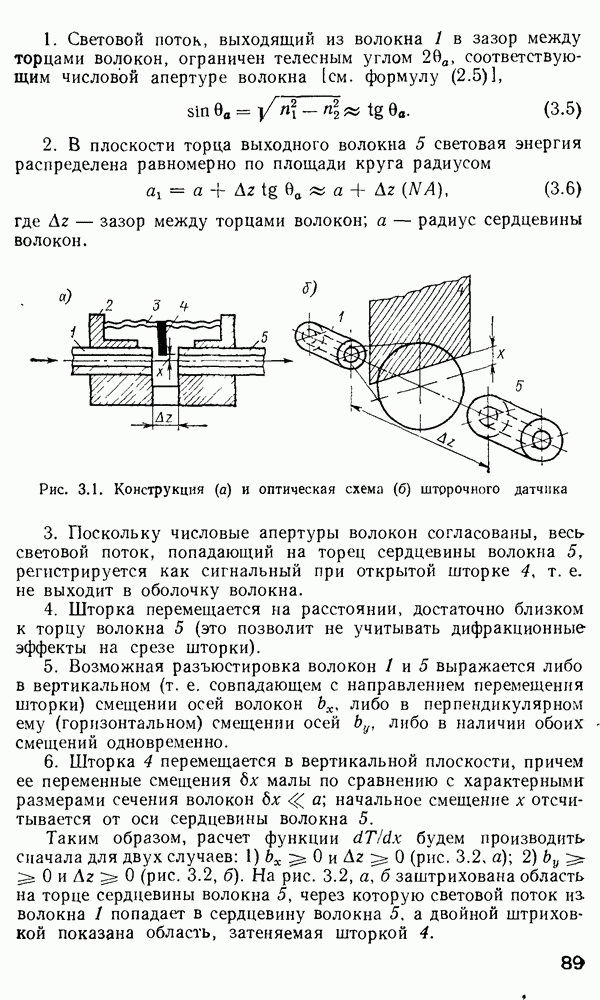
Рис. 3.16. Типичные зависимости функции пропускания  и модуляционной функции
и модуляционной функции  вблизи правильно выбранной рабочей точки
вблизи правильно выбранной рабочей точки 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
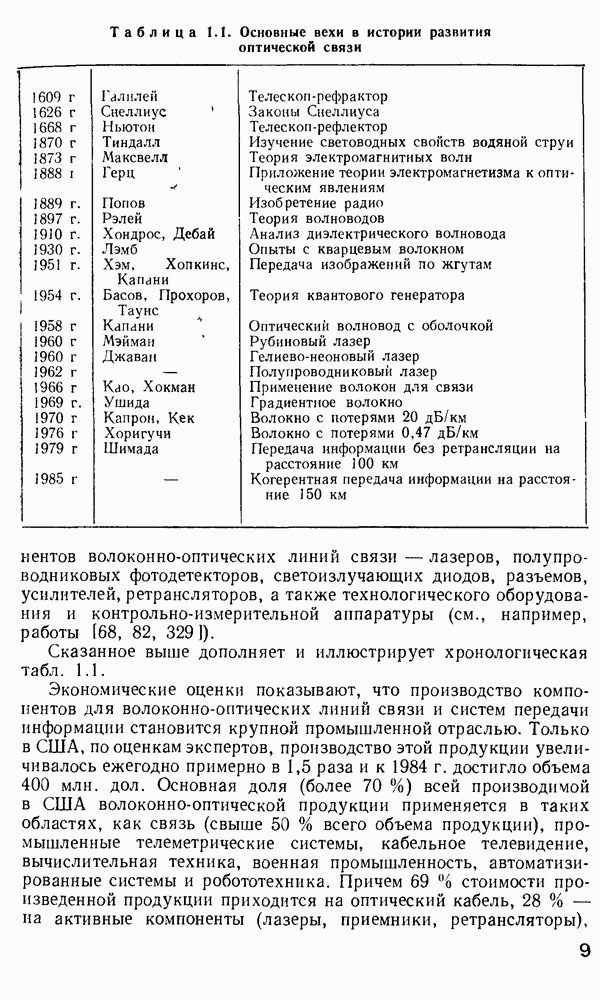
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
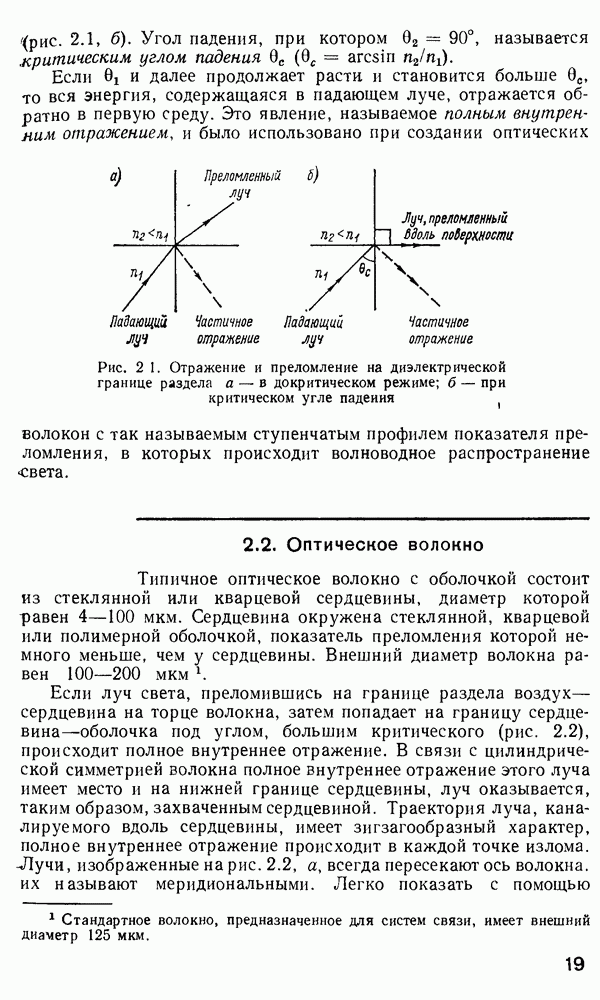
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
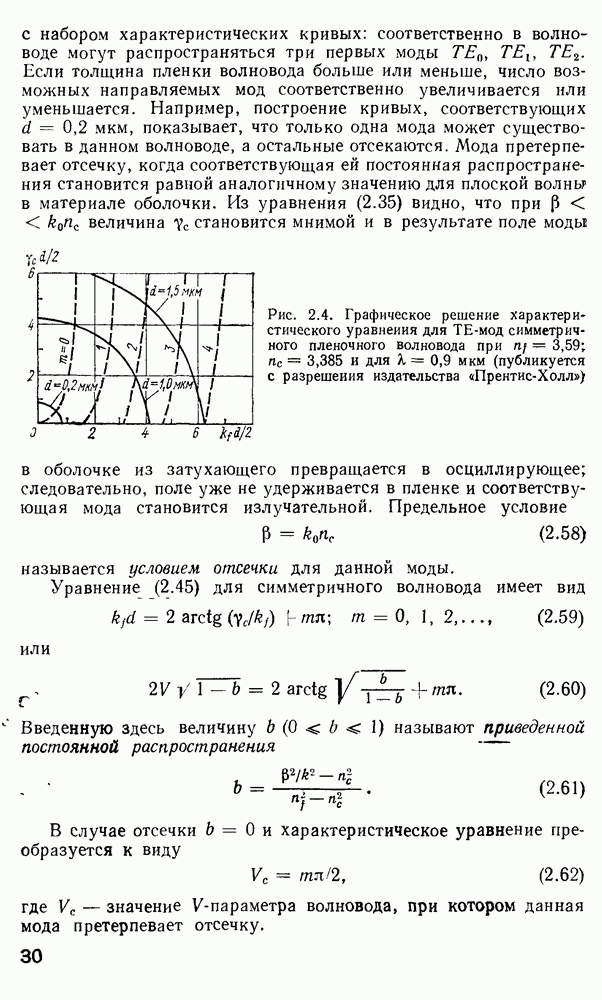
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
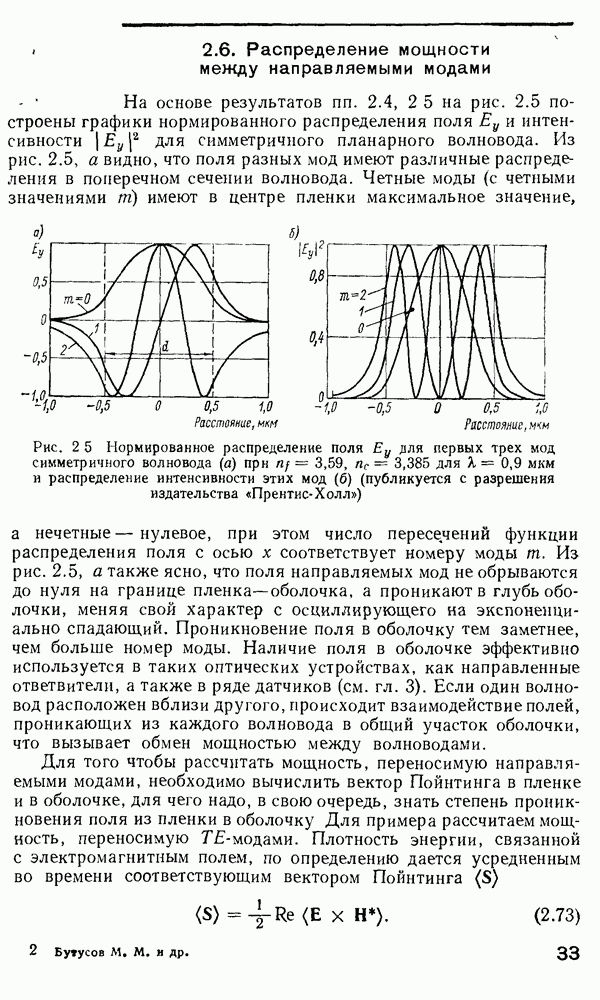
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
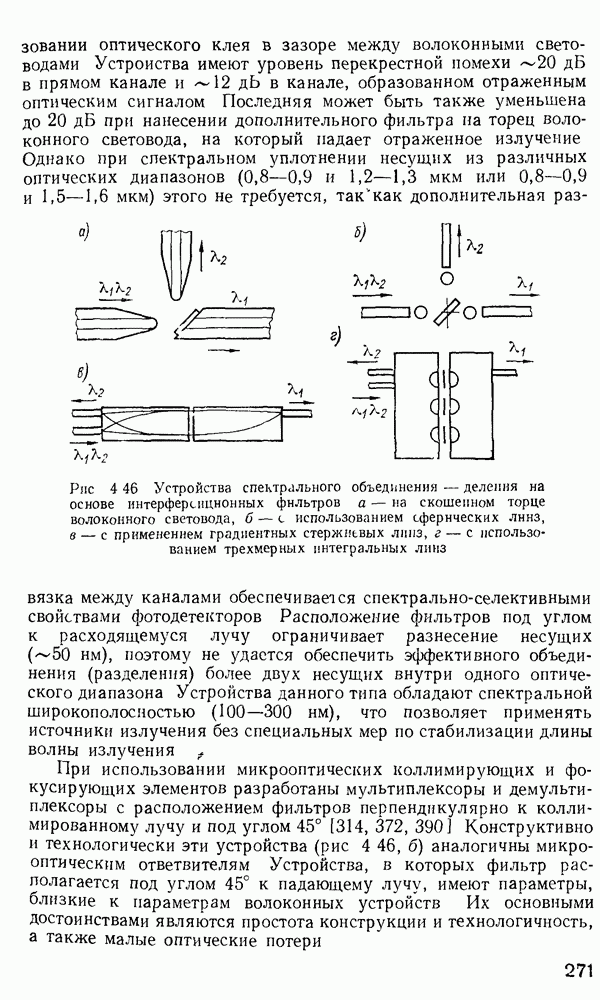
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
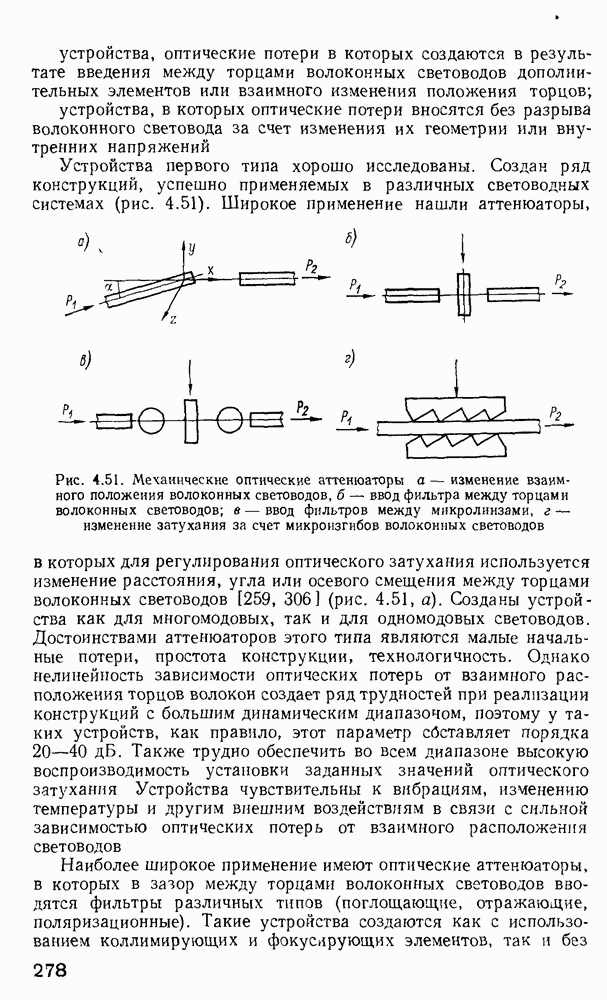
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
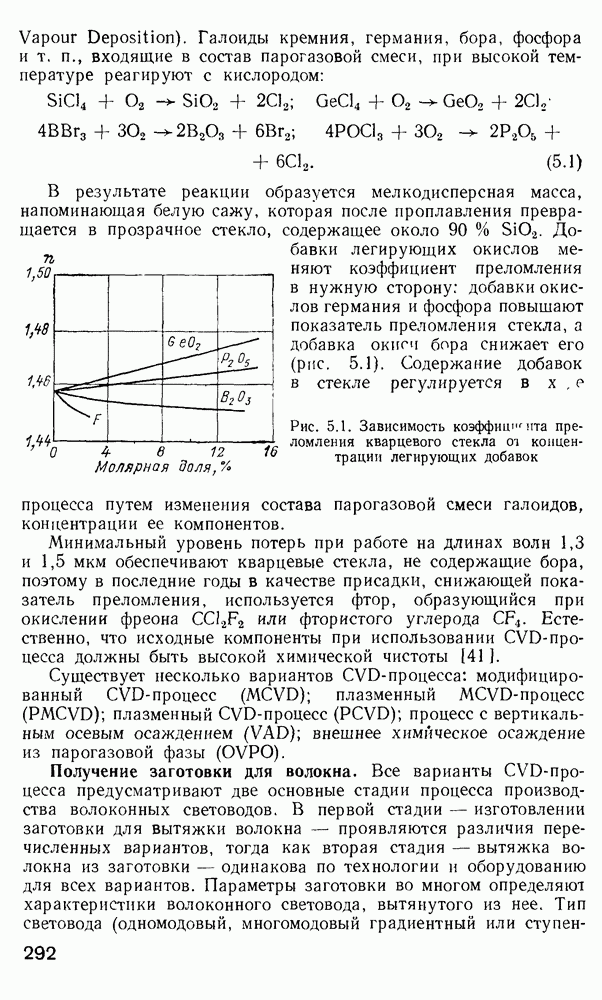
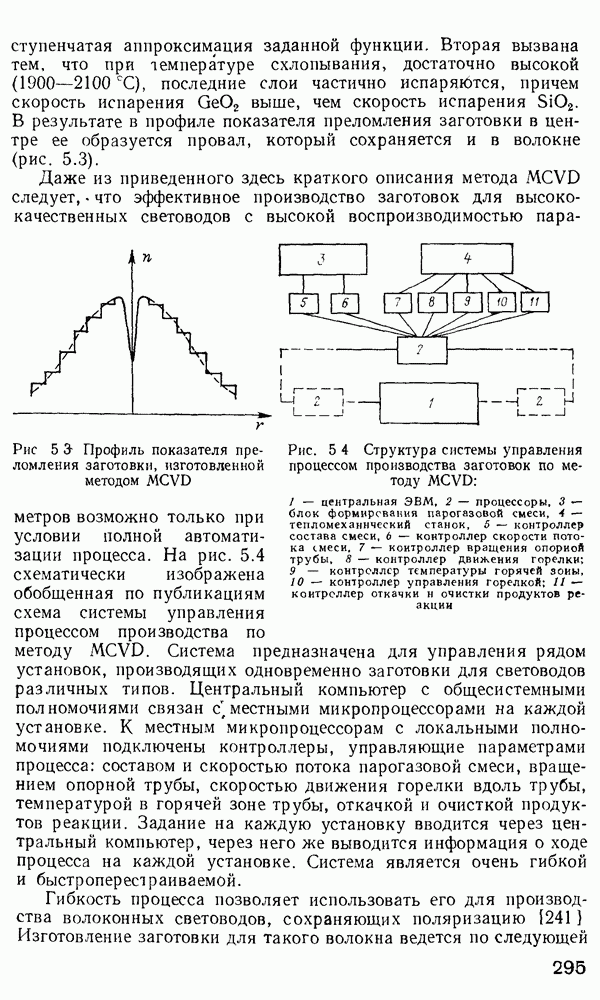
- Получение заготовки для волокна.
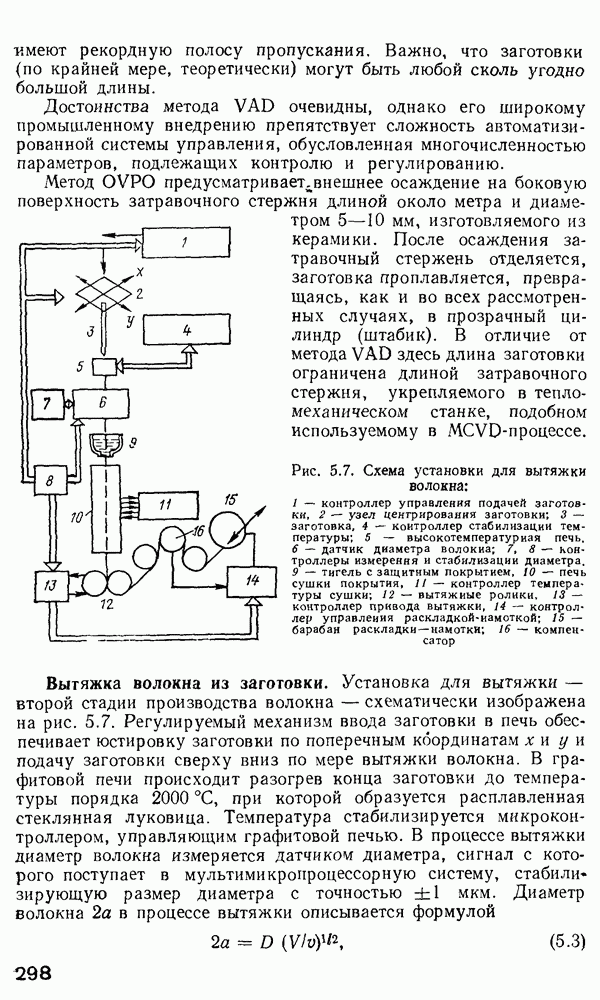
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
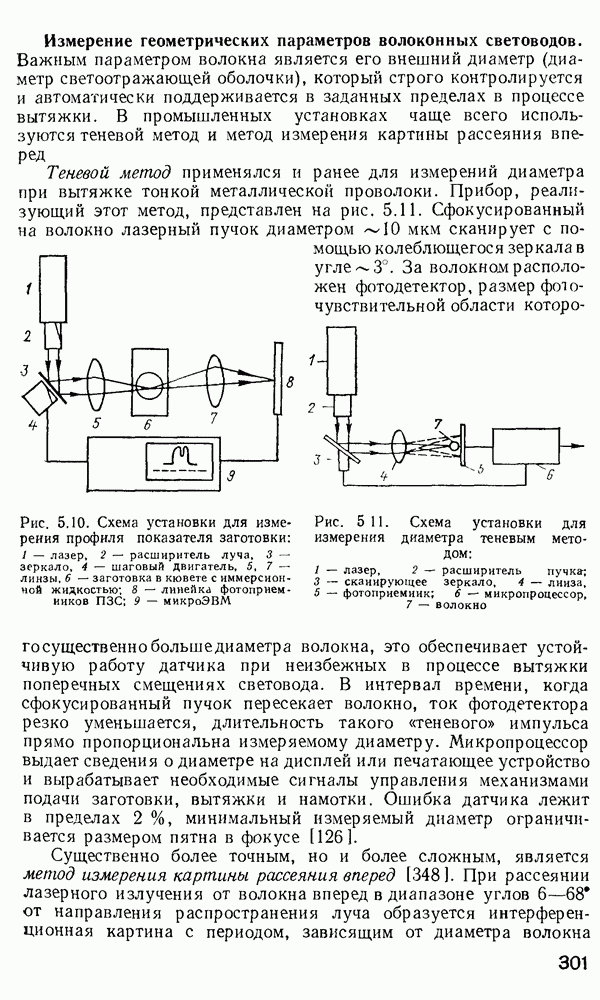
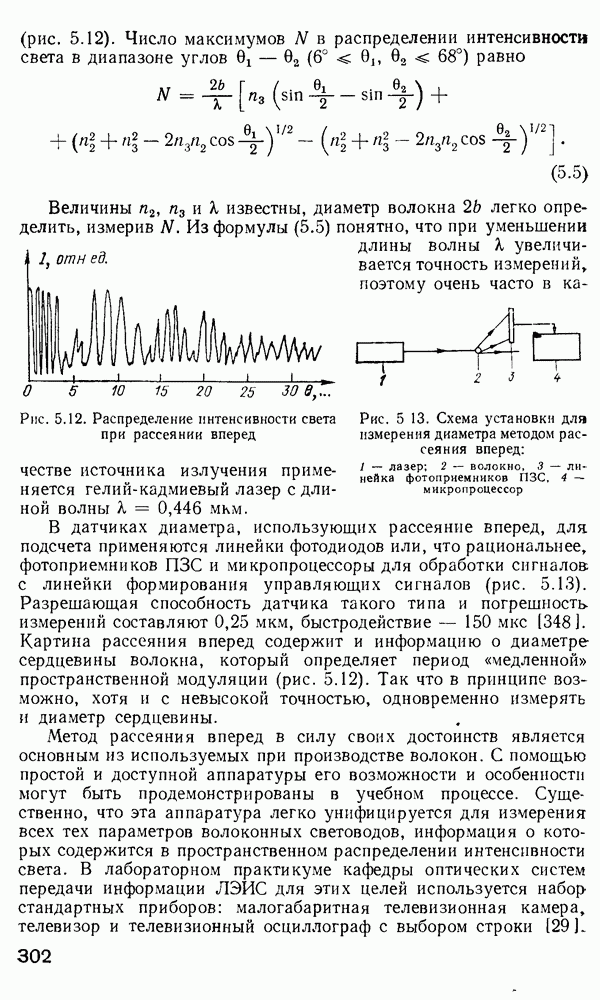
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
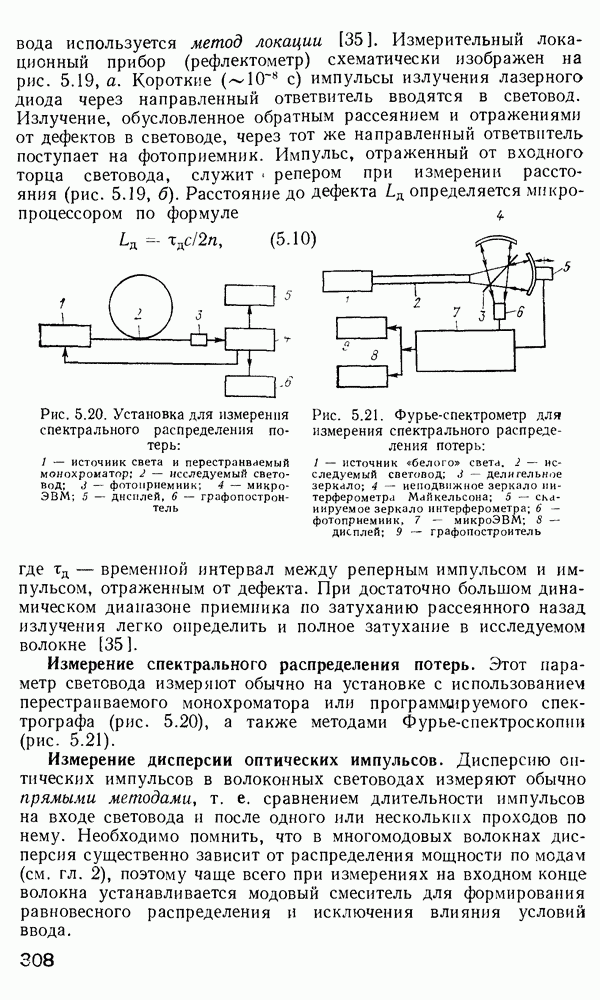
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ