| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
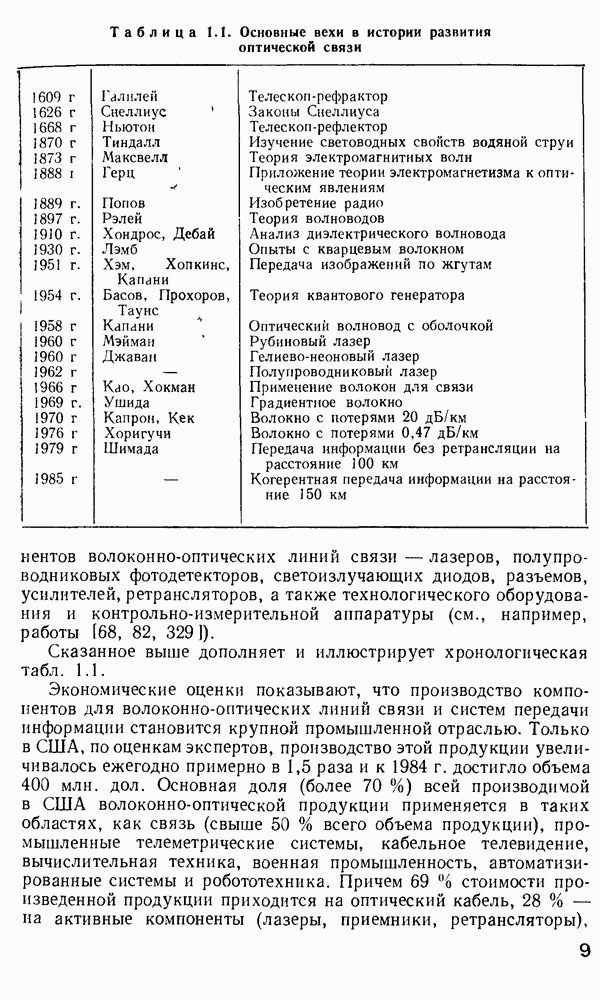
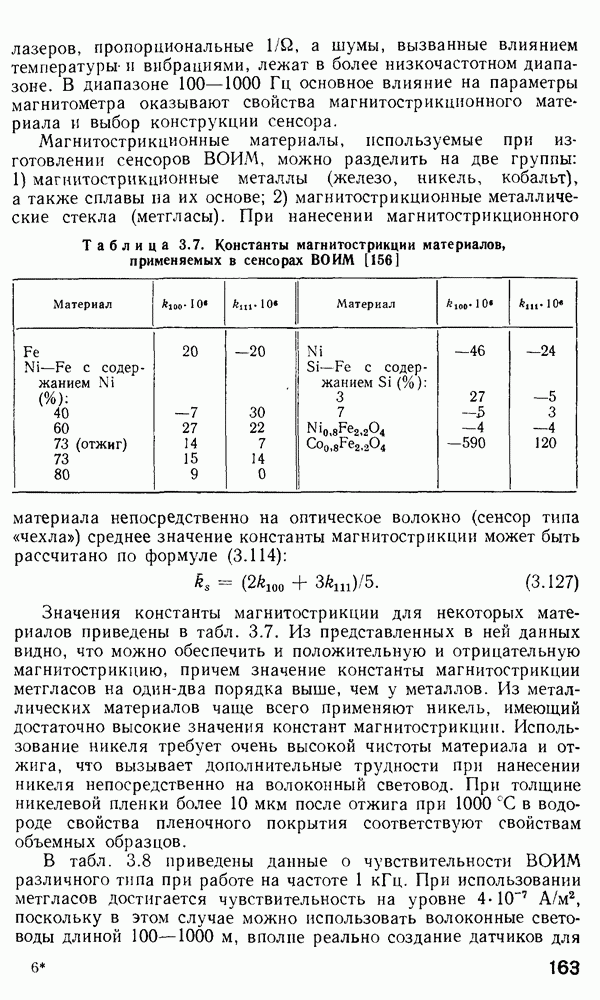
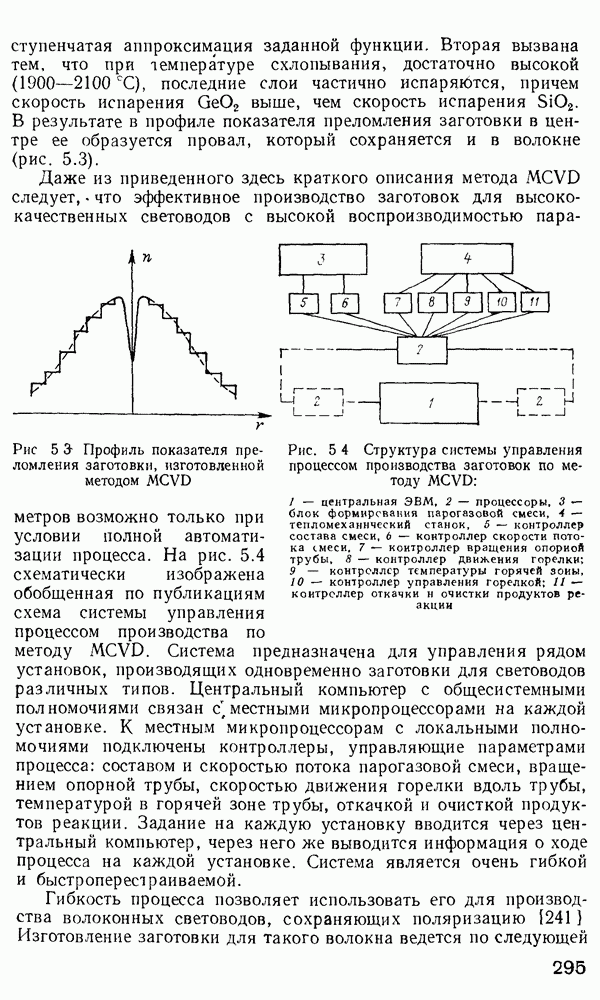
Дисперсия импульсов в одномодовых волокнах.
Как было показано выше (см. п. 2.8), если К-параметр ступенчатого волокна составляет менее чем 2,405, в волокне распространяется только одна мода. Очевидно, что в таком одномодовом волокне межмодовая дисперсия невозможна и уширение импульса вызвано внутримодовой дисперсией, которая, в свою очередь, состоит из материальной и волноводной, причем оба эти явления связаны с конечной шириной спектра практически используемых источников света. Здесь предполагается, что уширение спектра, создаваемое импульсной модуляцией в соответствии с принципом неопределенности, пренебрежимо мало.
Согласно выражению (2.189), время прохождения моды по

где  — волновое число в свободном пространстве. Если
— волновое число в свободном пространстве. Если  — ширина спектра вблизи центральной длины волны излучения
— ширина спектра вблизи центральной длины волны излучения  можно считать, что импульс переносится большим количеством близко расположенных спектральных несущих, времена распространения которых различны из-за дисперсии. Тогда уширение импульса
можно считать, что импульс переносится большим количеством близко расположенных спектральных несущих, времена распространения которых различны из-за дисперсии. Тогда уширение импульса  соотносится с шириной спектра
соотносится с шириной спектра  , как
, как

Теперь, опираясь на выражение (2.221), получаем, что

Итак, внутримодовая дисперсия существенно зависит от второй производной  и (в нашем случае) от так называемого
и (в нашем случае) от так называемого
«дисперсионного коэффициента»  выражаемого обычно в
выражаемого обычно в  Для того чтобы оценить значение внутримодовой дисперсии в одномодовом волокне, рассмотрим выражение (2.138) для нормализованной постоянной распространения
Для того чтобы оценить значение внутримодовой дисперсии в одномодовом волокне, рассмотрим выражение (2.138) для нормализованной постоянной распространения 
В слабонаправляющих волокнах  это выражение можно переписать в виде
это выражение можно переписать в виде

Постоянная распространения, таким образом, нмеег два компонента: один — чисто материальный  другой — связан как с параметром моды
другой — связан как с параметром моды  так и со свойствами материала. Если временно пренебречь зависимостью свойств материала от длины волны (т. е. материальной и профильной дисперсией), то из формулы (2.224) можно получить:
так и со свойствами материала. Если временно пренебречь зависимостью свойств материала от длины волны (т. е. материальной и профильной дисперсией), то из формулы (2.224) можно получить:

следовательно, 

Значит, коэффициент волноводной дисперсии

Отсюда следует, что  прежде всего определяется выражением
прежде всего определяется выражением  Строго говоря, чтобы получить зависимость
Строго говоря, чтобы получить зависимость  для одномодового волокна, надо решать уравнение (2.135) для случая
для одномодового волокна, надо решать уравнение (2.135) для случая  т. е. для моды
т. е. для моды  Существует, однако, эмпирическая зависимость для диапазона
Существует, однако, эмпирическая зависимость для диапазона  обеспечивающая расчет с точностью до
обеспечивающая расчет с точностью до 

Если же временно пренебречь волноводной дисперсией, то из формул (2.223) и (2.224) можно получить коэффициент материальной дисперсии

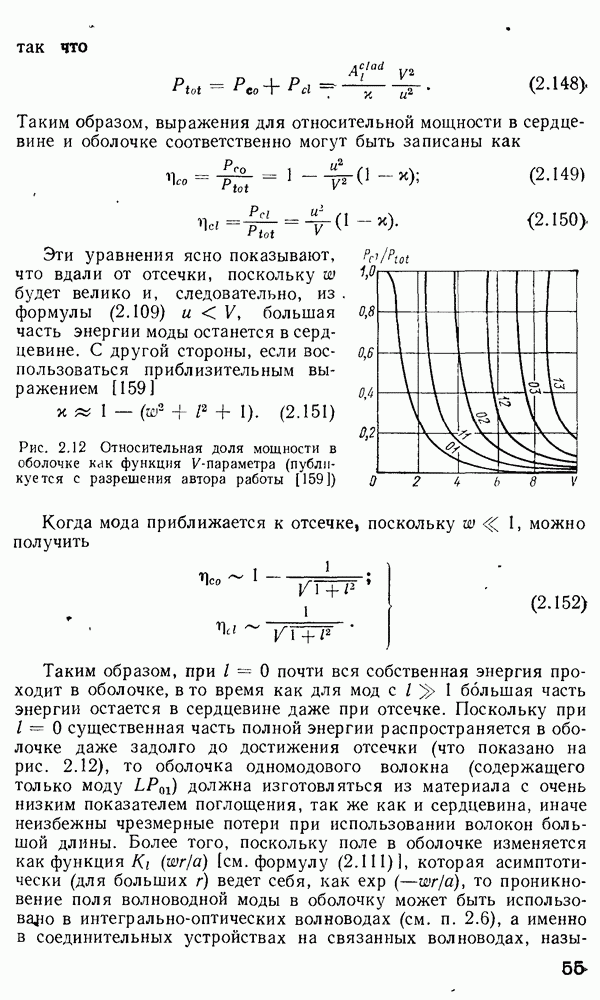
Интересно, что в градиентных волокнах для устройств связи, где базовым веществом является плавленый кварц, зависимость коэффициента оболочки  от к проходит через ноль в области к
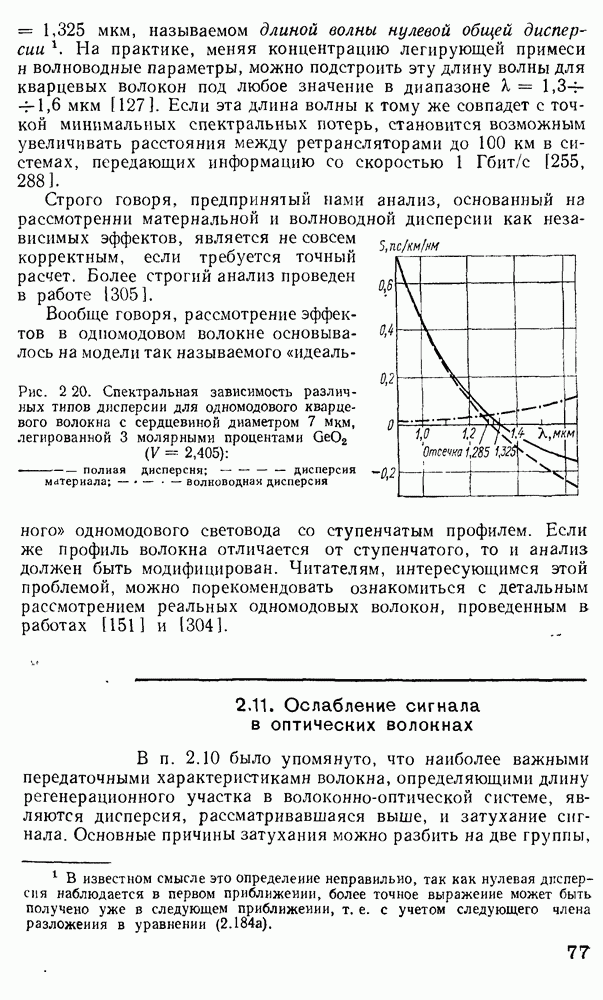
от к проходит через ноль в области к  мкм, а в легированном кварце это значение несколько больше (штриховая линия на рис. 2.20) [307]. Суммарная дисперсионная кривая на рис. 2.20, полученная численным дифференцированием из уравнения (2.223), проходит через 0 при
мкм, а в легированном кварце это значение несколько больше (штриховая линия на рис. 2.20) [307]. Суммарная дисперсионная кривая на рис. 2.20, полученная численным дифференцированием из уравнения (2.223), проходит через 0 при 
 мкм, называемом длиной волны нулевой общей дисперсии. На практике, меняя концентрацию легирующей примеси и волноводные параметры, можно подстроить эту длину волны для кварцевых волокон под любое значение в диапазоне
мкм, называемом длиной волны нулевой общей дисперсии. На практике, меняя концентрацию легирующей примеси и волноводные параметры, можно подстроить эту длину волны для кварцевых волокон под любое значение в диапазоне  мкм [127]. Если эта длина волны к тому же совпадет с точкой минимальных спектральных потерь, становится возможным увеличивать расстояния между ретрансляторами до 100 км в системах, передающих информацию со скоростью 1 Гбит/с [255, 288].
мкм [127]. Если эта длина волны к тому же совпадет с точкой минимальных спектральных потерь, становится возможным увеличивать расстояния между ретрансляторами до 100 км в системах, передающих информацию со скоростью 1 Гбит/с [255, 288].
Строго говоря, предпринятый нами анализ, основанный на рассмотрении материальной и волноводной дисперсии как независимых эффектов, является не совсем корректным, если требуется точный расчет. Более строгий анализ проведен в работе [305].
Вообще говоря, рассмотрение эффектов в одпомодовом волокне основывалось на модели так называемого «идеального» одномодового световода со ступенчатым профилем.

Рис. 2 20. Спектральная зависимость различных типов дисперсии для одномодового кварцевого волокна с сердцевиной диаметром 7 мкм, легированной 3 молярными процентами  - полная дисперсия;
- полная дисперсия;  дисперсия материала;
дисперсия материала;  — волноводная дисперсия
— волноводная дисперсия
Если же профиль волокна отличается от ступенчатого, то и анализ должен быть модифицирован. Читателям, интересующимся этой проблемой, можно порекомендовать ознакомиться с детальным рассмотрением реальных одномодовых волокон, проведенным в работах [151] и [304].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
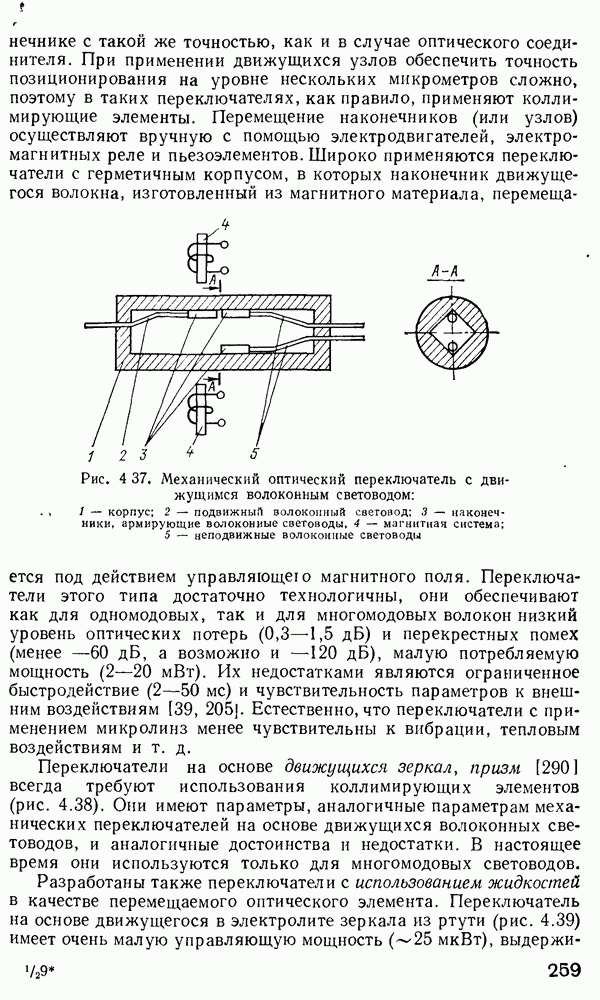
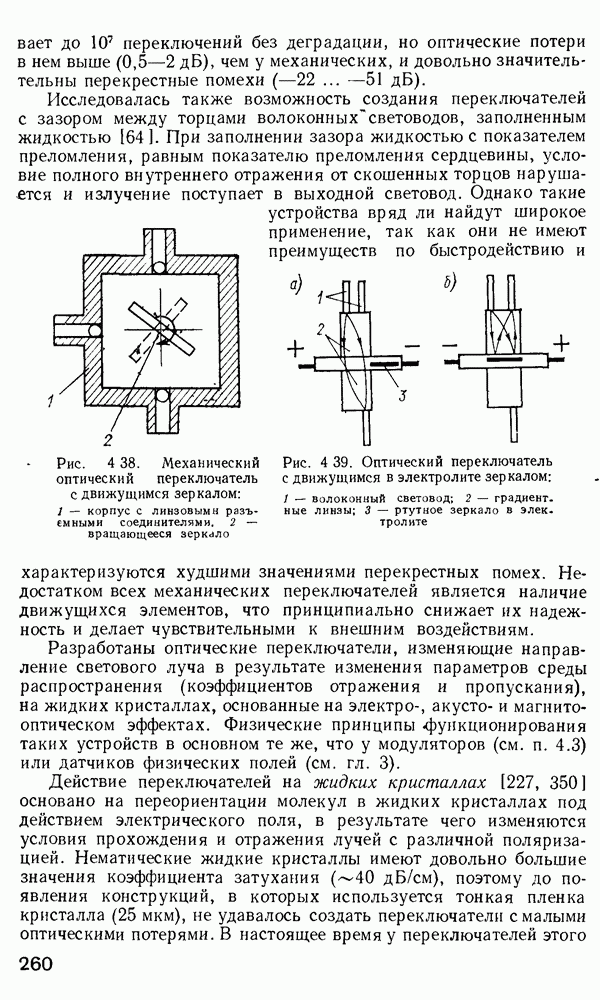
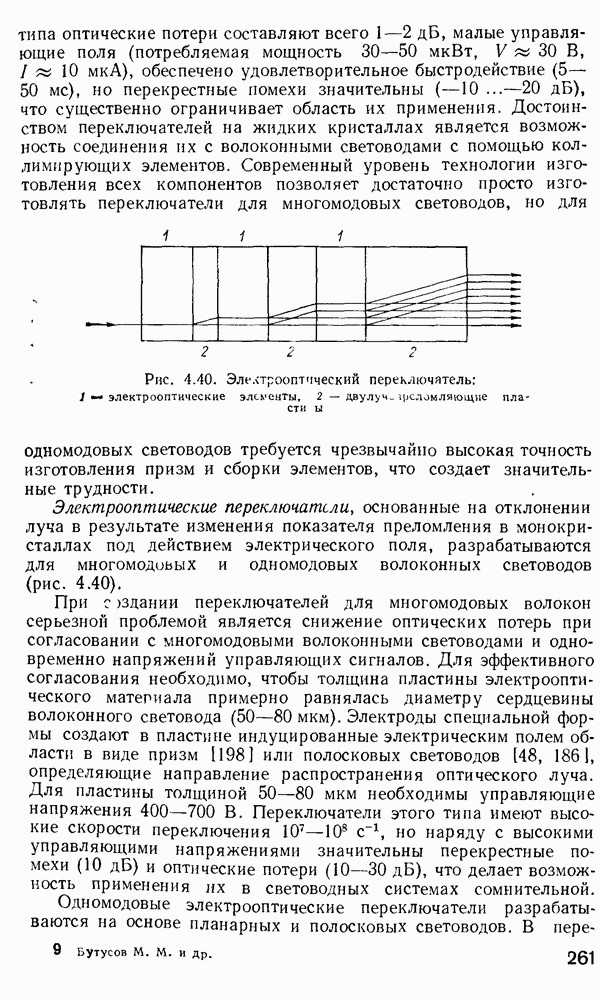
- 4.7. Волоконно-оптические переключатели
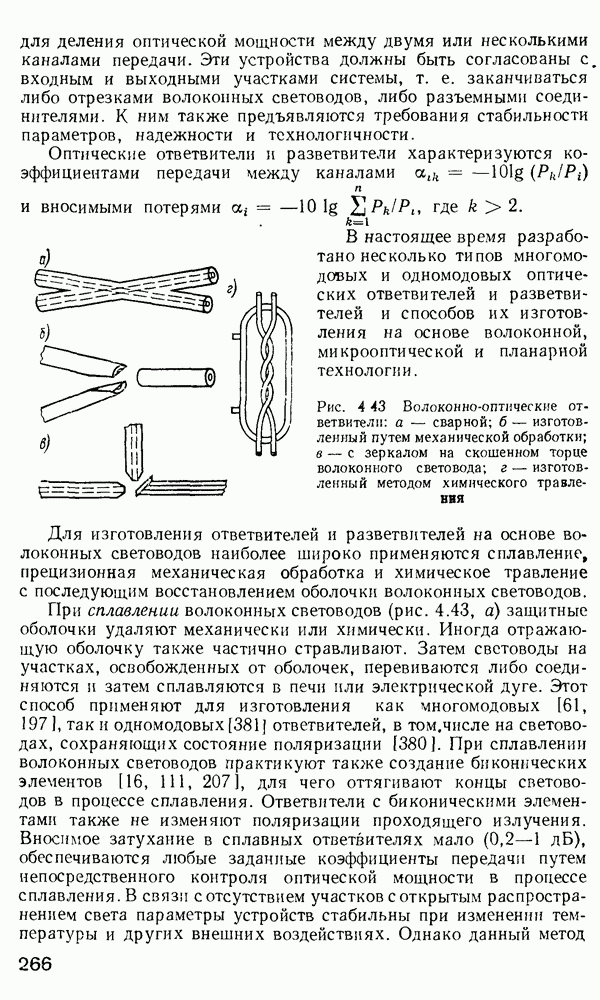
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
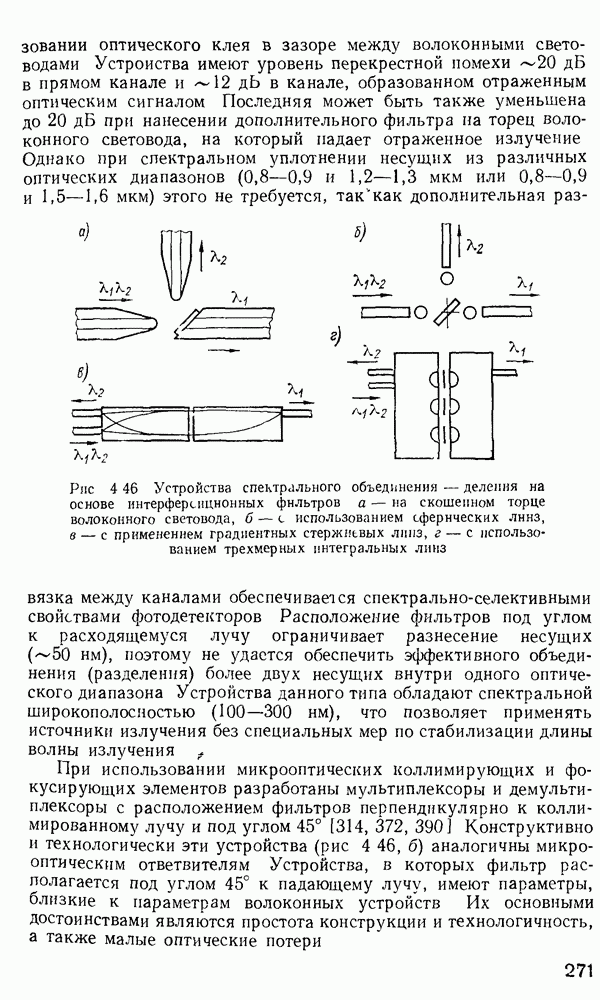
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
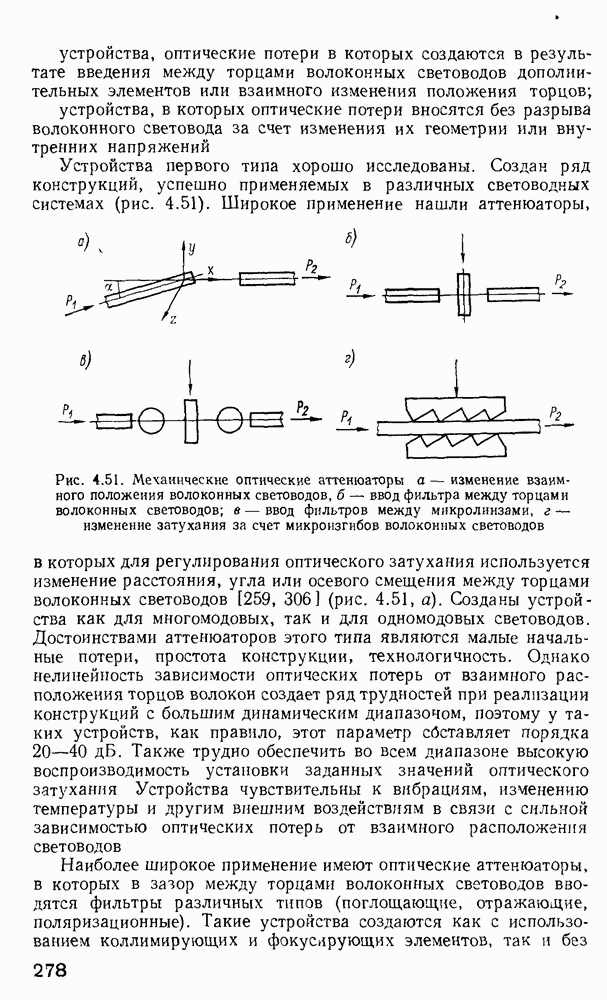
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
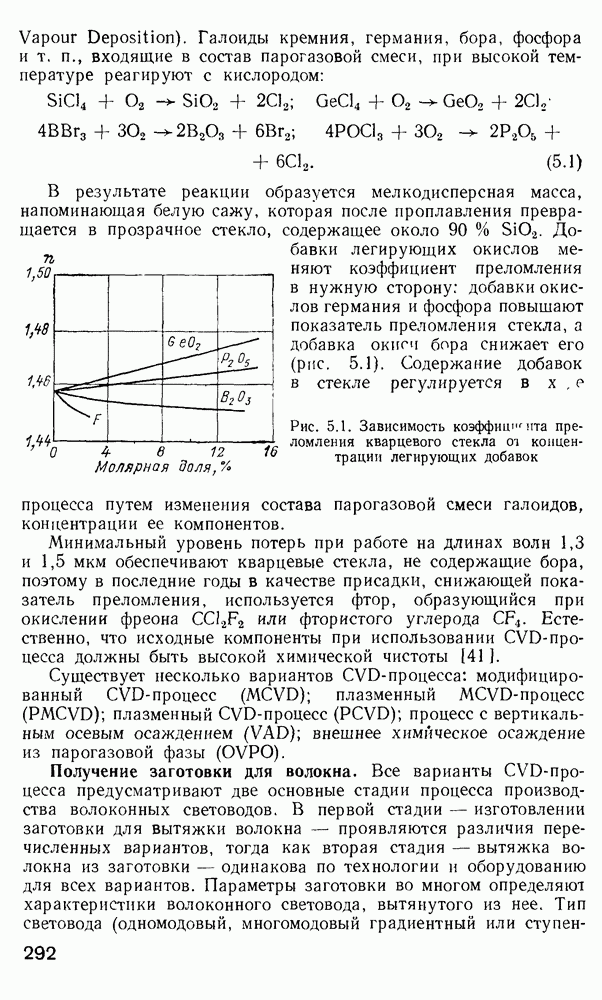
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ