| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
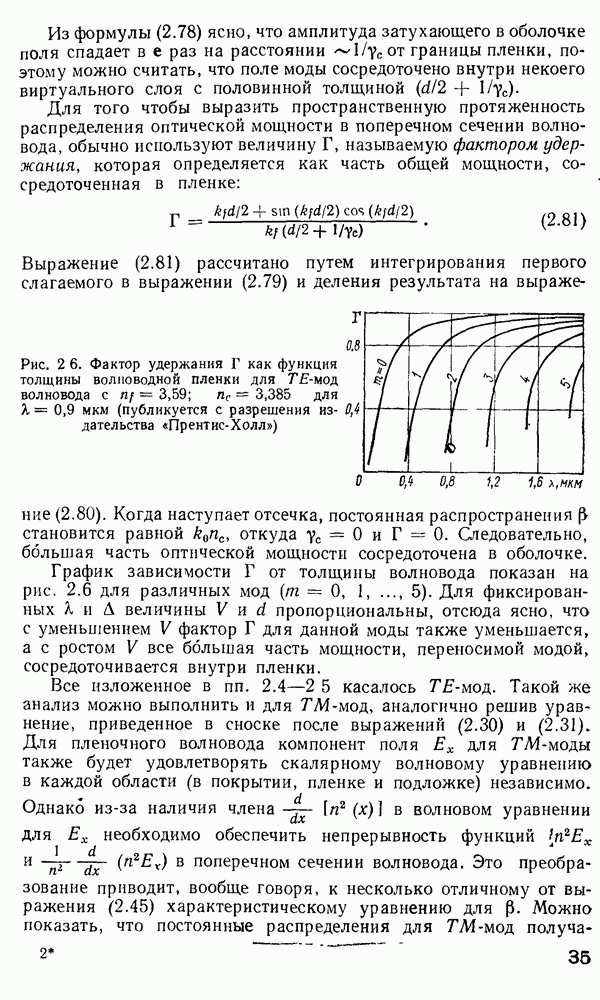
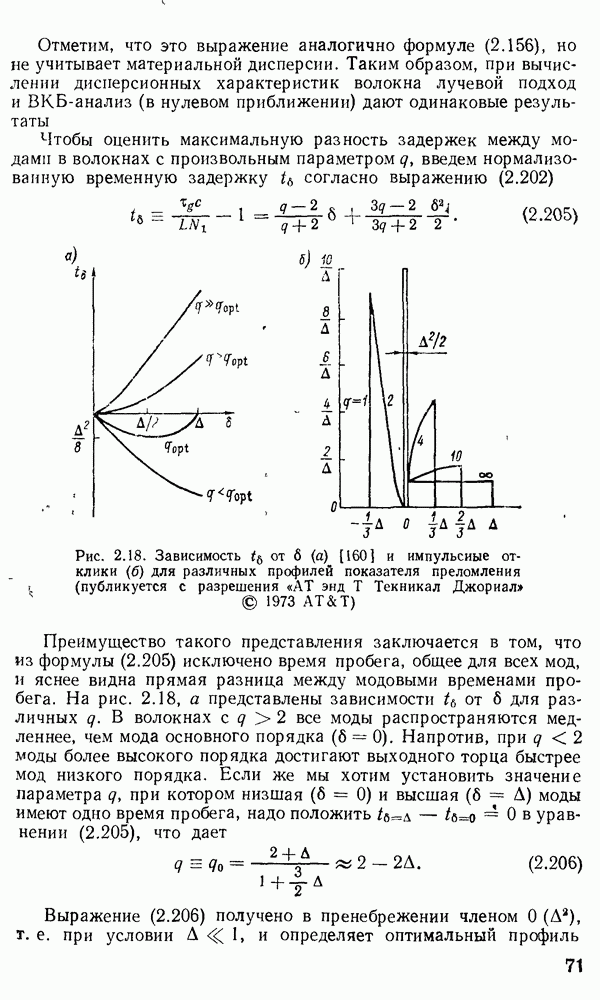
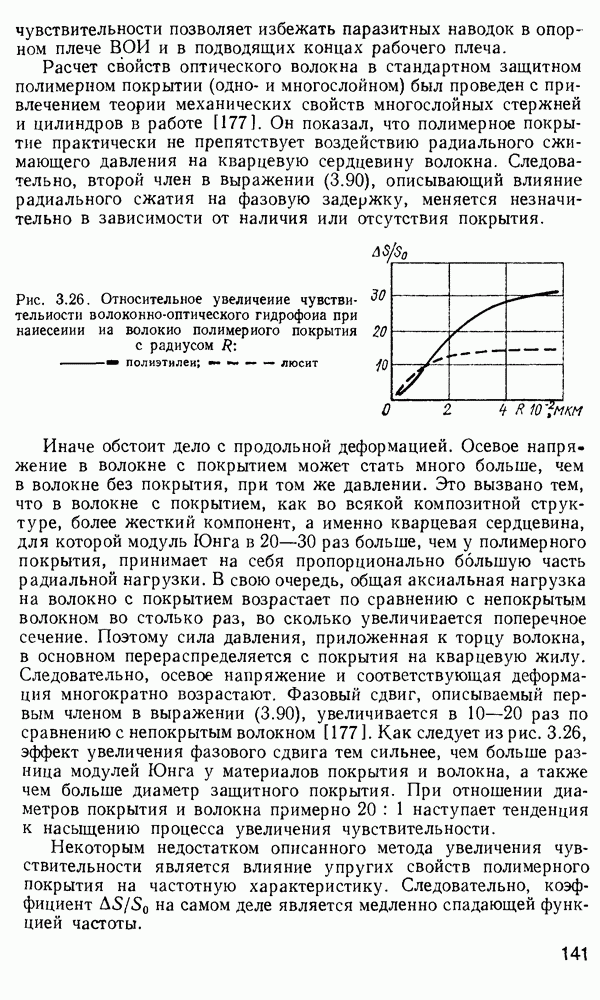
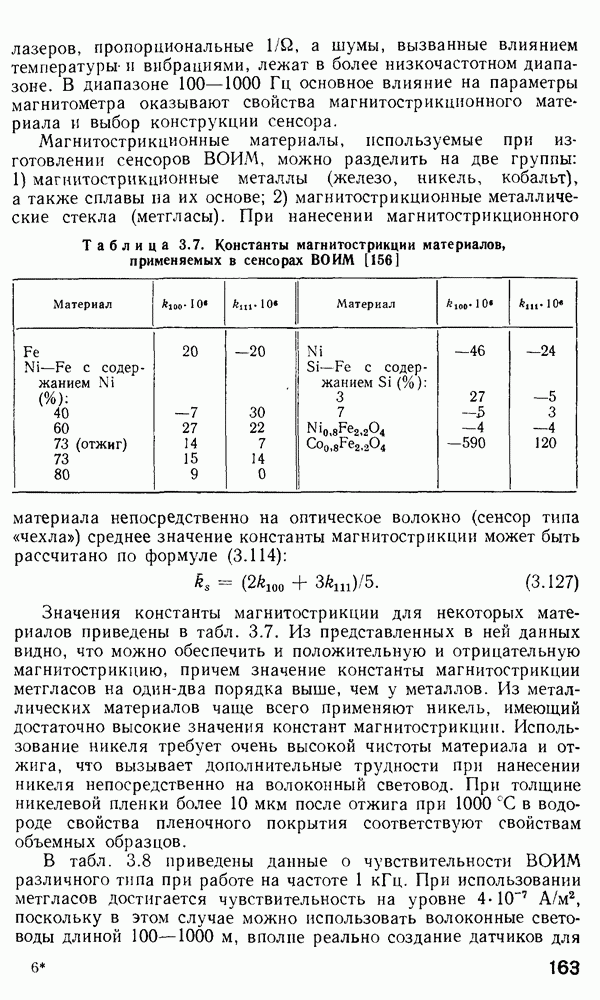
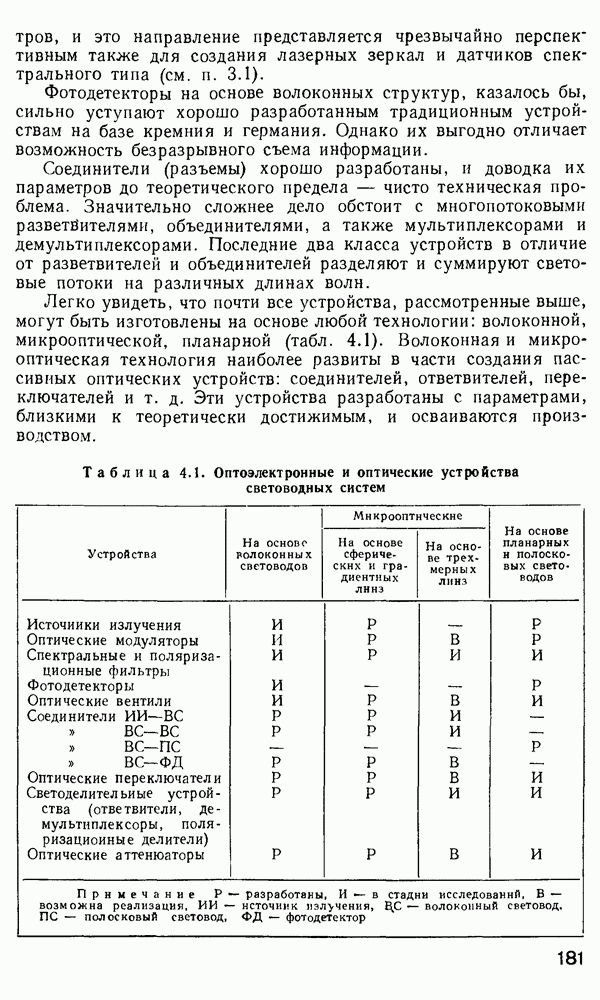
Распределение мощности направляемых мод в поперечном сечении волокна.
По аналогии с расчетом потока энергии в планарных волноводах, представленном в  заметим, что
заметим, что  -компонент вектора Пойнтинга [см. формулу (2.73)], проинтегрированный по поперечному сечению волновода, даст выражение для потока мощности, распространяющейся вдоль волновода. Таким образом:
-компонент вектора Пойнтинга [см. формулу (2.73)], проинтегрированный по поперечному сечению волновода, даст выражение для потока мощности, распространяющейся вдоль волновода. Таким образом:

где  Вместо компонентов поля
Вместо компонентов поля  в сердцевине и оболочке из формул (2.125) и (2.127), выполнив интегрирование с помощью стандартных интегралов функций Бесселя, можно получить:
в сердцевине и оболочке из формул (2.125) и (2.127), выполнив интегрирование с помощью стандартных интегралов функций Бесселя, можно получить:

где  Поскольку
Поскольку  непрерывны при
непрерывны при  можно получить при условии непрерывности
можно получить при условии непрерывности  что
что

Используем рекуррентные соотношения

совместно с определением

Уравнения (2.143) преобразуются тогда в

так что

Таким образом, выражения для относительной мощности в сердцевине и оболочке соответственно могут быть записаны как

Эти уравнения ясно показывают, что вдали от отсечки, поскольку до будет велико и, следовательно, из  формулы
формулы  большая часть энергии моды останется в сердцевине. С другой стороны, если воспользоваться приблизительным выражением [159]
большая часть энергии моды останется в сердцевине. С другой стороны, если воспользоваться приблизительным выражением [159]


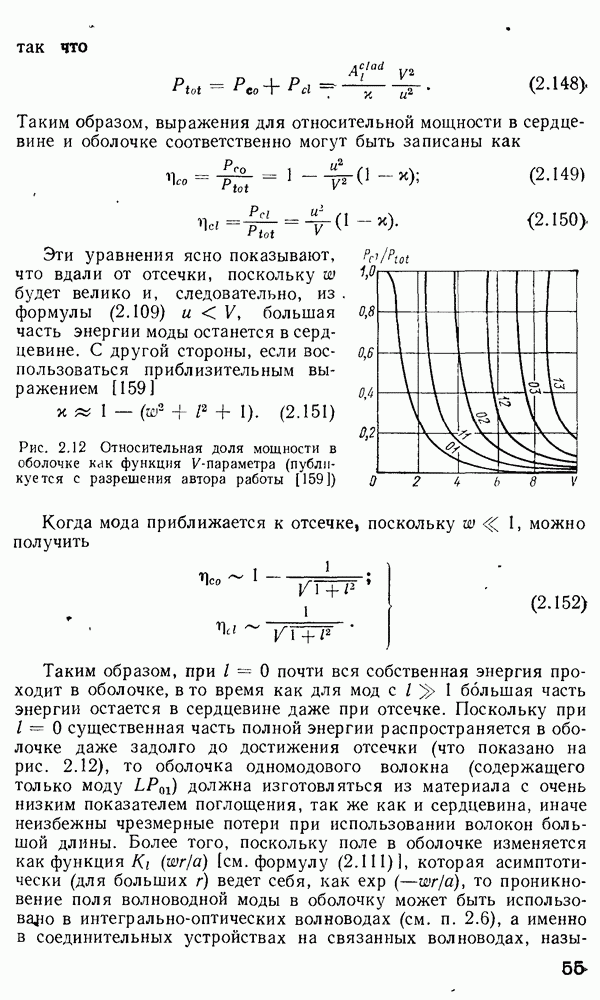
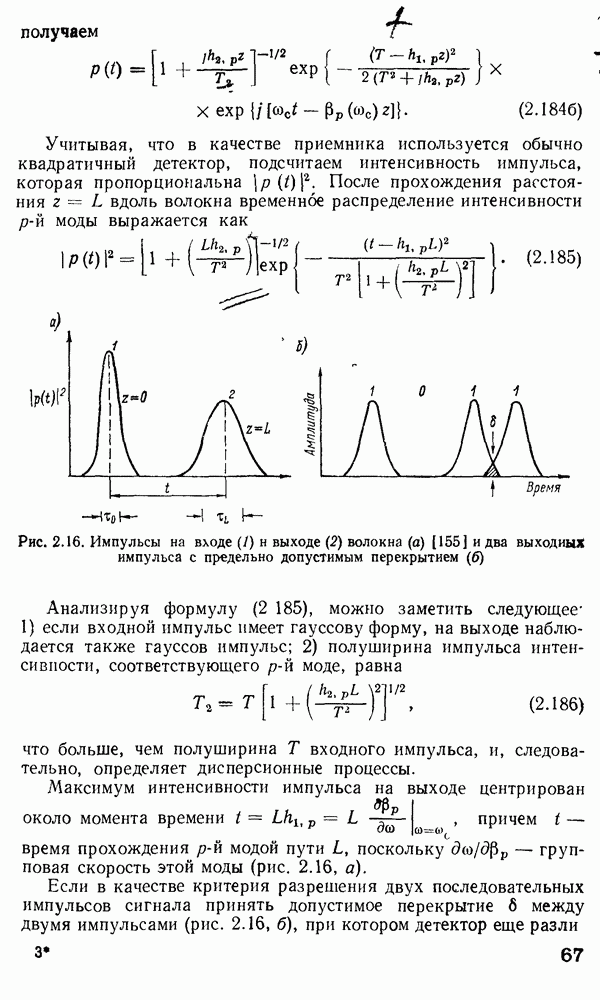
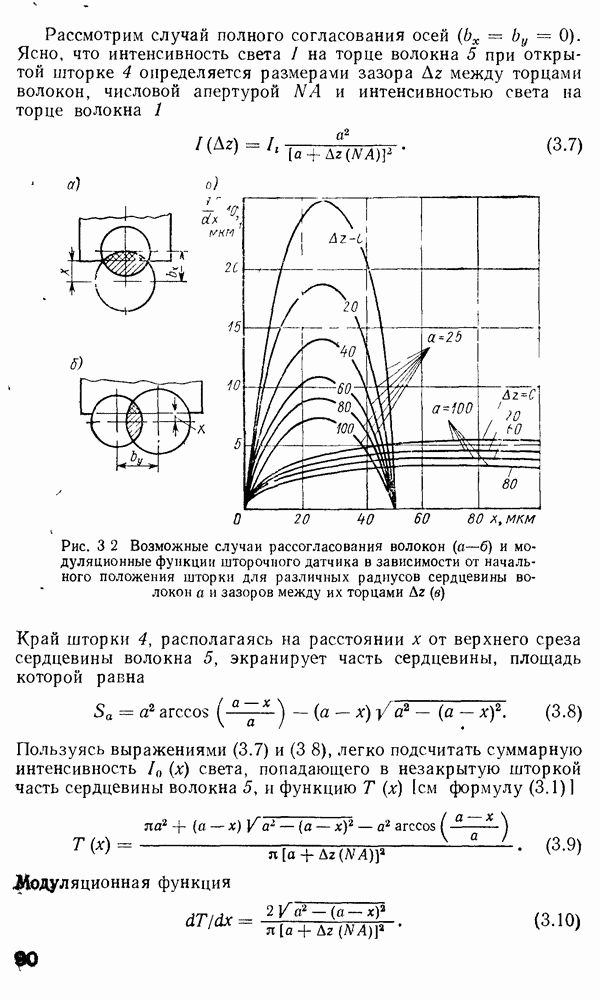
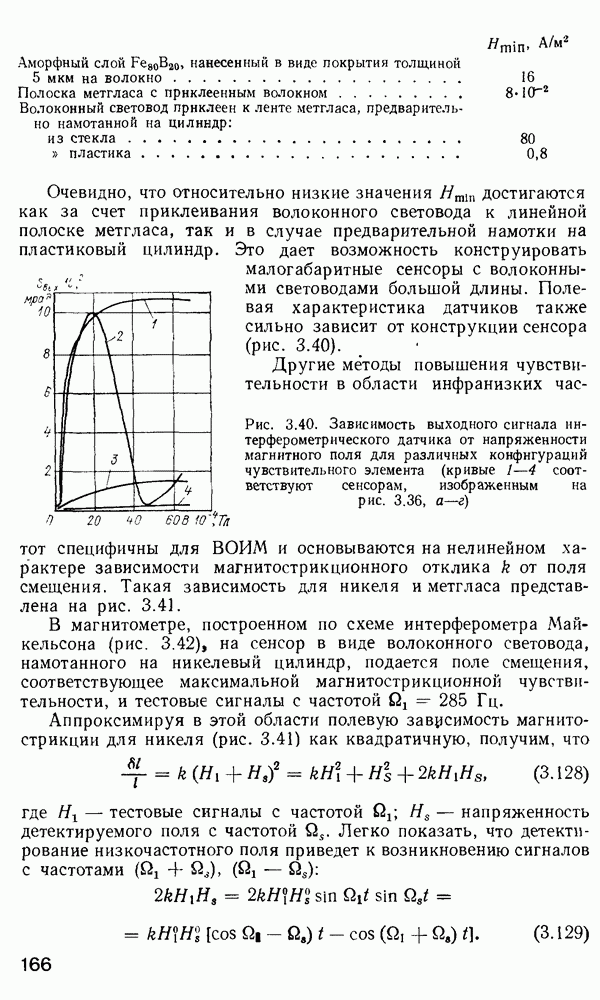
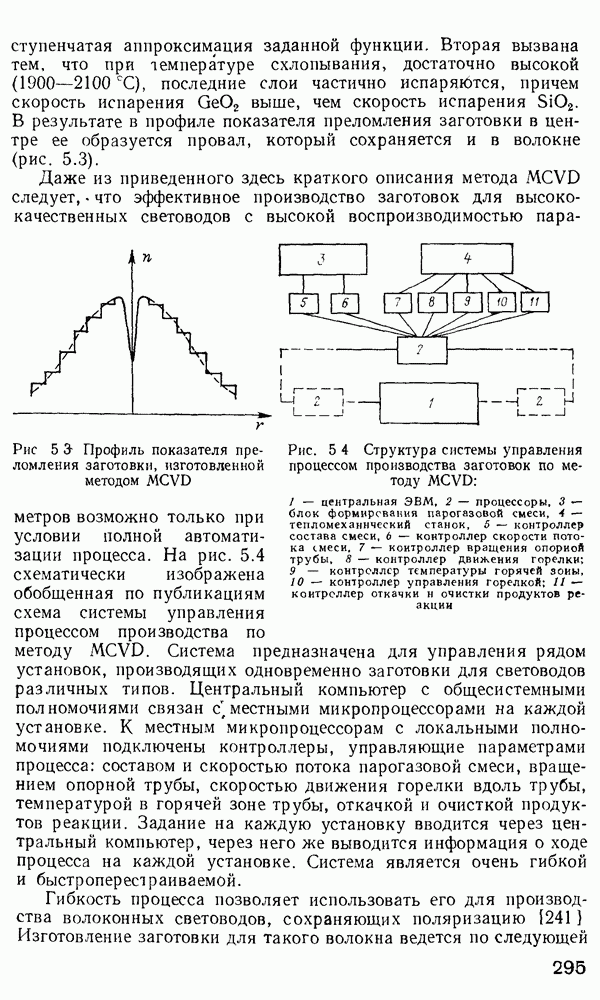
Рис. 2.12 Относительная доля мощности в оболочке как функция У-параметра (публикуется с разрешения автора работы [159])
Когда мода приближается к отсечке, поскольку  можно получить
можно получить

Таким образом, при  почти вся собственная энергия проходит в оболочке, в то время как для мод с
почти вся собственная энергия проходит в оболочке, в то время как для мод с  большая часть энергии остается в сердцевине даже при отсечке. Поскольку при
большая часть энергии остается в сердцевине даже при отсечке. Поскольку при  существенная часть полной энергии распространяется в оболочке даже задолго до достижения отсечки (что показано на рис. 2.12), то оболочка одномодового волокна (содержащего только моду
существенная часть полной энергии распространяется в оболочке даже задолго до достижения отсечки (что показано на рис. 2.12), то оболочка одномодового волокна (содержащего только моду  должна изготовляться из материала с очень низким показателем поглощения, так же как и сердцевина, иначе неизбежны чрезмерные потери при использовании волокон большой длины. Более того, поскольку поле в оболочке изменяется как функция
должна изготовляться из материала с очень низким показателем поглощения, так же как и сердцевина, иначе неизбежны чрезмерные потери при использовании волокон большой длины. Более того, поскольку поле в оболочке изменяется как функция  [см. формулу (2.111)], которая асимптотически (для больших
[см. формулу (2.111)], которая асимптотически (для больших  ) ведет себя, как
) ведет себя, как  то проникновение поля волноводной моды в оболочку может быть использовало в интегрально-оптических волноводах (см. п. 2.6), а именно в соединительных устройствах на связанных волноводах,
то проникновение поля волноводной моды в оболочку может быть использовало в интегрально-оптических волноводах (см. п. 2.6), а именно в соединительных устройствах на связанных волноводах,
называемых волоконными направленными ответвителями. Эти элементы обычно являются весьма важными в волоконно-оптических приборах. Если мы определим эффективный радиус для данной моды как  т. е. как расстояние, на котором максимальное значение поля моды в оболочке спадает в
т. е. как расстояние, на котором максимальное значение поля моды в оболочке спадает в  раз, то [83]
раз, то [83]
 ]
]
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
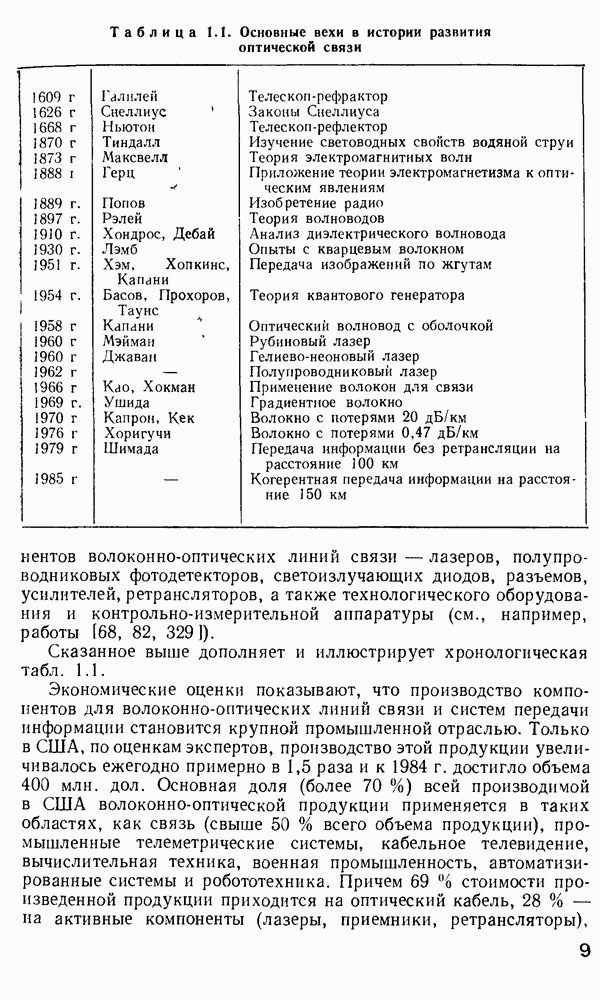
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
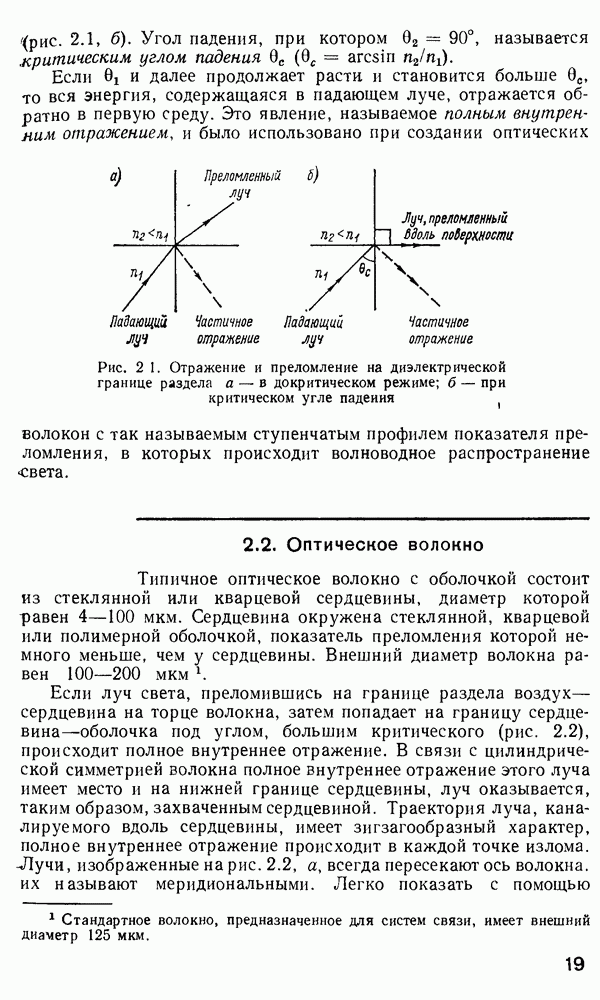
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
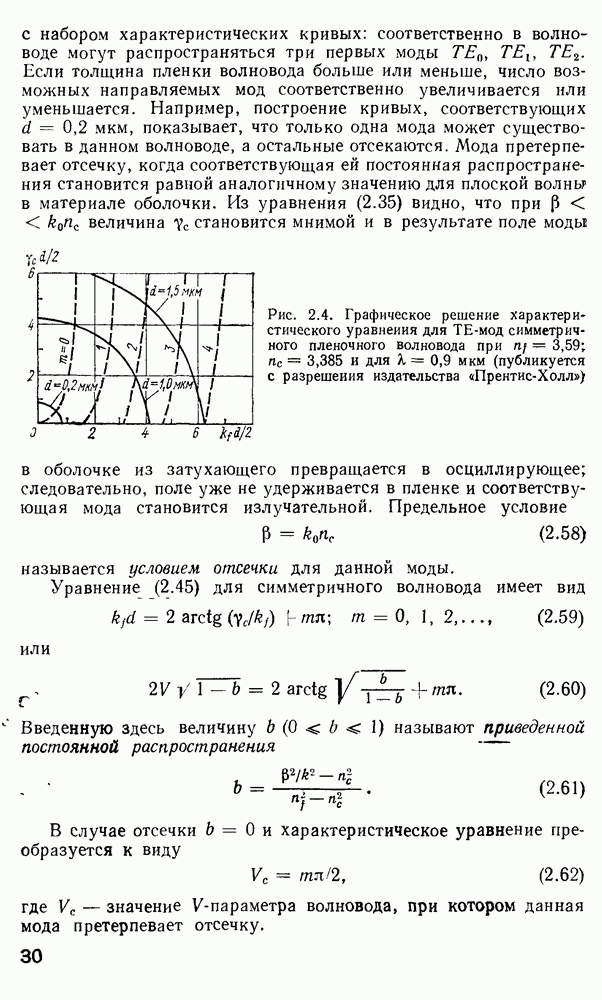
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
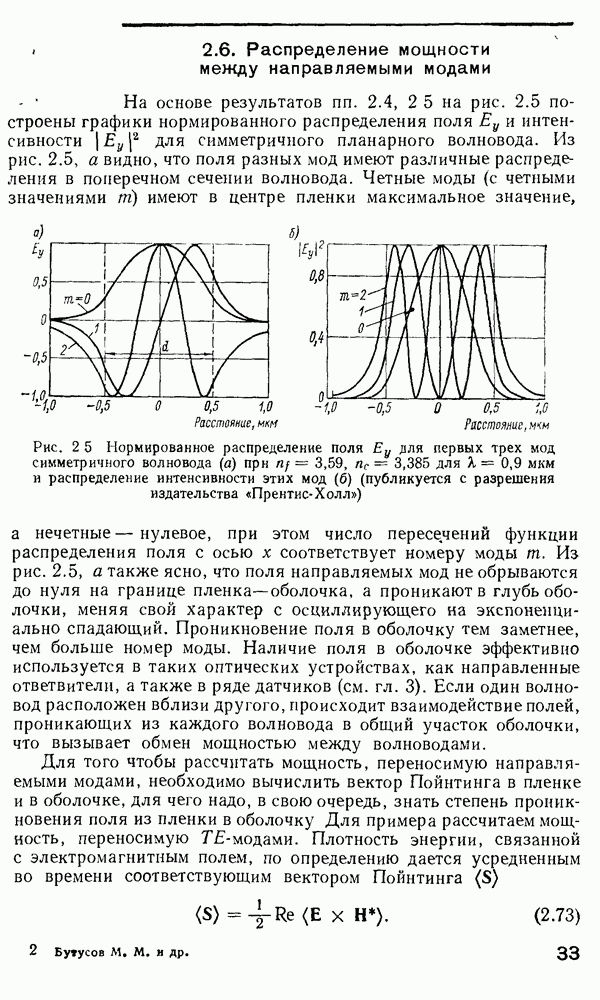
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
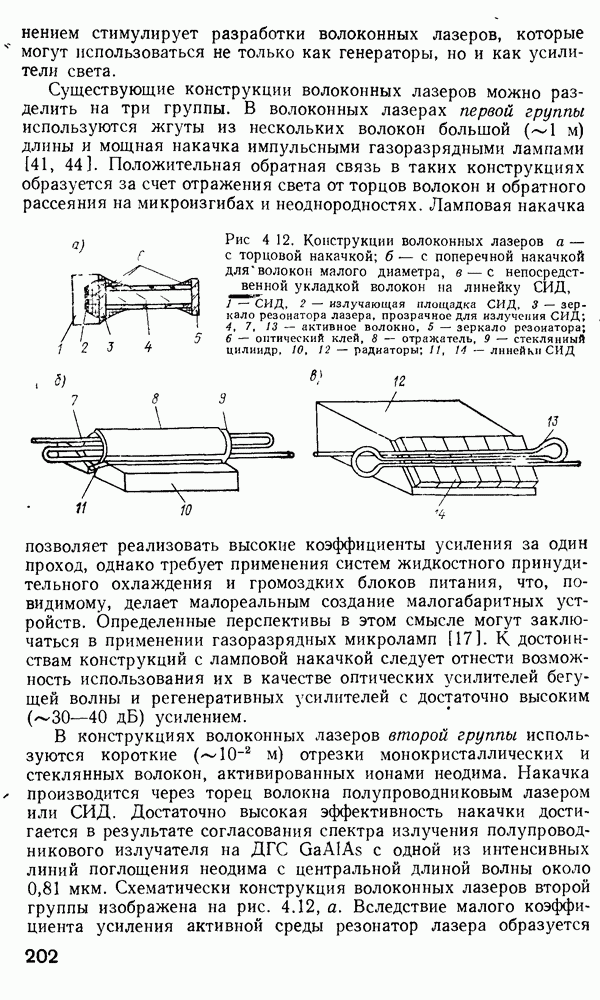
- Волоконные лазеры.
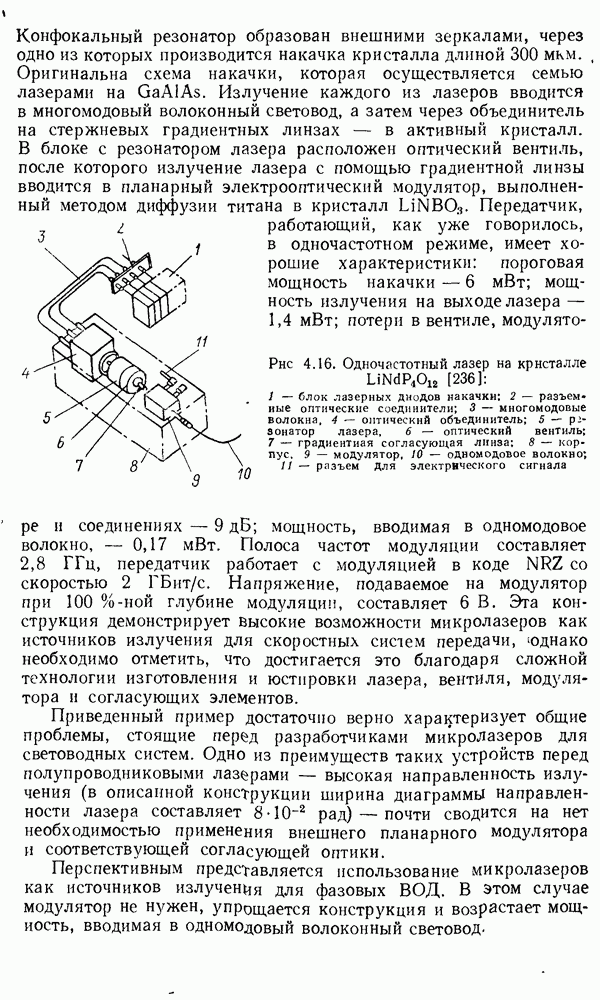
- Объемные микролазеры.
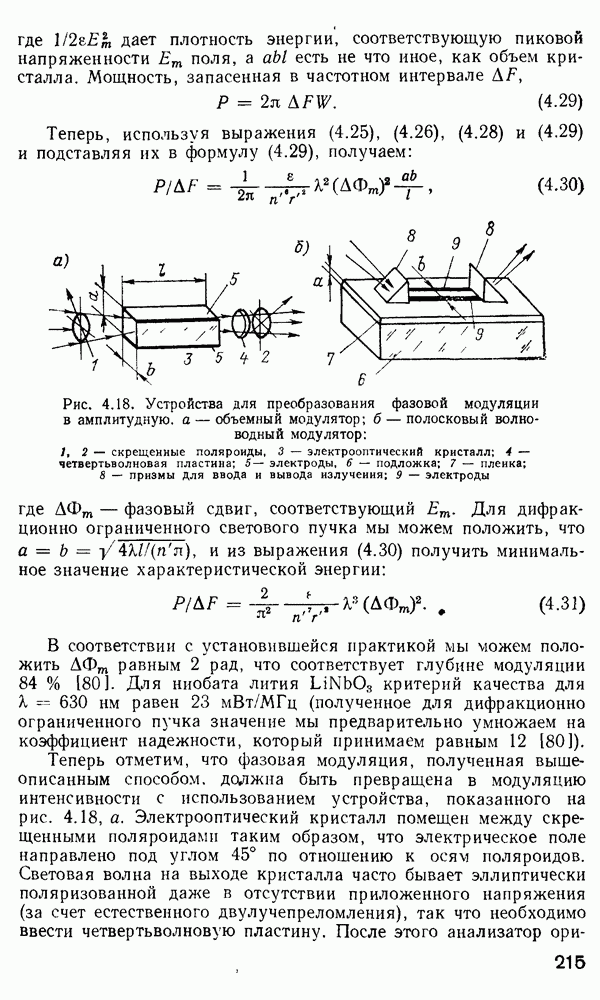
- 4.3. Оптические модуляторы
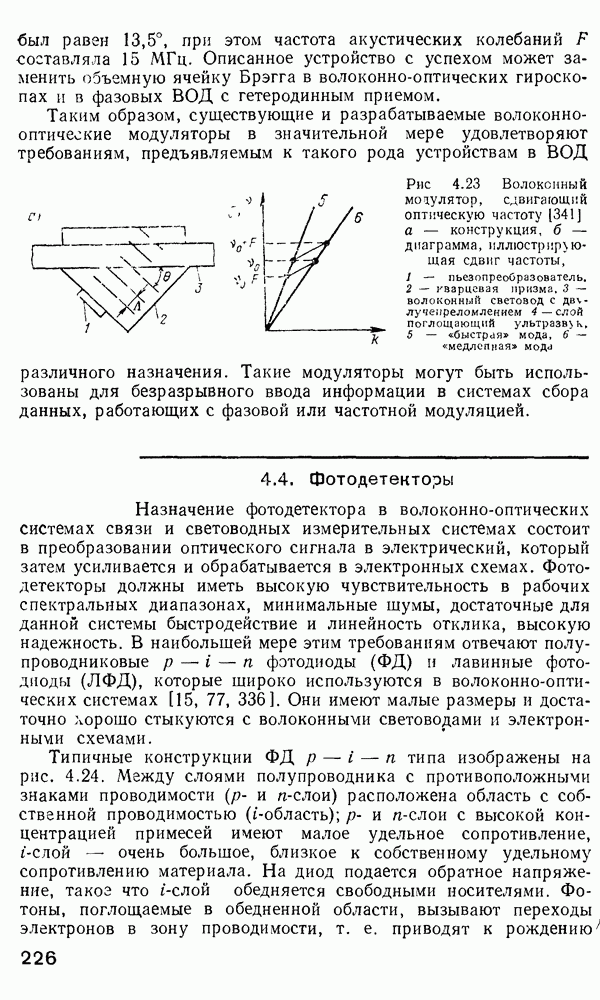
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
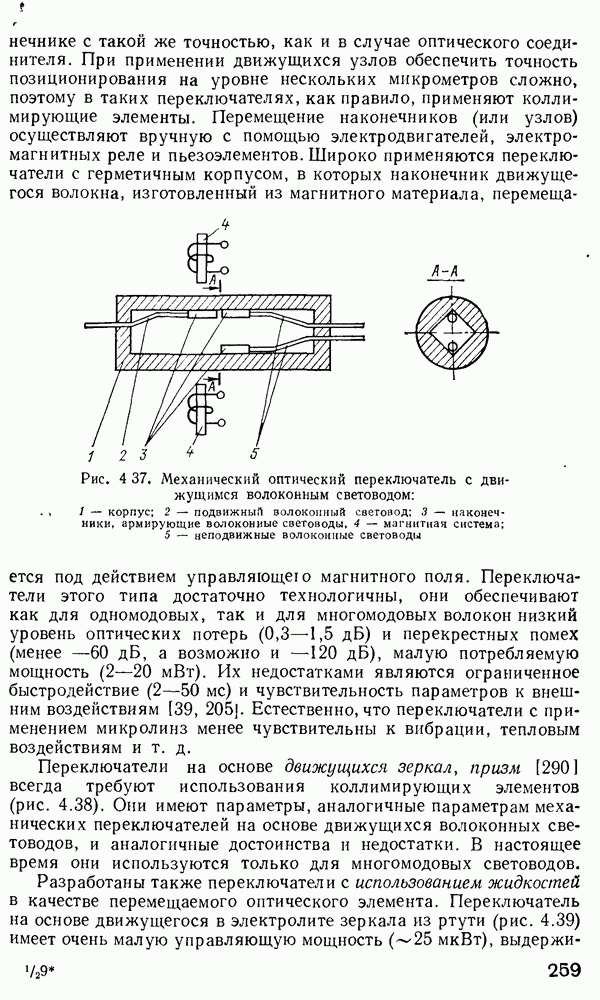
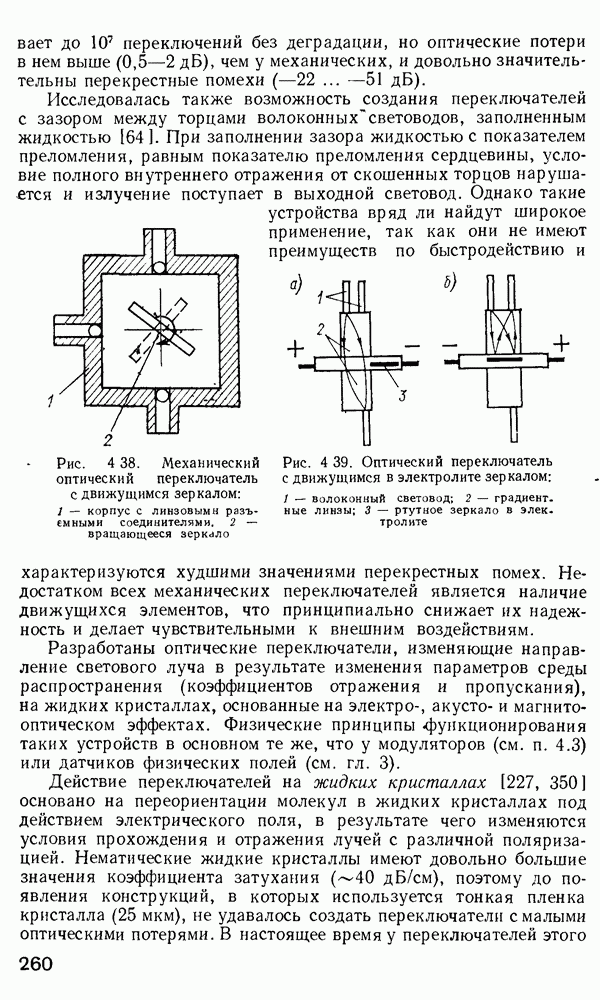
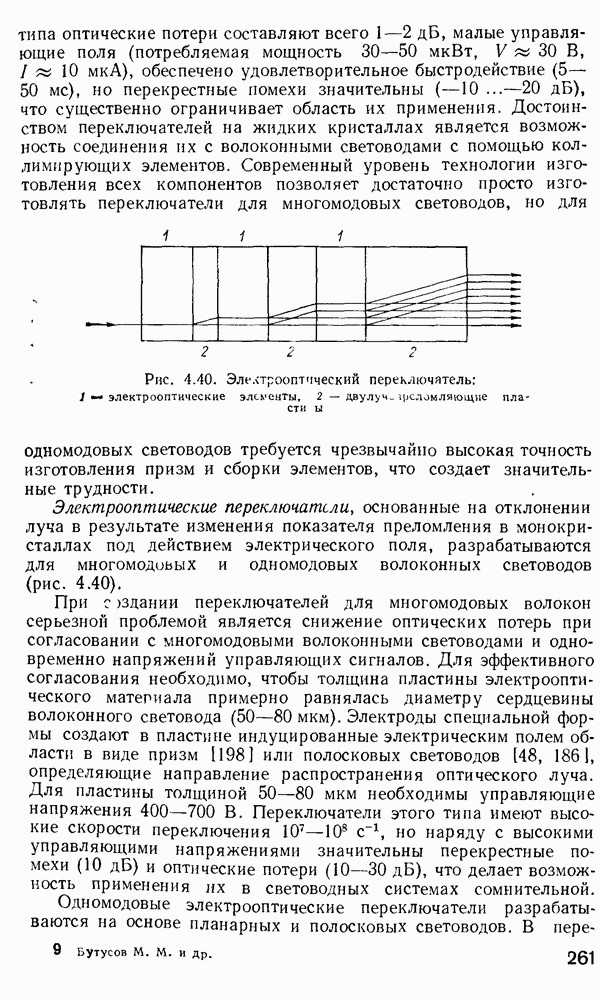
- 4.7. Волоконно-оптические переключатели
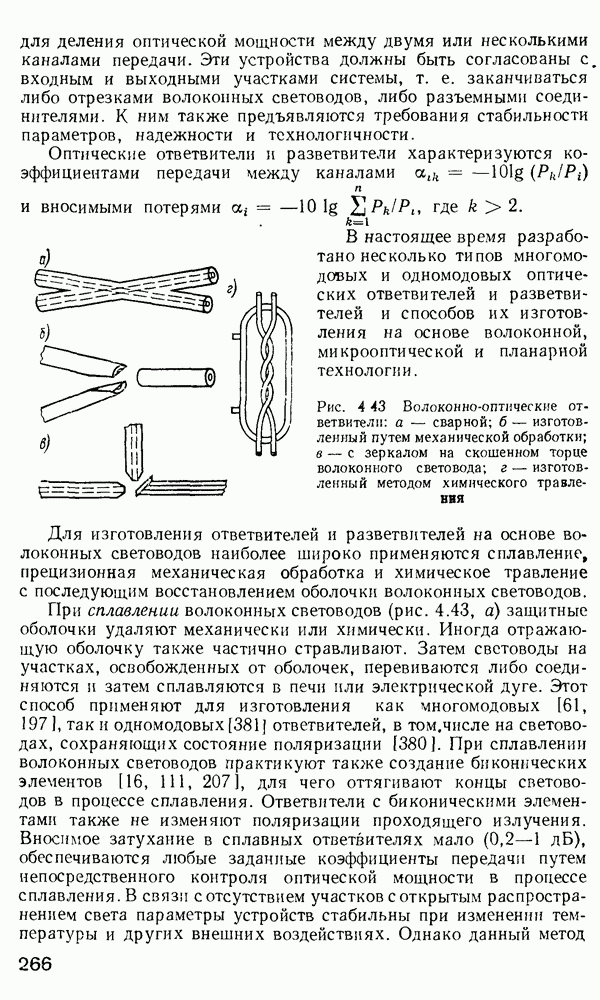
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
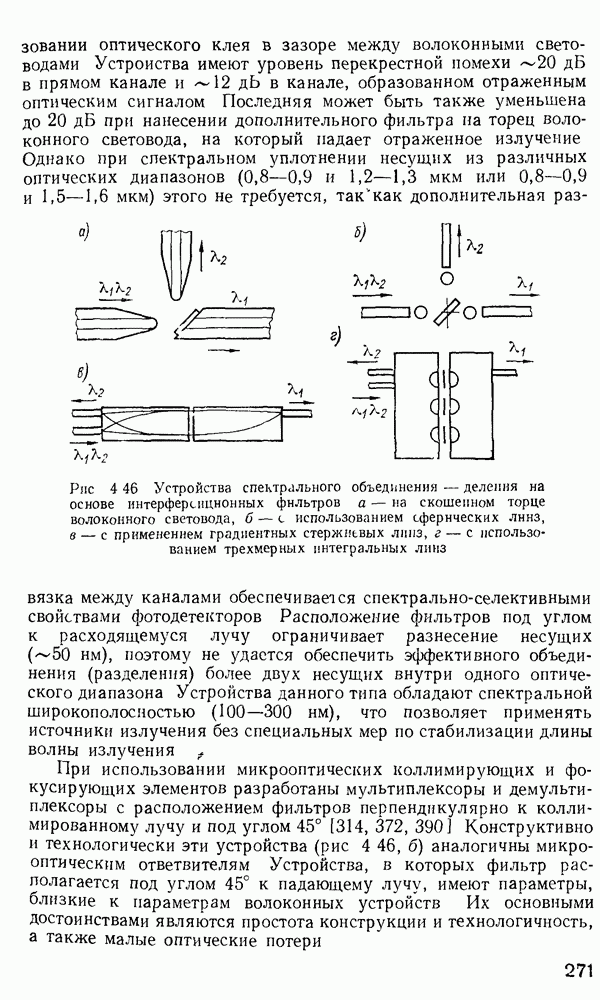
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
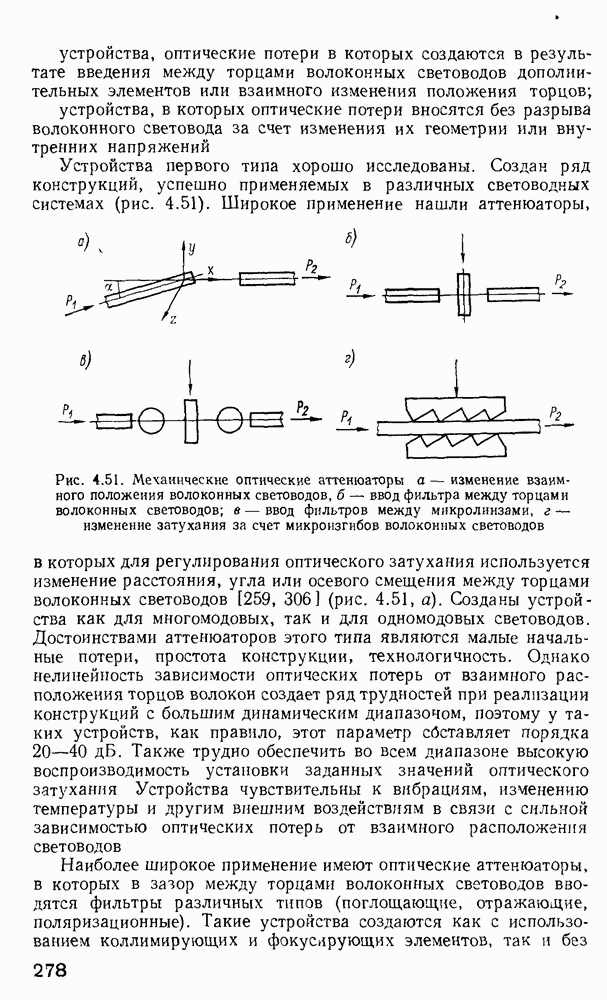
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
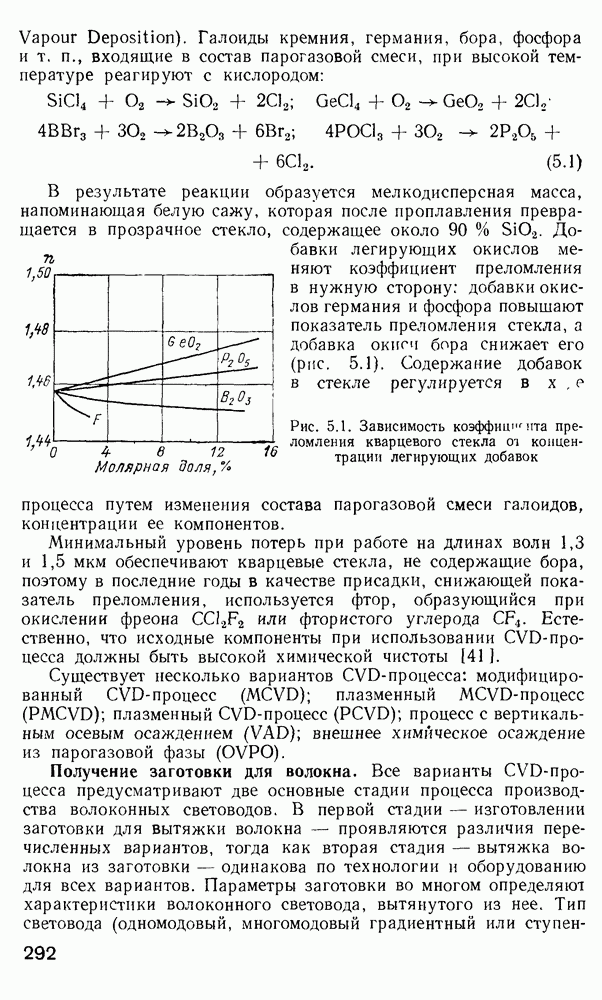
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ