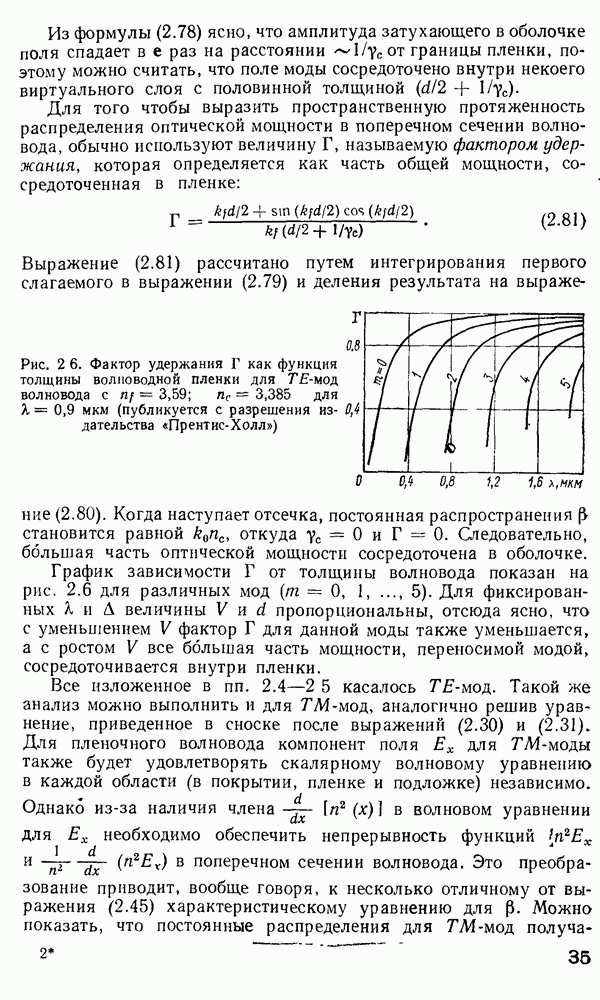
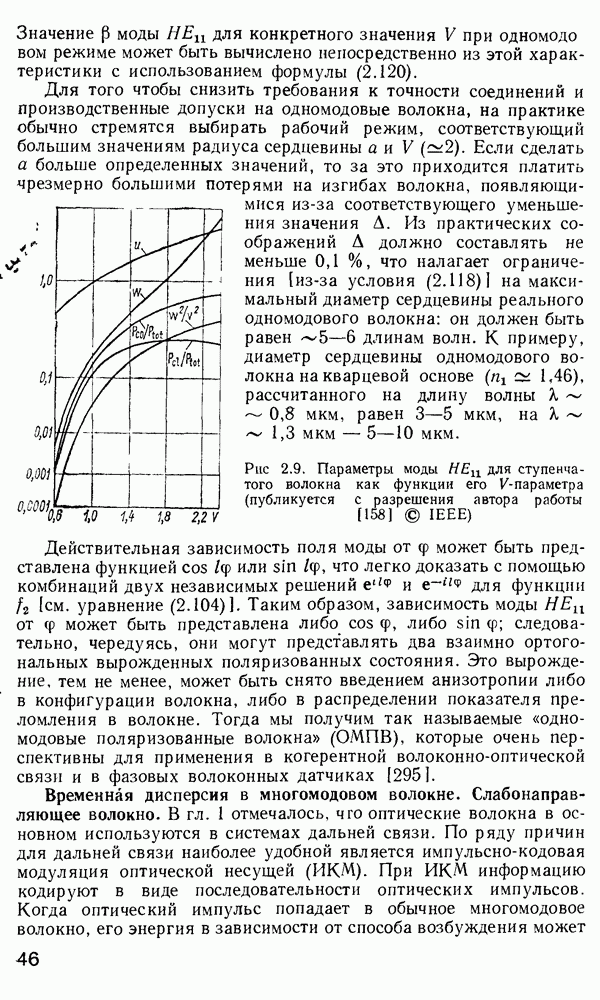
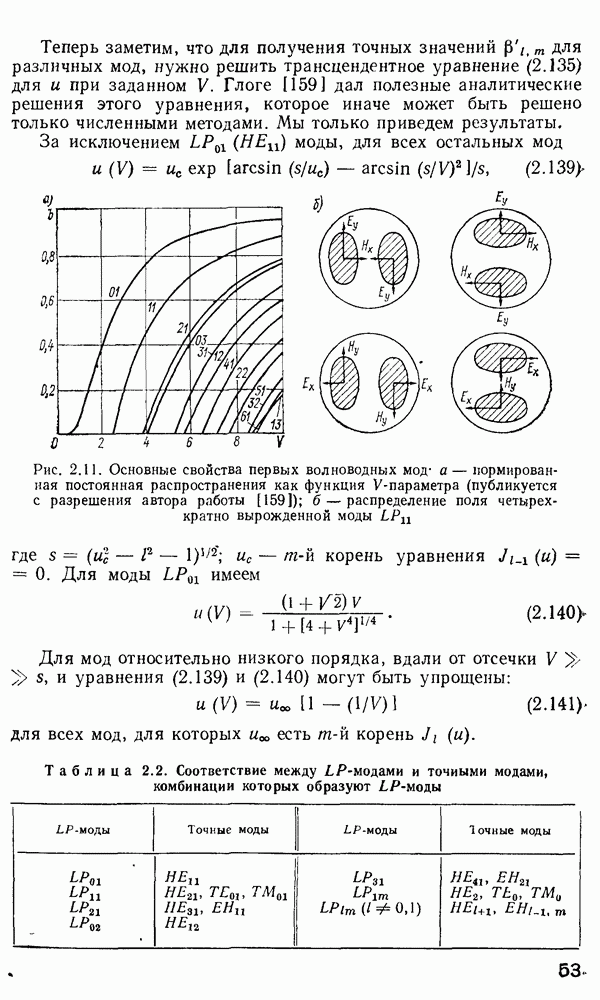
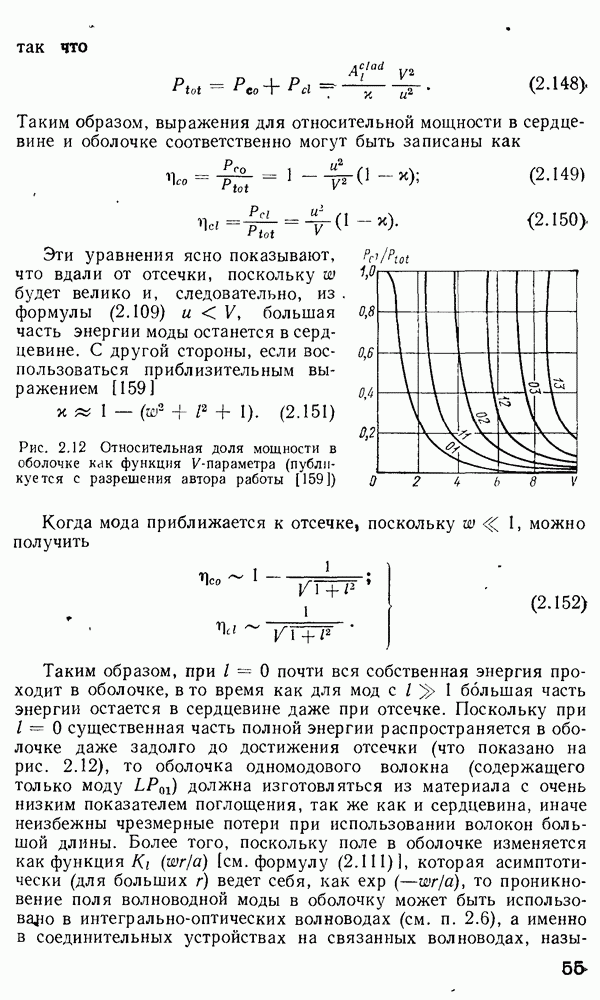
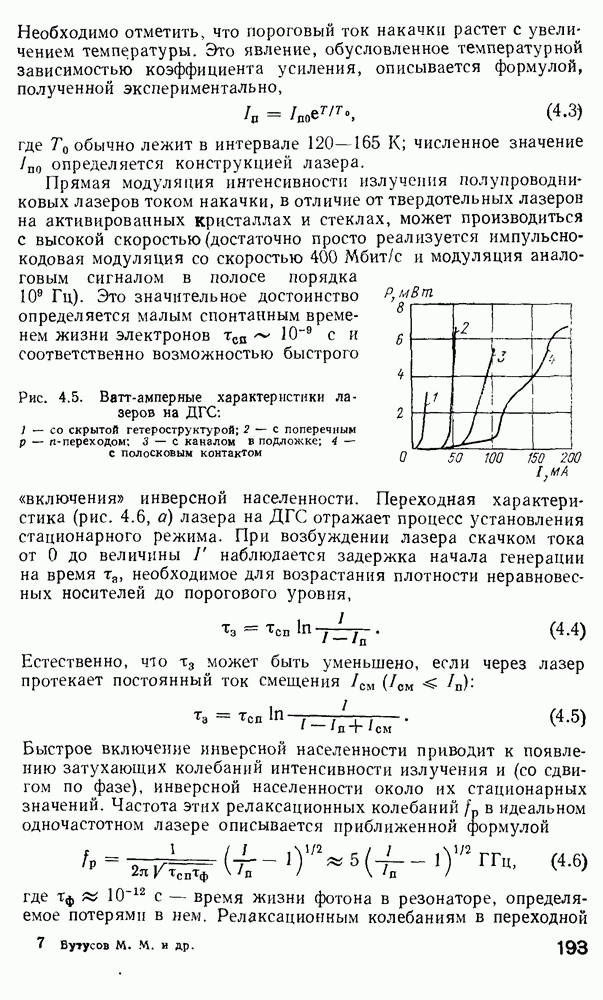
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
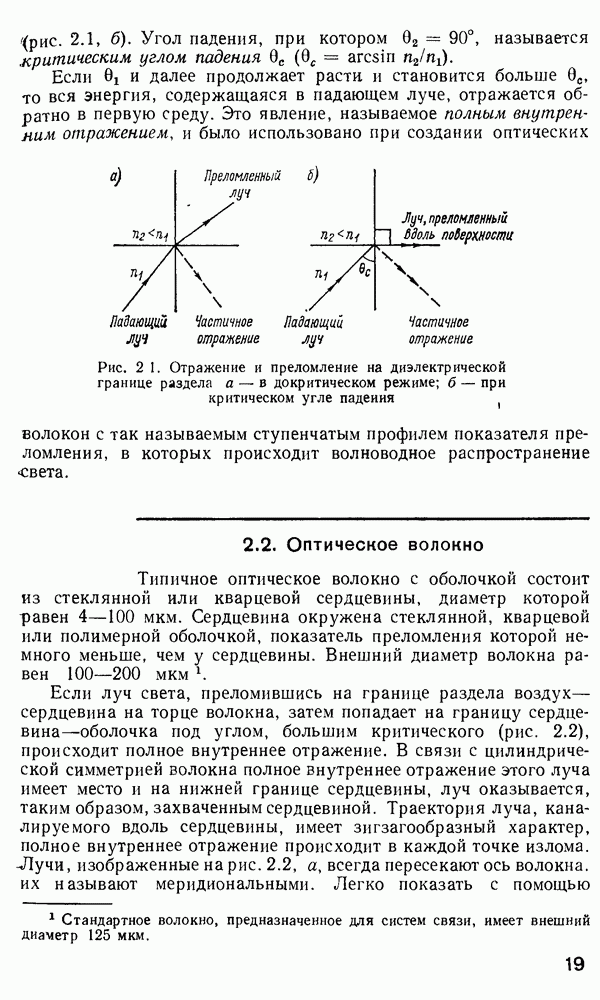
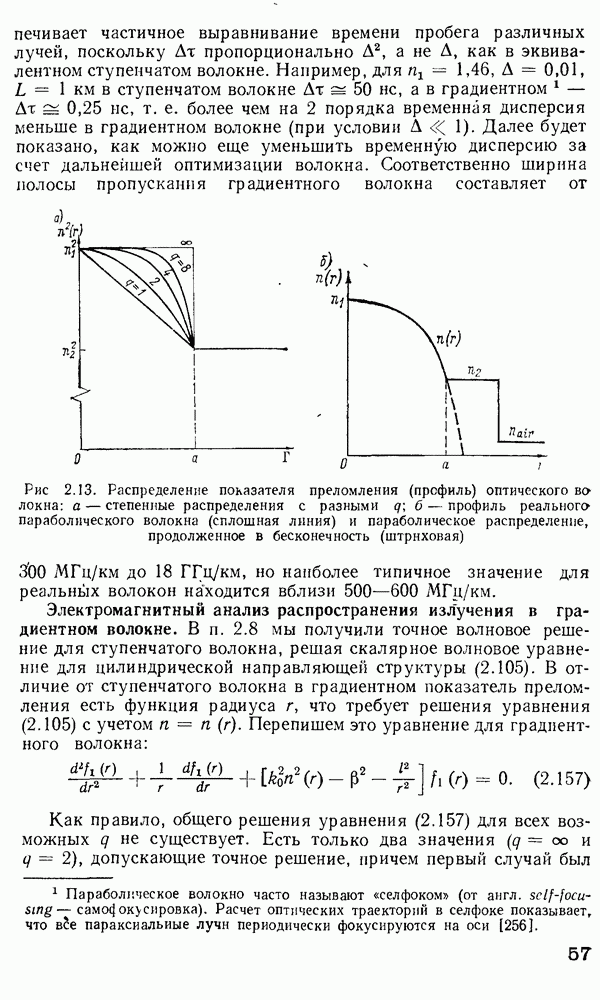
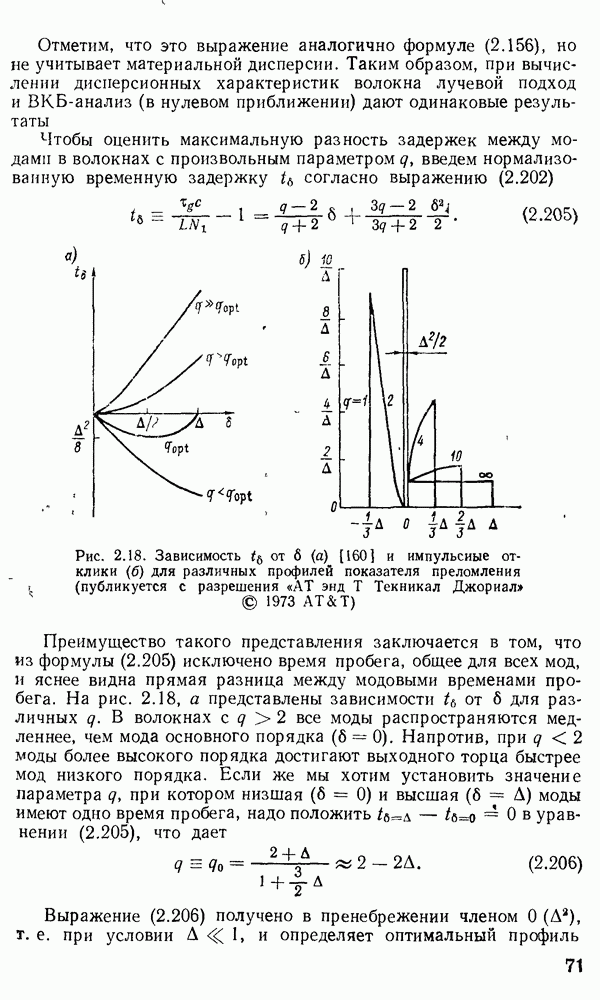
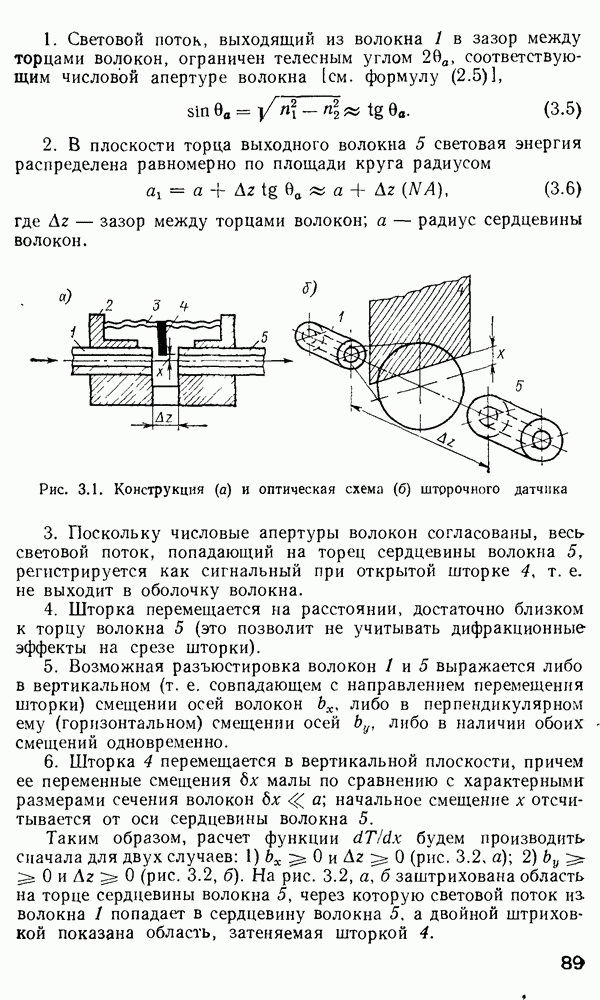
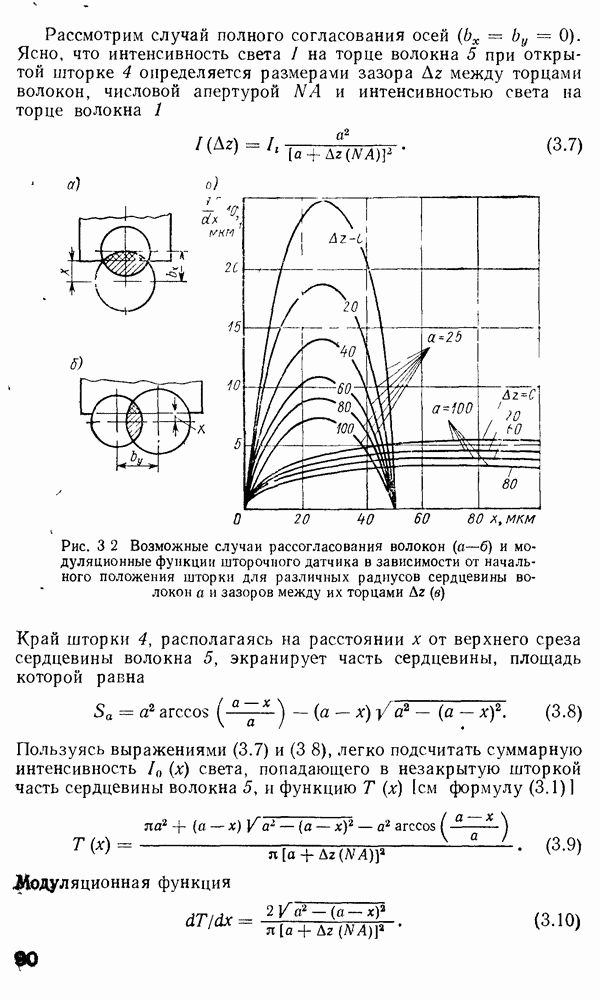
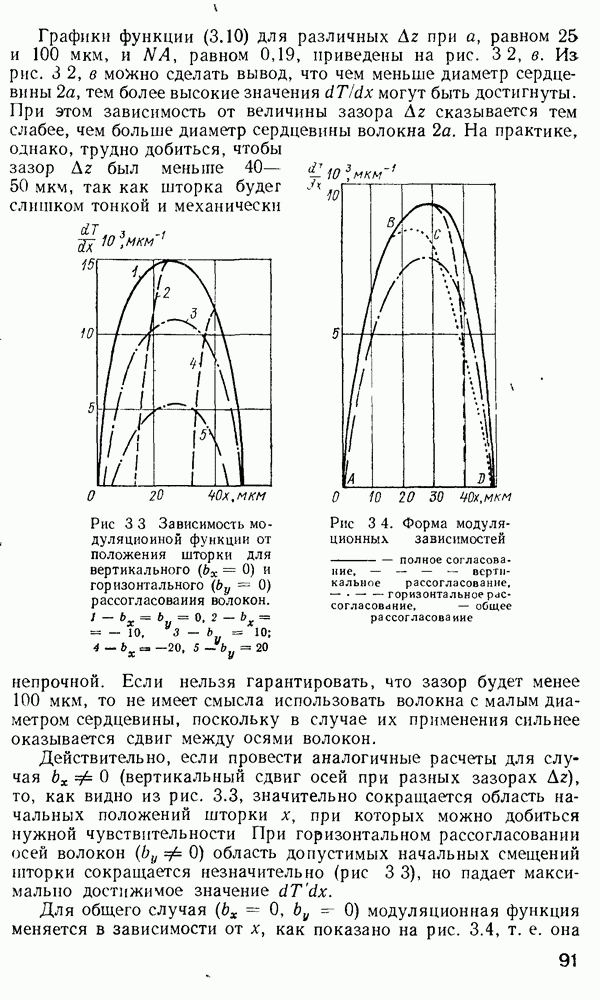
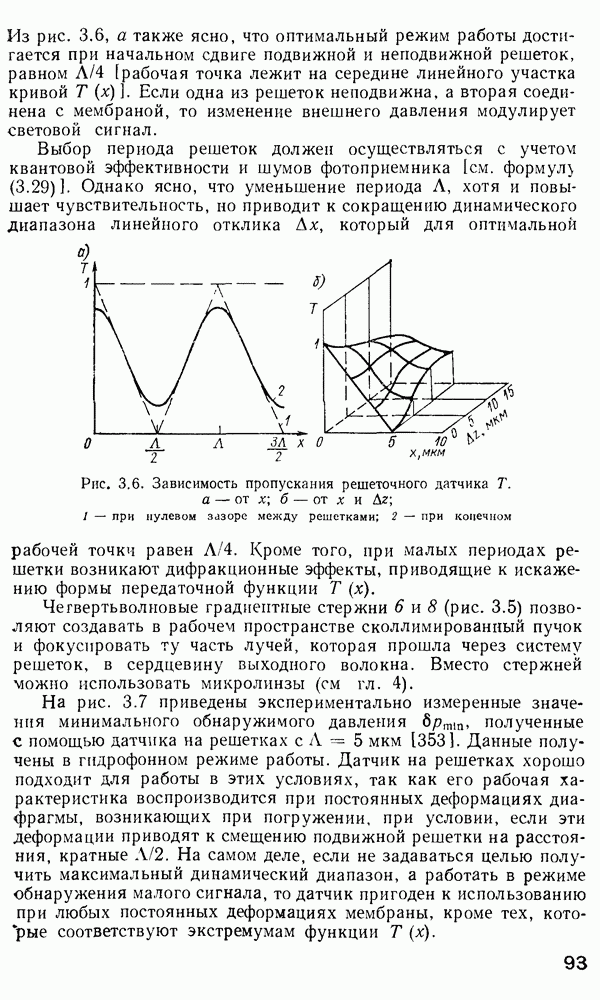
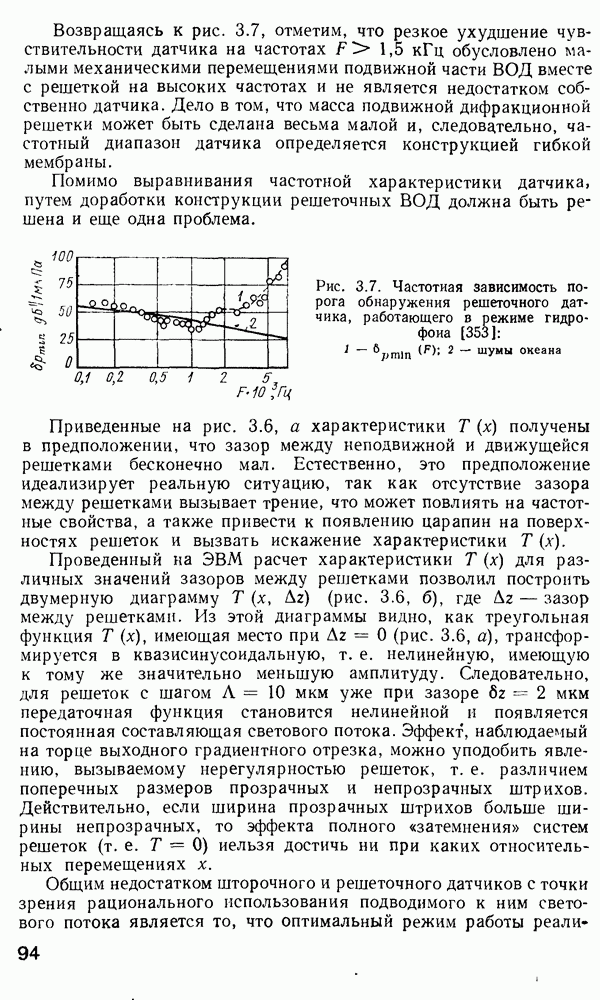
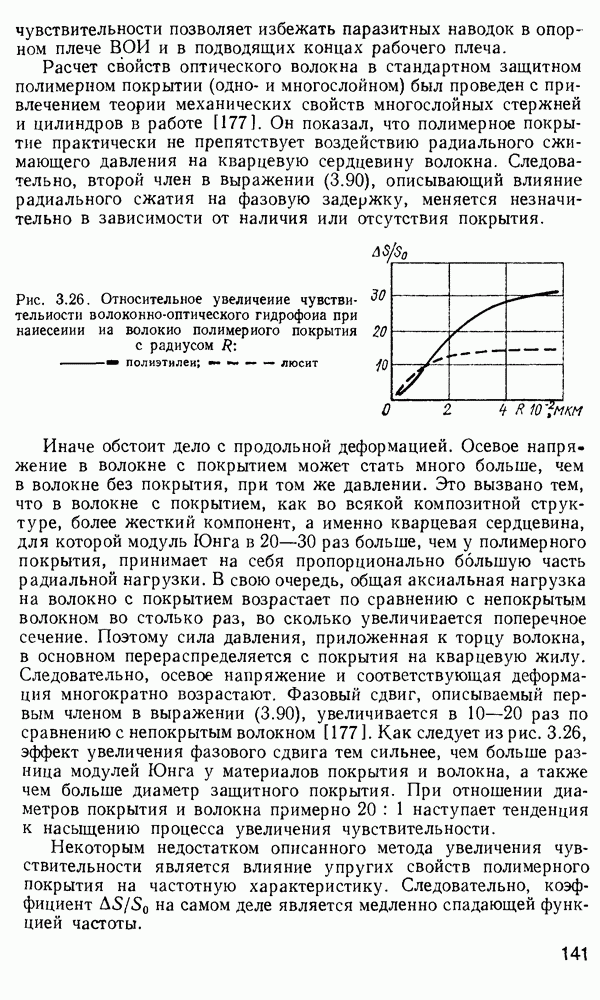
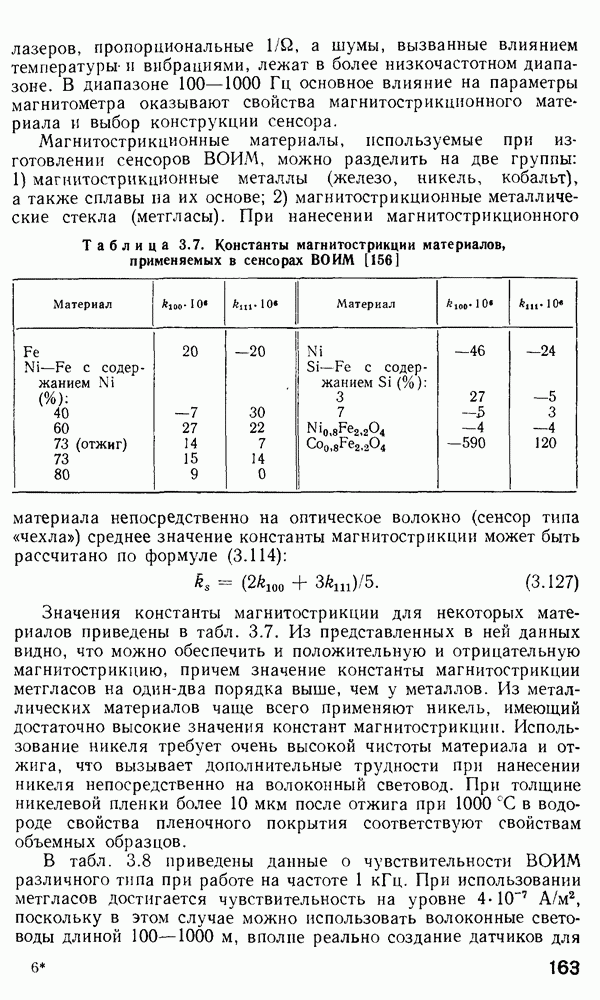
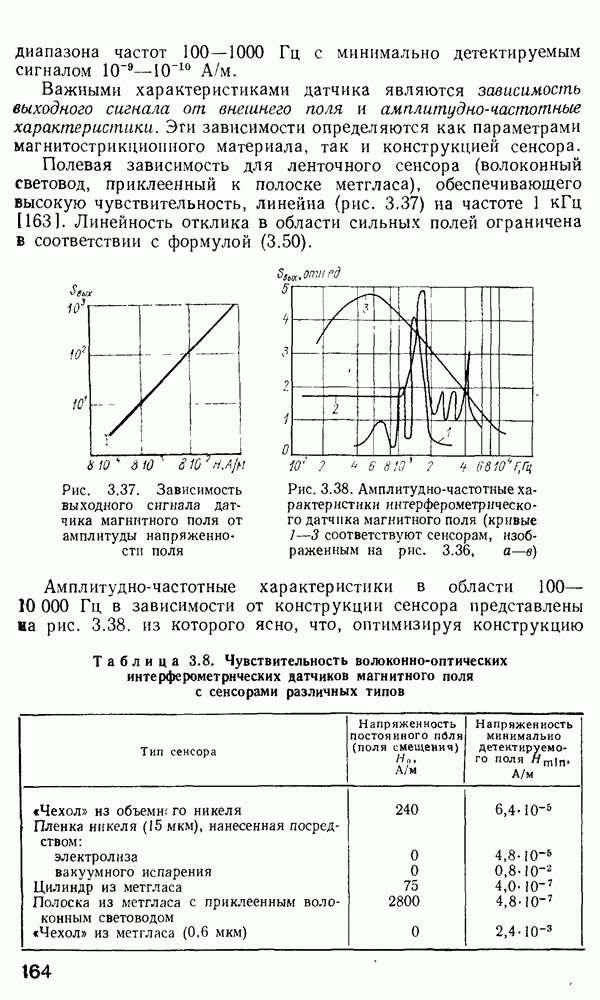
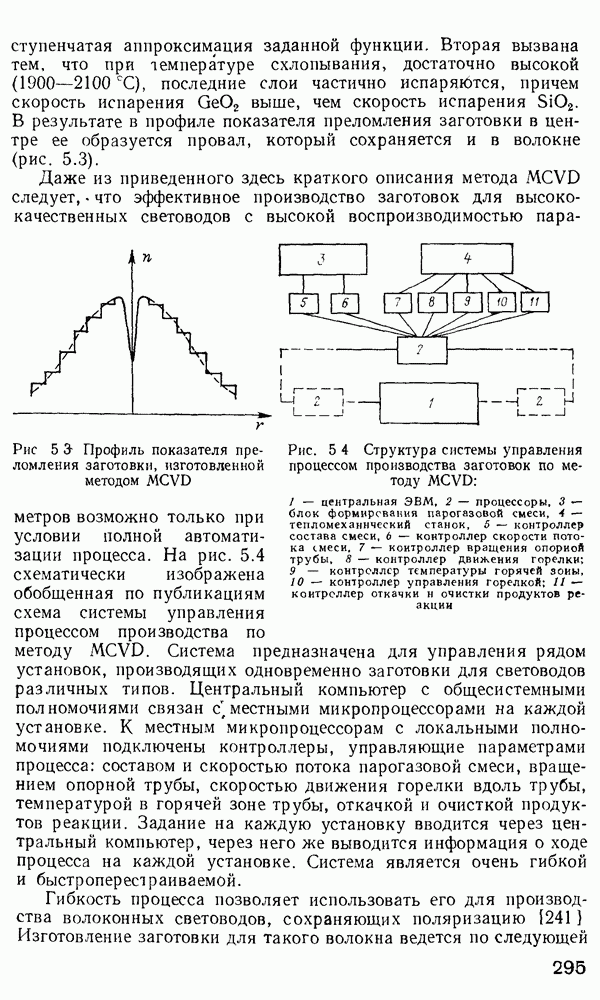
Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
В гл. 1 отмечалось, что оптические волокна в основном используются в системах дальней связи. По ряду причин для дальней связи наиболее удобной является импульсно-кодовая модуляция оптической несущей  При
При  информацию кодируют в виде последовательности оптических импульсов. Когда оптический импульс попадает в обычное многомодовое волокно, его энергия в зависимости от способа возбуждения может
информацию кодируют в виде последовательности оптических импульсов. Когда оптический импульс попадает в обычное многомодовое волокно, его энергия в зависимости от способа возбуждения может
быть распределена между большим числом разрешенных волноводных мод. Каждая из этих мод будет распространяться по длине волокна со скоростью  характерной для данной модовой группы. На выходе волокна энергия различных мод суммируется и образуется импульс, как правило, большей длительности, чем входной. Эффект «расплывания» импульса известен как временная дисперсия. Временная дисперсия является одной из определяющих характеристик при расчете многомодовых волокон, так как она определяет ширину полосы пропускания волокон. Поскольку в одномодовых волокнах распространяется лишь одна мода и, следовательно, возможна лишь одна групповая скорость, то временная дисперсия, казалось бы, должна отсутствовать. Однако в действительности это не так. Как мы увидим в дальнейшем, вследствие конечности ширины спектра реально возможного светового излучения всегда будет наблюдаться некоторая остаточная временная дисперсия даже в одномодовом волокне. В многомодовых волокнах грубая оценка временного расплывания импульса может быть сделана с помощью вычисления разности времен прохождения по волокну между низшей и высшей разрешенными модами. Конкретная мода волокна со ступенчатым профилем показателя преломления имеет возможность распространяться под характеристическим углом
характерной для данной модовой группы. На выходе волокна энергия различных мод суммируется и образуется импульс, как правило, большей длительности, чем входной. Эффект «расплывания» импульса известен как временная дисперсия. Временная дисперсия является одной из определяющих характеристик при расчете многомодовых волокон, так как она определяет ширину полосы пропускания волокон. Поскольку в одномодовых волокнах распространяется лишь одна мода и, следовательно, возможна лишь одна групповая скорость, то временная дисперсия, казалось бы, должна отсутствовать. Однако в действительности это не так. Как мы увидим в дальнейшем, вследствие конечности ширины спектра реально возможного светового излучения всегда будет наблюдаться некоторая остаточная временная дисперсия даже в одномодовом волокне. В многомодовых волокнах грубая оценка временного расплывания импульса может быть сделана с помощью вычисления разности времен прохождения по волокну между низшей и высшей разрешенными модами. Конкретная мода волокна со ступенчатым профилем показателя преломления имеет возможность распространяться под характеристическим углом  создаваемым вектором плоской волны с осью волокна, который определяют из формулы, аналогичной выражению (2.66),
создаваемым вектором плоской волны с осью волокна, который определяют из формулы, аналогичной выражению (2.66),

где  — структурный номер моды, соответствующий конкретным значениям
— структурный номер моды, соответствующий конкретным значениям  . Как понятно из рис. 2.2, а, время, затрачиваемое обычным лучом на прохождение расстояния
. Как понятно из рис. 2.2, а, время, затрачиваемое обычным лучом на прохождение расстояния  в волокне,
в волокне,

Таким образом, если по волноводу одновременно распространяются под углом  изменяющимся между 0 и
изменяющимся между 0 и  различные лучи, имеющие одинаковую мощность, то эти лучи затратят различное время на прохождение по волокну и разница во времени между прохождением по кратчайшему (соответствующему
различные лучи, имеющие одинаковую мощность, то эти лучи затратят различное время на прохождение по волокну и разница во времени между прохождением по кратчайшему (соответствующему  и наиболее длинному (соответствующему
и наиболее длинному (соответствующему  путям, составит
путям, составит

Для  Таким образом
Таким образом

где  (см. п. 2.2). Если допустить, что
(см. п. 2.2). Если допустить, что  то в ступенчатом волокне длиной 1 км
то в ступенчатом волокне длиной 1 км  нс, т. е. импульс бесконечно малой временной ширины после прохождения 1 км
нс, т. е. импульс бесконечно малой временной ширины после прохождения 1 км
волокна становится импульсом продолжительностью приблизительно 50 не. Так что для получения достаточного временного разрешения на конце волокна передаваемые импульсы должны следовать друг за другом через 50 не и более, чтобы приемник разрешал их как отдельные импульсы.
Такова ситуация в цифровых оптических линиях передачи, в которых используются волокна со ступенчатым профилем показателя преломления длиной порядка 1 км. Поскольку в соответствии с выражением  пропорционально А, то для увеличения скорости передачи импульса в градиентных волокнах для дальней связи необходимо, чтобы А было не более 0,01-0,02. Волокна, характеризующиеся
пропорционально А, то для увеличения скорости передачи импульса в градиентных волокнах для дальней связи необходимо, чтобы А было не более 0,01-0,02. Волокна, характеризующиеся  называют слабонаправляющими.
называют слабонаправляющими.
Побочным результатом условия  , вызванного практической необходимостью, является то, что для слабонаправляющих волокон значительно упрощается описание волноводных мод. В этом можно убедиться, подставив
, вызванного практической необходимостью, является то, что для слабонаправляющих волокон значительно упрощается описание волноводных мод. В этом можно убедиться, подставив  в уравнение (2.113). Используя рекуррентные соотношения типа
в уравнение (2.113). Используя рекуррентные соотношения типа  получаем следующее характеристическое уравнение
получаем следующее характеристическое уравнение

Погрешность при расчете с помощью этой формулы, как показано в работе [343], составляет  для
для  для
для 
Другим следствием слабой направляемости является то, что распространение волны по волокну будет более эффективным при малых углах между волновым вектором и волноводной осью [см. уравнения (2.4) и (2.5)]. НЕ-моды порядка  и ЕН-моды порядка
и ЕН-моды порядка  становятся почти вырожденными, т. е. собственные значения постоянных распространения
становятся почти вырожденными, т. е. собственные значения постоянных распространения  стано-вятсяфактически почти одинаковыми в пределе
стано-вятсяфактически почти одинаковыми в пределе  Из-за этого почти полного вырождения в таких волноводах можно создать с помощью линейной суперпозиции
Из-за этого почти полного вырождения в таких волноводах можно создать с помощью линейной суперпозиции  мод почти линейно поляризованные моды, содержащие в поперечном по отношению к оси поле только один преобладающий компонент электрического и один магнитного поля. После длительных алгебраических преобразований, используя декартовы координаты, можно получить следующее соотношение для компонентов поля
мод почти линейно поляризованные моды, содержащие в поперечном по отношению к оси поле только один преобладающий компонент электрического и один магнитного поля. После длительных алгебраических преобразований, используя декартовы координаты, можно получить следующее соотношение для компонентов поля 

Можно также показать, что учет условия  действительно приводит к тому, что либо
действительно приводит к тому, что либо  либо для ортогональной поляризации
либо для ортогональной поляризации  Таким образом поперечные поля существенно поляризованы в одном направлении и имеют только четыре ненулевых компонента поля
Таким образом поперечные поля существенно поляризованы в одном направлении и имеют только четыре ненулевых компонента поля  (или
(или
для ортогональной поляризации  вместо шести ненулевых компонентов в первоначальном (не слабонаправляющем) волокне. Вместо рассмотренного выше довольно сложного метода расчета можно воспользоваться преобразованиями, предложенными Глоге в работе [159] для того, чтобы показать, что для
вместо шести ненулевых компонентов в первоначальном (не слабонаправляющем) волокне. Вместо рассмотренного выше довольно сложного метода расчета можно воспользоваться преобразованиями, предложенными Глоге в работе [159] для того, чтобы показать, что для  волноводные моды почти линейно поляризованы и имеют только один преобладающий поперечный электрический или магнитный компонент поля.
волноводные моды почти линейно поляризованы и имеют только один преобладающий поперечный электрический или магнитный компонент поля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
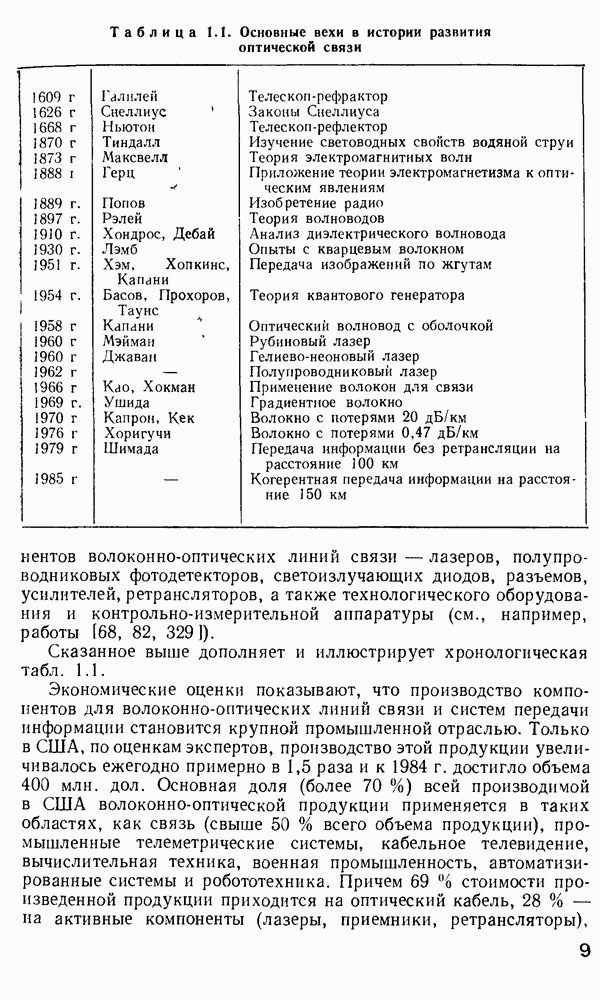
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
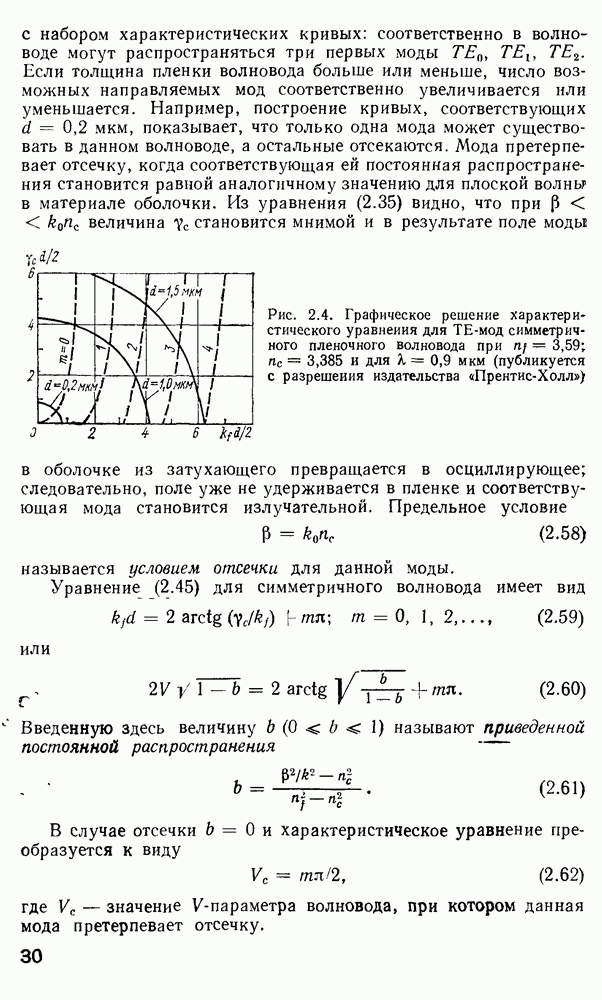
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
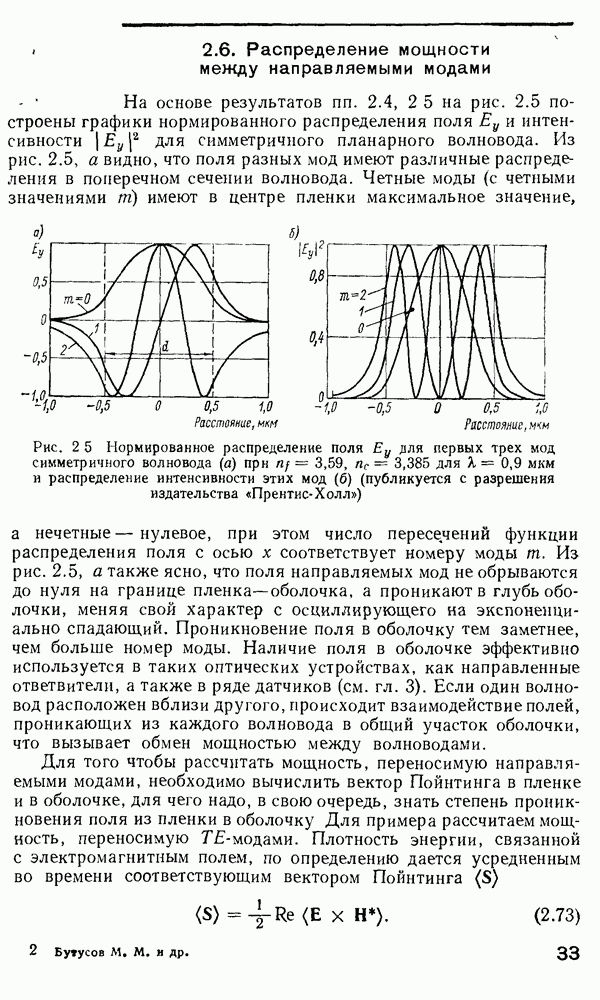
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
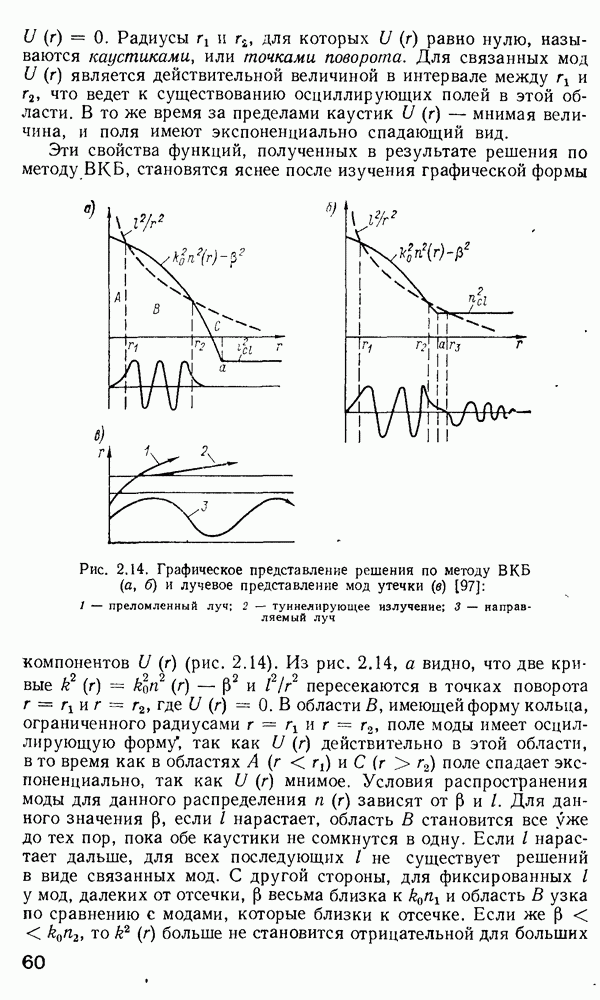
- Решение уравнения (2.157) методом ВКБ.
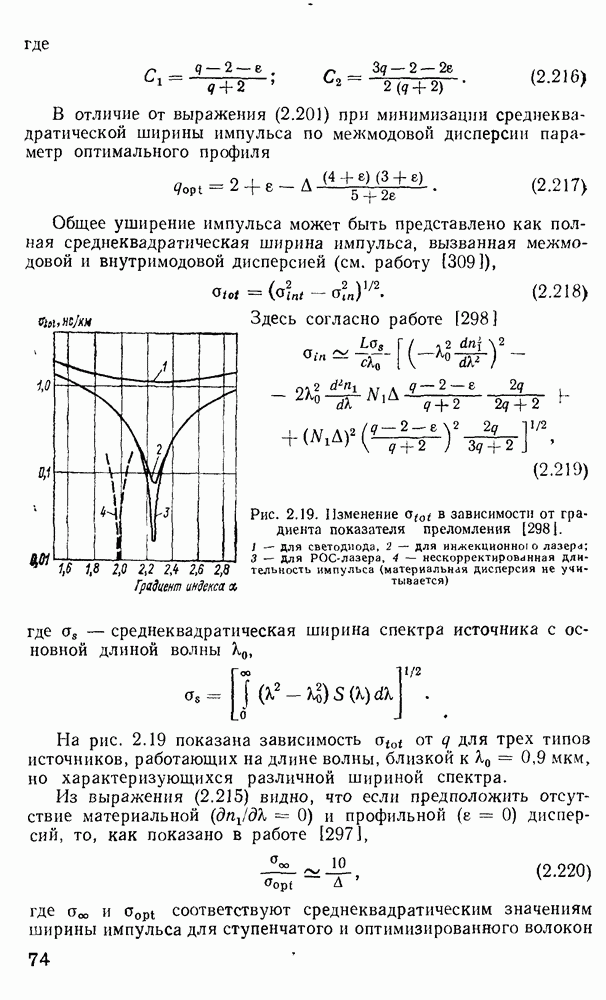
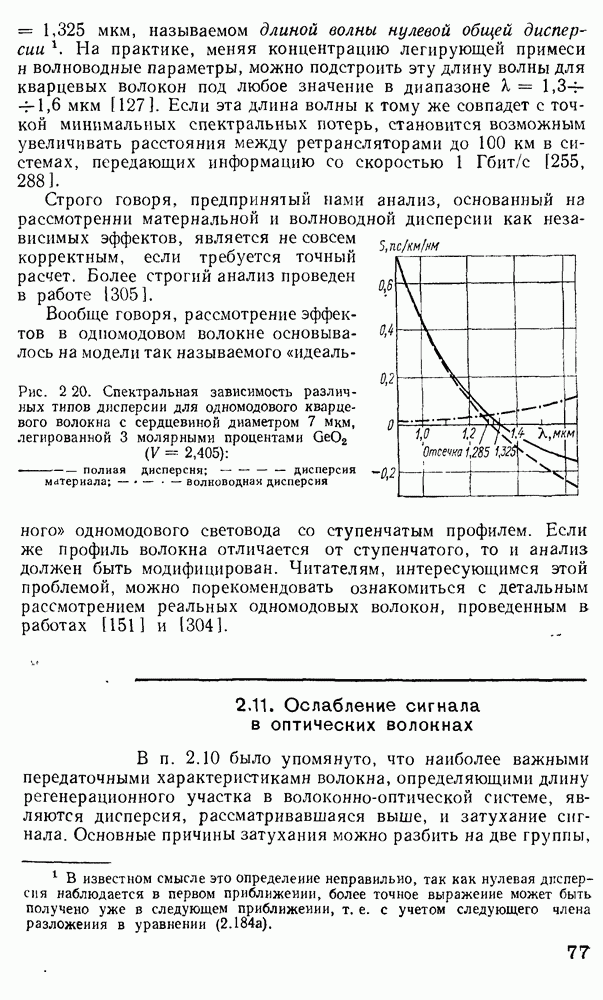
- 2.10. Дисперсия в оптических волокнах
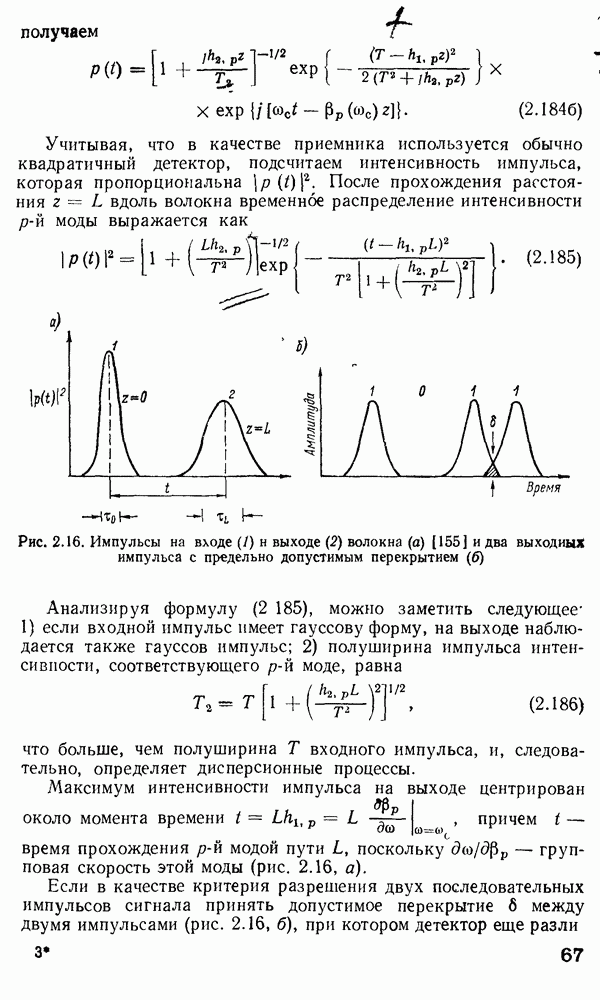
- Распространение импульса в оптических волокнах.
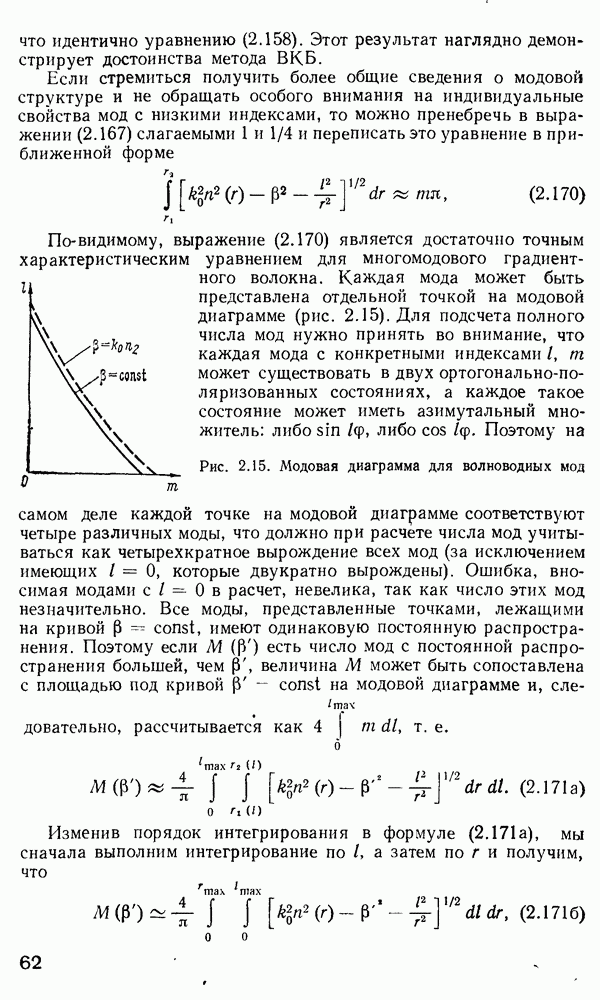
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
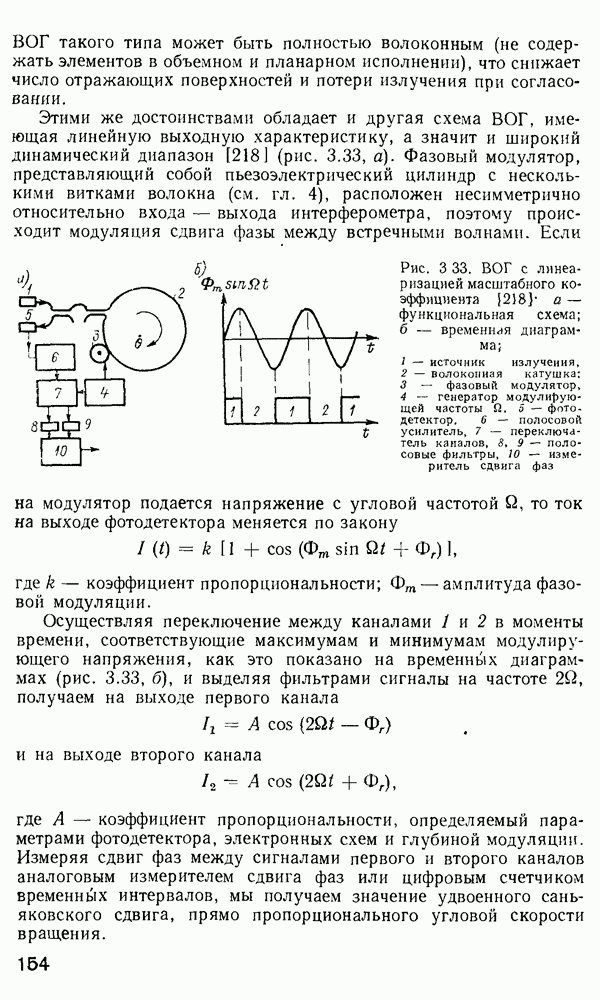
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
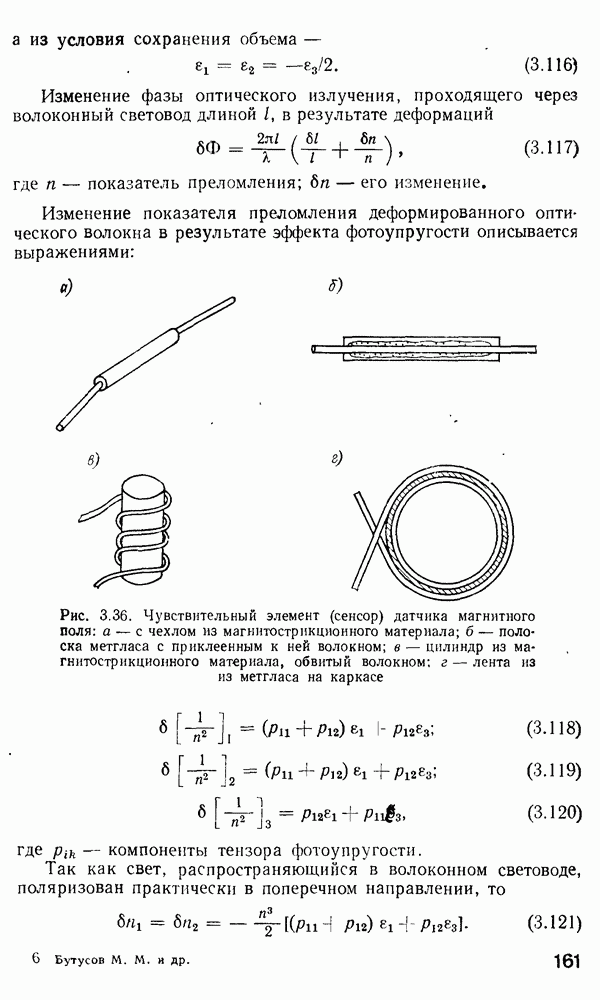
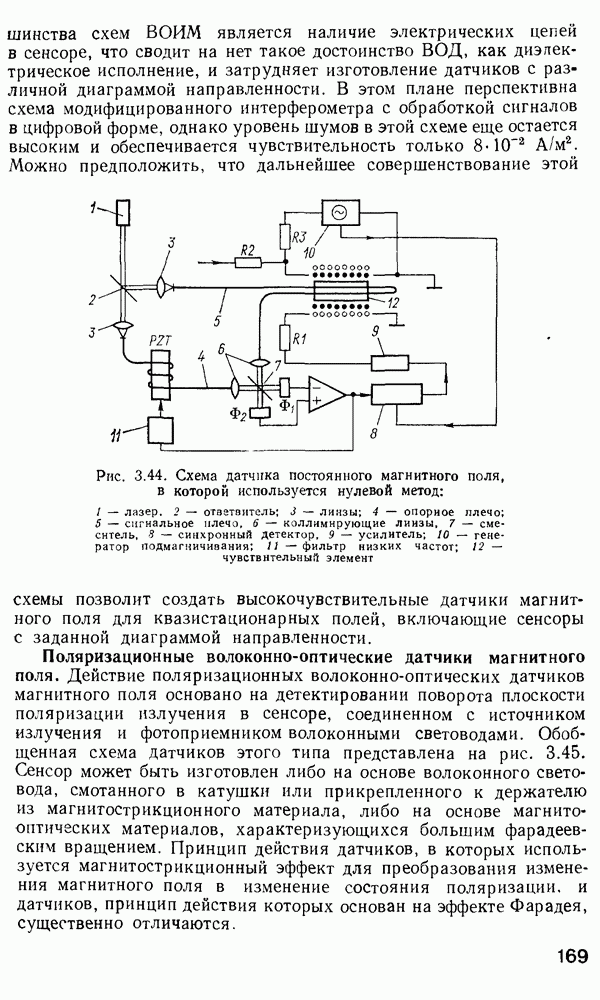
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
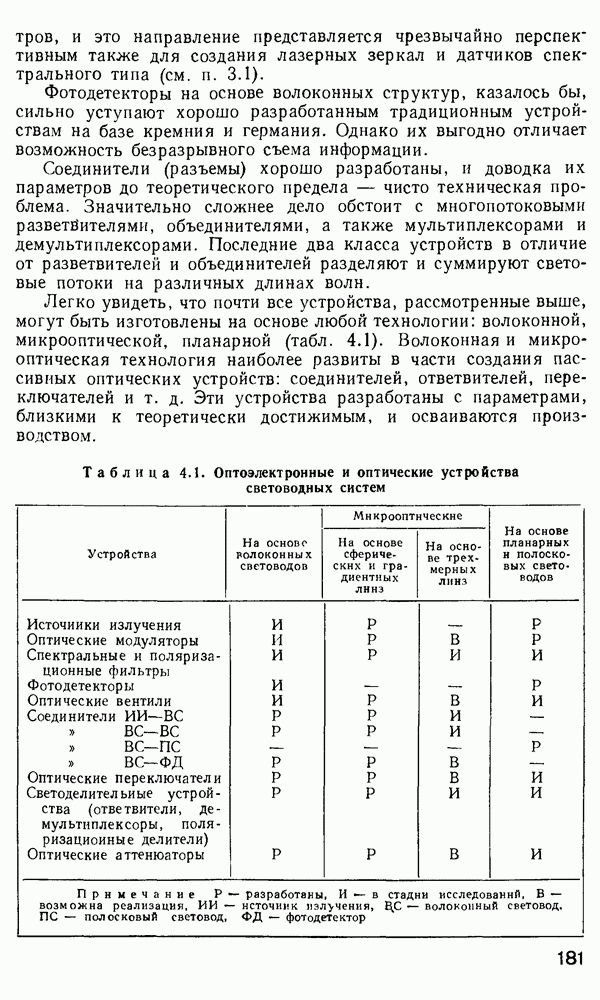
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
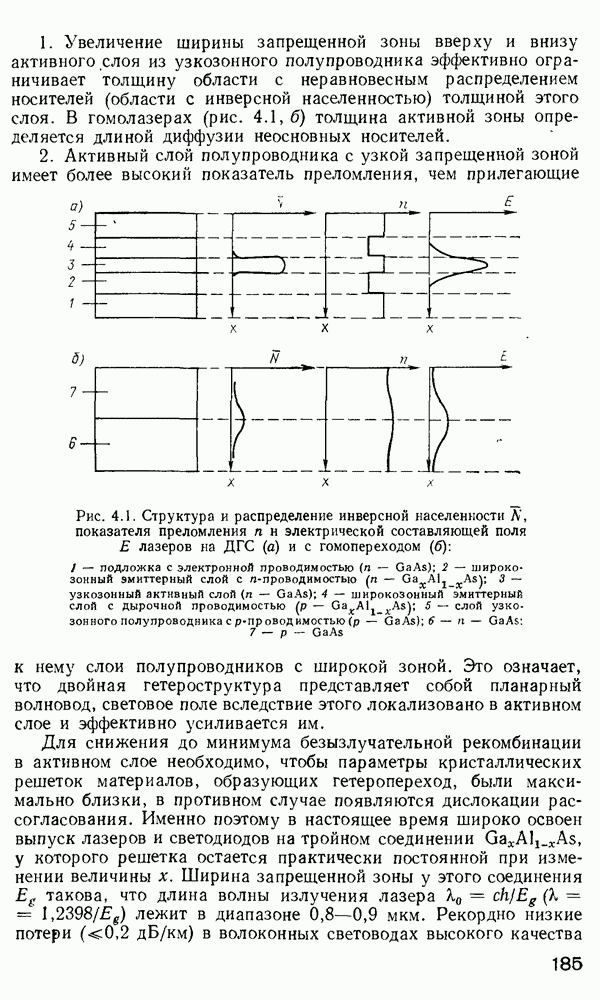
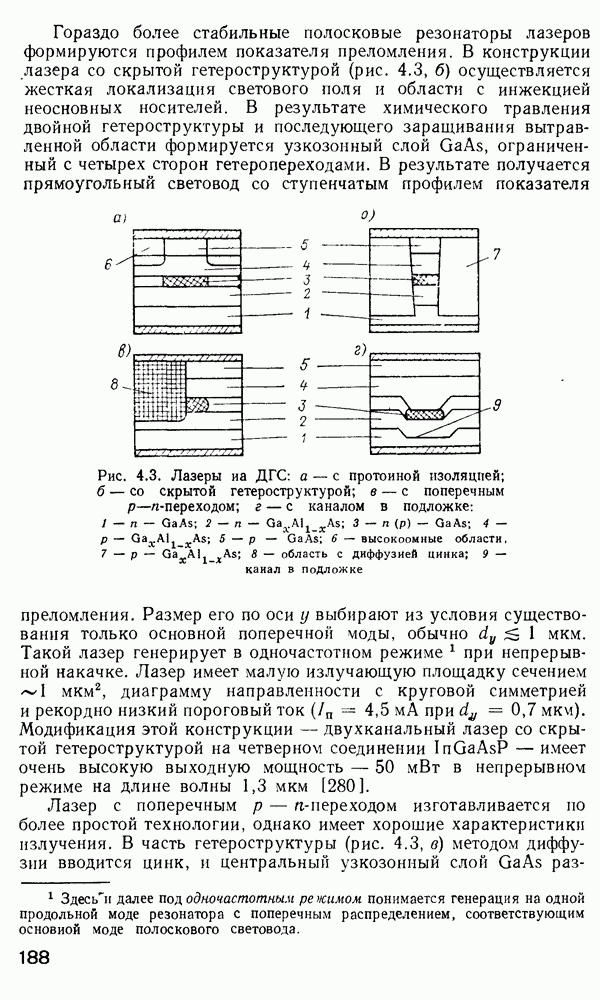
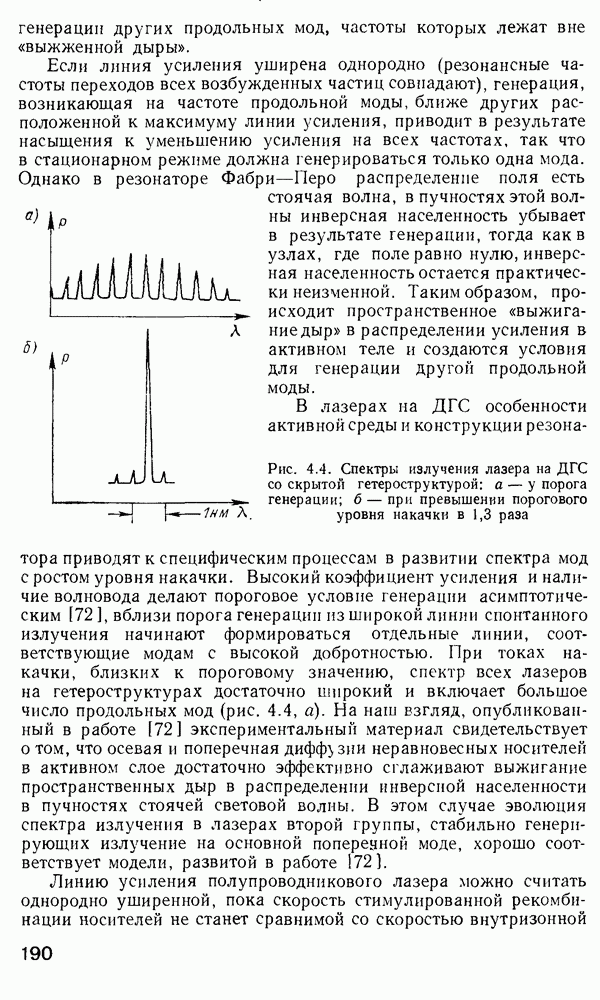
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
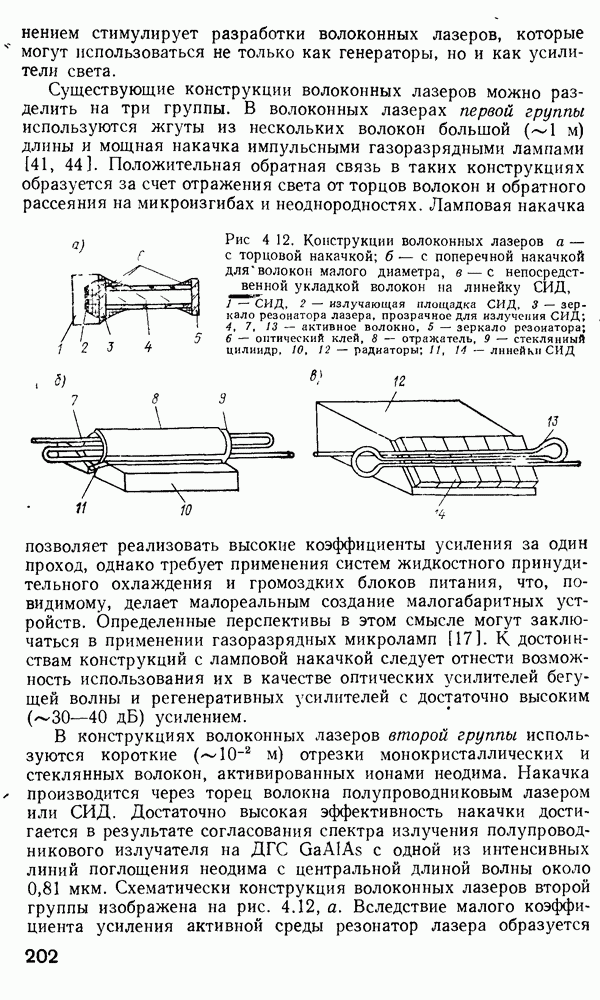
- Волоконные лазеры.
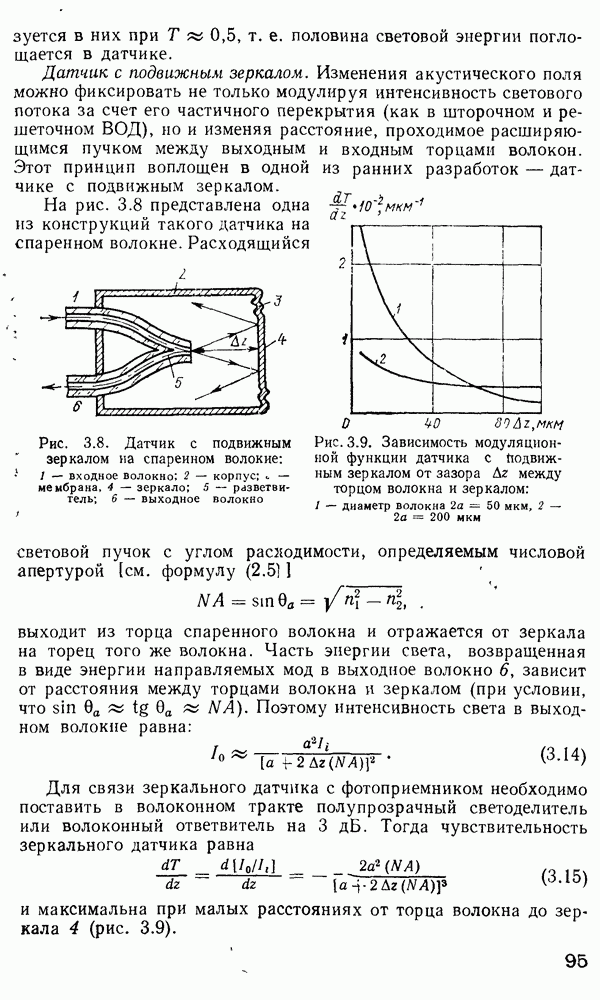
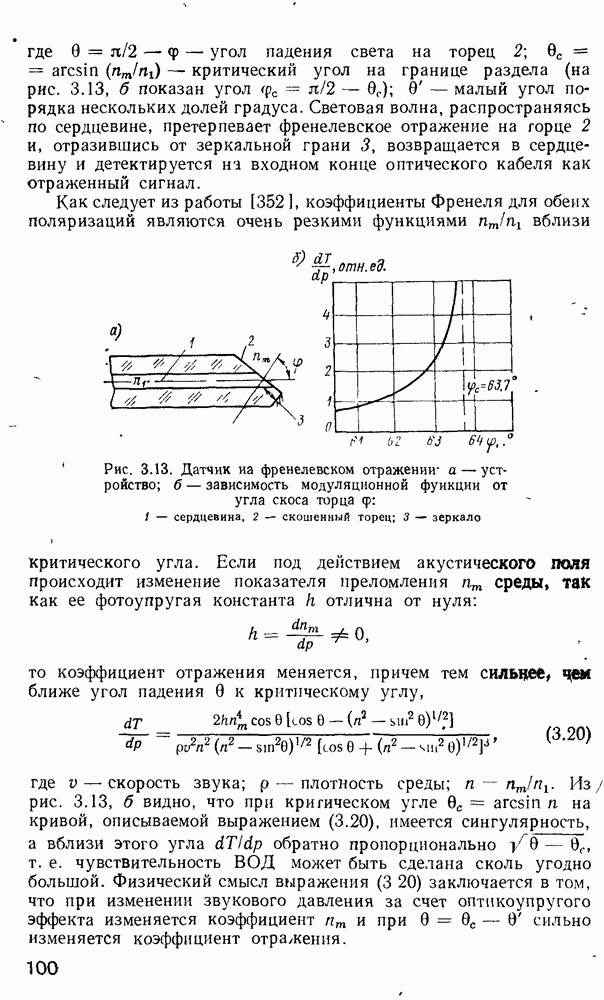
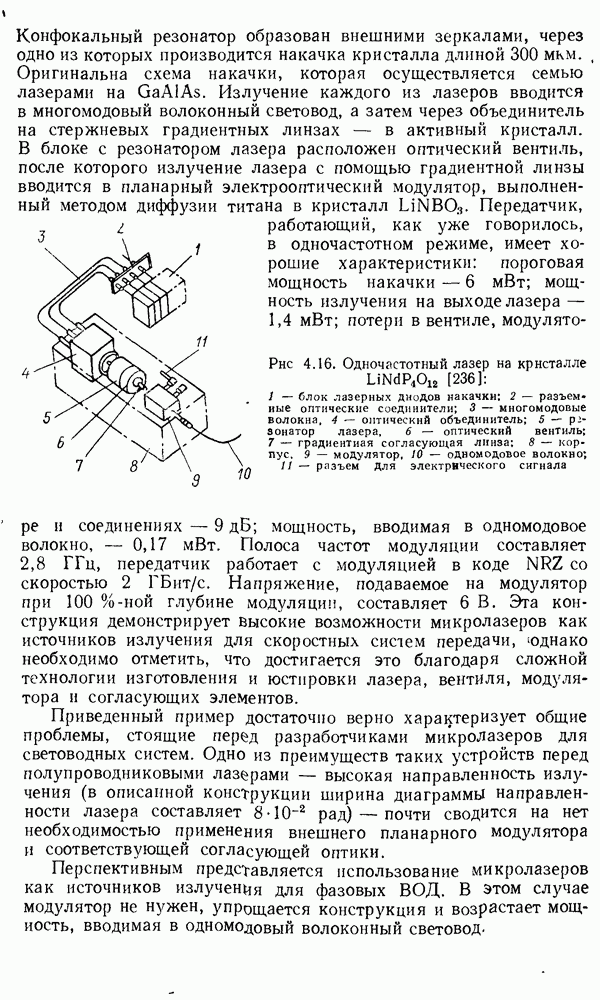
- Объемные микролазеры.
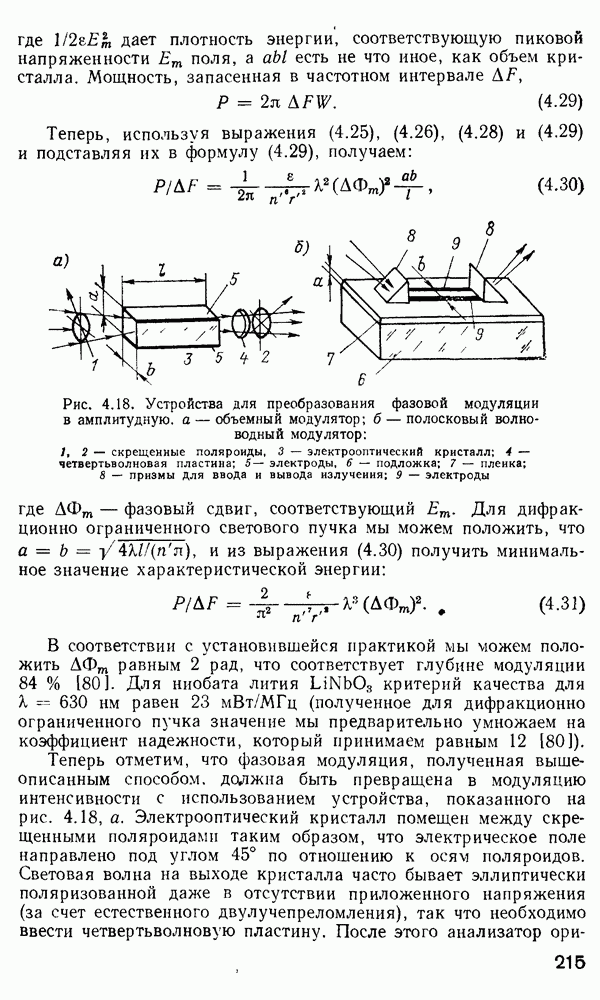
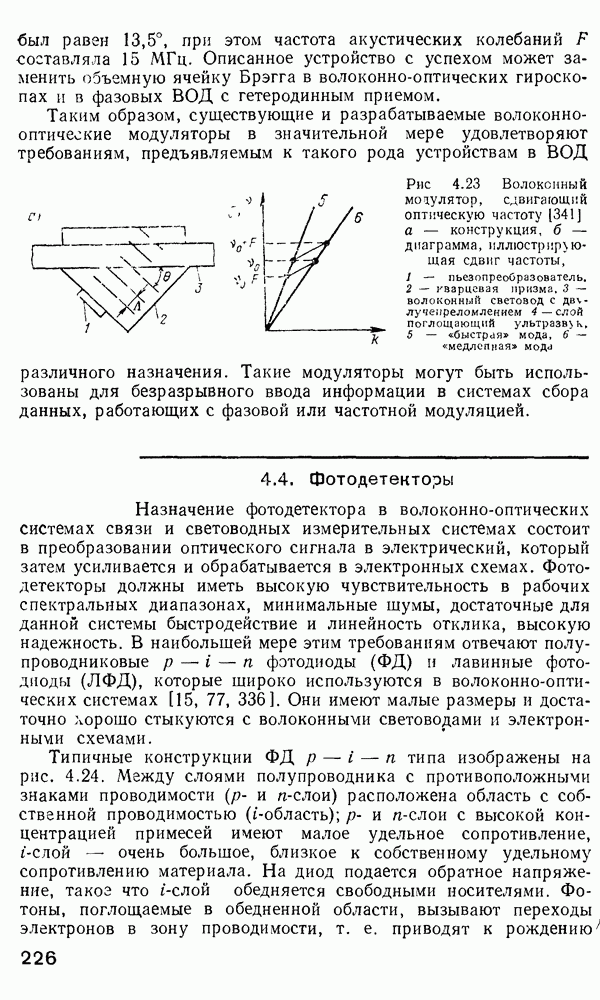
- 4.3. Оптические модуляторы
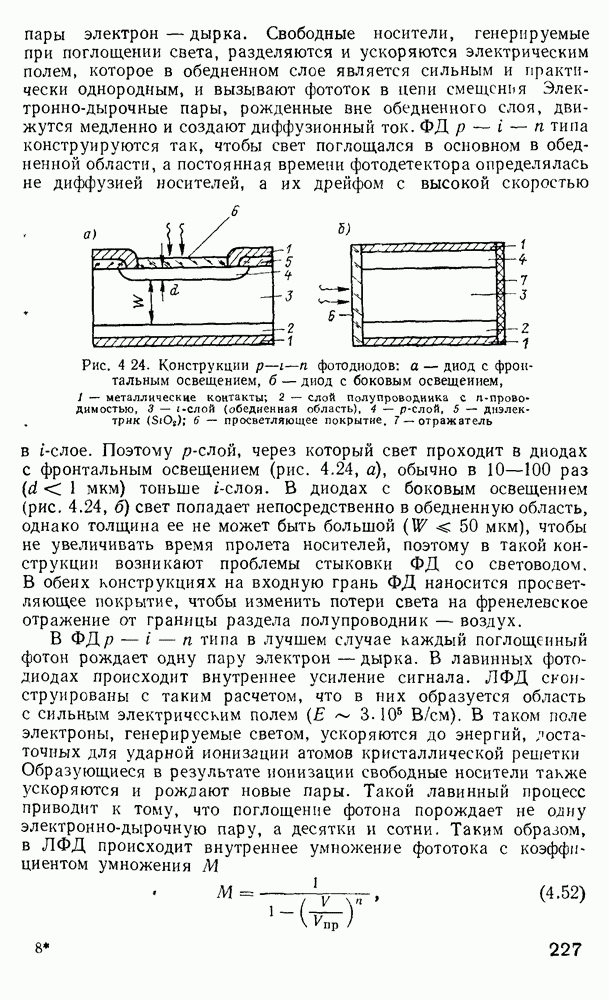
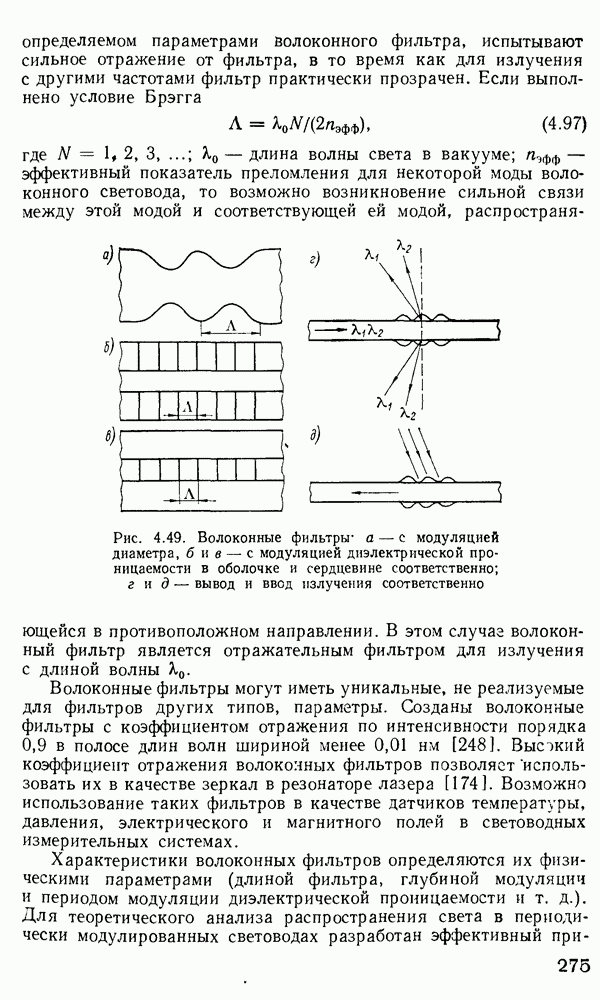
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
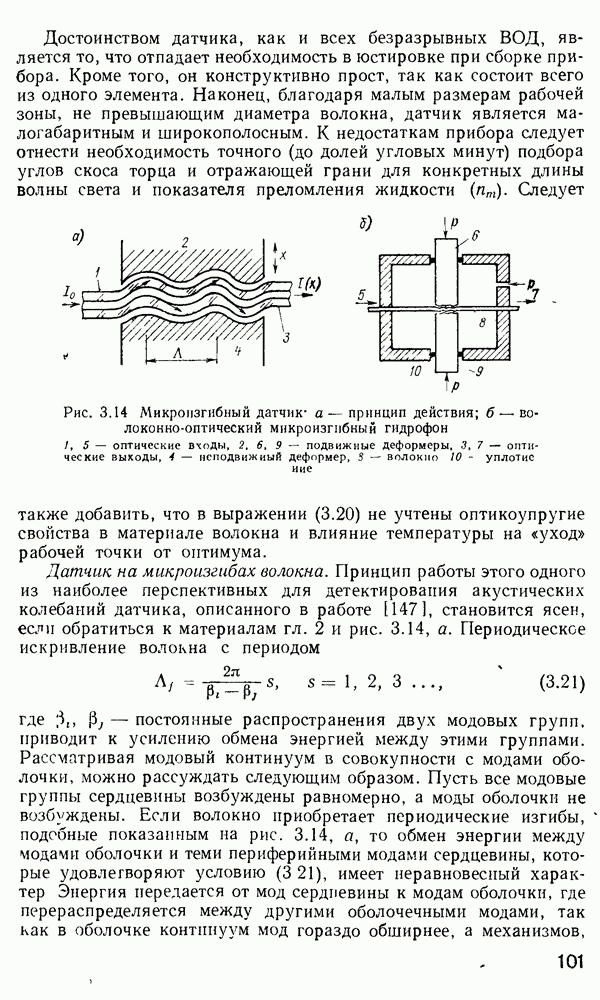
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
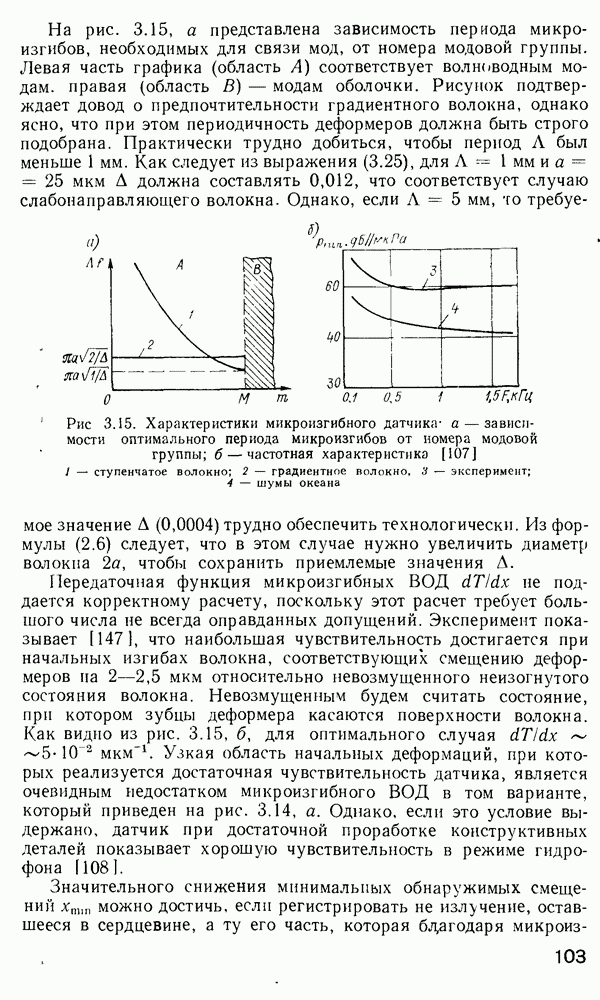
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
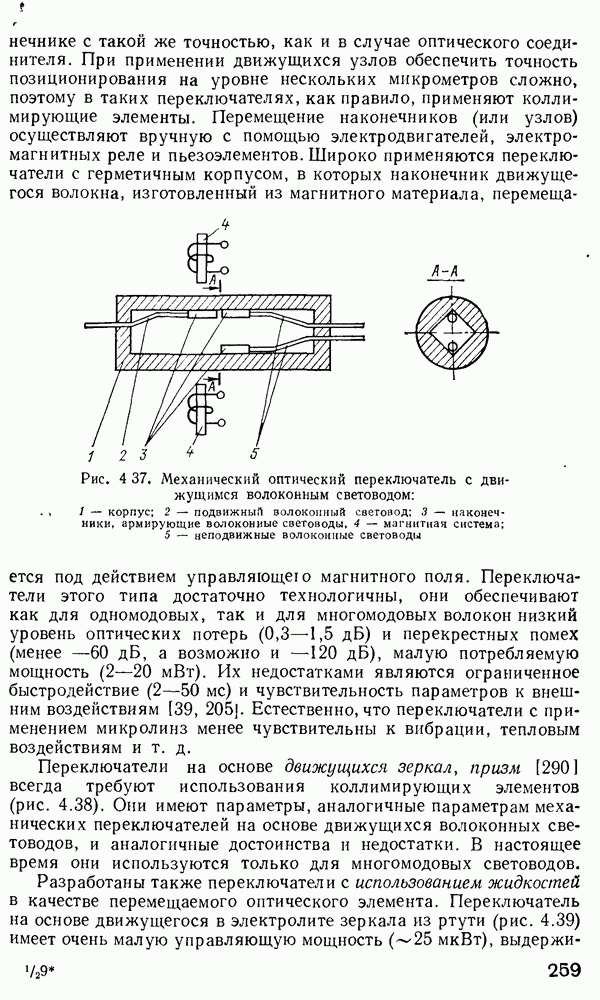
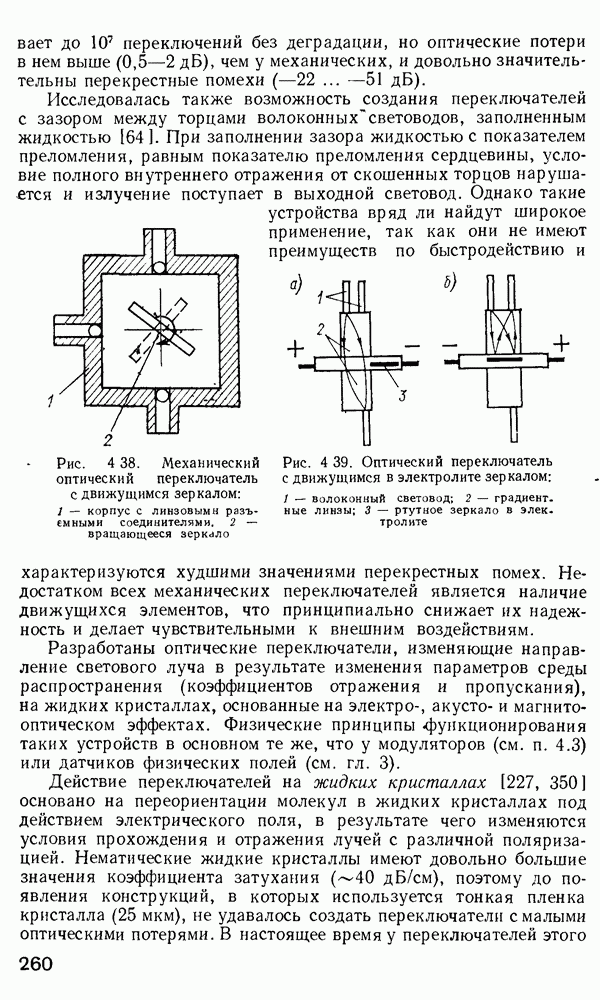
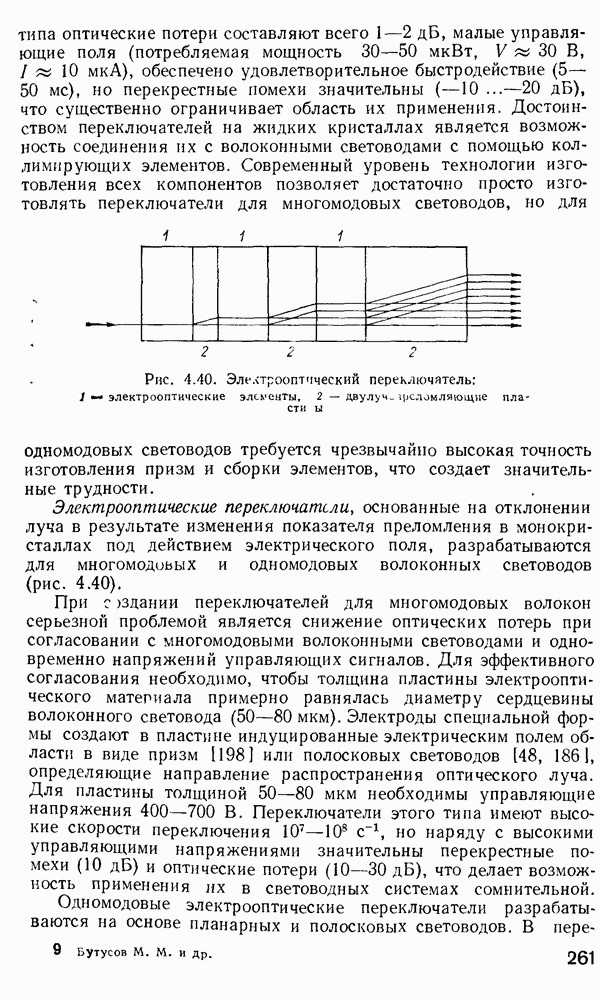
- 4.7. Волоконно-оптические переключатели
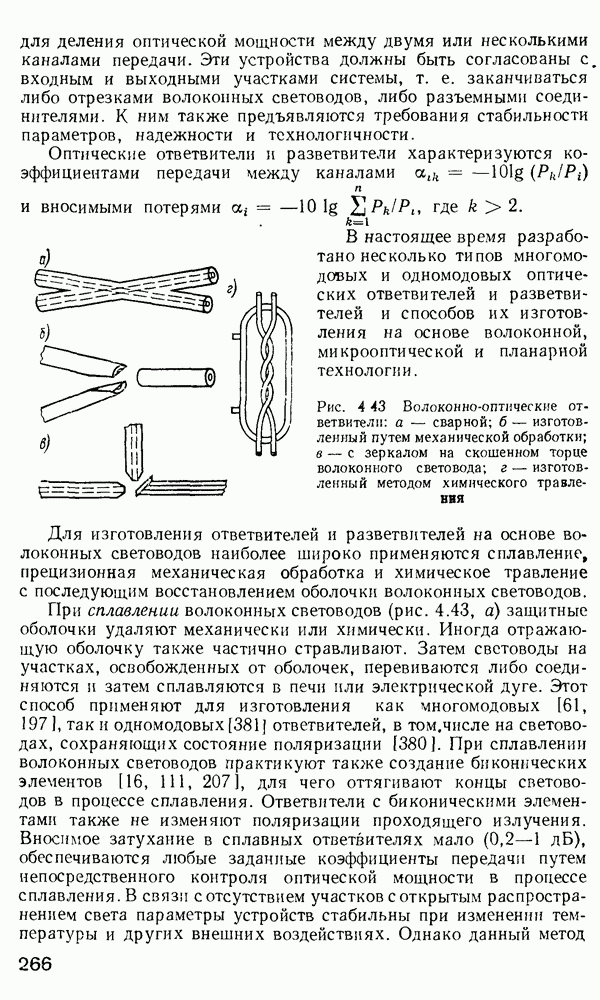
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
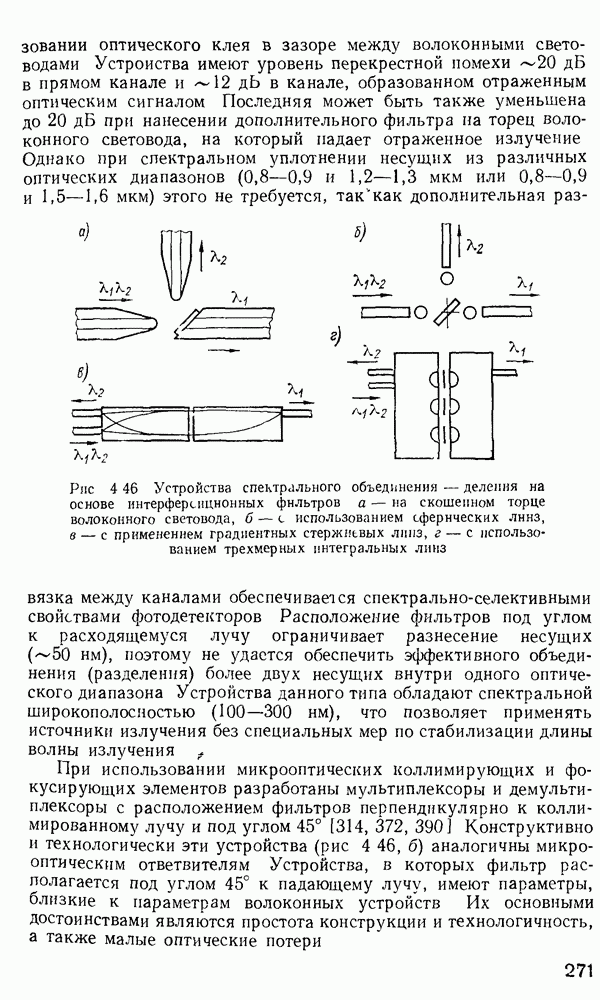
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
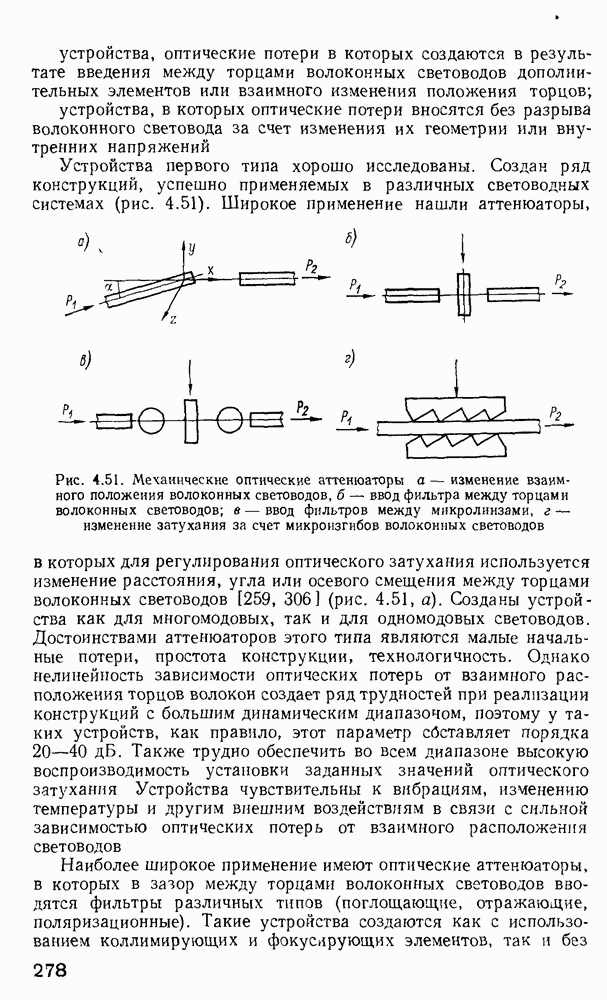
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
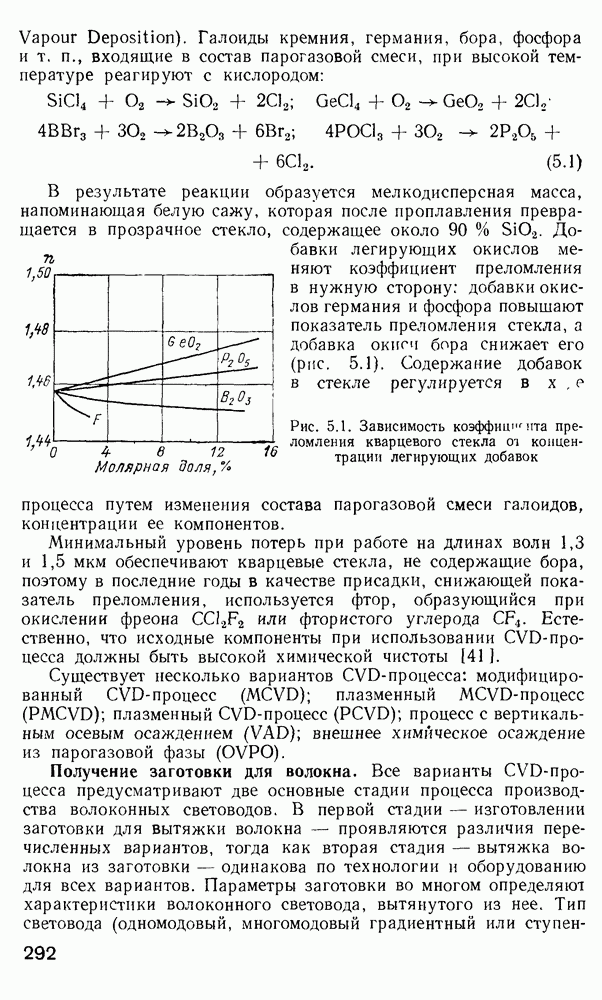
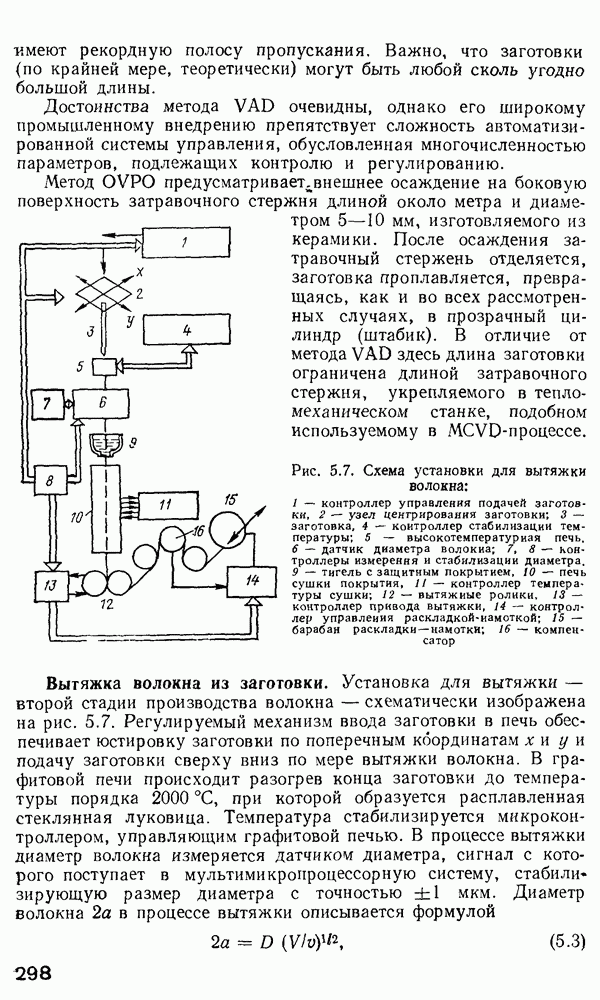
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
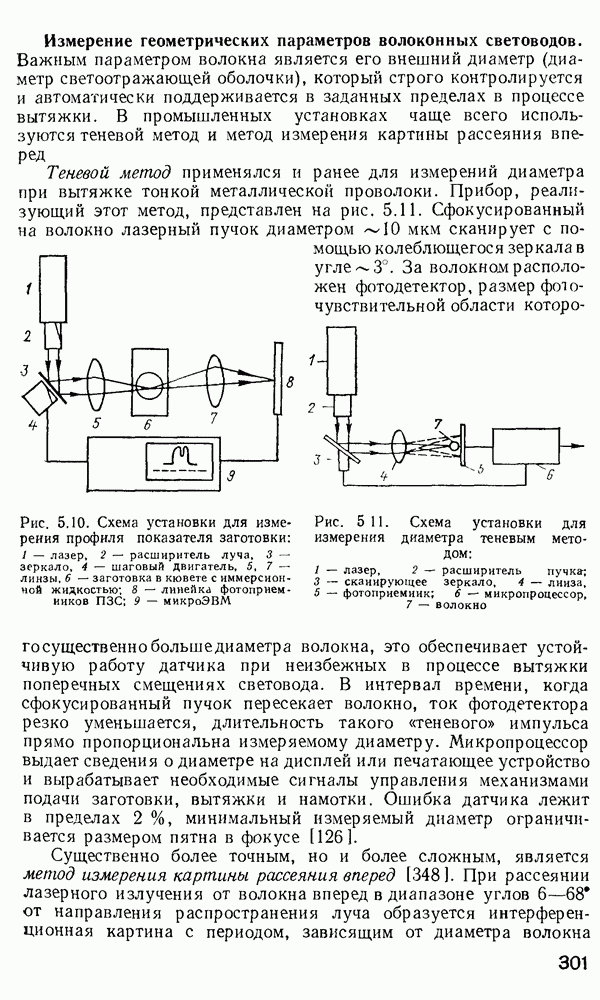
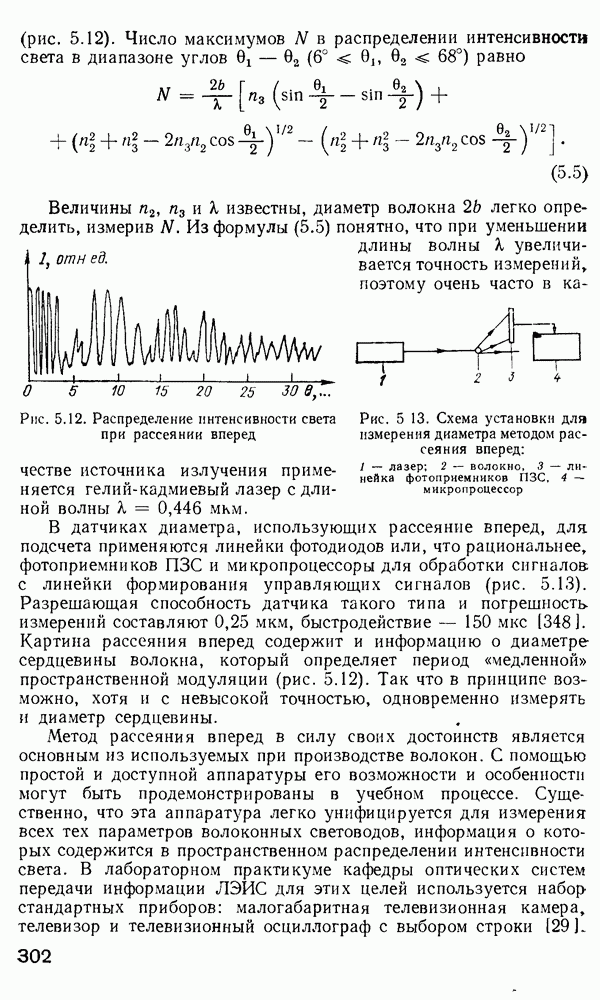
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ