| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
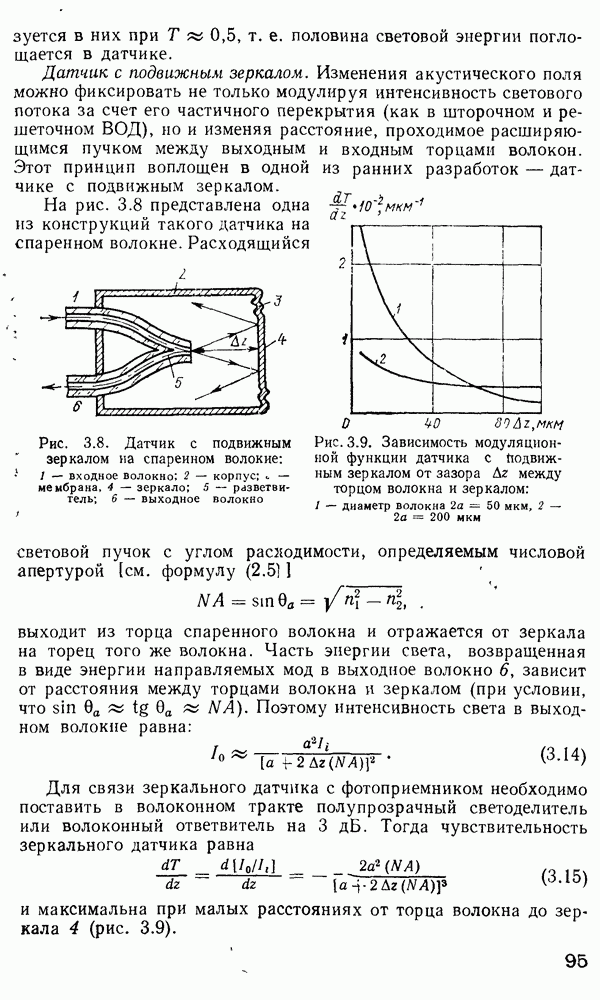
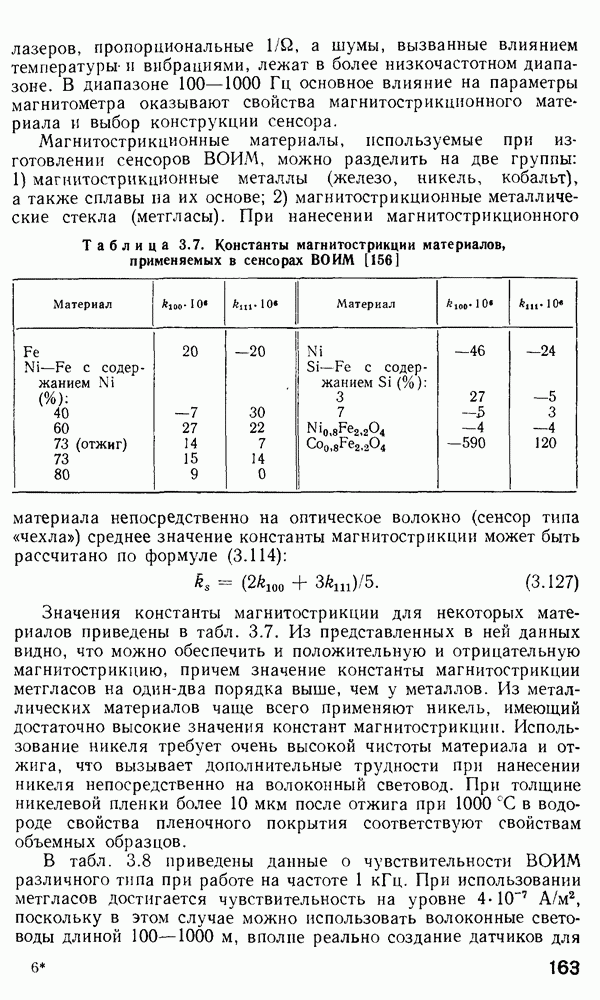
2.4. Характеристическое уравнение и условие отсечки
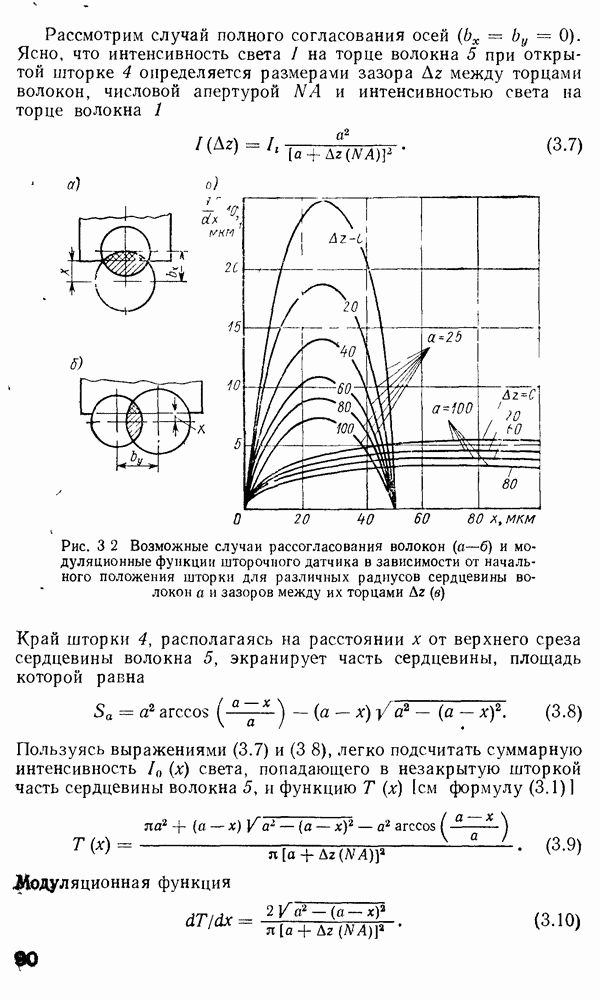
В п. 2.3 мы показали, что, решая характеристические уравнения (2.44) или (2.45), можно получить значения  для ассиметричного
для ассиметричного  пленочного волновода. В симметричном волноводе
пленочного волновода. В симметричном волноводе  уравнение (2.44) преобразуется к виду
уравнение (2.44) преобразуется к виду

Индекс с теперь относится к среде, окружающей волновод с обеих сторон (оболочке). Уравнение (2.52) можно привести к двум трансцендентным уравнениям:

Выбирая первое решение, мы с помощью уравнения (2.48) получаем выражение для поля в пленке 

представляющее собой симметричную функцию координаты х относительно середины пленки 
Если воспользоваться выражением (2.54) для определения Р, то выражение для поля внутри пленки приобретет вид

т. е. поле есть антисимметричная функция относительно плоскости 
Таким образом, уравнение (2.55) определяет четные, а уравнение (2.56) — нечетные собственные функции симметричного пленочного волновода.
Для получения численных значений  для разных мод надо решить уравнения (2.53) или (2.54) графическим или численным методами. Для удобства графического решения введем
для разных мод надо решить уравнения (2.53) или (2.54) графическим или численным методами. Для удобства графического решения введем  -параметр волновода [см. формулу (2.6)]
-параметр волновода [см. формулу (2.6)]

Уравнение (2.57) определяет окружность в плоскости вспомогательных координат X и Y, где  . Легко показать, что построение этой окружности в плоскости
. Легко показать, что построение этой окружности в плоскости  одновременно с построением кривых, описываемых уравнениями (2.53) и (2.54), позволяет найти постоянные распространения как точки пересечения кривых с окружностью (рис. 2.4). Это построение оказывается очень наглядным, так как позволяет показать, что постоянная распространения ТЕ-моды для данных значений половинной толщины волновода
одновременно с построением кривых, описываемых уравнениями (2.53) и (2.54), позволяет найти постоянные распространения как точки пересечения кривых с окружностью (рис. 2.4). Это построение оказывается очень наглядным, так как позволяет показать, что постоянная распространения ТЕ-моды для данных значений половинной толщины волновода  и показателей преломления пленки и оболочки
и показателей преломления пленки и оболочки  может быть получена нахождением координат точки пересечения кривых типа (2.53), (2.54) для различных мод и окружности (2.57), характеризующей свойства волновода.
может быть получена нахождением координат точки пересечения кривых типа (2.53), (2.54) для различных мод и окружности (2.57), характеризующей свойства волновода.
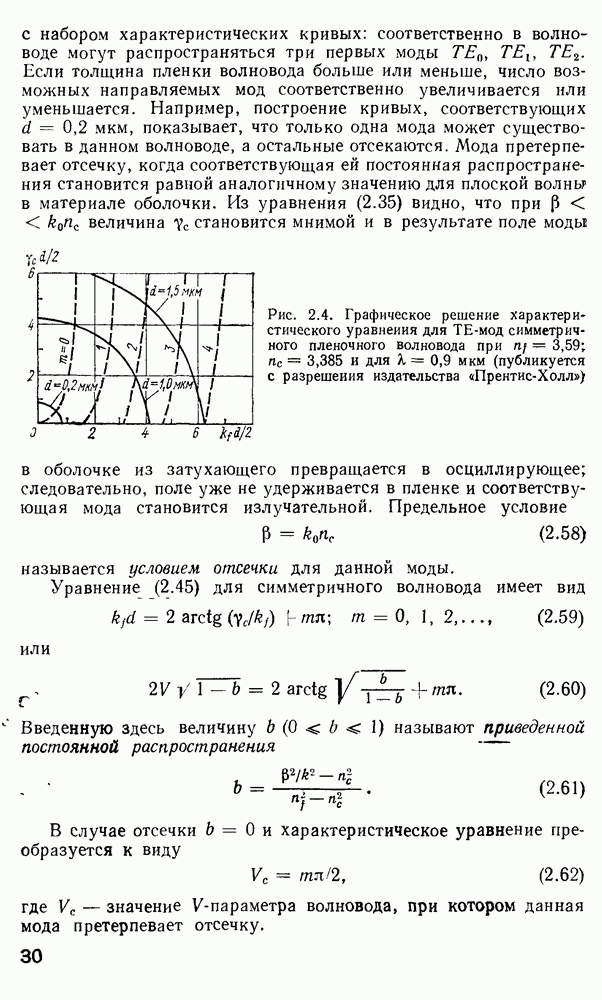
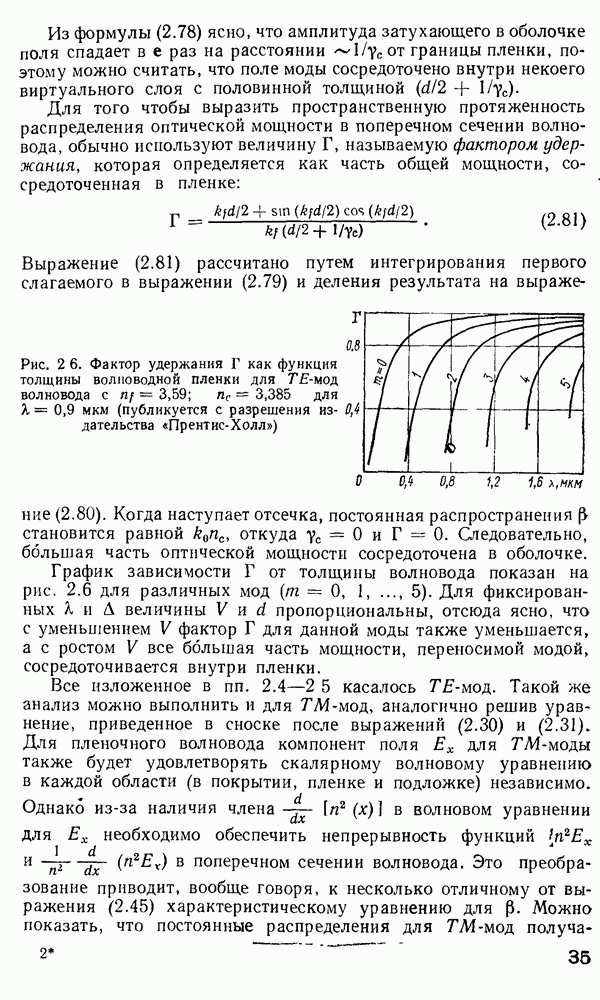
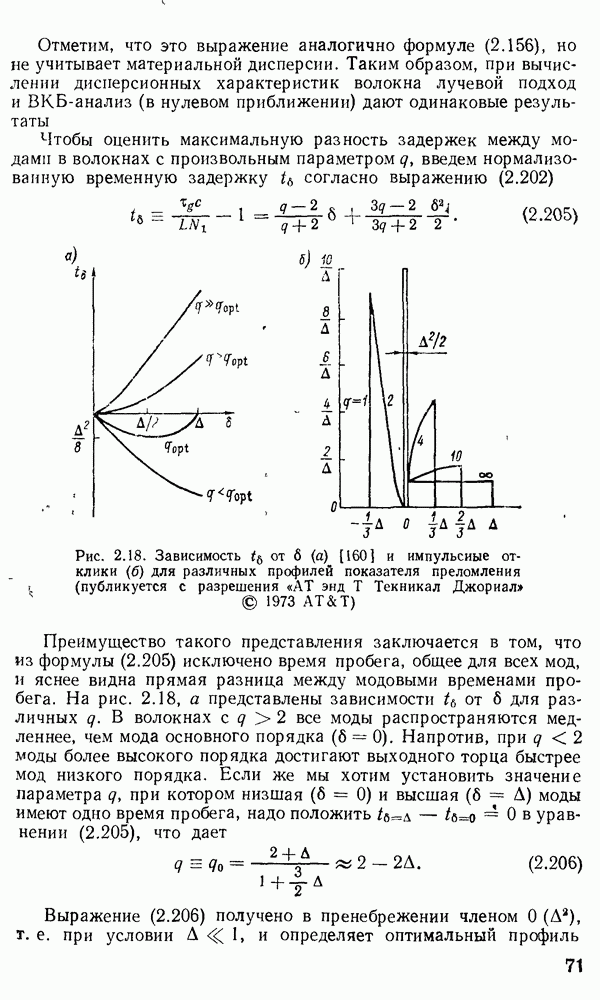
С помощью рис. 2.4 можно также определить число направляемых мод, поддерживаемых волноводом. Например, для типичной толщины пленки 1 мкм имеется три точки пересечения окружности
с набором характеристических кривых: соответственно в волноводе могут распространяться три первых моды  Если толщина пленки волновода больше или меньше, число возможных направляемых мод соответственно увеличивается или уменьшается. Например, построение кривых, соответствующих
Если толщина пленки волновода больше или меньше, число возможных направляемых мод соответственно увеличивается или уменьшается. Например, построение кривых, соответствующих  мкм, показывает, что только одна мода может существовать в данном волноводе, а остальные отсекаются. Мода претерпевает отсечку, когда соответствующая ей постоянная распространения становится равной аналогичному значению для плоской волны в материале оболочки. Из уравнения (2.35) видно, что при
мкм, показывает, что только одна мода может существовать в данном волноводе, а остальные отсекаются. Мода претерпевает отсечку, когда соответствующая ей постоянная распространения становится равной аналогичному значению для плоской волны в материале оболочки. Из уравнения (2.35) видно, что при  величина
величина  становится мнимой и в результате поле моды в оболочке из затухающего превращается в осциллирующее; следовательно, поле уже не удерживается в пленке и соответствующая мода становится излучательной.
становится мнимой и в результате поле моды в оболочке из затухающего превращается в осциллирующее; следовательно, поле уже не удерживается в пленке и соответствующая мода становится излучательной.

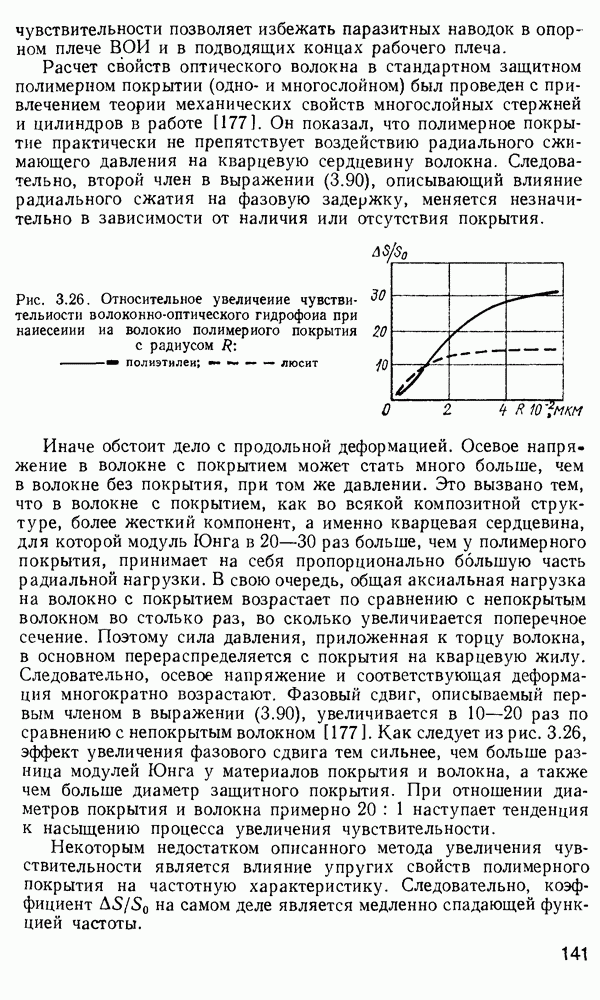
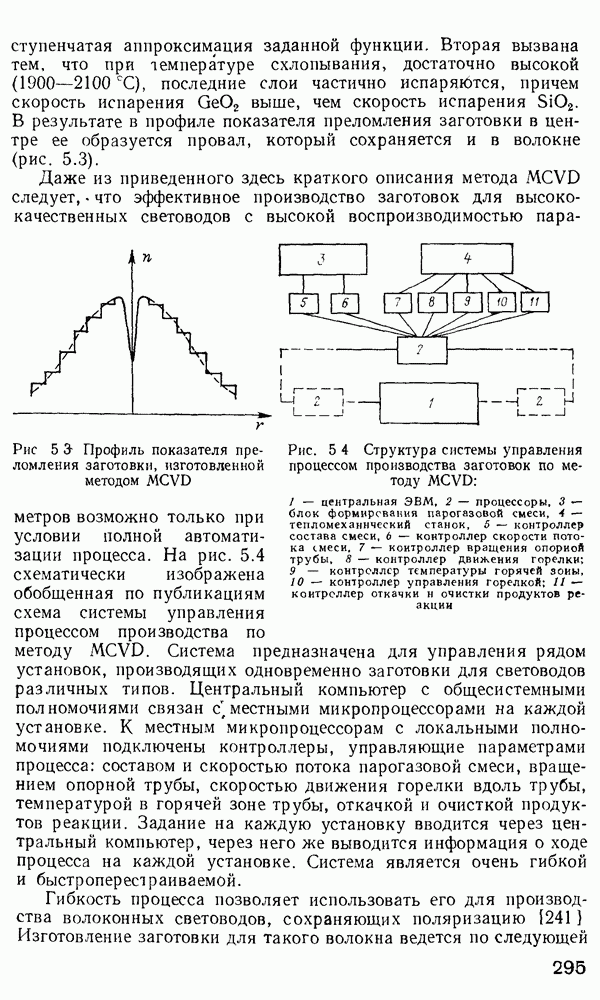
Рис. 2.4. Графическое решение характеристического уравнения для ТЕ-мод симметричного пленочного волновода при  и для
и для  мкм (публикуется с разрешения издательства «Прентис-Холл»)
мкм (публикуется с разрешения издательства «Прентис-Холл»)
Предельное условие

называется условием отсечки для данной моды.
Уравнение (2.45) для симметричного волновода имеет вид

или

Введенную здесь величину  называют приведенной постоянной распространения
называют приведенной постоянной распространения

В случае отсечки  и характеристическое уравнение преобразуется к виду
и характеристическое уравнение преобразуется к виду

где  — значение
— значение  -параметра волновода, при котором данная мода претерпевает отсечку.
-параметра волновода, при котором данная мода претерпевает отсечку.
Для фундаментальной моды  т. е. в симметричном волноводе фундаментальная мода не претерпевает отсечки и распространяется, какой бы малой ни была толщина волновода. При
т. е. в симметричном волноводе фундаментальная мода не претерпевает отсечки и распространяется, какой бы малой ни была толщина волновода. При  начинается распространение моды
начинается распространение моды  т. е. диапазон
т. е. диапазон  определяет одномодовый режим работы волновода.
определяет одномодовый режим работы волновода.
Для любой моды с индексом  из уравнений (2.61) и (2.57) можно найти критическую толщину волновода, при которой происходит отсечка моды,
из уравнений (2.61) и (2.57) можно найти критическую толщину волновода, при которой происходит отсечка моды,

С другой стороны, если толщина волновода неизменна, а меняется длина волны распространяющегося излучения, то можно найти длину волны отсечки  для данной моды
для данной моды

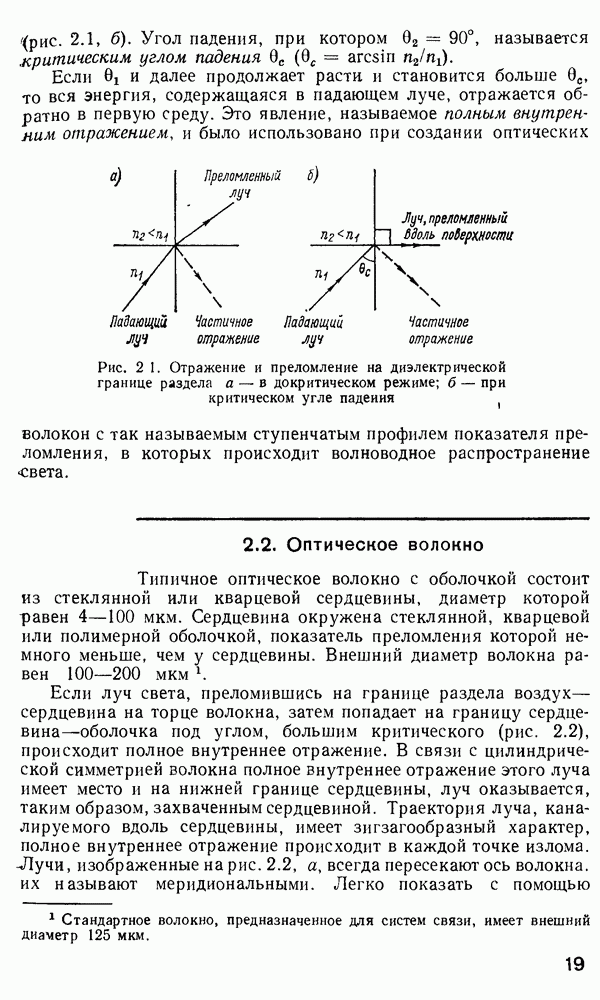
Интересно отметить, что условия отсечки моды можно сопоставить с условиями, соответствующими ситуации, когда плоская волна, описывающая данную моду, более не претерпевает полного внутреннего отражения на границе пленка—оболочка.
Из уравнений (2.51) и (2.58) мы находим, что для возникновения отсечки надо, чтобы

т. е.

Определения критического угла для полного внутреннего отражения [см. формулу (2.31) ] и угла данной моды  (см. рис. 2.3) ясно показывают, что условие (2.65) есть не что иное, как условие нарушения полного внутреннего отражения на границе раздела пленка—оболочка.
(см. рис. 2.3) ясно показывают, что условие (2.65) есть не что иное, как условие нарушения полного внутреннего отражения на границе раздела пленка—оболочка.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
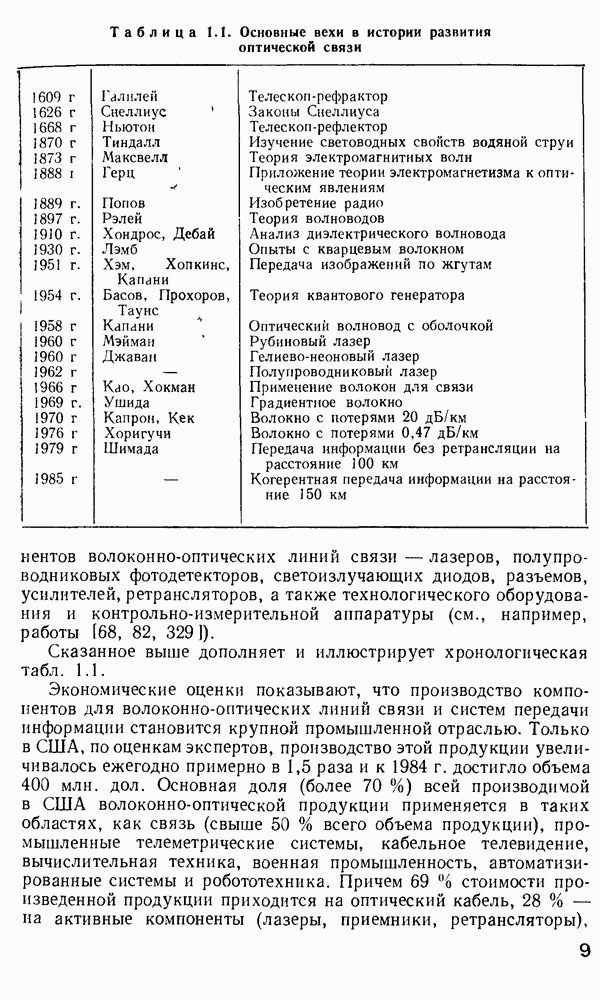
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
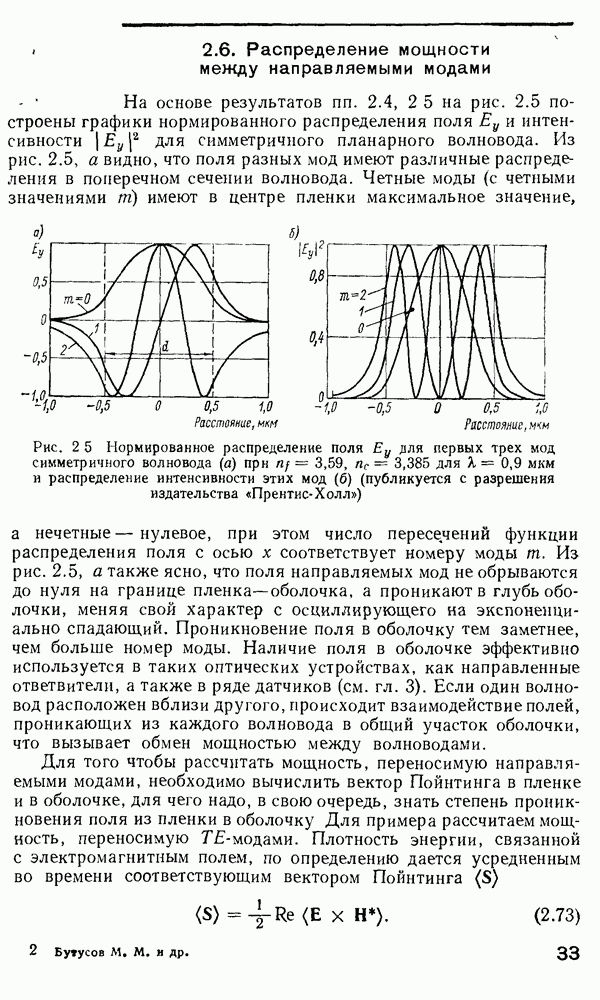
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
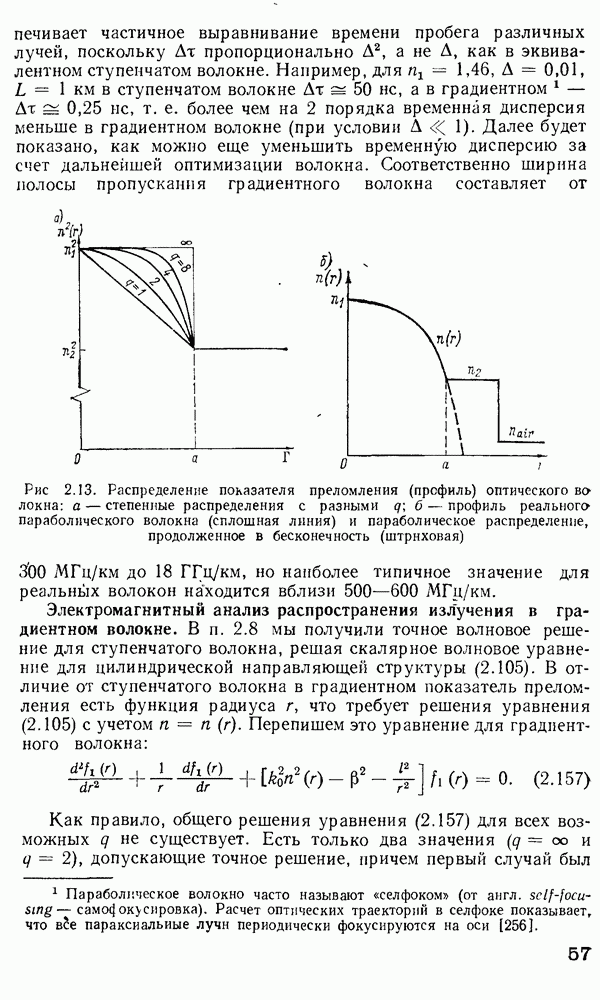
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
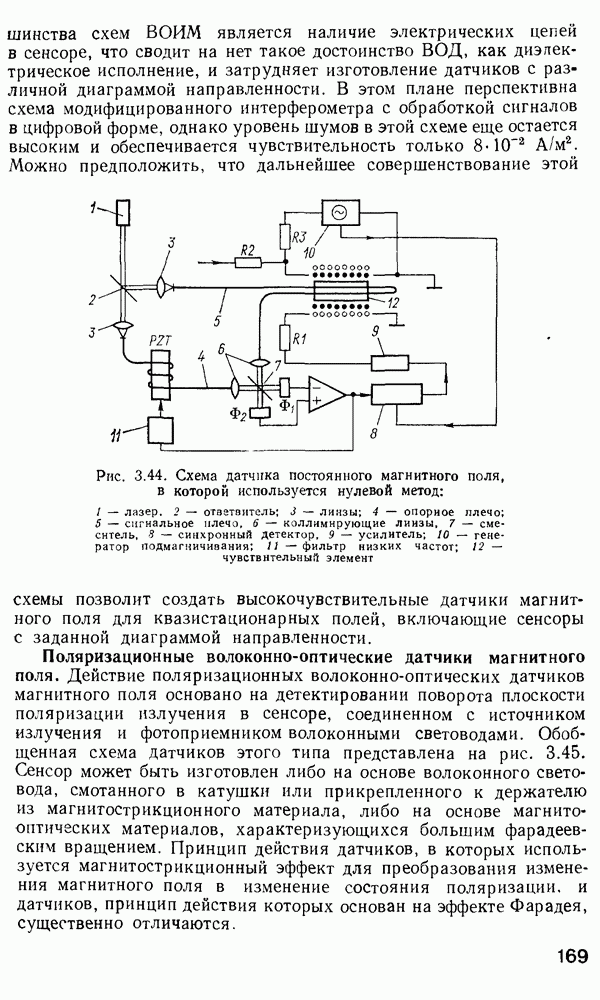
- 3.7. Фазовые и поляризационные датчики магнитного поля
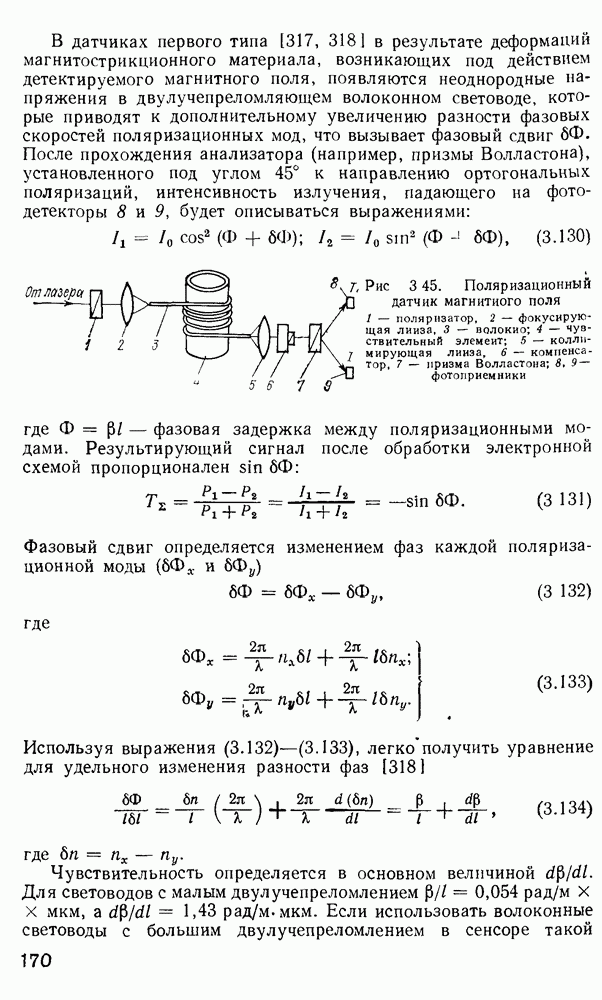
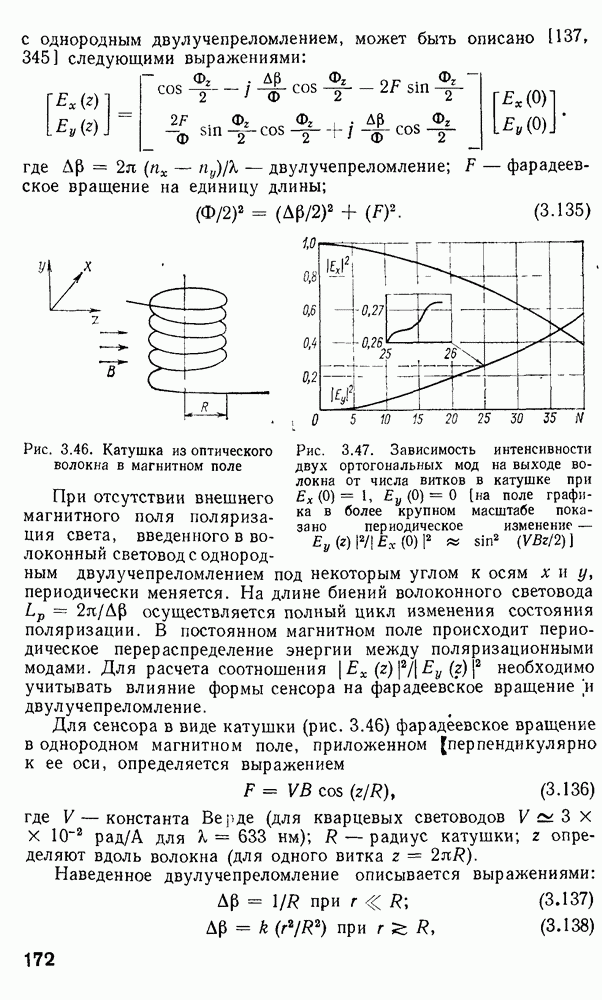
- Поляризационные волоконно-оптические датчики магнитного поля.
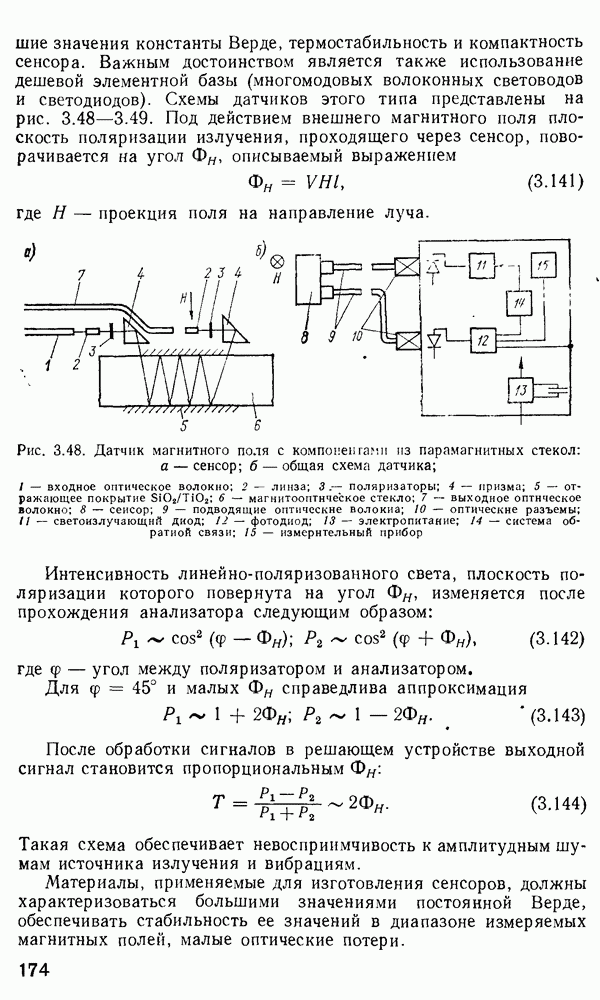
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
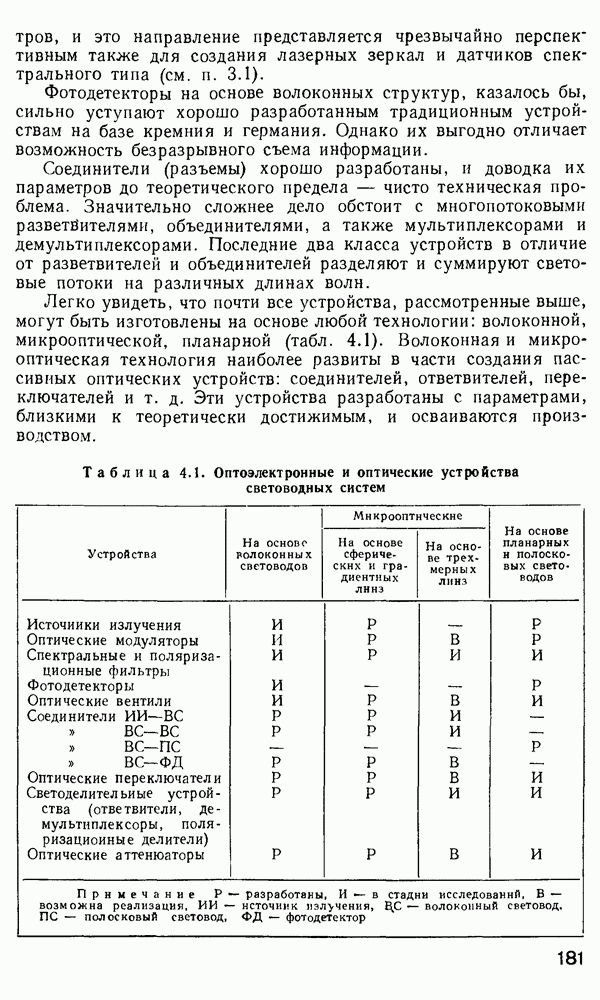
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
- Волоконные лазеры.
- Объемные микролазеры.
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
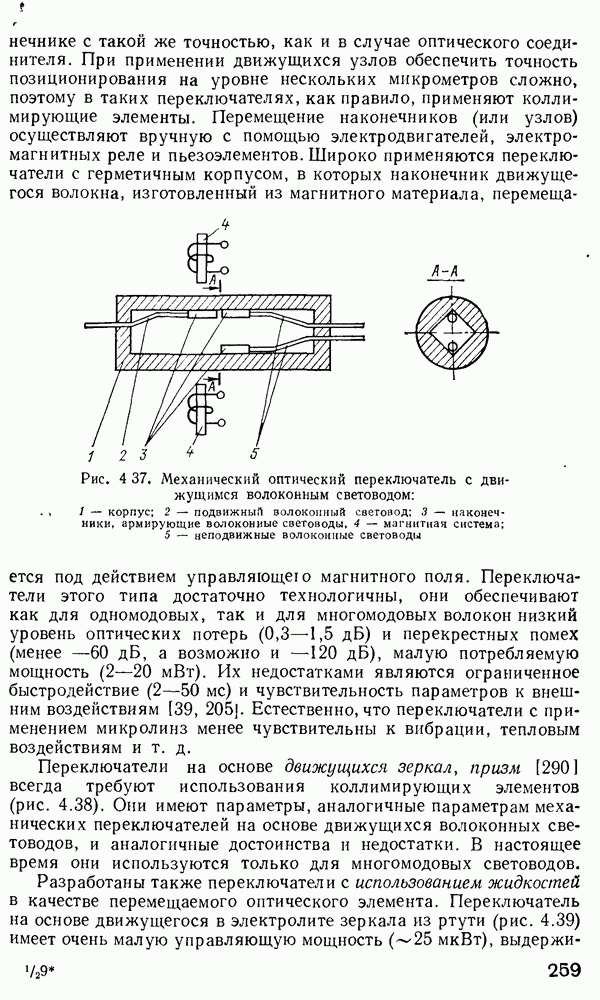
- 4.7. Волоконно-оптические переключатели
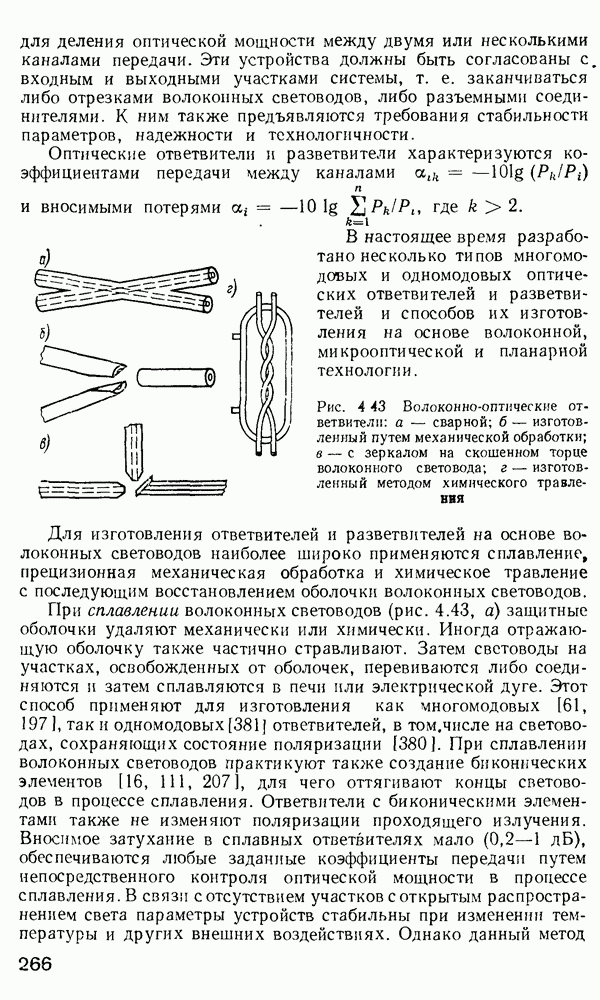
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
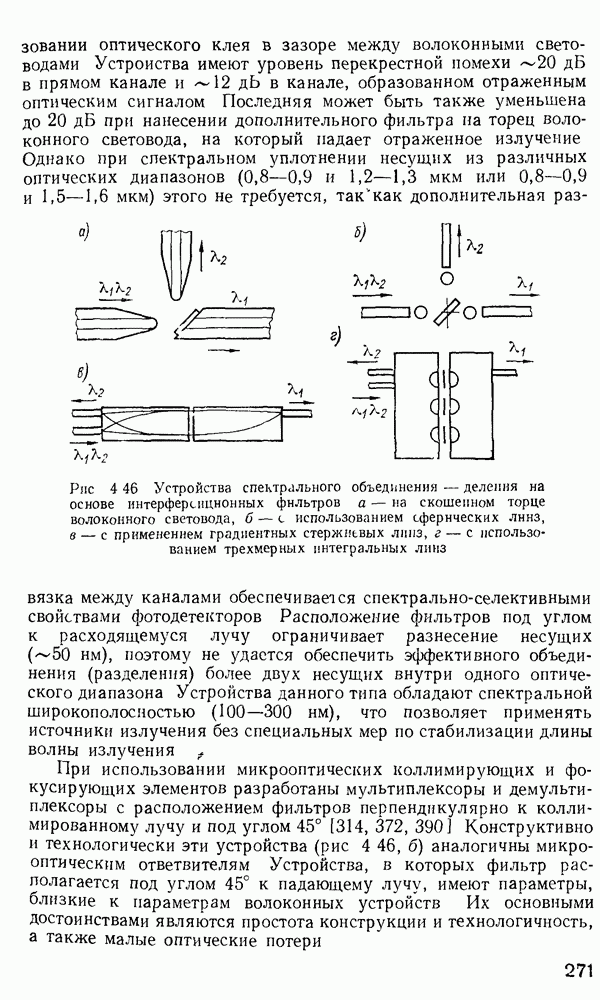
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
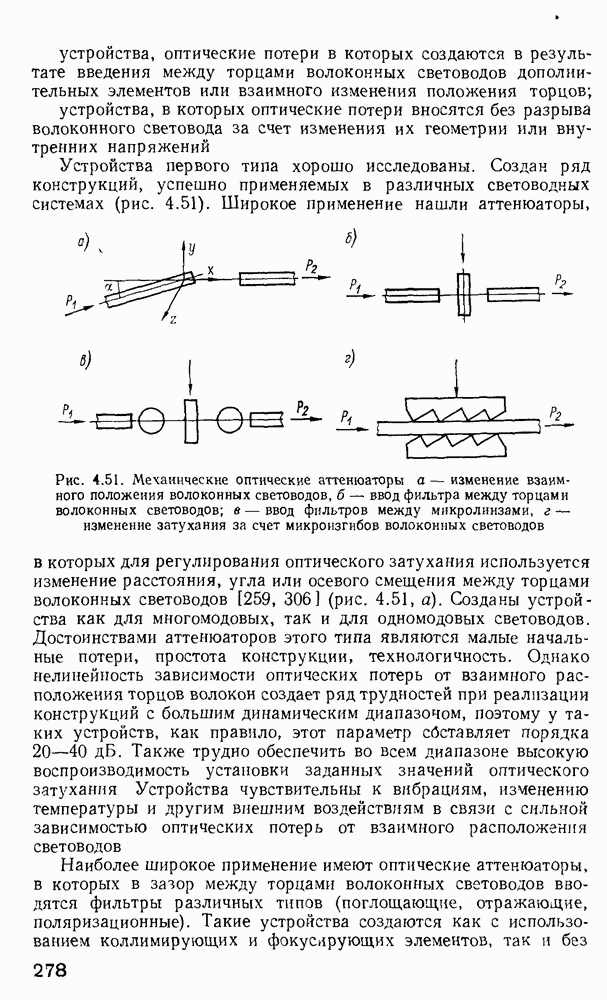
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
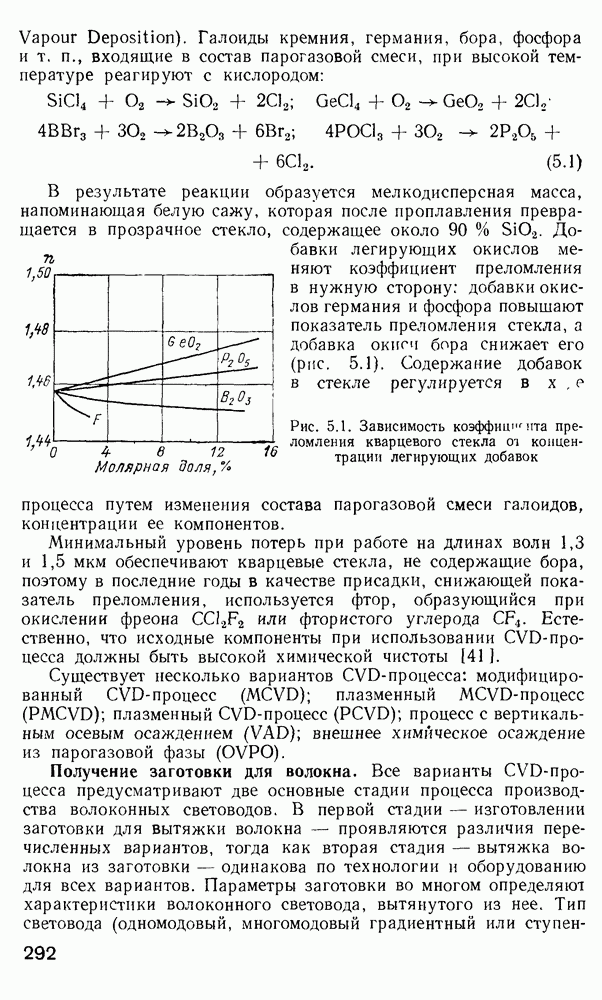
- Получение заготовки для волокна.
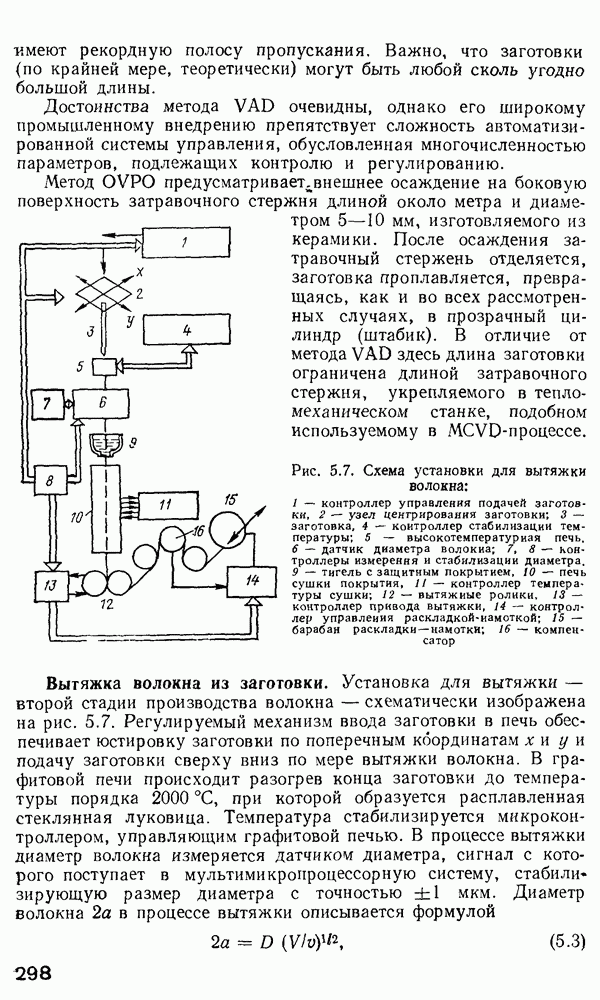
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
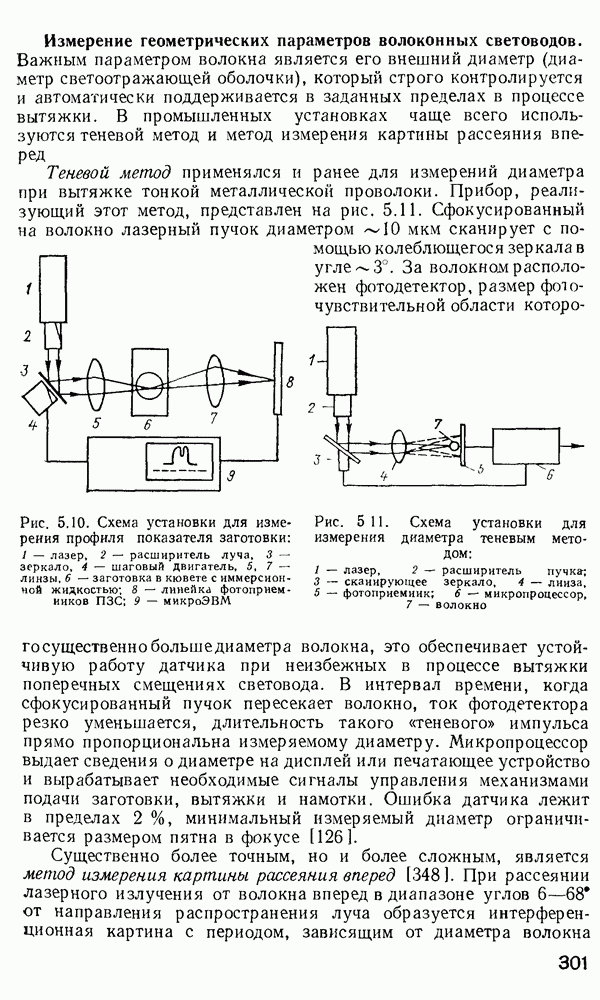
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ