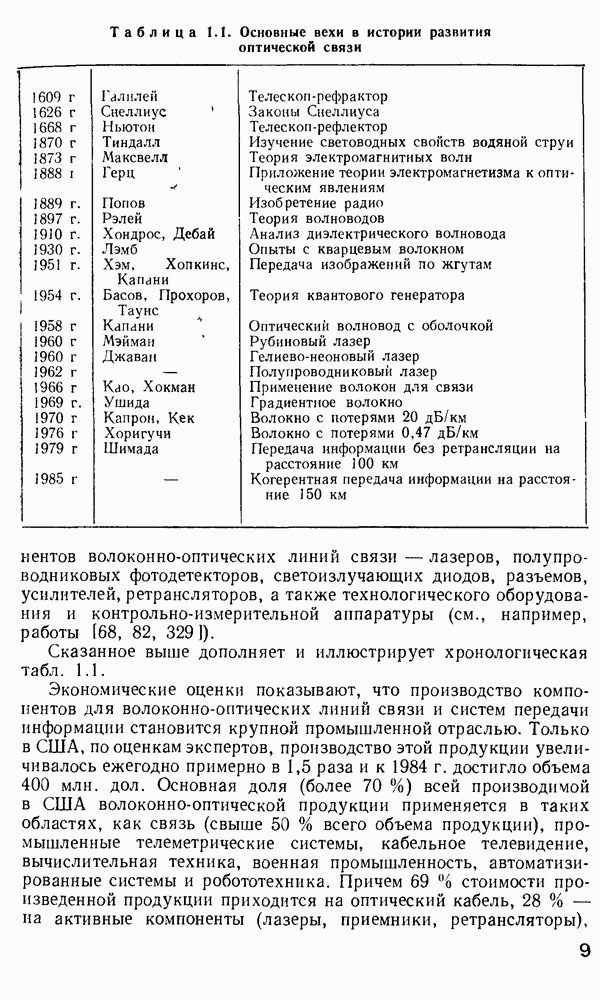
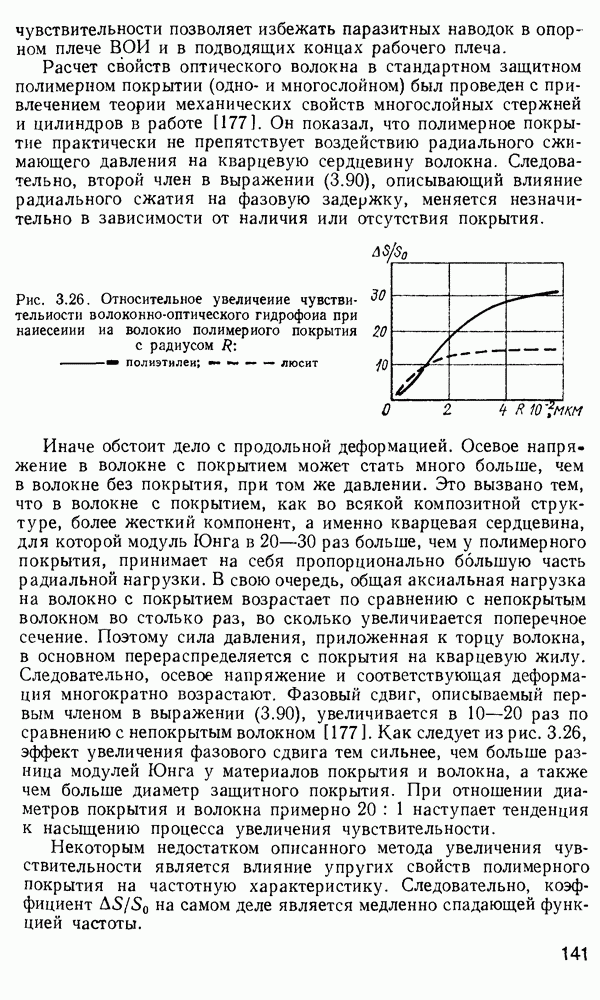
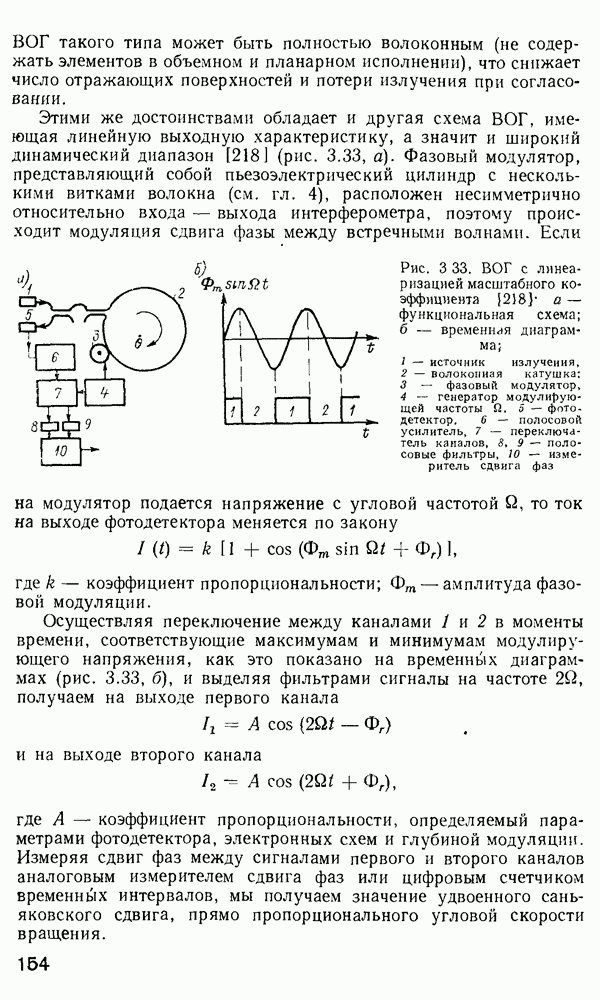
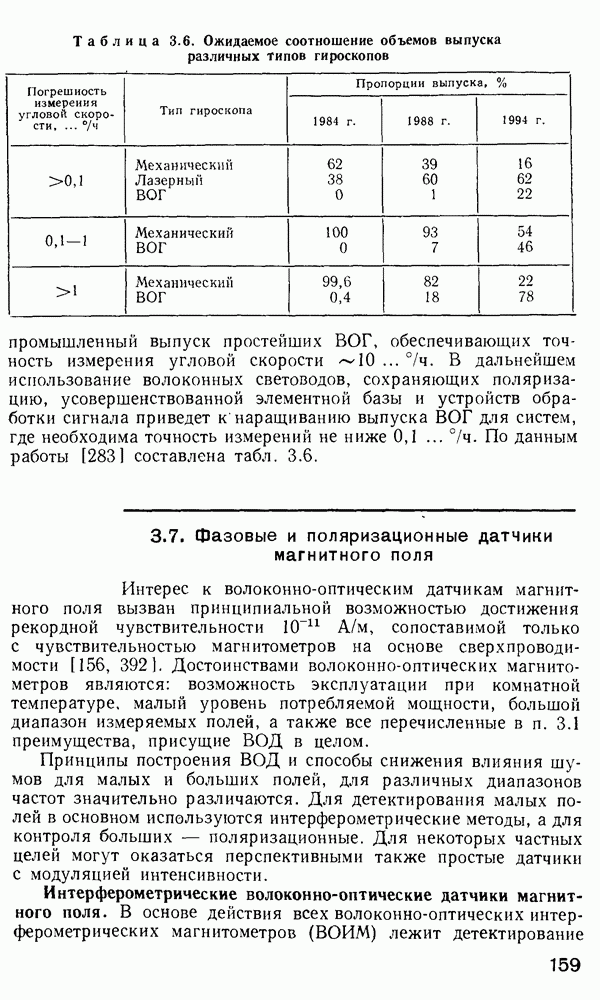
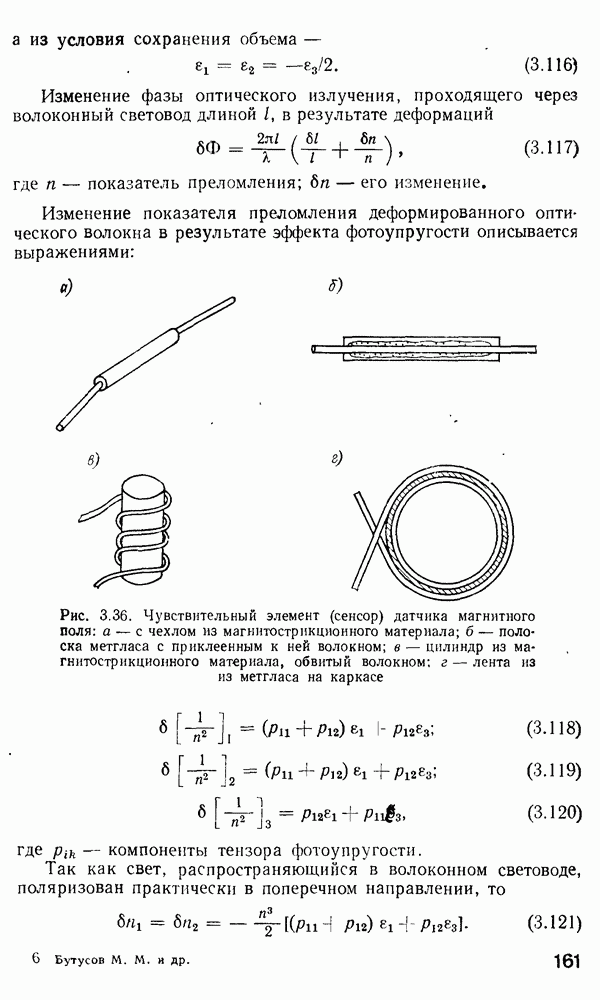
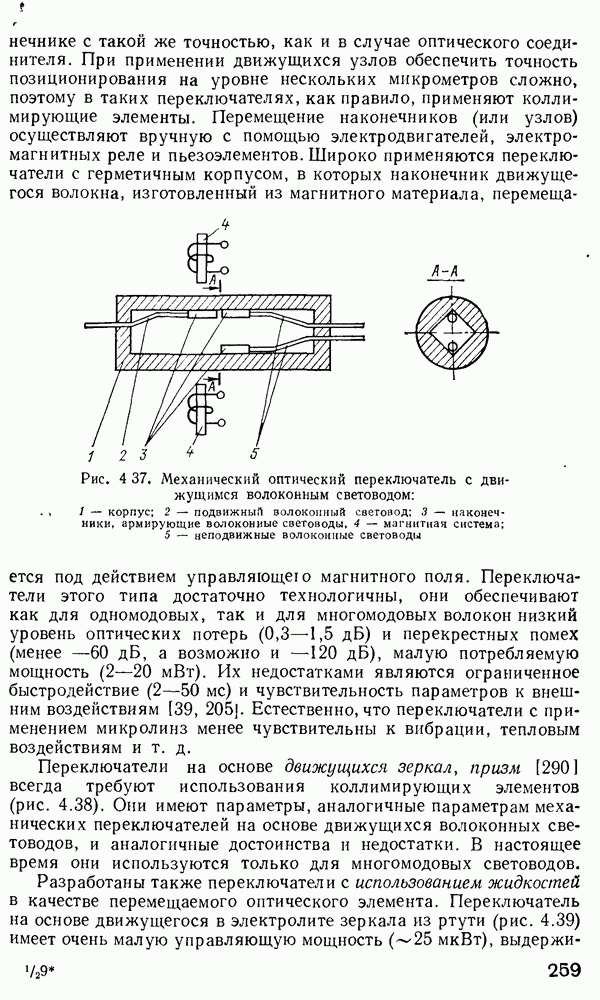
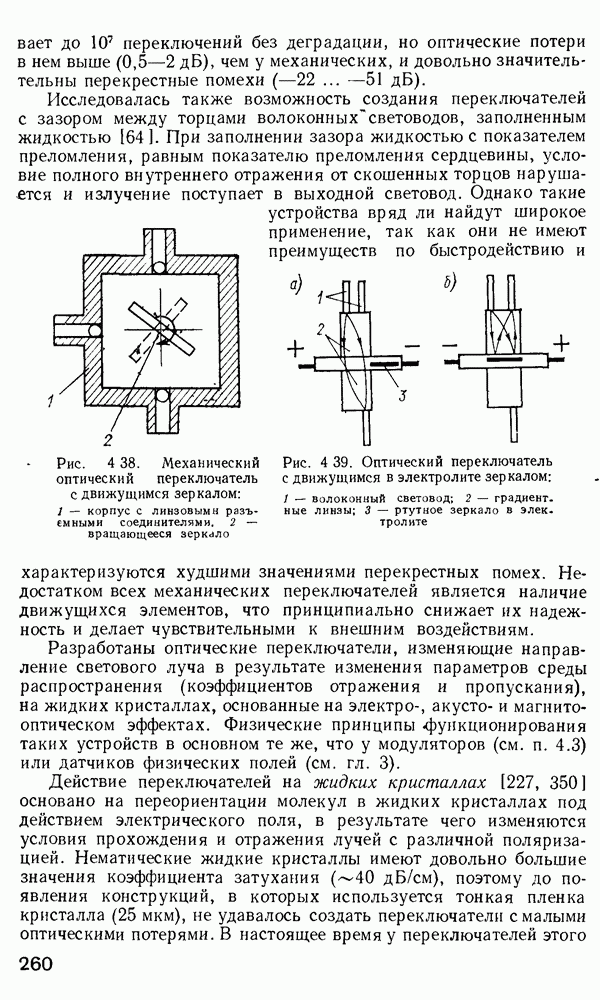
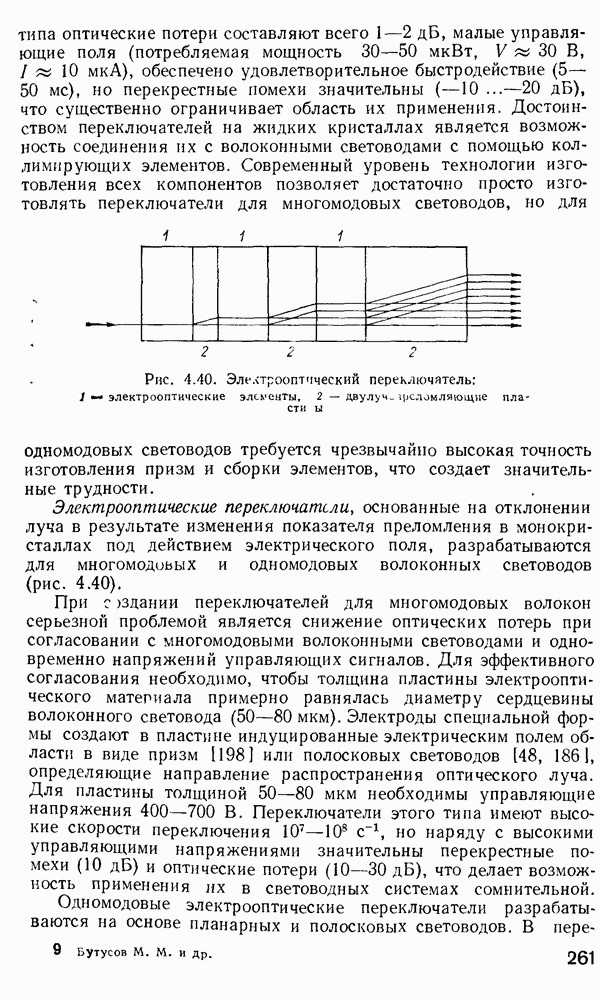
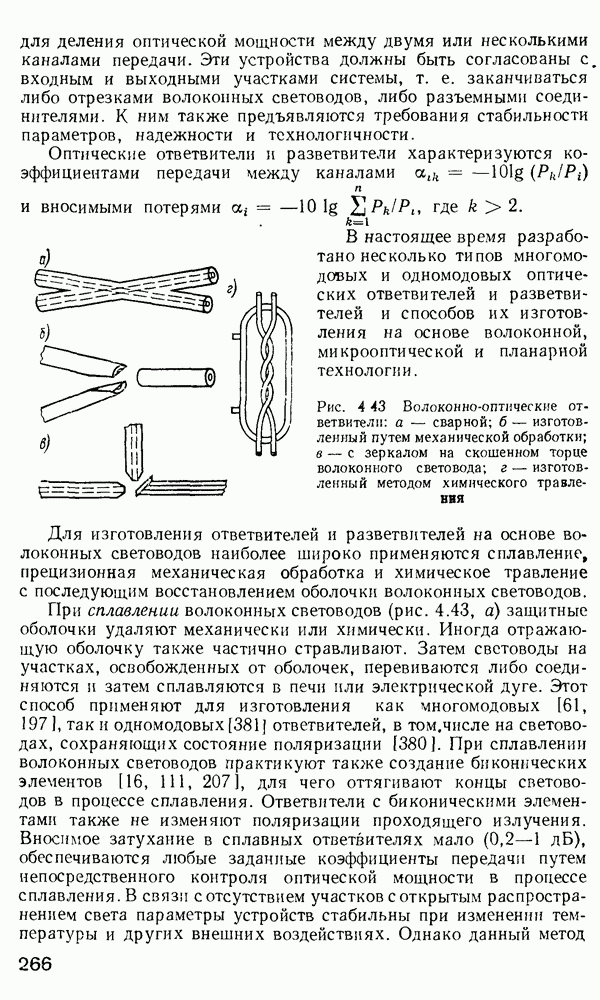
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
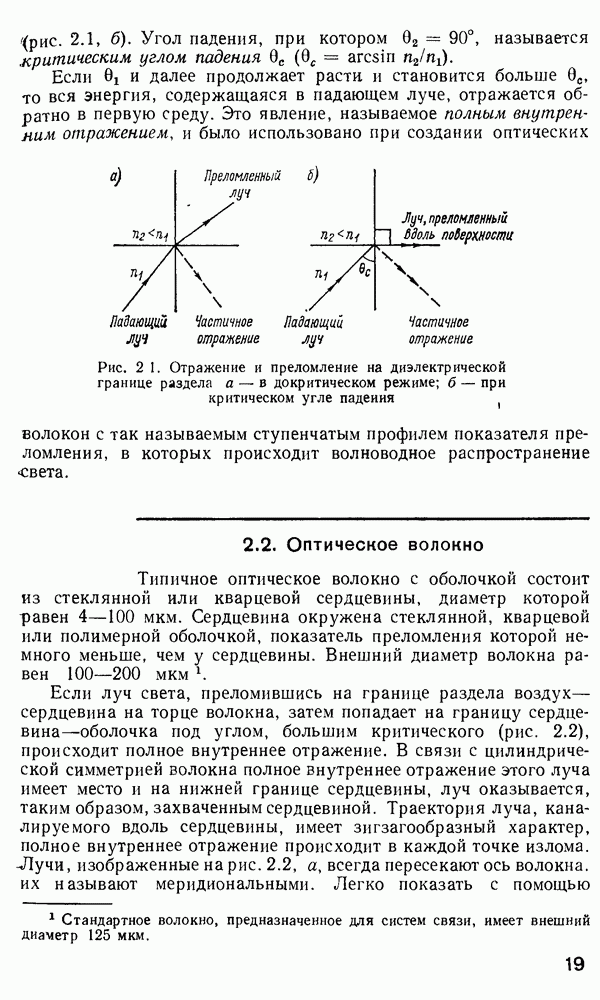
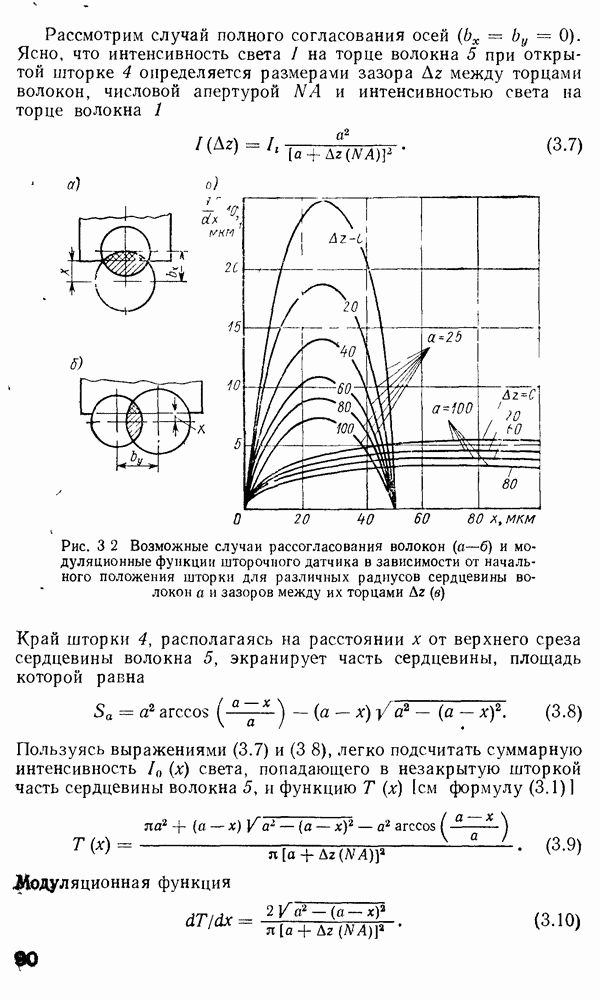
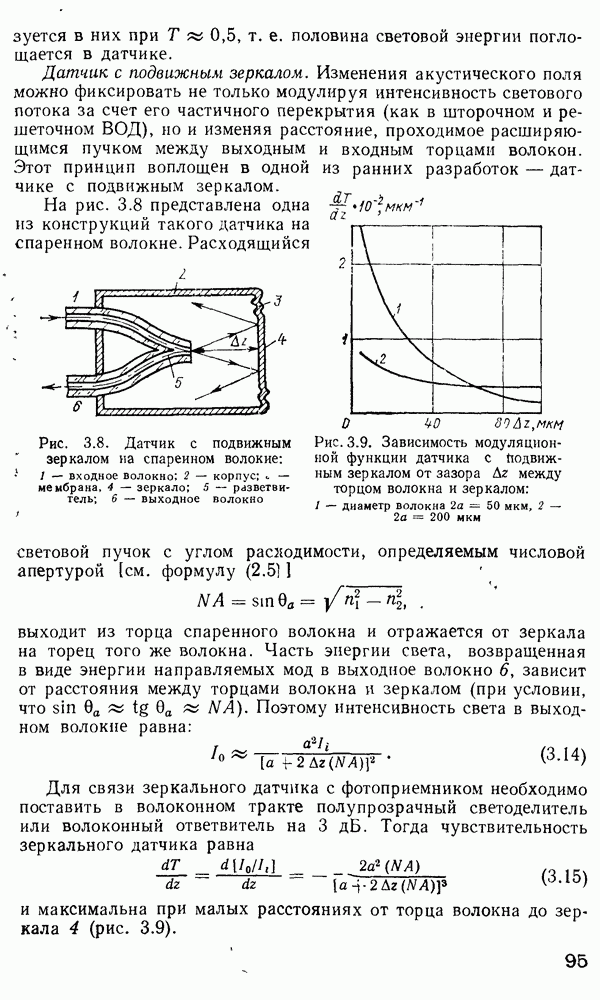
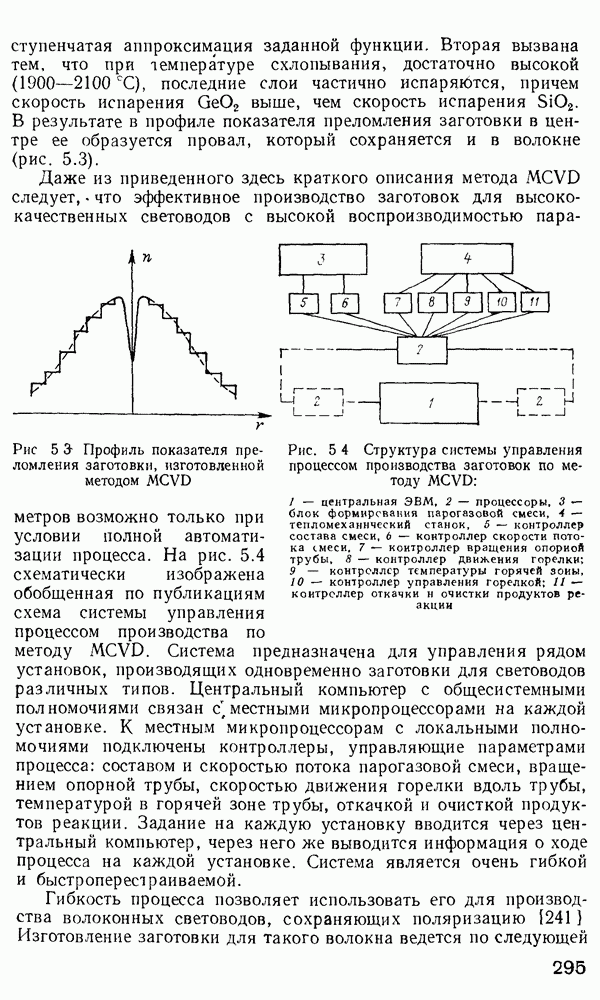
Одномодовое волокно.
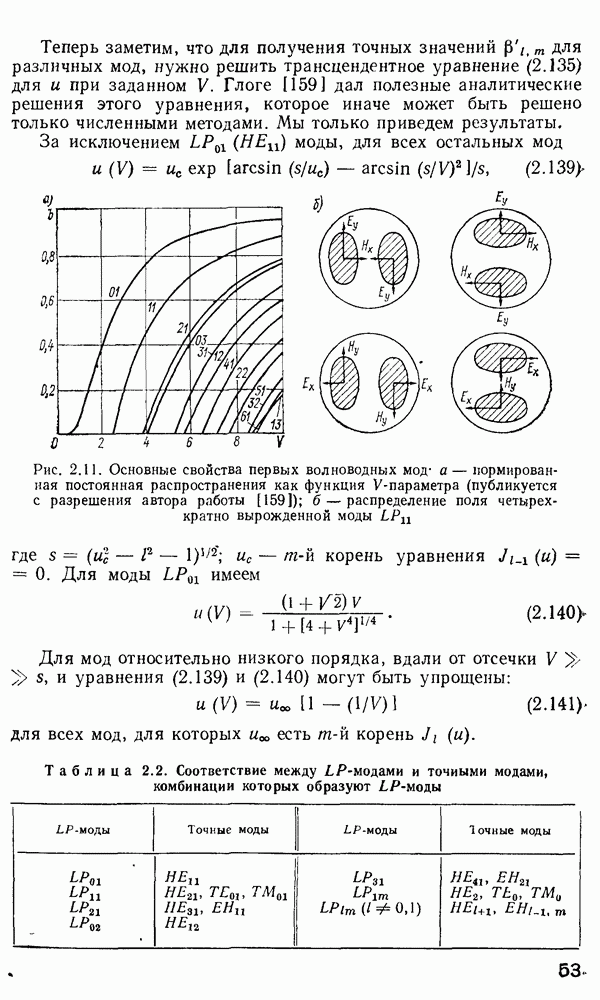
При достижении отсечки моды по аналогии с рассуждениями, приведенными в п. 2.4, мы должны иметь  Используя рекуррентные соотношения, связывающие
Используя рекуррентные соотношения, связывающие 
с  и Ко с Ко, приходим к характеристическому уравнению при отсечке для
и Ко с Ко, приходим к характеристическому уравнению при отсечке для  к ТМ-мод
к ТМ-мод

Поскольку  есть осциллирующая функция аргумента и для заданного I, то должно существовать
есть осциллирующая функция аргумента и для заданного I, то должно существовать  корней уравнений (2.114) и (2.115), подчиняющихся ограничениям, выраженным условием (2.110). В соответствии с этим
корней уравнений (2.114) и (2.115), подчиняющихся ограничениям, выраженным условием (2.110). В соответствии с этим  и ТМ-моды в оптическом волокне могут обозначаться двумя индексами:
и ТМ-моды в оптическом волокне могут обозначаться двумя индексами:  соответствующими первому, второму и т. д. нулям функции
соответствующими первому, второму и т. д. нулям функции  . Ситуации, соответствующие
. Ситуации, соответствующие  , являются гораздо более сложными. Не углубляясь в детальные расчеты, приведем условия отсечки для различных гибридных мод [122]:
, являются гораздо более сложными. Не углубляясь в детальные расчеты, приведем условия отсечки для различных гибридных мод [122]:

так как нули функции  имеют место при
имеют место при  то мода
то мода  не имеет отсечки. Поскольку при отсечке
не имеет отсечки. Поскольку при отсечке  из уравнения (2.109) можно получить, что и
из уравнения (2.109) можно получить, что и  где
где  — некая граничная величина.
— некая граничная величина.
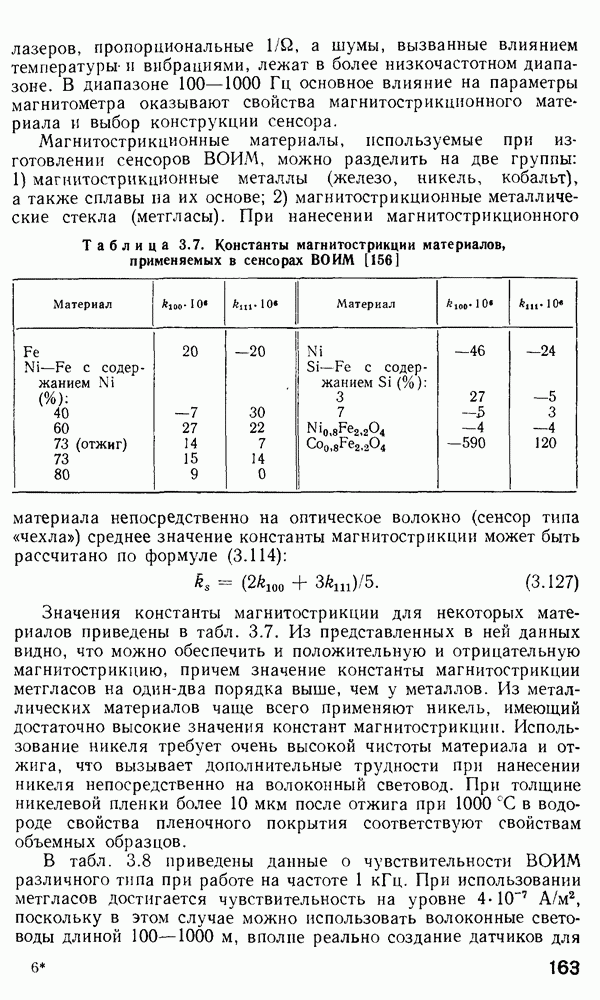
Значения  -параметра, соответствующие отсечкам различных мод, показаны в табл. 2.1.
-параметра, соответствующие отсечкам различных мод, показаны в табл. 2.1.
Таким образом, поскольку  для моды
для моды  , эта мода, являющаяся самой низкой разрешенной модой в оптическом волокне, в принципе может распространяться при произвольно малом радиусе сердцевины а и произвольно малой относительной разности показателей преломления сердцевины и оболочки — А. Следующие более высокие разрешенные моды —
, эта мода, являющаяся самой низкой разрешенной модой в оптическом волокне, в принципе может распространяться при произвольно малом радиусе сердцевины а и произвольно малой относительной разности показателей преломления сердцевины и оболочки — А. Следующие более высокие разрешенные моды —  частота отсечки которых задается первым нулем
частота отсечки которых задается первым нулем  который имеет место при и
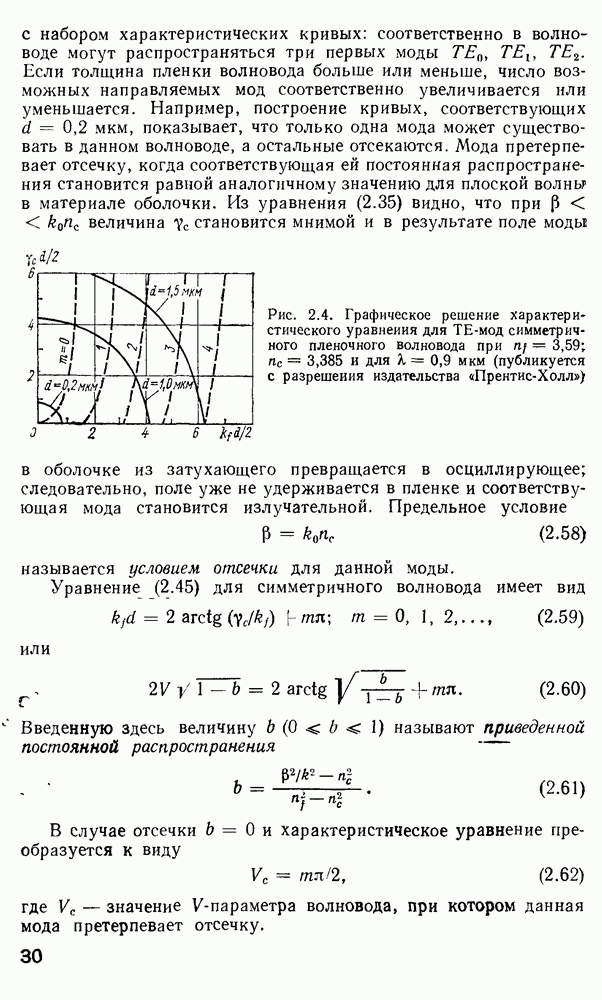
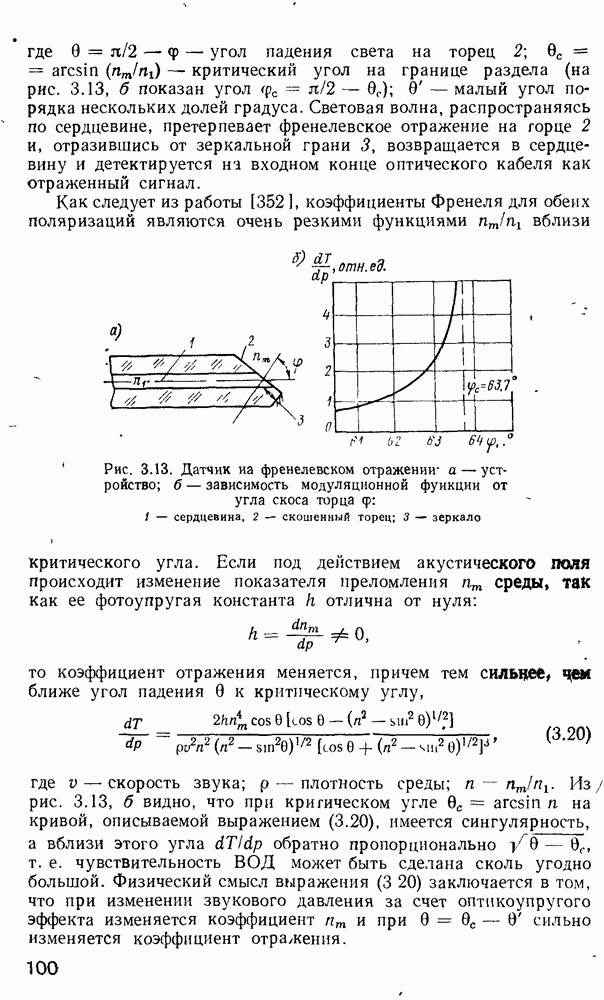
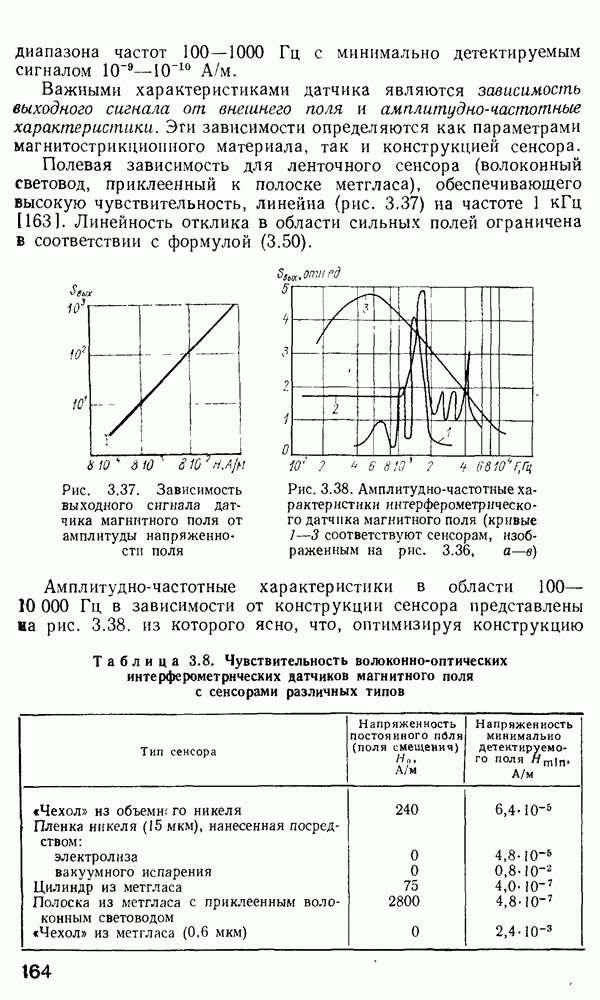
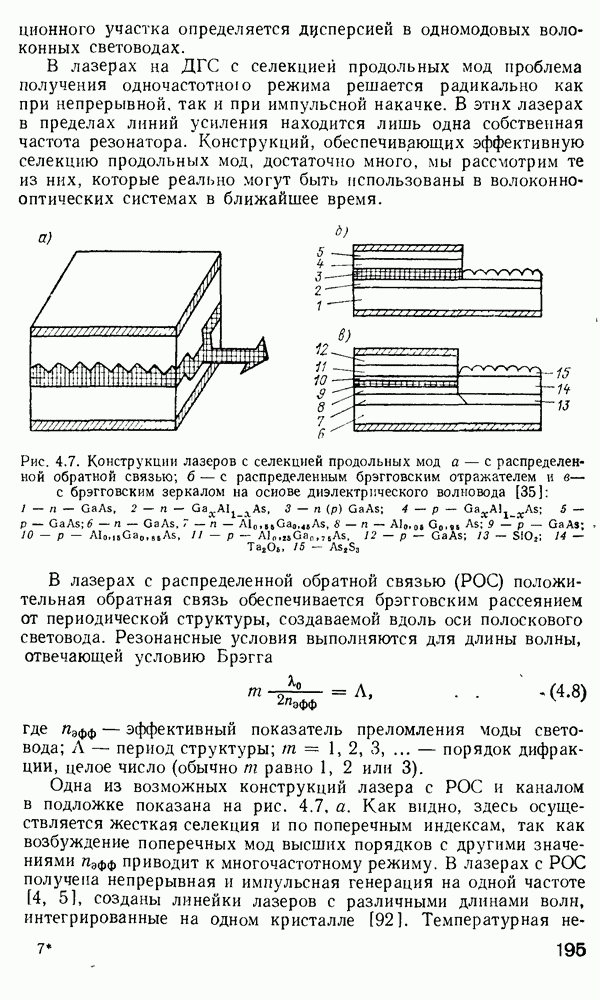
который имеет место при и  Вид различных функций Бесселя для получения условий отсечки представлен на рис. 2.8.
Вид различных функций Бесселя для получения условий отсечки представлен на рис. 2.8.
Таблица 2.1. Критические значения  -параметра для
-параметра для  и ЕН-мод в ступенчатом волокне с
и ЕН-мод в ступенчатом волокне с 

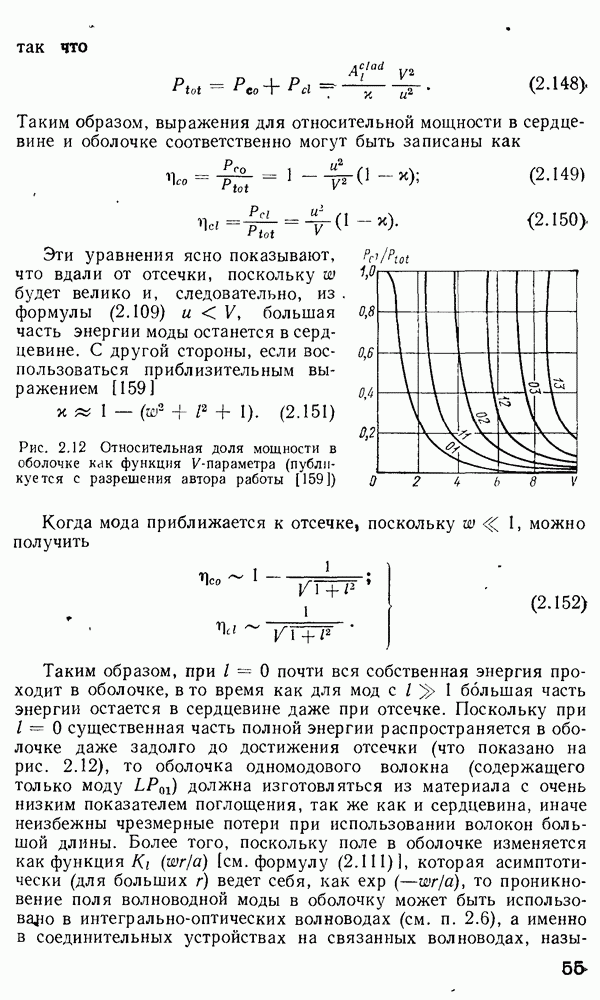
Если подобрать такие значения радиуса сердцевины а и относительной разности показателя преломления А, чтобы  так что другие моды, кроме низшей разрешенной
так что другие моды, кроме низшей разрешенной  не смогут распространяться в волокне, то можно получить так называемые «одномодовые волокна». Они обладают рядом достоинств, в числе которых крайне большая ширина полосы пропускания. Одномодовые волокна в наибольшей мере подходят для использования с интегрально-оптическими устройствами и изготовления волоконно-оптических фазовых датчиков
не смогут распространяться в волокне, то можно получить так называемые «одномодовые волокна». Они обладают рядом достоинств, в числе которых крайне большая ширина полосы пропускания. Одномодовые волокна в наибольшей мере подходят для использования с интегрально-оптическими устройствами и изготовления волоконно-оптических фазовых датчиков  Условие
Условие

может быть использовано в расчете волноводов при выборе значений а и А для получения одномодовых волокон (со ступенчатым профилем показателя преломления), рассчитанных на определенную длину волны X. Условие отсечки в оптическом волокне также часто выражается через длину волны отсечки  аналогично плоскому волноводу [см. уравнение (2.64)].
аналогично плоскому волноводу [см. уравнение (2.64)].

Рис. 2.8 Функции Бесселя 
В данном случае

для данного волокна, имеющего определенные  и А. Для любой X, большей
и А. Для любой X, большей  данное волокно будет всегда одномодовым. С другой стороны, при
данное волокно будет всегда одномодовым. С другой стороны, при  оно становится многомодовым. В этом смысле величина
оно становится многомодовым. В этом смысле величина  очень важна, потому что выбор значения
очень важна, потому что выбор значения  фактически диктуемый такими соображениями, как снижение потерь при передаче и увеличение ширины полосы пропускания, определяет длину волны, при которой эффективности источника и детектора максимальны, что в конечном счете определяет и выбор значений а и А для конструирования одномодовых волокон с хорошими рабочими параметрами.
фактически диктуемый такими соображениями, как снижение потерь при передаче и увеличение ширины полосы пропускания, определяет длину волны, при которой эффективности источника и детектора максимальны, что в конечном счете определяет и выбор значений а и А для конструирования одномодовых волокон с хорошими рабочими параметрами.
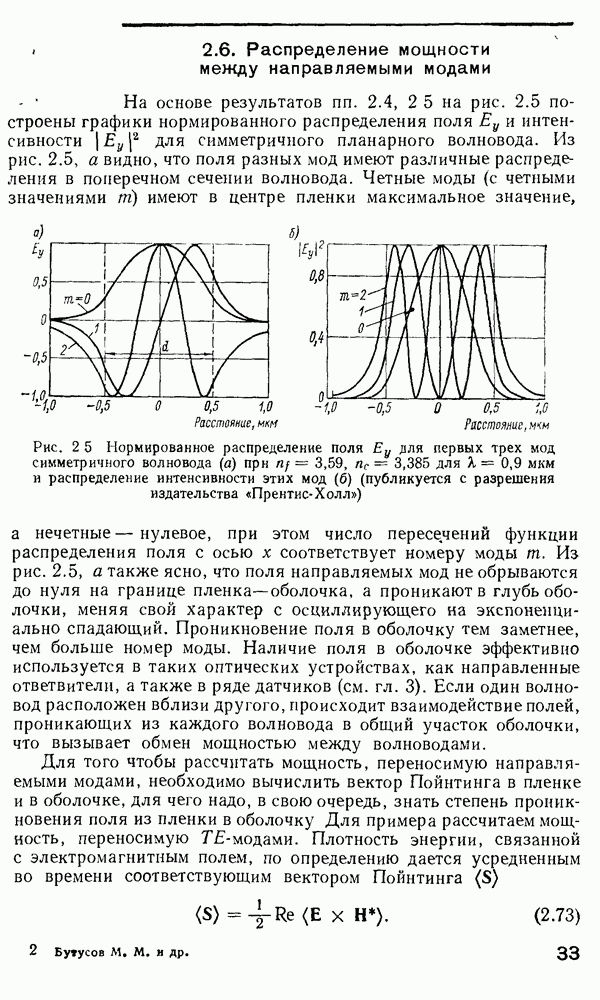
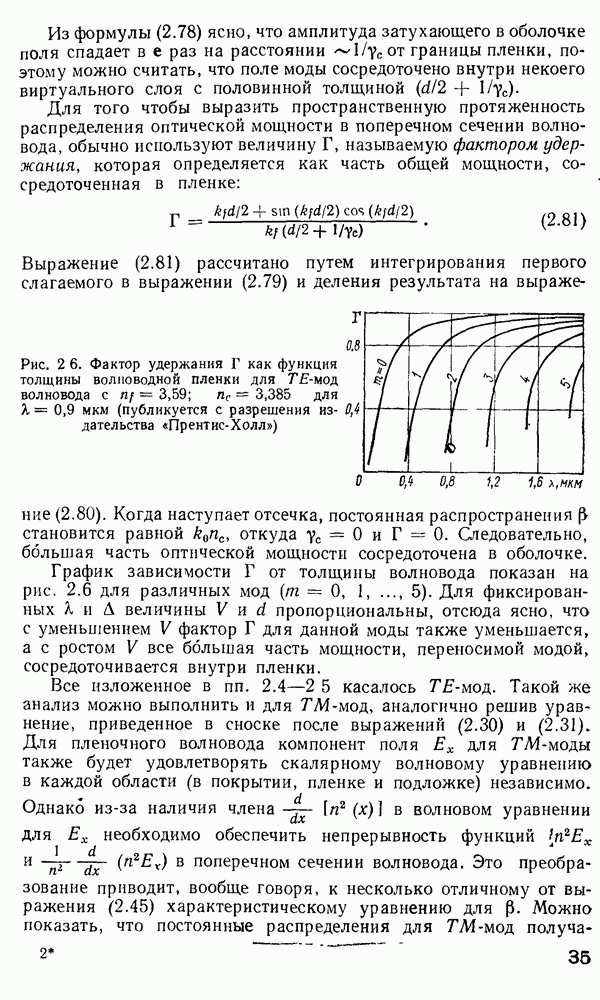
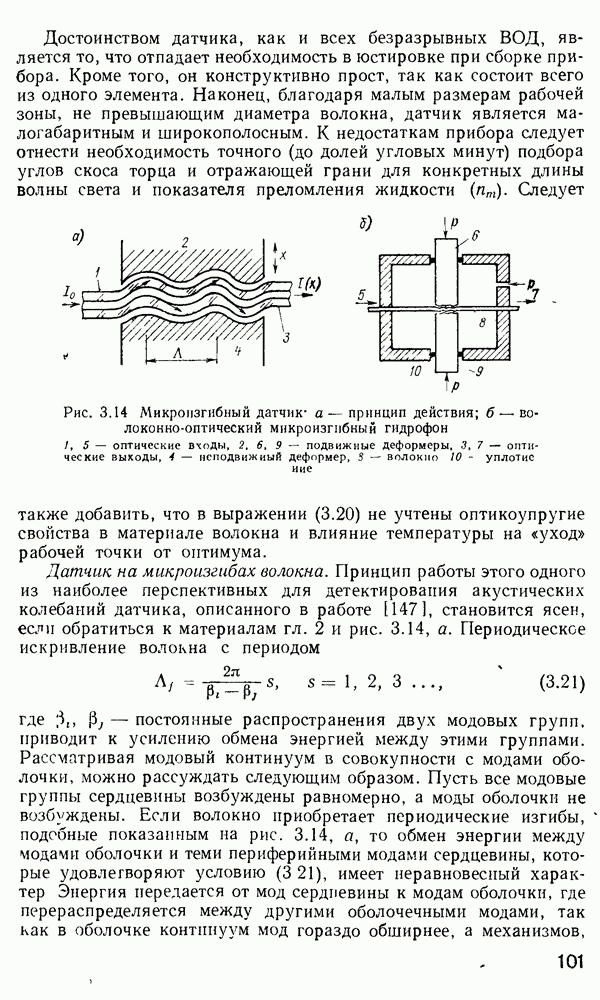
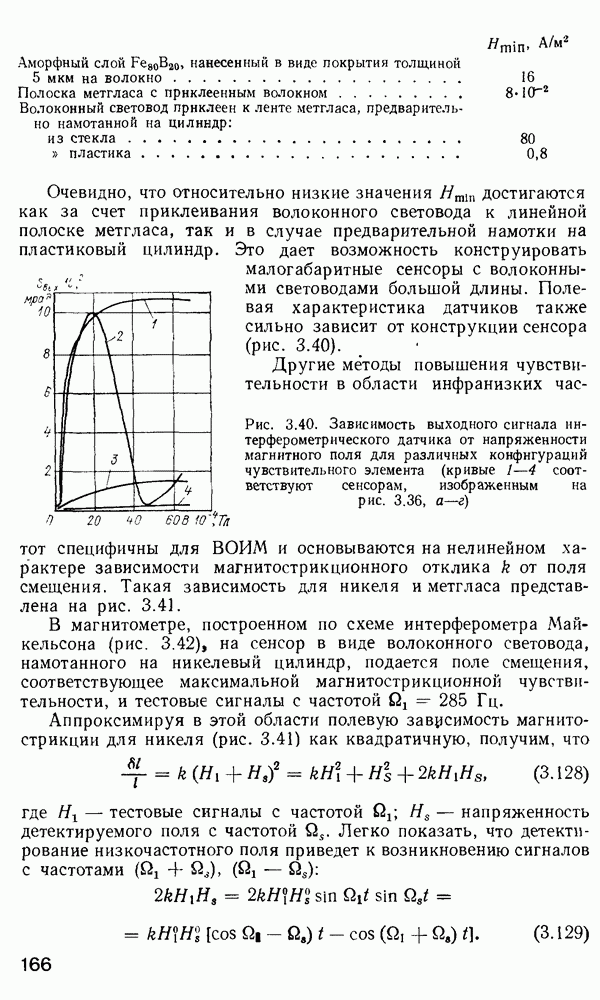
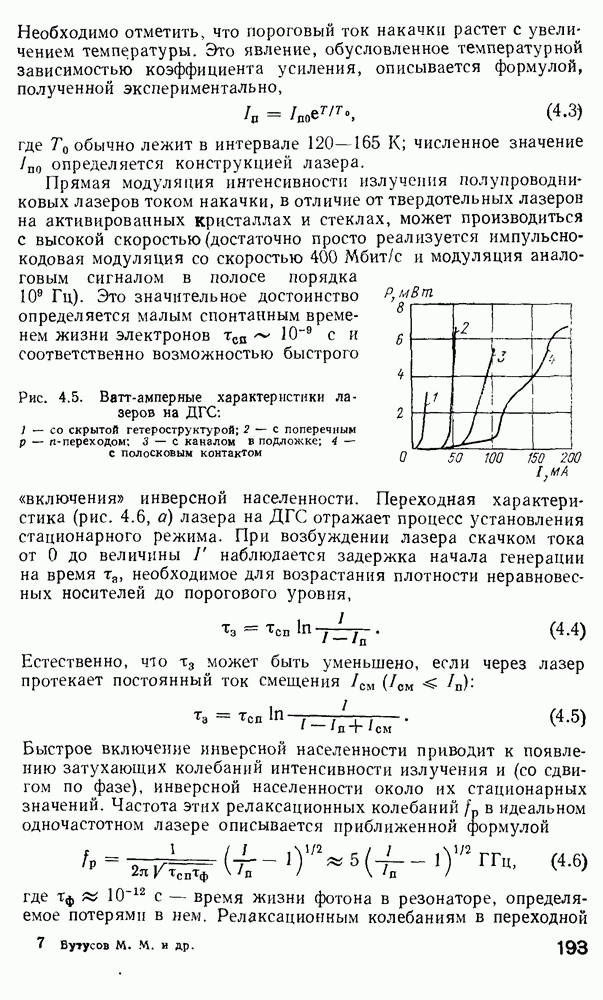
Различные важные характеристики основной моды  приведены на рис. 2.9 для
приведены на рис. 2.9 для  Исходя из определений и и V [см. уравнения (2.108)], можно легко показать, что
Исходя из определений и и V [см. уравнения (2.108)], можно легко показать, что

Для иллюстрации характера изменения  построен график
построен график  наряду с кривыми для других интересующих нас величин (которые мы обсудим позднее в связи с расчетами потока мощности).
наряду с кривыми для других интересующих нас величин (которые мы обсудим позднее в связи с расчетами потока мощности).
Значение  моды
моды  для конкретного значения V при одномодо
для конкретного значения V при одномодо  режиме может быть вычислено непосредственно из этой характеристики с использованием формулы (2.120).
режиме может быть вычислено непосредственно из этой характеристики с использованием формулы (2.120).
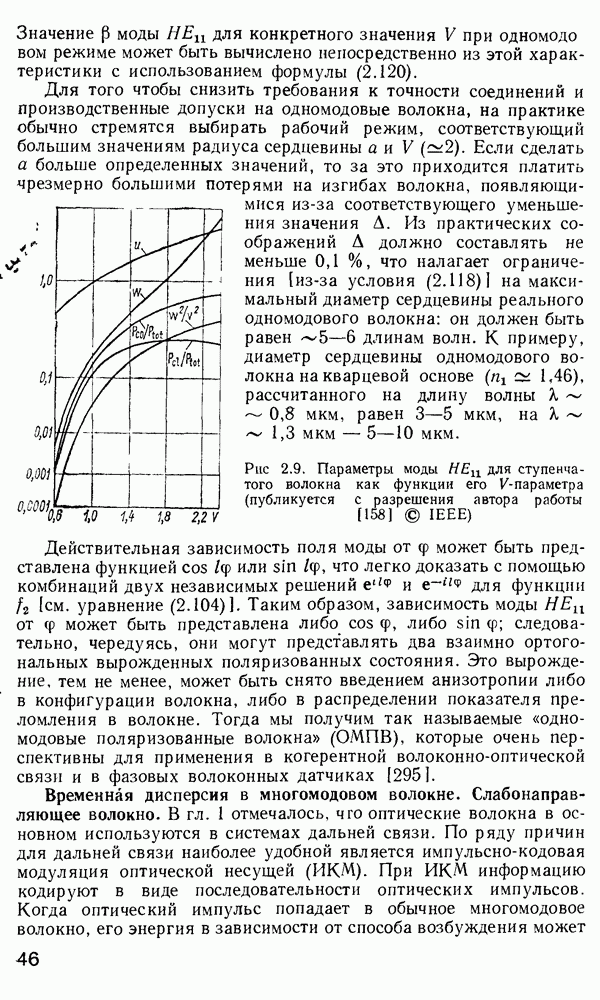
Для того чтобы снизить требования к точности соединений и производственные допуски на одномодовые волокна, на практике обычно стремятся выбирать рабочий режим, соответствующий большим значениям радиуса сердцевины а и  . Если сделать а больше определенных значений, то за это приходится платить чрезмерно большими потерями на изгибах волокна, появляющимися из-за соответствующего уменьшения значения
. Если сделать а больше определенных значений, то за это приходится платить чрезмерно большими потерями на изгибах волокна, появляющимися из-за соответствующего уменьшения значения  Из практических соображений А должно составлять не меньше
Из практических соображений А должно составлять не меньше  что налагает ограничения [из-за условия (2.118)] на максимальный диаметр сердцевины реального одномодового волокна: он должен быть равен
что налагает ограничения [из-за условия (2.118)] на максимальный диаметр сердцевины реального одномодового волокна: он должен быть равен  длинам волн. К примеру, диаметр сердцевины одномодового волокна на кварцевой основе
длинам волн. К примеру, диаметр сердцевины одномодового волокна на кварцевой основе  рассчитанного на длину волны
рассчитанного на длину волны 
— 0,8 мкм, равен 3—5 мкм, на  мкм — 5—10 мкм.
мкм — 5—10 мкм.

Рис. 2.9. Параметры моды  для ступенчатого волокна как функции его К-параметра (публикуется с разрешения автора работы
для ступенчатого волокна как функции его К-параметра (публикуется с разрешения автора работы 
Действительная зависимость поля моды от  может быть представлена функцией
может быть представлена функцией  или
или  что легко доказать с помощью комбинаций двух независимых решений
что легко доказать с помощью комбинаций двух независимых решений  для функции
для функции  [см. уравнение (2.104)]. Таким образом, зависимость моды
[см. уравнение (2.104)]. Таким образом, зависимость моды  от
от  может быть представлена либо
может быть представлена либо  либо
либо  следовательно, чередуясь, они могут представлять два взаимно ортогональных вырожденных поляризованных состояния. Это вырождение, тем не менее, может быть снято введением анизотропии либо в конфигурации волокна, либо в распределении показателя преломления в волокне. Тогда мы получим так называемые «одномодовые поляризованные волокна»
следовательно, чередуясь, они могут представлять два взаимно ортогональных вырожденных поляризованных состояния. Это вырождение, тем не менее, может быть снято введением анизотропии либо в конфигурации волокна, либо в распределении показателя преломления в волокне. Тогда мы получим так называемые «одномодовые поляризованные волокна»  которые очень перспективны для применения в когерентной волоконно-оптической связи и в фазовых волоконных датчиках [295].
которые очень перспективны для применения в когерентной волоконно-оптической связи и в фазовых волоконных датчиках [295].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
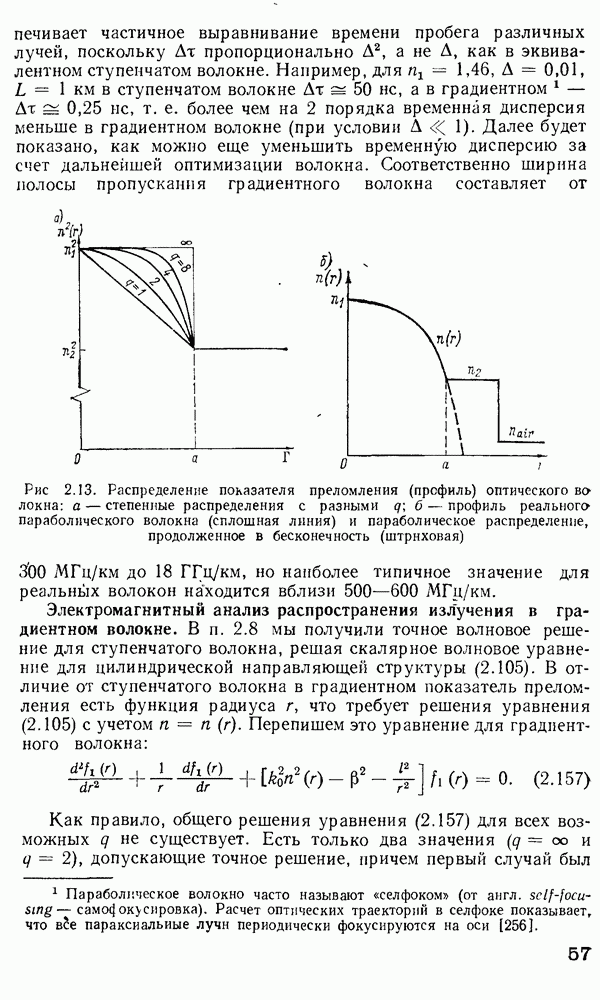
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
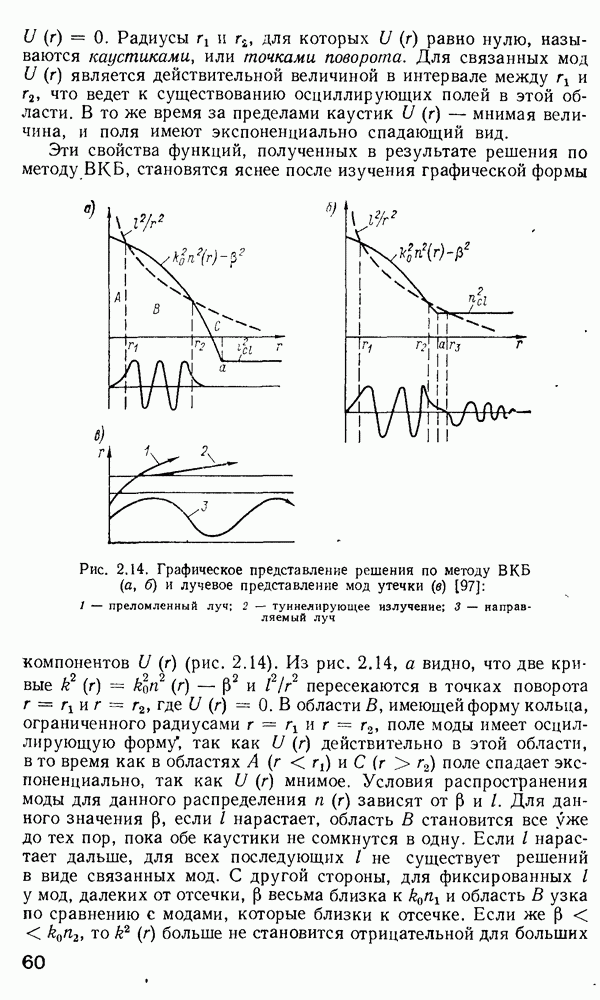
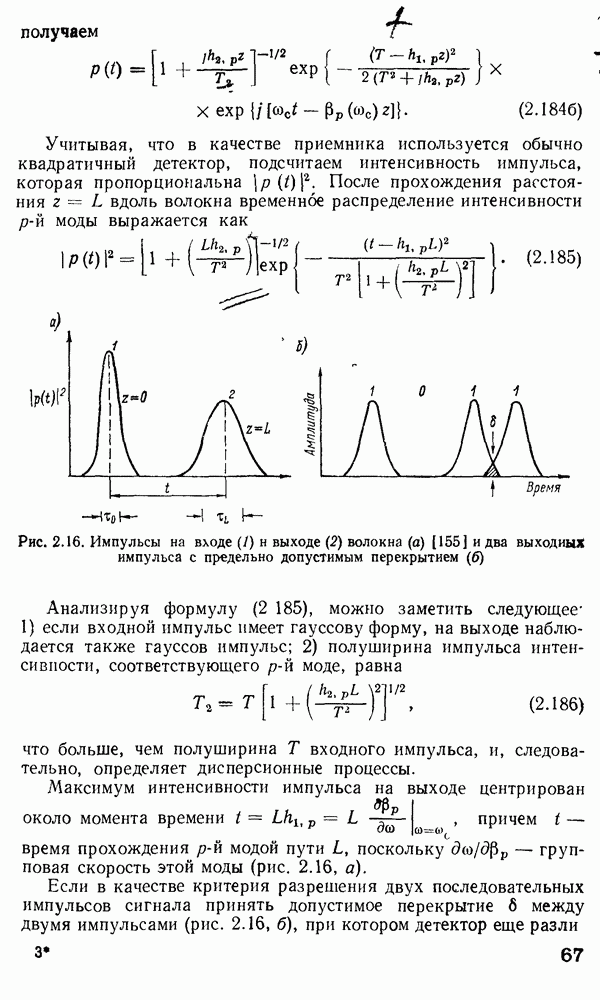
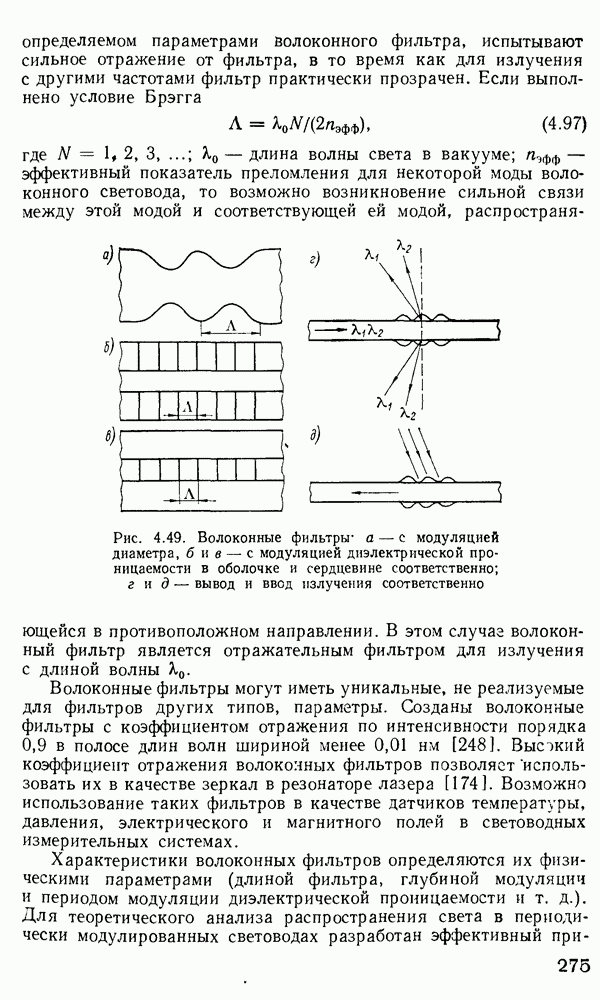
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
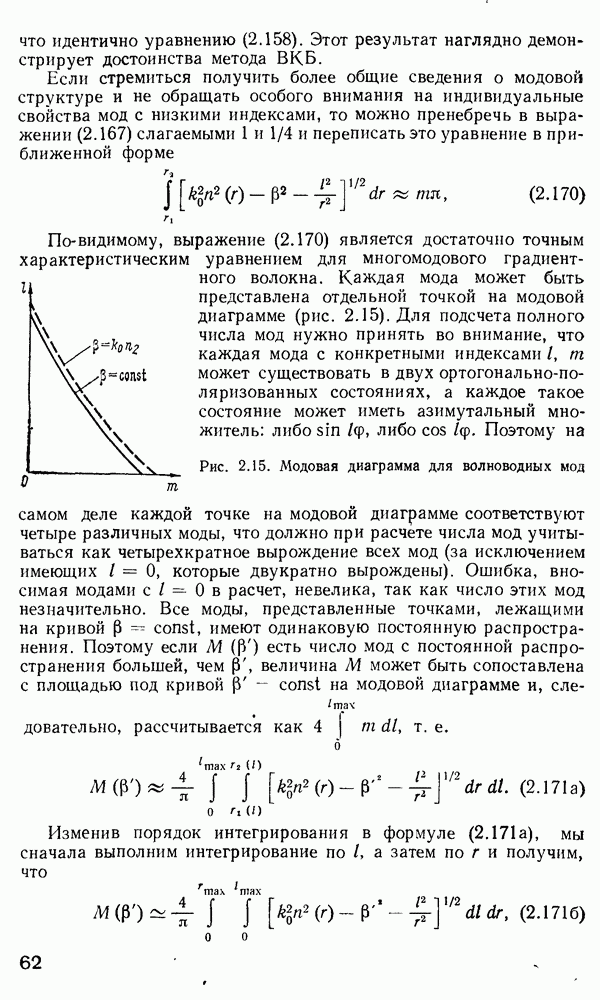
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
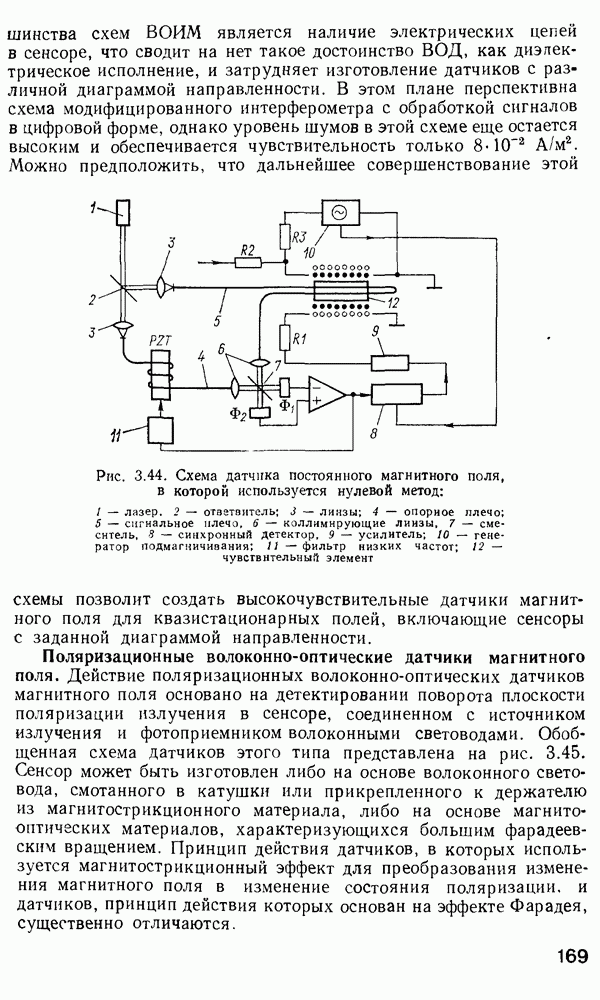
- 3.7. Фазовые и поляризационные датчики магнитного поля
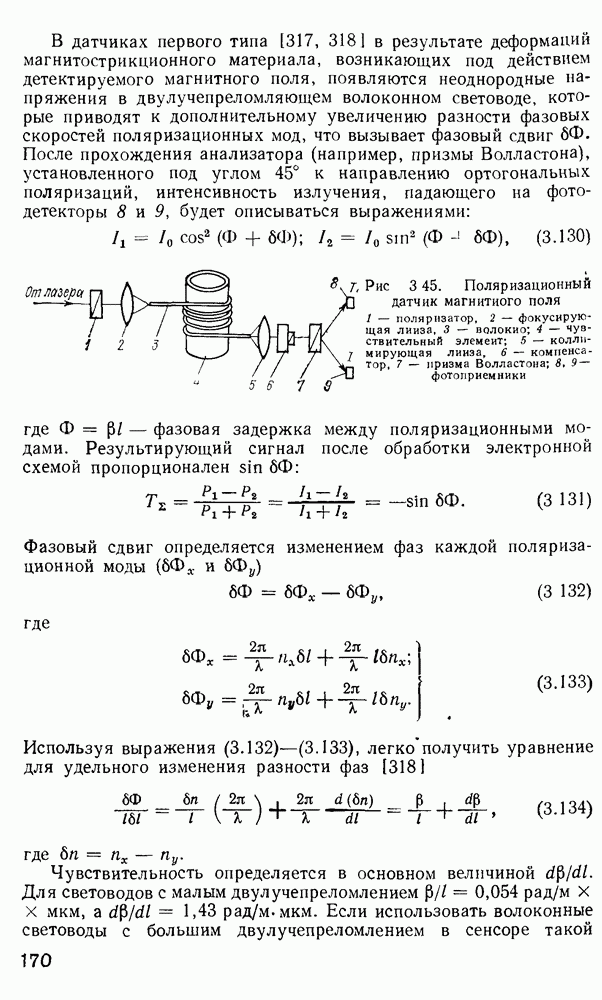
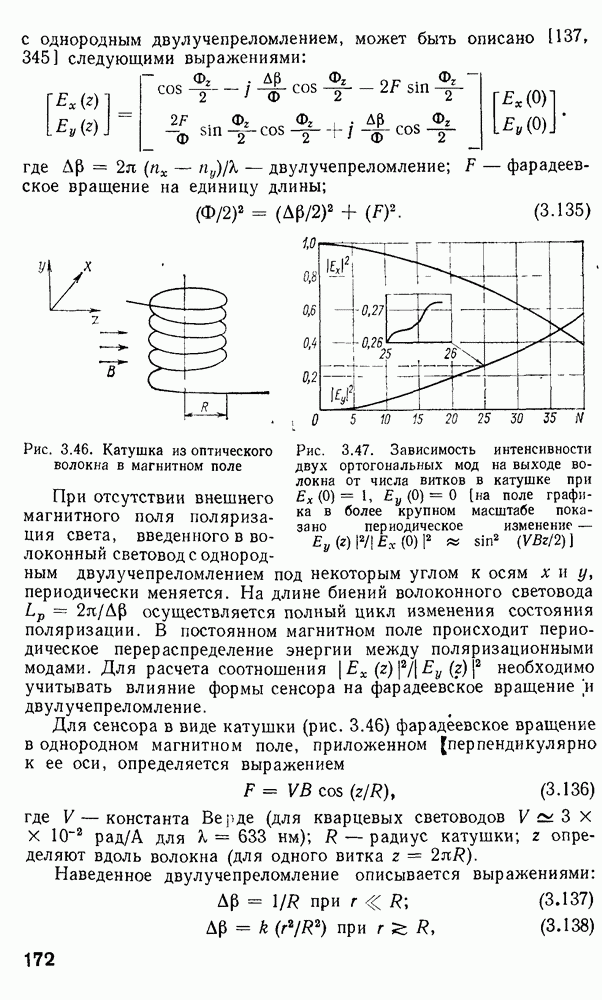
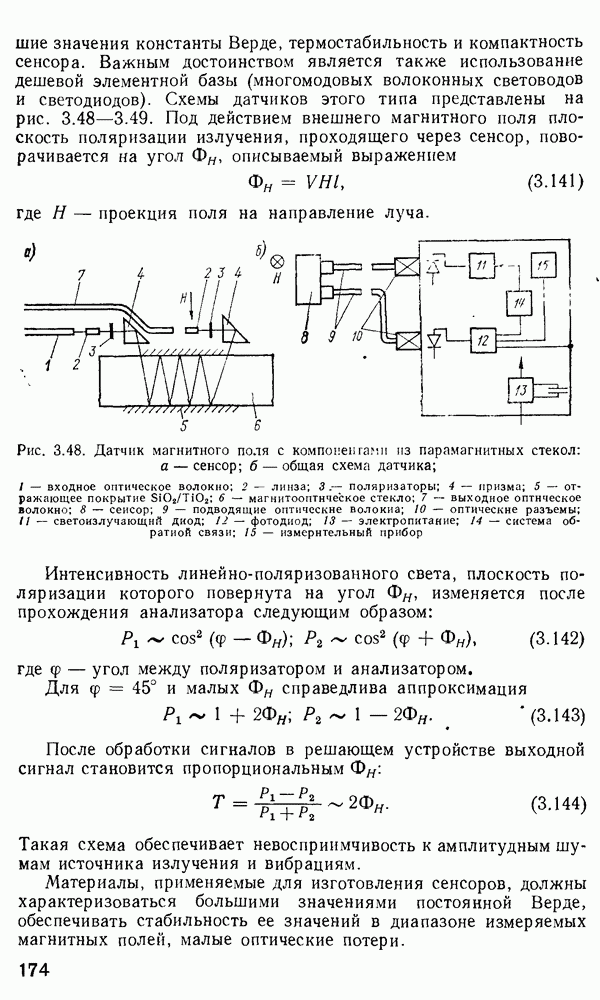
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
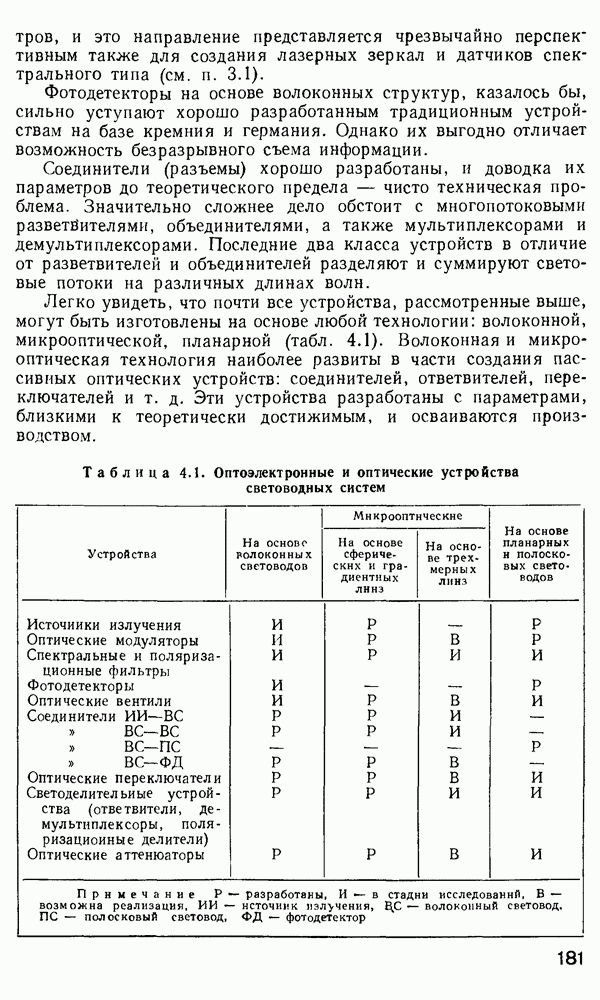
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
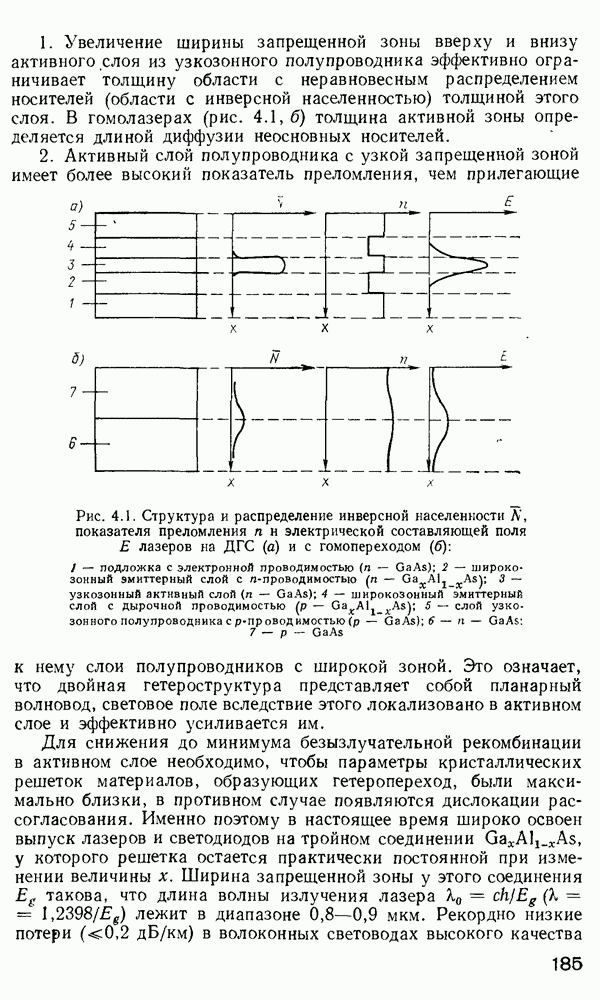
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
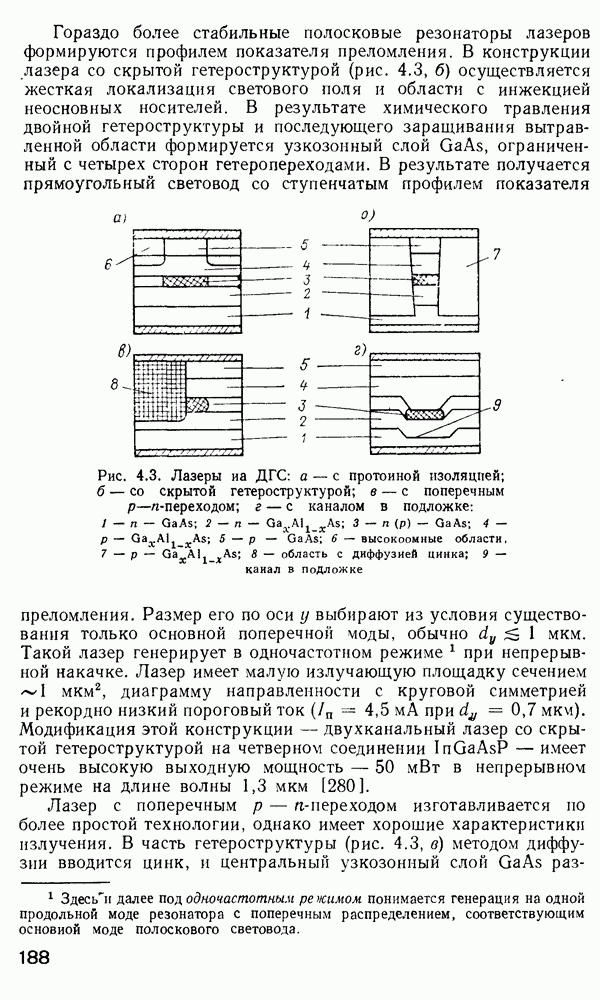
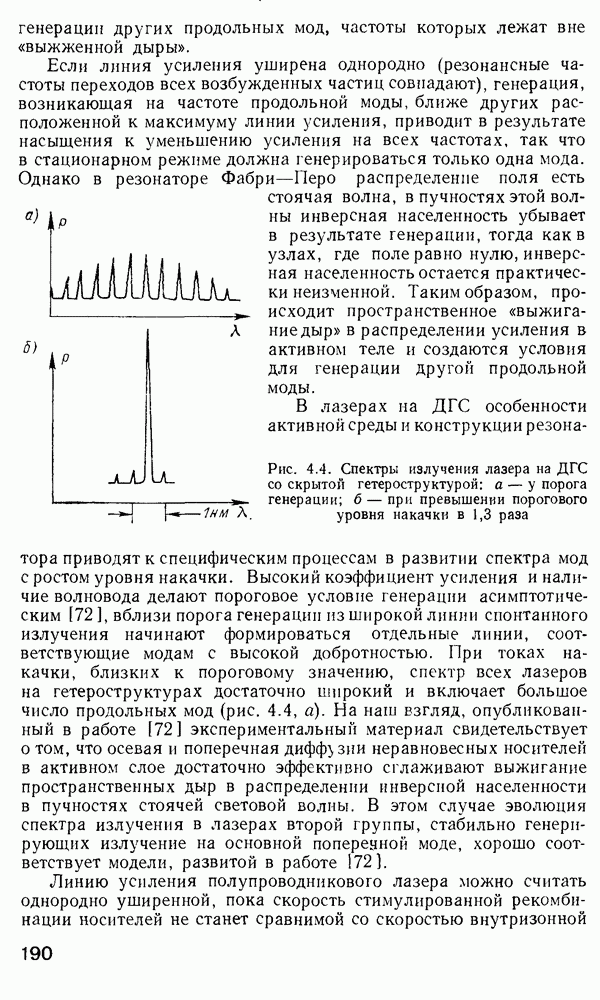
- Полупроводниковые источники излучения.
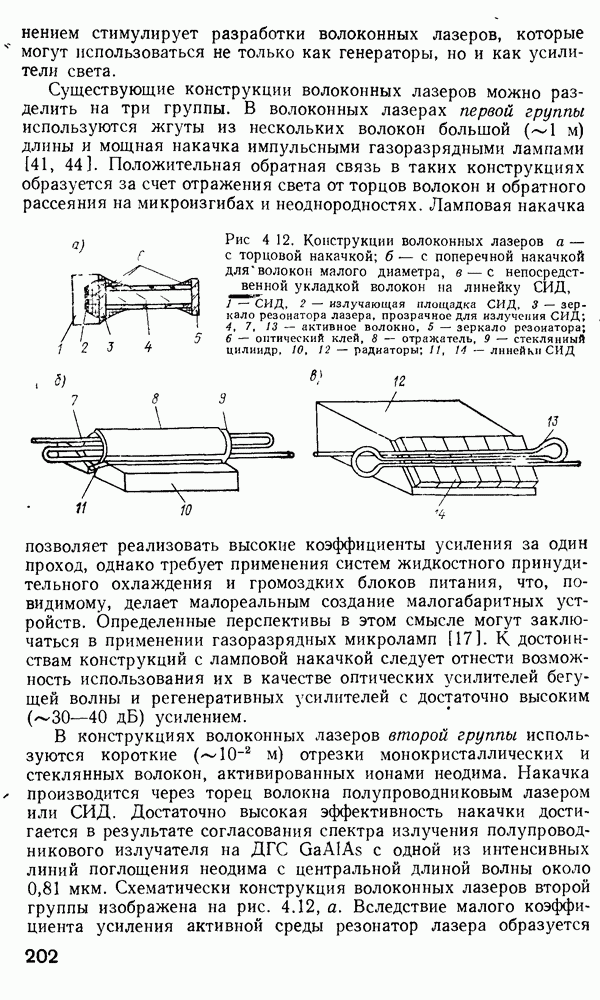
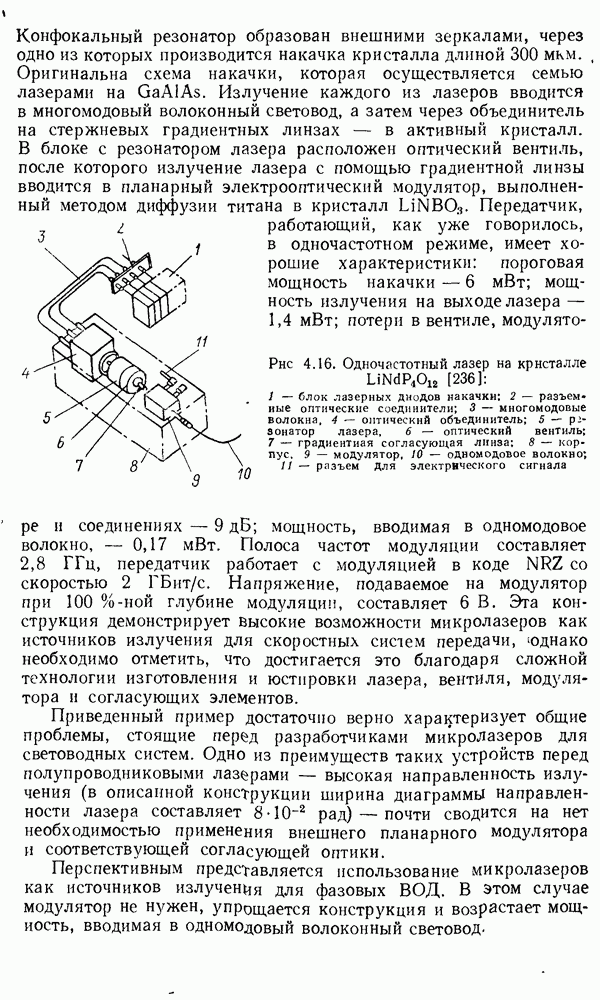
- Волоконные лазеры.
- Объемные микролазеры.
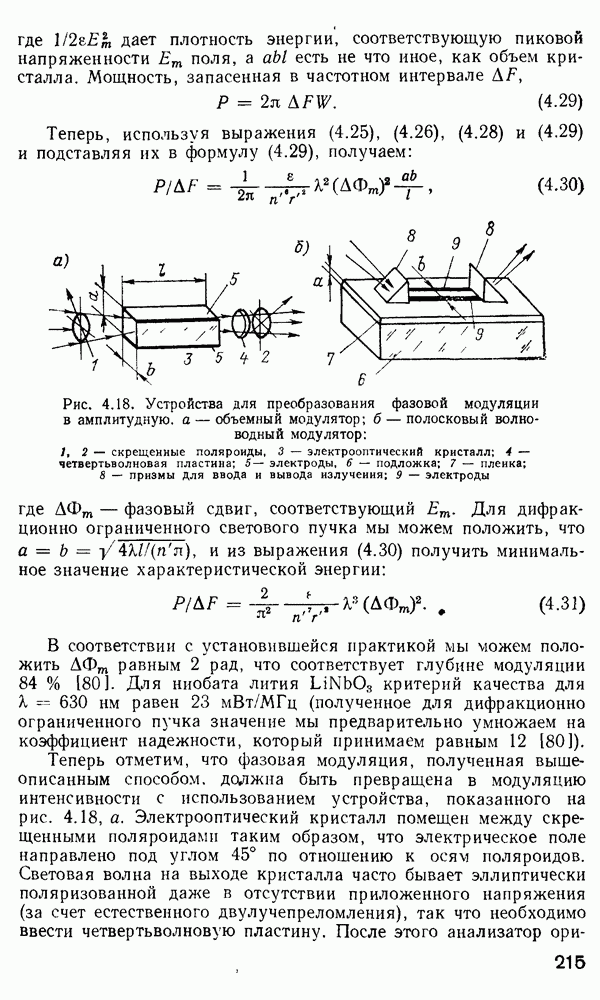
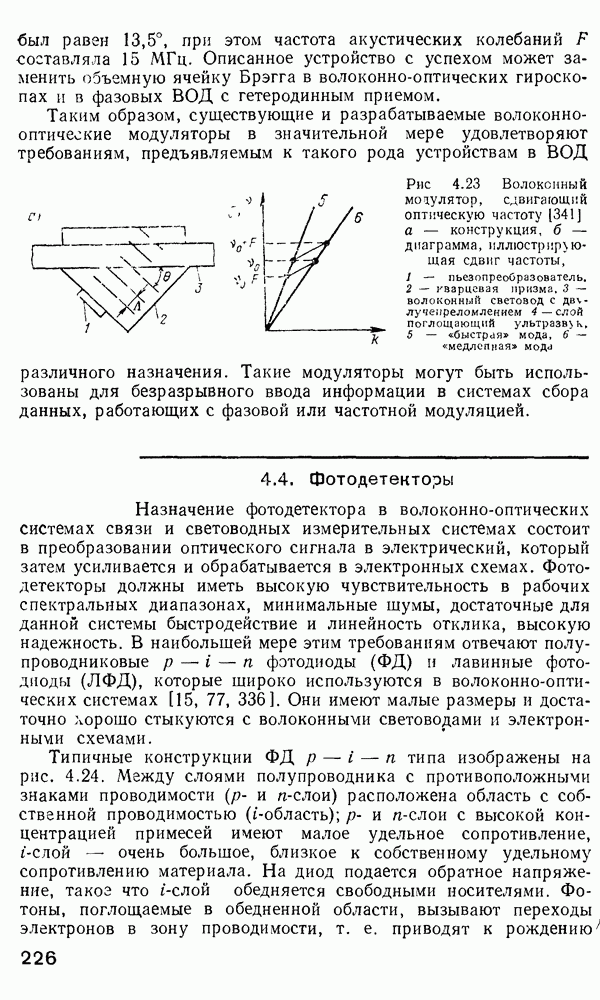
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
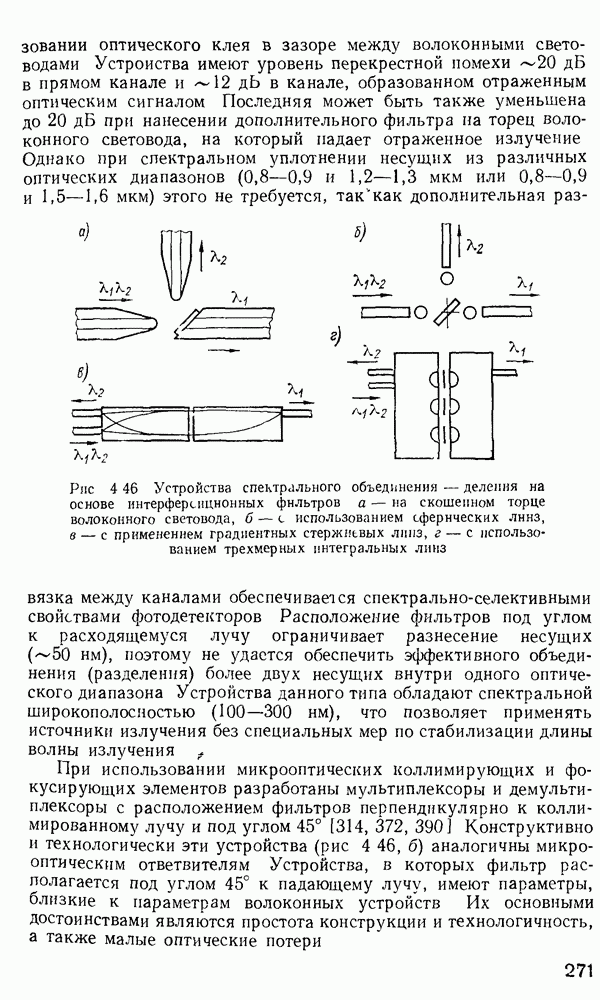
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
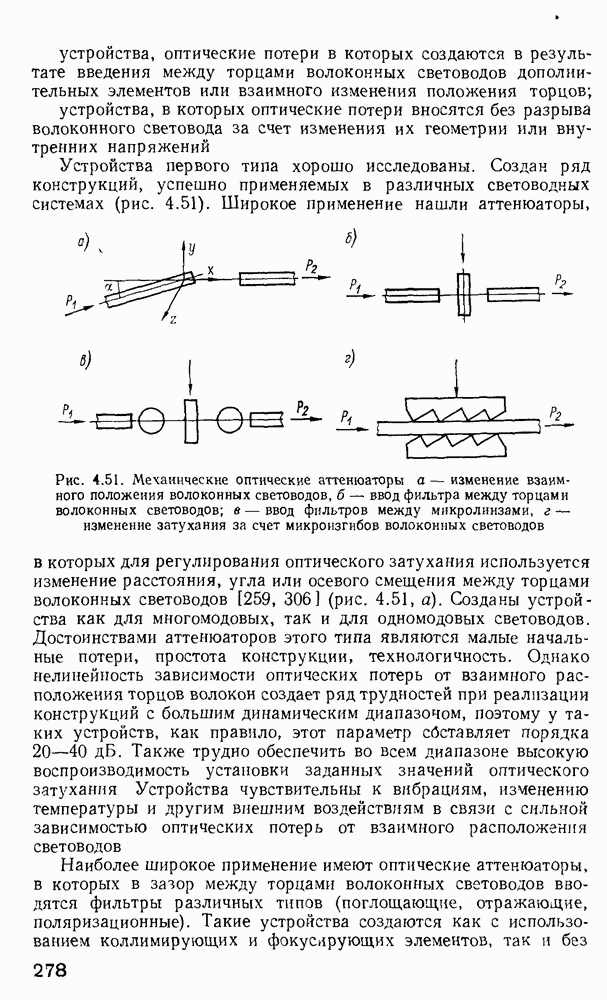
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
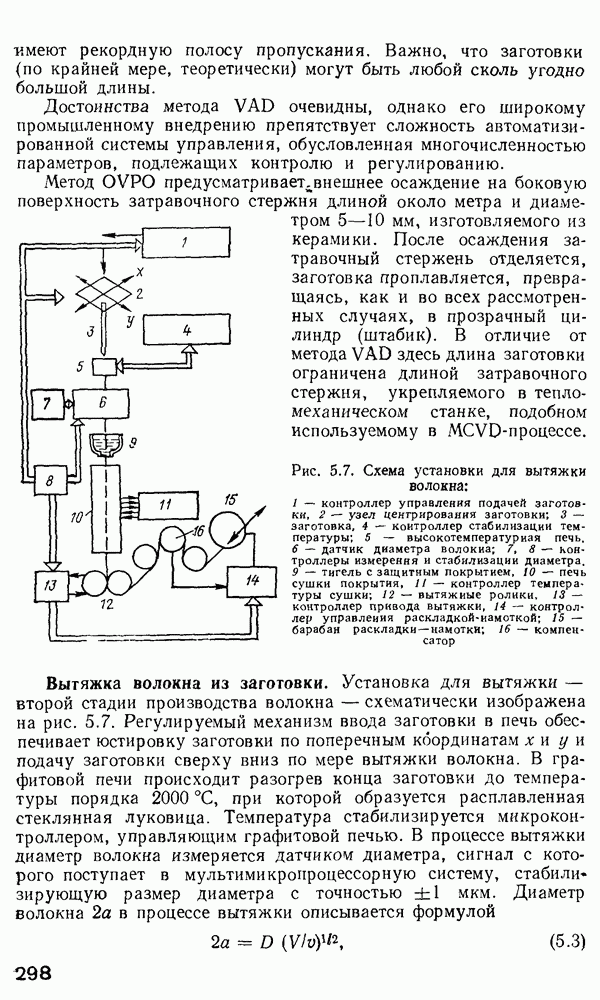
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
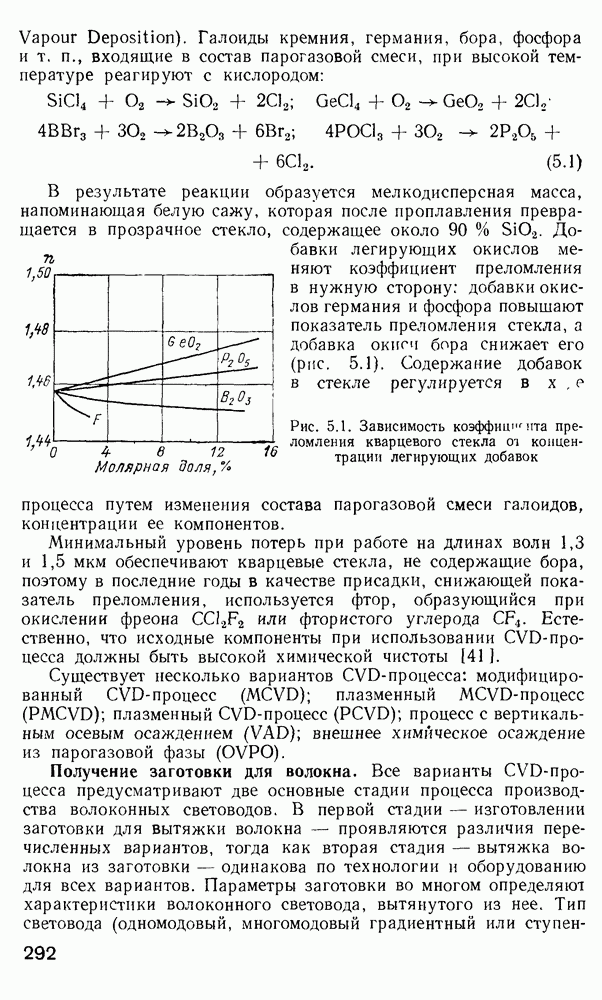
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
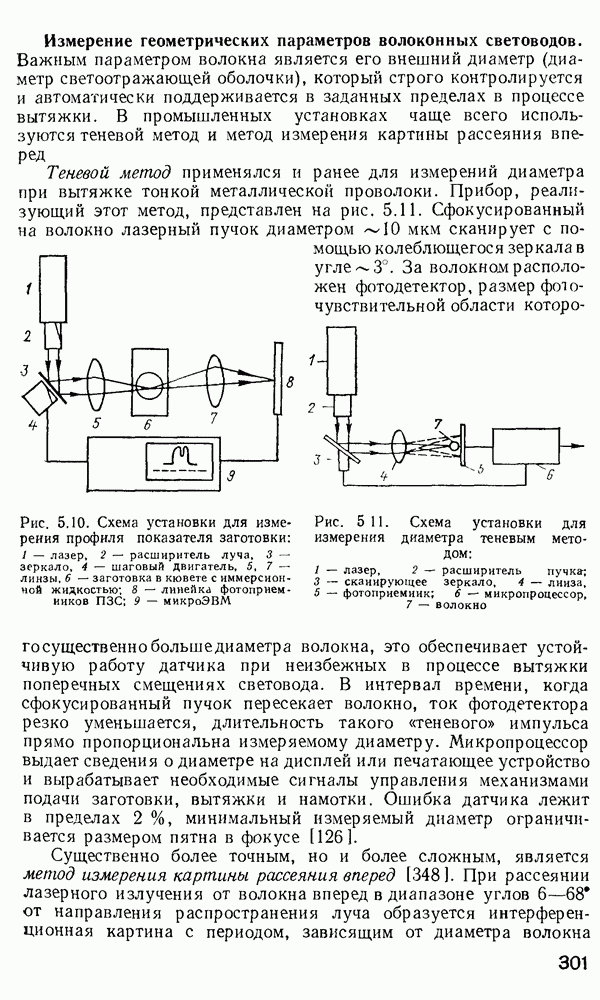
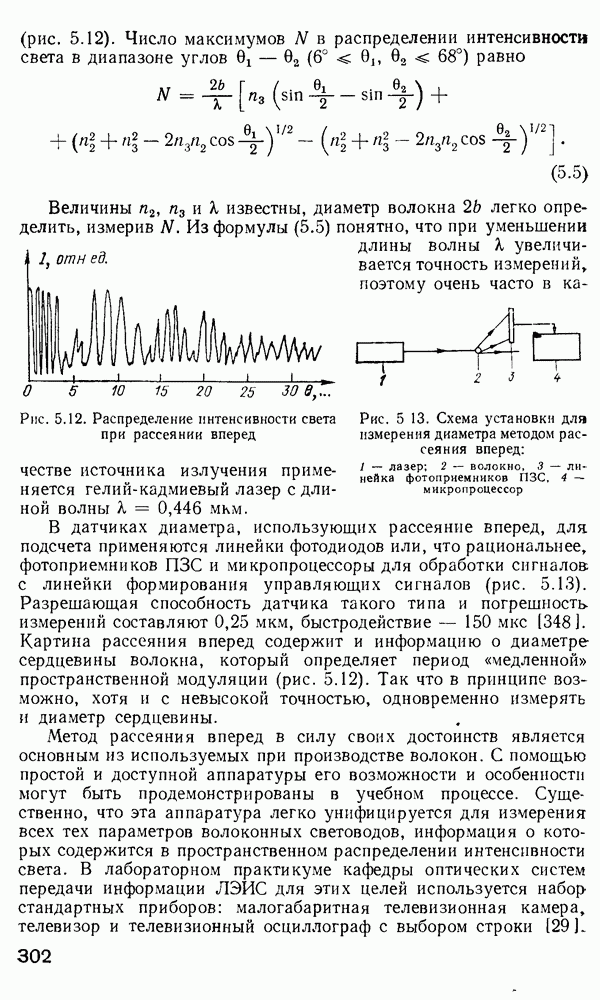
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ