| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
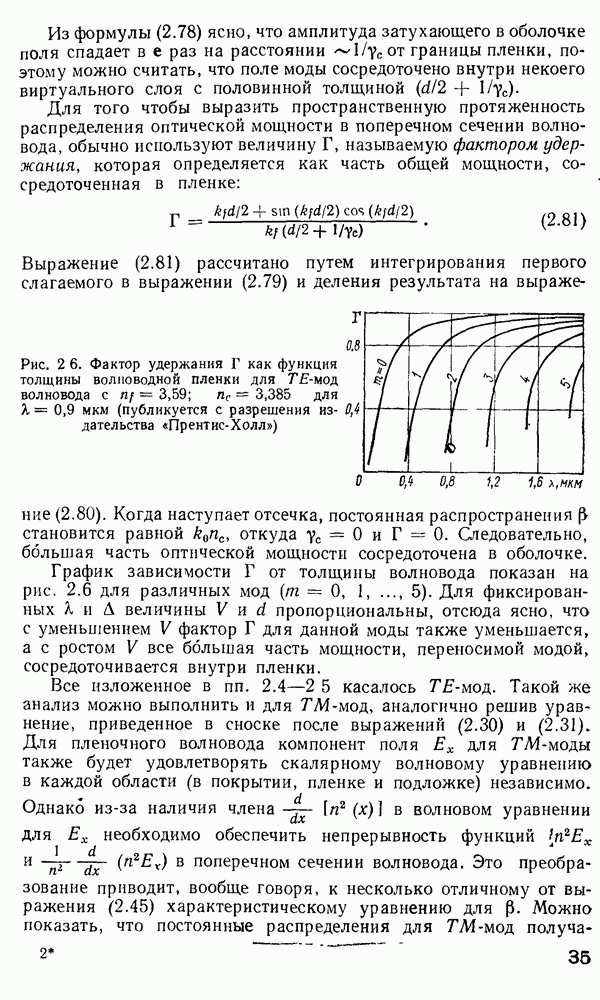
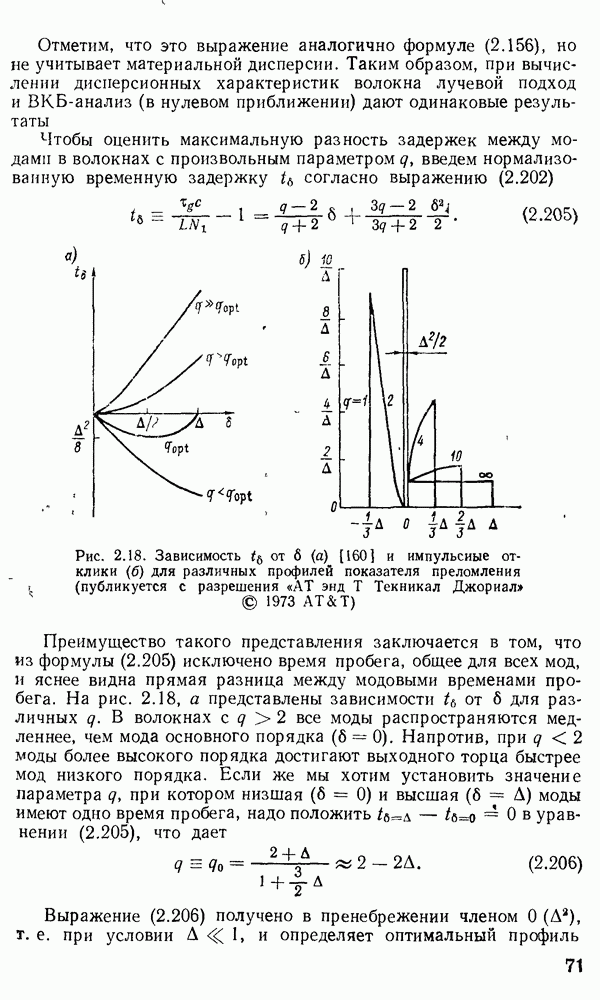
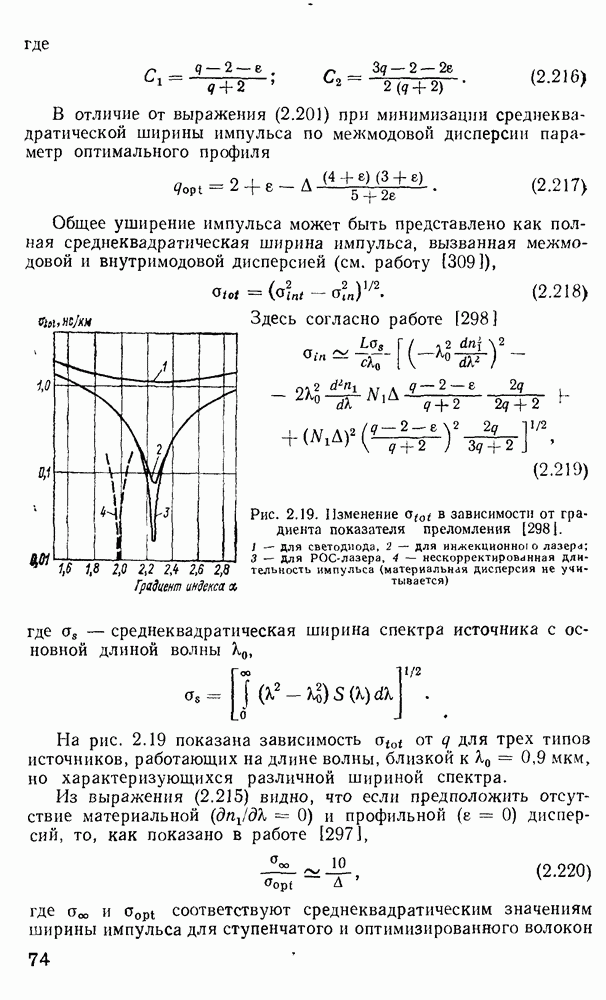
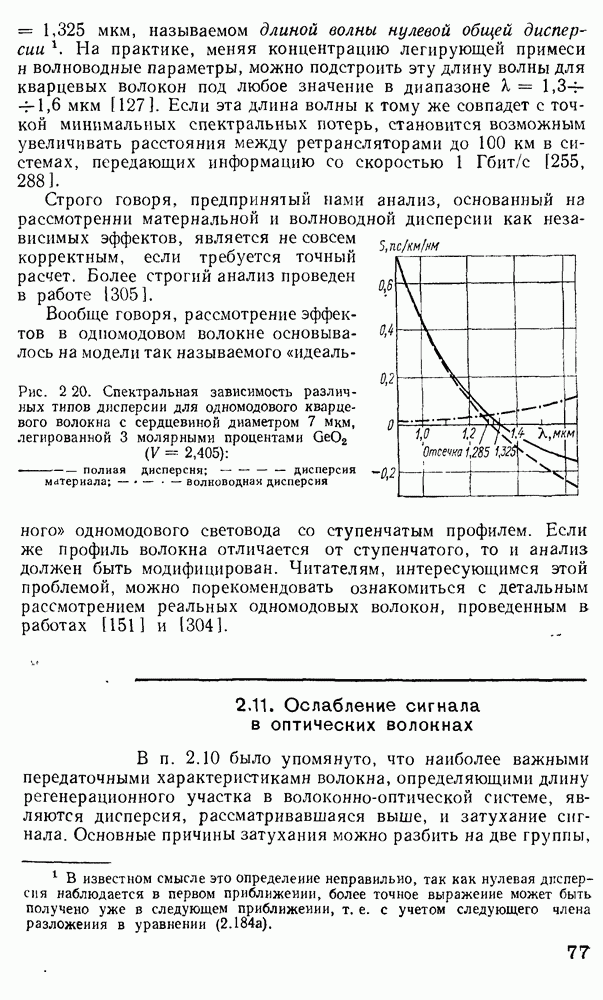
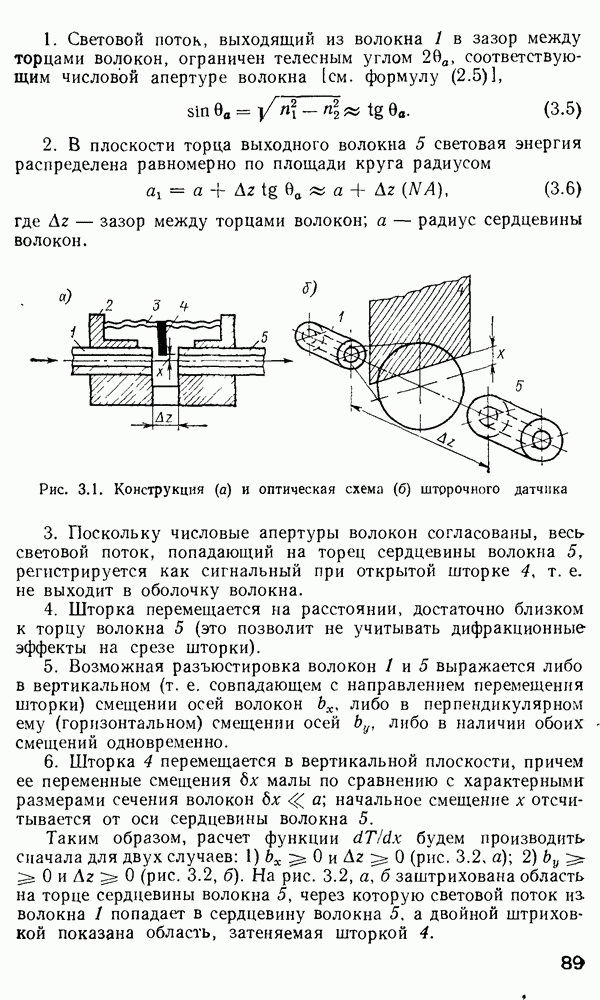
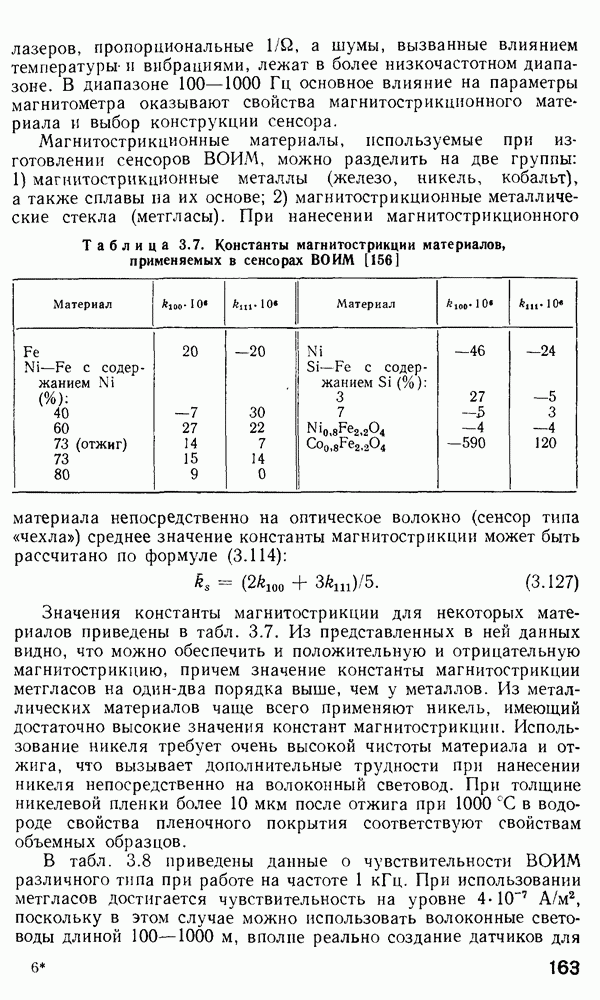
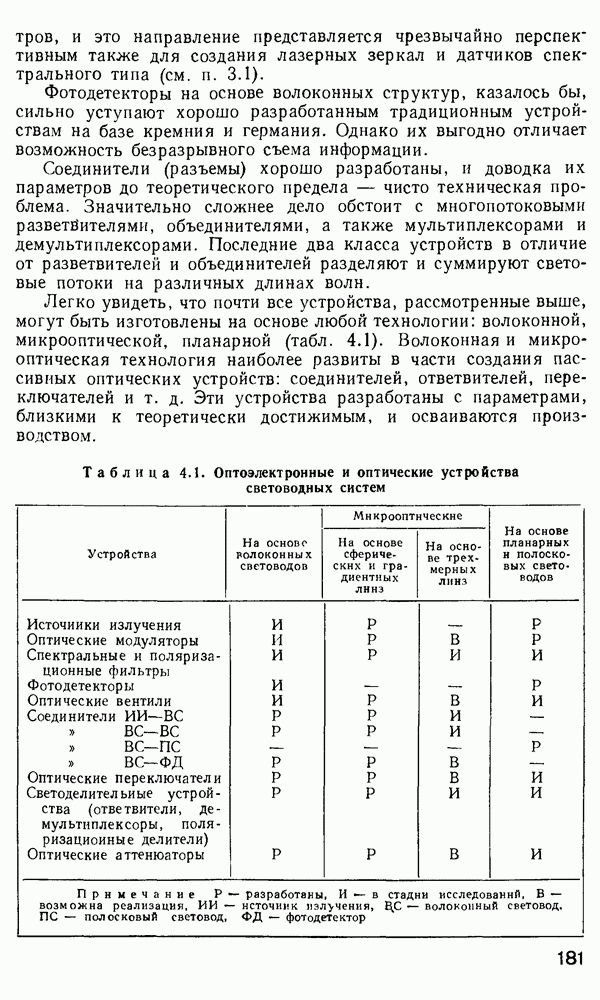
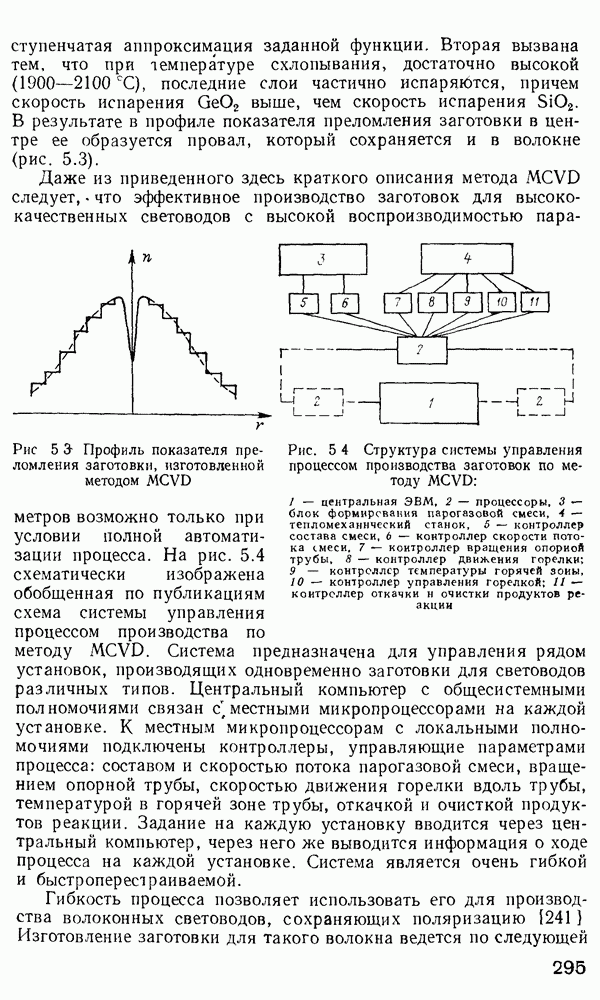
2.3. Электромагнитная теория распространения излучения в оптических волноводах
Известно, что наиболее правильные результаты при описании любого оптического явления можно получить, применив математический аппарат волновой оптики, т. е. анализ распространения электромагнитных волн. В п. 2.2 мы показали, что основной механизм, обеспечивающий волноводное распространение в оптических волокнах, может быть полностью описан в рамках полного внутреннего отражения лучей.
Следует отметить, что оптико-геометрический подход оказывается полезным до тех пор, пока диаметр сердцевины волокна  и величина А не становятся меньше некоторых значений. Чтобы представить себе примерные значения
и величина А не становятся меньше некоторых значений. Чтобы представить себе примерные значения  при которых геометрическая интерпретация достаточно правильна, оба эти параметра, а также длину волны распространяющегося излучения
при которых геометрическая интерпретация достаточно правильна, оба эти параметра, а также длину волны распространяющегося излучения  объединяют в один общий параметр, называемый нормализованной частотой, или
объединяют в один общий параметр, называемый нормализованной частотой, или  -параметром, который определяется как
-параметром, который определяется как

Если  геометрический подход, основанный на лучевом приближении, дает точные результаты при рассмотрении большинства явлений распространения излучения в волокне [154]. При
геометрический подход, основанный на лучевом приближении, дает точные результаты при рассмотрении большинства явлений распространения излучения в волокне [154]. При  геометрическая оптика уже не может использоваться при анализе свойств оптических волокон и требуется полный электромагнитный анализ, основанный на положениях волновой оптики.
геометрическая оптика уже не может использоваться при анализе свойств оптических волокон и требуется полный электромагнитный анализ, основанный на положениях волновой оптики.
В качественном приближении можно рассуждать так: если диаметр сердцевины сравним с длиной волны света, тогда оптическое волокно можно рассматривать только как волновод, работающий на оитических частотах, аналогично тому, как рассматриваются металлические волноводы для  диапазона.
диапазона.

Рис. 2.3. Сечение пленочного волновода, однородное в плоскости  а — геометрическая структура волновода;
а — геометрическая структура волновода;  — схематическое представление компонента
— схематическое представление компонента  - моды, показывающее падающую, отраженную и затухающую волны в различных областях волновода
- моды, показывающее падающую, отраженную и затухающую волны в различных областях волновода
С другой стороны, некоторые результаты, полученные с помощью волновой теории, могут быть сведены к результатам геометрического расчета, если предположить, что к 
Хорошо известно, что ограниченный оптический пучок диаметром  распространяющийся в однородной среде, характеризуется дифракционной расходимостью
распространяющийся в однородной среде, характеризуется дифракционной расходимостью

Однако при распространении по волокну, в котором и сердцевина, и оболочка однородны, большинство лучей, формирующих пучок, совершает многократные полные внутренние отражения, тем самым влияние дифракционной расходимости существенно ограничивается и пучок продолжает сохранять свое поперечное сечение [78].
На практике самым простым примером оптического волновода является пленочный (рис. 2.3). Пленочный волновод представляет собой двумерную структуру, состоящую из однородной пленки толщиной в несколько микрометров с показателем преломления  не ограниченную в направлении у. Эта пленка нанесена на подложку с показателем преломления
не ограниченную в направлении у. Эта пленка нанесена на подложку с показателем преломления  Сверху над пленкой расположен материал покрытия с показателем преломления
Сверху над пленкой расположен материал покрытия с показателем преломления
 Таким образом, планарная геометрия структуры такова, что она бесконечна в направлении плоскости
Таким образом, планарная геометрия структуры такова, что она бесконечна в направлении плоскости  и имеет толщину
и имеет толщину  в направлении х.
в направлении х.
Планарная структура интересует нас прежде всего потому, что на ее примере с помощью простых вычислений можно выявить основные особенности явления волноводного распространения света. Физические особенности волноводного распространения в оптических волокнах, характеризующихся цилиндрической симметрией, для анализа которых требуются громоздкие вычисления, могут быть в общих чертах предсказаны на основе результатов, полученных при рассмотрении планарной структуры. Пленочные и несколько более сложные полосковые структуры (в которых волновод ограничен в направлениях х и у), имеют также важное практическое значение при разработке интегрально-оптических устройств. Некоторые оптические датчики, создаваемые в настоящее время, основаны на применении интегрально-оптических структур.
Проблема распространения электромагнитной волны в оптическом волноводе требует решения (с учетом граничных условий) известных уравнений Максвелла, которые в системе МКС имеют вид [78]:

совместно с материальными уравнениями, определяющими свойства среды, в которой происходило распространение:

где Е и Н — напряженность электрического и магнитного полей соответственно;  и В — электрическая и магнитная индукция;
и В — электрическая и магнитная индукция;  — плотность тока;
— плотность тока;  и [Л — проводимость, диэлектрическая и магнитная проницаемость рассматриваемой среды.
и [Л — проводимость, диэлектрическая и магнитная проницаемость рассматриваемой среды.
Уравнения Максвелла (2.8)-(2.11), хотя и являются дифференциальными уравнениями первого порядка, образуют систему связанных дифференциальных уравнений, решение которой с учетом граничных условий иногда представляет существенные трудности. Эти трудности можно преодолеть, если записать так называемое «волновое» уравнение, которое является уравнением второго порядка с разделяющимися переменными и решеиие которого в
зависимости от граничных условий, т. е. от свойств среды, дает характеристики волноводного распространения в достаточно простой форме.
Чтобы вывести волновое уравнение, соответствующее диэлектрической пленочной структуре (см. рис. 2.3), мы должны положить, что  и — поскольку среда немагнитная —
и — поскольку среда немагнитная —  (
( — магнитная проницаемость свободного пространства). Применив к выражению (2.8) оператор ротора, мы получим
— магнитная проницаемость свободного пространства). Применив к выражению (2.8) оператор ротора, мы получим

Подставляя в формулу (2.15) уравнение  и используя векторное тождество
и используя векторное тождество

мы преобразуем ее к виду

Аналогично можно получить уравнение для вектора Н

Уравнения (2.17) и (2.18) известны как векторные волновые уравнения. Если мы предположим, что  т. е. свойства среды не меняются вдоль направления распространения волны, то решение уравнения (2.17) можно записать в такой форме:
т. е. свойства среды не меняются вдоль направления распространения волны, то решение уравнения (2.17) можно записать в такой форме:

где направление распространения выбрано вдоль оси  а Р называется постоянной распространения.
а Р называется постоянной распространения.
Аналогичным образом можно предположить, что решение для магнитного поля имеет форму

Уравнения (2.18) и (2.20) описывают плоские волны, являющиеся решениями волновых уравнений для данного значения постоянной распространения  значения которой, в свою очередь, определяются параметрами волновода. На самом же деле, граничные условия, накладываемые параметрами волновода, допускают существование только определенных дискретных значений
значения которой, в свою очередь, определяются параметрами волновода. На самом же деле, граничные условия, накладываемые параметрами волновода, допускают существование только определенных дискретных значений  Поперечные распределения поля
Поперечные распределения поля  соответствующие этим значениям
соответствующие этим значениям  называются в соответствии с применяемой терминологией модами волновода. Волноводная мода определяется как некоторое особое распределение поля, которое распространяется вдоль волновода с сохранением определенного состояния поляризации, постоянной групповой скоростью
называются в соответствии с применяемой терминологией модами волновода. Волноводная мода определяется как некоторое особое распределение поля, которое распространяется вдоль волновода с сохранением определенного состояния поляризации, постоянной групповой скоростью  и без изменения структуры своего первоначального
и без изменения структуры своего первоначального
поперечного распределения. В зависимости от геометрии и физических характеристик волновода последний может поддерживать распространение нескольких мод или только одной моды. В первом случае волновод называется многомодовым, во втором — одномодовым. На практике в большинстве случаев полное выражение для поля в волноводе, возбуждаемом оптическим пучком, может быть представлено в виде суммы мод, которые распространяются внутри волновода (так называемые направляемые волноводные моды) и континуума излучательных, т. е. не направляемых волноводом, мод.
Ниже мы рассмотрим планарные волноводы, в которых диэлектрическая постоянная считается зависящей только от одной координаты, т. е.  . В этом случае зависимость электрического и магнитного полей от координаты у выражается в форме
. В этом случае зависимость электрического и магнитного полей от координаты у выражается в форме

где у — положительная константа, что непосредственно вытекает из формул (2.17) и (2.18). В пленочном волноводе, геометрия которого позволяет считать его размеры бесконечными в плоскости  (см. рис. 2.3), мы можем без потери общности положить
(см. рис. 2.3), мы можем без потери общности положить  Это означает, что волна распространяется вдоль оси
Это означает, что волна распространяется вдоль оси  Таким образом, решения выражений (2.17) и (2.18) надо искать в форме
Таким образом, решения выражений (2.17) и (2.18) надо искать в форме

Для того чтобы получить точное выражение для  непосредственно накладывая граничные условия на уравнение (2.17), мы используем иную процедуру, допускающую более ясную физическую трактовку. Подставляя решение в форме выражений (2.22) и (2.23) в уравнения Максвелла (2.8) и (2.9) и выписывая х, у, z — составляющие результирующих уравнений, получаем следующую систему уравнений:
непосредственно накладывая граничные условия на уравнение (2.17), мы используем иную процедуру, допускающую более ясную физическую трактовку. Подставляя решение в форме выражений (2.22) и (2.23) в уравнения Максвелла (2.8) и (2.9) и выписывая х, у, z — составляющие результирующих уравнений, получаем следующую систему уравнений:

Уравнения (2.24)-(2.29) показывают, что начальные максвелловские уравнения распадаются на две группы. Одна содержит компоненты  связанные с помощью формул (2.24)- (2.26). Другая группа — выражения (2.27)-(2.29) — связывает
связанные с помощью формул (2.24)- (2.26). Другая группа — выражения (2.27)-(2.29) — связывает
компоненты  и Ну. Первая группа уравнений определяет поперечные электрические Т-моды, у которых продольный компонент электрического поля
и Ну. Первая группа уравнений определяет поперечные электрические Т-моды, у которых продольный компонент электрического поля  равен 0. Вторая группа соответственно описывает поперечные магнитные ТМ-моды
равен 0. Вторая группа соответственно описывает поперечные магнитные ТМ-моды 
Далее из формул  видно, что для описания ТЕ-мод достаточно знать единственный не нулевой компонент электрического поля, т. е.
видно, что для описания ТЕ-мод достаточно знать единственный не нулевой компонент электрического поля, т. е.  так как
так как  однозначно определяются с помощью этих уравнений. Аналогично знания
однозначно определяются с помощью этих уравнений. Аналогично знания  достаточно для однозначного описания
достаточно для однозначного описания  -мод.
-мод.
Дифференцируя выражение (2.25) и исключая  из уравнений (2.24) и (2.26), мы получаем волновое уравнение для компонента
из уравнений (2.24) и (2.26), мы получаем волновое уравнение для компонента  в виде
в виде

где

Величина  в формуле (2.31) есть поперечная составляющая волнового вектора
в формуле (2.31) есть поперечная составляющая волнового вектора  в волноводе, а его продольная составляющая равна
в волноводе, а его продольная составляющая равна  Уравнение (2.30) называется скалярным волновым уравнением, решением которого являются
Уравнение (2.30) называется скалярным волновым уравнением, решением которого являются  -моды пленочного планарного волновода 1. Решения выражения (2.30) для покрытия, пленки и подложки имеют вид:
-моды пленочного планарного волновода 1. Решения выражения (2.30) для покрытия, пленки и подложки имеют вид:

Здесь А, В, С, D — константы;

Из общих соображений поле направляемой волны должно спадать до малых значений в подложке и в покрытии, а в пленке может иметь осциллирующий характер. Следовательно, параметры  должны быть положительными. Поэтому для направляемой моды постоянная распространения Р должна удовлетворять соотношению
должны быть положительными. Поэтому для направляемой моды постоянная распространения Р должна удовлетворять соотношению

Теперь, чтобы найти точные значения, которые может иметь Р в интервале (2.38), надо наложить граничные условия, а именно: тангенциальные компоненты  и их производные для ТЕ-мод непрерывны на границах
и их производные для ТЕ-мод непрерывны на границах  рис. 2.3), т. е.
рис. 2.3), т. е.

Здесь индексы  при компонентах
при компонентах  соответствуют значениям этих полей в покрытии, пленке и подложке.
соответствуют значениям этих полей в покрытии, пленке и подложке.
Учет граничных условий приводит к системе четырех уравнений:

Исключая из формул (2.40) и (2.41) величину  а из формул (2.42), (2.43) — величину А и решая получившиеся уравнения, находим, что
а из формул (2.42), (2.43) — величину А и решая получившиеся уравнения, находим, что

С помощью простых алгебраических операций из формулы (2.44) получаем

где

Поскольку  принимает только дискретные значения, подстановка уравнения (2.30) в уравнение (2.45) и последующее решение получившегося уравнения дадут значения
принимает только дискретные значения, подстановка уравнения (2.30) в уравнение (2.45) и последующее решение получившегося уравнения дадут значения  для различных ТЕ-мод волновода, соответствующие разным значениям
для различных ТЕ-мод волновода, соответствующие разным значениям  Случай
Случай  соответствует фундаментальной моде
соответствует фундаментальной моде  Уравнения (2.45) называются характеристическими — они определяют постоянные распространения различных мод рт.
Уравнения (2.45) называются характеристическими — они определяют постоянные распространения различных мод рт.
Решая уравнения (2.40) и (2.41), мы можем выразить В и С через  следующим образом:
следующим образом:

Следовательно, полное выражение для поля внутри пленки (2.33) приобретает вид

Используя формулы (2.46), мы преобразуем выражение (2.48) следующим образом:

где  Физический смысл выражения (2.49) состоит в следующем: поле
Физический смысл выражения (2.49) состоит в следующем: поле  моды внутри волновода формируется двумя плоскими волнами, распространяющимися в направлениях
моды внутри волновода формируется двумя плоскими волнами, распространяющимися в направлениях  и составляющими с осью
и составляющими с осью  углы
углы  соответственно (см. рис. 2.3). Угол
соответственно (см. рис. 2.3). Угол  определяют с помощью выражения
определяют с помощью выражения

Следовательно,

Интересно отметить, что если бы не было условий для волноводного распространения, т. е. если бы пленка превратилась в бесконечно толстый слой однородного материала, то плоская волна в нем имела бы постоянную распространения  Поскольку каждой моде соответствует определенное дискретное значение
Поскольку каждой моде соответствует определенное дискретное значение  то в соответствии с выражением (2.51) и углы распространения разных мод различны и имеют дискретные значения.
то в соответствии с выражением (2.51) и углы распространения разных мод различны и имеют дискретные значения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
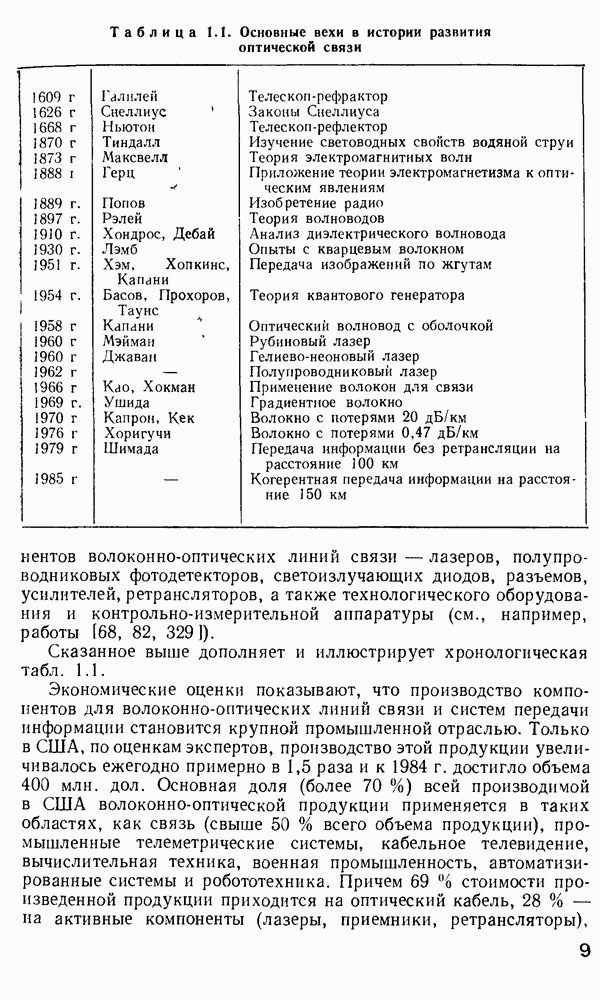
- 1. ВОЛОКОННАЯ ОПТИКА — ИСТОРИЯ И ПЕРСПЕКТИВЫ
- 2. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛНОВОДАХ
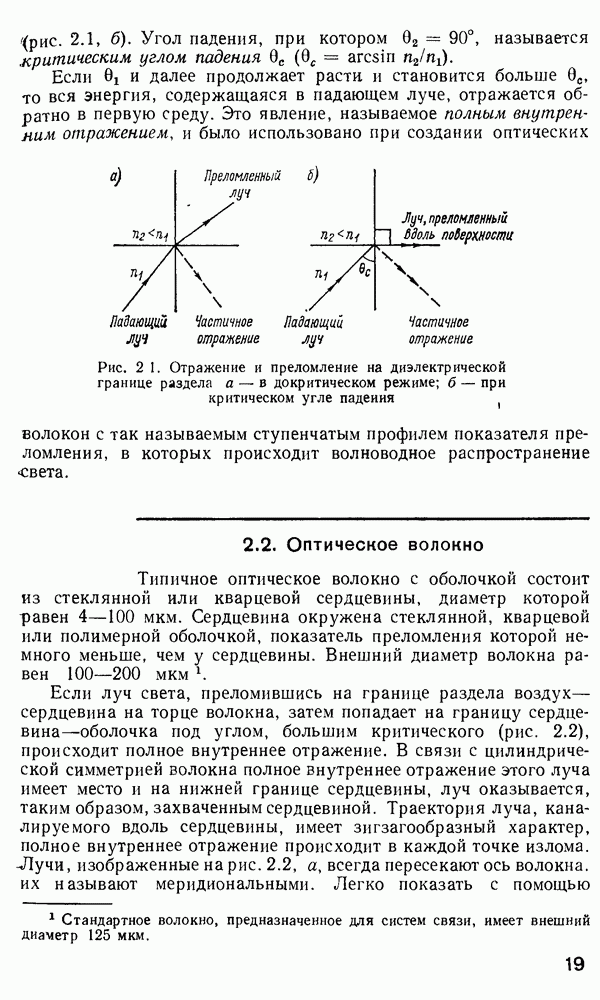
- 2.2. Оптическое волокно
- 2.3. Электромагнитная теория распространения излучения в оптических волноводах
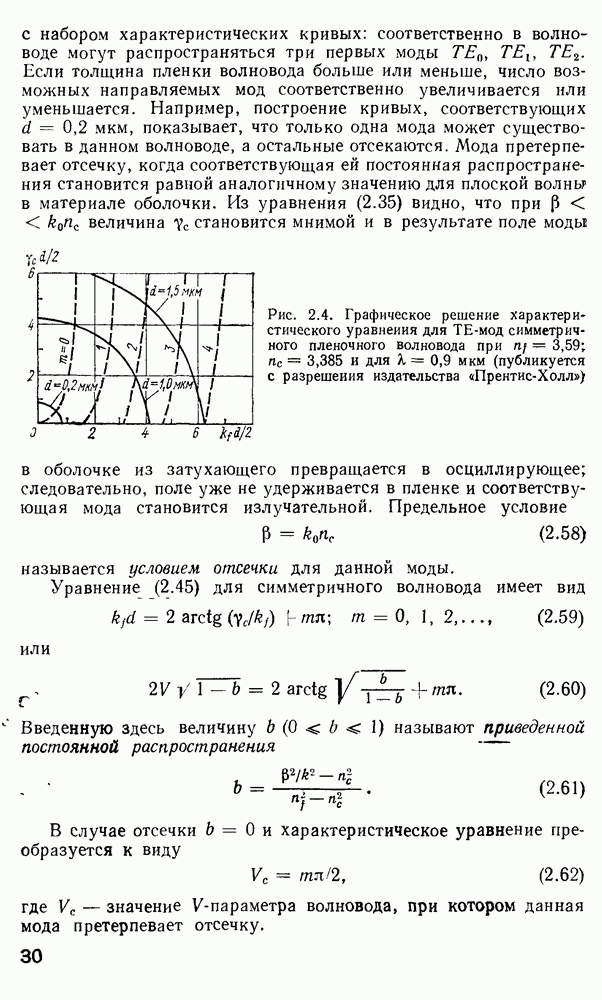
- 2.4. Характеристическое уравнение и условие отсечки
- 2.5. Лучевой вывод характеристического уравнения
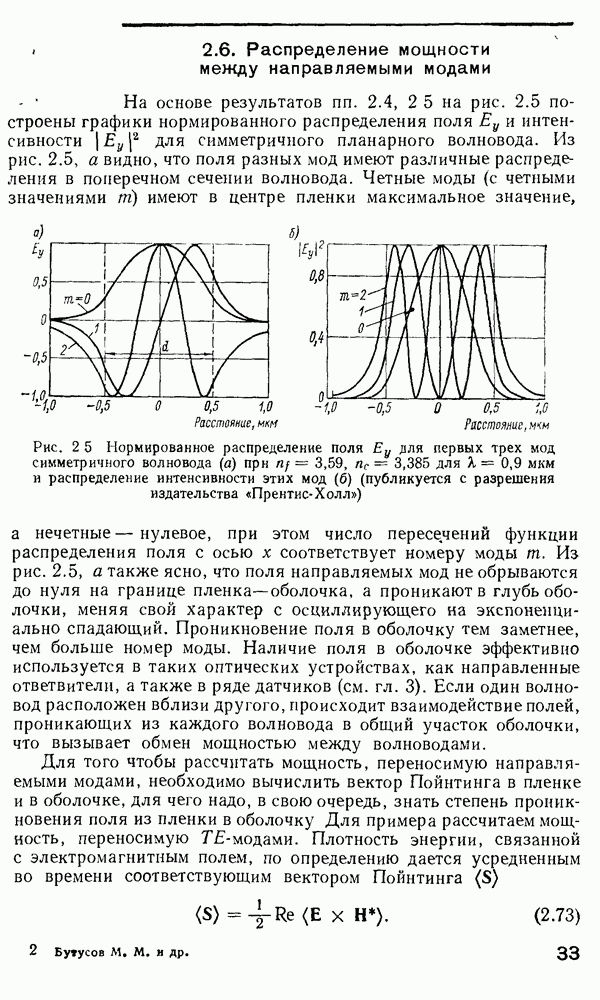
- 2.6. Распределение мощности между направляемыми модами
- 2.7. Прямоугольные волноводы
- 2.8. Электромагнитная теория распространения волн в оптических волокнах со ступенчатым профилем показателя преломления
- Решение уравнения (2.105) для волокна со ступенчатым профилем.
- Одномодовое волокно.
- Временная дисперсия в многомодовом волокне. Слабонаправляющее волокно.
- Линейно-поляризованные моды в слабонаправляющих волокнах.
- Распределение мощности направляемых мод в поперечном сечении волокна.
- 2.9. Градиентное оптическое волокно
- Решение уравнения (2.157) методом ВКБ.
- 2.10. Дисперсия в оптических волокнах
- Распространение импульса в оптических волокнах.
- Применение метода ВКБ для многомодовых градиентных волокон.
- Дисперсия импульсов в одномодовых волокнах.
- 2.11. Ослабление сигнала в оптических волокнах
- 3. ВОЛОКОННО-ОПТИЧЕСКИЕ ДАТЧИКИ
- 3.2. Датчики акустических полей с модуляцией интенсивности
- Разрывные акустические ВОД.
- Безразрывные акустические ВОД с модуляцией интенсивности.
- Расчет минимально обнаружимых смещений и динамического диапазона.
- 3.3. ВОД с модуляцией интенсивности для регистрации других физических величин
- 3.4. Волоконно-оптические интерферометры на одномодовых волокнах
- Методы стабилизации и обработки сигналов ВОИ.
- Применение многомодовых волокон в ВОИ.
- Поляризационные ВОД.
- 3.5. Фазовые датчики акустических колебаний
- 3.6. Волоконно-оптические гироскопы
- Принципы построения волоконно-оптических гироскопов.
- Технология изготовления и перспективы внедрения ВОГ.
- 3.7. Фазовые и поляризационные датчики магнитного поля
- Поляризационные волоконно-оптические датчики магнитного поля.
- Волоконно-оптические датчики магнитного поля с модуляцией интенсивности.
- 4. КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ И УСТРОЙСТВ
- 4.1. Основные направления и проблемы в создании волоконно-оптических функциональных устройств
- 4.2. Источники излучения. Требования к источникам излучения для волоконно-оптических систем
- Полупроводниковые источники излучения.
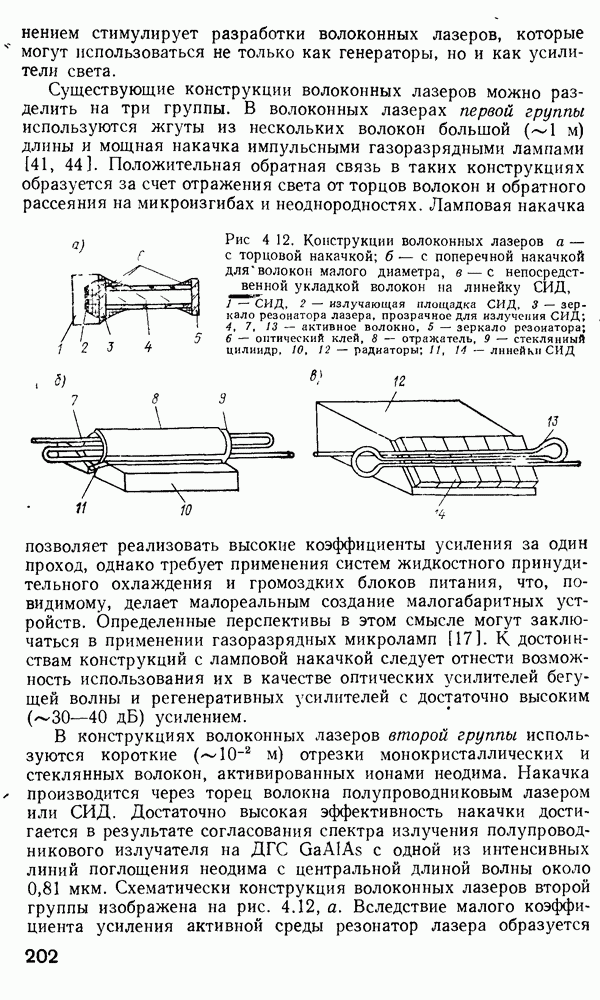
- Волоконные лазеры.
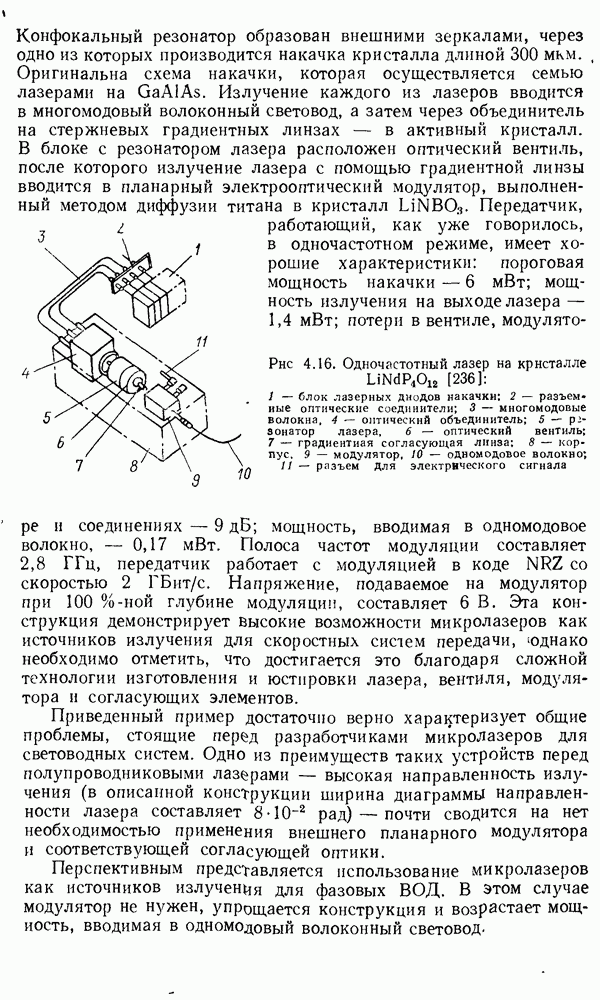
- Объемные микролазеры.
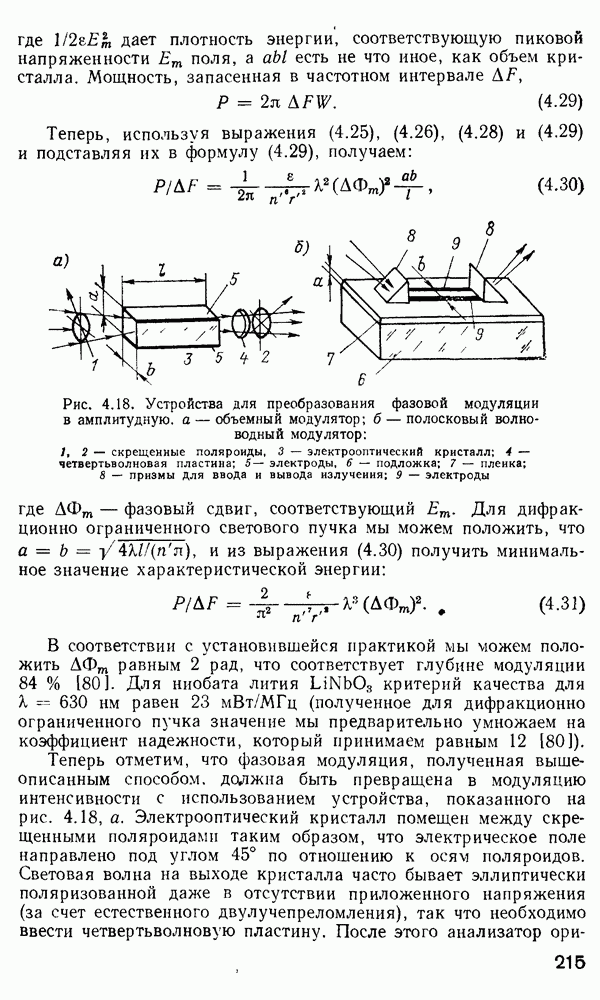
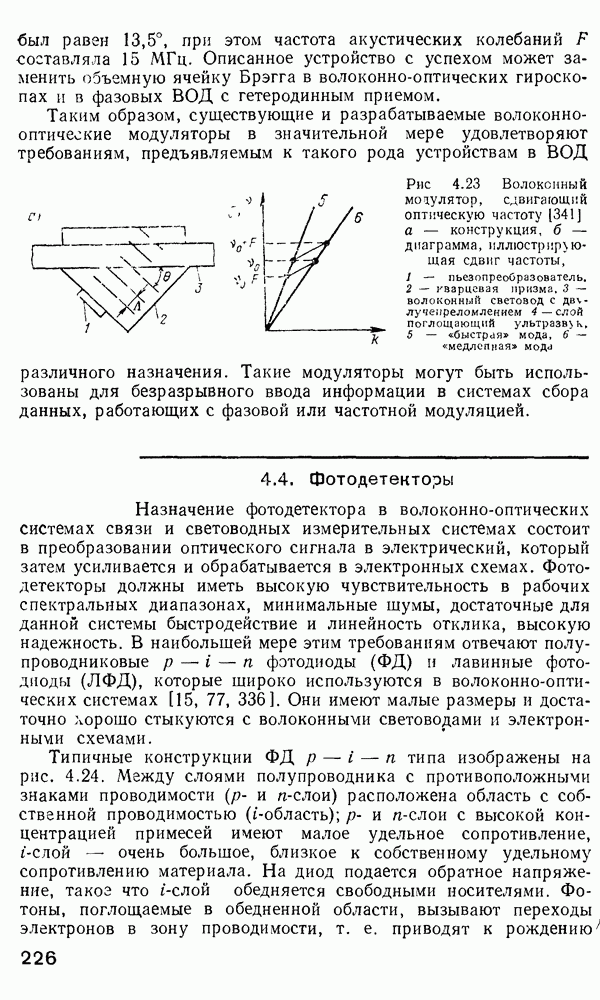
- 4.3. Оптические модуляторы
- 4.4. Фотодетекторы
- 4.5. Оптические вентили
- 4.6. Оптические соединители
- Соединители источников излучения с волоконными световодами ИИ-ВС.
- Соединители волоконных световодов с фотодетекторами ВС-ФД.
- Соединители волоконных световодов с планарными и полосковыми световодами ВС-ПС.
- 4.7. Волоконно-оптические переключатели
- 4.8. Ответвители и разветвители. Мультиплексоры и демультиплексоры
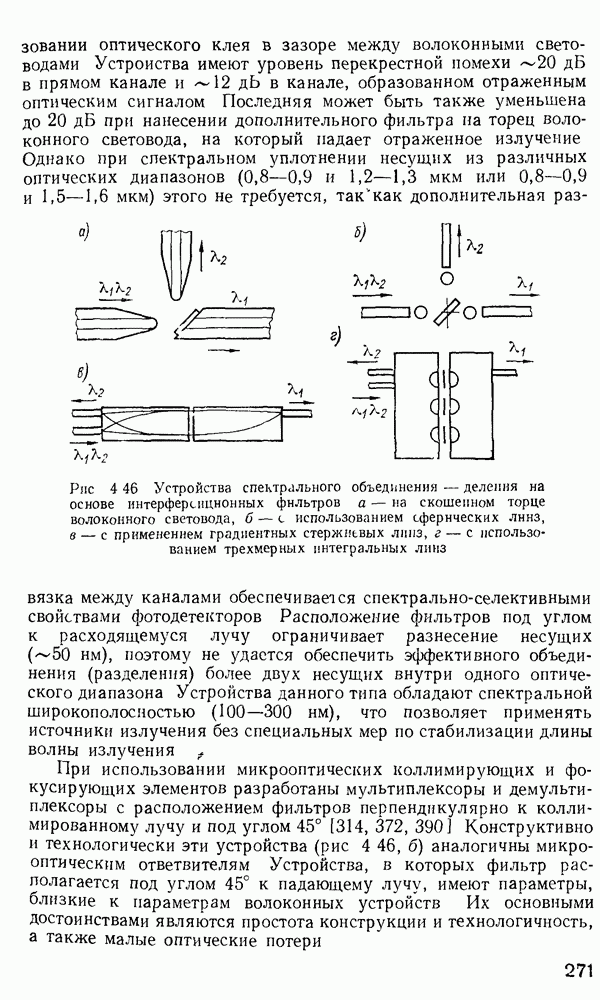
- Устройства спектрального объединения и деления (мультиплексоры и демультиплексоры).
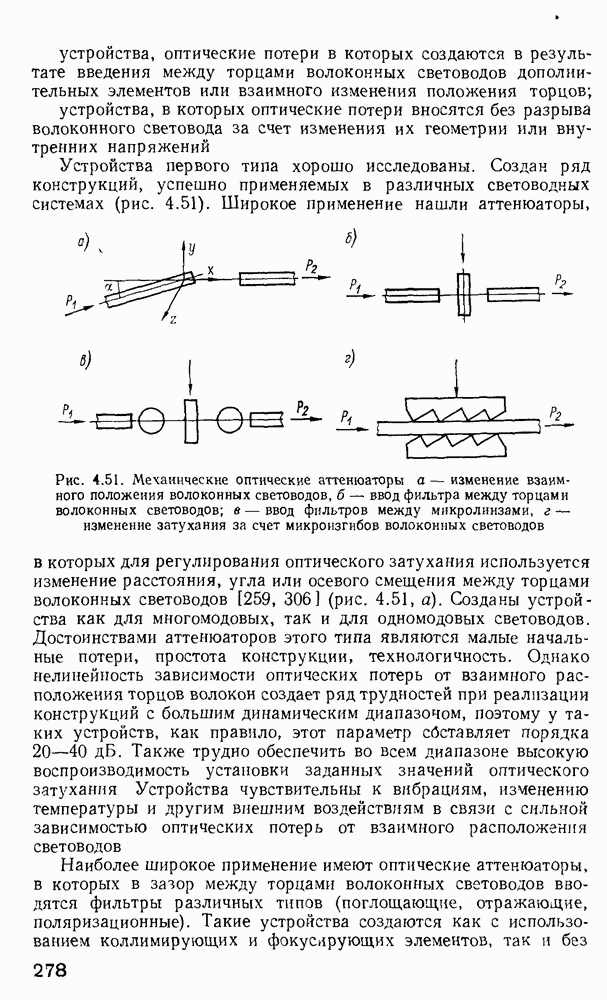
- 4.9. Оптические аттенюаторы
- 4.10. Направления интеграции элементов световодных измерительных систем
- 4.11. Особенности технологии изготовления устройств для волоконно-оптических систем
- Изготовление волоконных элементов.
- Изготовление планарных элементов.
- Сборка волоконно-оптических устройств.
- 5. ПРОИЗВОДСТВО ВОЛОКОННЫХ СВЕТОВОДОВ И ИЗМЕРЕНИЕ ИХ ХАРАКТЕРИСТИК
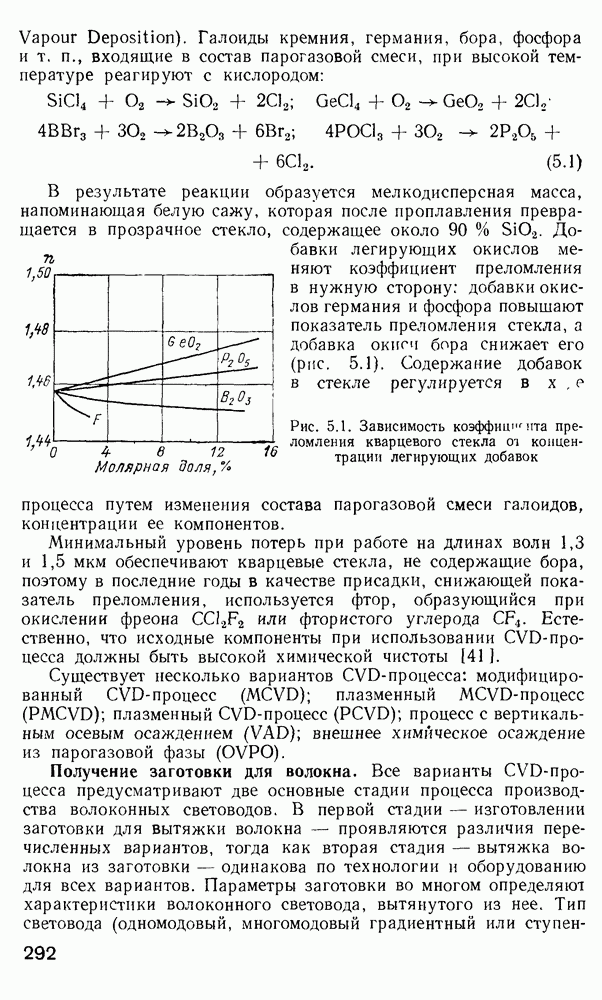
- Получение заготовки для волокна.
- Вытяжка волокна из заготовки.
- 5.2. Методы и аппаратура для измерений характеристик заготовок и волоконных световодов
- Измерение геометрических параметров волоконных световодов.
- Контроль профиля показателя преломления волоконных световодов.
- Контроль затухания излучения в волоконных световодах.
- Измерение дисперсии оптических импульсов.
- СПИСОК ЛИТЕРАТУРЫ