| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2.2. Матрица попарных сходств или различий
Для многомерного шкалирования существенным является определенная организация исходного экспериментального материала в так называемую матрицу сходств. Элементом матрицы 
ляется некоторая мера сходства между парой стимулов  и
и  или обратная ей величина
или обратная ей величина  мера различия.
мера различия.
Оценки различий можно получить от испытуемого разными методами. В каждом случае выбор метода шкалирования различий зависит от конкретных экспериментальных условий. Но существует разделение этих методов на два больших класса, которое зависит только от того, какая модель многомерного шкалирования используется для анализа матрицы различий — метрическая или неметрическая.
Условия, налагаемые на элементы матрицы различий в метрическом многомерном шкалировании, строго соответствуют аксиомам расстояния в геометрическом пространстве.
1. Рефлексивность различия:

подразумевает, что различие между двумя идентичными стимулами (диагональные элементы матрицы различий) должно равняться нулю.
2. Симметричность различий:

означает, что оценка различия не должна зависеть от временных или пространственных перестановок стимулов относительно друг друга при оценивании (симметричные элементы матрицы различий относительно главной диагонали).
3. Аксиома треугольника

требует, чтобы суммарное различие между любыми двумя парами из трех данных стимулов было не меньше, чем различие между оставшейся парой стимулов.
В терминах теории измерений это означает, что субъективные оценки различий должны представлять собой величины на шкале отношений. Только в этом случае их можно рассматривать непосредственно как расстояние между точками в психологическом пространстве или субъективные расстояния.
Методы для шкалирования психологического расстояния между сложными стимулами в большей части прямо аналогичны методам одномерного шкалирования. Большинство методов вполне могут быть расширены до шкалирования многомерных различий. Однако в каждом случае испытуемый делает более сложное суждение. Прямое расширение моделей требует некоторой модификации [203]. Эти изменения определяются, во-первых, усложнением стимулов и, во-вторых, сменой содержания оценочных суждений. В одномерном случае оценка представляет величину стимула на шкале, тогда как в многомерном шкалировании оценивается психологическое расстояние между парами стимулов. Если в ситуации одномерного шкалирования шкала отношений или
интервалов строилась для самих оценок стимулов, то теперь эти шкалы строятся для межстимульных различий.
Несколько более слабые ограничения налагает на элементы матрицы различий модель неметрического многомерного шкалирования. В общем случае достаточно, чтобы оценки различий удовлетворяли отношениям, установленным для шкалы порядка. Методы порядкового шкалирования основываются на ясных и простых принципах, которые легко реализуются в большинстве экспериментальных ситуаций.
Например, испытуемому могут быть предъявлены все пары стимулов одновременно и он должен упорядочить их по степени сходства. Иногда порядок различия оценивается в баллах или в рангах [30].
В некоторых случаях информацию о сходствах можно получить из данных о смешении стимулов. Информацию о смешениях можно получить на основе идентификации испытуемым предъявляемых стимулов. Тогда в клетку  матрицы заносится число, равное числу случаев, когда испытуемый идентифицировал стимул
матрицы заносится число, равное числу случаев, когда испытуемый идентифицировал стимул  как
как  Частота случаев идентификации стимула
Частота случаев идентификации стимула  как
как  может служить мерой их сходства. Испытуемому можно предложить упорядочить все стимулы в один ряд. Такое упорядочивание производится по отношению к каждому стимулу. Сходство двух стимулов оценивается по частоте их попадания в соседние участки ряда.
может служить мерой их сходства. Испытуемому можно предложить упорядочить все стимулы в один ряд. Такое упорядочивание производится по отношению к каждому стимулу. Сходство двух стимулов оценивается по частоте их попадания в соседние участки ряда.
Пристального внимания заслуживает вариант, в котором предлагается упростить работу испытуемого, заменив задачу оценивания попарных различий более простой задачей классификации стимулов.
Пусть имеется множество многомерных стимулов (цвета, шрифта, вкусовые качества пищевых продуктов, геометрические фигуры и т. п.). Для данного множества стимулов  выбирается произвольный набор классов
выбирается произвольный набор классов  (категорий, наименований) так, чтобы каждый стимул всегда можно было бы отнести по крайней мере к какому-нибудь одному классу. Набор классов должен исчерпывать классификацию стимулов. Например, для множества вкусовых качеств пищевых продуктов можно предложить набор из четырех основных классов (кислый, сладкий, горький, соленый). Классификация заключается в отнесении каждого данного стимула к одному или нескольким классам. Причем если стимул относится к одному классу, например «кислый» для вкуса, то класс заполняется полным весом стимула, или единицей, если же стимул относится сразу к двум классам, например «кисло-сладкий», то каждому классу приписывается по половине веса стимула. Если имеет значение место класса в названии, то тому классу, который ставится на первое место, надо приписать больше веса. Процедура распределения весов стимулов при классификации может быть самой различной, необходимо лишь, чтобы сохранялось порядковое соответствие между распределением весов по классам и предпочтением при классификации стимулов.
(категорий, наименований) так, чтобы каждый стимул всегда можно было бы отнести по крайней мере к какому-нибудь одному классу. Набор классов должен исчерпывать классификацию стимулов. Например, для множества вкусовых качеств пищевых продуктов можно предложить набор из четырех основных классов (кислый, сладкий, горький, соленый). Классификация заключается в отнесении каждого данного стимула к одному или нескольким классам. Причем если стимул относится к одному классу, например «кислый» для вкуса, то класс заполняется полным весом стимула, или единицей, если же стимул относится сразу к двум классам, например «кисло-сладкий», то каждому классу приписывается по половине веса стимула. Если имеет значение место класса в названии, то тому классу, который ставится на первое место, надо приписать больше веса. Процедура распределения весов стимулов при классификации может быть самой различной, необходимо лишь, чтобы сохранялось порядковое соответствие между распределением весов по классам и предпочтением при классификации стимулов.
В результате классификации стимулов по данному набору классов строится матрица  в которой строка определяется номером стимула
в которой строка определяется номером стимула  а столбец указывает класс
а столбец указывает класс  Элементом матрицы
Элементом матрицы  является число, показывающее вес стимула
является число, показывающее вес стимула  по классу
по классу  просуммированный по числу предъявлений.
просуммированный по числу предъявлений.
Каждая строка матрицы представляет собой вектор  компонентами которого служат элементы строки
компонентами которого служат элементы строки  Все строки образуют векторное пространство реакций размерности
Все строки образуют векторное пространство реакций размерности  (по числу классов). В этом пространстве вводится некоторая мера различия между векторами, и тогда попарные различия всех векторов дадут матрицу субъективных различий между стимулами. Полученная таким образом матрица различий вводит данные в систему многомерного шкалирования.
(по числу классов). В этом пространстве вводится некоторая мера различия между векторами, и тогда попарные различия всех векторов дадут матрицу субъективных различий между стимулами. Полученная таким образом матрица различий вводит данные в систему многомерного шкалирования.
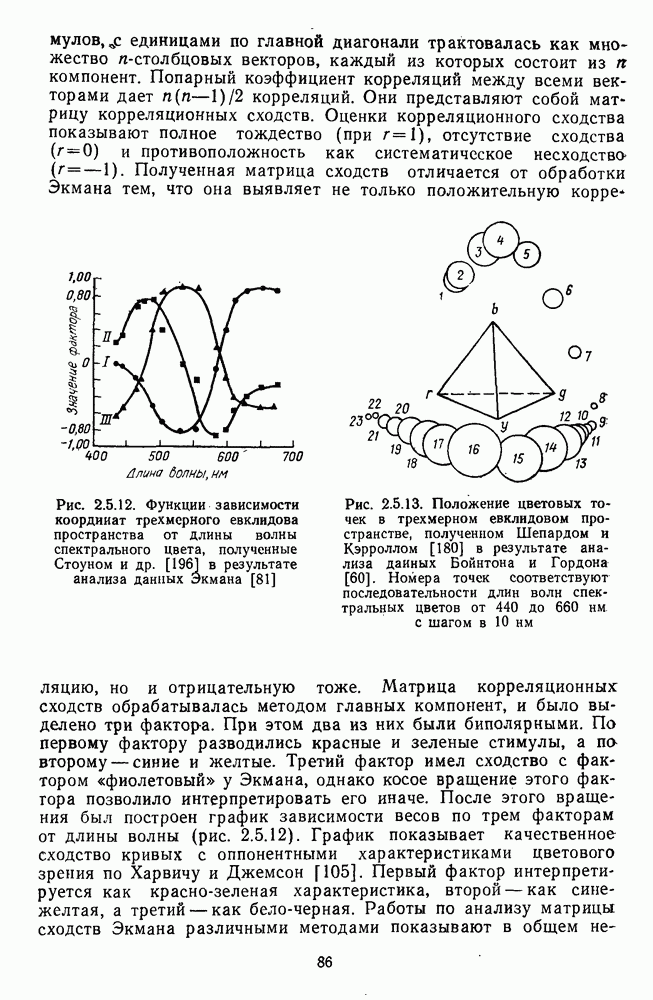
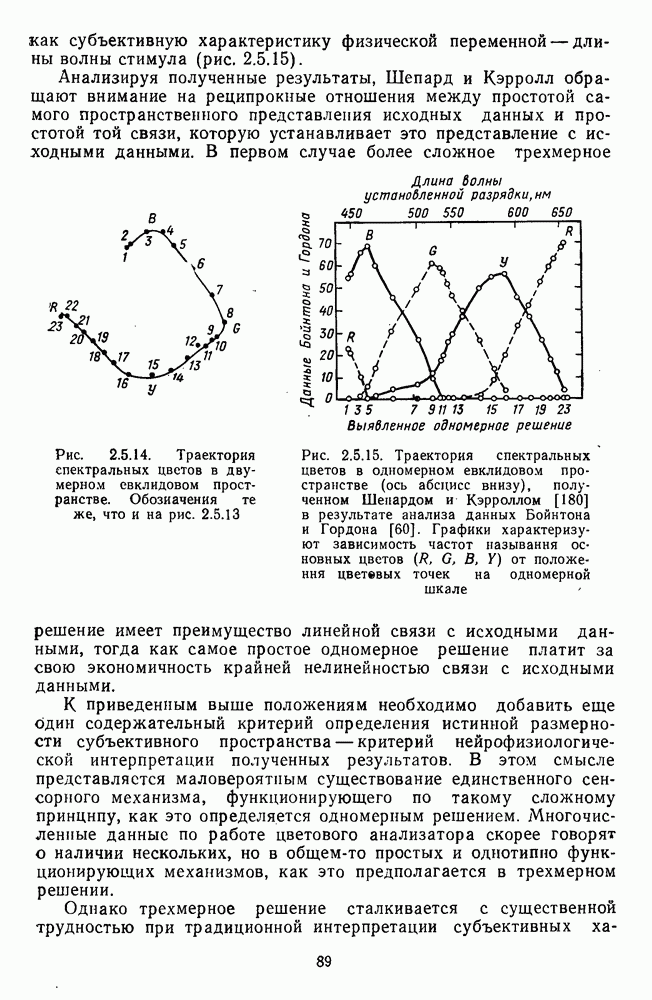
Такая процедура успешно применялась Шепардом, Кэрролом [180] и Измайловым [11] к данным называния цветов Бойнтона и Гордона [60] для построения пространства цветоразличения.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
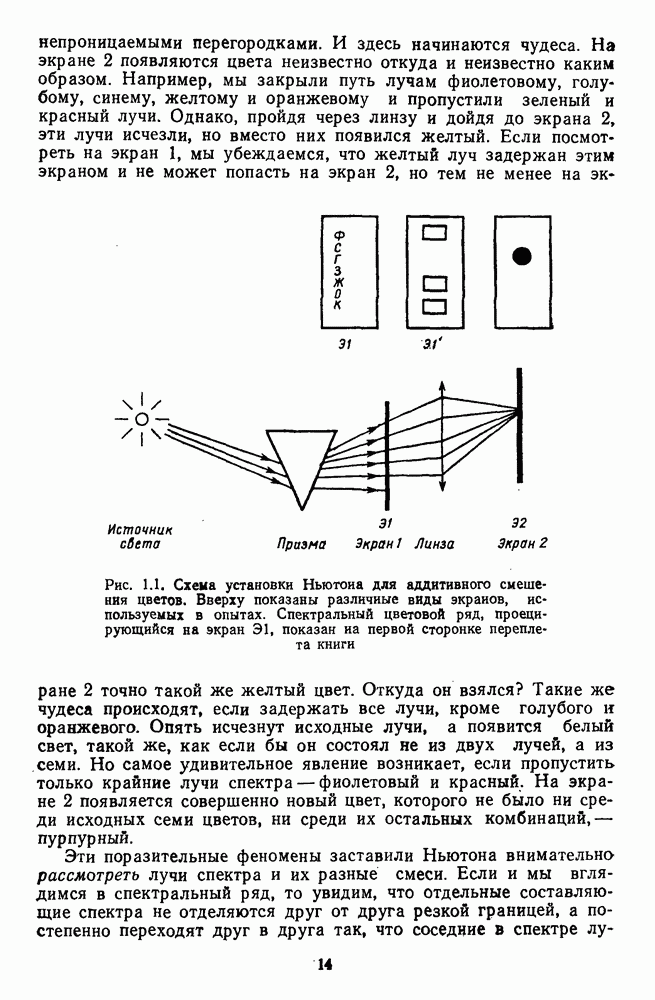
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
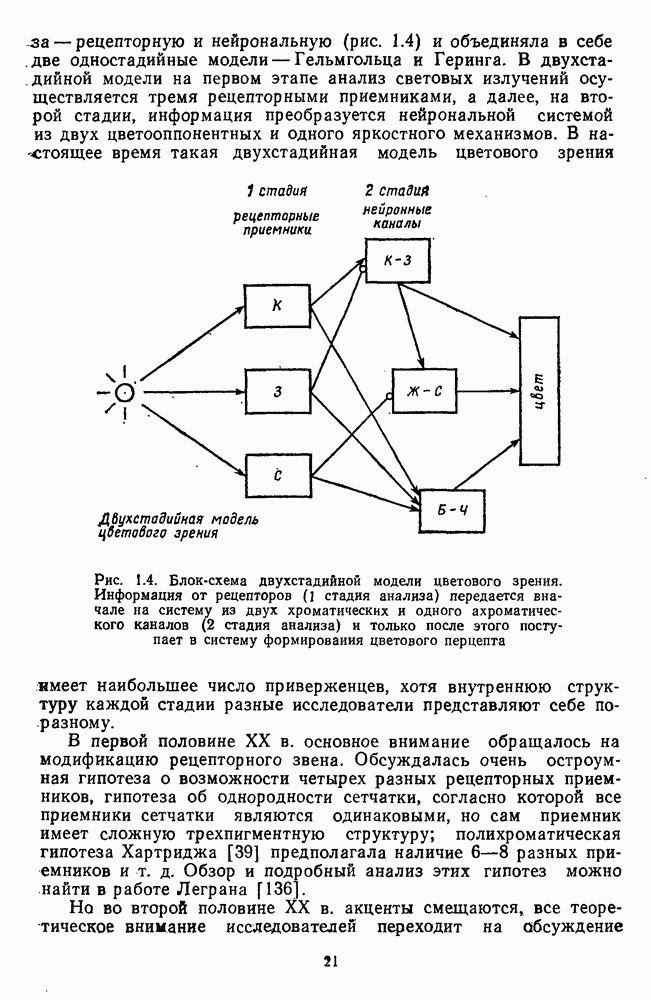
- 1.8. Двухстадийная теория цветового зрения
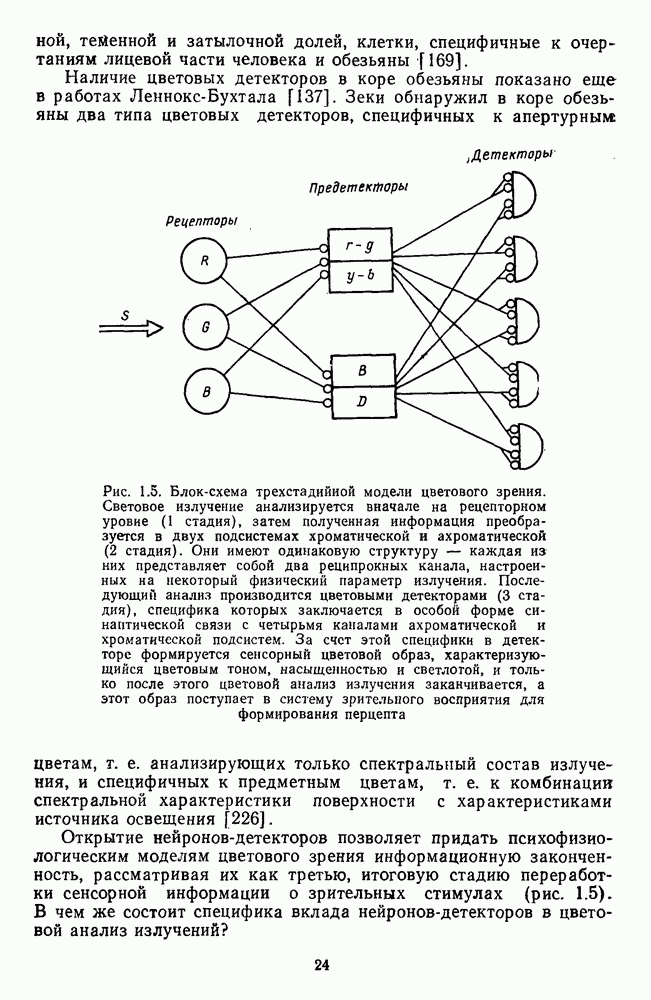
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
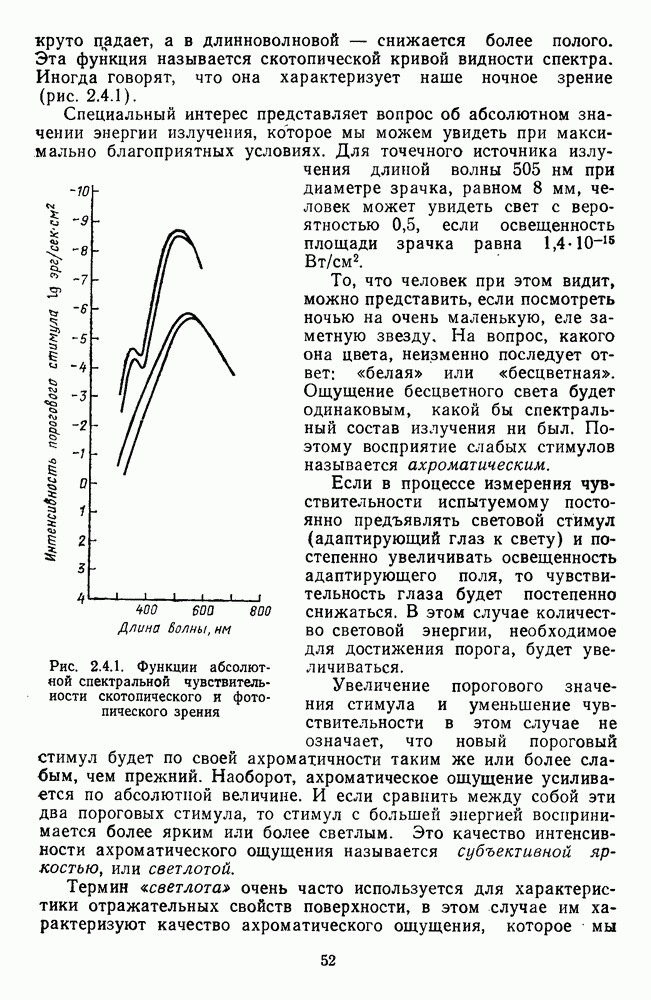
- 2.4.1. Спектральная чувствительность зрения
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- 4.3.2. Модель Гуса
- 4.3.3. Трехстадийная модель ахроматического зрения
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА