| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
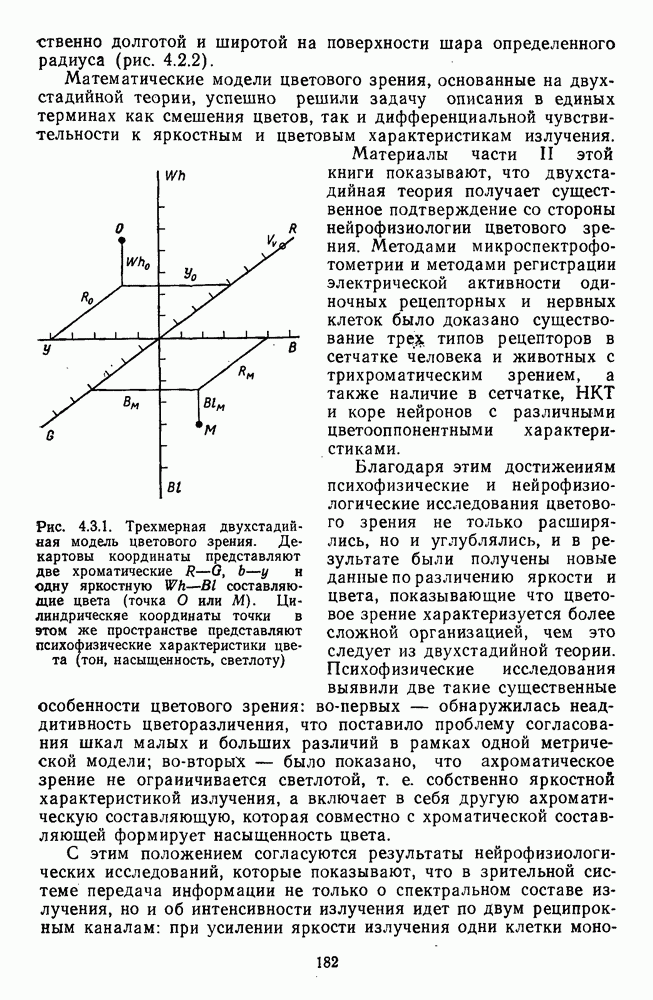
Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
4.2.1. Модель Харвича и Джемсон
В историческом экскурсе в начале книги мы рассматривали причины отвержения одностадийной концепции и замены ее двухстадийной. И хотя первые идеи о втором звене цветового анализатора появились еще в начале нашего века, реально, в качестве сформировавшейся теории, двухстадийная концепция появляется только в 50-е годы. Первую математическую модель, основанную на широком круге экспериментальных измерений, предложили американские исследователи Харвич и Джемсон [104; 105].
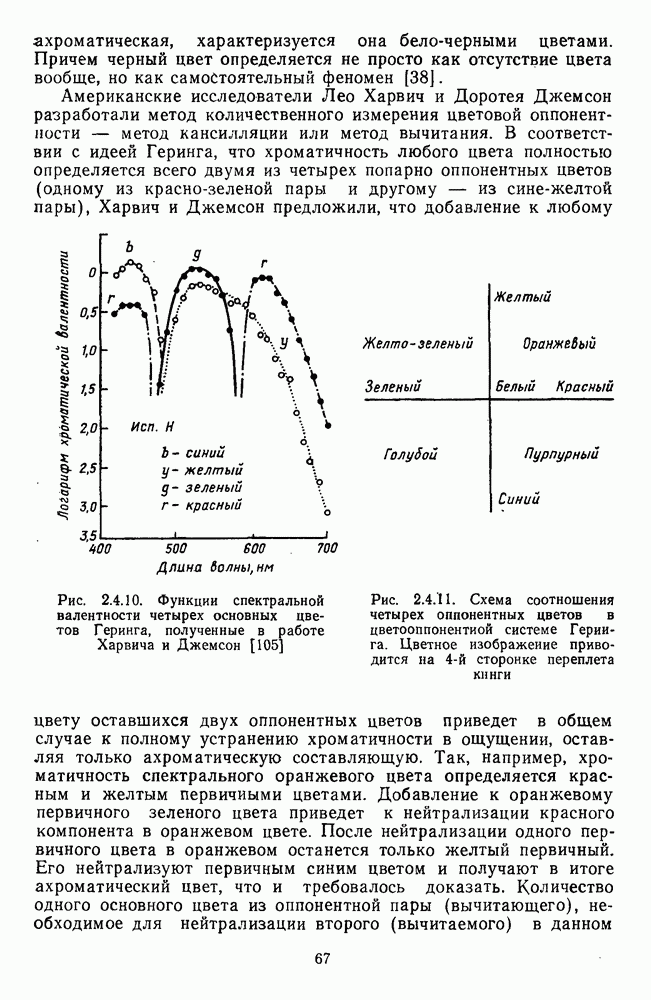
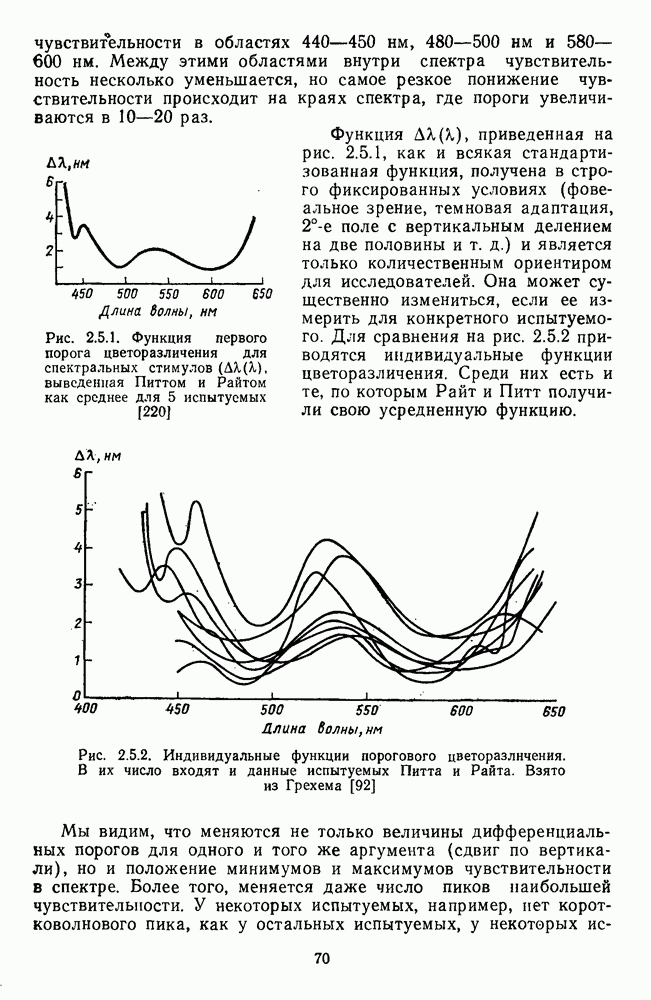
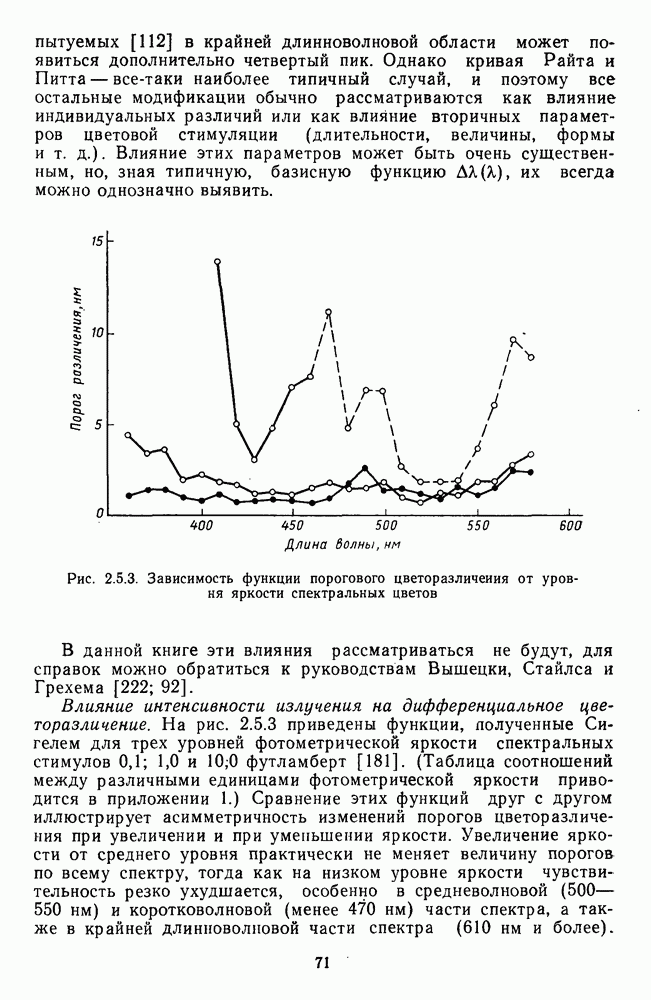
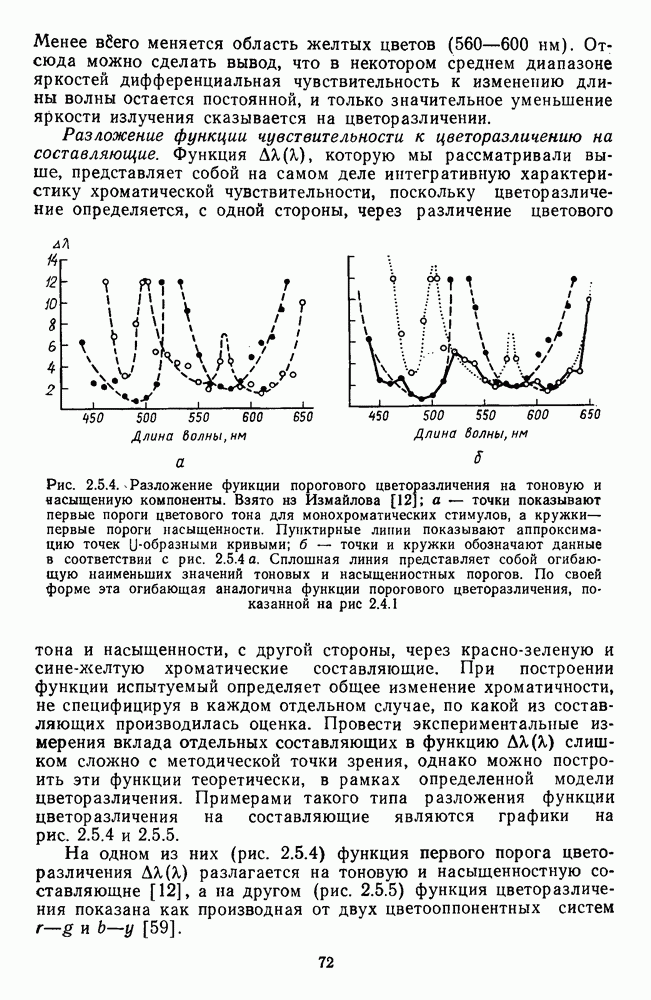
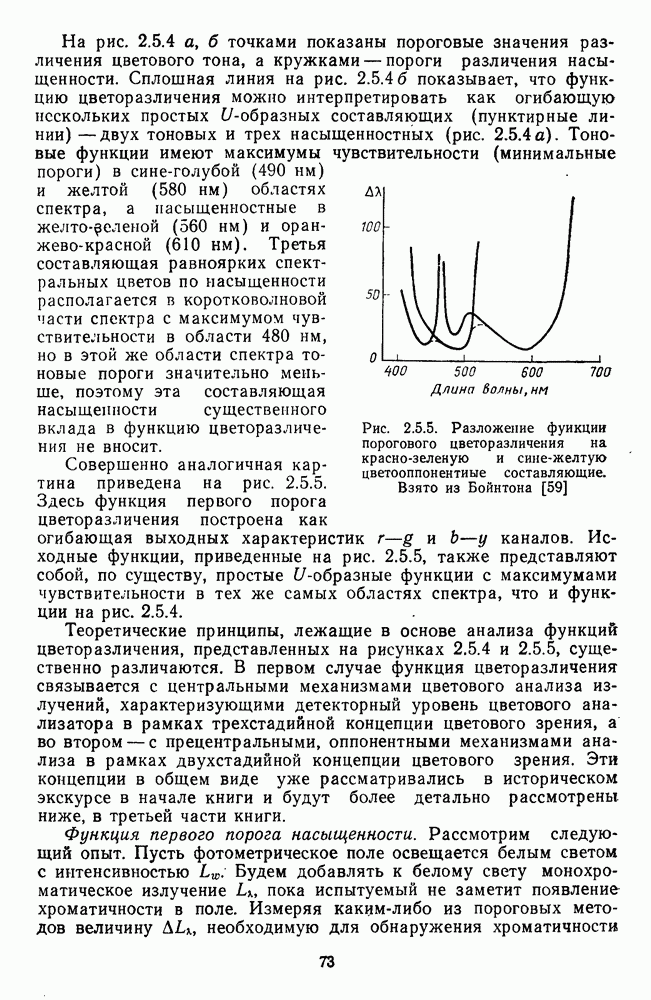
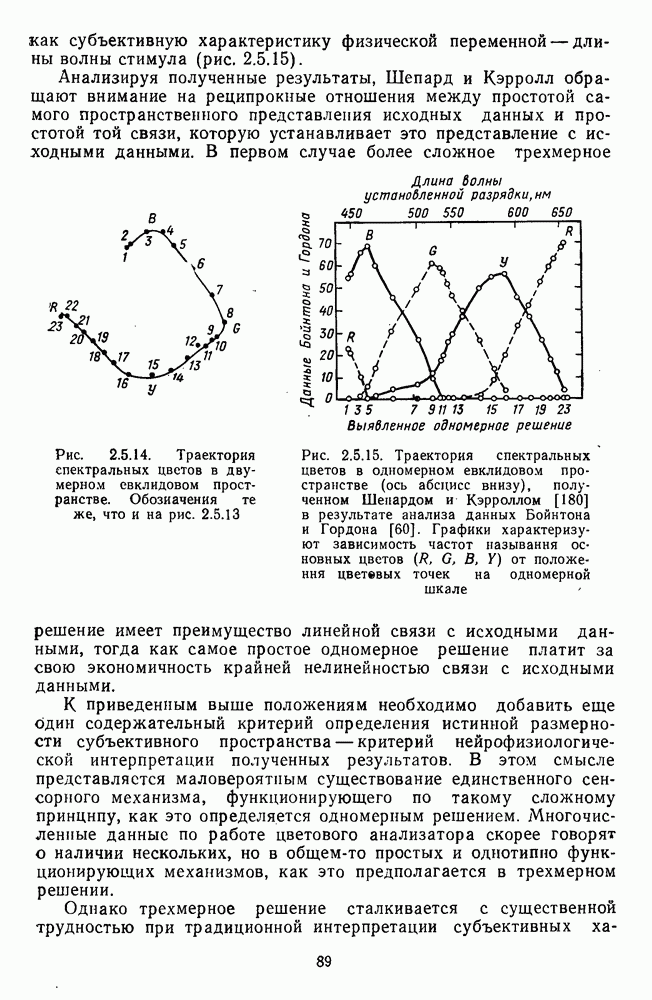
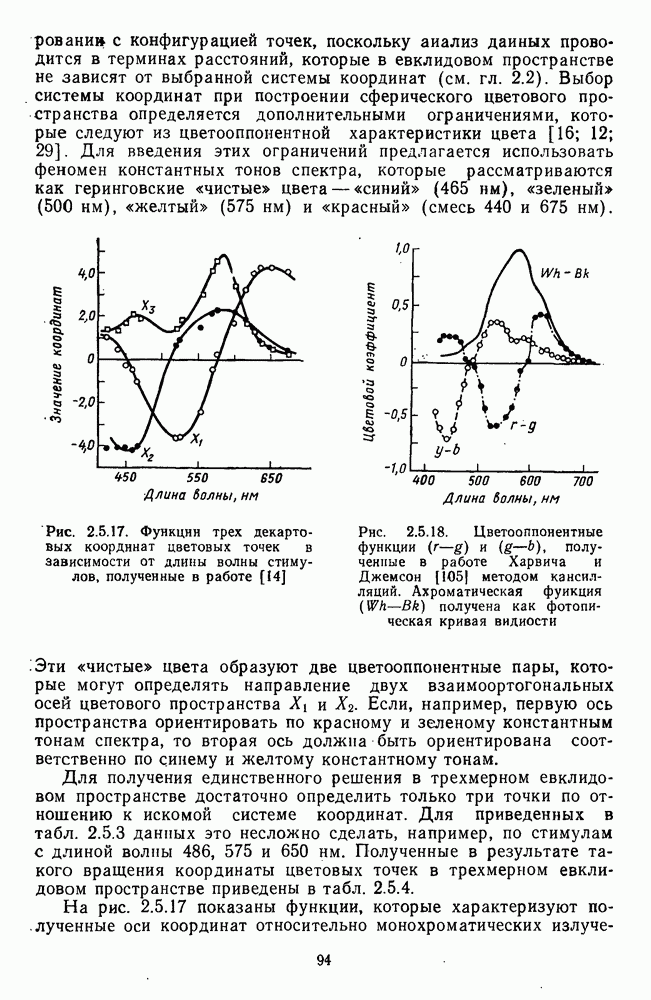
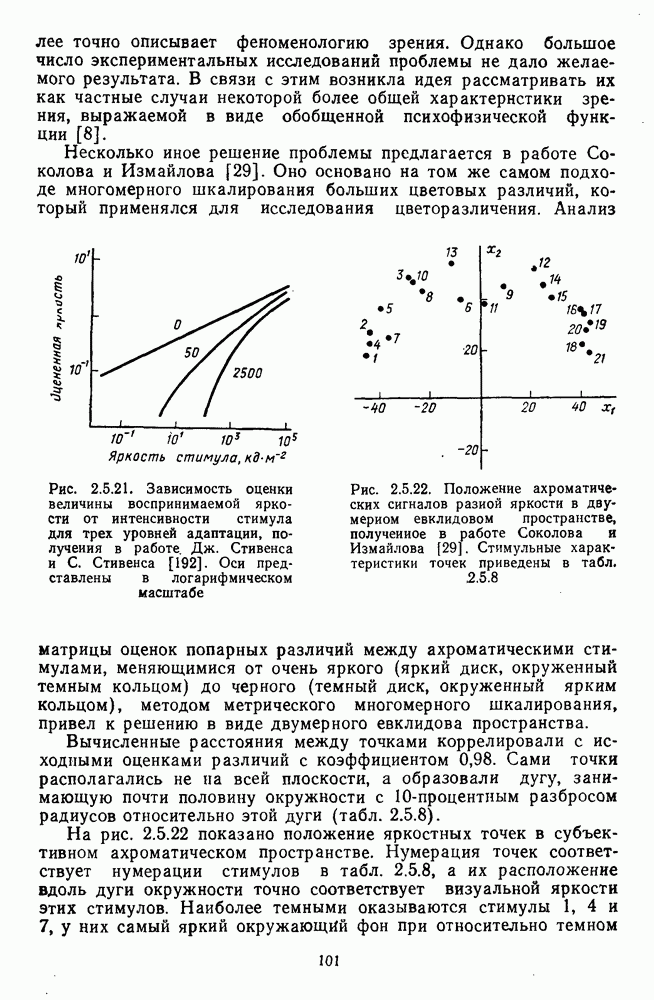
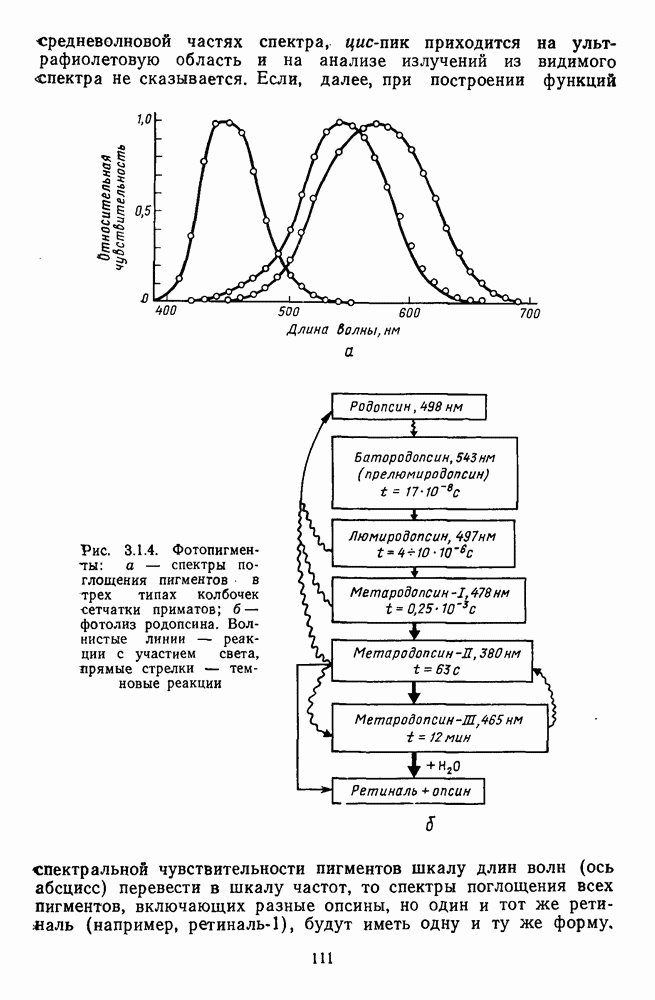
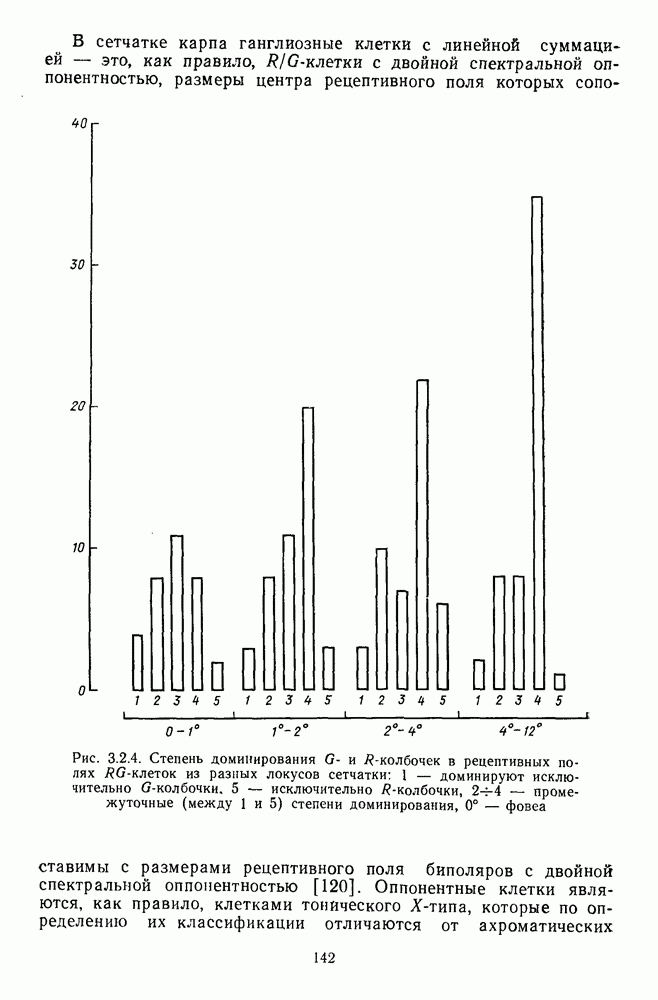
Исходным массивом экспериментальных данных, которые использовали Харвич и Джемсон для построения своей модели, послужили функции спектральной валентности четырех геринговских цветов, которые были измерены методом кансилляций (рис. 2.4.10 и 2.5.18).
Поскольку эти функции были получены для равноэнергетического спектра, Харвич и Джемсон определили матрицу линейных коэффициентов, которые связывают функции спектральной валентности с функциями смешения цветов. (Как и большинство исследователей, Харвич и Джемсон использовали для этого функции Стандартного Наблюдателя МКО-31). Это показало, что в модели
Харвича и Джемсон выполняется вся феноменология смешения цветов:

Последняя функция  от длины волны представляет дифференциальную активность четырех нейрональных механизмов
от длины волны представляет дифференциальную активность четырех нейрональных механизмов  имеющих одинаковые значения относительной спектральной чувствительности, но разные — абсолютной, она представляет ахроматическую составляющую в модели Харвича и Джемсон. Коэффициенты
имеющих одинаковые значения относительной спектральной чувствительности, но разные — абсолютной, она представляет ахроматическую составляющую в модели Харвича и Джемсон. Коэффициенты  зависят от яркостного уровня стимулов и, в частности, для условий экспериментов Харвича и Джемсон они равны:
зависят от яркостного уровня стимулов и, в частности, для условий экспериментов Харвича и Джемсон они равны:

Нетрудно видеть, что, варьируя коэффициенты, можно очень гибко управлять структурой модели, но отсутствие содержательной интерпретации этих коэффициентов существенно умаляет их ценность и приближает саму модель к типу моделей ad hoc.
Мы не будем здесь подробно рассматривать математические выкладки, позволяющие рассчитать то большое число цветовых функций, которые приводятся в работах Харвича и Джемсон. Все подробности можно найти в руководстве Грехема [92]. В качестве примера рассмотрим только, как измеряется в модели Харвича и Джемсон первый порог насыщенности. (Экспериментальные измерения этой функции уже приводились на рис. 2.5.6.) Исходя из уравнений (4.2.1) показатель насыщенности спектрального света определяется следующим образом:

Выражение (4.2.2) определяет вклад хроматической и ахроматической компонент в показатель насыщенности Р. для единицы яркости. Для любого выбранного значения яркости  надо вместо единицы в числителе и знаменателе проставить это значение и тогда получится
надо вместо единицы в числителе и знаменателе проставить это значение и тогда получится

Условия эксперимента для измерения первого порога насыщенности (см. ч. 2, гл. 5) предусматривают, что не только ахроматическая компонента спектрального света участвует в выражении (4.2.3), но и константная ахроматическая компонента белого
света, к которому подмешивается спектральный. Поэтому для смеси белого и спектрального света выражение (4.2.3) примет вид

Пороговое значение  также есть некоторая константа, поскольку в однородном цветовом пространстве пороговая величина везде сохраняется константной по определению. Таким образом, в уравнении (2.4) оказываются известными все параметры, за исключением
также есть некоторая константа, поскольку в однородном цветовом пространстве пороговая величина везде сохраняется константной по определению. Таким образом, в уравнении (2.4) оказываются известными все параметры, за исключением  Подставив для каждой длины волны в выражении (4.2.4) значения
Подставив для каждой длины волны в выражении (4.2.4) значения  из уравнений (4.2.1) и пользуясь константами
из уравнений (4.2.1) и пользуясь константами  можно определить
можно определить  и рассматривать его как приращение от нулевого значения, т. е.
и рассматривать его как приращение от нулевого значения, т. е.

и соответственно определить для каждой длины волны отношение


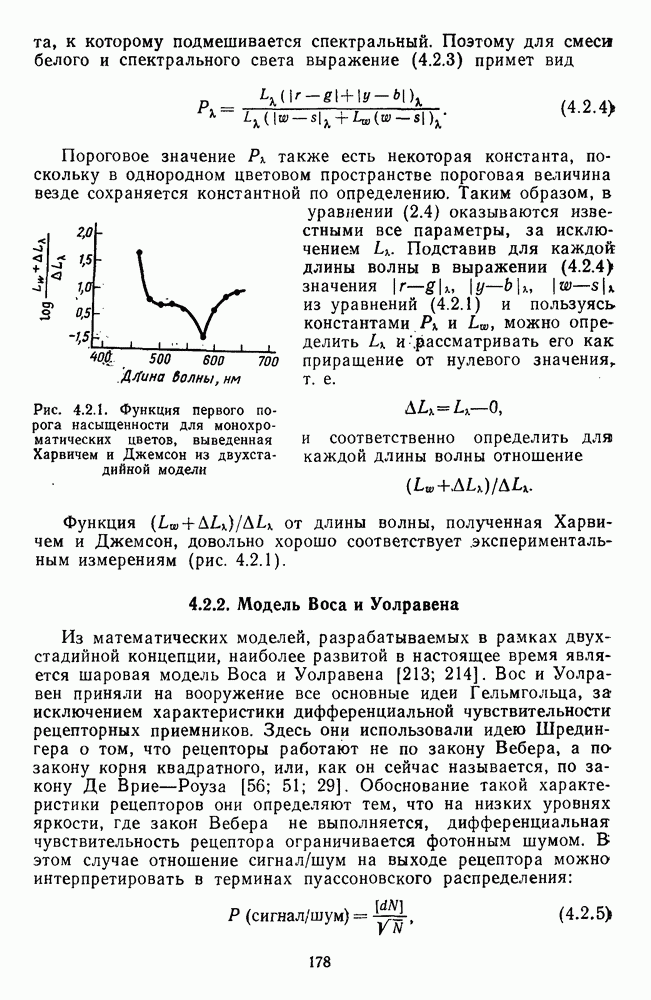
Рис. 4.2.1. Функция первого порога насыщенности для монохроматических цветов, выведенная Харвичем и Джемсон из двухстадийной модели
Функция  от длины волны, полученная Харвичем и Джемсон, довольно хорошо соответствует экспериментальным измерениям (рис. 4.2.1).
от длины волны, полученная Харвичем и Джемсон, довольно хорошо соответствует экспериментальным измерениям (рис. 4.2.1).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
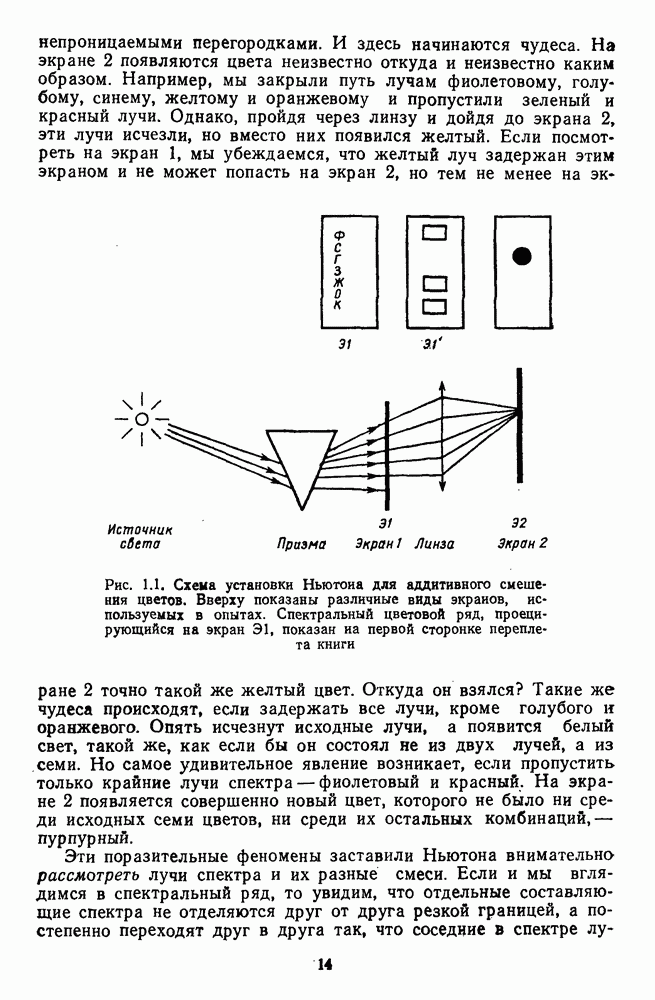
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
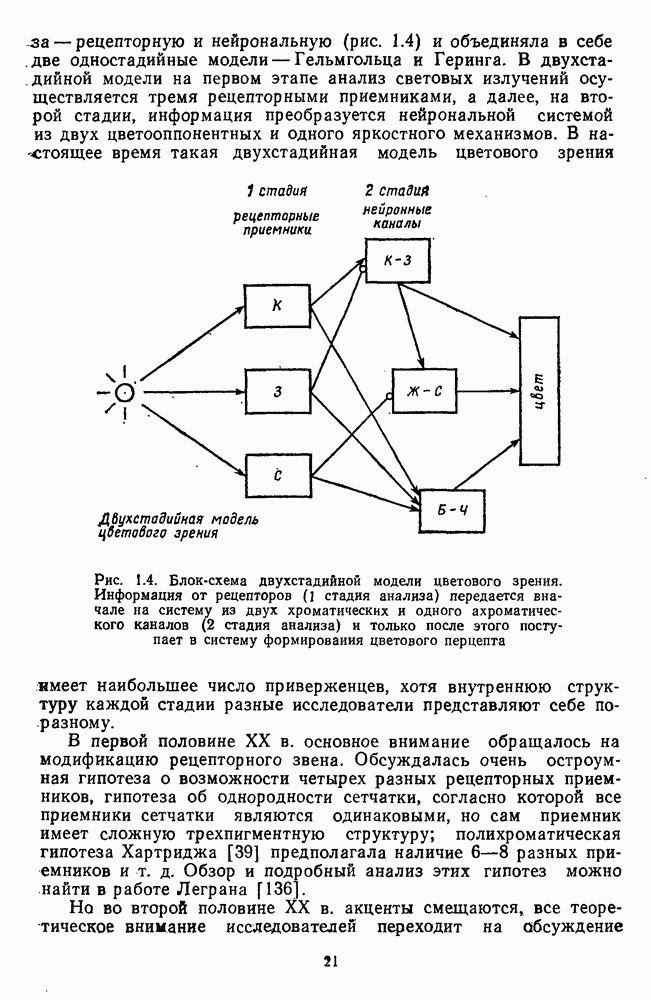
- 1.8. Двухстадийная теория цветового зрения
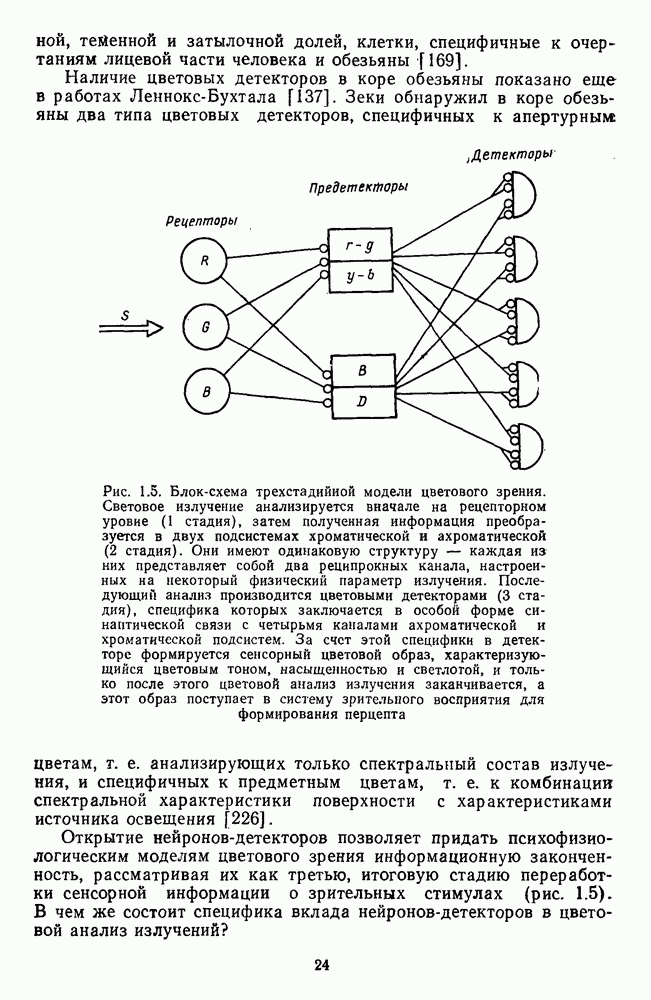
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
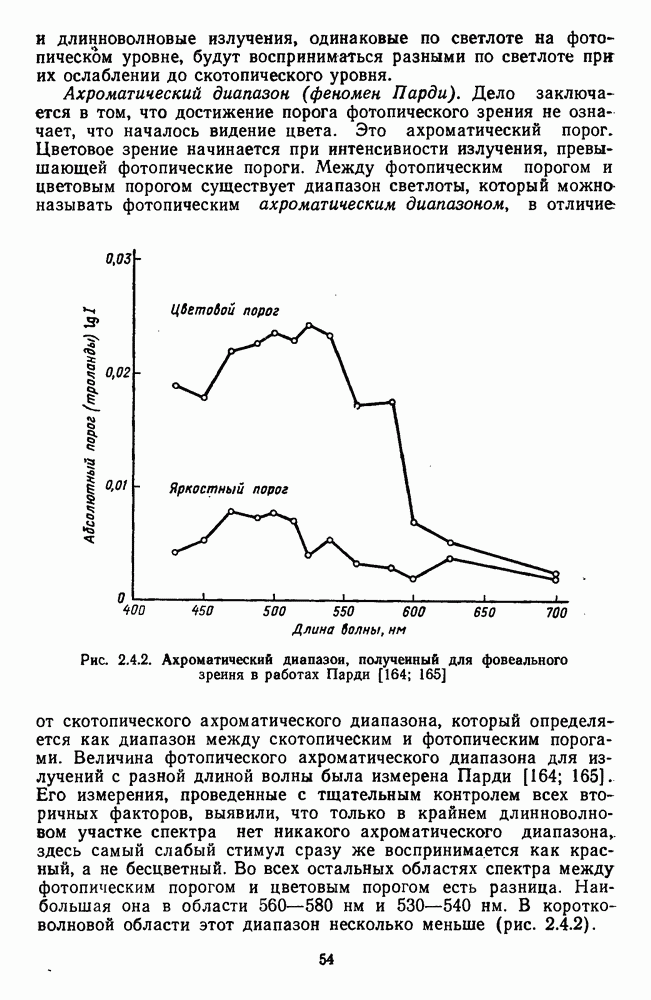
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
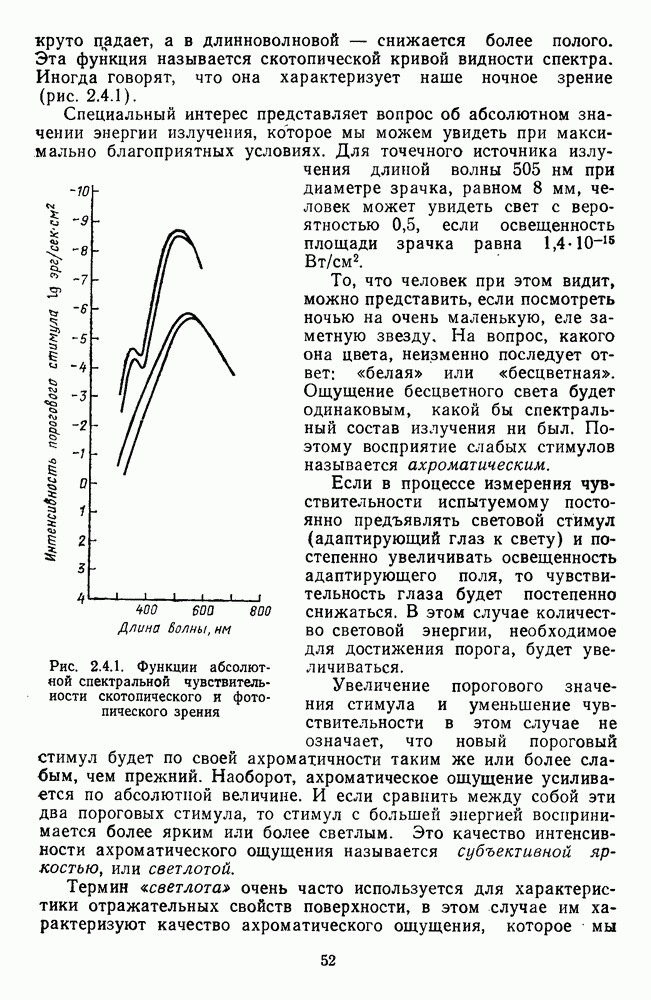
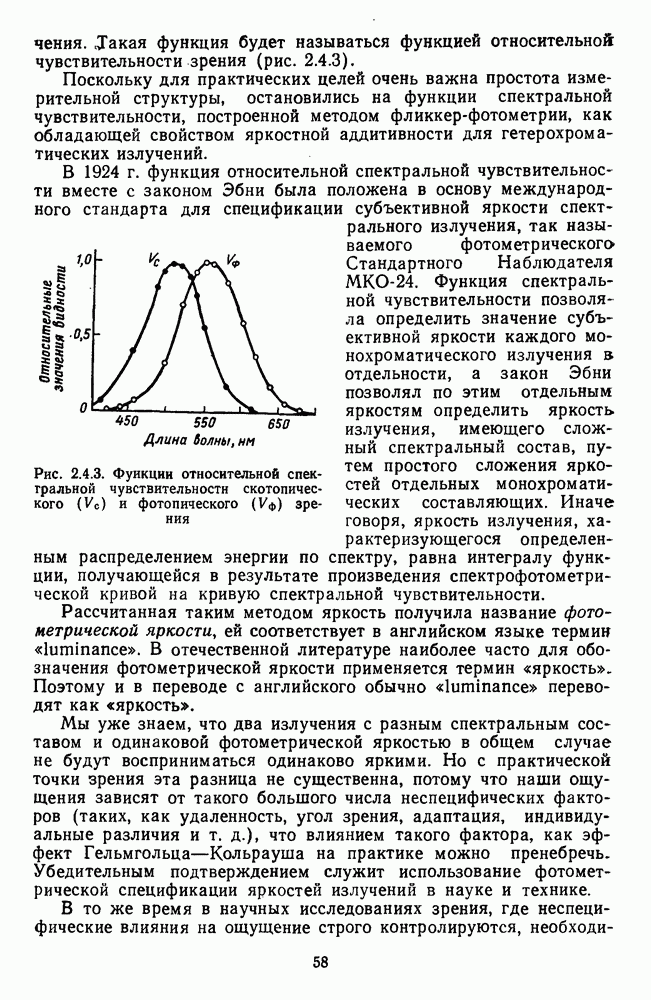
- 2.4.1. Спектральная чувствительность зрения
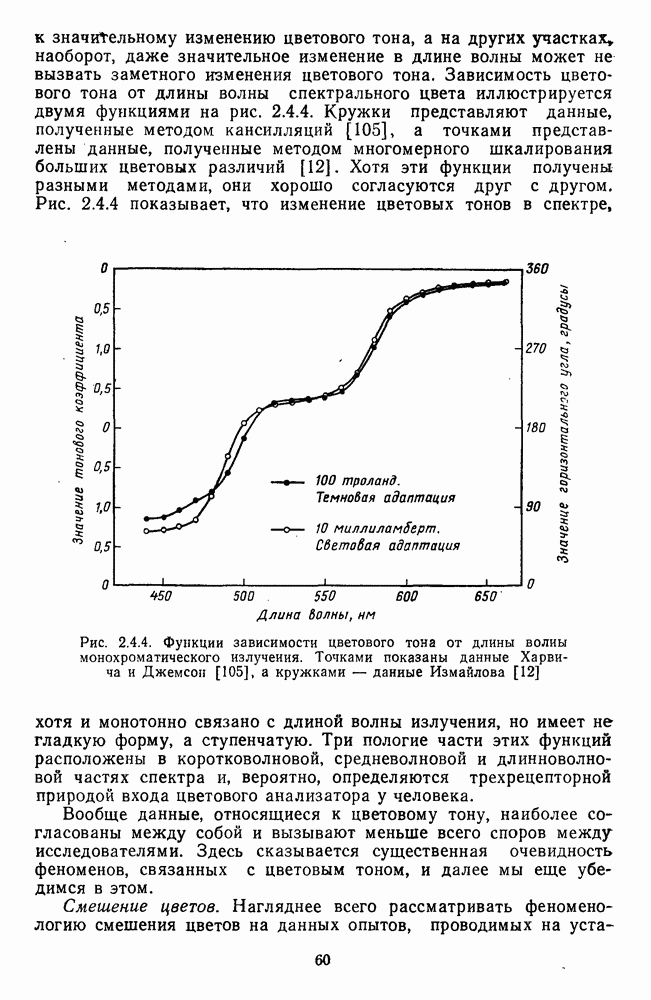
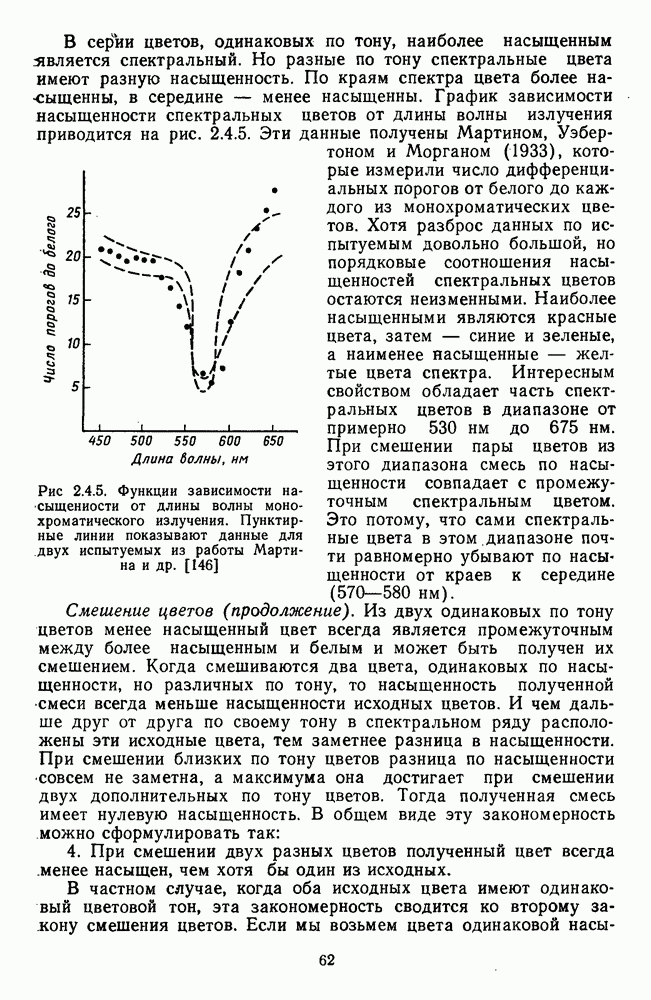
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
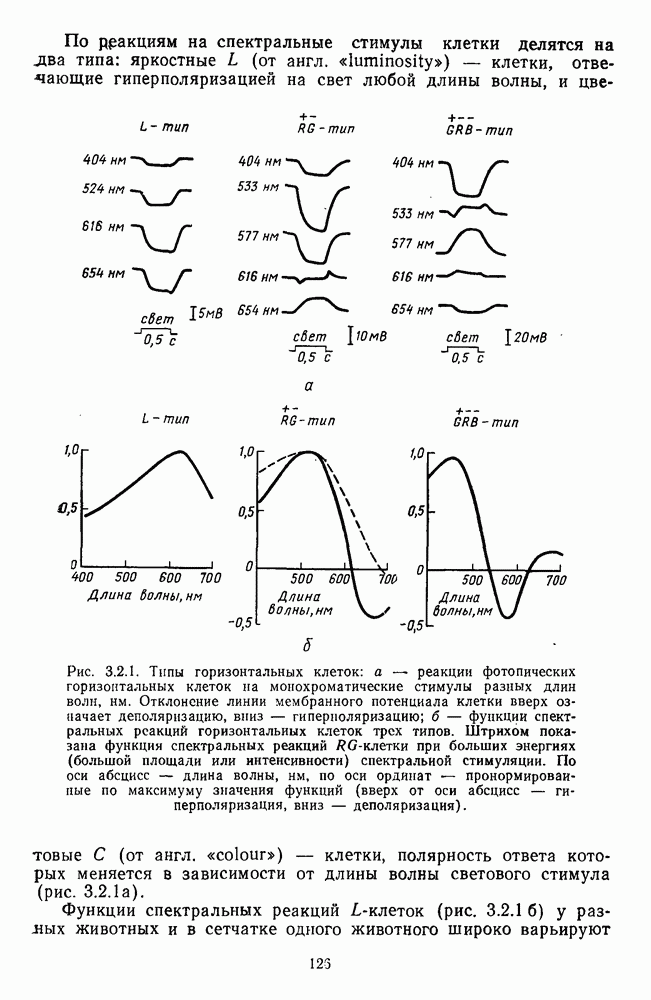
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
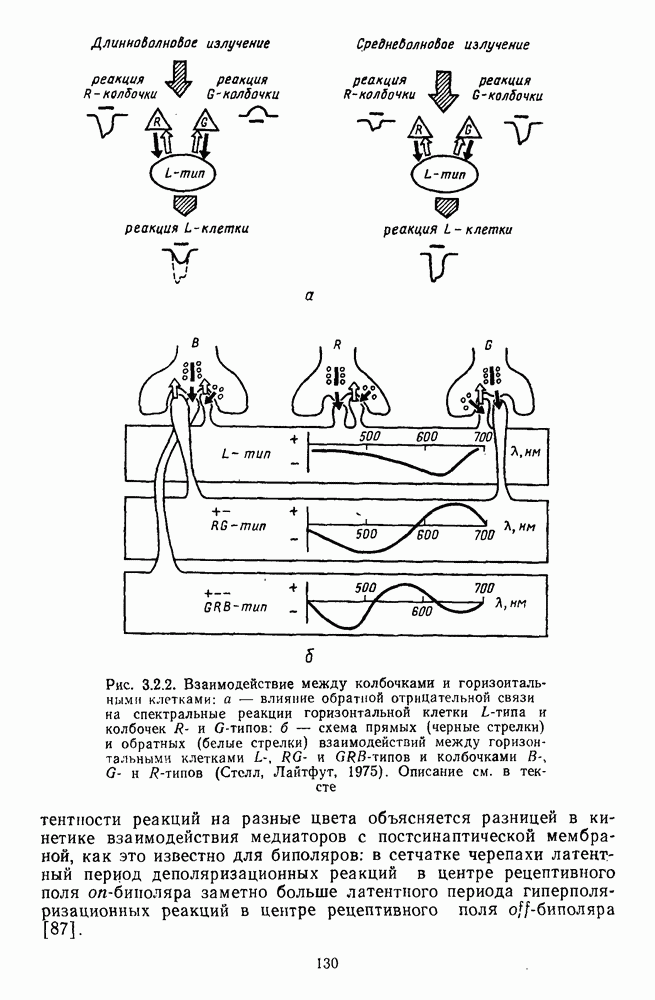
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
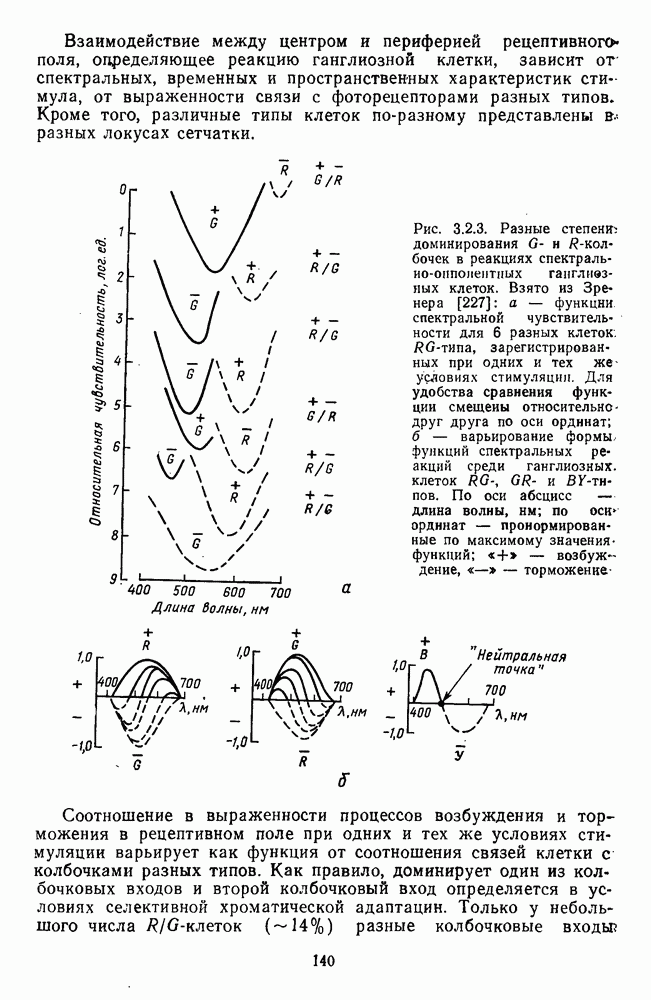
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
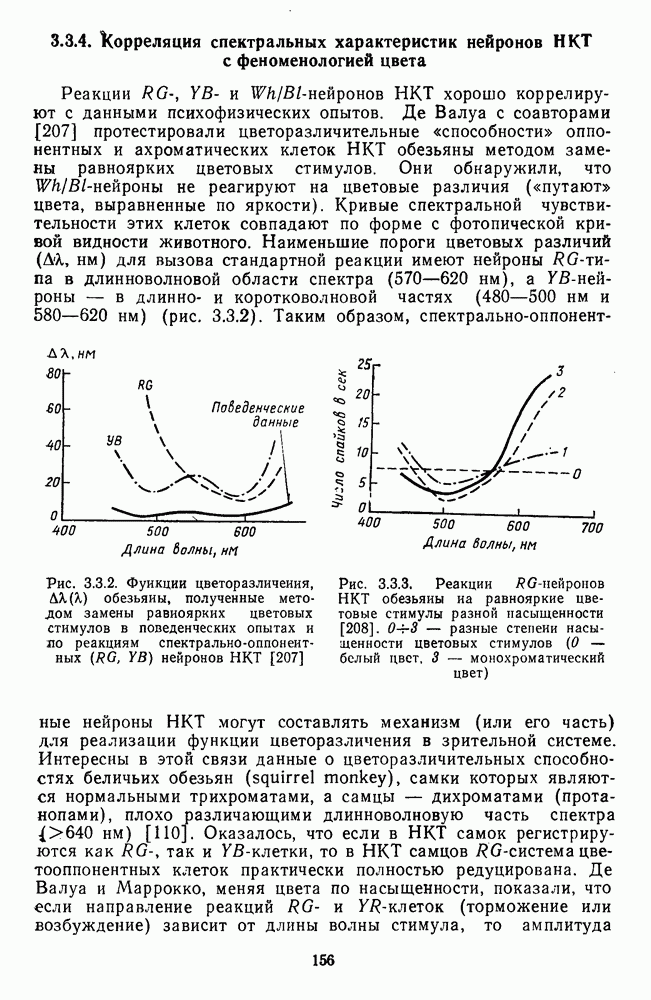
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
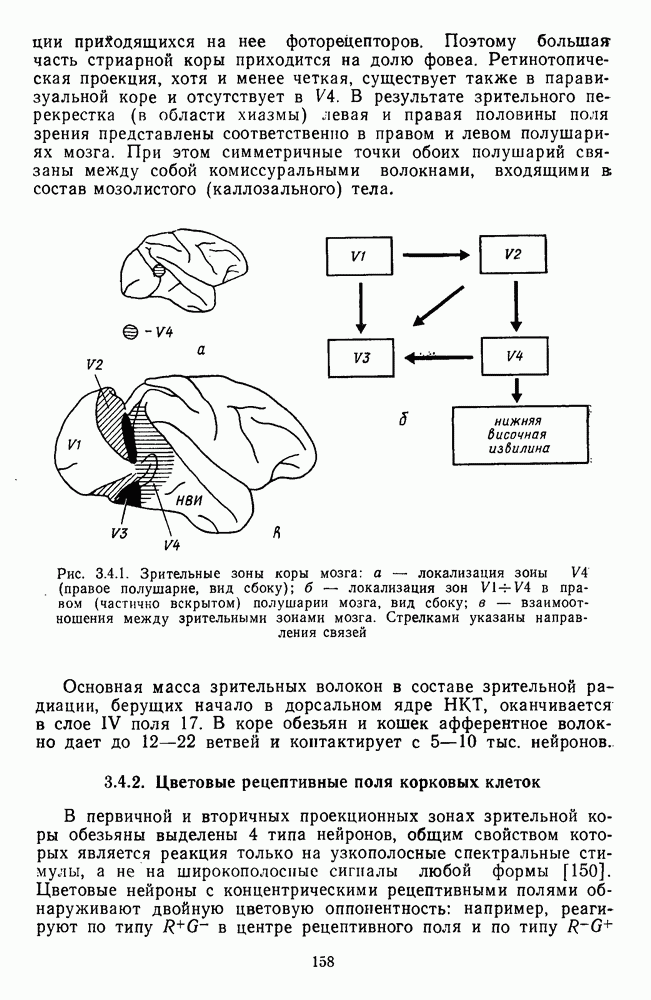
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
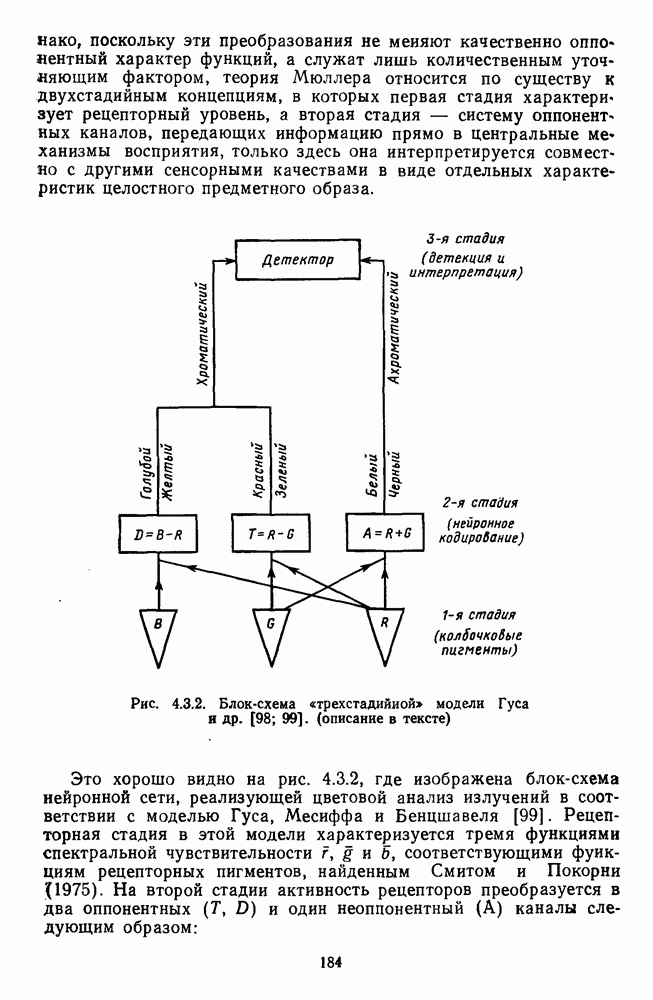
- 4.3.2. Модель Гуса
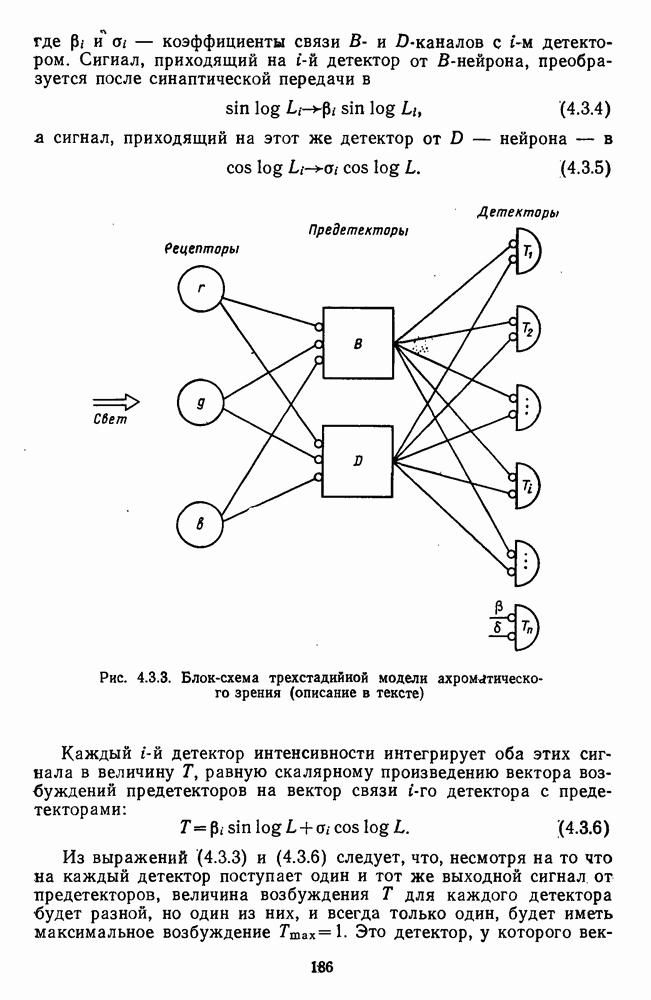
- 4.3.3. Трехстадийная модель ахроматического зрения
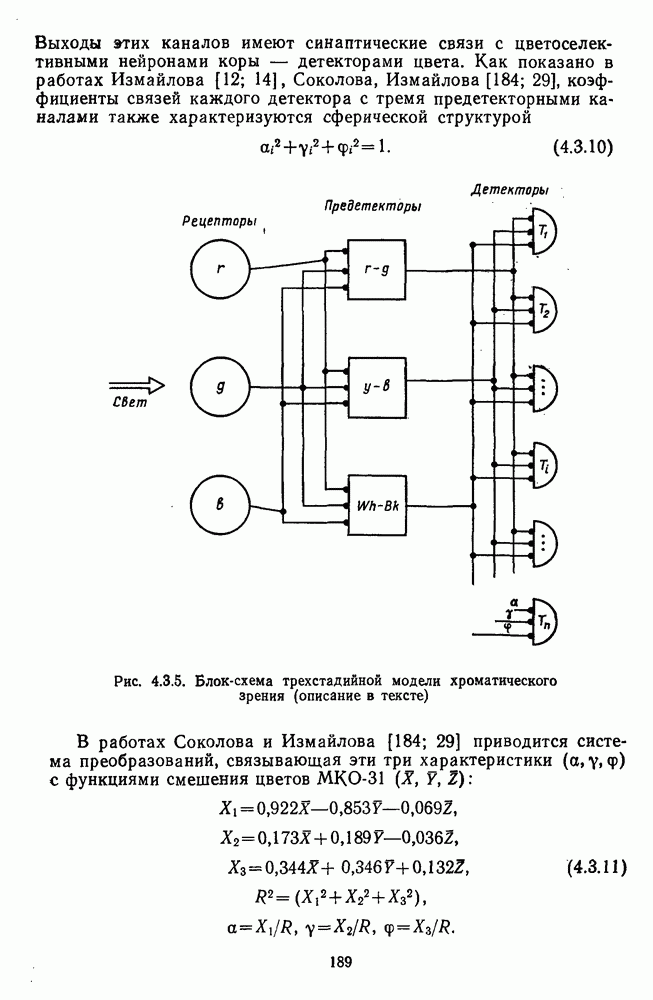
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА