| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5.5. Неевклидовость ахроматического пространства
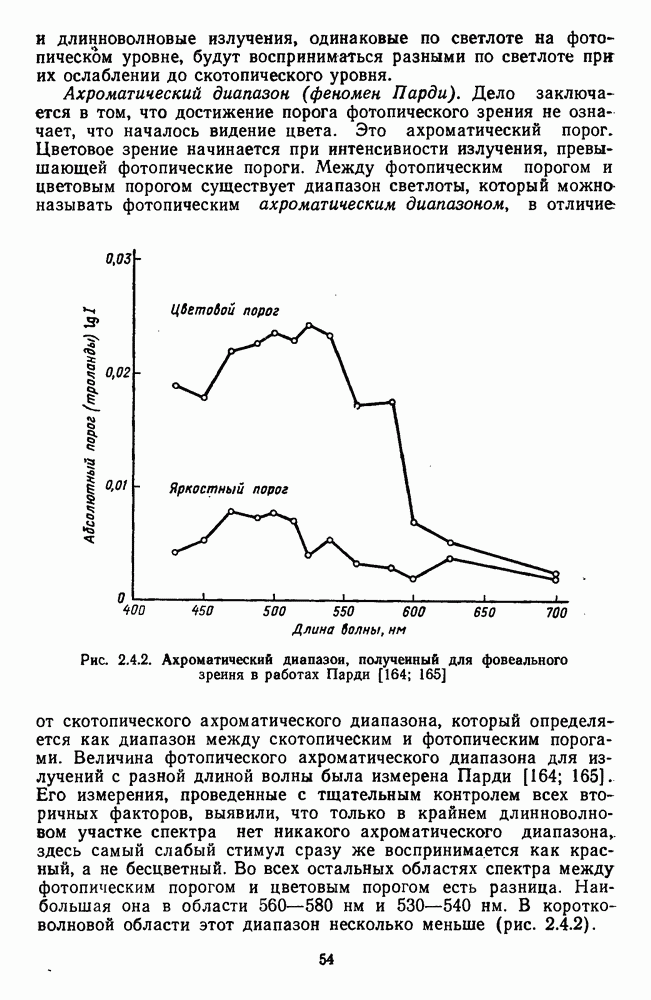
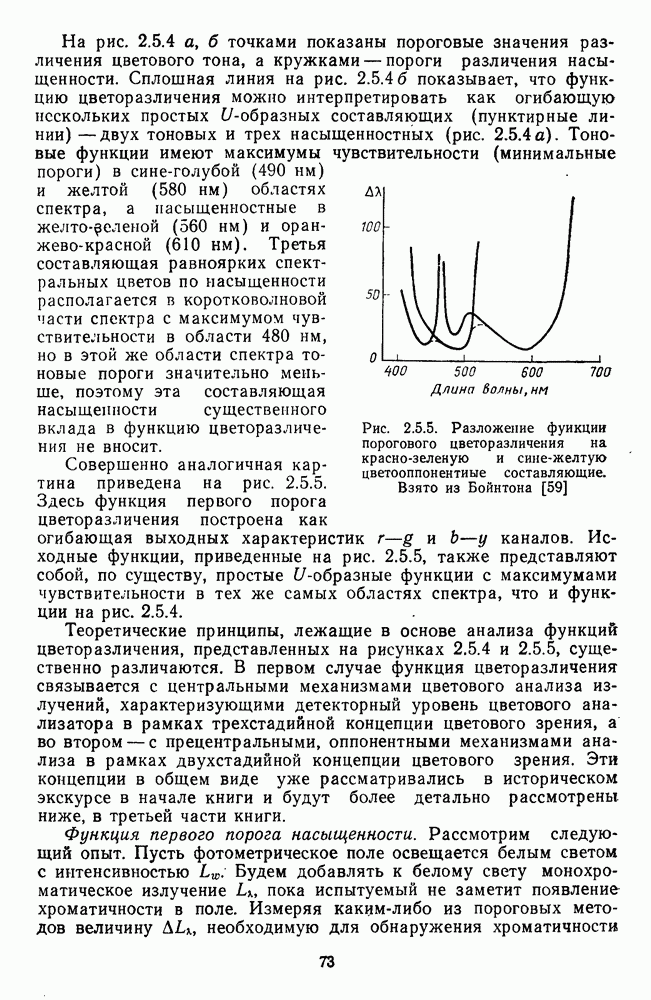
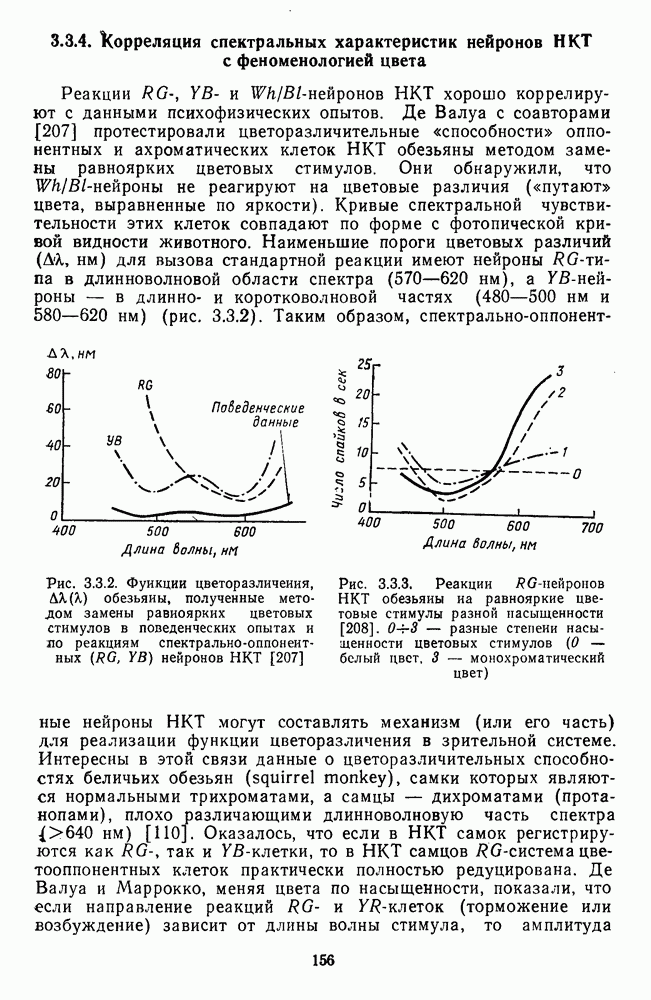
Основной ахроматической составляющей апертурного цвета является светлота. Диапазон ее изменения от ослепительно яркого цвета до очень темного вмещает в себя значительно больше дифференциальных порогов ( = 300 е.з.р.), чем диапазон изменений цветового тона (~ 150 е. з. р., включая пурпурные) или насыщенности (от 10 до 30 е. з.р.). Основываясь на характеристиках дифференциальной чувствительности (рис. 2.5.7), Фехнер вывел психофизическую функцию светлоты в виде

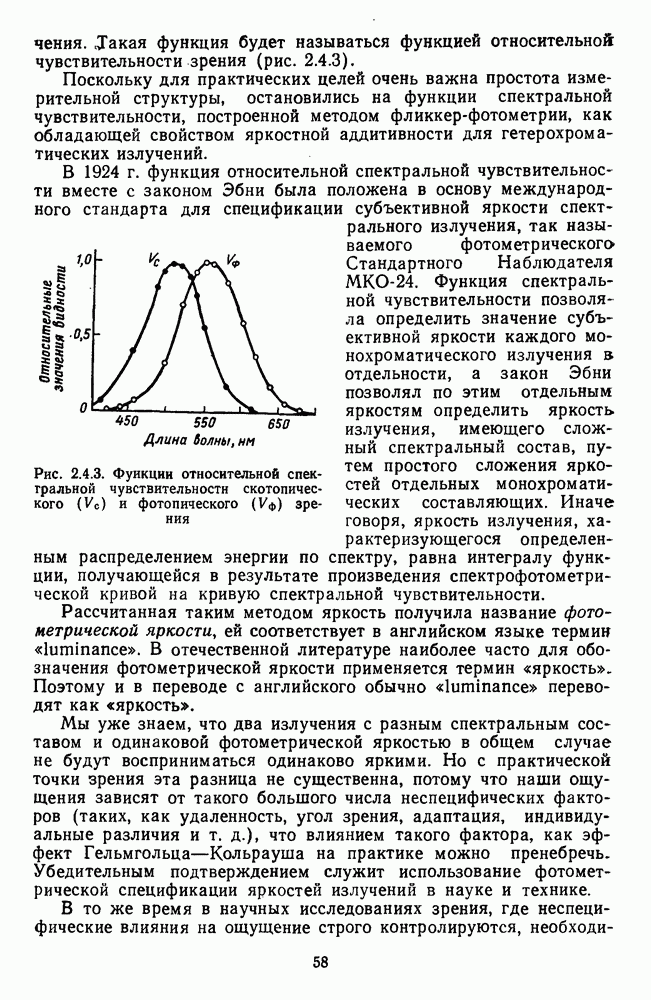
Шкалирование надпороговых значений стимулов, которое применил Стивенс [190; 191], а вслед за ним и другие исследователи (Экман и др. [83]), дало результаты, представляющие не логарифмическую, а степенную функцию:

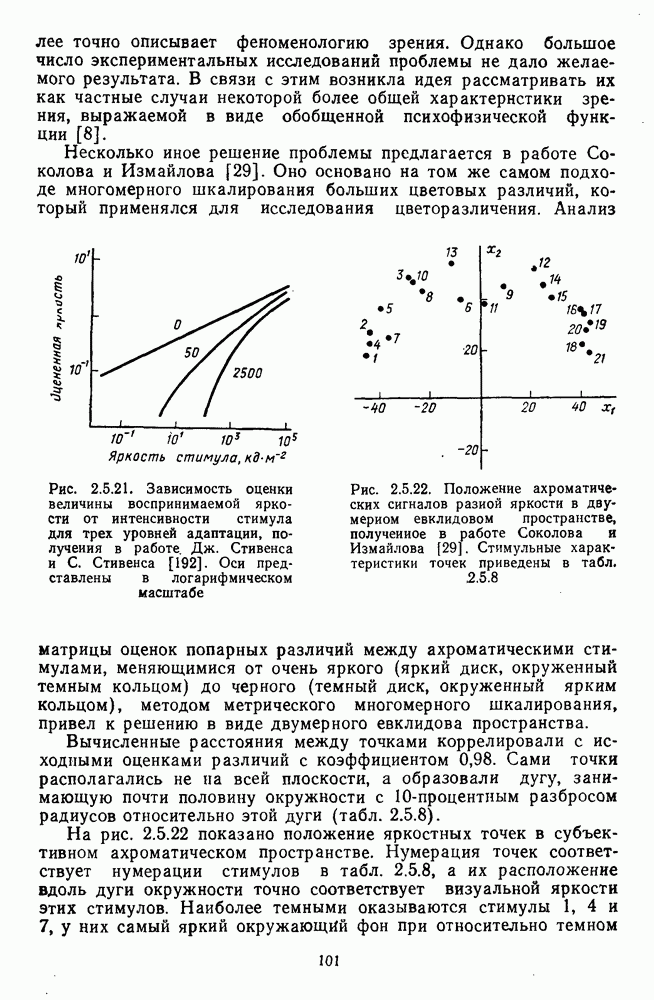
Эта функция показана на рис. 2.5.21. Ее оси заданы в логарифмических координатах.
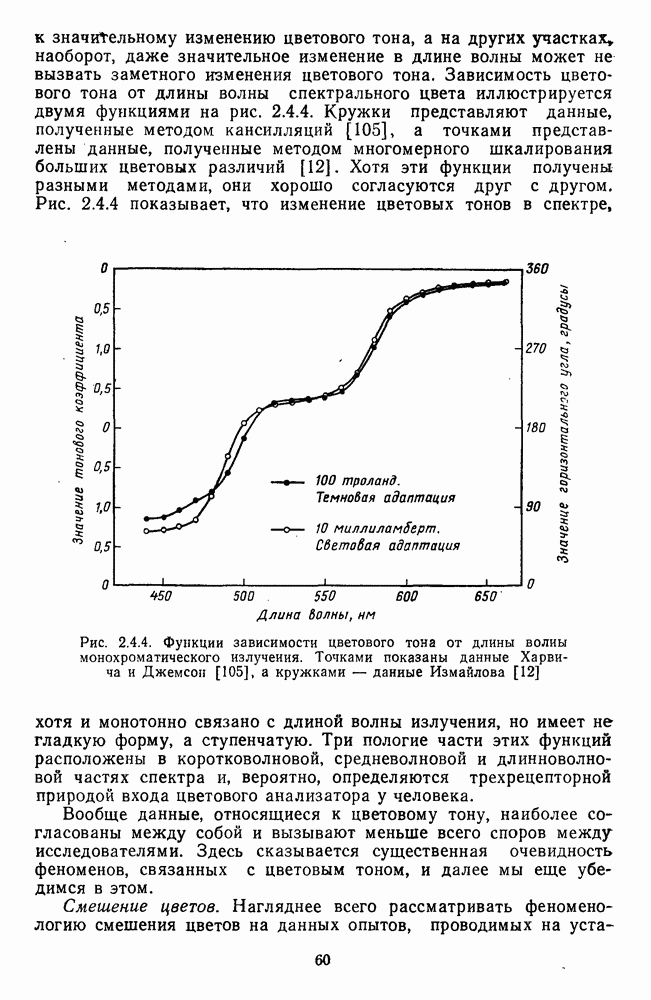
Расхождение между двумя психофизическими функциями вызвало оживленные дискуссии и попытки выяснить, какая из них
более точно описывает феноменологию зрения. Однако большое число экспериментальных исследований проблемы не дало желаемого результата. В связи с этим возникла идея рассматривать их как частные случаи некоторой более общей характеристики зрения, выражаемой в виде обобщенной психофизической функции [8].
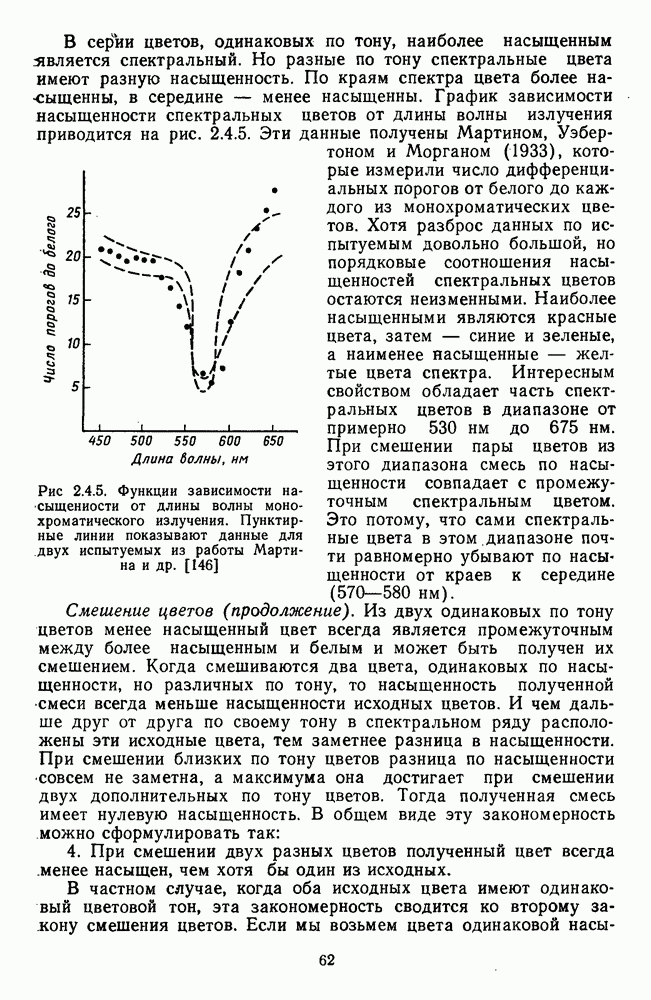
Несколько иное решение проблемы предлагается в работе Соколова и Измайлова [29]. Оно основано на том же самом подходе многомерного шкалирования больших цветовых различий, который применялся для исследования цветоразличения.

Рис. 2.5.21. Зависимость оценки величины воспринимаемой яркости от интенсивности стимула для трех уровней адаптации, получения в работе Дж. Стивенса и С. Стивенса [192]. Оси представлены в логарифмическом масштабе

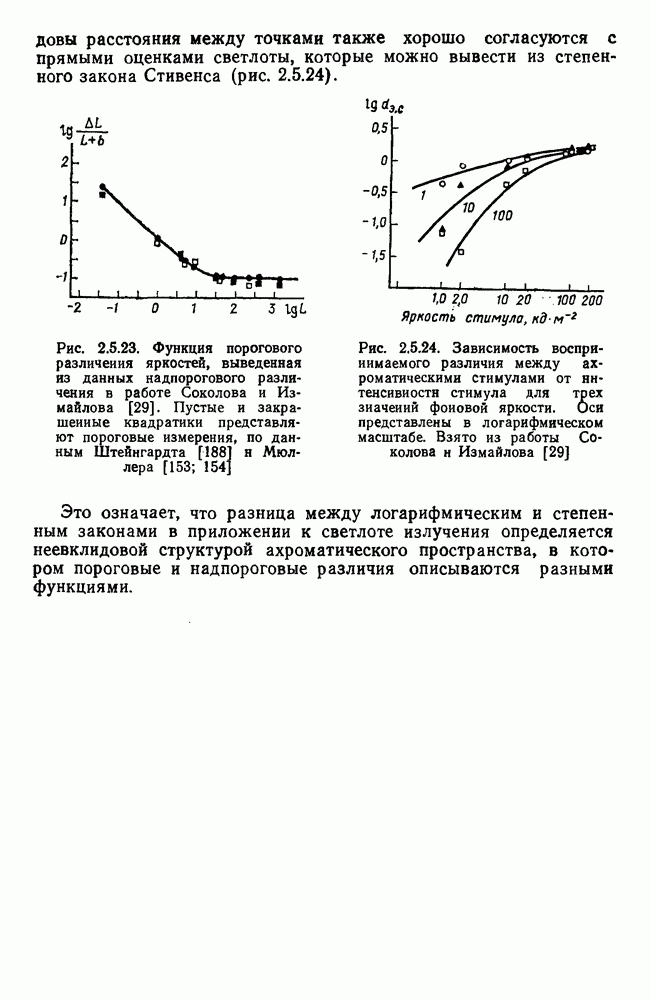
Рис. 2.5.22. Положение ахроматических сигналов разной яркости в двумерном евклидовом пространстве, полученное в работе Соколова и Измайлова [29]. Стимульные характеристики точек приведены в табл. 2.5.8
Анализ матрицы оценок попарных различий между ахроматическими стимулами, меняющимися от очень яркого (яркий диск, окруженный темным кольцом) до черного (темный диск, окруженный ярким кольцом), методом метрического многомерного шкалирования, привел к решению в виде двумерного евклидова пространства.
Вычисленные расстояния между точками коррелировали с исходными оценками различий с коэффициентом 0,98. Сами точки располагались не на всей плоскости, а образовали дугу, занимающую почти половину окружности с 10-процентным разбросом радиусов относительно этой дуги (табл. 2.5.8).
На рис. 2.5.22 показано положение яркостных точек в субъективном ахроматическом пространстве. Нумерация точек соответствует нумерации стимулов в табл. 2.5.8, а их расположение вдоль дуги окружности точно соответствует визуальной яркости этих стимулов. Наиболее темными оказываются стимулы 1, 4 и 7, у них самый яркий окружающей фон при относительно темном
Таблица 2.5.8 (см. скан) Координаты цветовых точек в двумерном евклидовом пространстве и показатели сферичности полученной конфигурации точек (средний радиус, стандартное отклонение радиусов от среднего, коэффициент вариации радиусов)
центральном диске, а наиболее светлыми являются стимулы 18 и 20, у которых, наоборот, наиболее темный фон по сравнению с очень ярким центральным диском. В соответствии с этим они располагаются на противоположных концах дуги.
Расположение ахроматических цветов на дуге окружности, полученное исходя из условия евклидовой метрики различий между стимулами, показывает, что ахроматические различия также характеризуются неаддитивностью, как и хроматические. Как мы уже обсуждали, в этом случае неизбежно должно возникать расхождение между измерениями пороговых различий и надпороговых.
В сферическом пространстве ахроматических цветов, приведенном на рис. 2.5.22, абсолютное значение светлоты определяется горизонтальным углом, отсчитываемым от оси  против часовой стрелки. Величины этого угла для экспериментальных точек хорошо согласуются со значениями яркости, полученными в соответствии с логарифмическим законом Фехнера (рис. 2.5.23). А евклидовы
против часовой стрелки. Величины этого угла для экспериментальных точек хорошо согласуются со значениями яркости, полученными в соответствии с логарифмическим законом Фехнера (рис. 2.5.23). А евклидовы
расстояния между точками также хорошо согласуются с прямыми оценками светлоты, которые можно вывести из степенного закона Стивенса (рис. 2.5.24).

Рис. 2.5.23. Функция порогового различения яркостей, выведенная из данных надпорогового различения в работе Соколова и Измайлова [29]. Пустые и закрашенные квадратики представляют пороговые измерения, по данным Штейнгардта [1881 и Мюллера [153; 154]

Рис. 2.5.24. Зависимость воспринимаемого различия между ахроматическими стимулами от интенсивности стимула для трех значений фоновой яркости. Оси представлены в логарифмическом масштабе. Взято из работы Соколова и Измайлова [29]
Это означает, что разница между логарифмическим и степенным законами в приложении к светлоте излучения определяется неевклидовой структурой ахроматического пространства, в котором пороговые и надпороговые различия описываются разными функциями.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
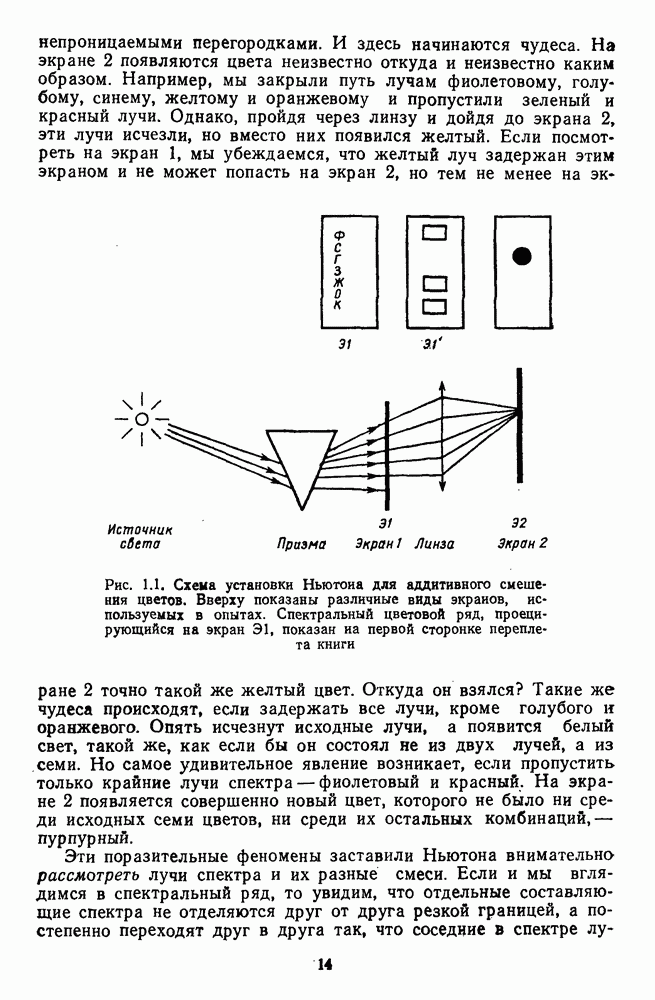
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
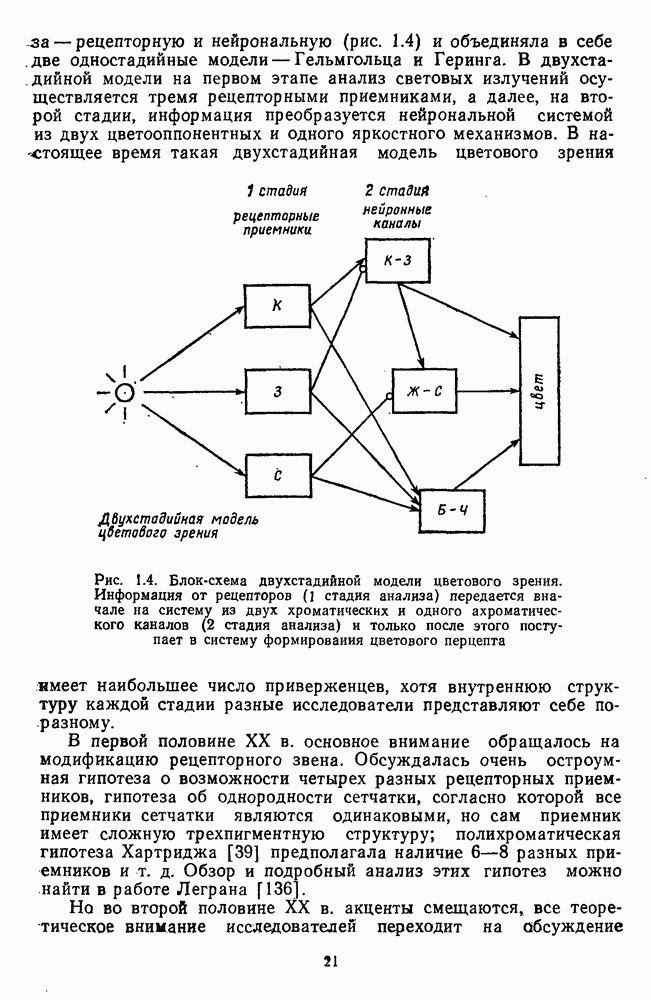
- 1.8. Двухстадийная теория цветового зрения
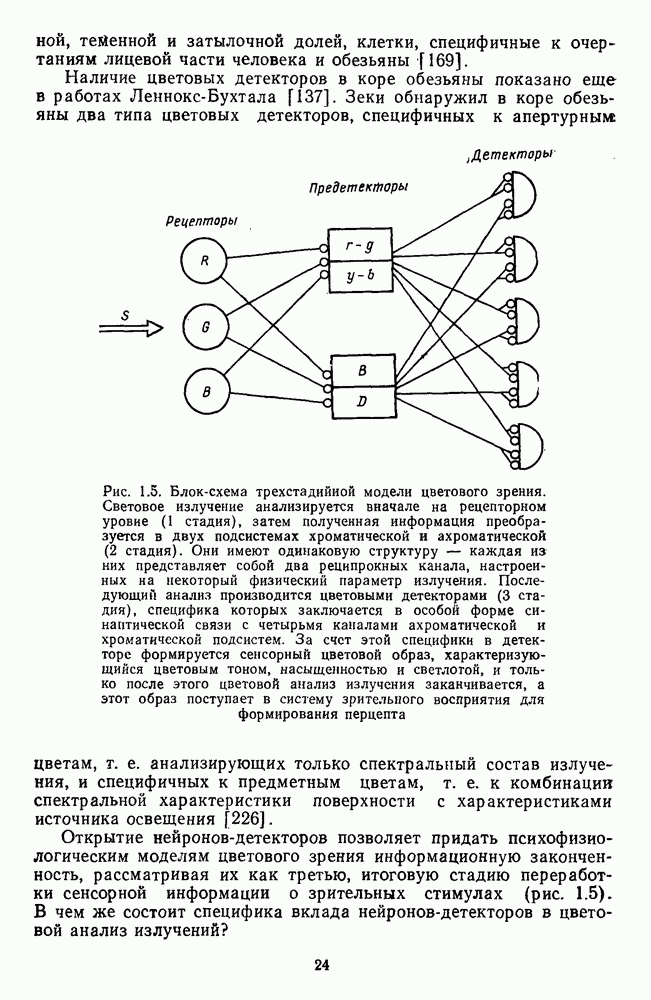
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
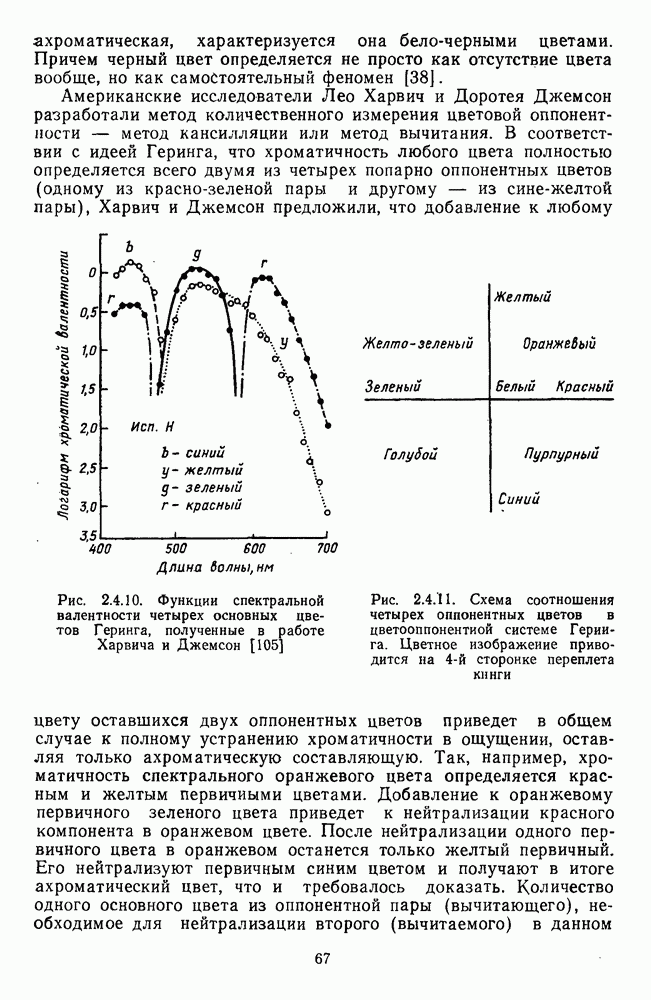
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
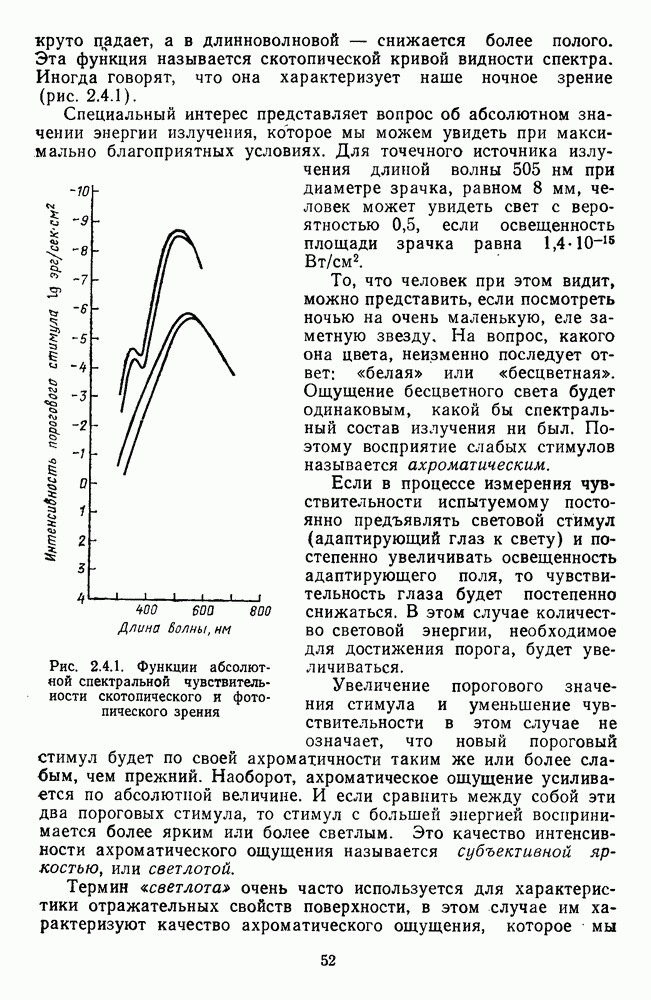
- 2.4.1. Спектральная чувствительность зрения
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
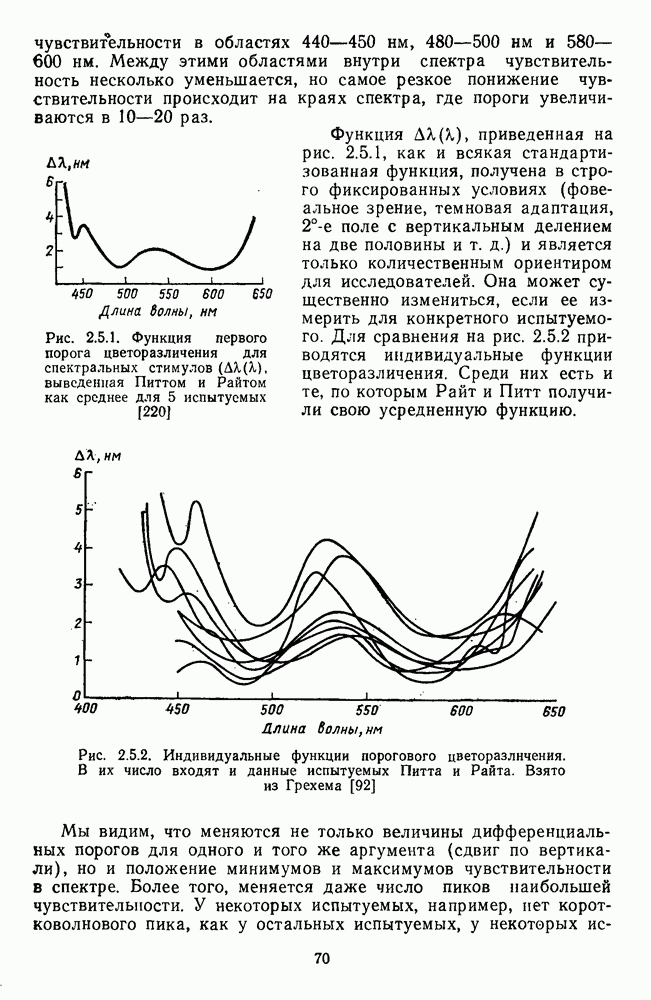
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
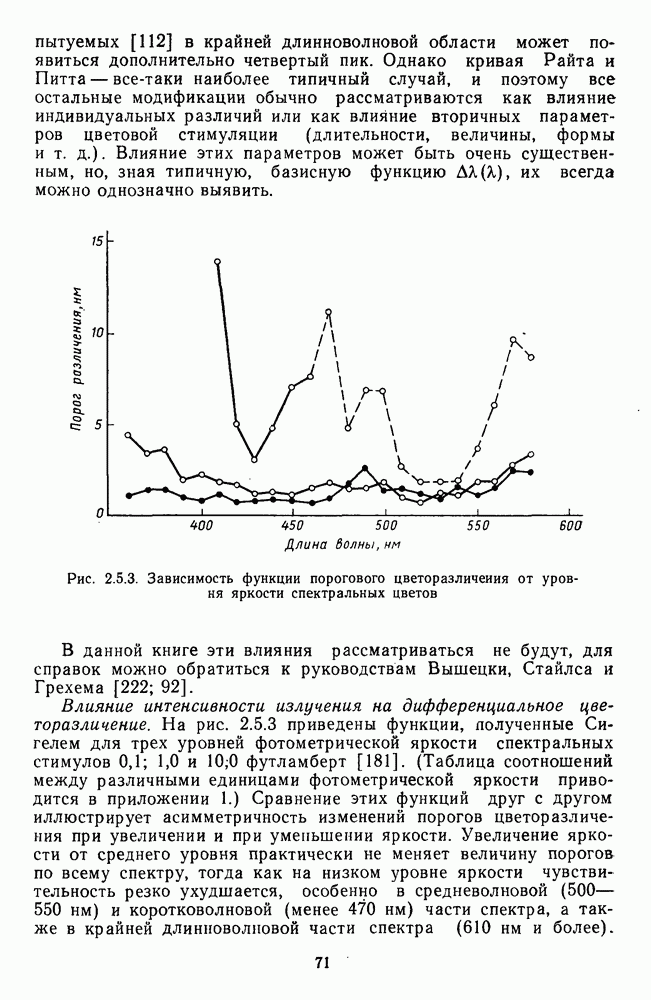
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
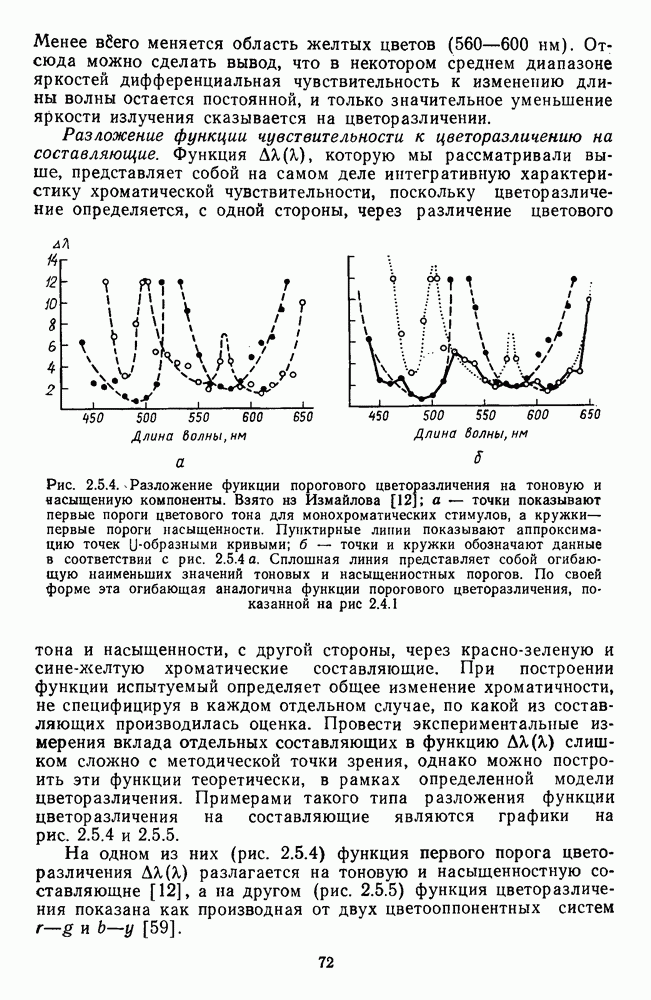
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
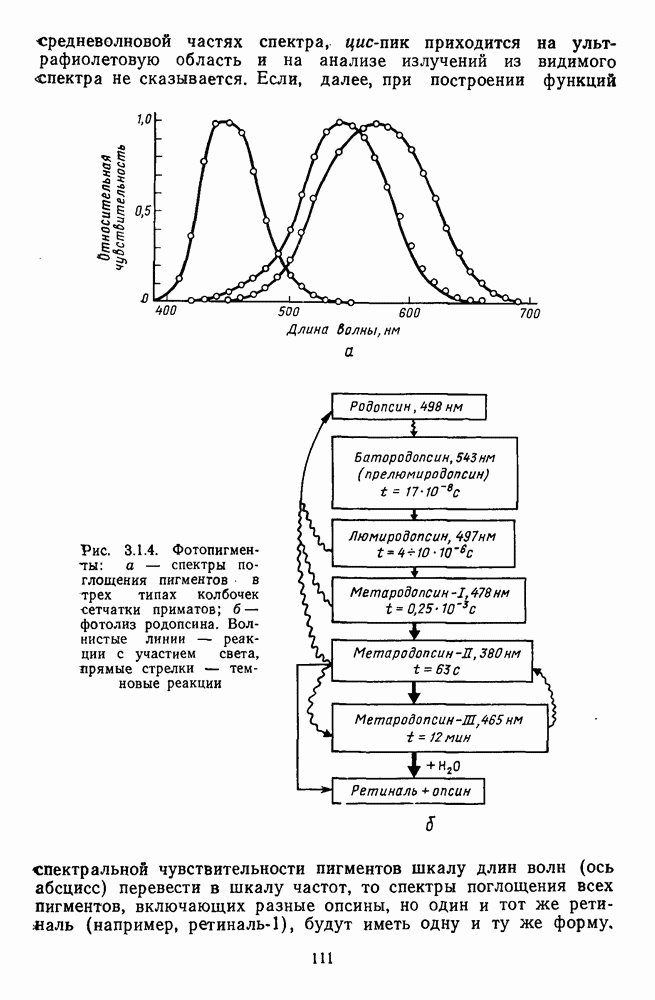
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
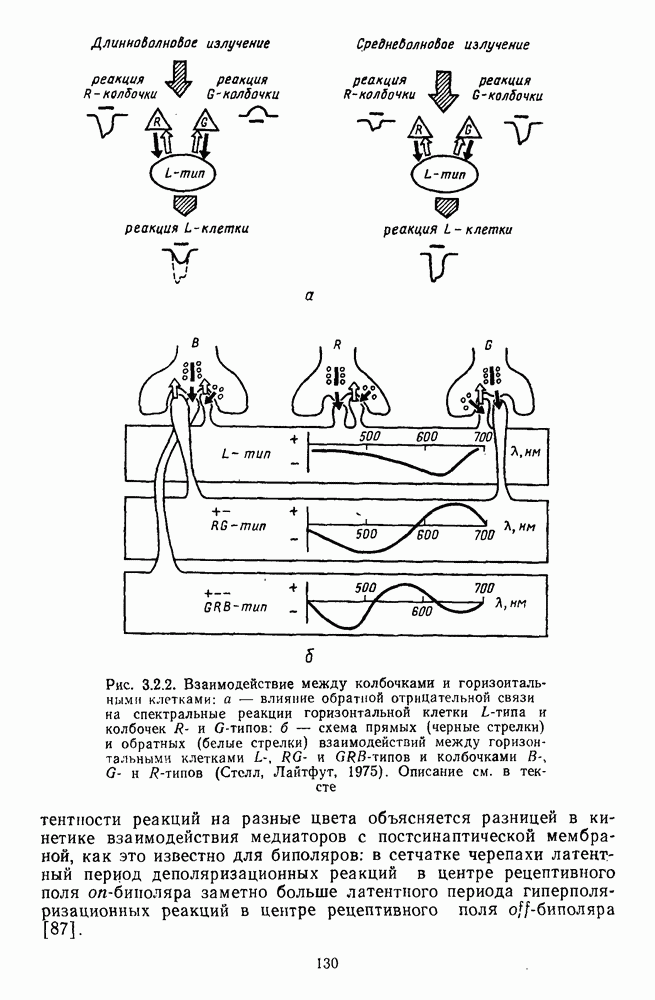
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
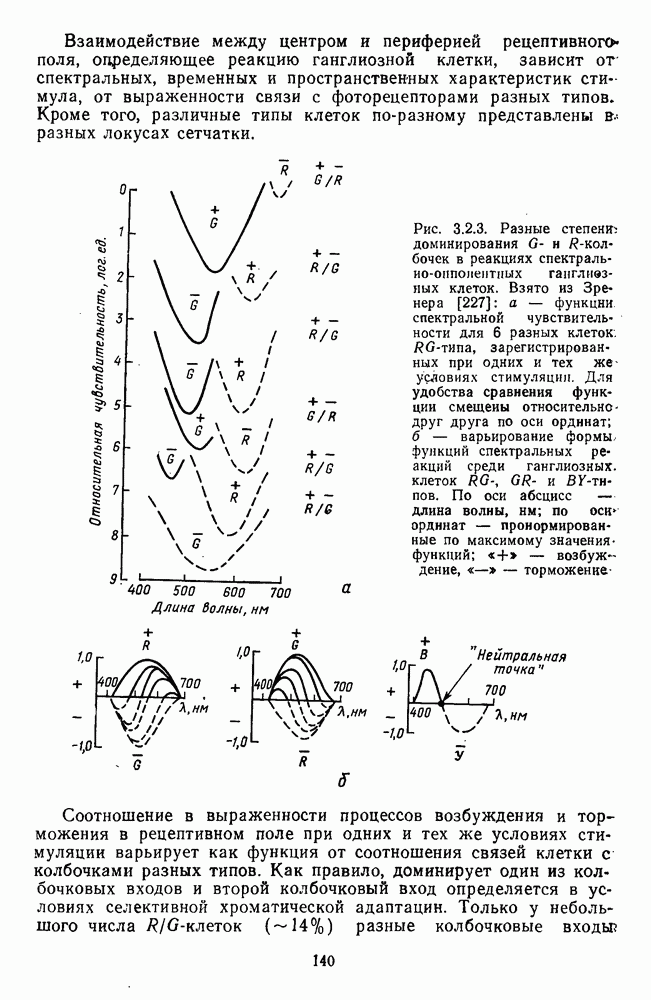
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
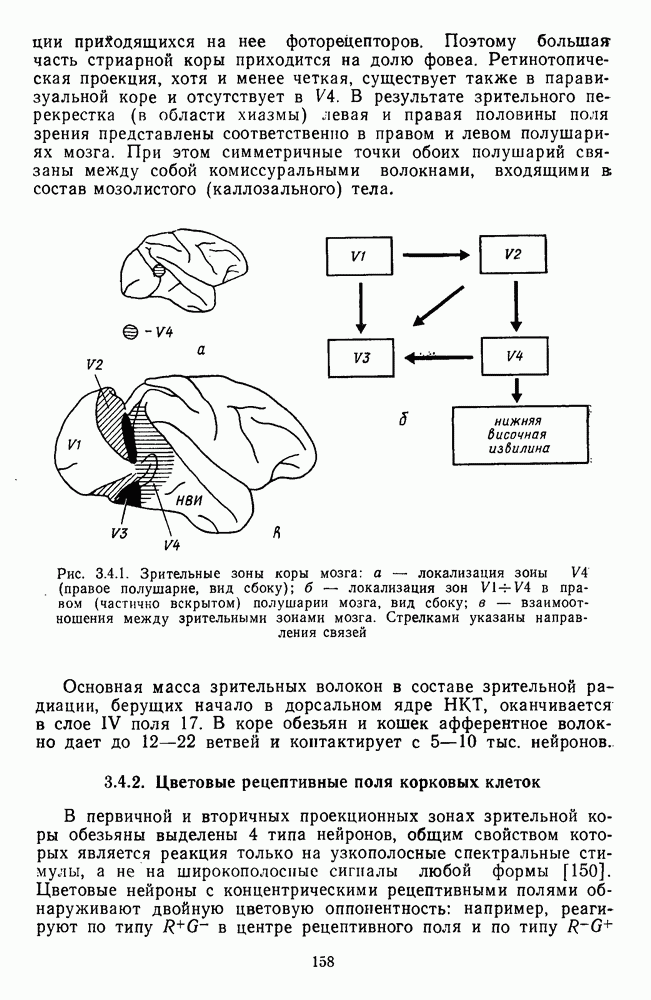
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
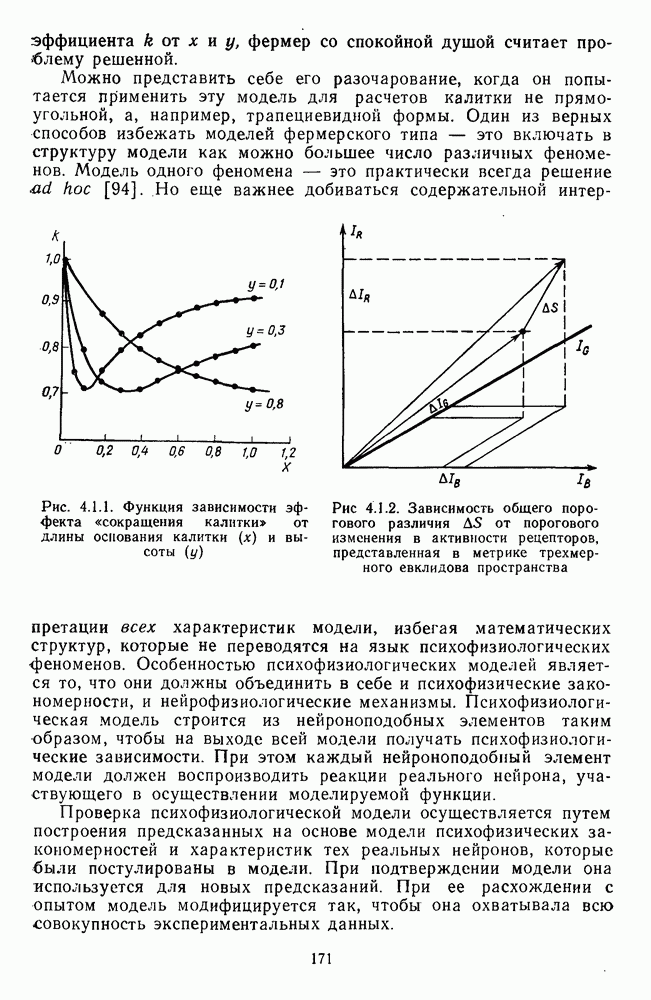
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
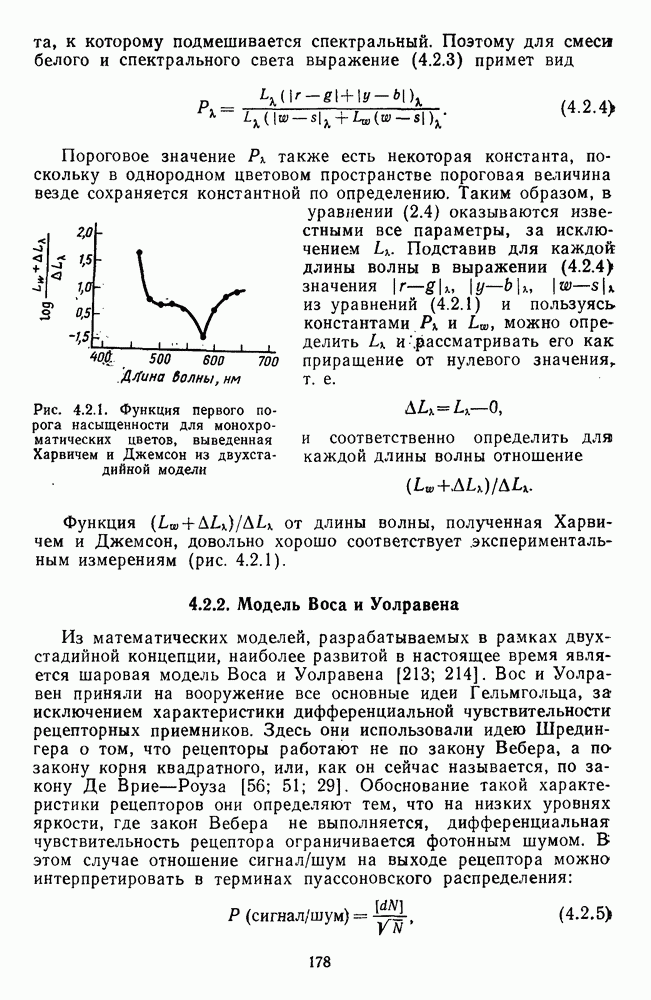
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
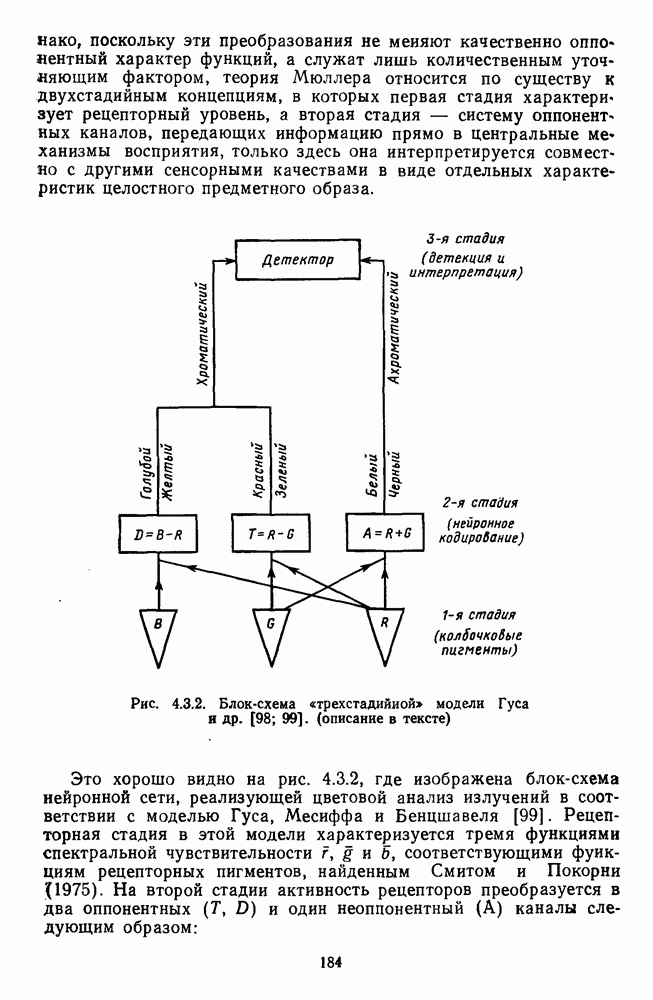
- 4.3.2. Модель Гуса
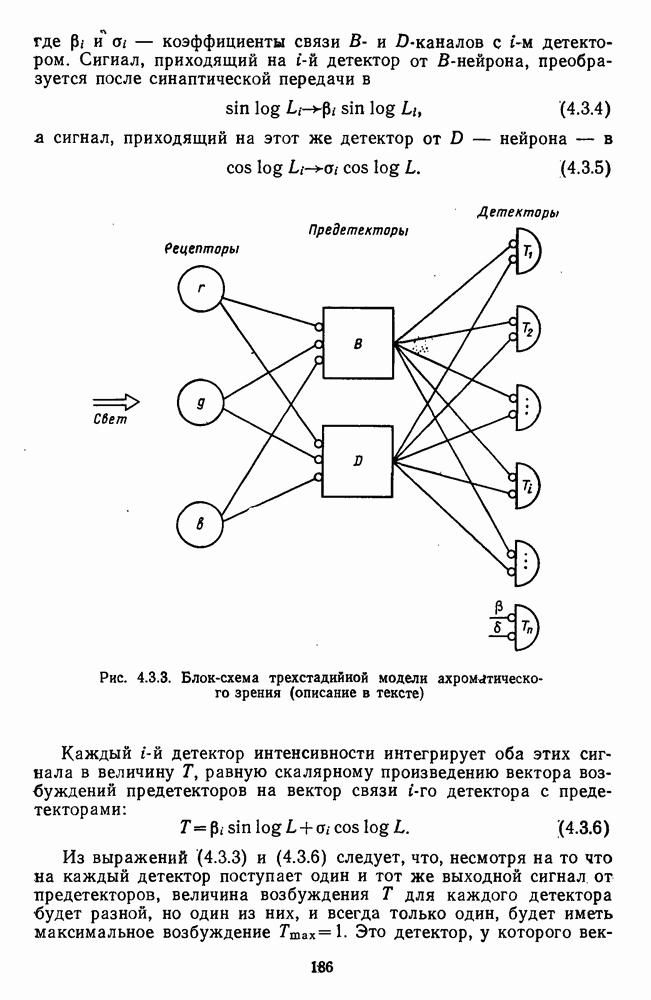
- 4.3.3. Трехстадийная модель ахроматического зрения
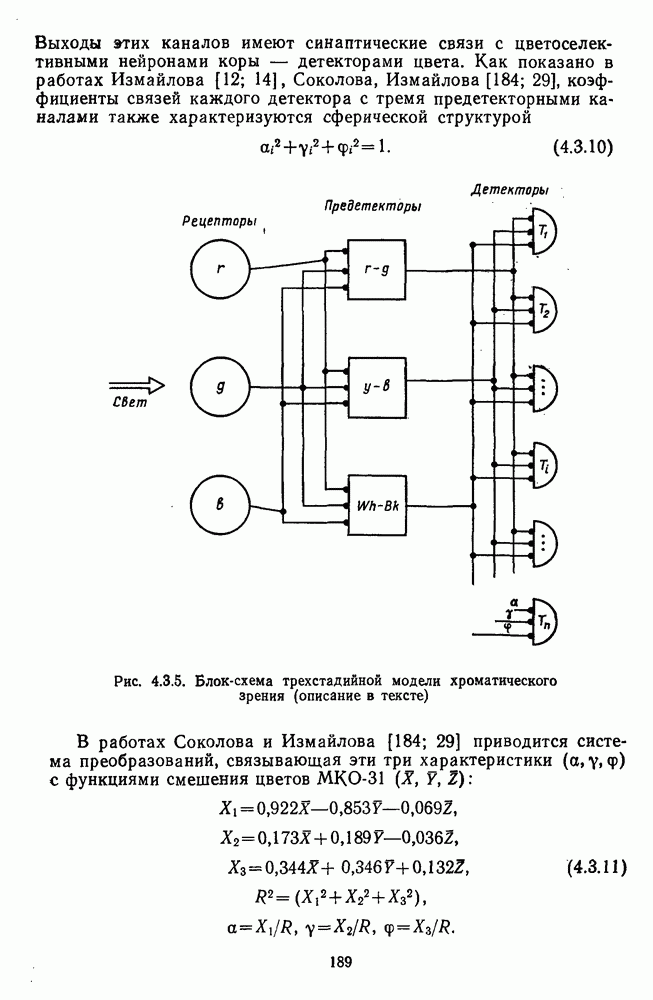
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА