| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.1.3. Модель Стайлса
Последняя серьезная попытка реанимации одностадийной трехкомпонентной теории была сделана Стайлсом [194]. Стайлс основывался на большом массиве измерений, проведенных методом двухцветного порога [193; 222]. По результатам этих измерений Стайлс вывел свои функции спектральной чувствительности рецепторов сетчатки. Это привело его к выводу, что вклад каждого приемника в цветоразличение не одинаков, он рассчитал пропорции вкладов приемников и изменил выражение (4.1.3) следующим образом:

где 
Функция  по Стайлсу характеризуется выражением
по Стайлсу характеризуется выражением

Тогда общее выражение для цветового различия будет иметь вид

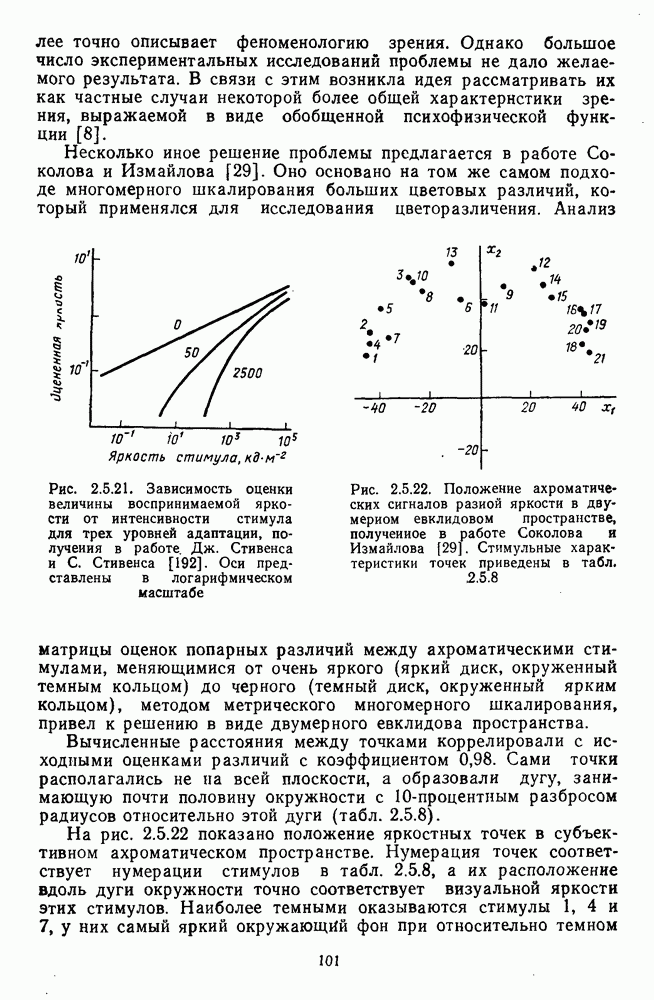
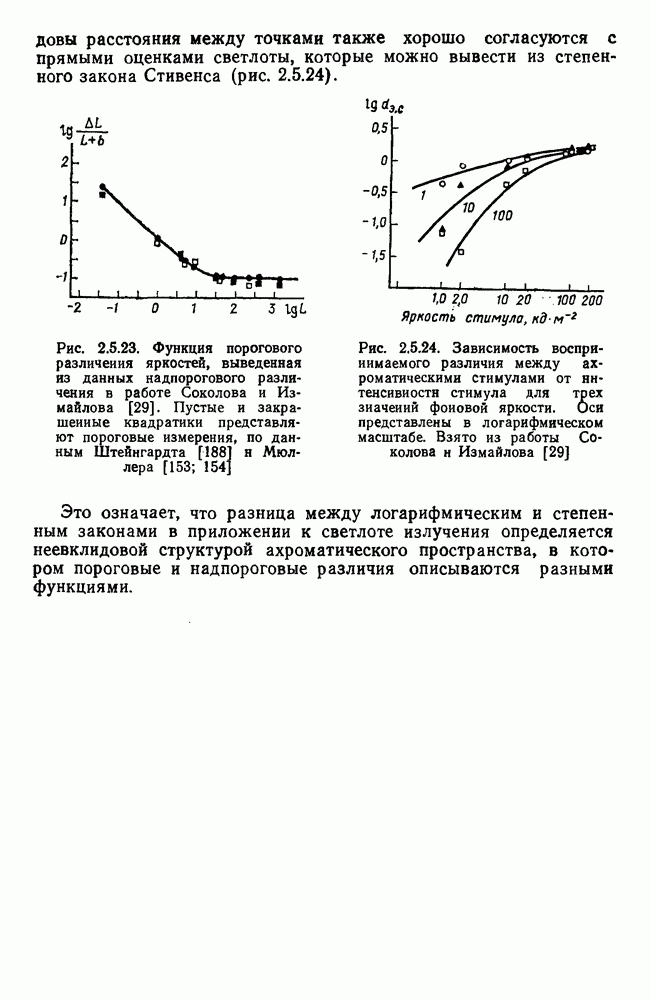
Из модели Стайлса оказалось возможным вывести значительно больше цветовых функций, чем из всех предыдущих моделей, построенных в рамках трехкомпонентной теории. В частности, Стайлс вывел функцию чувствительности к яркости для фотопического зрения, которая очень хорошо согласовывалась с экспериментальной функцией, полученной методом последовательного сдвига по спектру (рис. 4.1.4); далее, Стайлс показал, что функция цветоразличения  выведенная из его модели, также хорошо согласуется с экспериментальными данными. Некоторые проблемы возникли у Стайлса при построении на основе его модели однородного хроматического пространства. Построение такого пространства Стайлс основывал на определении метрических коэффициентов для локусов порогового различения, аналогичных эллипсам Мак Адама. В результате Стайлс получил поверхность с отрицательной кривизной, причем кривизна ее была максимальной для пурпурных цветов (на хроматической диаграмме МКО-31 это область с координатами
выведенная из его модели, также хорошо согласуется с экспериментальными данными. Некоторые проблемы возникли у Стайлса при построении на основе его модели однородного хроматического пространства. Построение такого пространства Стайлс основывал на определении метрических коэффициентов для локусов порогового различения, аналогичных эллипсам Мак Адама. В результате Стайлс получил поверхность с отрицательной кривизной, причем кривизна ее была максимальной для пурпурных цветов (на хроматической диаграмме МКО-31 это область с координатами  а от этой области во все стороны монотонно убывала. Это означало су
а от этой области во все стороны монотонно убывала. Это означало су
существенное расхождение с результатами Мак Адама. Кривизна поверхности по эллипсам Мак Адама получается положительной на большей центральной части хроматической диаграммы и только по краям диаграммы имеет отрицательные значения [139; 182]. Необходимо учитывать, однако, что представленные на хроматической диаграмме МКО-31 расчеты Стайлса качественно хорошо согласуются с экспериментальными данными Мак Адама, расхождения метрических коэффициентов нельзя считать принципиальными, поскольку уже 15%-ная ошибка измерений (при цветовом подравнивании ошибка может достигать и 30%) не позволяет оценить достаточно надежно кривизну поверхности по данным локального цветоразличения [85].
Попытки Стайлса расширить класс цветовых функций, выведенных из модели, оказались неудачными [222], и дальнейшего развития модель Стайлса уже не имела, На наш взгляд, причина отхода модели Стайлса на второй план заключалась не столько в отдельных недостатках самой модели (модель Стайлса как раз отличается большими возможностями для Дальнейшего развития по отдельным характеристикам), сколько в общем изменении отношения к одностадийной концепции цветового зрения. Именно в 50-е и 60-е гг. в цветовой науке произошел коренной переход от одностадийной к двухстадийной концепции цветового зрения.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
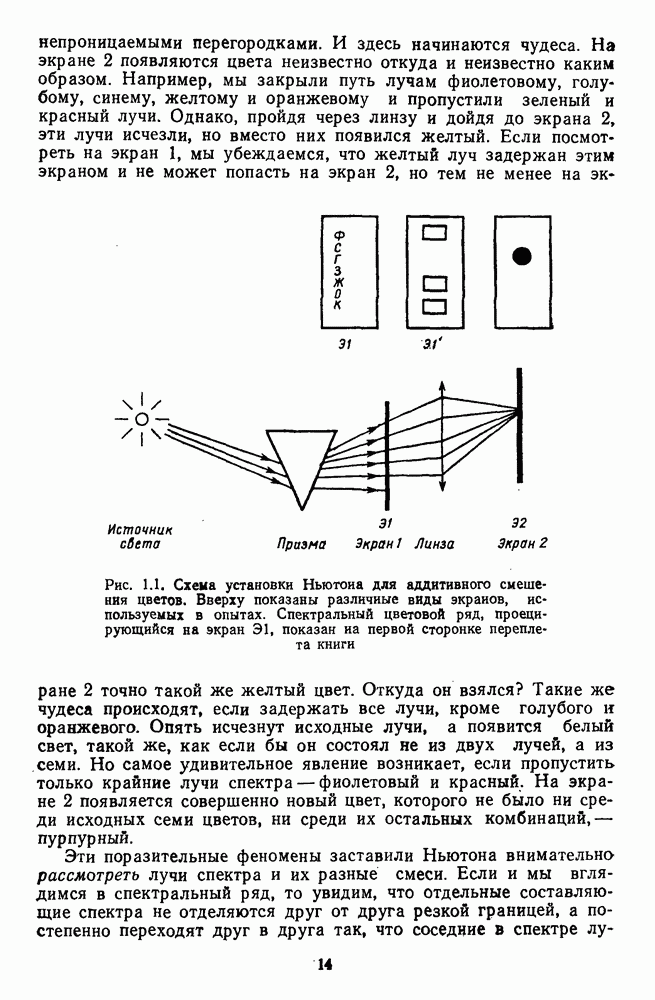
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
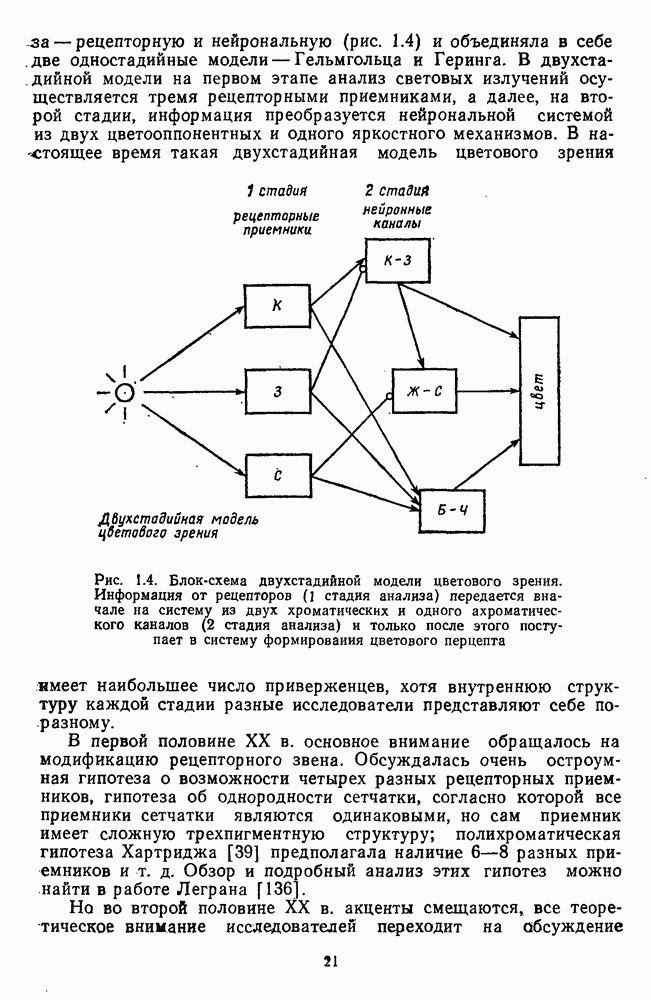
- 1.8. Двухстадийная теория цветового зрения
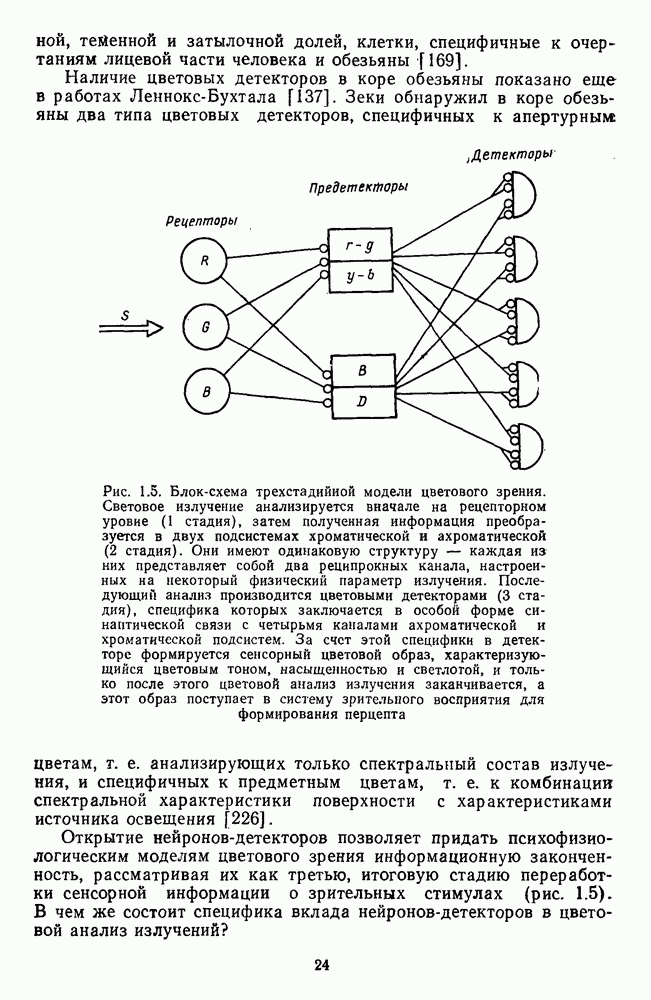
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
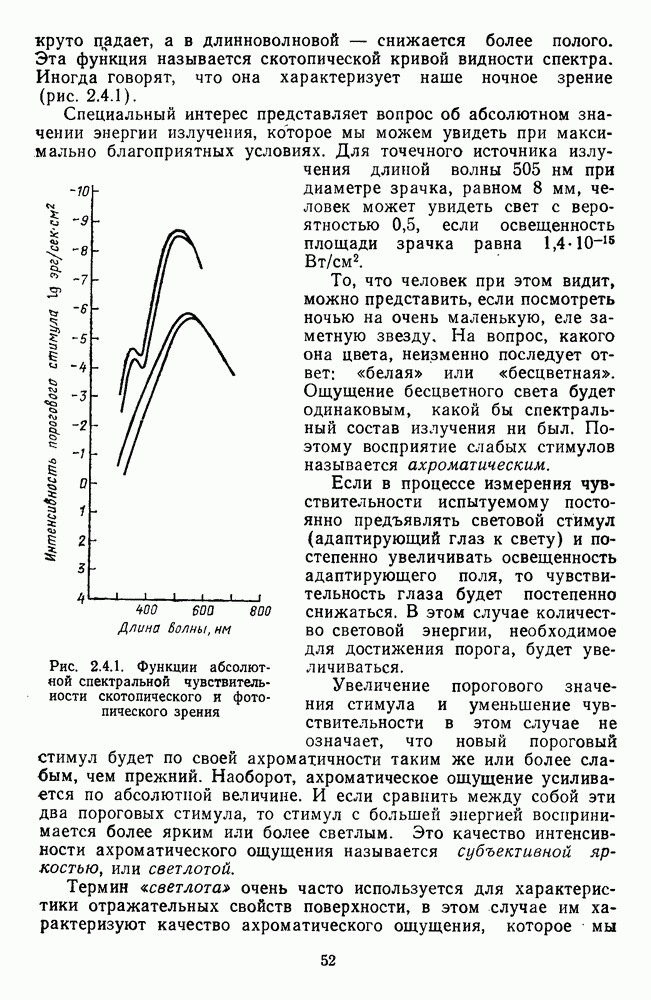
- 2.4.1. Спектральная чувствительность зрения
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
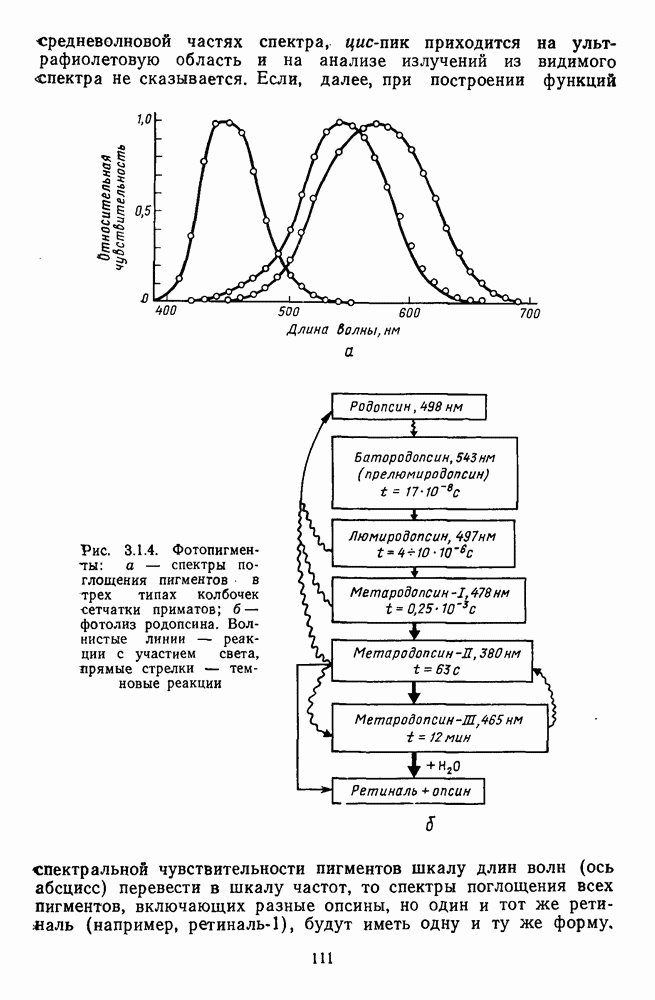
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
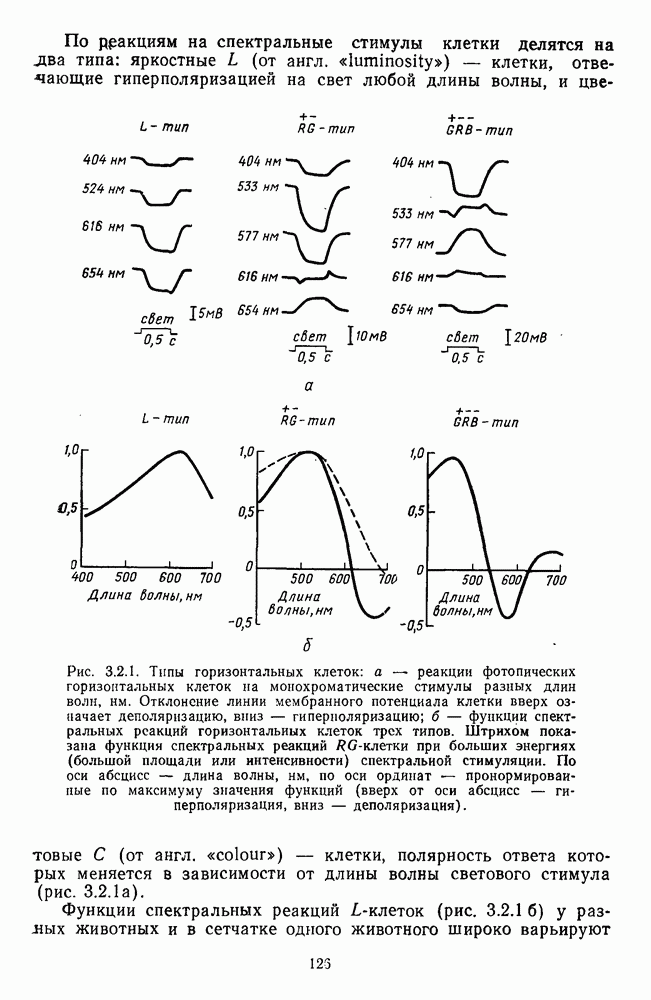
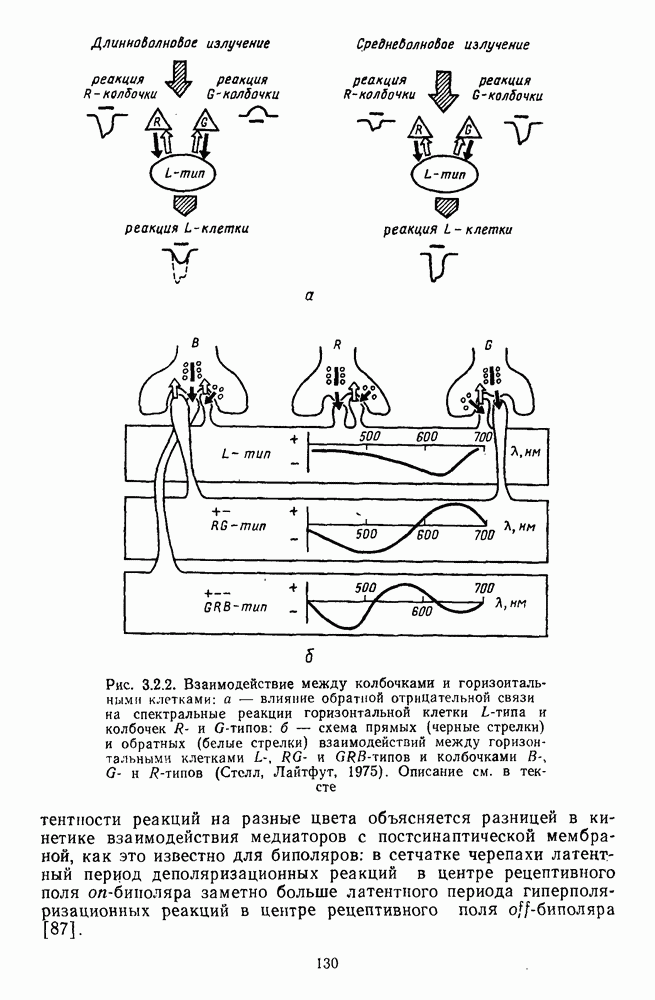
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
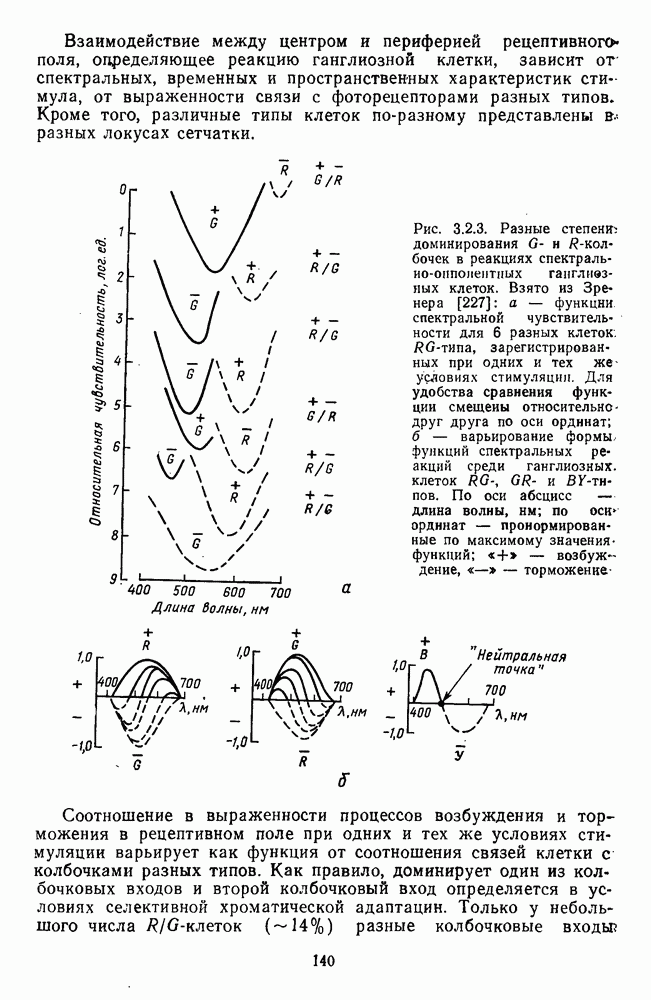
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
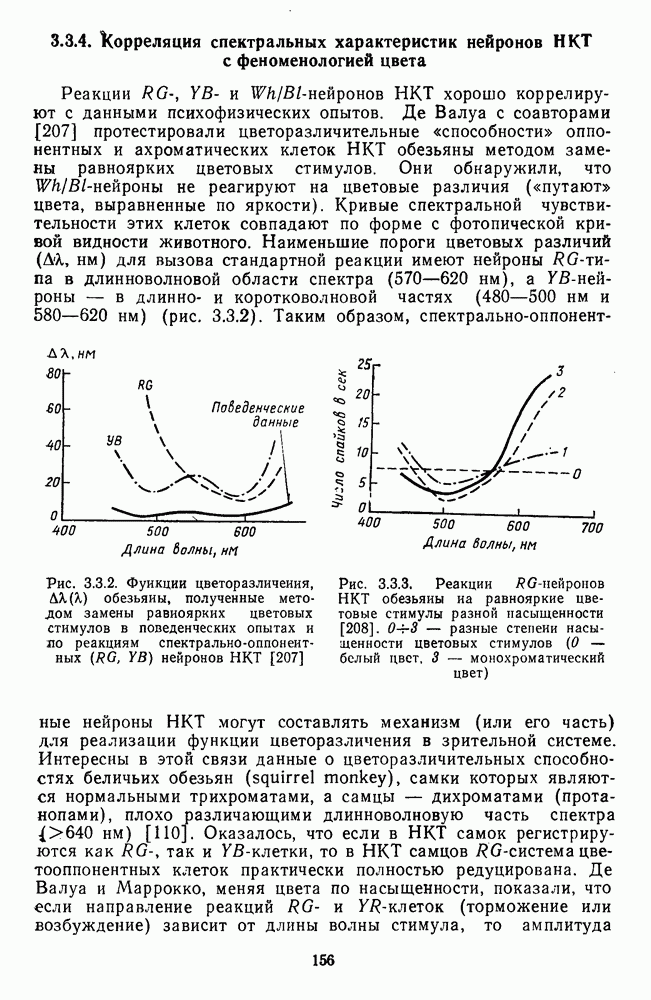
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
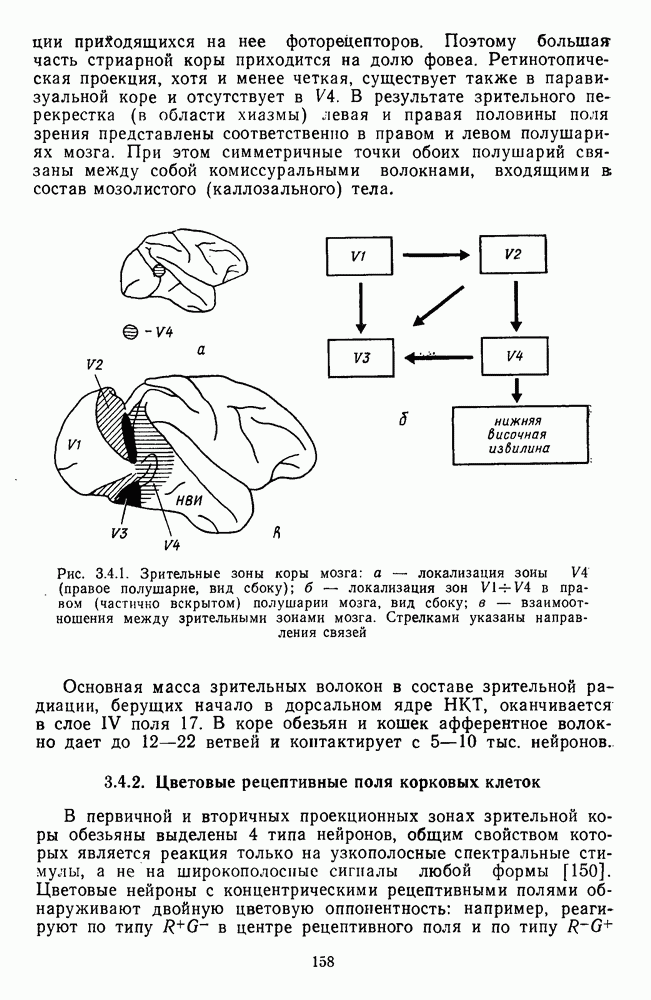
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
- 4.3.2. Модель Гуса
- 4.3.3. Трехстадийная модель ахроматического зрения
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА