| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2.2. Модель Воса и Уолравена
Из математических моделей, разрабатываемых в рамках двухстадийной концепции, наиболее развитой в настоящее время является шаровая модель Воса и Уолравена [213; 214]. Вос и Уолравен приняли на вооружение все основные идеи Гельмгольца, за исключением характеристики дифференциальной чувствительности рецепторных приемников. Здесь они использовали идею Шредингера о том, что рецепторы работают не по закону Вебера, а по закону корня квадратного, или, как он сейчас называется, по закону Де Врие—Роуза [56; 51; 29]. Обоснование такой характеристики рецепторов они определяют тем, что на низких уровнях яркости, где закон Вебера не выполняется, дифференциальная чувствительность рецептора ограничивается фотонным шумом. В этом случае отношение сигнал/шум на выходе рецептора можно интерпретировать в терминах пуассоновского распределения:

 среднее число поглощенных квантов энергии за единицу времени.
среднее число поглощенных квантов энергии за единицу времени.
Оставляя в силе положение Гельмгольца, что общие выходные характеристики приемников сетчатки должны быть положительны  определяться квадратичной формой,
определяться квадратичной формой,  и Уолравен определяют первую (рецепторную) стадию следующим образом:
и Уолравен определяют первую (рецепторную) стадию следующим образом:

где  — выходные реакции рецепторов.
— выходные реакции рецепторов.
Выражение (4.2.6), представленное в виде системы взаимо-ортогональных координат  и В, характеризует цветовой стимул как точку в трехмерном евклидовом пространстве с осями
и В, характеризует цветовой стимул как точку в трехмерном евклидовом пространстве с осями  Длина радиуса-вектора цветовой точки в таком лространстве, определенная как
Длина радиуса-вектора цветовой точки в таком лространстве, определенная как

 характеризовать яркость цвета как сумму реакций рецепторов
характеризовать яркость цвета как сумму реакций рецепторов

В этом случае цветовое пространство Воса и Уолравена представляет собой шар в трехмерном евклидовом пространстве, где декартова система координат интерпретируется как активность трех рецепторов сетчатки, а длина радиуса-вектора цветовой точки внутри шара представляет яркость цветового стимула. Равнояркие цвета располагаются в этом пространстве на поверхности шара фиксированного радиуса.
Однако различение сигналов связано не с первой стадией анализа, а со второй. Вторую стадию анализа представляют один яркостный (неоппонентный) канал Т (уравнение 4.2.8) и два хроматических (оппонентных) канала  и
и  Хроматические каналы так же, как и яркостный, определяются из выходных реакций рецепторов:
Хроматические каналы так же, как и яркостный, определяются из выходных реакций рецепторов:

Цветовое различие определяется работой этих трех каналов  и
и  следующим образом:
следующим образом:

В уравнении (4.2.10) параметры  характеризуют фактор неопределенности стимула, а константы
характеризуют фактор неопределенности стимула, а константы  определяют вес каждого из каналов на второй стадии в цветоразличении.
определяют вес каждого из каналов на второй стадии в цветоразличении.
В шаровой модели Воса и Уолравена оппонентные каналы  и
и  представлены широтой и долготой так, что каждый стимул,
представлены широтой и долготой так, что каждый стимул,
представленный точкой шара, может быть задан как в системе декартовых координат  и В, так и в системе полярных координат
и В, так и в системе полярных координат  и Т (рис. 4.2.2).
и Т (рис. 4.2.2).
С помощью основных уравнений (4.2.6; 4.2.10) Вос и Уолравен смогли вывести целый ряд цветовых функций для разных уровней яркости и для разных типов цветового зрения (трихроматического и дихроматического). Хотя количественное совпадение теоретических и экспериментальных функций не всегда было одинаково хорошим, качественно теоретические функции полностью соответствовали экспериментальным.

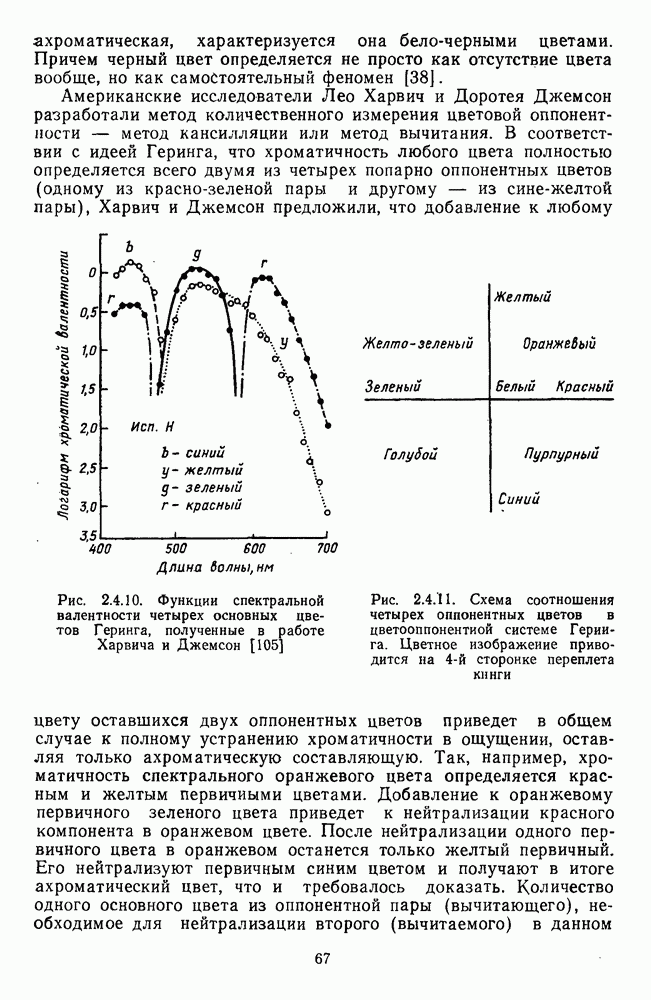
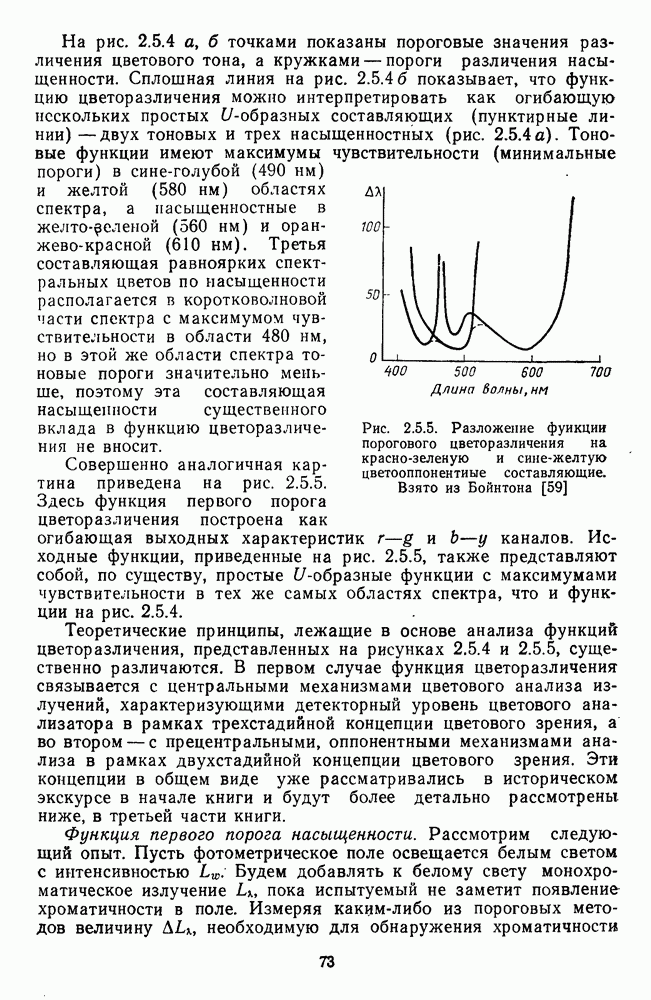
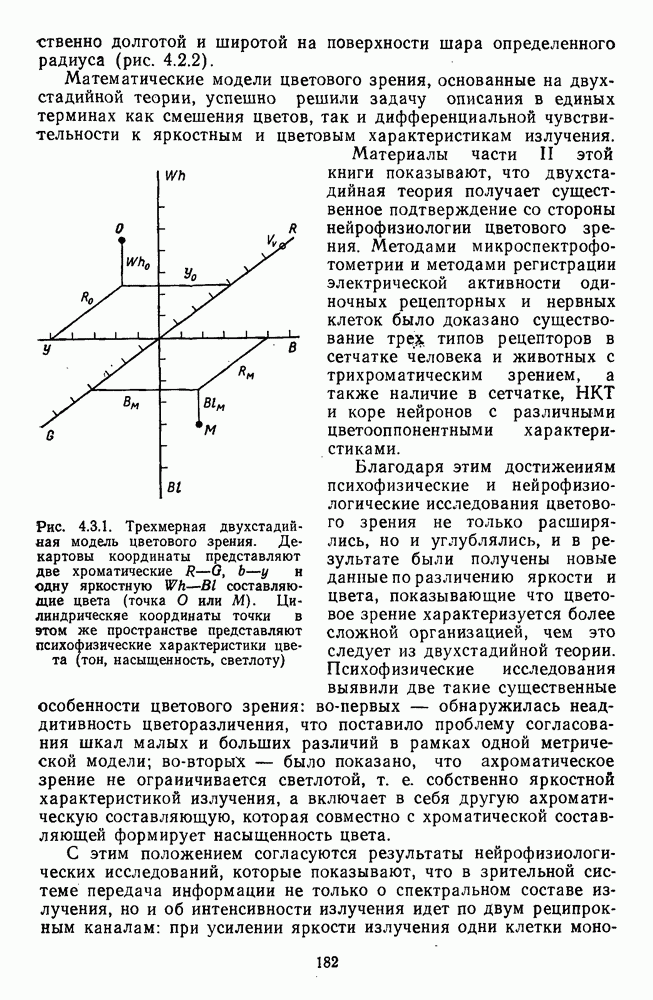
Рис. 4.2.2. Шаровая модель Воса и Уолравена. Три декартовы координаты представляют три рецепторных механизма, а три шаровые координаты — красно-зеленую, сине-желтую и яркостную характеристики. Взято из Воса и Уолравена [213; 214]

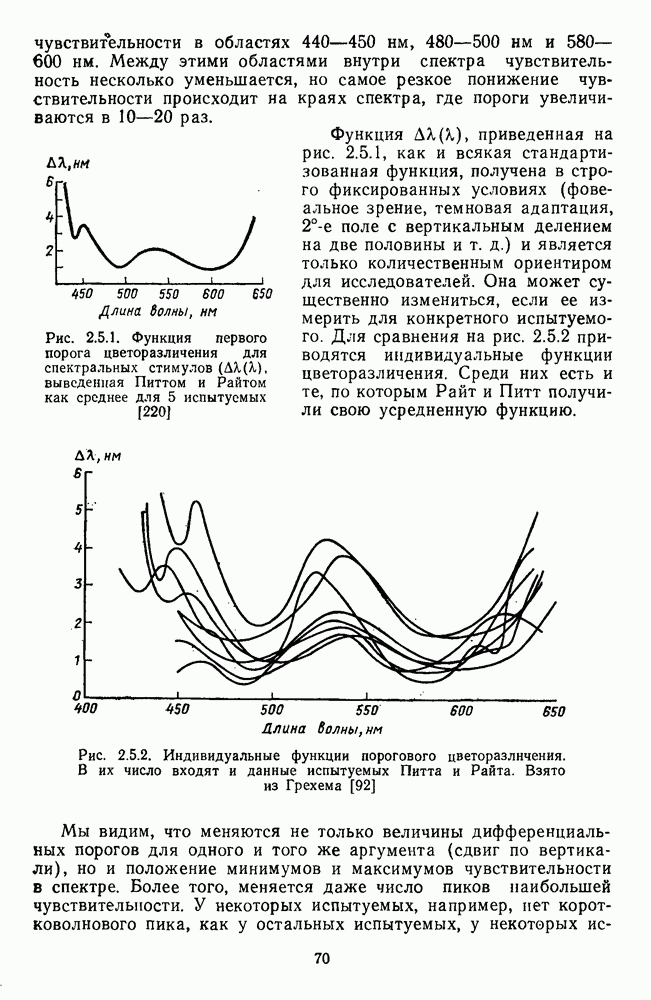
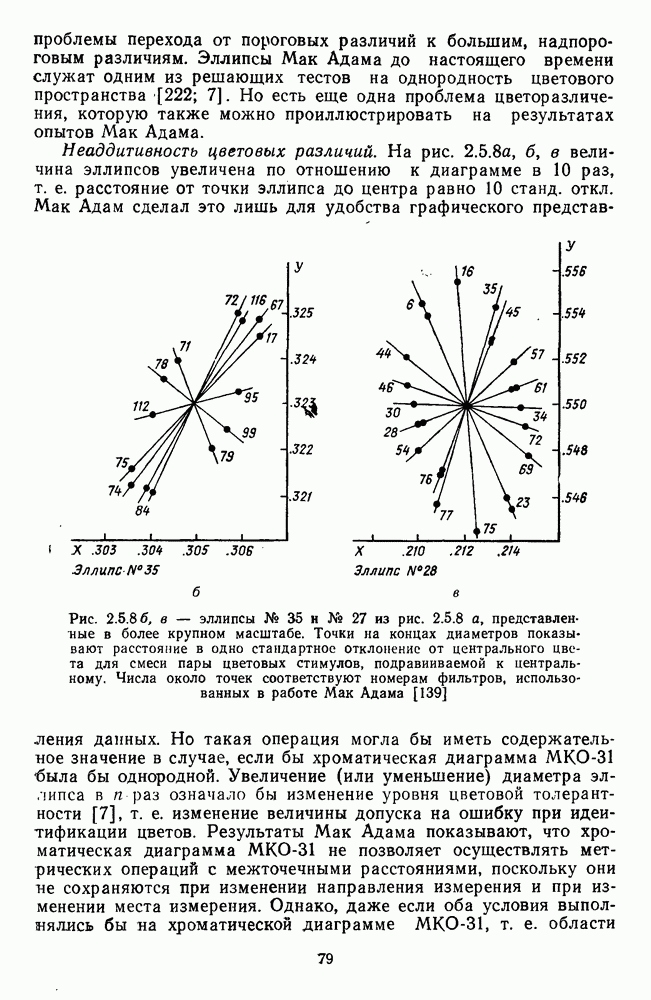
Рис. 4.2.3. Функции цветоразличения для низкого, среднего и высокого уровней яркости спектральных цветов, выведенные Восом и Уолравеном из двухстадийной модели. Взято из Воса и Уолравена [213; 214]
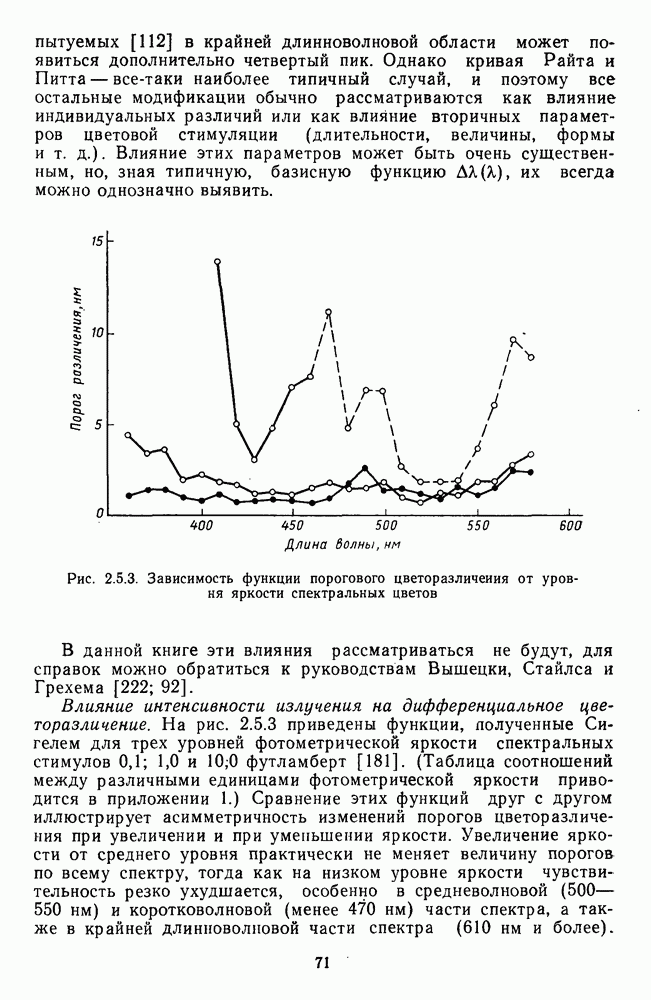
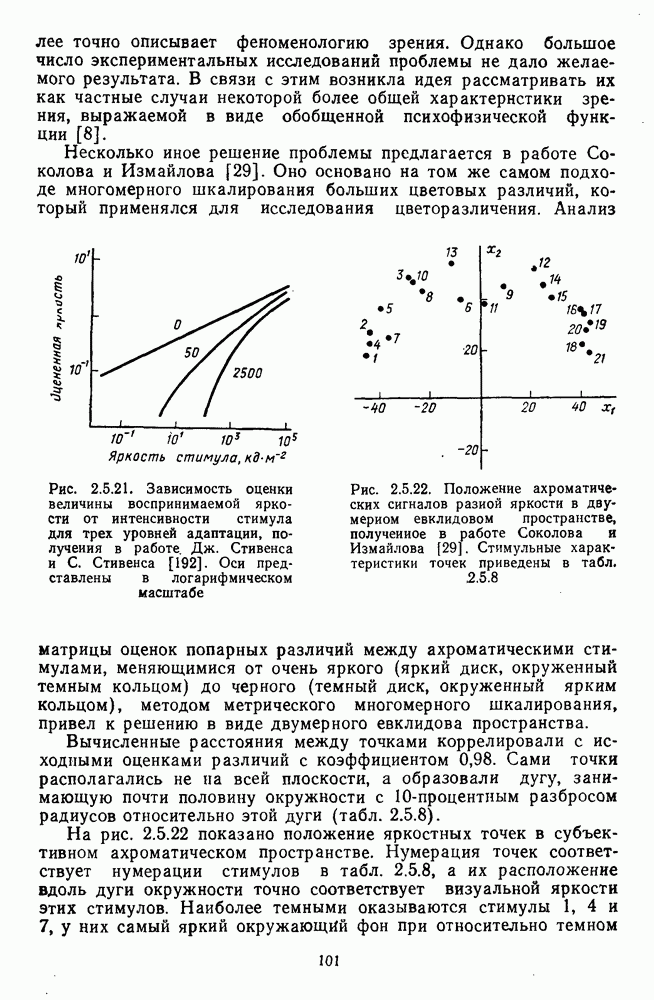
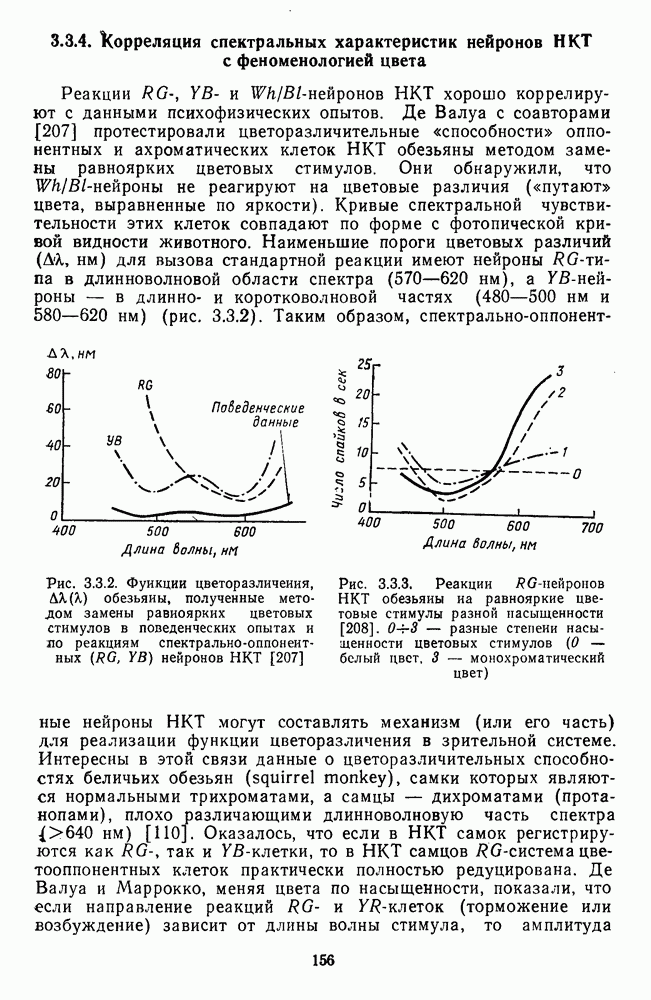
В качестве примера на рис. 4.2.3 приведены функции цветоразличения  для трех уровней яркости: низкого, среднего и высокого. Их можно сравнить с рис. 2.5.3, на котором приводятся аналогичные данные Сигеля [181].
для трех уровней яркости: низкого, среднего и высокого. Их можно сравнить с рис. 2.5.3, на котором приводятся аналогичные данные Сигеля [181].
Вывод цветовых функций с учетом разных уровней яркости в модели Воса и Уолравена является существенным продвижением в разработке двухстадийной концепции, однако отсутствие содержательной интерпретации коэффициентов в уравнении (4.2.10) (как и в примере с моделью Харвича и Джемсон) дает слишком много степеней свободы модели и тем самым ограничивает ее психофизиологический смысл.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
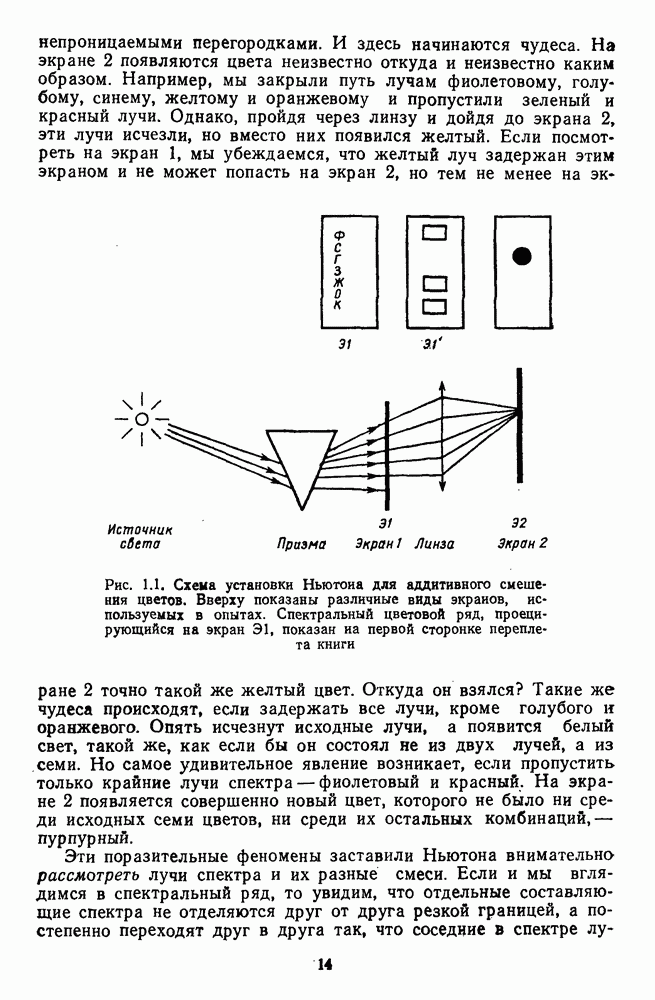
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
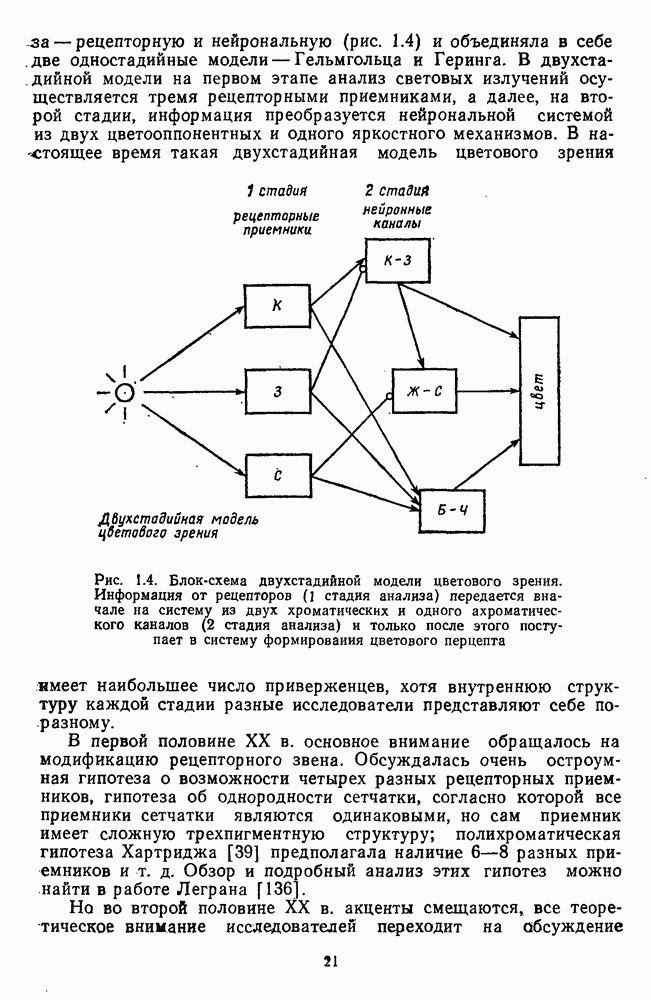
- 1.8. Двухстадийная теория цветового зрения
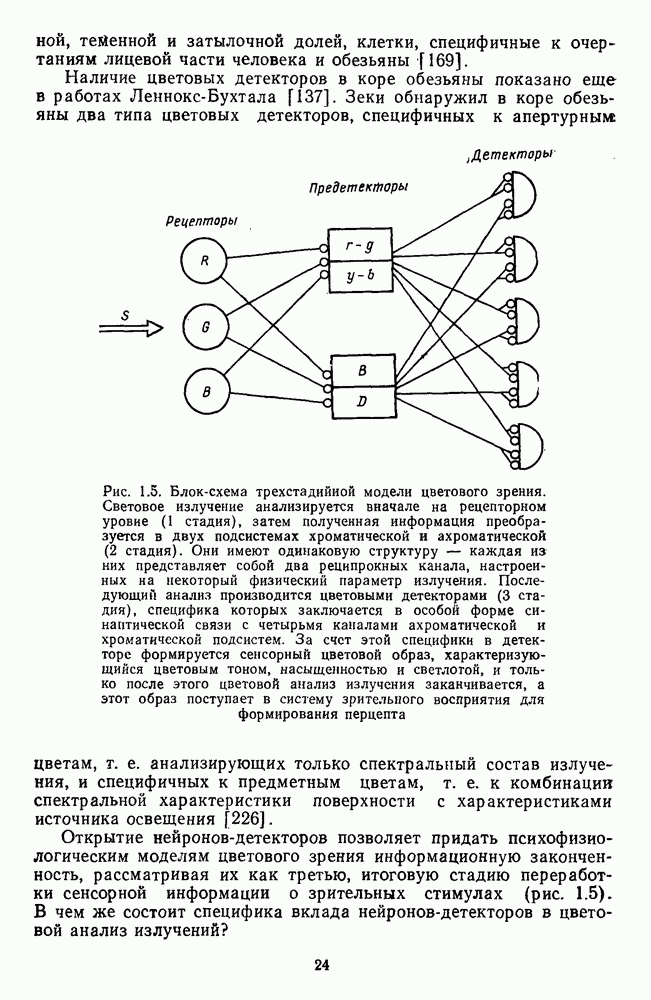
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
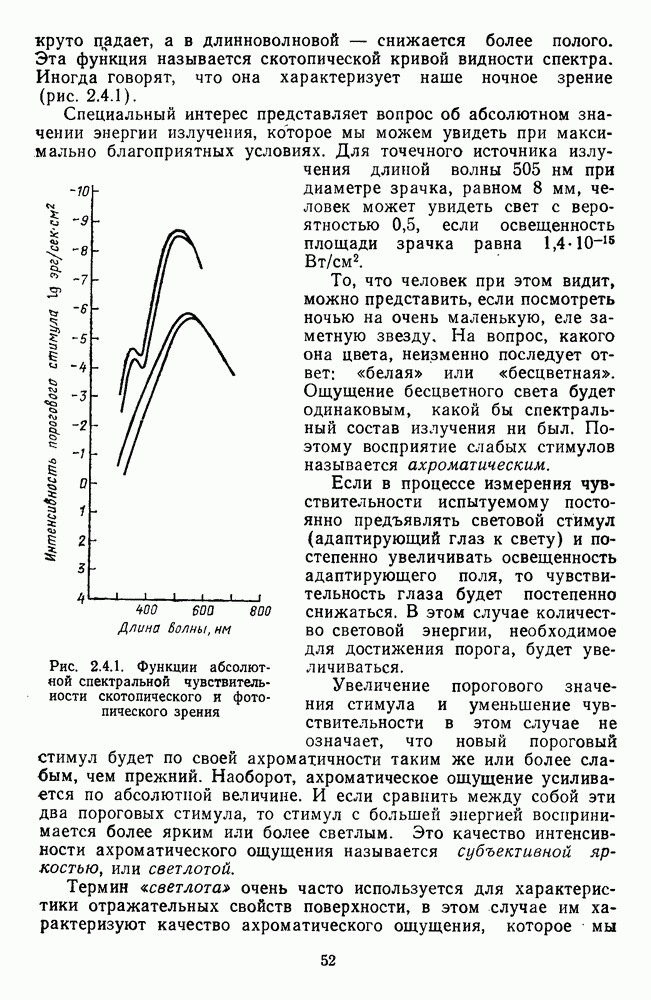
- 2.4.1. Спектральная чувствительность зрения
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
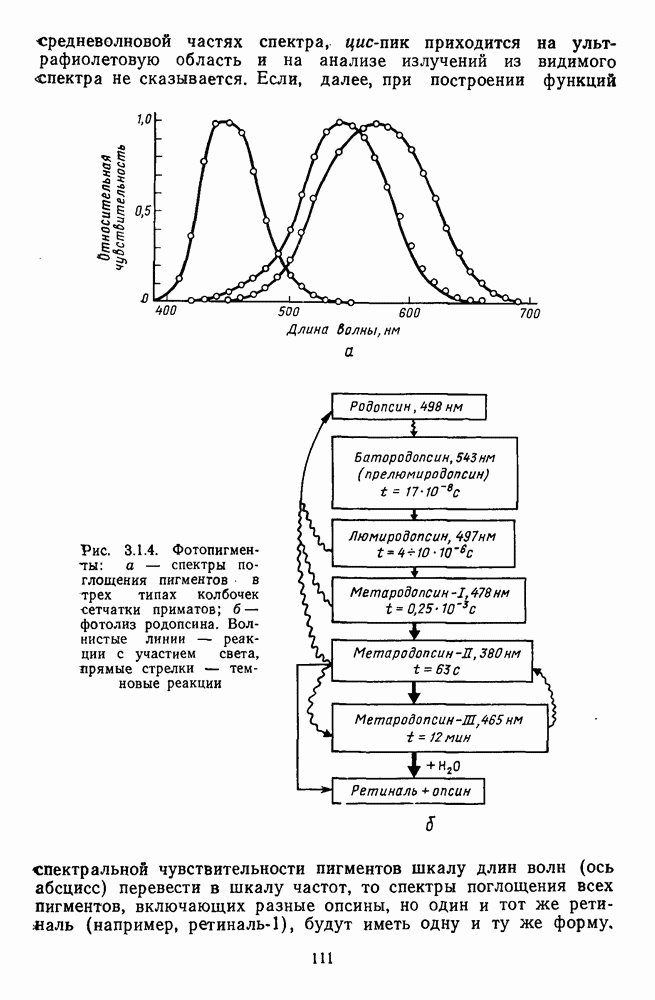
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
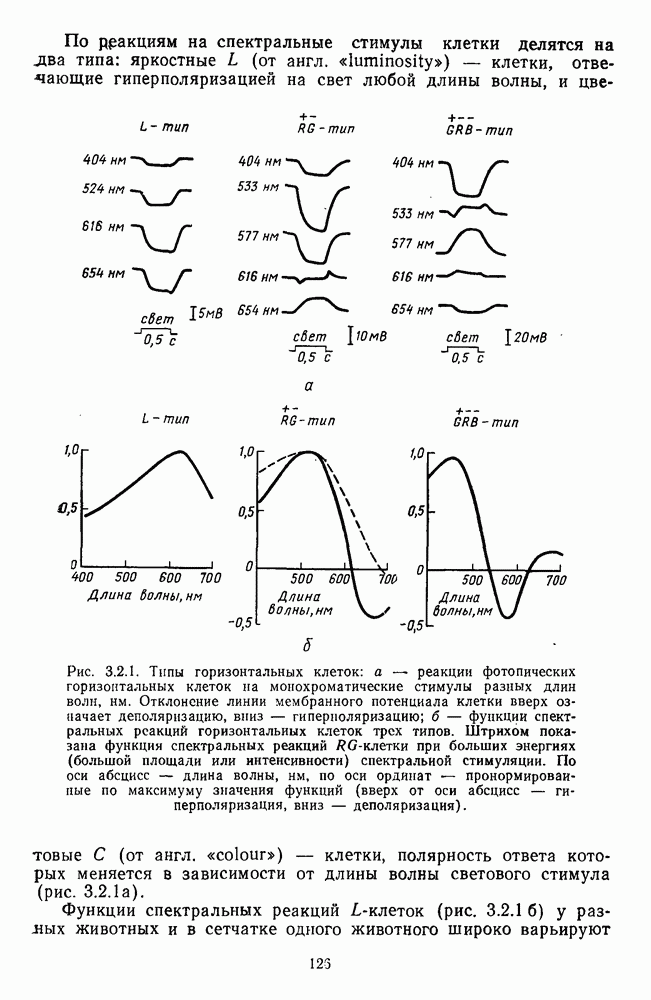
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
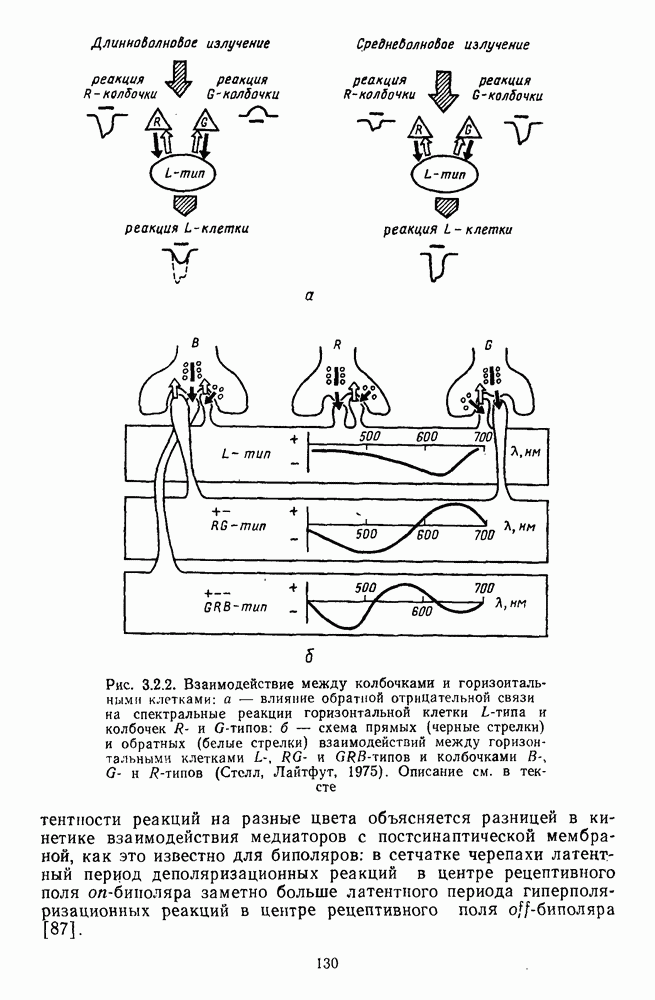
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
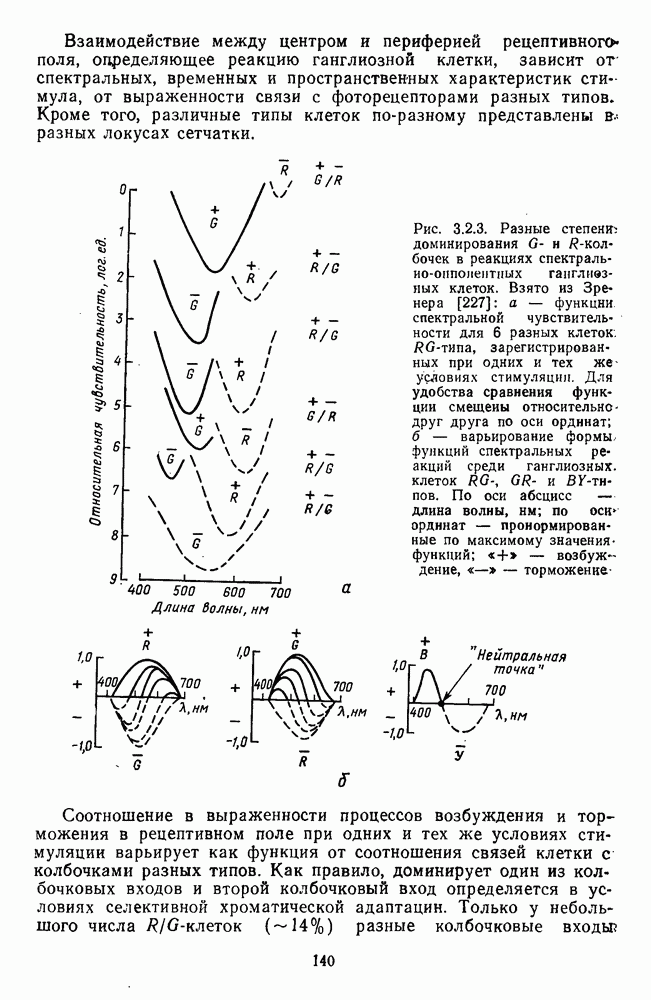
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
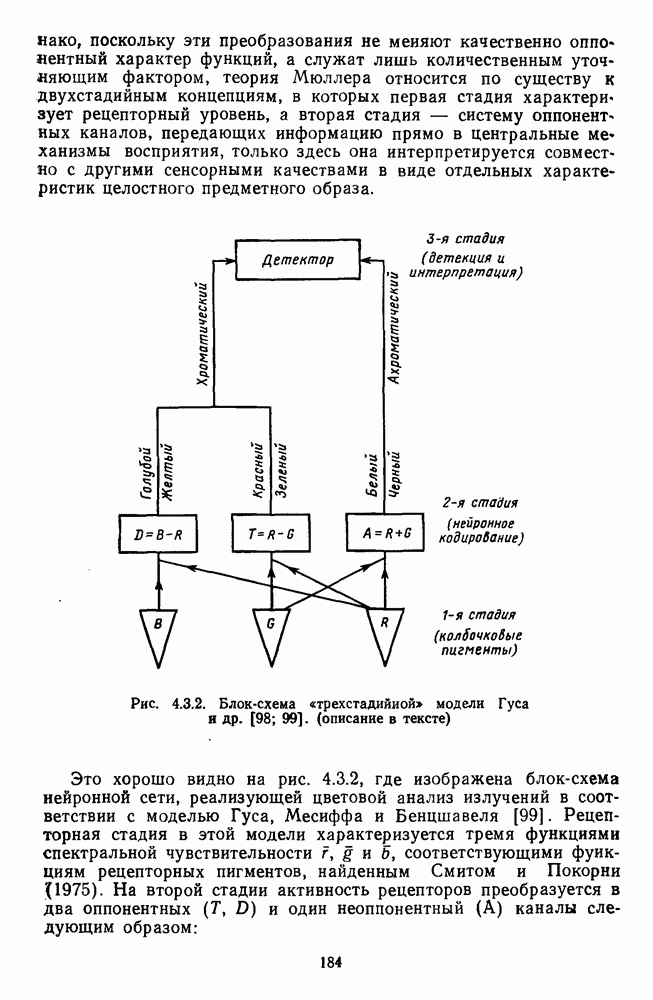
- 4.3.2. Модель Гуса
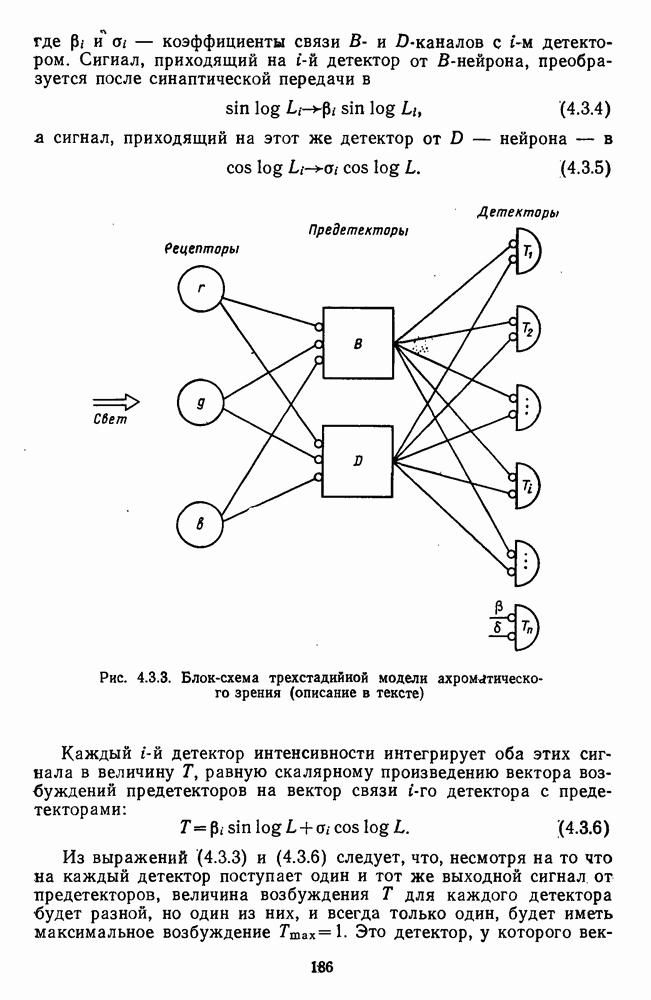
- 4.3.3. Трехстадийная модель ахроматического зрения
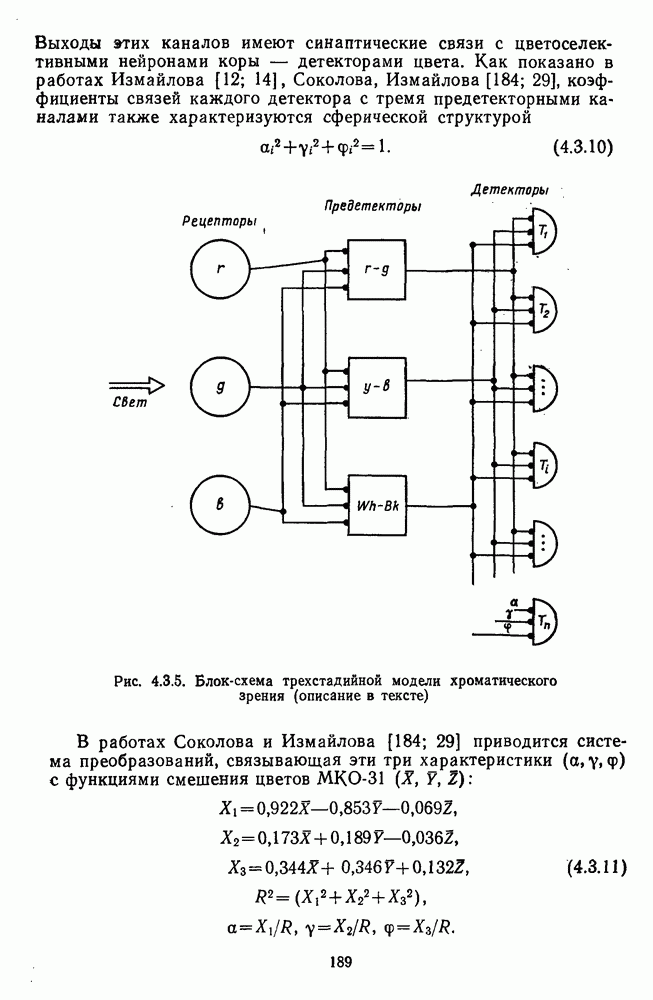
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА