| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
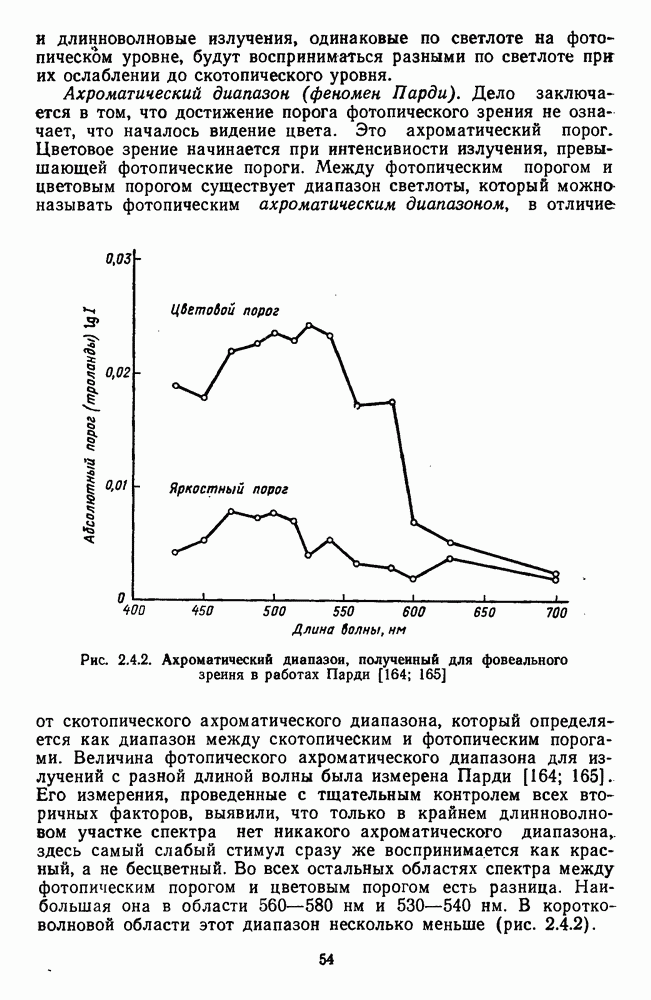
4.1.2. Модель Гельмгольца
Автором первой математической модели различения цветов был Герман фон Гельмгольц [103; 162]. Он разработал ее незадолго до смерти в 1894 г., основываясь на своей теории цветового зрения. На модель Гельмгольца уже много лет ссылаются только как на начальную точку в истории математических моделей цветоразличения [92; 222]. Действительно, модель Гельмгольца очень быстро обнаружила свою несостоятельность в решении проблемы цветоразличения, но тем не менее она имеет не только исторический, но и теоретический интерес. Целый ряд идей, лежащих в основе модели Гельмгольца, без изменений входит во все последующие модели. Такова, например, идея применения в качестве модели различения цветов метрического многомерного пространства, в котором точки представляют отдельные цвета, а межточечные расстояния — соответственно цветовые различия. Затем Гельмгольцу принадлежит также идея физиологической интерпретации осей цветового пространства. В связи с этим будет полезно рассмотреть главные положения модели Гельмгольца.
Построение модели Гельмгольц начал с решения следующей проблемы: как можно различать цвета, основываясь на изменении интенсивности трех базисных процессов  , протекающих в приемниках сетчатки?
, протекающих в приемниках сетчатки?
Пусть  представляют минимальные величины изменения интенсивности, приводящие к активации соответствующие приемники,
представляют минимальные величины изменения интенсивности, приводящие к активации соответствующие приемники,  — величина минимального цветового различия. Тогда ответом на вопрос будет следующее уравнение:
— величина минимального цветового различия. Тогда ответом на вопрос будет следующее уравнение:

Каким психофизиологическим требованием должна удовлетворять функция  в выражении
в выражении  Во-первых,
Во-первых,  не может быть отрицательным, поскольку цветовое различие не может быть меньше нуля (т. е. различия двух идентичных цветов). Далее, при
не может быть отрицательным, поскольку цветовое различие не может быть меньше нуля (т. е. различия двух идентичных цветов). Далее, при  должно выполняться
должно выполняться  поскольку цветовое различие может исчезнуть только в том случае, если ни один из приемников не меняет своей активности. Самая простая функция, которая удовлетворяет таким требованиям, это:
поскольку цветовое различие может исчезнуть только в том случае, если ни один из приемников не меняет своей активности. Самая простая функция, которая удовлетворяет таким требованиям, это:

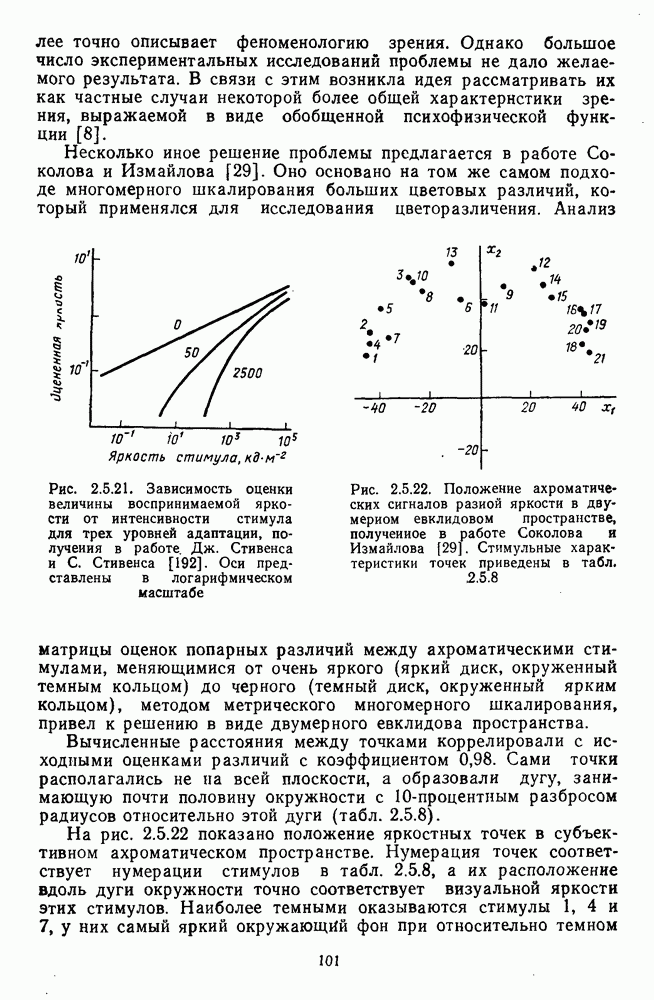
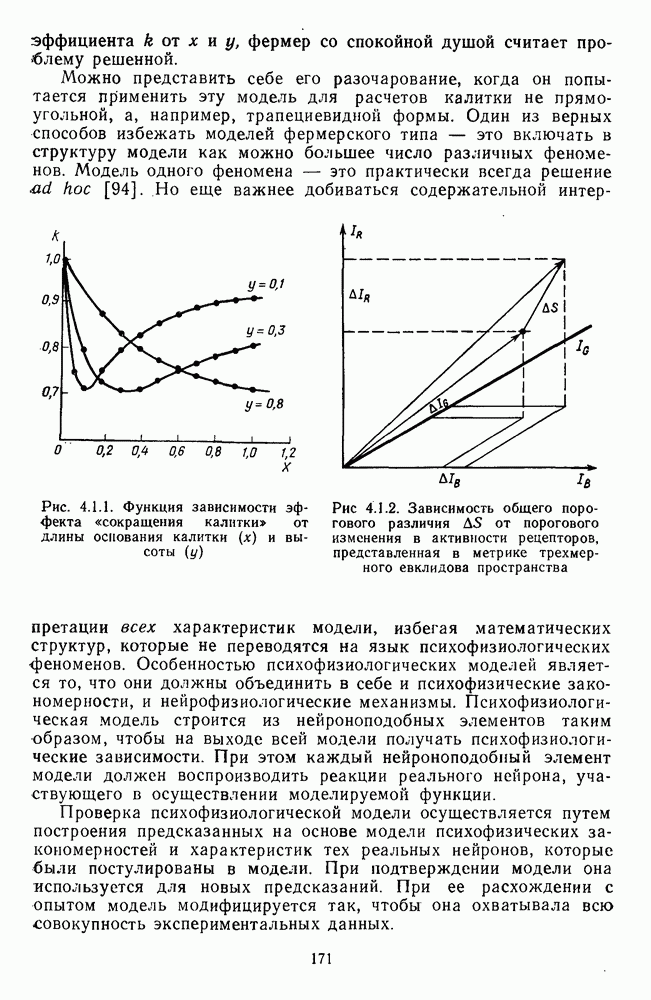
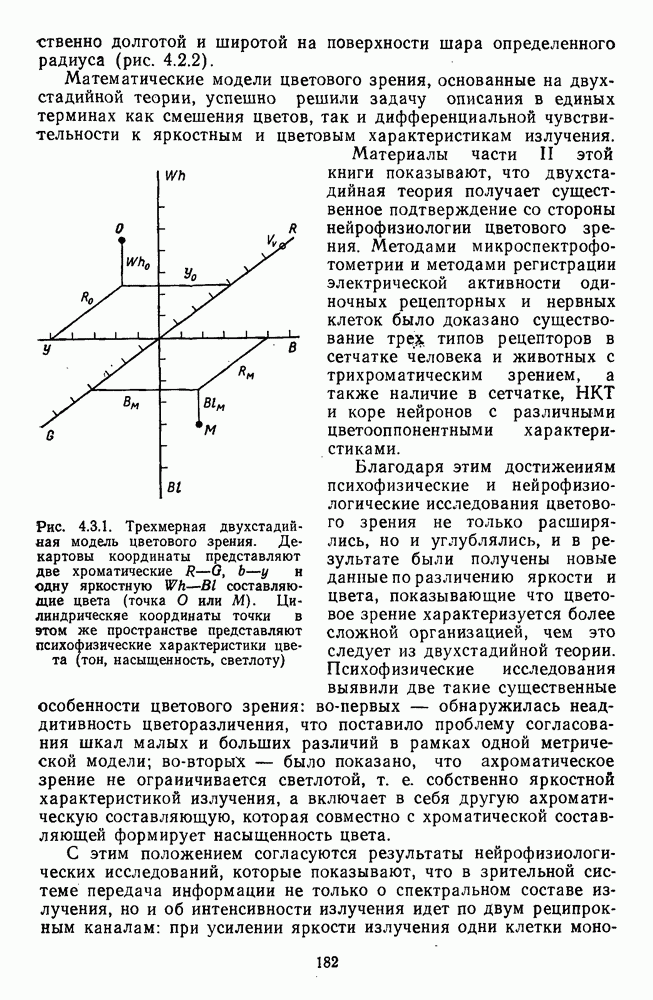
что в геометрических терминах может быть представлено как расстояние в трехмерном евклидовом пространстве (рис. 4.1.2).
Следующий вопрос, на который отвечал Гельмгольц, касалсяг психофизической характеристики чувствительности приемников-сетчатки. Здесь Гельмгольц принял Фехнеровскую идею

для каждого из приемников, но несколько модифицировал выражение (4.3), введя константы для учета изменений на очень низких и очень высоких уровнях интенсивности:

где

и

Константы  интерпретировались Гельмгольцем как характеристики «собственного света» сетчатки, а термин Н был введен для сохранения закона Вебера при максимальных уровнях яркости света.
интерпретировались Гельмгольцем как характеристики «собственного света» сетчатки, а термин Н был введен для сохранения закона Вебера при максимальных уровнях яркости света.
Проверку своей модели Гельмгольц начал с расчета величины расстояния, соответствующей едва заметному различию. Для этого он упростил задачу, перейдя к измерению только яркостного различия между цветами.
Допустим, мы изменили яркость цвета на некоторую величину. Различие между бывшим и новым цветами также выражается как  При этом изменении активность цветоприемников изменяется в одном и том же отношении так, что
При этом изменении активность цветоприемников изменяется в одном и том же отношении так, что

Отсюда, учитывая уравнения (4.1.2) и (4.1.4), можно записать

Принимая, что на высоких уровнях яркости  и В приближаются к константе
и В приближаются к константе  Гельмгольц получил
Гельмгольц получил

Использовав теперь для расчета экспериментальные данные Кенига и Дитеричи [125] по различению яркостей, Гельмгольц вывел, что величина  равна 0,018. Эту константу он использовал для вычисления функции цветоразличения
равна 0,018. Эту константу он использовал для вычисления функции цветоразличения  и получил хорошее соответствие между теоретической и экспериментальной функциями. На рис. 4.1.3 показаны две эти функции, сплошная линия.
и получил хорошее соответствие между теоретической и экспериментальной функциями. На рис. 4.1.3 показаны две эти функции, сплошная линия.
представляет экспериментальные измерения Кенига и Дитеричи, а пунктирная — расчеты в модели Гельмгольца.
Когда же Гельмгольц попытался вывести из своей модели функции спектральной чувствительности первичных приемников, которые были бы согласованы с уже выведенной функцией цвето-различения, он потерпел неудачу. Полученные функции спектральной чувствительности имели два пика и очень мало соответствова-. ли характеристикам приемников, на которых базировалась трехкомпонентная теория.

Рис. 4.1.3. Сравнение экспериментальной функции цветоразличе-ния [125] с теоретической функцией, выведенной из одностадийной модели Гельмгольца. Взято из Грехема [92]

Рис. 4.1.4. Функция фотоцической спектральной чувствительности, полученная методом последовательного сдвига по спектру (точки). Линия представляет теоретические данные, выведенные из модели Стайлса
Такие функции спектральной чувствительности, хорошо согласующиеся с требованиями трехкомпонентной теории, уже были выведены Кеиигом и Дитеричи на основании экспериментов по смешению цветов [126].
После Гельмгольца многие исследователи пытались найти более удачное решение, модифицируя различные параметры модели. В частности, Шредингер [175] модифицировал модель Гельмгольца, заменив выражение (4.1.3) следующей формой:

Шредингер вывел из своей модели функции спектральной чувствительности первичных приемников, которые были согласованы с данными смешения цветов Кенига и Дитеричи [126], однако в этом случае оказалось невозможным вывести функцию цветораз-. личения из модели Шредингера [222].
Таким образом, модели Гельмгольца и Шредингера показывали, что функция цветоразличения не имеет прямой связи с функциями чувствительности приемников сетчатки, что служило решающим аргументом для отвержения трехкомпонентной одностадийной теории цветового зрения.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть 1. ПРИРОДА СВЕТА И ЦВЕТА
- 1.1. Обыденные представления о цвете и свете
- 1.3. Античные представления о природе света
- 1.4. Гипотезы о физической природе цвета
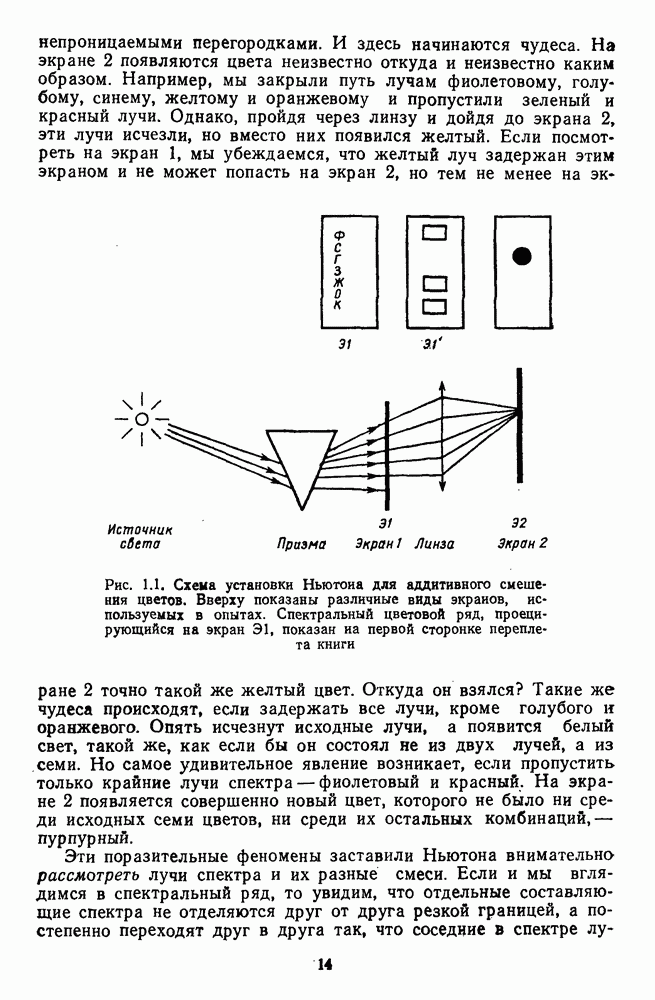
- 1.5. Цветовые опыты Ньютона
- 1.6. Развитие идеи о психофизиологической природе цвета
- 1.7. Одностадийная теория цветового зрения
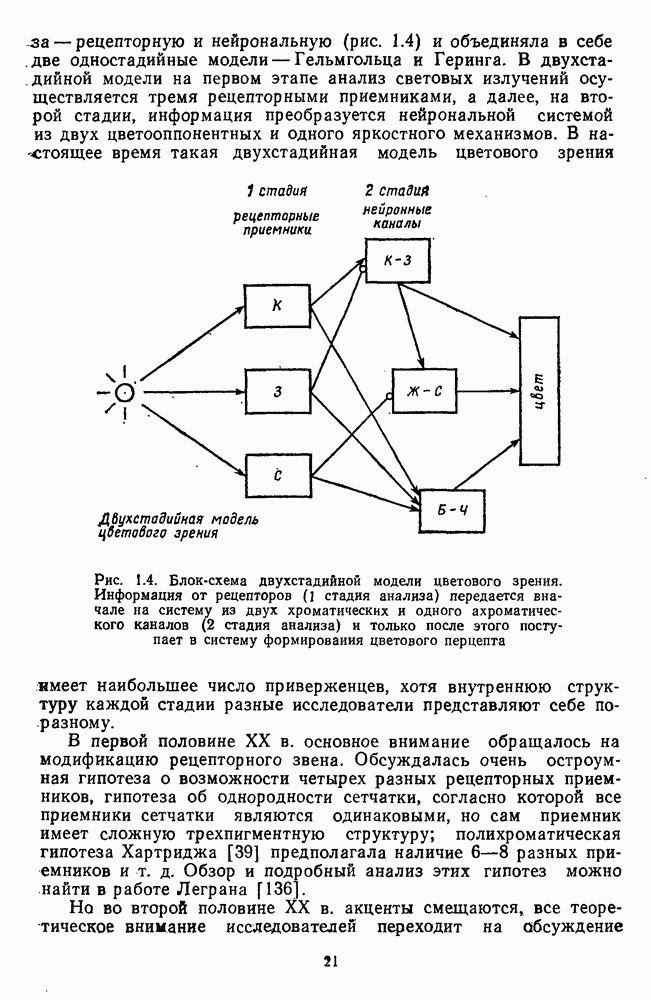
- 1.8. Двухстадийная теория цветового зрения
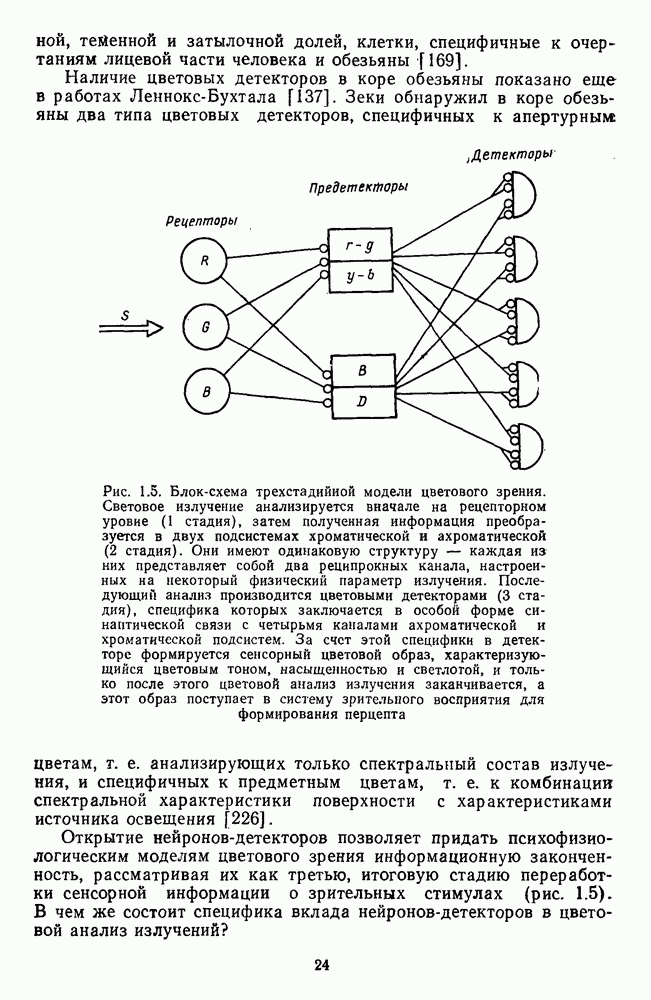
- 1.9. Трехстадийная концепция цветового зрения
- Часть 2. ПСИХОФИЗИКА ЦВЕТОВОГО ЗРЕНИЯ
- Глава 2.1. ОСНОВНЫЕ ПРИНЦИПЫ ПСИХОФИЗИКИ
- 2.1.2. Психологические шкалы
- 2.1.3. «Сильные» (метрические) шкалы
- 2.1.4. Производные шкалы
- 2.1.5. Модель шкалирования Терстона
- Глава 2.2. МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
- 2.2.2. Матрица попарных сходств или различий
- 2.2.3. Построение пространственной модели стимулов
- 2.2.4. Построение метрической модели субъективных различий
- Глава 2.3. ЦВЕТОВОЙ СТИМУЛ И ЦВЕТ
- 2.3.1. Ощущение и восприятие цвета
- 2.3.2. Цветовой стимул
- 2.3.3. Взаимоотношение апертурных и предметных цветов
- Глава 2.4. ПСИХОФИЗИЧЕСКАЯ ФЕНОМЕНОЛОГИЯ ЦВЕТА
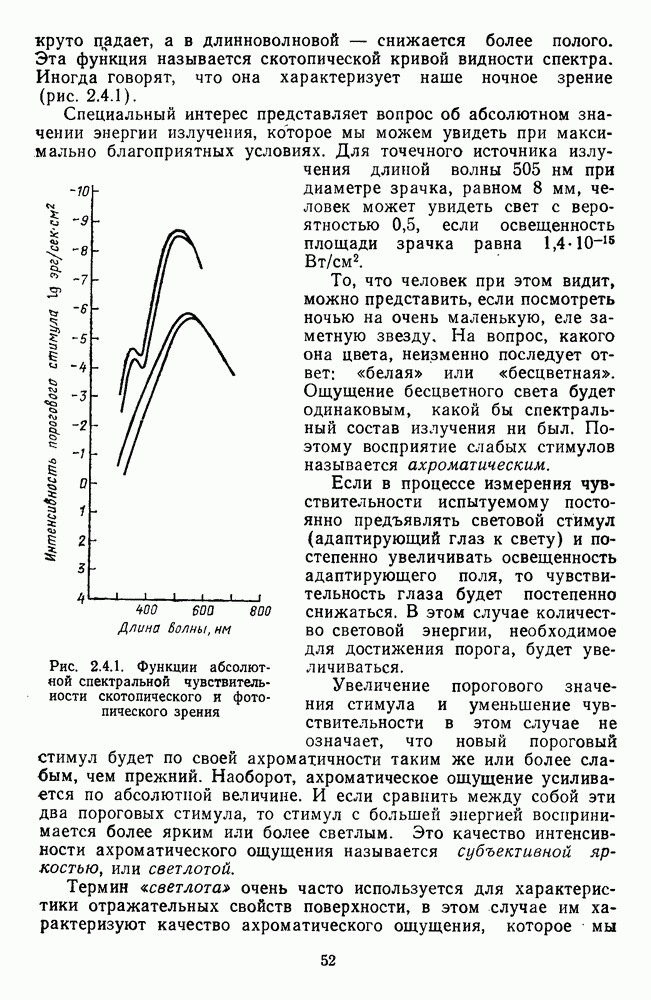
- 2.4.1. Спектральная чувствительность зрения
- 2.4.2. Хроматические характеристики цвета
- 2.4.3. Влияние яркости на хроматичность спектральных цветов
- 2.4.4. Геометрическая модель смешения цветов
- 2.4.5. Цветовые сходства и различия
- Глава 2.5. ЦВЕТОРАЗЛИЧЕНИЕ
- 2.5.2. Надпороговые цветовые различия
- 2.5.3. Субъективное цветовое пространство
- 2.5.4. Неевклидовость цветового пространства
- 2.5.5. Неевклидовость ахроматического пространства
- Часть 3. НЕЙРОФИЗИОЛОГИЧЕСКИЕ ОСНОВЫ ЦВЕТОВОГО ЗРЕНИЯ
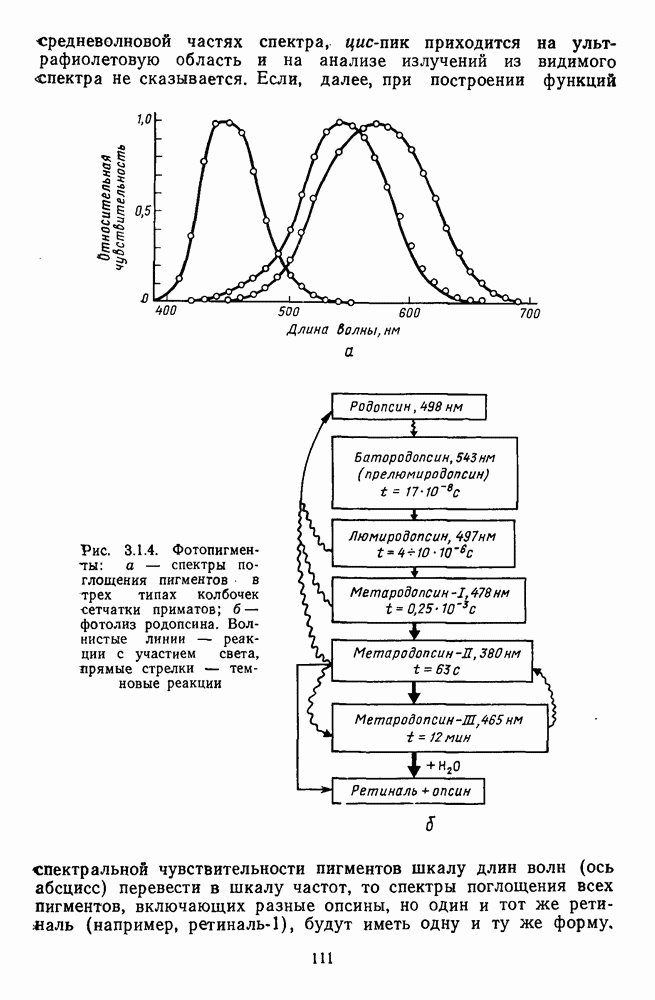
- 3.1.2. Зрительные фотопигменты
- 3.1.3. Электрофизиология фоторецепторов
- 3.1.4. Реакции фоторецепторов на световое излучение
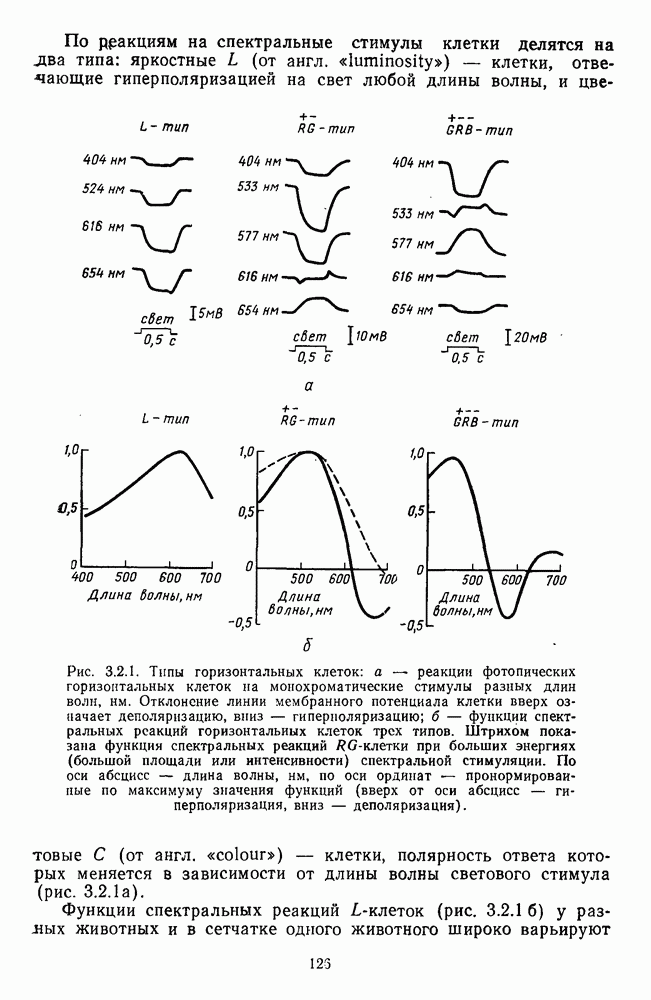
- Глава 3.2. АНАЛИЗ СПЕКТРАЛЬНОГО СОСТАВА ИЗЛУЧЕНИЙ НЕЙРОНАМИ СЕТЧАТКИ
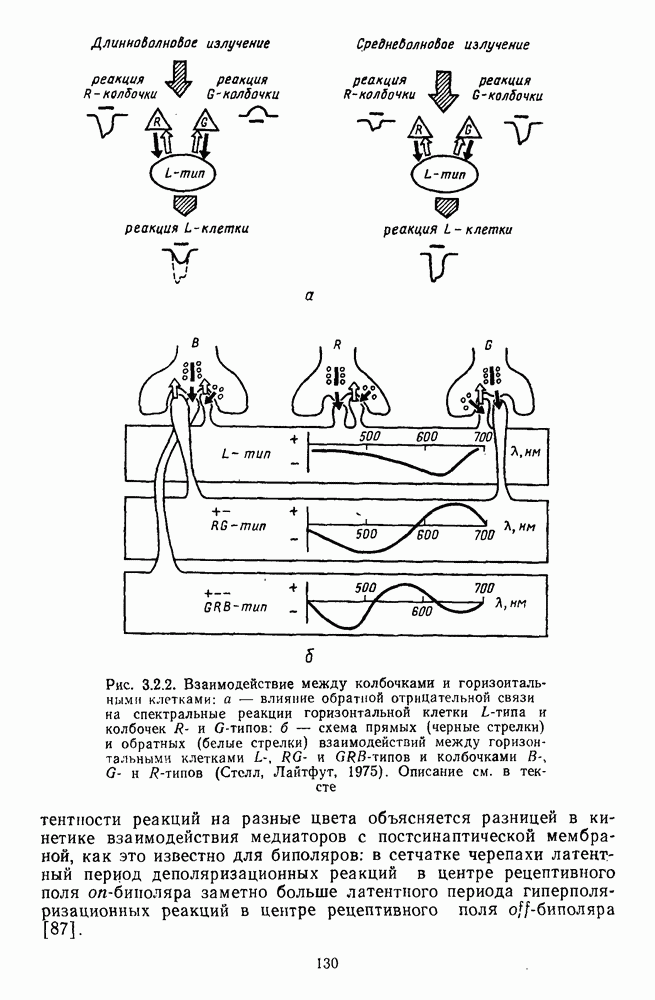
- 3.2.2. Биполярные клетки
- 3.2.3. Амакриновые клетки
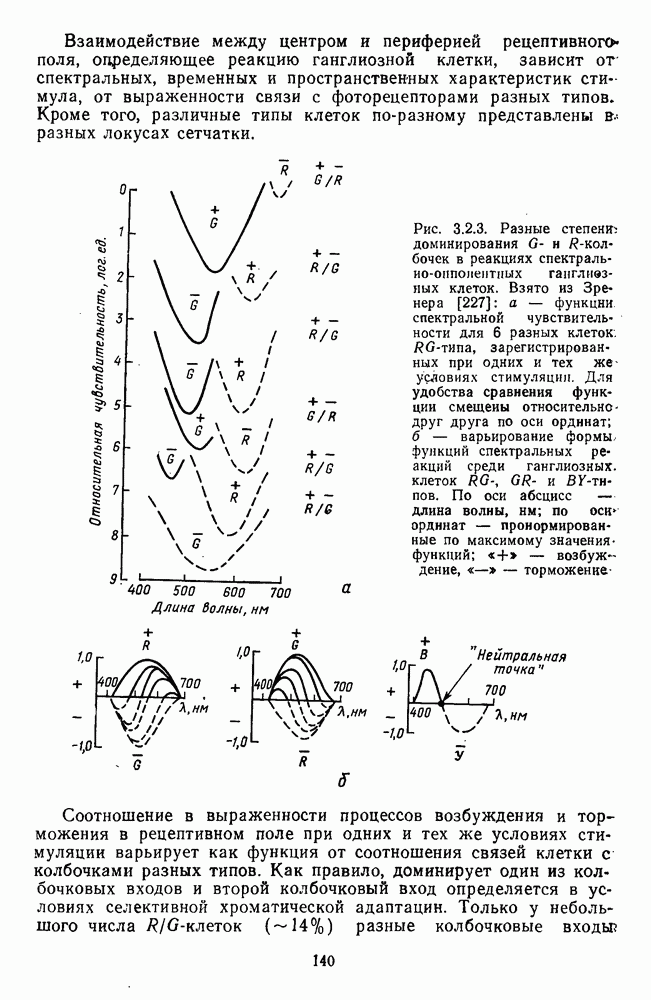
- 3.2.4. Ганглиозные клетки
- 3.2.5. Мюллеровские клетки. Электроретинограмма
- Глава 3.3. НЕЙРОННЫЕ МЕХАНИЗМЫ КОДИРОВАНИЯ ЦВЕТА В НАРУЖНОМ КОЛЕНЧАТОМ ТЕЛЕ
- 3.3.2. Спектрально-оппонентные и ахроматические нейроны
- 3.3.3. Особенности нейронов парво- и магноцеллюлярных слоев
- 3.3.4. Корреляция спектральных характеристик нейронов НКТ с феноменологией цвета
- Глава 3.4. КОРКОВЫЕ МЕХАНИЗМЫ ЦВЕТОВОГО ЗРЕНИЯ
- 3.4.1. Зрительные зоны коры мозга
- 3.4.2. Цветовые рецептивные поля корковых клеток
- 3.4.3. Детекторы спектральных излучений
- 3.4.4. Организация каналов из тонических неоппонентных клеток
- 3.4.5. Цветовые колонки
- 3.4.6. Особенности процессов кодирования цвета в престриарной зоне V4
- Часть 4. МАТЕМАТИЧЕСКАЯ ПСИХОФИЗИОЛОГИЯ ЦВЕТОВОГО ЗРЕНИЯ
- 4.1.2. Модель Гельмгольца
- 4.1.3. Модель Стайлса
- Глава 4.2. ДВУХСТАДИИНАЯ ТЕОРИЯ И ЕЕ МОДЕЛИ
- 4.2.1. Модель Харвича и Джемсон
- 4.2.2. Модель Воса и Уолравена
- Глава 4.3. ТРЕХСТАДИЙНАЯ МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ
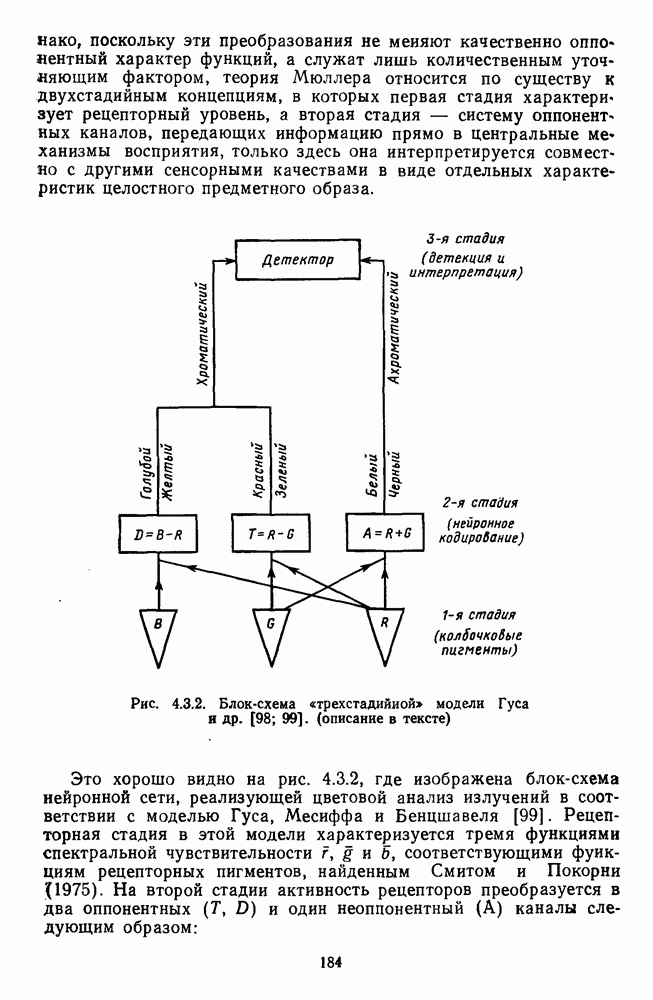
- 4.3.2. Модель Гуса
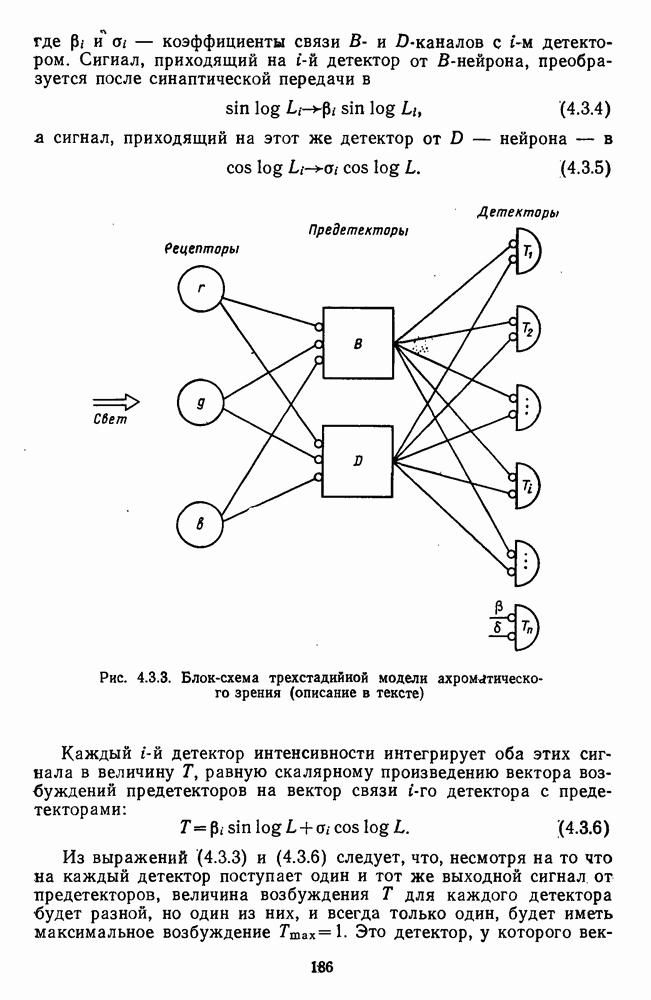
- 4.3.3. Трехстадийная модель ахроматического зрения
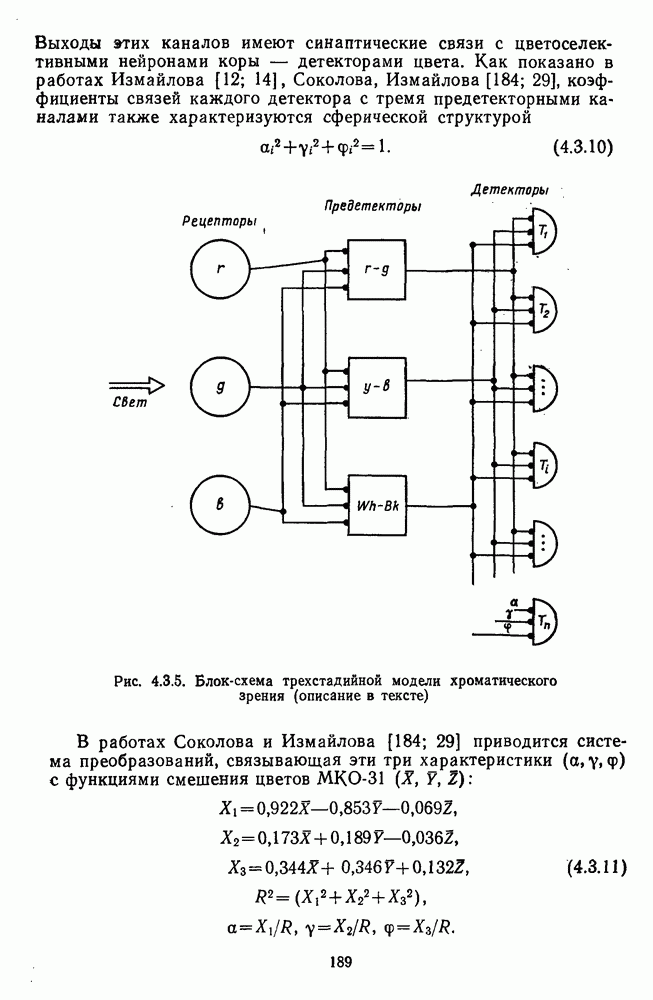
- 4.3.4. Трехстадийиая модель хроматического зрения
- 4.3.5. Общая трехстадийная модель цветового зрения
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА