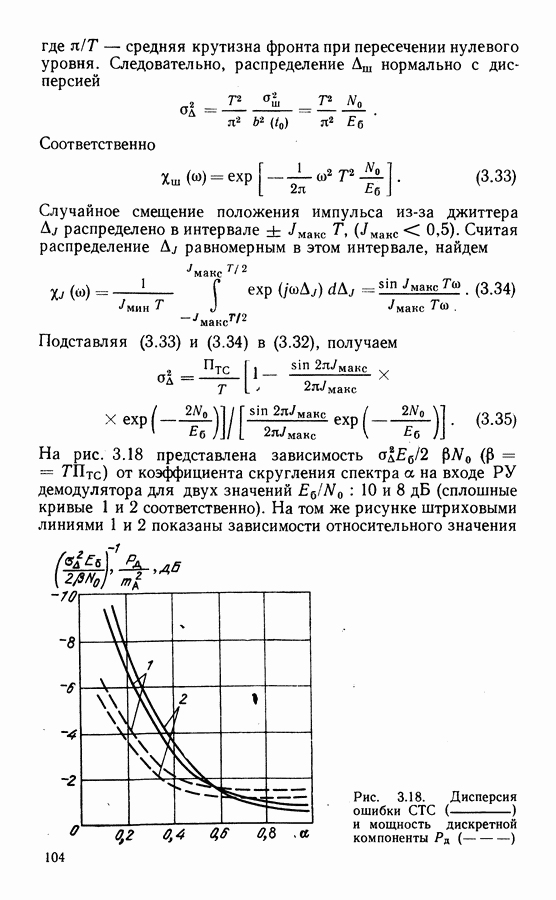
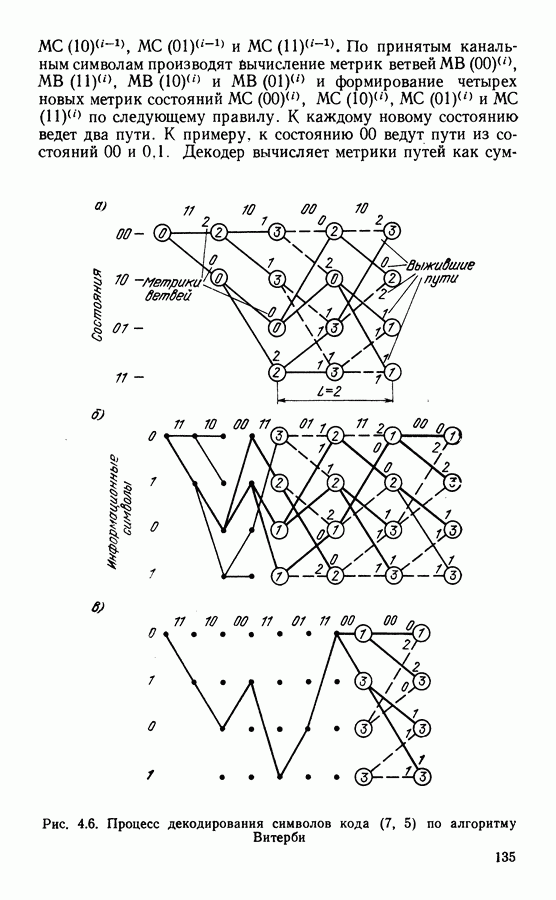
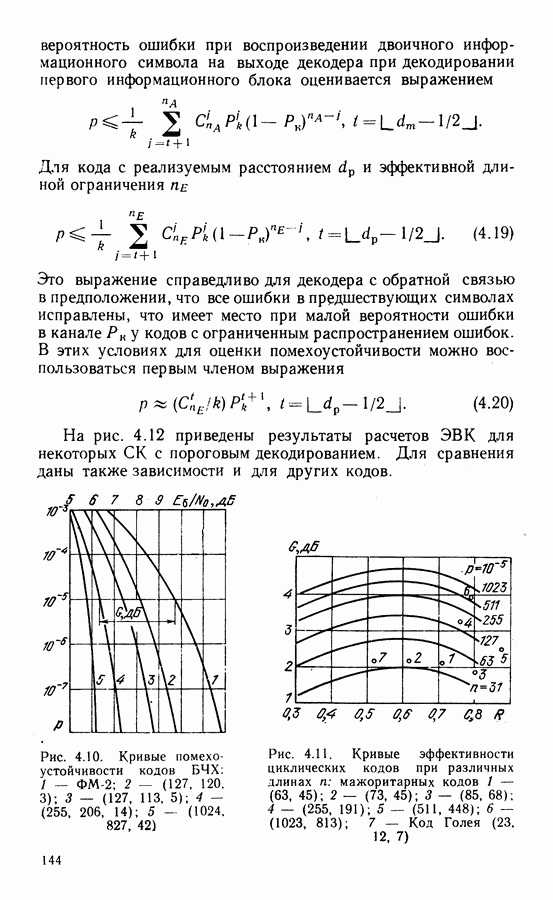
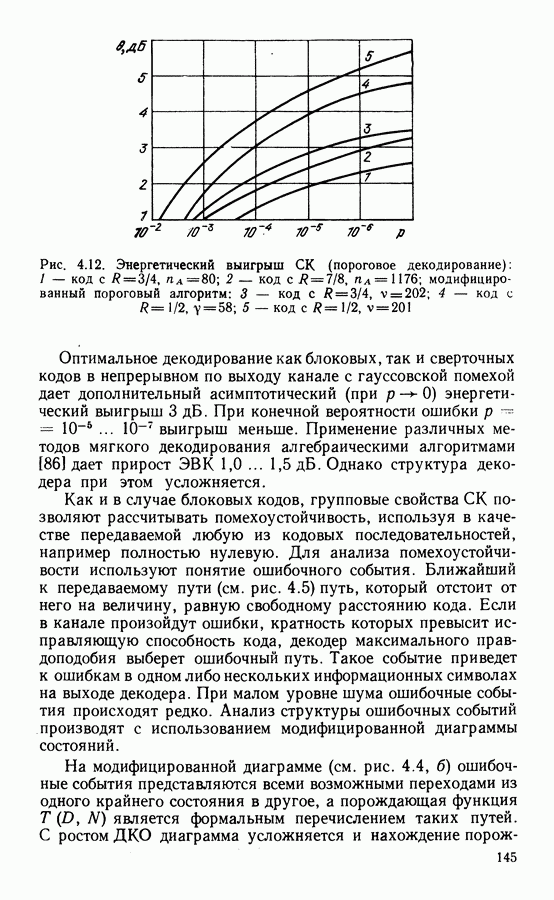
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РАЗДЕЛ II. МОДУЛЯЦИЯ
ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
2.1. ДИСКРЕТНЫЕ СИГНАЛЫ В СПУТНИКОВЫХ КАНАЛАХ
Основная тенденция развития современных ЦССС - повышение помехоустойчивости и эффективности передачи информации. Внедряются новые методы, обеспечивающие повышение скорости передачи, снижение влияния помех в каналах и экономное расходование полосы частот. При этом возможно достижение высоких показателей информационной, энергетической и частотной эффективности [33, 34].
Решению этих задач способствует рациональный выбор сигналов, используемых для передачи информации по спутниковым каналам, методов их формирования и обработки на приеме. В современных спутниковых системах широко используют сигналы с фазовой модуляцией и когерентный прием. Наряду с двоичными применяют и многопозиционные ансамбли сигналов. Возрастает интерес к сигналам с постоянной огибающей и непрерывно меняющейся фазой.
Рассмотрим основные виды сигналов и методы их формирования, используемые в ЦССС. Искажения сигналов при передаче по каналам на первом этапе учитываться не будут. Подробный анализ влияния искажений содержится в § 2.5, 2.6.
В общем виде колебание модулированной несущей с частотой 

Здесь функции  определяют закон модуляции амплитуды и фазы несущей. Сигнал М — позиционной фазовой модуляции
определяют закон модуляции амплитуды и фазы несущей. Сигнал М — позиционной фазовой модуляции  на интервале одного символа
на интервале одного символа 

Дискретные значения фазы сигнала  число возможных сигналов,
число возможных сигналов,  -ичные символы
-ичные символы  выбираются из множества
выбираются из множества  Обычно
Обычно  Тогда каждый М-ичный символ
Тогда каждый М-ичный символ  соответствует набору из
соответствует набору из  двоичных информационных символов V, а его длительность
двоичных информационных символов V, а его длительность  где Т — длительность двоичного символа.
где Т — длительность двоичного символа.
Энергия ФМ сигнала постоянна и составляет  Она может быть выражена через энергию
Она может быть выражена через энергию  затрачиваемую на передачу одной двоичной единицы (бита) как
затрачиваемую на передачу одной двоичной единицы (бита) как  Длительность бита Т определяет скорость модуляции
Длительность бита Т определяет скорость модуляции  в двоичных символах в секунду.
в двоичных символах в секунду.
При  получаем сигналы двоичной фазовой модуляции
получаем сигналы двоичной фазовой модуляции  Сигналы с одинаковыми энергиями удобно характеризовать коэффициентом корреляции:
Сигналы с одинаковыми энергиями удобно характеризовать коэффициентом корреляции:

Сигналы ФМ-2 противоположны и коэффициент корреляции
Модулированный сигнал (2.1) представим в виде суммы квадратурных составляющих:

Выражения в квадратных скобках определяются видом передаваемой информации и модулируют ортогональные несущие  Обозначим
Обозначим  Вид модулирующих функций
Вид модулирующих функций  задает метод модуляции и определяет свойства сигналов. Представим их в виде
задает метод модуляции и определяет свойства сигналов. Представим их в виде  информационные символы
информационные символы  элементарные модулирующие сигналы в квадратурных каналах. Последовательности символов а и
элементарные модулирующие сигналы в квадратурных каналах. Последовательности символов а и  получают расщеплением исходной информационной последовательности
получают расщеплением исходной информационной последовательности  на четные и нечетные символы. Символы
на четные и нечетные символы. Символы  могут быть как двоичными, так и многоуровневыми.
могут быть как двоичными, так и многоуровневыми.
Обычно модулирующие сигналы выбирают такими, чтобы при последовательной передаче в каждом из квадратурных каналов они не перекрывались во времени. Это условие выполняется, если длительность каждого сигнала  или
или
 равна
равна  . В этом случае имеет место модуляция полным откликом и в формируемых в модуляторе сигналах отсутствует межсимвольная интерференция. Такие методы достаточно просты и их широко используют на практике. При модуляции частичным откликом длительность сигналов
. В этом случае имеет место модуляция полным откликом и в формируемых в модуляторе сигналах отсутствует межсимвольная интерференция. Такие методы достаточно просты и их широко используют на практике. При модуляции частичным откликом длительность сигналов  превышает
превышает  допускаются взаимное перекрытие сигналов и межсимвольная интерференция. Процесс обработки и демодуляции при этом усложняется, но такие сигналы обладают лучшими спектральными свойствами. Возможности их применения в ЦССС рассматриваются в гл. 8.
допускаются взаимное перекрытие сигналов и межсимвольная интерференция. Процесс обработки и демодуляции при этом усложняется, но такие сигналы обладают лучшими спектральными свойствами. Возможности их применения в ЦССС рассматриваются в гл. 8.
Для сигналов с постоянной огибающей должно выполняться условие

Такому условию удовлетворяют элементарные модулирующие сигналы в виде прямоугольных импульсов

при этом двоичные информационные символы полагаются равными  . В этом случае получаем сигналы двукратной ФМ. На интервале длительностью
. В этом случае получаем сигналы двукратной ФМ. На интервале длительностью  четыре возможные комбинации символов
четыре возможные комбинации символов  задают следующие варианты сигналов четырехпозиционной ФМ (ФМ-4):
задают следующие варианты сигналов четырехпозиционной ФМ (ФМ-4):

Они образуют биортогональный ансамбль, так как сигнал  а сигналы
а сигналы  взаимно ортогональны
взаимно ортогональны 
Представление сигналов в виде суммы квадратурных составляющих определяет простой способ их формирования в модуляторе. В частности, сигналы ФМ-4 можно получить как сумму двух сигналов ФМ-2, несущие колебания которых отличаются по фазе на  Схема модулятора показана на рис.2.1,а, а временнйе диаграммы на рис. 2.2. Двоичная последовательность
Схема модулятора показана на рис.2.1,а, а временнйе диаграммы на рис. 2.2. Двоичная последовательность

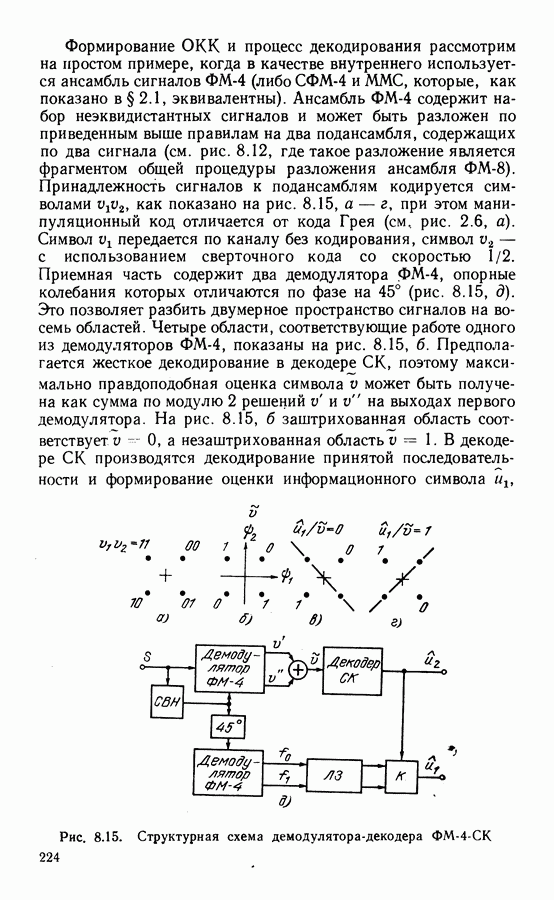
Рис. 2.1. Структурные схемы модуляторов: а - ФМ-4; б - ММС
информационных символов  в коммутаторе К разделяется на последовательности а и
в коммутаторе К разделяется на последовательности а и  которые модулируют квадратурные несущие
которые модулируют квадратурные несущие  Длительность каждого символа
Длительность каждого символа  равна Т, а длительности символов а и
равна Т, а длительности символов а и  равны
равны  Сигналы ФМ-2 квадратурных каналов складываются, образуя четырехфазный сигнал ФМ-4.
Сигналы ФМ-2 квадратурных каналов складываются, образуя четырехфазный сигнал ФМ-4.
При одновременной смене символов в каждом из квадратурных каналов модулятора в сигнале ФМ-4 происходит скачок фазы на  . Прохождение ФМ сигнала через полосовые фильтры тракта сопровождается изменениями огибающей в моменты, соответствующие скачкам фазы. Скачки на
. Прохождение ФМ сигнала через полосовые фильтры тракта сопровождается изменениями огибающей в моменты, соответствующие скачкам фазы. Скачки на  вызывают провалы огибающей до нуля. Такая паразитная модуляция сигнала нежелательна. Исключить скачки фазы
вызывают провалы огибающей до нуля. Такая паразитная модуляция сигнала нежелательна. Исключить скачки фазы

Рис. 2.2. Временные диаграммы при формировании сигналов ММС

Рис. 2.3. Формы элементарных модулирующих сигналов
на  возможно, если разнести во времени моменты смены фаз в квадратурных каналах. Обычно модулирующие сигналы водном из каналов смещают величину на
возможно, если разнести во времени моменты смены фаз в квадратурных каналах. Обычно модулирующие сигналы водном из каналов смещают величину на  Например, выбирая элементарные модулирующие сигналы в виде
Например, выбирая элементарные модулирующие сигналы в виде

и полагая что  получаем сигналы смещенной
получаем сигналы смещенной 
Формы элементарных модулирующих сигналов при различных видах модуляции показаны на рис. 2.3. Модулятор СФМ-4 отличается от модулятора ФМ-4 наличием в одном из каналов задержки символов на время  На рис. 2.1, а элемент задержки показан штриховой линией, на
На рис. 2.1, а элемент задержки показан штриховой линией, на  модулирующая последовательность
модулирующая последовательность  смещена на
смещена на  по сравнению с
по сравнению с 
Если символы а и  в квадратурных каналах многоуровневые, в схеме рис. 2.1,а возможно формирование различных многопозиционных сигналов с фазовой и амплитудно-фазовой модуляцией
в квадратурных каналах многоуровневые, в схеме рис. 2.1,а возможно формирование различных многопозиционных сигналов с фазовой и амплитудно-фазовой модуляцией  Например, выбирая при
Например, выбирая при  значения символов в соответствии с табл. 2.1, получаем сигналы ФМ-8.
значения символов в соответствии с табл. 2.1, получаем сигналы ФМ-8.
Если модулирующие символы в квадратурных каналах принимают значения  ±1 и
±1 и  то в каждом из каналов модулятора будут четырехуровневые сигналы, а в целом на выходе модулятора получим сигнал с амплитудно-фазовой модуляцией АФМ-16. Использование элементарных модулирующих сигналов вида (2.6) дает смещенную амплитудно-фазовую модуляцию
то в каждом из каналов модулятора будут четырехуровневые сигналы, а в целом на выходе модулятора получим сигнал с амплитудно-фазовой модуляцией АФМ-16. Использование элементарных модулирующих сигналов вида (2.6) дает смещенную амплитудно-фазовую модуляцию 
Опорная несущая, необходимая для когерентного приема в демодуляторах, выделяется, как правило, из принимаемого сигнала. При этом возникает неоднозначность фазы, когда
Таблица 2.1

выделение возможно с ошибкой, кратной величине  Анализ способов формирования несущей и причин появления неоднозначности приведен в § 3.2.
Анализ способов формирования несущей и причин появления неоднозначности приведен в § 3.2.
Передача ФМ в каналах с неоднозначностью требует применения специальных мер. Чаще других используют относительное кодирование информации по правилу

где  символы на выходе относительного кодера, и — символы на входе кодера,
символы на выходе относительного кодера, и — символы на входе кодера,  задержанные на такт выходные символы
задержанные на такт выходные символы  символ задержки),
символ задержки),  сложение по модулю М.
сложение по модулю М.
Символы относительного кода подают на модулятор  получая на выходе сигнал относительной фазовой модуляции
получая на выходе сигнал относительной фазовой модуляции 
В демодуляторе производится обратное преобразование. Пусть принятые символы  и неоднозначность фазы в канале обозначается символом
и неоднозначность фазы в канале обозначается символом  Информационные символы определяют, производя вычитание (по модулю М)
Информационные символы определяют, производя вычитание (по модулю М)  Поскольку величина неоднозначности на большом интервале времени остается неизменной
Поскольку величина неоднозначности на большом интервале времени остается неизменной  в результате вычитания получаем
в результате вычитания получаем  Относительное кодирование необходимо применять и при амплитудно-фазовой модуляции для кодирования фазовых позиций сигнала.
Относительное кодирование необходимо применять и при амплитудно-фазовой модуляции для кодирования фазовых позиций сигнала.
Сужение спектра модулированных сигналов производится как узкополосными фильтрами на выходе модулятора, так и за счет скругления элементарных модулирующих сигналов. Оптимизация параметров фильтров рассматривается в § 2.5. Одна из широко используемых форм скругления соответствует полупериоду косинусоиды, когда сигналы выбирают в виде

Символы  в квадратурных каналах должны быть смещены на время Т. Тогда модулированный сигнал имеет вид
в квадратурных каналах должны быть смещены на время Т. Тогда модулированный сигнал имеет вид

Временные диаграммы функций  и модулирующих сигналов в квадратурных каналах
и модулирующих сигналов в квадратурных каналах  и
и  показаны на рис. 2.2. Функции (2.8) удовлетворяют условию (2.4), и рассматриваемый сигнал имеет постоянную огибающую. Он оказывается модулированным по частоте с индексом модуляции
показаны на рис. 2.2. Функции (2.8) удовлетворяют условию (2.4), и рассматриваемый сигнал имеет постоянную огибающую. Он оказывается модулированным по частоте с индексом модуляции  Текущая фаза сигнала в произвольный момент времени
Текущая фаза сигнала в произвольный момент времени  а мгновенная частота
а мгновенная частота  Модулирующие символы в квадратурных каналах а и
Модулирующие символы в квадратурных каналах а и  имеют длительность
имеют длительность  и смещены на время Т, т. е. смена знаков происходит через Т. Основная модулирующая частота
и смещены на время Т, т. е. смена знаков происходит через Т. Основная модулирующая частота  девиация частоты
девиация частоты  индекс частотной модуляции
индекс частотной модуляции  Такой метод модуляции называется модуляцией минимального частотного сдвига (ММС).
Такой метод модуляции называется модуляцией минимального частотного сдвига (ММС).
Определим формы сигналов ММС (2.9) на интервале  с учетом четырех возможных комбинаций знаков символов а и
с учетом четырех возможных комбинаций знаков символов а и 

Вычисляя коэффициент корреляции по формуле (2.2), получаем:  Таким образом, на интервале длиной
Таким образом, на интервале длиной  сигналы ММС образуют ансамбль биортогональных сигналов. Если информационные символы а и
сигналы ММС образуют ансамбль биортогональных сигналов. Если информационные символы а и  многоуровневые, то использование функций (2.8) позволяет получить многоуровневую модуляцию с минимальным частотным сдвигом.
многоуровневые, то использование функций (2.8) позволяет получить многоуровневую модуляцию с минимальным частотным сдвигом.
Модулятор сигналов ММС показан на  Он состоит из квадратурного модулятора сигналов ФМ-4 и дополнительной схемы, в которой производится умножение информационных сигналов а и
Он состоит из квадратурного модулятора сигналов ФМ-4 и дополнительной схемы, в которой производится умножение информационных сигналов а и  на функции скругления
на функции скругления 
Сравнение свойств различных сигналов удобно производить, используя геометрическое представление сигналов [34]. В качестве ортов используют векторы, соответствующие

Рис. 2.4. Ансамбли сигналов
колебаниям с единичной энергией  Каждый сигнал изображают на плоскости вектором, длина которого равна
Каждый сигнал изображают на плоскости вектором, длина которого равна  Например, полагая амплитуду
Например, полагая амплитуду  сигналы ансамбля М-4 (2.5) можно представить так:
сигналы ансамбля М-4 (2.5) можно представить так:

и изобразить в виде точек (концов векторов) на плоскости.
На рис. 2.4 показаны типичные ансамбли сигналов с ФМ и АФМ. Энергия ФМ сигналов в процессе модуляции не изменяется и геометрическим местом сигнальных точек является окружность. Ансамбли АФМ сигналов содержат точки, находящиеся на различном расстоянии от начала координат. При АФМ энергия сигналов не постоянна и зависит от конкретной реализации передаваемого сигнала. Расстояние между сигналами определяют как  При сравнении ансамблей важным является в первую очередь, минимальное расстояние между
При сравнении ансамблей важным является в первую очередь, минимальное расстояние между
сигналами  Для ансамблей, показанных на рис. 2.4, значение минимальных расстояний, выраженное через среднюю энергию
Для ансамблей, показанных на рис. 2.4, значение минимальных расстояний, выраженное через среднюю энергию  следующее:
следующее: 
В виде вектора может быть представлена также и каждая реализация помехи  при этом проекции помехи на орты будут случайными величинами с нормальным распределением. Если помеха — белый шум с односторонней спектральной плотностью энергетического спектра
при этом проекции помехи на орты будут случайными величинами с нормальным распределением. Если помеха — белый шум с односторонней спектральной плотностью энергетического спектра  то дисперсия каждой из проекций будет равна
то дисперсия каждой из проекций будет равна  [33,34].
[33,34].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
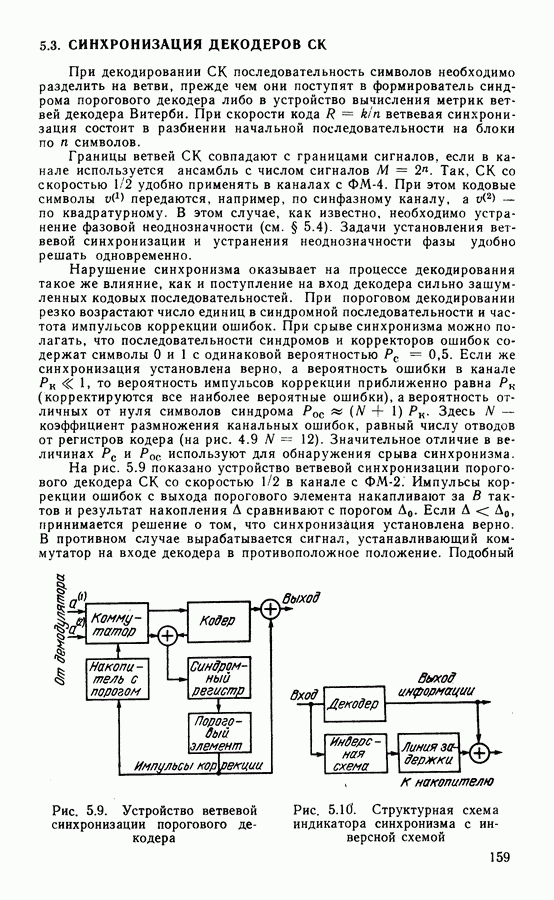
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ