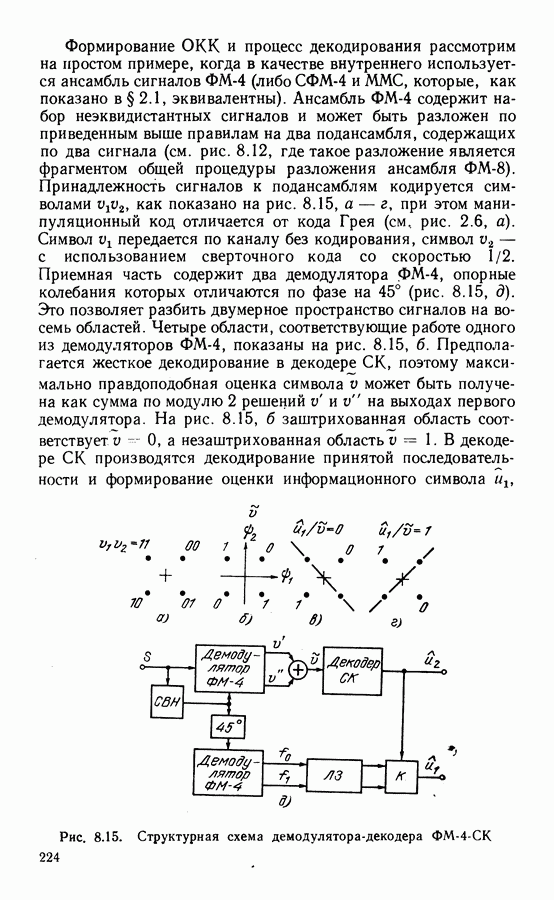
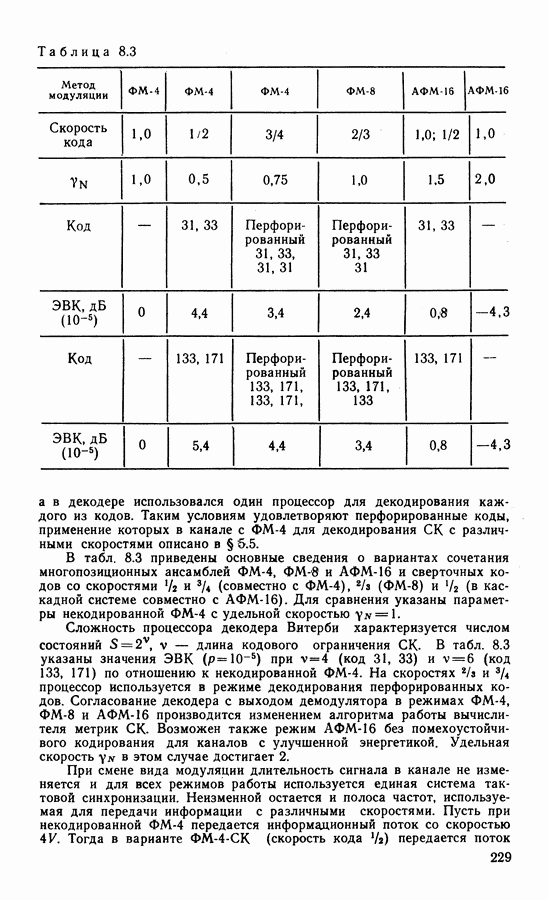
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
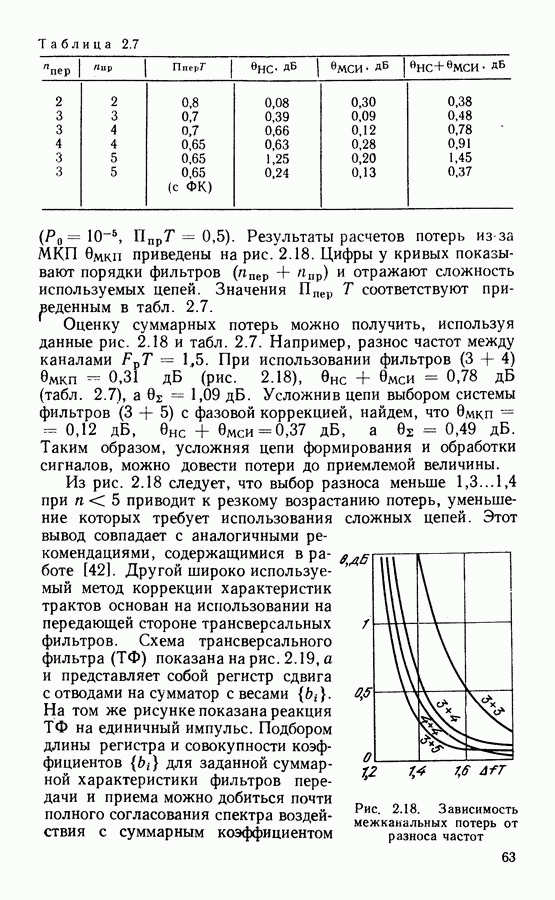
6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
Для уменьшения мешающего действия сигналов спутниковых систем на системы связи, работающие в той же полосе частот, применяется рассеивание энергии передаваемых сигналов с помощью дисперсии. Наиболее чувствительными к помехам оказываются системы передачи типа ОКН.
Наибольшую опасность для таких систем представляет мешающий ТВ-ЧМ сигнал при его модуляции только сигналом дисперсии. Вопросам расчета допустимого уровня помех на системы ОКН посвящены работы  также Отчет № 384-2 МККР [107]. В [102] расчет влияния помех проводился в предположении медленного сигнала дисперсии (с частотой кадров), в [104] — по экспериментальным данным.
также Отчет № 384-2 МККР [107]. В [102] расчет влияния помех проводился в предположении медленного сигнала дисперсии (с частотой кадров), в [104] — по экспериментальным данным.
Рассмотрим воздействие ЧМ сигнала, модулированного напряжением дисперсии, на приемник ФМ сигнала. В качестве сигнала дисперсии, как правило, используется треугольное (рис. 6.9, а) или пилообразное (рис. 6.9, б) напряжение. Обозначим размах девиации, обусловленный сигналом дисперсии, через А, а индекс модуляции  где
где  частота сигнала дисперсии. При большом индексе модуляции спектр сигнала является дискретным и равномерным в полосе А (рис. 6.10, а). В полосу приемника ФМ сигнала с шириной В при
частота сигнала дисперсии. При большом индексе модуляции спектр сигнала является дискретным и равномерным в полосе А (рис. 6.10, а). В полосу приемника ФМ сигнала с шириной В при  попадает ограниченнее число дискретных компонентов ЧМ сигнала с дисперсией (рис. 6.10, б), и огибающая помехи на выходе фильтра будет иметь непрерывный характер. Проанализируем вероятность ошибки в дискретном канале на примере передачи сигналов ФМ-2. Как будет показано в дальнейшем, такой анализ справедлив и для сигналов ФМ-4. Предполагается, что приемный фильтр — идеальный с полосой пропускания В.
попадает ограниченнее число дискретных компонентов ЧМ сигнала с дисперсией (рис. 6.10, б), и огибающая помехи на выходе фильтра будет иметь непрерывный характер. Проанализируем вероятность ошибки в дискретном канале на примере передачи сигналов ФМ-2. Как будет показано в дальнейшем, такой анализ справедлив и для сигналов ФМ-4. Предполагается, что приемный фильтр — идеальный с полосой пропускания В.
Допустим, что частота повторения сигнала дисперсии больше полосы пропускания приемника, т. е.  Тогда в полосу приемного фильтра может попасть не более одного
Тогда в полосу приемного фильтра может попасть не более одного

Рис. 6.9. Форма сигнала дисперсии

Рис. 6.10. Спектр ЧМ сигнала с дисперсией
спектрального компонента с уровнем  где
где  уровень компонента,
уровень компонента,  уровень ЧМ помехи с дисперсией на входе приемного фильтра,
уровень ЧМ помехи с дисперсией на входе приемного фильтра,  число спектральных компонентов помехи. Напряжение на выходе фильтра
число спектральных компонентов помехи. Напряжение на выходе фильтра  При когерентном детектировании напряжение на выходе фазового детектора приемника
При когерентном детектировании напряжение на выходе фазового детектора приемника  Это выражение совпадает с выражением (6.1), и для оценки
Это выражение совпадает с выражением (6.1), и для оценки  можно воспользоваться соответствующими формулами (6.5) и (6.6).
можно воспользоваться соответствующими формулами (6.5) и (6.6).
Если частота дисперсии  то в полосу приемника могут попасть уже два спектральных компонента с разносом, равным частоте дисперсии. При дальнейшем уменьшении частоты дисперсии в полосу приемника попадут три компоненты и т. д. Для оценки
то в полосу приемника могут попасть уже два спектральных компонента с разносом, равным частоте дисперсии. При дальнейшем уменьшении частоты дисперсии в полосу приемника попадут три компоненты и т. д. Для оценки  можно использовать формулы (6.9) и (6.10). При числе компонентов больше четырех следует учитывать фазовые соотношения между отдельными спектральными составляющими, что представляет весьма сложную задачу (формула (6.9) получена в предположении независимости фаз
можно использовать формулы (6.9) и (6.10). При числе компонентов больше четырех следует учитывать фазовые соотношения между отдельными спектральными составляющими, что представляет весьма сложную задачу (формула (6.9) получена в предположении независимости фаз  Поэтому оценим
Поэтому оценим  при низкой дисперсии соотношением [102]:
при низкой дисперсии соотношением [102]:

Здесь  вероятность ошибки при попадании мгновенной частоты помехи в полосу ФМ приемника;
вероятность ошибки при попадании мгновенной частоты помехи в полосу ФМ приемника;  вероятность этого события;
вероятность этого события;  вероятность ошибки при отсутствии помех. Согласно данным работы [104] формула (6.16) применима при
вероятность ошибки при отсутствии помех. Согласно данным работы [104] формула (6.16) применима при 
На основании этих соображений в [103] дан расчет допустимого уровня  помехи при следующем предположении. Уровень помехи
помехи при следующем предположении. Уровень помехи  считается допустимым, если
считается допустимым, если  увеличивается со значения
увеличивается со значения  в отсутствие помехи до
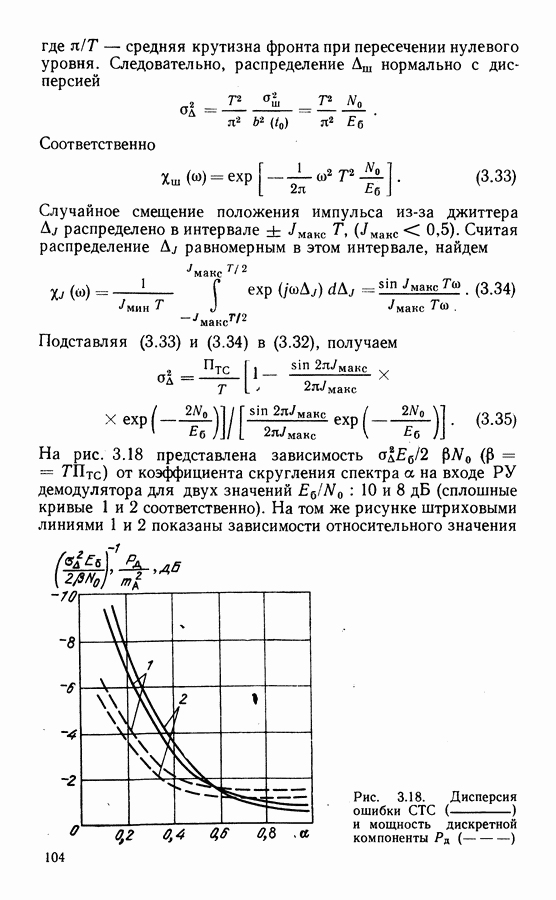
в отсутствие помехи до  при ее наличии. На рис. 6.11 представлена зависимость (кривая 1)
при ее наличии. На рис. 6.11 представлена зависимость (кривая 1)  от частоты сигнала дисперсии при девиации дисперсии
от частоты сигнала дисперсии при девиации дисперсии  и полосе приемного фильтра
и полосе приемного фильтра  . На том же рисунке (прямая 2) представлена гауссовская аппроксимация действия
. На том же рисунке (прямая 2) представлена гауссовская аппроксимация действия  помехи, при этом считалось, что ее мощность в полосе приемного фильтра равна
помехи, при этом считалось, что ее мощность в полосе приемного фильтра равна  Из приведенных зависимостей следует, что существует оптимальная частота дисперсии, лежащая в диапазоне
Из приведенных зависимостей следует, что существует оптимальная частота дисперсии, лежащая в диапазоне  , и разность в допустимом уровне помехи при медленной и оптимальной дисперсии составляет около
, и разность в допустимом уровне помехи при медленной и оптимальной дисперсии составляет около  Результаты этого анализа показывают, что дисперсия со строчной частотой близка к оптимальной с точки зрения мешающего влияния на каналы
Результаты этого анализа показывают, что дисперсия со строчной частотой близка к оптимальной с точки зрения мешающего влияния на каналы  ИКМ/ФМ. Гауссовская оценка
ИКМ/ФМ. Гауссовская оценка

Рис. 6.11. Зависимость допустимого  от частоты сигнала дисперсии
от частоты сигнала дисперсии

Рис. 6.12. Комбинированный сигнал дисперсии
действия  помехи дает значительную ошибку, особенно для случая медленного сигнала дисперсии, существенно завышая допустимый уровень помех по сравнению с реальными условиями.
помехи дает значительную ошибку, особенно для случая медленного сигнала дисперсии, существенно завышая допустимый уровень помех по сравнению с реальными условиями.
В рекомендациях  нормируется среднеминутная мощность помех в полосе
нормируется среднеминутная мощность помех в полосе  [106]. Максимальная допустимая
[106]. Максимальная допустимая  получается при частоте сигнала дисперсии
получается при частоте сигнала дисперсии  поскольку при низкой частоте дисперсии мощность помех
поскольку при низкой частоте дисперсии мощность помех  а при
а при  в полосу
в полосу  попадает один спектральный компонент и
попадает один спектральный компонент и  следует, что
следует, что  Из этих соотношений следует, что к выбору частоты повторения сигнала дисперсии, с точки зрения выполнения норм на мощность помех в полосе
Из этих соотношений следует, что к выбору частоты повторения сигнала дисперсии, с точки зрения выполнения норм на мощность помех в полосе  и минимального влияния на каналы типа ОКН—ИКМ/ФМ, предъявляются противоречивые требования. Кроме того, как было отмечено в [102], применение быстрого сигнала дисперсии может создать значительную помеху в каналах наземных РРЛ из-за биений дискретных компонентов
и минимального влияния на каналы типа ОКН—ИКМ/ФМ, предъявляются противоречивые требования. Кроме того, как было отмечено в [102], применение быстрого сигнала дисперсии может создать значительную помеху в каналах наземных РРЛ из-за биений дискретных компонентов  сигнала с остатком несущей спектра
сигнала с остатком несущей спектра  Отметим также, что при значительном уровне сигнала дисперсии со строчной частотой возникают трудности его компенсации на приемной стороне.
Отметим также, что при значительном уровне сигнала дисперсии со строчной частотой возникают трудности его компенсации на приемной стороне.
В связи с указанным целесообразно использование комбинированного сигнала дисперсии, состоящего из суммы медленного (с частотой кадров) и быстрого (со строчной частотой) сигналов дисперсии (рис. 6.12). Введение медленной дисперсии обеспечивает выполнение норм на мощность помех в полосе  а быстрого — уменьшение мешающего действия
а быстрого — уменьшение мешающего действия  сигнала на каналы
сигнала на каналы  ИКМ/ФМ [103].
ИКМ/ФМ [103].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
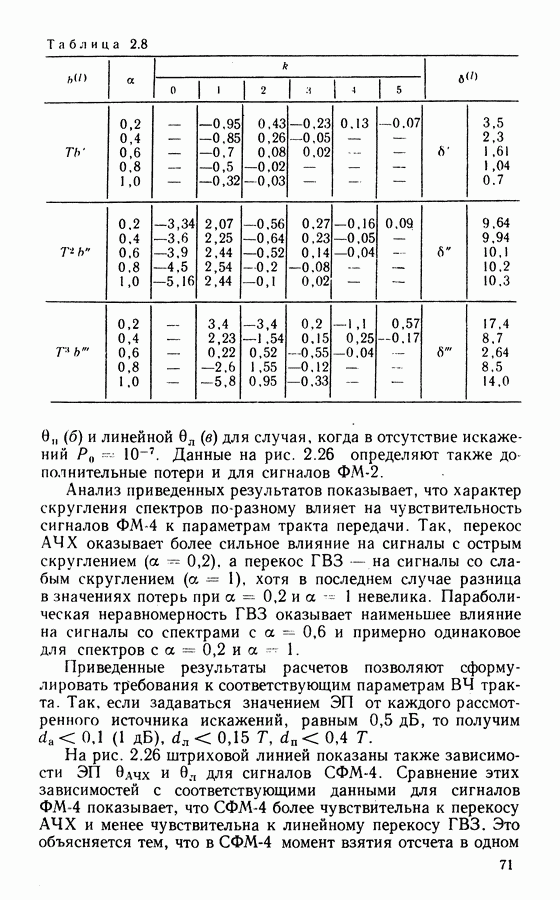
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
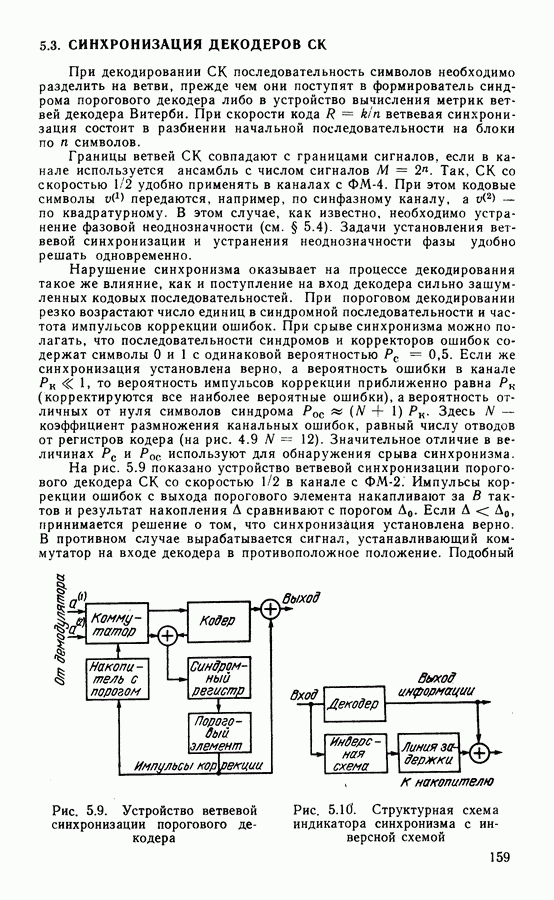
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
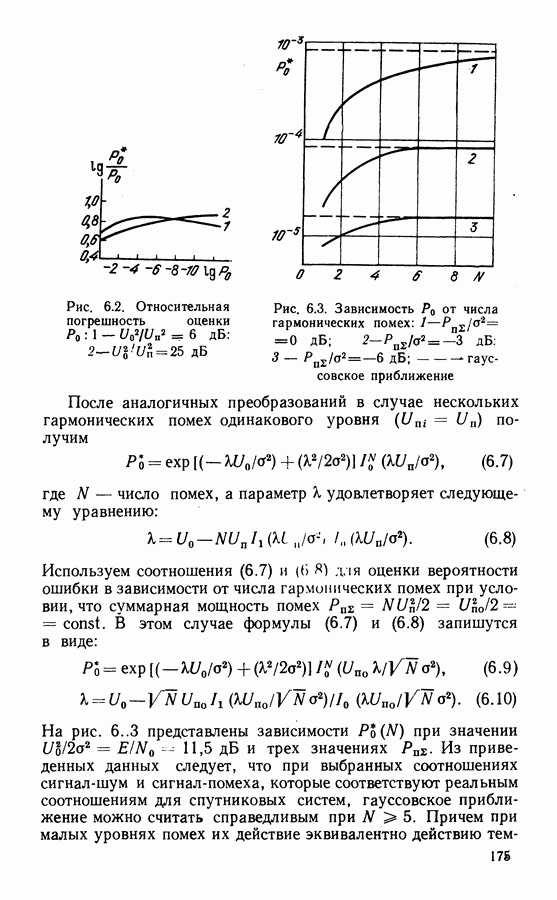
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
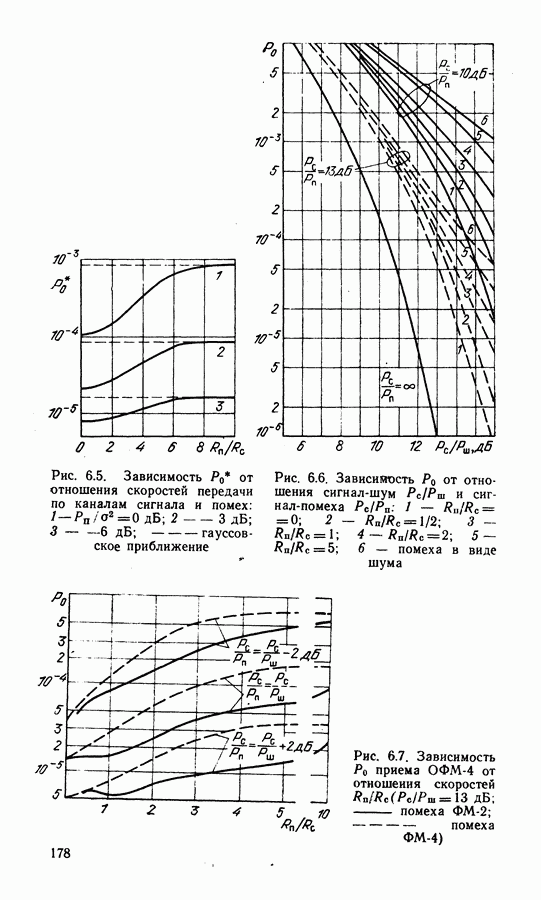
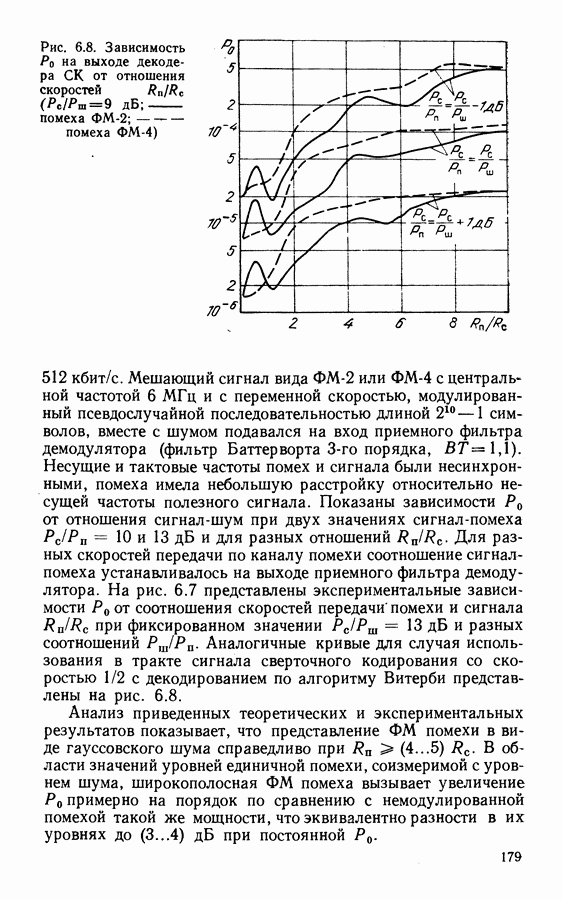
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
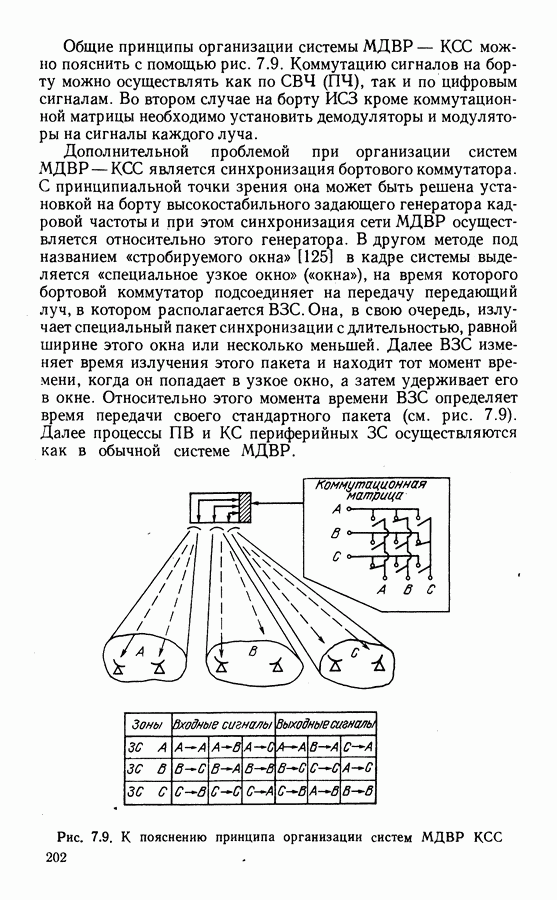
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ