| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
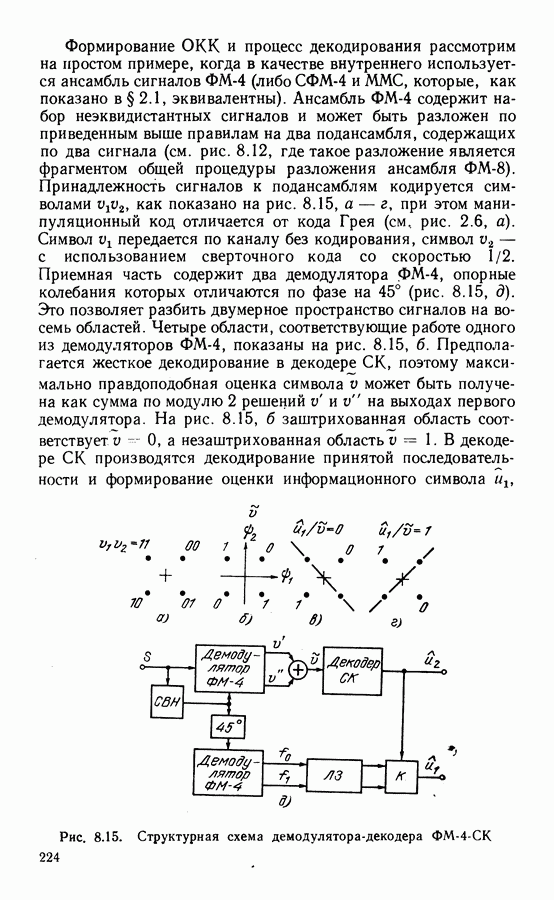
В § 3.2 показано, что принципиальным недостатком всех способов формирования несущей из принимаемого ФМ сигнала является неоднозначность фазы выделенной несущей. Порядок неоднозначности равен числу фаз сигнала. В системах с двоичной ФМ наблюдается «обратная работа», когда на выход демодулятора принимаемые символы поступают в инверсном виде. При демодуляции сигналов ФМ-4 картина будет сложнее.
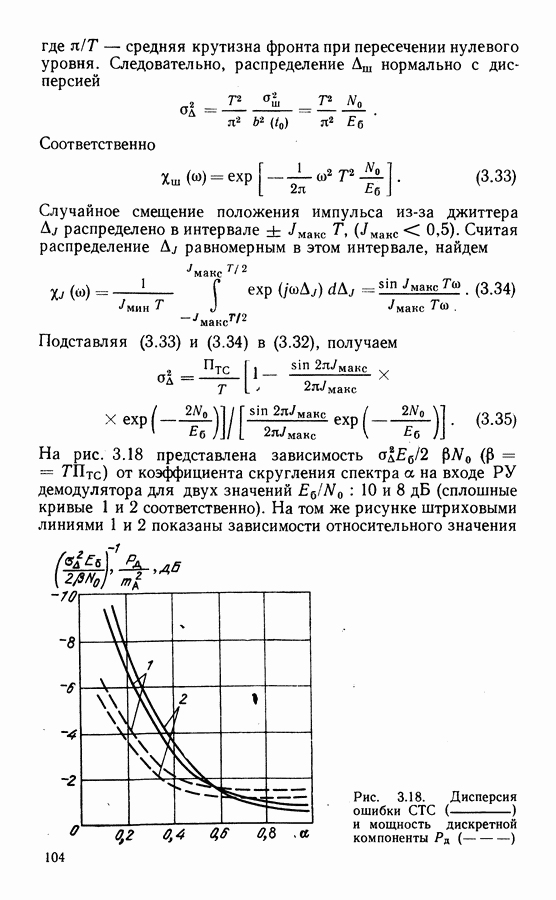
На рис. 3.19 показаны векторные диаграммы передаваемых сигналов  опорных колебаний
опорных колебаний  при различных значениях начальной фазы
при различных значениях начальной фазы  а также модели каналов, соответствующие этим фазам. Данные с квадратурных выходов
а также модели каналов, соответствующие этим фазам. Данные с квадратурных выходов  демодулятора могут поступать не только в инверсном виде (фаза
демодулятора могут поступать не только в инверсном виде (фаза  ), но и перекрещенными между каналами (фаза
), но и перекрещенными между каналами (фаза  ). Как отмечено в § 2.1, переход к относительной фазовой модуляции обеспечивает передачу сигналов по каналу с неоднозначностью.
). Как отмечено в § 2.1, переход к относительной фазовой модуляции обеспечивает передачу сигналов по каналу с неоднозначностью.
В соответствии с выражением (2.11) при относительной передаче информация содержится в парах последовательно передаваемых символов. Перескоки фазы опорной несущей происходят достаточно редко, так что на длительном интервале фазу можно считать постоянной, но выбранной случайным образом из множества возможных значений фазы. Передачу информации по такому каналу удобно рассматривать с использованием алгебраической модели канала [341.
Множество дискретных значений фазы сигнала в такой модели заменяется множеством символов  где М — число фаз. Символы
где М — число фаз. Символы  образуют циклическую группу. В простейшем случае при
образуют циклическую группу. В простейшем случае при  символы
символы  а операции над ними совершаются по известным правилам сложения по модулю 2. Неоднозначность фазы также отображается символом
а операции над ними совершаются по известным правилам сложения по модулю 2. Неоднозначность фазы также отображается символом  который принадлежит
который принадлежит

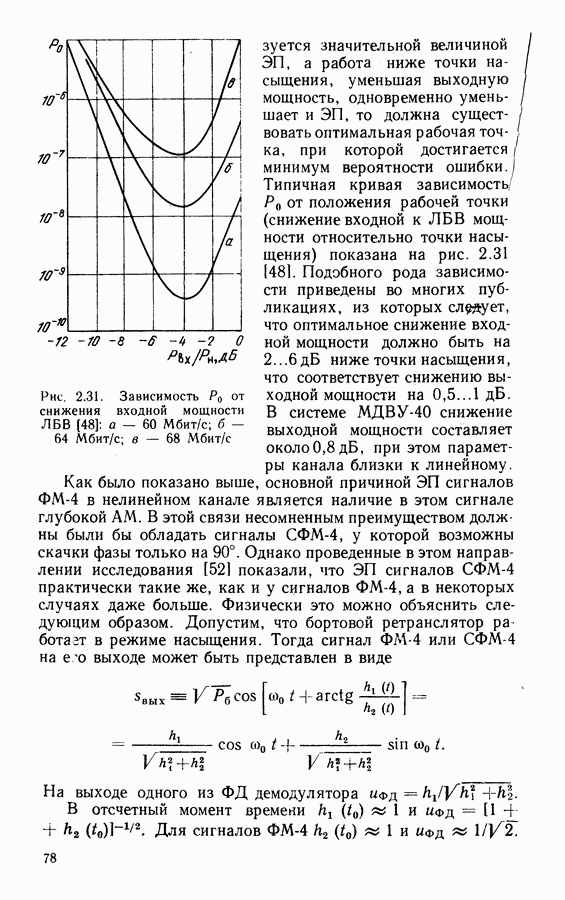
Рис. 3.19. Модели канала ФМ-4 с неоднозначностью фазы

Рис. 3.20. Алгебраическая модель канала с относительным кодированием
к множеству  Тогда принятые символы определяются как сумма по модулю М переданных символов и символов неоднозначности
Тогда принятые символы определяются как сумма по модулю М переданных символов и символов неоднозначности 
Представим последовательность  -ичных символов
-ичных символов  передаваемых по каналу в виде формальных рядов
передаваемых по каналу в виде формальных рядов

Можно проверить делением, что  Пусть
Пусть  передаточная функция относительного декодера на выходе канала с неоднозначностью (рис. 3.20, а). Тогда последовательность символов на его выходе имеет вид и
передаточная функция относительного декодера на выходе канала с неоднозначностью (рис. 3.20, а). Тогда последовательность символов на его выходе имеет вид и  где знак
где знак  означает сложение по модулю М. Если положить
означает сложение по модулю М. Если положить  то при подаче на вход относительного декодера последовательности символов неоднозначности (3.36) на его выходе получим единственный ненулевой символ
то при подаче на вход относительного декодера последовательности символов неоднозначности (3.36) на его выходе получим единственный ненулевой символ  в момент
в момент  так как
так как  . В последующие моменты времени при
. В последующие моменты времени при  символы неоднозначности на выходе декодера равны нулю. Очевидно, что передаточная функция относительного кодера должна быть обратной, т. е.
символы неоднозначности на выходе декодера равны нулю. Очевидно, что передаточная функция относительного кодера должна быть обратной, т. е. 
Функциональные схемы относительного кодера и декодера показаны на рис. 3.20, б.
Декодер состоит из устройства вычисления разности символов (по модулю М) и элемента задержки символов на

Рис. 3.21. Функциональная схема устройства вычитания по модулю 4
один такт. В системах с ФМ-2 функции вычитающего устройства выполняет сумматор по модулю 2. В кодере используют сумматор по модулю М.
Для каналов с многопозиционной ФМ относительное кодирование и декодирование реализуют устройствами с двоичным представлением УИ-ичных символов. На рис. 3.21 показана функциональная схема устройства, реализующего вычитание  Входные и выходные символы представлены в двоичном двухразрядном коде Грея. Такое устройство является составным элементом кодера и декодера в системе с ОФМ-4. Синтез схем для ОФМ другой кратности может быть выполнен по известным правилам синтеза устройств дискретной автоматики.
Входные и выходные символы представлены в двоичном двухразрядном коде Грея. Такое устройство является составным элементом кодера и декодера в системе с ОФМ-4. Синтез схем для ОФМ другой кратности может быть выполнен по известным правилам синтеза устройств дискретной автоматики.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
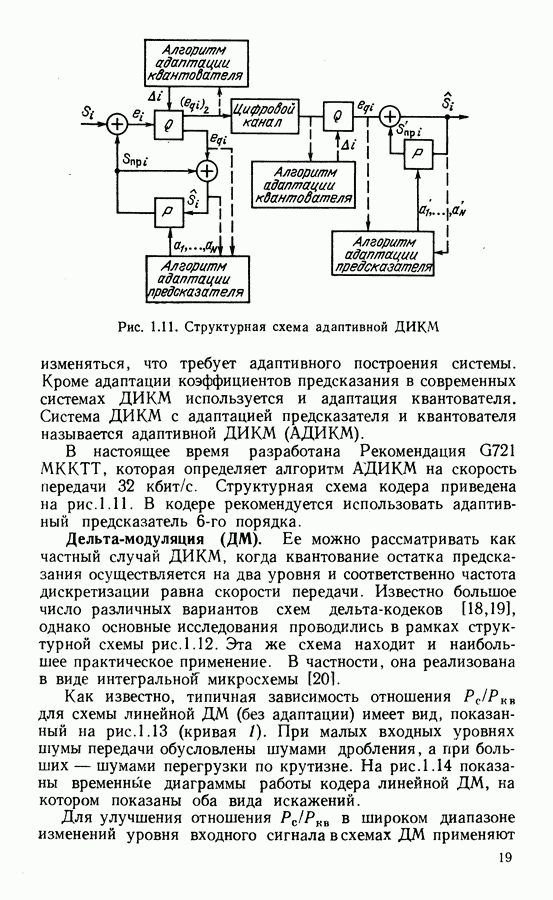
- Дифференциальная ИКМ (ДИКМ).
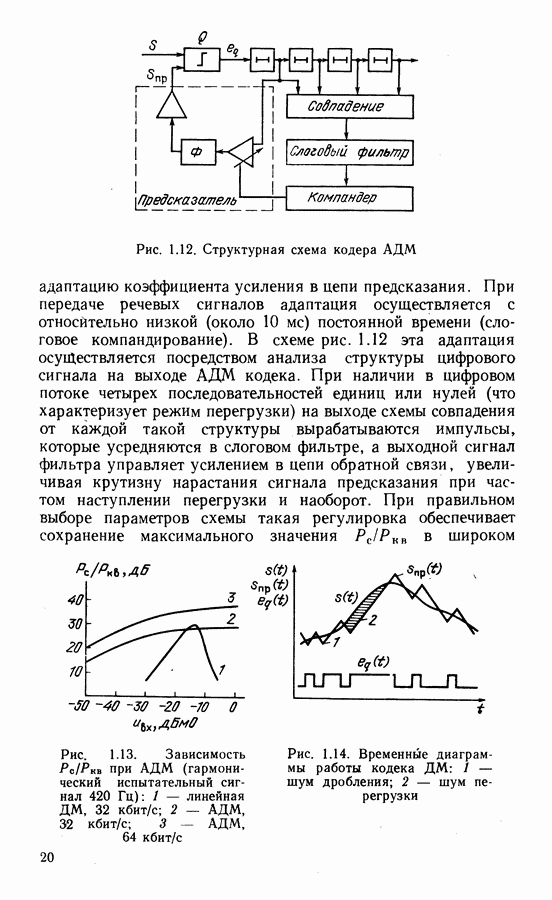
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
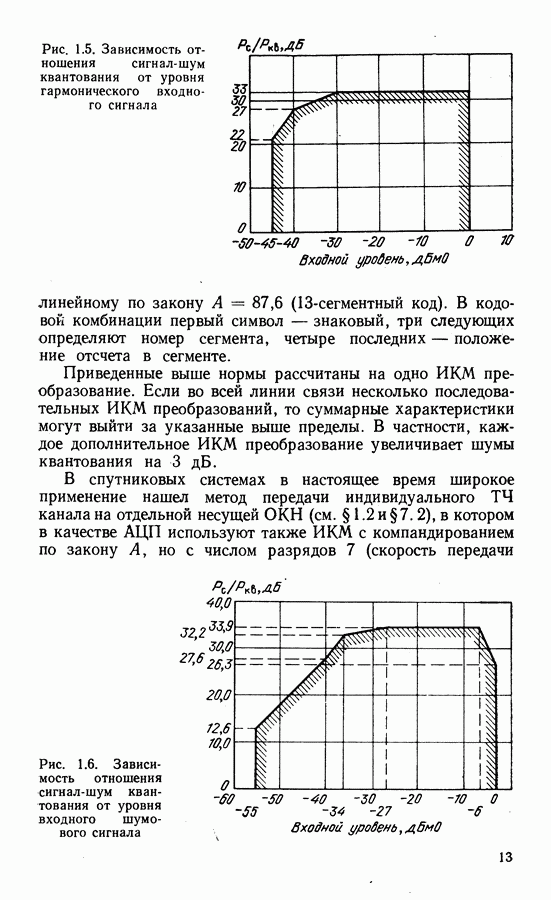
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
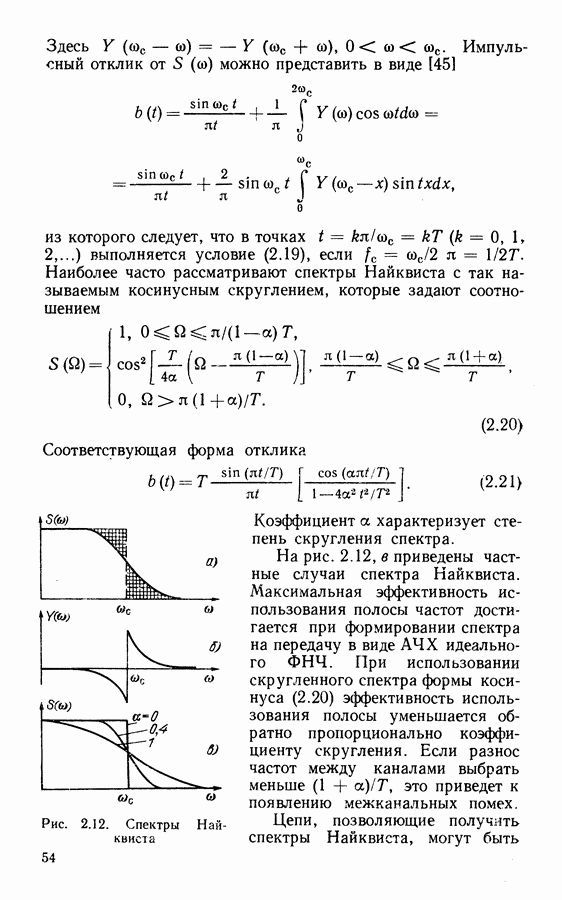
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
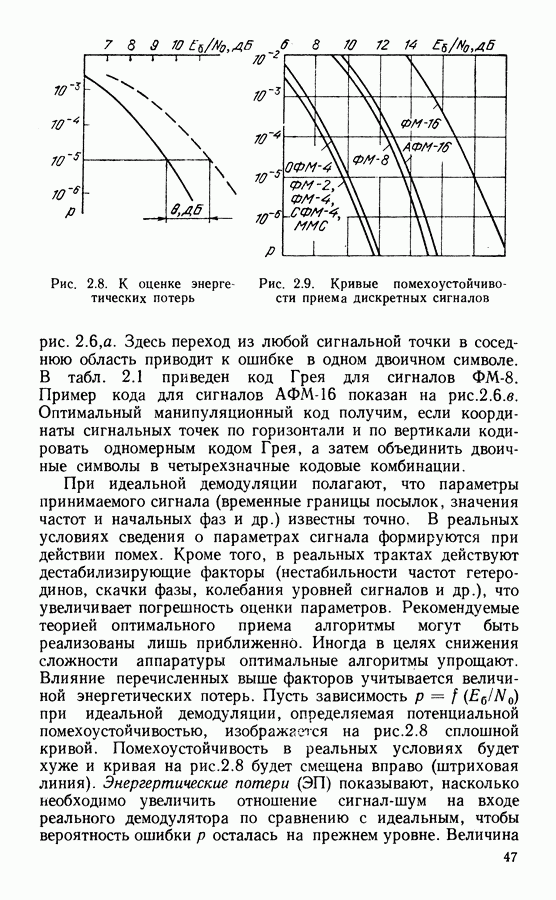
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
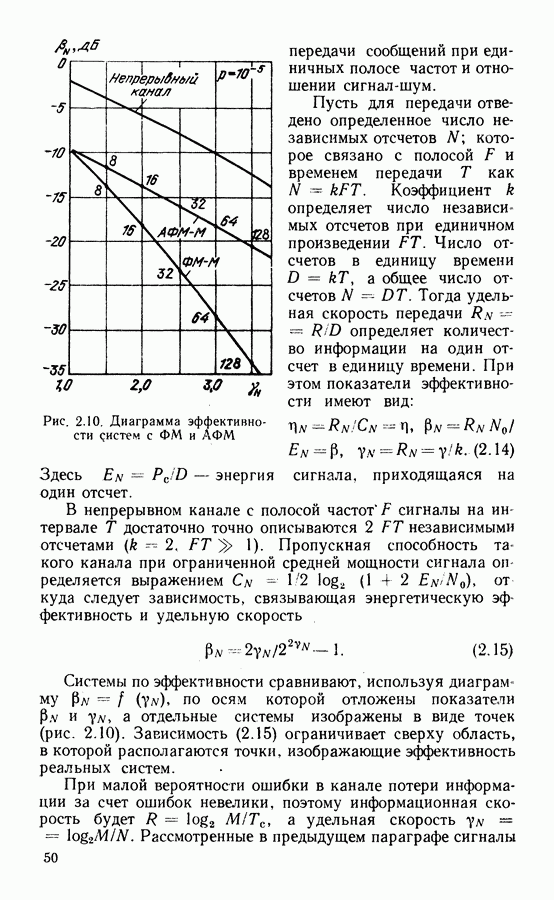
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
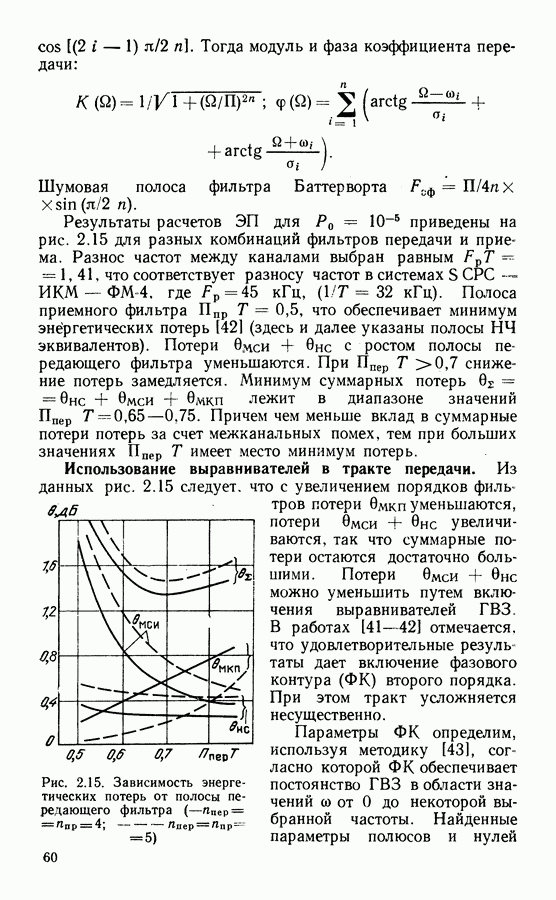
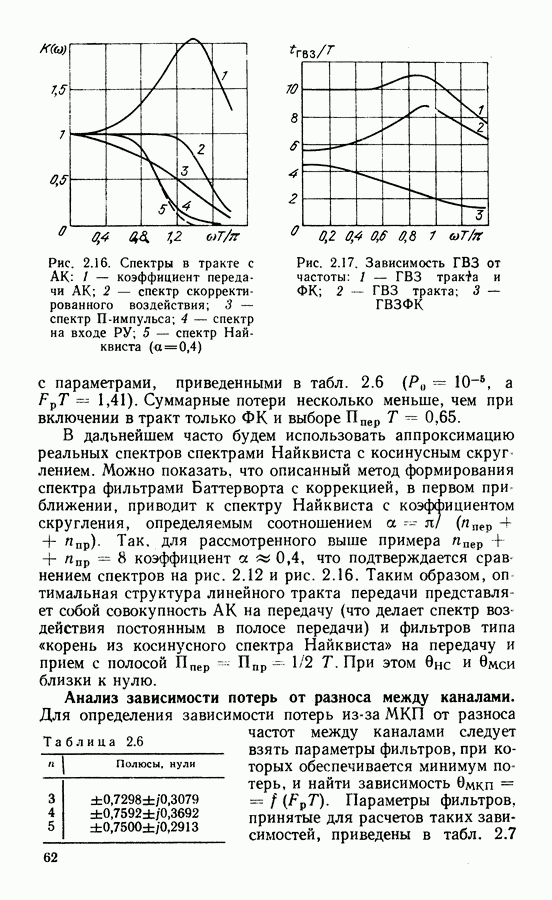
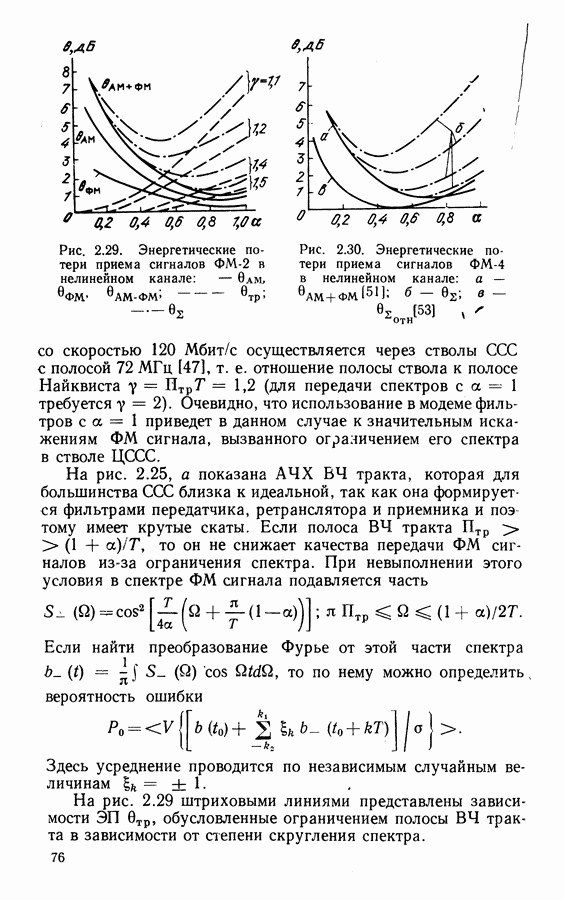
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
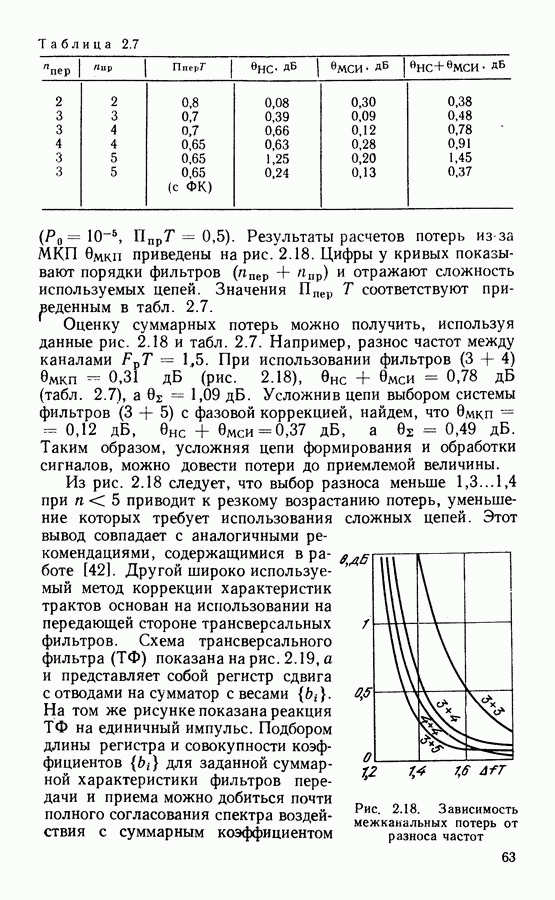
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
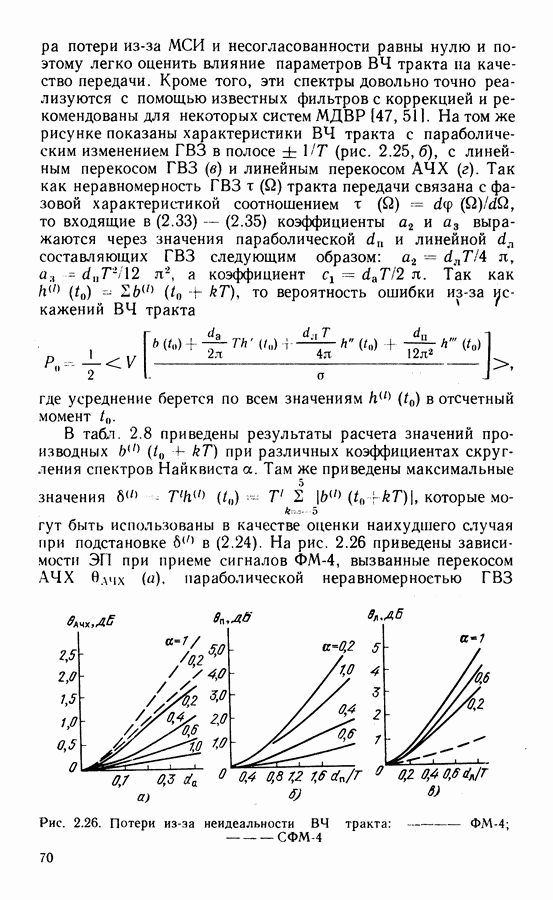
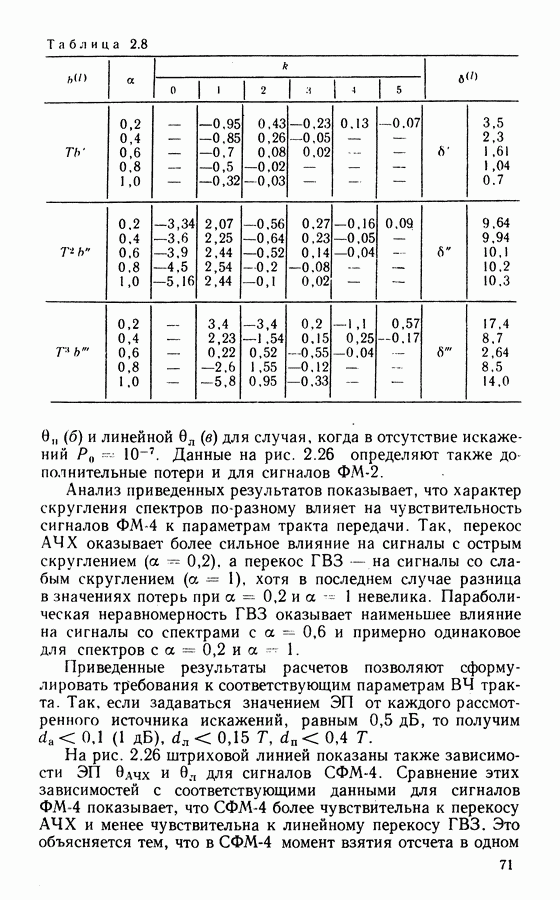
- Энергетические потери в системе с ФМ-4.
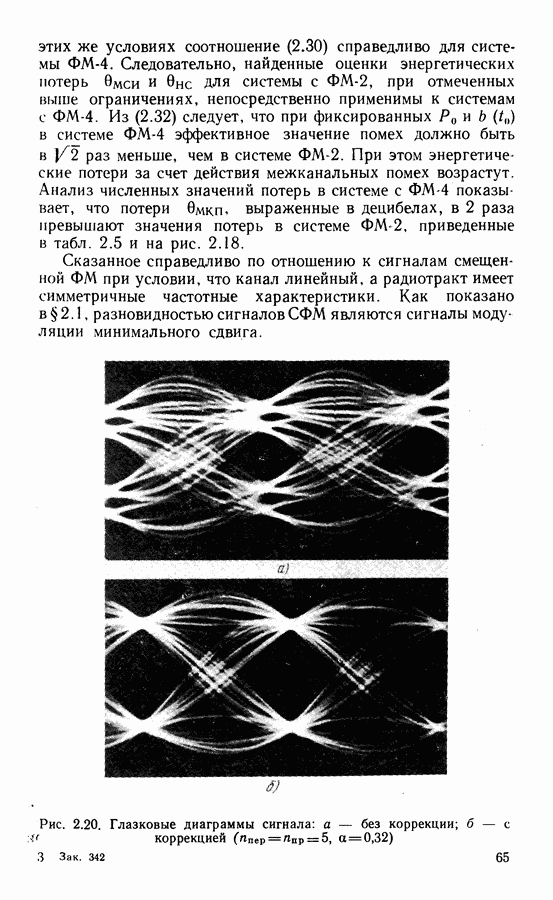
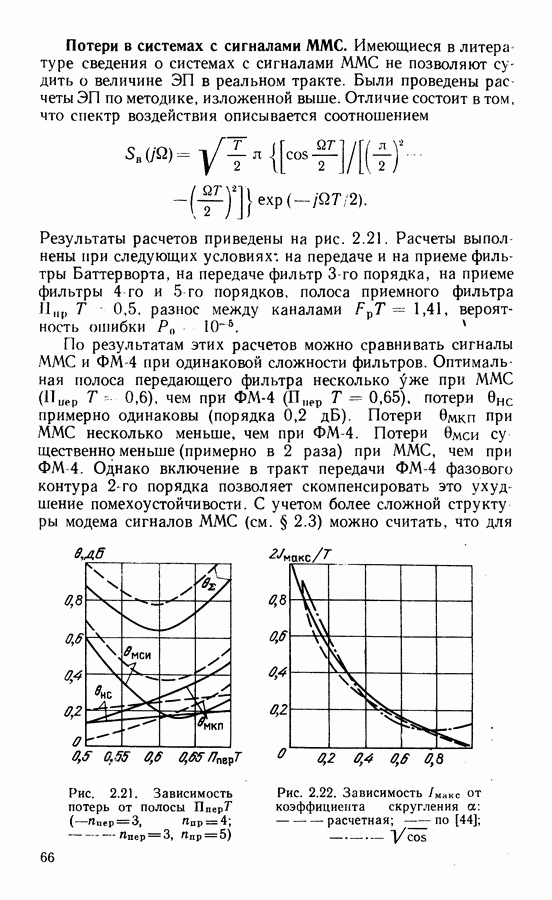
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
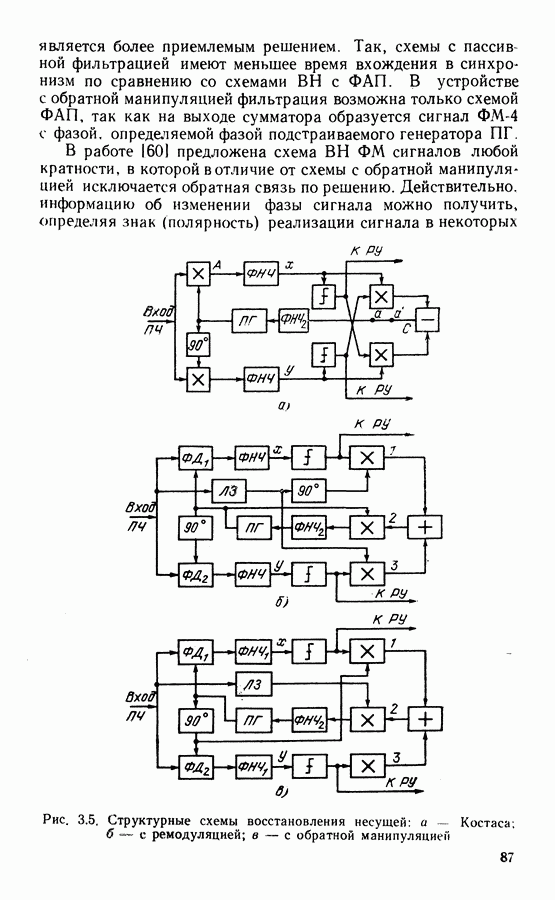
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
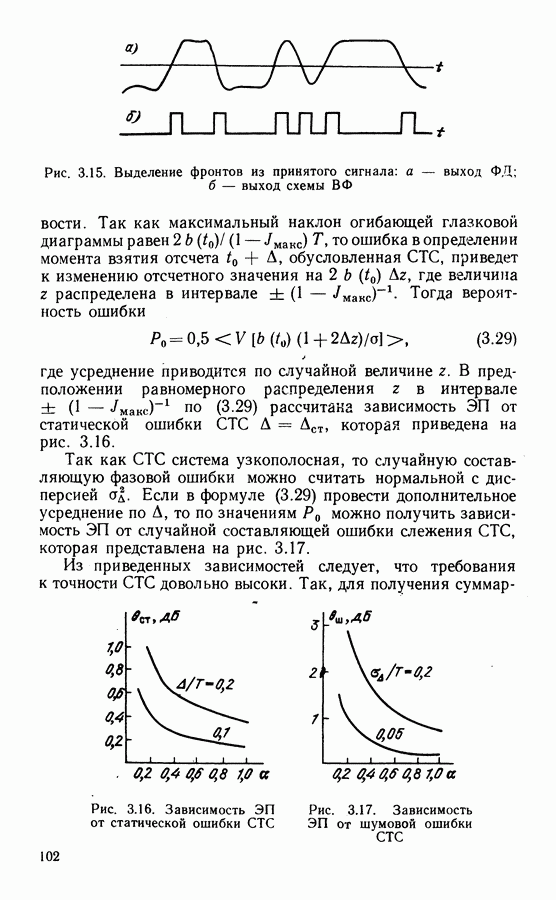
- Требования к точности работы системы ВН.
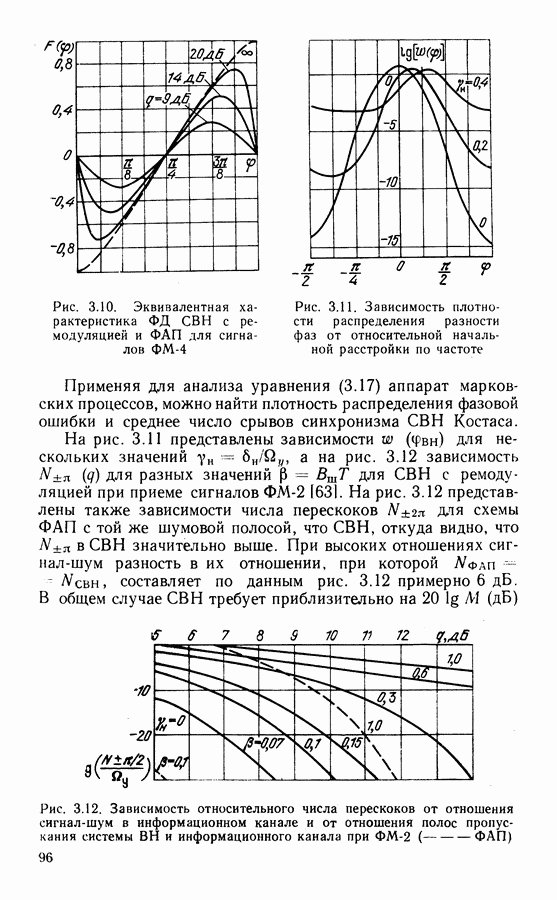
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
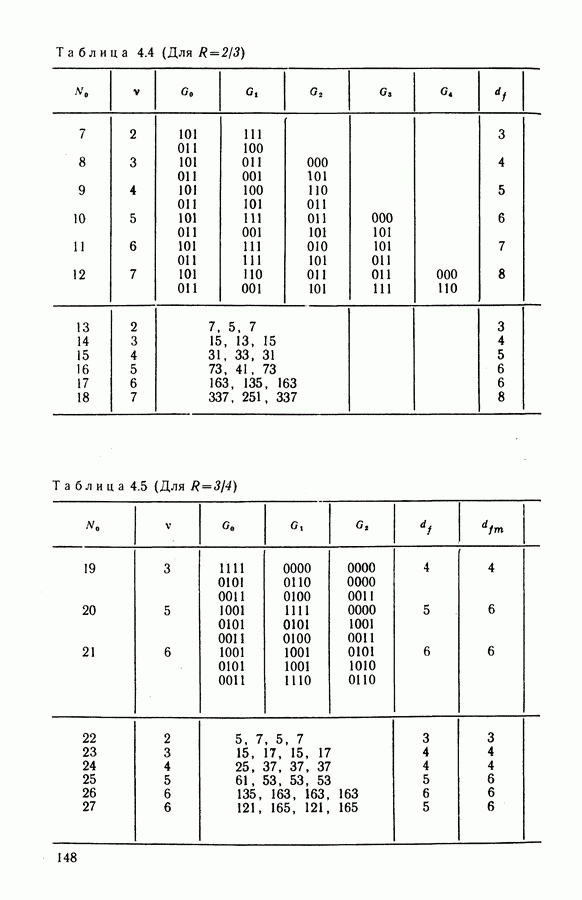
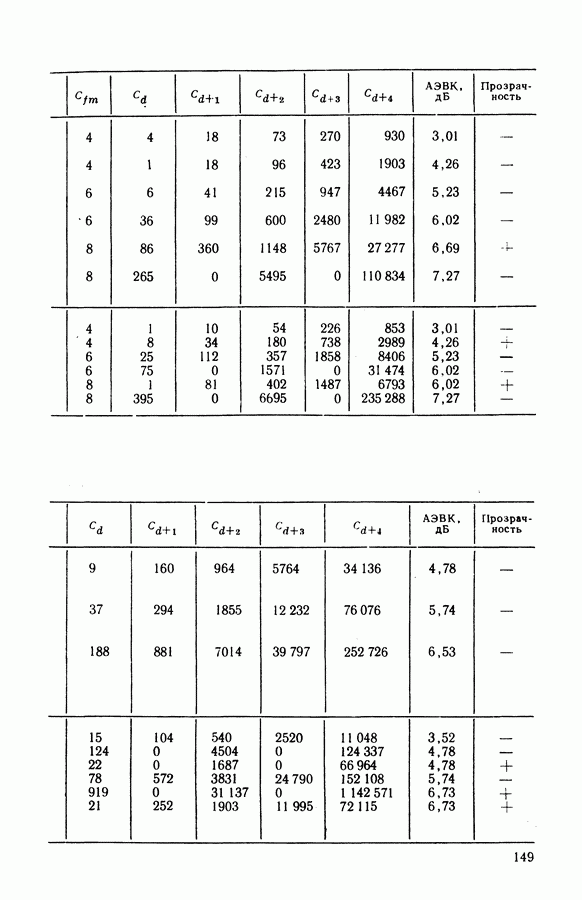
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
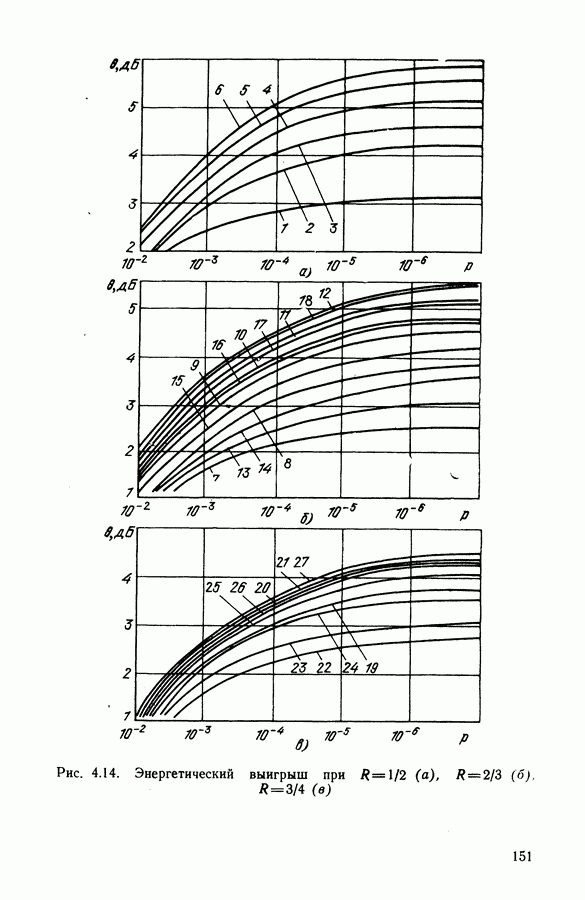
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
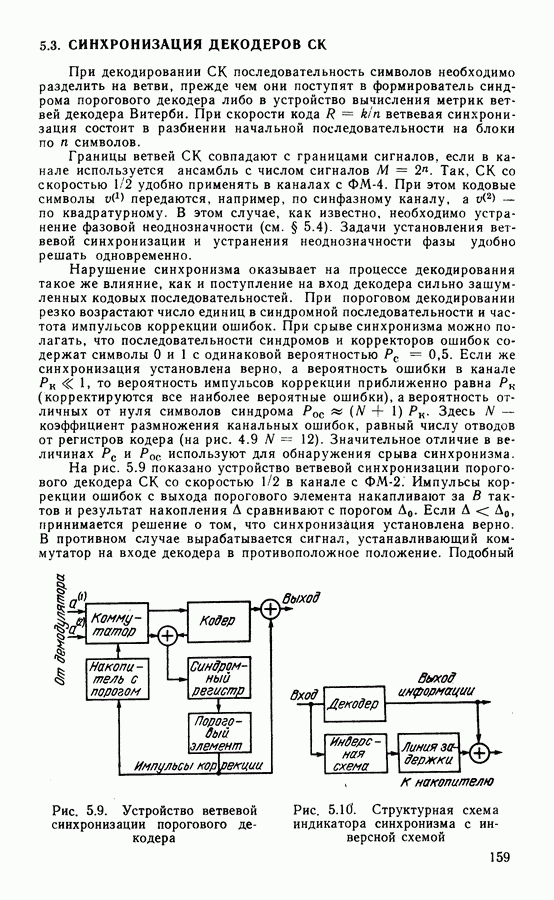
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
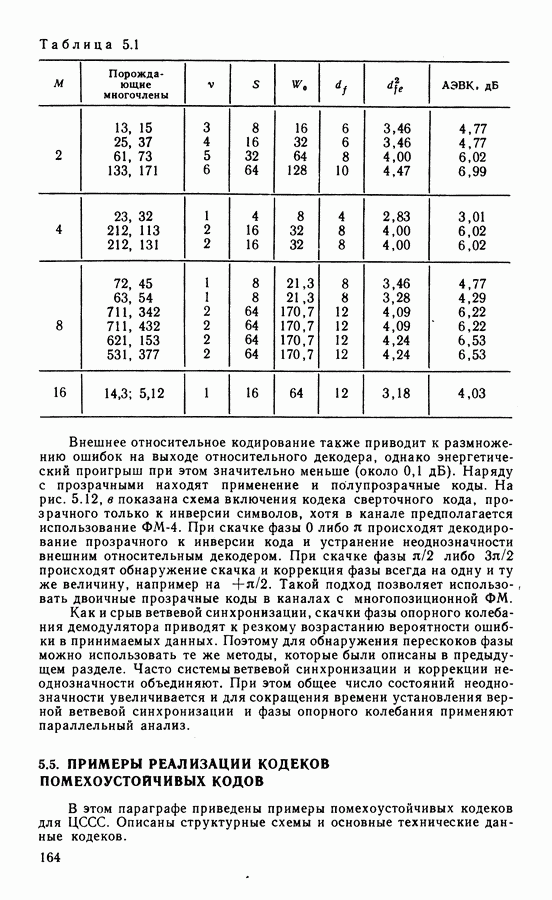
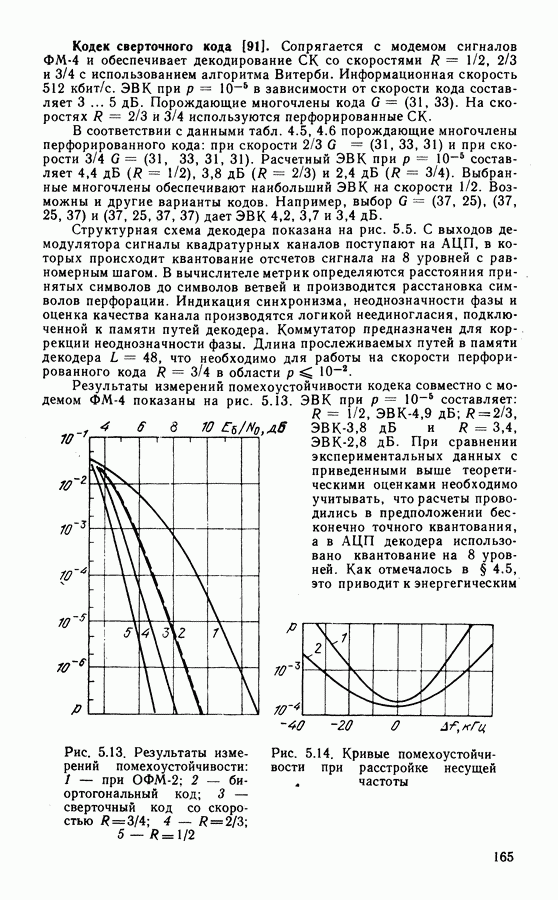
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
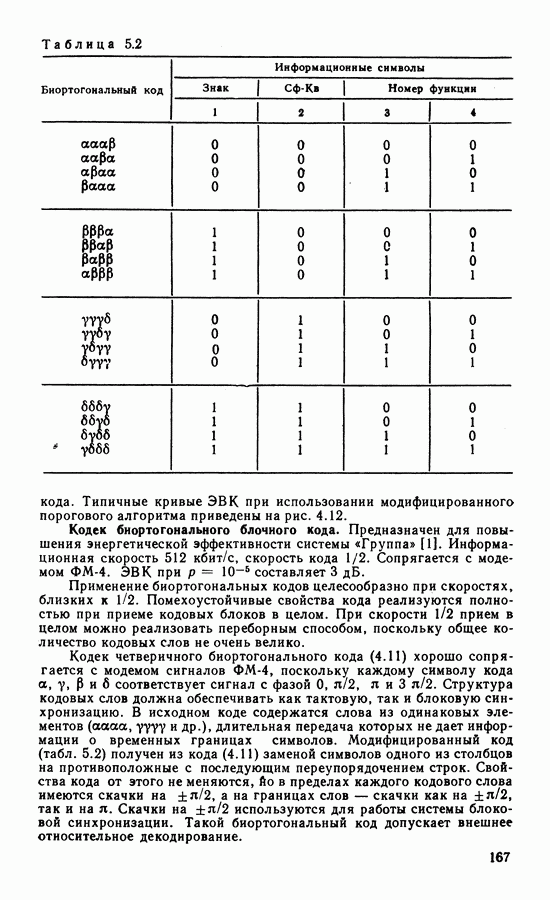
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
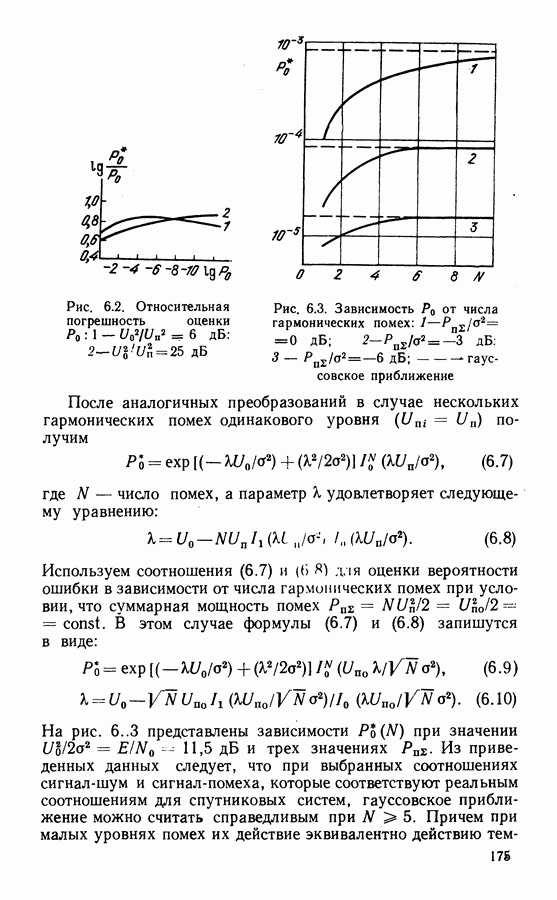
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
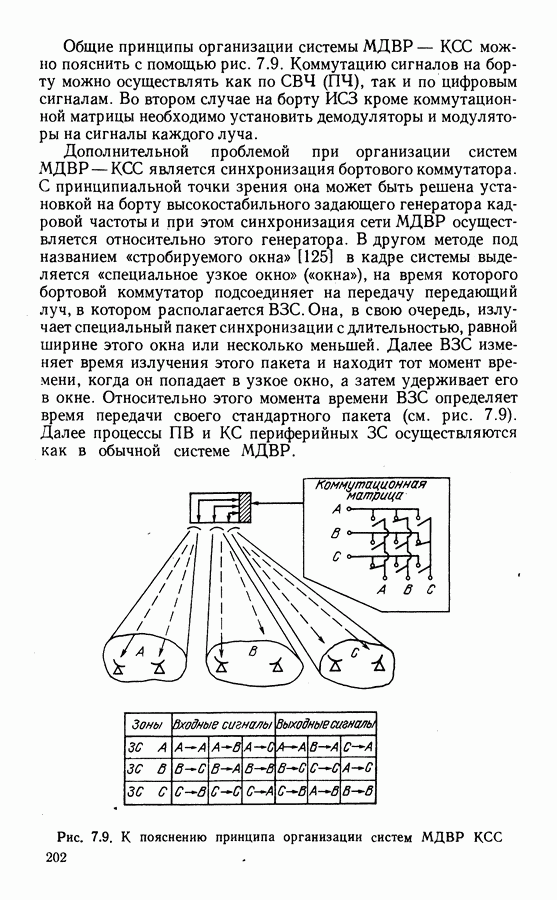
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
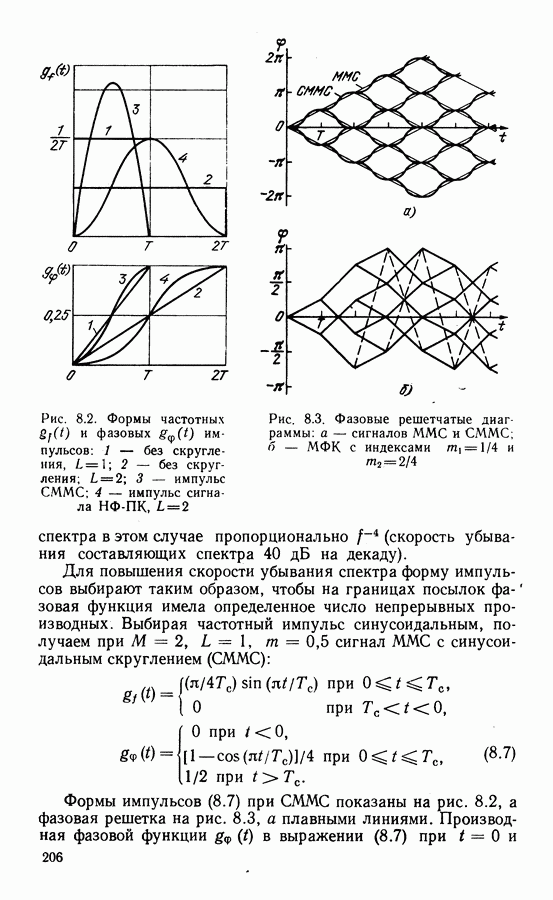
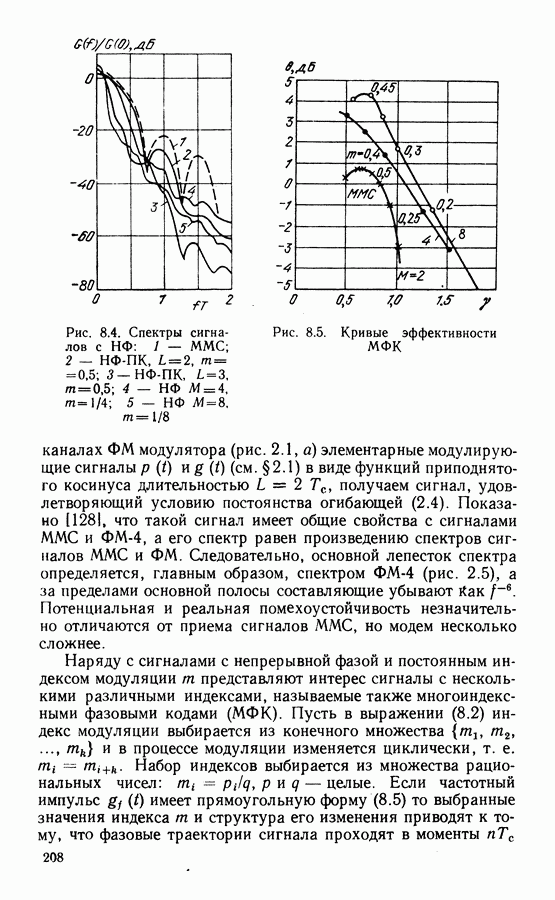
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
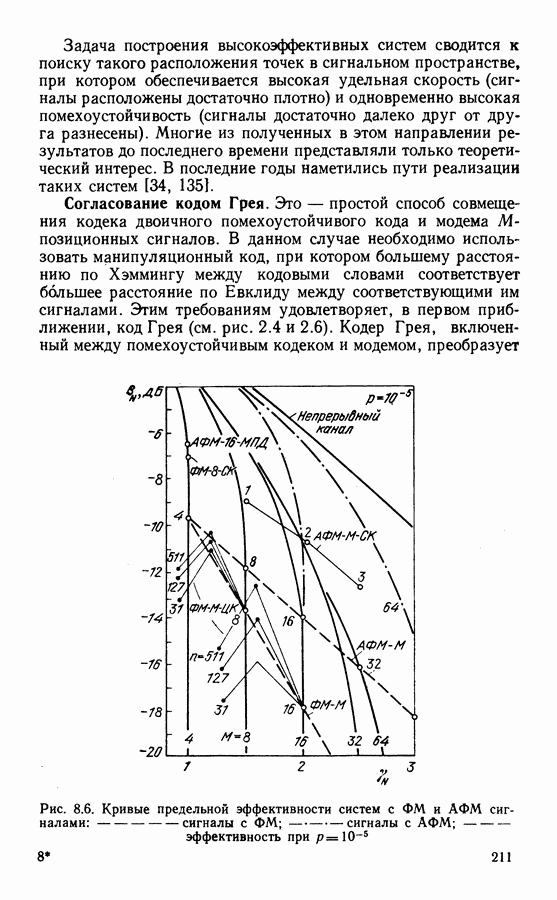
- Согласование кодом Грея.
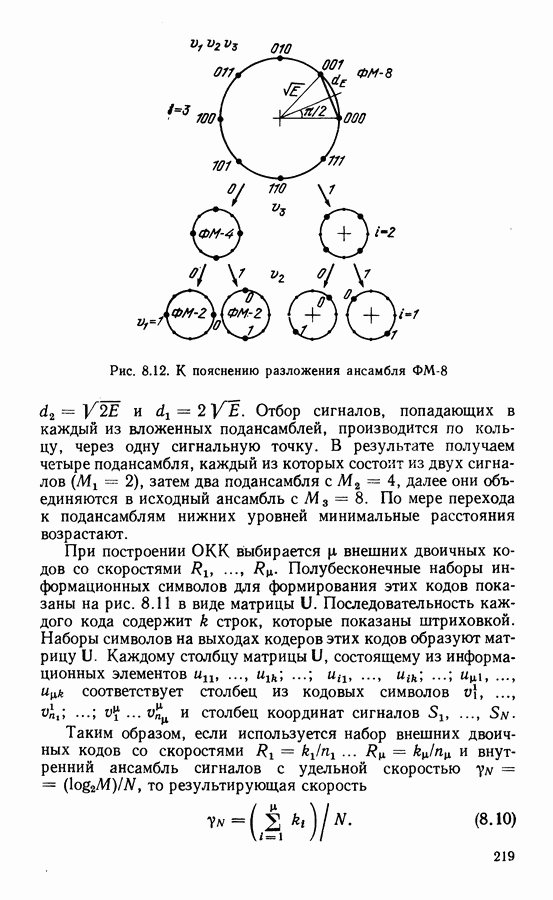
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ