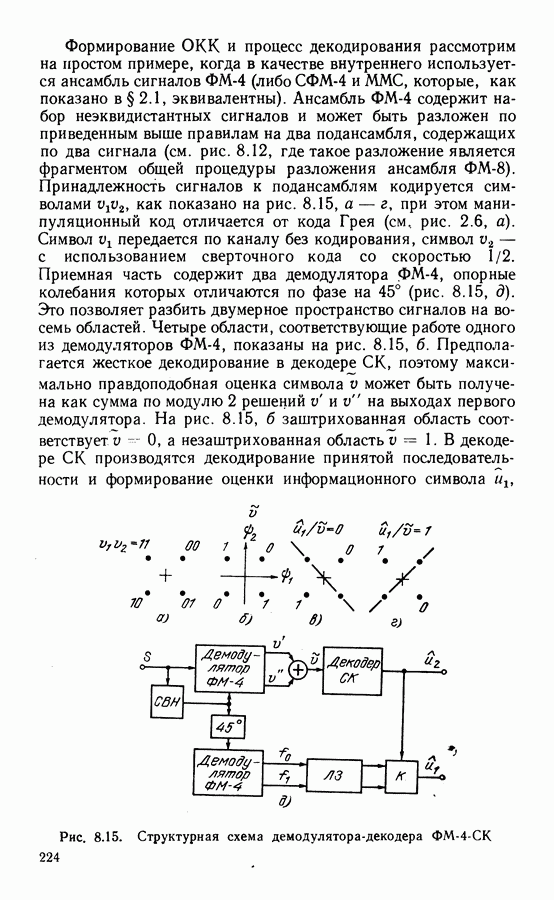
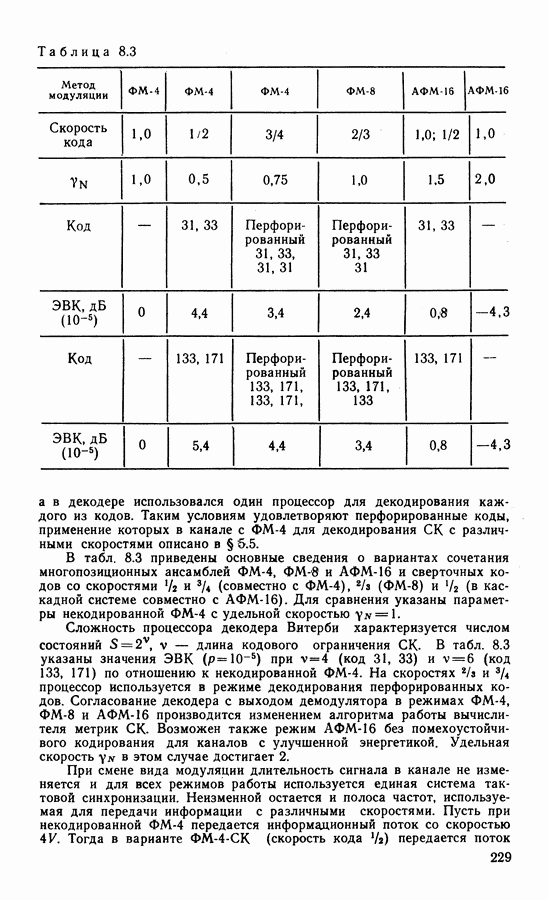
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
Для описания линейных кодов используют математический аппарат высшей алгебры. Подробные сведения по этому вопросу читатель может найти в книгах [74, 75]. Напомним элементы теории, необходимые для дальнейшего.
При блоковом кодировании наборы кодовых символов образуют кодовые слова  Символы слов
Символы слов  выбирают из поля Галуа
выбирают из поля Галуа  Множество слов длины
Множество слов длины  образует
образует  -мерное векторное пространство над полем
-мерное векторное пространство над полем  Для элементов этого пространства (векторов) определены операции сложения и умножения, умножение вектора на элемент поля, а также скалярное произведение векторов. Векторы
Для элементов этого пространства (векторов) определены операции сложения и умножения, умножение вектора на элемент поля, а также скалярное произведение векторов. Векторы  ортогональны, если их скалярное произведение
ортогональны, если их скалярное произведение  Совокупность линейно независимых векторов образует базис, который порождает
Совокупность линейно независимых векторов образует базис, который порождает  -мерное векторное пространство
-мерное векторное пространство  причем каждый из векторов этого пространства может быть получен как линейная комбинация базисных векторов. Подмножество векторов пространства
причем каждый из векторов этого пространства может быть получен как линейная комбинация базисных векторов. Подмножество векторов пространства  удовлетворяющее аксиомам векторного пространства, образует подпространство
удовлетворяющее аксиомам векторного пространства, образует подпространство 
В цифровых системах широко используют двоичные коды, так как их структура и реализация кодеков наиболее просты. При двоичном кодировании слова состоят из элементов поля 
Блоковый код длины  словами называется линейным
словами называется линейным  кодом, если его кодовые слова образуют
кодом, если его кодовые слова образуют  -мерное подпространство векторного
-мерное подпространство векторного  -мерного пространства
-мерного пространства  Подпространство V порождается базисом из к линейно независимых векторов, которые образуют строки порождающей матрицы
Подпространство V порождается базисом из к линейно независимых векторов, которые образуют строки порождающей матрицы  кода
кода

Если  матрица-строка информационного слова, то кодирование производят по правилу
матрица-строка информационного слова, то кодирование производят по правилу

где  матрица-строка кодового слова
матрица-строка кодового слова  кода.
кода.
Кодовые слова можно представить в систематической форме, образуя отдельно информационную часть из  символов и проверочную часть из
символов и проверочную часть из  символов. Порождающая матрица систематического кода имеет вид
символов. Порождающая матрица систематического кода имеет вид

Матрица  содержит единичную матрицу
содержит единичную матрицу  определяющую информационную часть слова, и матрицу Р, определяющую проверочные символы. Переход к систематической форме производится линейной комбинацией строк матрицы (4.1).
определяющую информационную часть слова, и матрицу Р, определяющую проверочные символы. Переход к систематической форме производится линейной комбинацией строк матрицы (4.1).
При декодировании проверочные соотношения устанавливают с использованием проверочной матрицы Н, пространство строк которой ортогонально пространству строк порождающей матрицы, т. е.

Здесь индекс Т — символ транспонирования. Если порождающая матрица задана в форме (4.2), для выполнения условия ортогональности проверочная матрица должна иметь вид

Каждое слово линейного кода  также удовлетворяет условию ортогональности
также удовлетворяет условию ортогональности

При передаче по каналу кодовые символы искажаются. Принятые слова имеют вид  где
где  а вектор ошибки ошибок
а вектор ошибки ошибок  На приеме вычисляют синдром
На приеме вычисляют синдром

Синдром зависит только от вектора ошибок:  Поскольку
Поскольку  синдром
синдром

Если  принятое слово
принятое слово  принадлежит к множеству кодовых слов. При
принадлежит к множеству кодовых слов. При  слово
слово  содержит ошибки. По значениям символов синдрома судят о конфигурации вектора ошибок. Этот принцип лежит в основе синдромного декодирования.
содержит ошибки. По значениям символов синдрома судят о конфигурации вектора ошибок. Этот принцип лежит в основе синдромного декодирования.
Для оценки обнаруживающей и исправляющей способности кода используют минимальное расстояние. Расстояние Хэмминга  между словами
между словами  равно числу символов, в которых они отличаются. Для вычисления расстояния
равно числу символов, в которых они отличаются. Для вычисления расстояния  между двоичными словами используют посимвольное сложение по модулю 2. Наименьшее из расстояний между любой парой кодовых слов называется минимальным расстоянием кода
между двоичными словами используют посимвольное сложение по модулю 2. Наименьшее из расстояний между любой парой кодовых слов называется минимальным расстоянием кода  Минимальное расстояние линейного кода равно наименьшему весу его ненулевых кодовых слов. При декодировании ошибка может быть обнаружена, если ее кратность
Минимальное расстояние линейного кода равно наименьшему весу его ненулевых кодовых слов. При декодировании ошибка может быть обнаружена, если ее кратность  (количество ошибочных символов на длине блока) не превышает
(количество ошибочных символов на длине блока) не превышает  Ошибка с весом
Ошибка с весом  может быть исправлена при
может быть исправлена при 
— нечетное). Таким образом, способность кода с минимальным расстоянием  корректировать случайные ошибки определяется неравенствами: кратность обнаруживаемой ошибки —1; кратность исправляемой ошибки
корректировать случайные ошибки определяется неравенствами: кратность обнаруживаемой ошибки —1; кратность исправляемой ошибки  нечетное) и
нечетное) и  четное).
четное).
С учетом расстояния систематические коды обозначают как  Важным параметром кода является кодовая скорость
Важным параметром кода является кодовая скорость  Одна из проблем теории кодирования состоит в поиске кодов, которые при заданной длине блока
Одна из проблем теории кодирования состоит в поиске кодов, которые при заданной длине блока  и кодовой скорости
и кодовой скорости  обеспечивают наибольшее расстояние
обеспечивают наибольшее расстояние  Пределы этих параметров определяются кодовыми границами, сведения о которых можно найти в [74—76].
Пределы этих параметров определяются кодовыми границами, сведения о которых можно найти в [74—76].
Существуют совершенные коды, позволяющие исправить все ошибки веса  и ни одной ошибки большего веса. К ним относятся, например, коды Хэмминга. Большинство кодов отличны от совершенных. Степень использования корректирующей способности кода зависит от алгоритма декодирования. При полном декодировании используют все возможности исправлять ошибки, вытекающие из свойств кода. Во многих случаях такое декодирование оказывается сложным. Прибегая к неполному декодированию, упрощают алгоритм в обмен на снижение помехоустойчивости.
и ни одной ошибки большего веса. К ним относятся, например, коды Хэмминга. Большинство кодов отличны от совершенных. Степень использования корректирующей способности кода зависит от алгоритма декодирования. При полном декодировании используют все возможности исправлять ошибки, вытекающие из свойств кода. Во многих случаях такое декодирование оказывается сложным. Прибегая к неполному декодированию, упрощают алгоритм в обмен на снижение помехоустойчивости.
Значительная часть используемых на практике блоковых кодов относится к классу циклических кодов  Это обусловлено упрощением процедур кодирования и декодирования на основе использования циклических свойств кода. Если
Это обусловлено упрощением процедур кодирования и декодирования на основе использования циклических свойств кода. Если  слово
слово  то его циклический сдвиг на произвольное число символов также является разрешенным кодовым словом. Например, слово
то его циклический сдвиг на произвольное число символов также является разрешенным кодовым словом. Например, слово  соответствует циклическому сдвигу
соответствует циклическому сдвигу  на один символ
на один символ
вправо. Свойства ЦК удобно изучать, представляя кодовые слова в виде многочленов по степеням формальной переменной  коэффициенты которых — символы кодового блока
коэффициенты которых — символы кодового блока  Сложение многочленов производится поэлементно и коэффициенты при одинаковых степенях
Сложение многочленов производится поэлементно и коэффициенты при одинаковых степенях  складывают по модулю 2, а умножение — по модулю многочлена
складывают по модулю 2, а умножение — по модулю многочлена  этом случае все возможные многочлены степени
этом случае все возможные многочлены степени  и меньше образуют алгебраическое кольцо многочленов
и меньше образуют алгебраическое кольцо многочленов 
Для построения циклического кода в кольце  выбирают подмножество многочленов — идеал
выбирают подмножество многочленов — идеал  Многочлен минимальной степени в этом подмножестве
Многочлен минимальной степени в этом подмножестве  называется порождающим многочленом
называется порождающим многочленом  Все многочлены идеала У, соответствующие кодовым словам
Все многочлены идеала У, соответствующие кодовым словам  делятся на
делятся на  без остатка и правило кодирования имеет вид
без остатка и правило кодирования имеет вид

Если степень многочлена и  равна к
равна к  степень
степень  не превышает
не превышает  то степень порождающего многочлена не превышает
то степень порождающего многочлена не превышает  Вводят понятие проверочного многочлена
Вводят понятие проверочного многочлена

степень которого не превышает 
Как и любой линейный код, ЦК представляют порождающей и проверочной матрицами. Первые  сдвигов порождающего многочлена образуют линейно независимые строки порождающей матрицы ЦК в несистематической форме:
сдвигов порождающего многочлена образуют линейно независимые строки порождающей матрицы ЦК в несистематической форме:

Используя условие ортогональности матриц (4.3), можно показать, что проверочная матрица

т. e. коэффициенты многочлена  представлены в строках матрицы Н в обратном порядке.
представлены в строках матрицы Н в обратном порядке.
Свойство делимости кодовых слов ЦК на порождающий многочлен используют для обнаружения ошибок в принятых
словах. Если  принятое слово, содержащее многочлен ошибок
принятое слово, содержащее многочлен ошибок  то в результате деления
то в результате деления

Здесь  многочлен синдрома, остаток от деления
многочлен синдрома, остаток от деления  на
на  Он имеет степень не выше
Он имеет степень не выше  отсутствие ошибок
отсутствие ошибок 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
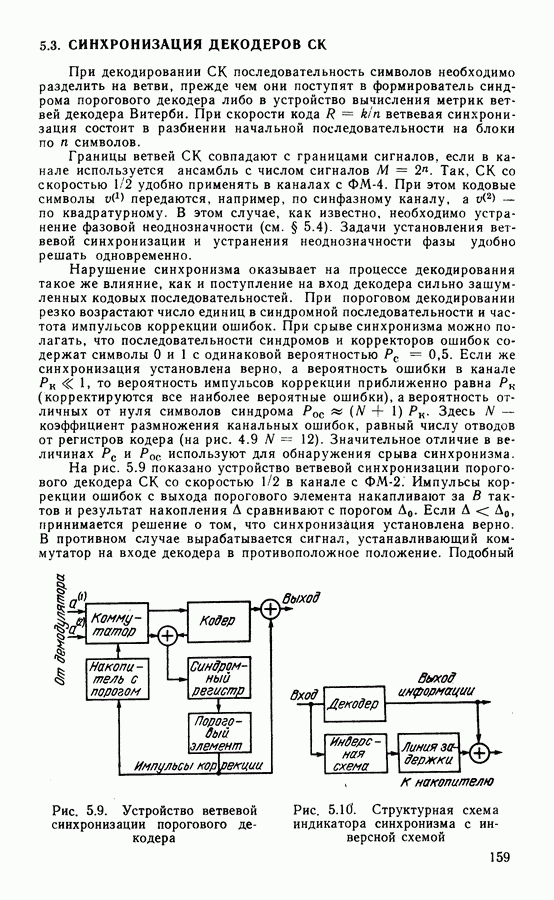
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ