| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
Наиболее удобным для реализации является случай, когда при объеме ансамбля сигналов  скорость сверточного кода выбирается равной
скорость сверточного кода выбирается равной  При этом результирующая удельная скорость
При этом результирующая удельная скорость  и каждый блок из
и каждый блок из  двоичных символов, соответствующий одному из ФМ сигналов, образует ветвь сверточного кода. Последовательности передаваемых сигналов ФМ-М образуют марковскую цепь, допускающую декодирование по алгоритму Витерби.
двоичных символов, соответствующий одному из ФМ сигналов, образует ветвь сверточного кода. Последовательности передаваемых сигналов ФМ-М образуют марковскую цепь, допускающую декодирование по алгоритму Витерби.
На рис. 8.8 показано согласование модема и кодека для случая ФМ-8 - СК со скоростью 2/3. Результирующая удельная скорость  совпадает со скоростью некодированной ФМ-4. Информационная последовательность символов и на входе кодера разбивается на два потока и
совпадает со скоростью некодированной ФМ-4. Информационная последовательность символов и на входе кодера разбивается на два потока и  и на выходе кодера на каждом такте образуется комбинация символов
и на выходе кодера на каждом такте образуется комбинация символов  . В модуляторе ФМ-8 используется код Грея. Соответствие символов ветви
. В модуляторе ФМ-8 используется код Грея. Соответствие символов ветви  и сигналов на выходе модулятора ФМ-8 определяется табл. 2.1. На приемной стороне
и сигналов на выходе модулятора ФМ-8 определяется табл. 2.1. На приемной стороне

Рис. 8.8. Структурная схема кодека-модема ФМ-8 СК
Таблица 8.1

в демодуляторе определяются проекции двумерного сигнала с помехой  на квадратурные оси х и у, по которым в декодере производятся вычисление метрик и декодирование по алгоритму Витерби, подробно описанному в § 4.5.
на квадратурные оси х и у, по которым в декодере производятся вычисление метрик и декодирование по алгоритму Витерби, подробно описанному в § 4.5.
Двоичные СК, оптимальные по критерию максимума свободного расстояния, были бы оптимальны и в таких многопозиционных каналах, если бы отображение двоичных подблоков в сигнальные точки ансамбля было таким, когда большему расстоянию Хэмминга соответствовало бы большее расстояние по Евклиду. При использовании кода Грея это условие Для всех вариантов отображения строго не выполняется, поэтому для каждого значения М необходимо производить поиск оптимальных кодов. В табл. 8.1 показаны комбинации двоичного кода для  расстояние по Хэммингу
расстояние по Хэммингу  и расстояние по Евклиду
и расстояние по Евклиду  при использовании манипуляционного кода Грея.
при использовании манипуляционного кода Грея.
Нижнюю границу свободного расстояния кода можно получить, если в качестве расстояния для каждой ветви использовать его минимальное значение 
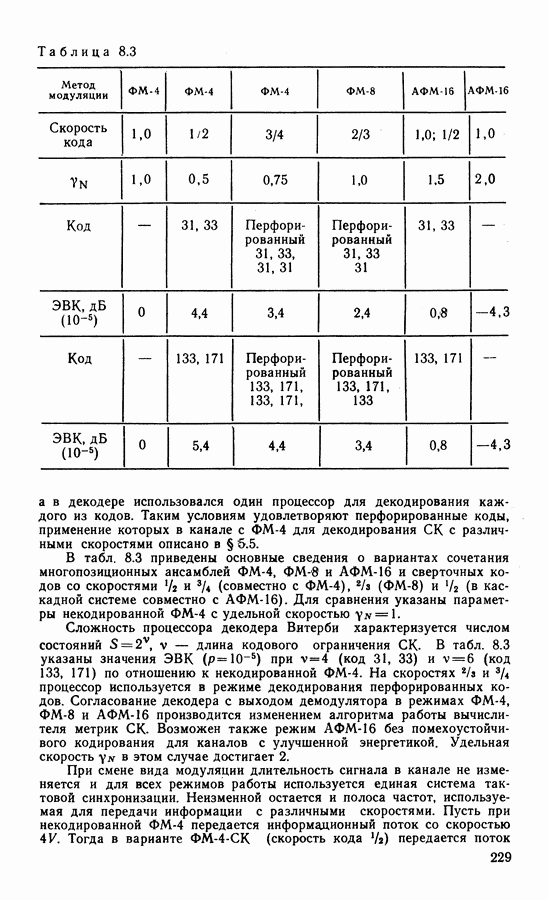
По методике, основанной на применении порождающих функций и рассмотренной в § 4.6, произведен перебор кодов с ограничениями на катастрофичность и найдены двоичные коды, оптимальные для каналов с ФМ-8. Основные параметры, значения АЭВК и ЭВК при  приведены в табл. 8.2 [139]. Поскольку в расчетах учитывалась нижняя оценка
приведены в табл. 8.2 [139]. Поскольку в расчетах учитывалась нижняя оценка  приводимые в табл. 8.2 значения ЭВК также несколько занижены.
приводимые в табл. 8.2 значения ЭВК также несколько занижены.
В таблице принята восьмеричная запись коэффициентов порождающей матрицы  соответственно для первого, второго и т. д. выходов кодера с номером
соответственно для первого, второго и т. д. выходов кодера с номером 
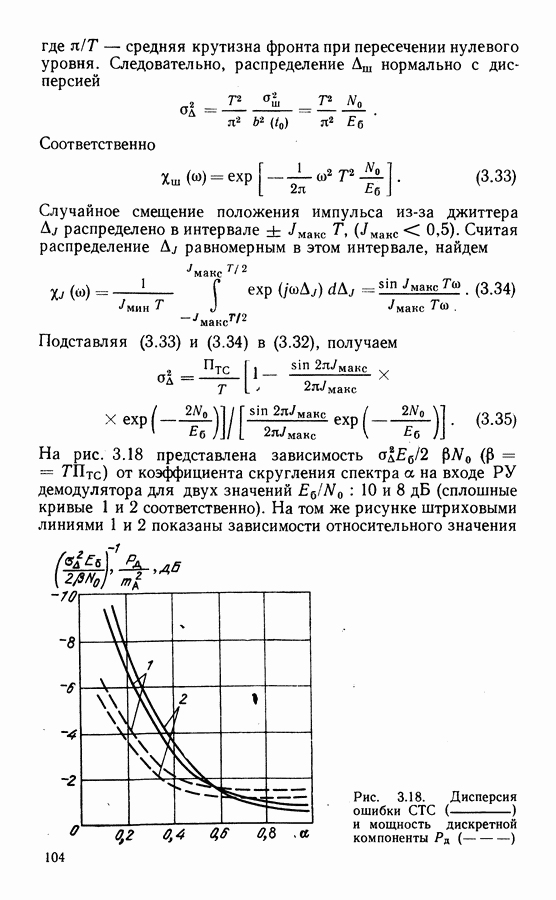
На рис. 8.9 показаны результаты расчетов вероятности ошибки для лучших вариантов кодов из табл.8.2 (номера кривых соответствуют номерам кодов) при условии декодирования по
Таблица 8.2

алгоритму Витерби с мягким решением. Анализ зависимости вероятности ошибки от длины памяти декодера показывает, что требования к длине памяти декодера примерно такие же, как и при применении перфорированных кодов (см. §4.6).
Как отмечалось в § 4.5, реализация кодов на скорость  значительно упрощается при использовании перфорированных кодов. В канале с ФМ-М вычисление метрик ветвей на перфорированном и неперфорированном шагах производится с учетом выбранного манипуляционного кода. К примеру, при скорости кода
значительно упрощается при использовании перфорированных кодов. В канале с ФМ-М вычисление метрик ветвей на перфорированном и неперфорированном шагах производится с учетом выбранного манипуляционного кода. К примеру, при скорости кода  символы ветви
символы ветви  разбиваются на две части:
разбиваются на две части:  неперфорированный шаг и
неперфорированный шаг и  перфорированный шаг. В соответствии с этим разбиением на рис. 8. 10 показаны области сигналов ФМ-8. Видно, что символы ветвей на каждом шаге передаются одним из двух сигналов ФМ-8, так что при декодировании по алгоритму Витерби вычисление метрик ветвей необходимо производить по составным гипотезам, когда метрики пропорциональны сумме условных
перфорированный шаг. В соответствии с этим разбиением на рис. 8. 10 показаны области сигналов ФМ-8. Видно, что символы ветвей на каждом шаге передаются одним из двух сигналов ФМ-8, так что при декодировании по алгоритму Витерби вычисление метрик ветвей необходимо производить по составным гипотезам, когда метрики пропорциональны сумме условных

Рис. 8.9. Кривые помехоустойчивости декодирования различных СКК: 1,3,5,7 — коды из табл. 8.2; моделирование систем; а — ФМ-8 - перфорированный код (31, 33, 31); б - АФМ-16 - код (31, 33); в - ФМ-16 - код (13, 15)

Рис. 8.10. К вычислению модифицированных метрик
вероятностей. Так, для ветви кода  получаем
получаем  . Метрики пар
. Метрики пар  вычисляются аналогично.
вычисляются аналогично.
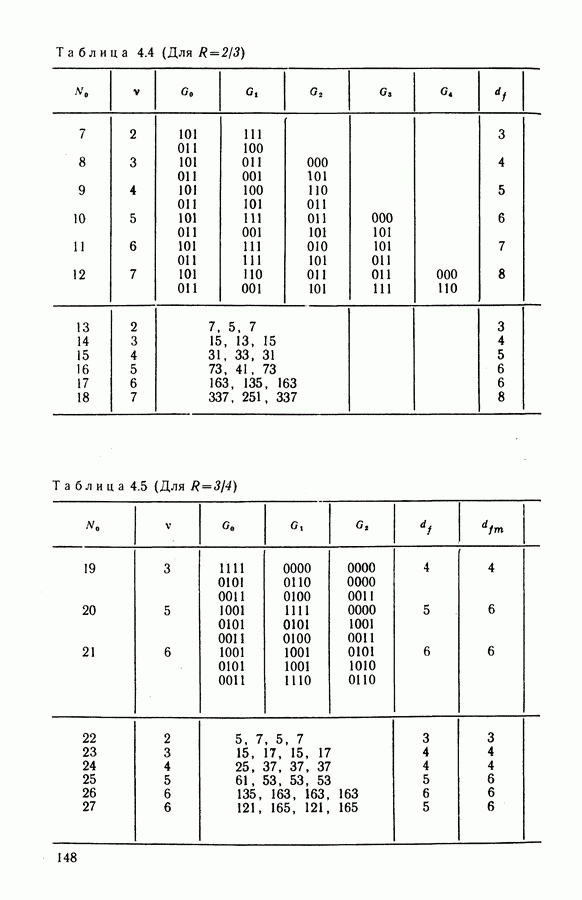
Алгоритм работы вычислителя метрик можно упростить и свести к описанному в § 5.1 алгоритму для сигналов ФМ-4, если метрики вычислять приближенно, как величины, пропорциональные расстояниям до точек, соответствующих центрам секторов сигналов (показаны на рис. 8.10 звездочкой). При этом вносится погрешность в каждую из таких модифицированных метрик, значение и знак которой имеют случайный характер, так что в целом влияние ошибки оказывается небольшим. На рис. 8.9 показаны результаты моделирования системы с ФМ-8 и перфорированным СК с порождающим многочленом  (31, 33, 31) (см. табл. 4.4, код 15), допускающим декодирование по решетке двоичного кода со скоростью 1/2. Проигрыш по ЭВК по сравнению с оптимальным кодом (код 1 на рис. 8.9) не превышает
(31, 33, 31) (см. табл. 4.4, код 15), допускающим декодирование по решетке двоичного кода со скоростью 1/2. Проигрыш по ЭВК по сравнению с оптимальным кодом (код 1 на рис. 8.9) не превышает  . В модифицированном вычислителе метрик декодера (см. рис. 8.8) производится последовательное вычисление метрик относительно точек-центров секторов сигналов на неперфорированном и перфорированном шагах соответственно. Квантование каждой координаты двумерного сигнального пространства при ФМ-8 на 16 зон дает потери в ЭВК не более
. В модифицированном вычислителе метрик декодера (см. рис. 8.8) производится последовательное вычисление метрик относительно точек-центров секторов сигналов на неперфорированном и перфорированном шагах соответственно. Квантование каждой координаты двумерного сигнального пространства при ФМ-8 на 16 зон дает потери в ЭВК не более  а при квантовании на 32 зоны потери практически равны нулю.
а при квантовании на 32 зоны потери практически равны нулю.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
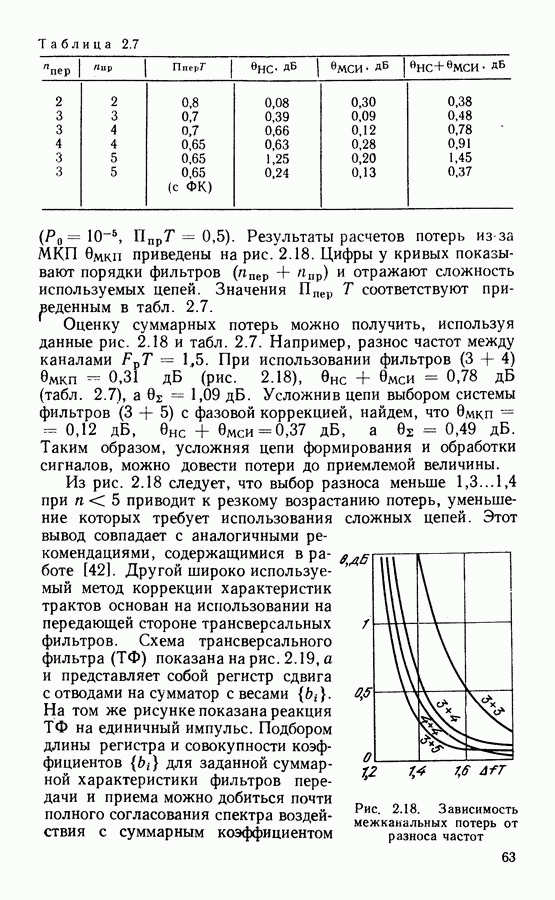
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
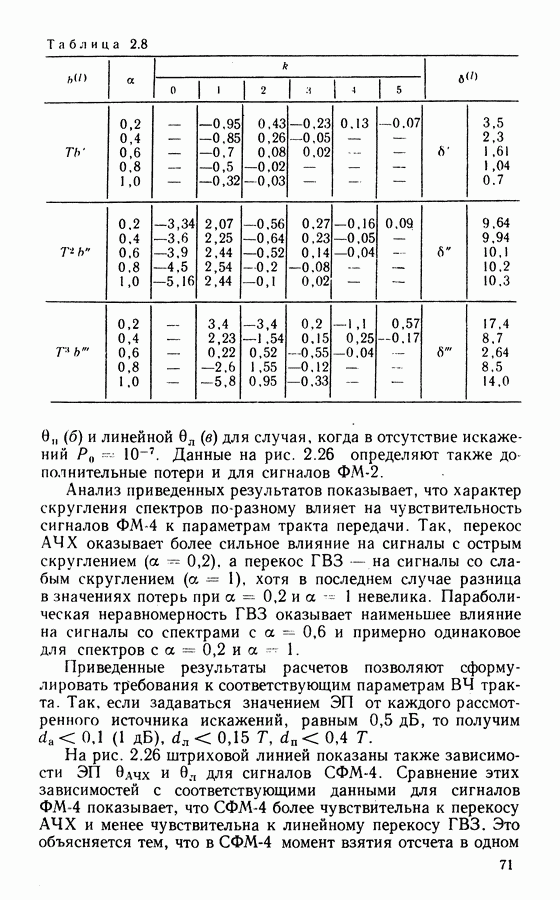
- Энергетические потери в системе с ФМ-4.
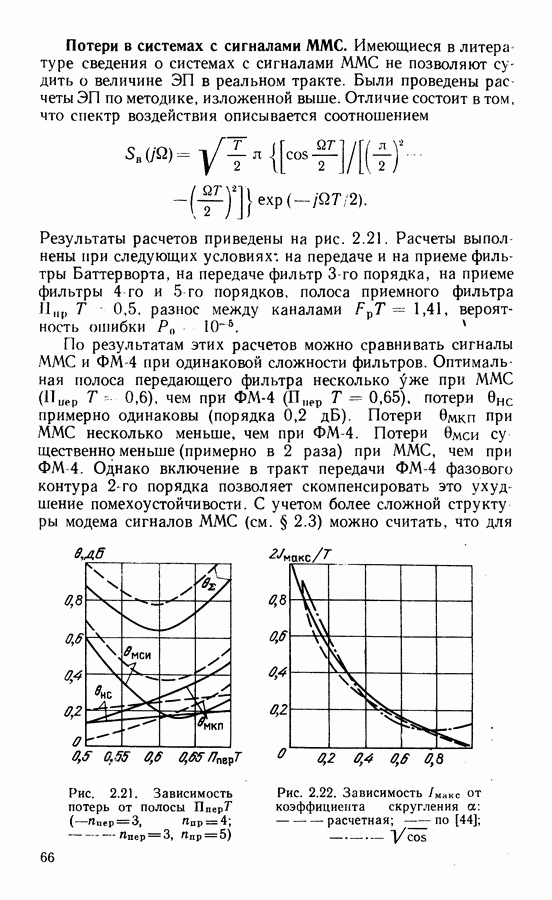
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
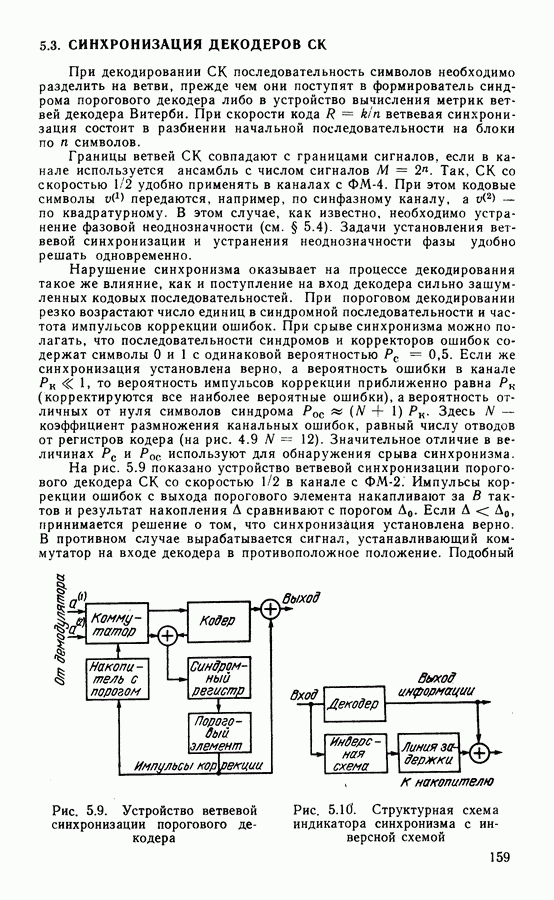
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
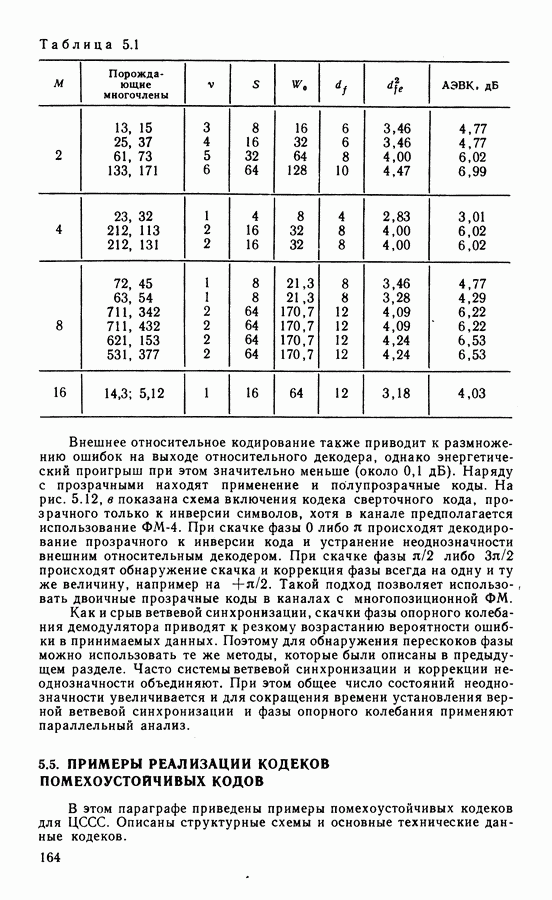
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
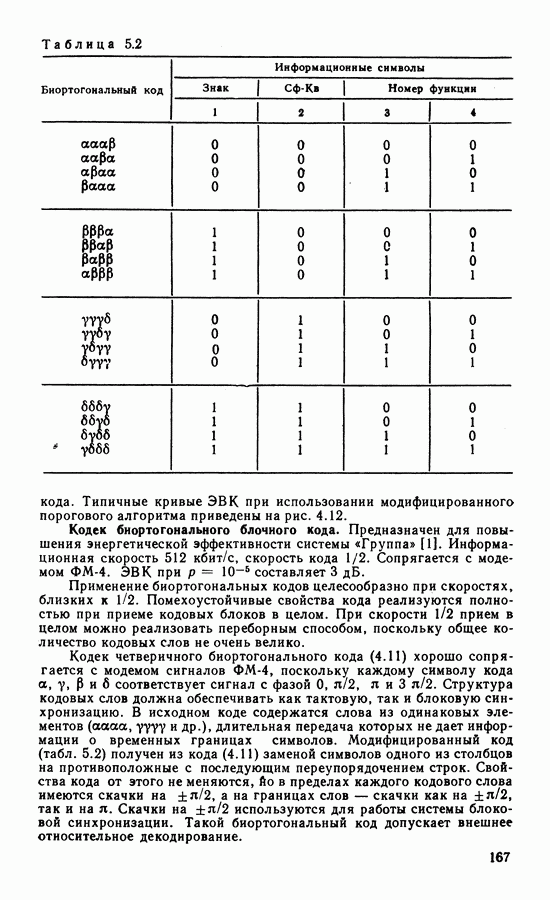
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
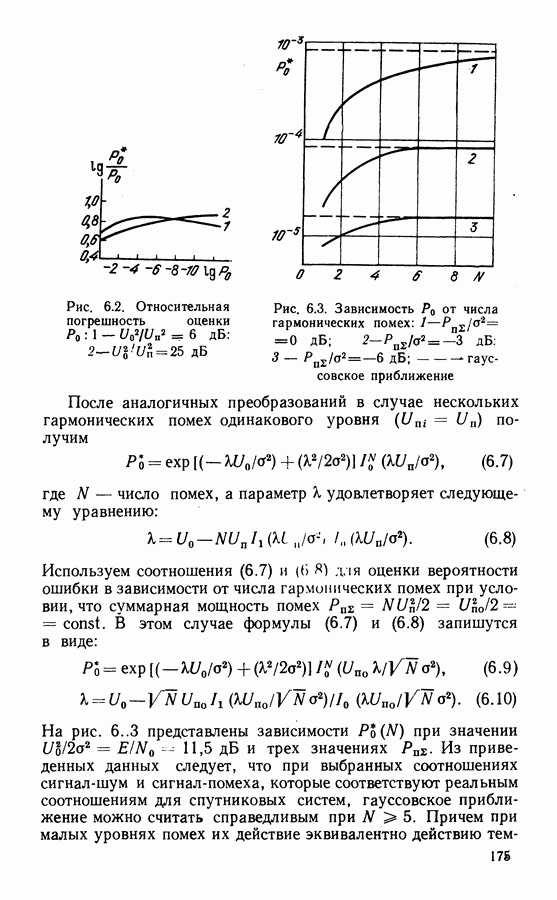
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
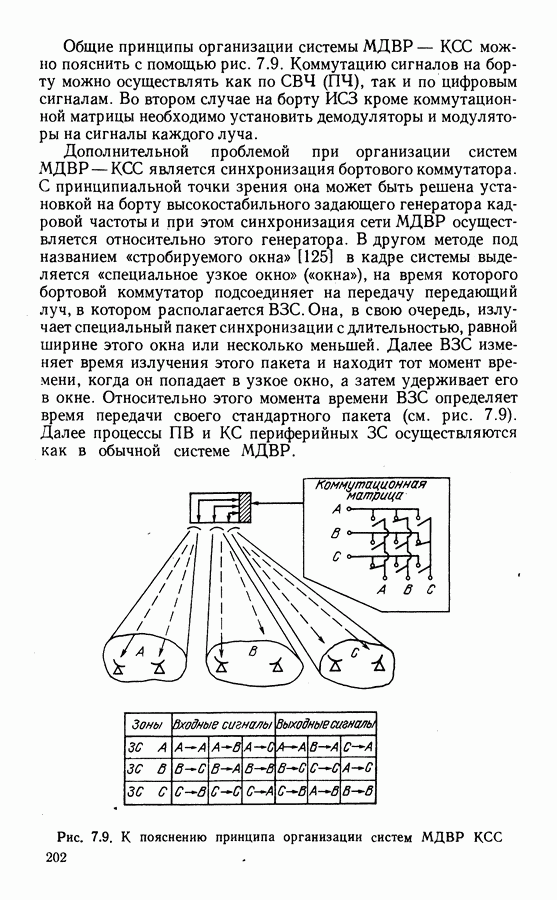
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
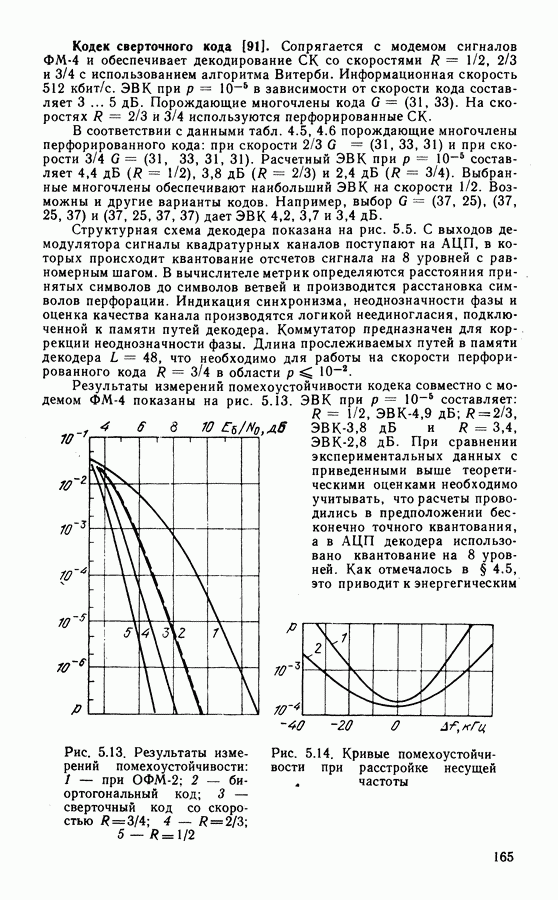
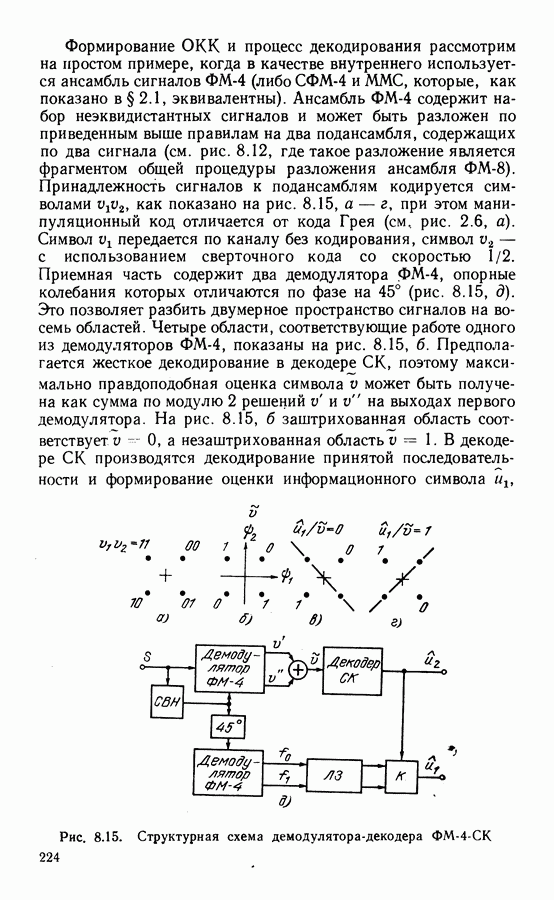
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ