| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
Согласование систем модуляции и кодирования возможно на основе построения обобщенных каскадных кодов (ОКК) [138]. Различные варианты блочных ОКК описаны в работах [34, 135, 136]. Ниже рассмотрен случай, когда внешние коды — сверточные. Пример конструкции со сверточными кодами, когда в канале используется ансамбль АФМ сигналов, приведен в работе [38].
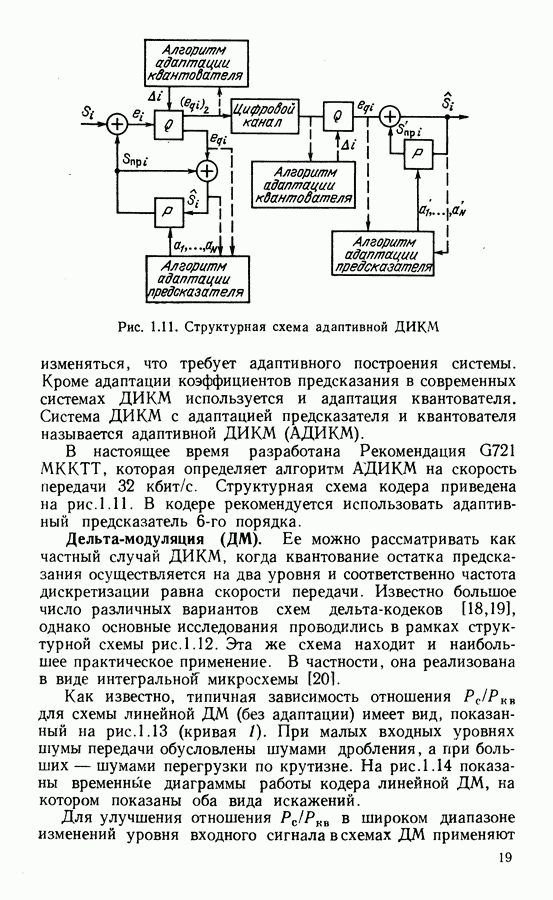
Конструкция обобщенного каскадного кода представлена на рис. 8.11. На входы внешних сверточных кодеров  поступают последовательности двоичных информационных символов
поступают последовательности двоичных информационных символов  . Скорости кодеров
. Скорости кодеров  На выходах кодеров получается последовательность и, состоящая из набора ветвей
На выходах кодеров получается последовательность и, состоящая из набора ветвей  Внутренний ансамбль сигналов, используемых для передачи информации по каналу, содержит
Внутренний ансамбль сигналов, используемых для передачи информации по каналу, содержит  сигналов,
сигналов,  число внешних кодов. Каждый сигнал ансамбля задается набором координат
число внешних кодов. Каждый сигнал ансамбля задается набором координат  Ансамбль разложен на набор вложенных подансамблей, удовлетворяющих следующим условиям:
Ансамбль разложен на набор вложенных подансамблей, удовлетворяющих следующим условиям:

Здесь индекс при  определяют объем соответствующего вложенного ансамбля
определяют объем соответствующего вложенного ансамбля  и минимальное евклидово расстояние между сигнальными точками этого ансамбля.
и минимальное евклидово расстояние между сигнальными точками этого ансамбля.
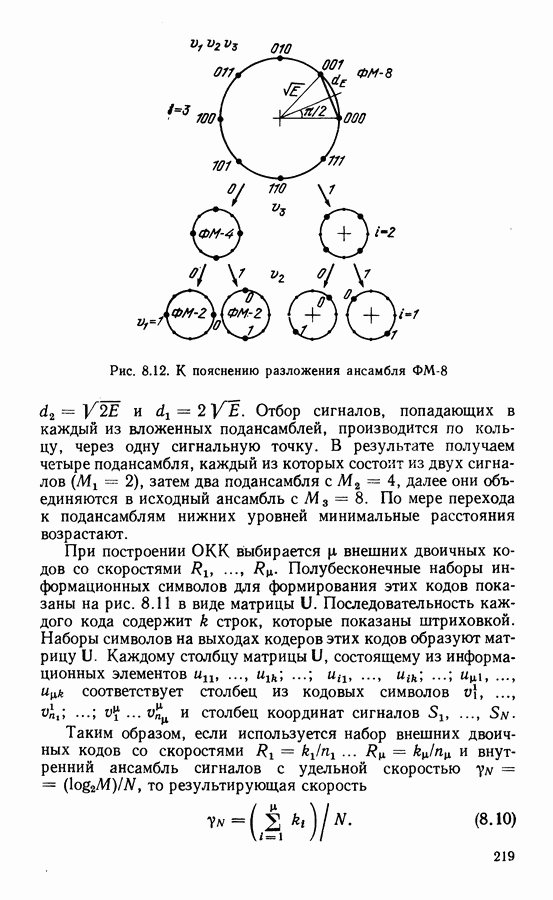
Пример разложения ансамбля сигналов ФМ-8 на три вложенных подансамбля показан на рис.  расстояния между ближайшими сигнальными точками в подансамблях
расстояния между ближайшими сигнальными точками в подансамблях 

Рис. 8.11. Конструкция обобщенного каскадного кода

Рис. 8.12. К пояснению разложения ансамбля 
Отбор сигналов, попадающих в каждый из вложенных подансамблей, производится по кольцу, через одну сигнальную точку. В результате получаем четыре подансамбля, каждый из которых состоит из двух сигналов  затем два подансамбля с
затем два подансамбля с  далее они объединяются в исходный ансамбль с
далее они объединяются в исходный ансамбль с  По мере перехода к подансамблям нижних уровней минимальные расстояния возрастают.
По мере перехода к подансамблям нижних уровней минимальные расстояния возрастают.
При построении ОКК выбирается  внешних двоичных кодов со скоростями
внешних двоичных кодов со скоростями  Полубесконечные наборы информационных символов для формирования этих кодов показаны на рис. 8.11 в виде матрицы
Полубесконечные наборы информационных символов для формирования этих кодов показаны на рис. 8.11 в виде матрицы  Последовательность каждого кода содержит
Последовательность каждого кода содержит  строк, которые показаны штриховкой. Наборы символов на выходах кодеров этих кодов образуют матрицу
строк, которые показаны штриховкой. Наборы символов на выходах кодеров этих кодов образуют матрицу  Каждому столбцу матрицы
Каждому столбцу матрицы  состоящему из информационных элементов
состоящему из информационных элементов  соответствует столбец из кодовых символов
соответствует столбец из кодовых символов  и столбец координат сигналов
и столбец координат сигналов  -Таким образом, если используется набор внешних двоичных кодов со скоростями
-Таким образом, если используется набор внешних двоичных кодов со скоростями  внутренний ансамбль сигналов с удельной скоростью ум
внутренний ансамбль сигналов с удельной скоростью ум  то результирующая скорость
то результирующая скорость

Минимальное расстояние ОКК определяется как минимальное расстояние среди всех возможных расстояний на каждой ступени вложенности, т. е.

где — квадрат евклидового расстояния  вложенного подансамбля;
вложенного подансамбля;  свободное расстояние по Хэммингу
свободное расстояние по Хэммингу  внешнего кода.
внешнего кода.
Рассмотрим подробнее процедуру разложения внутренних ансамблей сигналов на наборы вложенных подансамблей. Ансамбли могут быть представлены двумя основными классами сигналов: сигналы поверхностно-сферической укладки и сигналы объемно-сферической укладки [34]. К первым относятся сигналы с постоянной энергией  и др.). При геометрическом представлении сигнальные точки таких ансамблей сигналов располагаются на поверхности
и др.). При геометрическом представлении сигнальные точки таких ансамблей сигналов располагаются на поверхности  -мерной сферы. У сигналов объемной укладки сигнальные точки располагаются в объеме пространства сигналов, энергии разных сигналов имеют разную величину (например, сигналы с АФМ).
-мерной сферы. У сигналов объемной укладки сигнальные точки располагаются в объеме пространства сигналов, энергии разных сигналов имеют разную величину (например, сигналы с АФМ).
Ансамбли сигналов объемной укладки удобно строить на основе пространственной точечной решетки, пример которой показан на рис. 8.13. Здесь в двумерном пространстве на плоскости показано множество регулярно расположенных точек, образующих плоскую решетку. Особенностью регулярных решеток является периодическая повторяемость ее элементов при перемещениях вдоль определенных направлений (переносах), а также различные виды симметрий поворотов вокруг центров.
В качестве ансамбля сигналов выбирают компактно расположенное множество точек решетки, лежащих внутри замкнутого контура. На рис. 8.13 показаны представляющие практический интерес ансамбли с числом сигналов  Каждый из таких ансамблей может быть разложен на набор вложенных подансамблей, удовлетворяющих условиям вложенности (8.9).
Каждый из таких ансамблей может быть разложен на набор вложенных подансамблей, удовлетворяющих условиям вложенности (8.9).
Разложение производится в следующем порядке. На выбранной точечной решетке определяем множество точек, входящих в ансамбль сигналов (на рис. 8.14 ансамбль с  Соединяя точки решетки отрезками прямых, образуем многогранник, у которого внутри либо на гранях расположенно
Соединяя точки решетки отрезками прямых, образуем многогранник, у которого внутри либо на гранях расположенно  точек (на рис. 8.14 это квадрат с одной точкой внутри него). Последовательно перемещаем многогранник по решетке, совмещая его вершины с остальными точками решетки так, чтобы соседние многогранники не перекрывались и полностью заполняли все пространство. При этом исключаем из решетки всякий
точек (на рис. 8.14 это квадрат с одной точкой внутри него). Последовательно перемещаем многогранник по решетке, совмещая его вершины с остальными точками решетки так, чтобы соседние многогранники не перекрывались и полностью заполняли все пространство. При этом исключаем из решетки всякий

Рис. 8.13. Ансамбли АФМ на основе точечной решетки
раз точки, находящиеся внутри многогранника и на его гранях. Оставшиеся точки образуют подансамбль, вложенный в исходный ансамбль. Вычеркнутые точки принадлежат другим вложенным подансамблям. Процедуру следует повторить, произведя необходимое число шагов разложения. На рис. 8.14 штриховой линией показаны направления перемещения квадрата. Здесь  и на каждом шагу разложения подансамбль распадается вновь на два вложенных подансамбля. Показано два шага разложения, расстояния в подансамблях будут:
и на каждом шагу разложения подансамбль распадается вновь на два вложенных подансамбля. Показано два шага разложения, расстояния в подансамблях будут:  Кодирование принадлежности сигнальных точек к подансамблям производится
Кодирование принадлежности сигнальных точек к подансамблям производится  -ичным безызбыточным кодом. На рис. 8.14 показаны символы двоичного кода 1 и 0.
-ичным безызбыточным кодом. На рис. 8.14 показаны символы двоичного кода 1 и 0.

Рис. 8.14. К пояснению разложения ансамбля АФМ-16
Аналогично производится разложение на вложенные подансамбли сигналов решетчатой конфигурации размерности 
Для сигналов поверхностной укладки регулярный алгоритм разложения на вложенные подансамбли основан на использовании их групповых свойств. Пусть ансамбль сигналов объема М, состоящий из  -мерных векторов сигналов
-мерных векторов сигналов 
-  задается алгебраической группой
задается алгебраической группой  ортогональных матриц
ортогональных матриц  размером
размером  а также начальным вектором
а также начальным вектором  так что каждый вектор сигнала
так что каждый вектор сигнала  Матрица 0, определяет некоторый пространственный поворот начального вектора
Матрица 0, определяет некоторый пространственный поворот начального вектора  Совокупность векторов
Совокупность векторов  называют групповым кодом. Группа матриц
называют групповым кодом. Группа матриц  в общем случае может быть разложена на ряд из
в общем случае может быть разложена на ряд из  вложенных подгрупп
вложенных подгрупп  и фактор-групп
и фактор-групп  [74]. Это разложение используется для построения набора вложенных ансамблей сигналов. В качестве критериев оптимизации процесса разложения можно указать минимальное расстояние между сигналами, получение плотнейшей либо близкой к ней укладки сигналов в подансамблях, число ансамблей на каждом шаге разбиения и т. д. Выберем подгруппу Ну, удовлетворяющую принятым критериям на последнем шаге разбиения. Она задает один из вложенных ансамблей, а ее смежные классы определяют остальные подансамбли на
[74]. Это разложение используется для построения набора вложенных ансамблей сигналов. В качестве критериев оптимизации процесса разложения можно указать минимальное расстояние между сигналами, получение плотнейшей либо близкой к ней укладки сигналов в подансамблях, число ансамблей на каждом шаге разбиения и т. д. Выберем подгруппу Ну, удовлетворяющую принятым критериям на последнем шаге разбиения. Она задает один из вложенных ансамблей, а ее смежные классы определяют остальные подансамбли на  шаге разбиения. Дистанционные свойства сигналов в подансамблях будут одинаковы в силу их групповых свойств. Используя ряд подгрупп Н и фактор-групп
шаге разбиения. Дистанционные свойства сигналов в подансамблях будут одинаковы в силу их групповых свойств. Используя ряд подгрупп Н и фактор-групп  переходим к подгруппе
переходим к подгруппе  вновь производя разбиение на классы. Повторяем процедуру вплоть до
вновь производя разбиение на классы. Повторяем процедуру вплоть до  при необходимости объединяя несколько шагов разбиения в один.
при необходимости объединяя несколько шагов разбиения в один.
Например, ансамбль А из М двумерных сигналов  плотнейшей поверхностно-сферической укладки [34] задается начальным двумерным вектором
плотнейшей поверхностно-сферической укладки [34] задается начальным двумерным вектором  и циклической абелевой группой ортогональных матриц поворотов в двумерном пространстве с образующим элементом группы в виде
и циклической абелевой группой ортогональных матриц поворотов в двумерном пространстве с образующим элементом группы в виде

 При
При  группа
группа  содержит
содержит  вложенных подгрупп порядка
вложенных подгрупп порядка  что задает двоичные на каждом шаге разбиения А на подансамбли из 2 1 сигналов плотнейшей упаковки. Для случая
что задает двоичные на каждом шаге разбиения А на подансамбли из 2 1 сигналов плотнейшей упаковки. Для случая  пример такого разбиения показан на рис. 8.12. Конец начального вектора
пример такого разбиения показан на рис. 8.12. Конец начального вектора  отождествляется с сигнальной точкой ансамбля (0, 0, 0), группа
отождествляется с сигнальной точкой ансамбля (0, 0, 0), группа  из восьми сигналов распадается на две подгруппы,
из восьми сигналов распадается на две подгруппы,
состоящие из четырех и двух сигналов соответственно, которые порождают подансамбли из четырех и двух сигналов.
Декодирование обобщенных каскадных кодов производится за  шагов. На первом шаге производится декодирование первым кодом (см. рис. 8.11). По принятому сигналу с помехой
шагов. На первом шаге производится декодирование первым кодом (см. рис. 8.11). По принятому сигналу с помехой  демодулятор вырабатывает оценки правдоподобия (либо величины, им пропорциональные):
демодулятор вырабатывает оценки правдоподобия (либо величины, им пропорциональные):

Здесь суммирование ведется по всем возможным комбинациям символов  а символ
а символ  противоположен
противоположен  При жестком декодировании демодулятор вырабатывает оценки символов
При жестком декодировании демодулятор вырабатывает оценки символов  и, кроме того, информацию о том, к какому множеству сигналов из подансамблей следующей ступени разбиения ближе принятый сигнал
и, кроме того, информацию о том, к какому множеству сигналов из подансамблей следующей ступени разбиения ближе принятый сигнал  Эта информация необходима для коррекции сигналов после декодирования первым внешним кодом. Далее проводится декодирование первым внешним кодом. В соответствии с результатом декодирования ошибочные сигналы корректируются в ближайшие из других подансамблей, а набор декодированных символов
Эта информация необходима для коррекции сигналов после декодирования первым внешним кодом. Далее проводится декодирование первым внешним кодом. В соответствии с результатом декодирования ошибочные сигналы корректируются в ближайшие из других подансамблей, а набор декодированных символов  выдается получателю. Затем происходит переход к ансамблю меньшей кратности и процедура повторяется.
выдается получателю. Затем происходит переход к ансамблю меньшей кратности и процедура повторяется.
На каждом шаге декодирования необходимо вычислять вероятности, подобные приведенным в выражении (8.12). Сюда входят суммы экспонент, что затрудняет применение конструктивных алгоритмов с полным использованием информации с выхода демодулятора. Напомним, что при вычислении метрик для алгоритмов Витерби в соответствии с выражением (4.29) произведение экспонент заменялось суммой показателей их степеней. Рассмотрим квазиоптимальный алгоритм, когда в качестве оценки правдоподобия используется наибольшее слагаемое из суммы (8.12). На  шаге декодирования в каждую сумму (8.12) входит
шаге декодирования в каждую сумму (8.12) входит  слагаемых, каждое из которых соответствует определенному набору символов. Если вынесены максимально правдоподобные жесткие решения по символам
слагаемых, каждое из которых соответствует определенному набору символов. Если вынесены максимально правдоподобные жесткие решения по символам  то слагаемое
то слагаемое  в сумме (8.12) будет наибольшим. Оно используется для формирования оценки правдоподобия
в сумме (8.12) будет наибольшим. Оно используется для формирования оценки правдоподобия

С — постоянная.
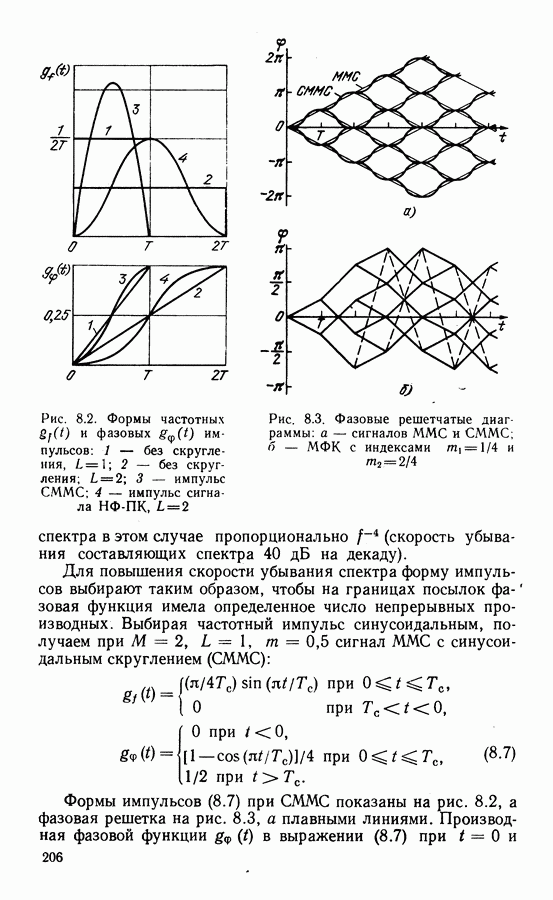
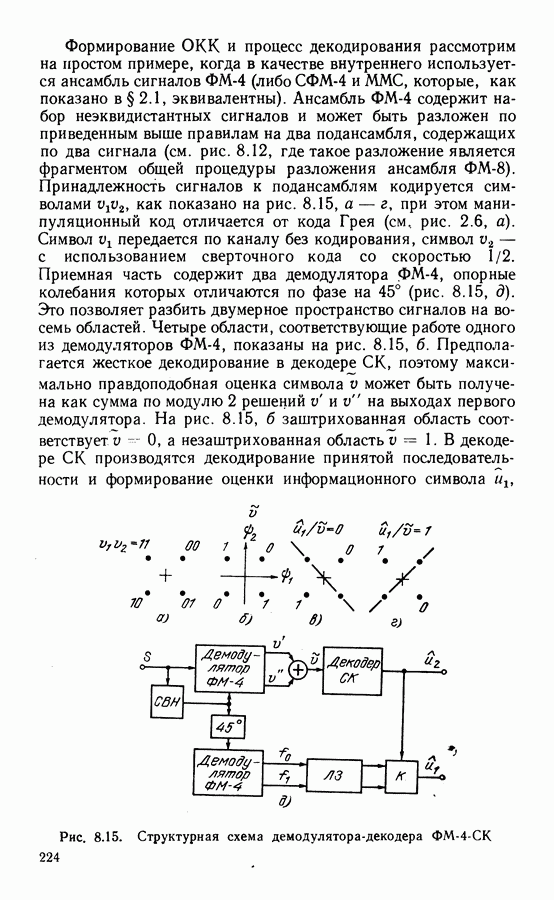
Формирование ОКК и процесс декодирования рассмотрим на простом примере, когда в качестве внутреннего используется ансамбль сигналов ФМ-4 (либо СФМ-4 и ММС, которые, как показано в § 2.1, эквивалентны). Ансамбль ФМ-4 содержит набор неэквидистантных сигналов и может быть разложен по приведенным выше правилам на два подансамбля, содержащих по два сигнала (см. рис. 8.12, где такое разложение является фрагментом общей процедуры разложения ансамбля ФМ-8). Принадлежность сигналов к подансамблям кодируется символами как показано на рис. 8.15, а  при этом манипуляционный код отличается от кода Грея (см, рис. 2.6, а). Символ
при этом манипуляционный код отличается от кода Грея (см, рис. 2.6, а). Символ  передается по каналу без кодирования, символ
передается по каналу без кодирования, символ  с использованием сверточного кода со скоростью 1/2. Приемная часть содержит два демодулятора ФМ-4, опорные колебания которых отличаются по фазе на 45° (рис. 8.15, д). Это позволяет разбить двумерное пространство сигналов на восемь областей. Четыре области, соответствующие работе одного из демодуляторов ФМ-4, показаны на рис. 8.15, б. Предполагается жесткое декодирование в декодере СК, поэтому максимально правдоподобная оценка символа
с использованием сверточного кода со скоростью 1/2. Приемная часть содержит два демодулятора ФМ-4, опорные колебания которых отличаются по фазе на 45° (рис. 8.15, д). Это позволяет разбить двумерное пространство сигналов на восемь областей. Четыре области, соответствующие работе одного из демодуляторов ФМ-4, показаны на рис. 8.15, б. Предполагается жесткое декодирование в декодере СК, поэтому максимально правдоподобная оценка символа  может быть получена как сумма по модулю 2 решений
может быть получена как сумма по модулю 2 решений  на выходах первого демодулятора. На рис. 8.15, б заштрихованная область соответствуете 0, а незаштрихованная область
на выходах первого демодулятора. На рис. 8.15, б заштрихованная область соответствуете 0, а незаштрихованная область  . В декодере СК производятся декодирование принятой последовательности и формирование оценки информационного символа
. В декодере СК производятся декодирование принятой последовательности и формирование оценки информационного символа 

Рис. 8.15. Структурная схема демодулятора-декодера ФМ-4-СК

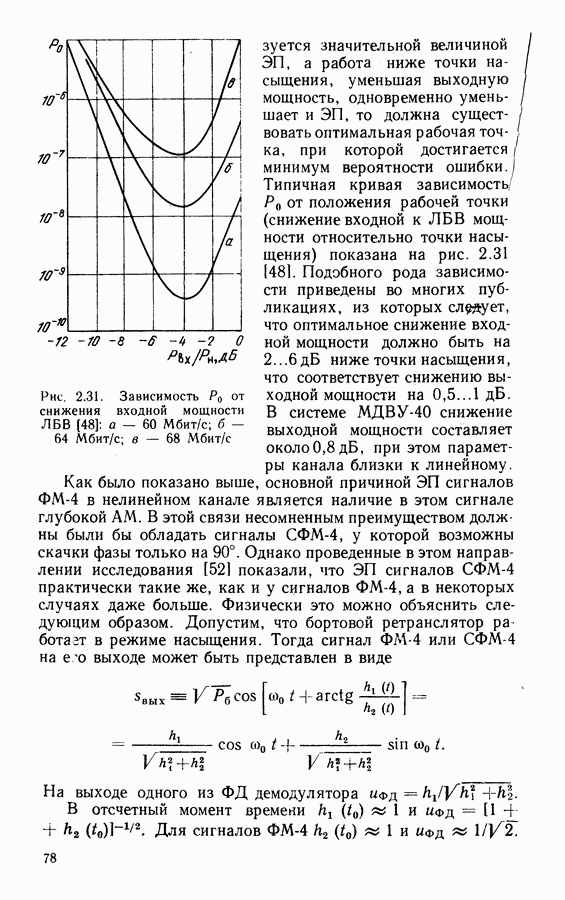
Рис. 8.16. Кривые помехоустойчивости  с пороговым декодированием и внутренним ансамблем ФМ-4
с пороговым декодированием и внутренним ансамблем ФМ-4
который поступает на выход к получателю, а также используется для коррекции решений, получаемых на выходе второго демодулятора.
Если оценка символа  в коммутаторе производится выбор значений первого информационного символа в соответствии с границами областей
в коммутаторе производится выбор значений первого информационного символа в соответствии с границами областей  сигналов, показанных на рис. 8.15, в. При
сигналов, показанных на рис. 8.15, в. При  границы показаны на рис.
границы показаны на рис. 
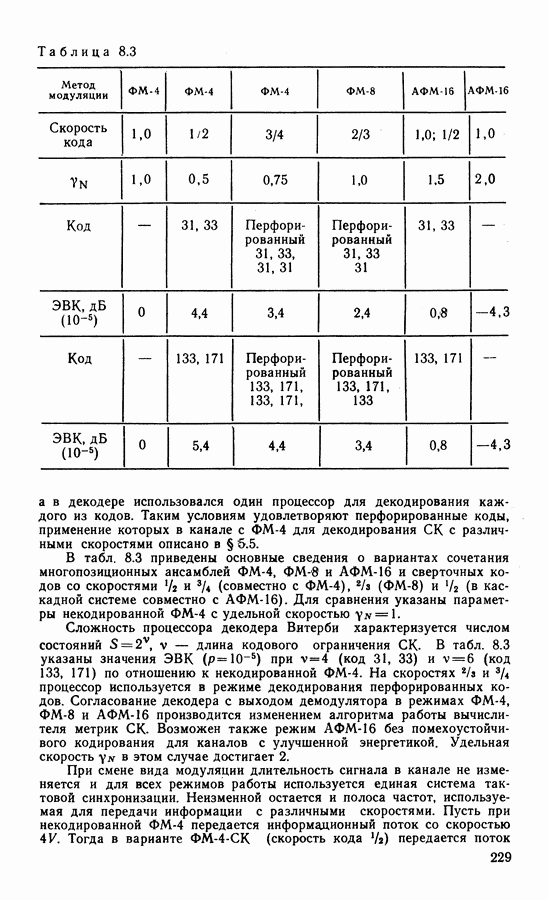
Поскольку в одном из каналов ФМ-4 передаются символы без избыточности, а в другом — со скоростью кода 1/2, результирующая скорость кода 2/3 и системы с  Более привлекательными такие системы оказываются при использовании высокоскоростных сверточных кодов. На рис. 8.16 показаны результаты расчетов вероятности ошибки при декодировании каскадных кодов с внутренним ансамблем сигналов ФМ-4 и пороговым алгоритмом декодирования сверточных кодов. Параметры кодов и систем следующие: кривая
Более привлекательными такие системы оказываются при использовании высокоскоростных сверточных кодов. На рис. 8.16 показаны результаты расчетов вероятности ошибки при декодировании каскадных кодов с внутренним ансамблем сигналов ФМ-4 и пороговым алгоритмом декодирования сверточных кодов. Параметры кодов и систем следующие: кривая  . ЭВК таких систем при
. ЭВК таких систем при  достигает
достигает  при удельных скоростях ум, близких к скорости некодированной
при удельных скоростях ум, близких к скорости некодированной  Достигается это некоторым усложнением демодулятора и применением кодека с простым пороговым алгоритмом декодирования.
Достигается это некоторым усложнением демодулятора и применением кодека с простым пороговым алгоритмом декодирования.
Использование в качестве внутренних ансамблей сигналов с более плотными сигналами, нежели ФМ-4, позволяет наряду с энергетическим выигрышем получать большую удельную скорость  . На рис. 8.16 приведены также результаты расчетов помехоустойчивости систем с самоортогональными кодами: кривая 4 — ансамбль АФМ-8, СК с неравной защитой символов,
. На рис. 8.16 приведены также результаты расчетов помехоустойчивости систем с самоортогональными кодами: кривая 4 — ансамбль АФМ-8, СК с неравной защитой символов,  кривая
кривая  кривая
кривая 
 кривая
кривая  Таким образом, при удельной скорости, превышающей
Таким образом, при удельной скорости, превышающей  ряд приведенных систем дает определенный ЭВК по сравнению с некодированной ФМ-4.
ряд приведенных систем дает определенный ЭВК по сравнению с некодированной ФМ-4.
Применение СК и декодирования по алгоритму Витерби с мягким решением позволяет значительно повысить эффективность таких систем.
На рис. 8.9 приведены результаты моделирования двух вариантов со следующими параметрами: кривая  ансамбль АФМ-16 (см. рис. 8.14), сверточный код со скоростью 1/2 и порождающими многочленами (31,33), результирующая удельная скорость
ансамбль АФМ-16 (см. рис. 8.14), сверточный код со скоростью 1/2 и порождающими многочленами (31,33), результирующая удельная скорость  кривая в — ансамбль ФМ-16, разложение на два вложенных подансамбля по 8 сигналов в каждом, сверточный код со скоростью,
кривая в — ансамбль ФМ-16, разложение на два вложенных подансамбля по 8 сигналов в каждом, сверточный код со скоростью,  удельная скорость
удельная скорость  проигрыш по ЭВК по сравнению с некодированной
проигрыш по ЭВК по сравнению с некодированной  При декодировании использовался алгоритм Витерби с мягким решением и описанным выше квазиоптимальным способом формирования оценок правдоподобия.
При декодировании использовался алгоритм Витерби с мягким решением и описанным выше квазиоптимальным способом формирования оценок правдоподобия.
Эффективность описанной здесь системы с АФМ сигналами показана на рис. 8.6 (АФМ-М-СК, точка  Переход к более сложным ансамблям с
Переход к более сложным ансамблям с  и 128 (точки 2 и 3 соответственно) позволяет повысить удельную скорость и продвинуться к предельным кривым, определяемым пропускной способностью канала.
и 128 (точки 2 и 3 соответственно) позволяет повысить удельную скорость и продвинуться к предельным кривым, определяемым пропускной способностью канала.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ I. ОСНОВЫ ПОСТРОЕНИЯ ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
- ГЛАВА 1. СПУТНИКОВЫЕ СИСТЕМЫ С МНОГОСТАНЦИОННЫМ ДОСТУПОМ
- 1.2. ПРЕОБРАЗОВАНИЕ АНАЛОГОВЫХ СИГНАЛОВ В ЦИФРОВУЮ ФОРМУ
- Адаптивная ИКМ.
- Дифференциальная ИКМ (ДИКМ).
- Дельта-модуляция (ДМ).
- Преобразование сигналов телевидения, многоканальной телефонии и вещания в цифровую форму.
- 1.3. СТАТИСТИЧЕСКОЕ УПЛОТНЕНИЕ В ЦССС
- 1.4. МНОГОСТАНЦИОННЫЙ ДОСТУП В ЦССС
- Многостанционный доступ с временным разделением каналов (МДВР).
- Многостанционный доступ с разделением сигналов по форме (МДФР).
- Многостанционный доступ со случайным доступом (МДСД).
- 1.5. НОРМИРОВАНИЕ ПАРАМЕТРОВ ЦССС
- РАЗДЕЛ II. МОДУЛЯЦИЯ
- ГЛАВА 2. МЕТОДЫ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.2. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СИГНАЛОВ
- 2.3. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИГНАЛОВ ПРИ ИДЕАЛЬНОМ ПРИЕМЕ
- 2.4. СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ
- 2.5. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДЧР
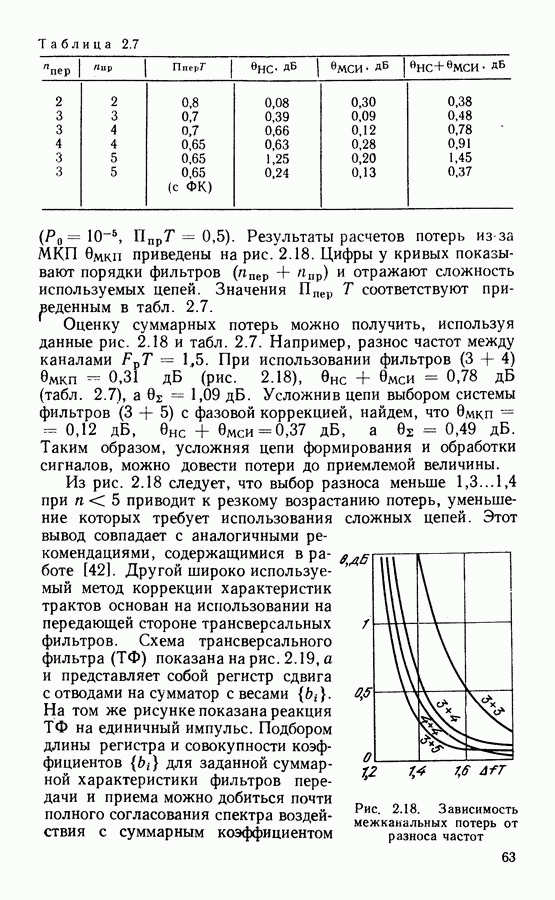
- Результаты расчетов потерь в системе с ФМ-2 и стандартными фильтрами.
- Использование выравнивателей в тракте передачи.
- Анализ зависимости потерь от разноса между каналами.
- Энергетические потери в системе с ФМ-4.
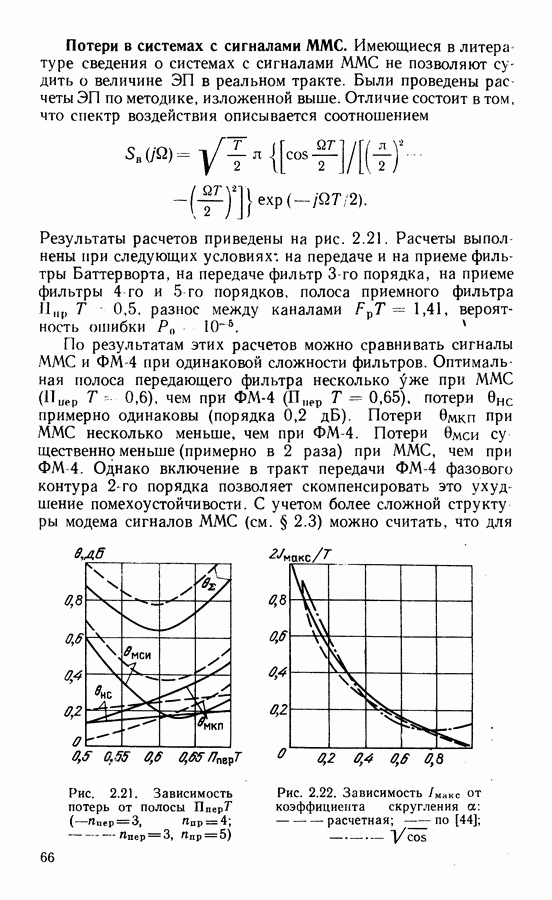
- Потери в системах с сигналами ММС.
- 2.6. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ ПРИ МДВР
- ГЛАВА 3. МОДЕМЫ
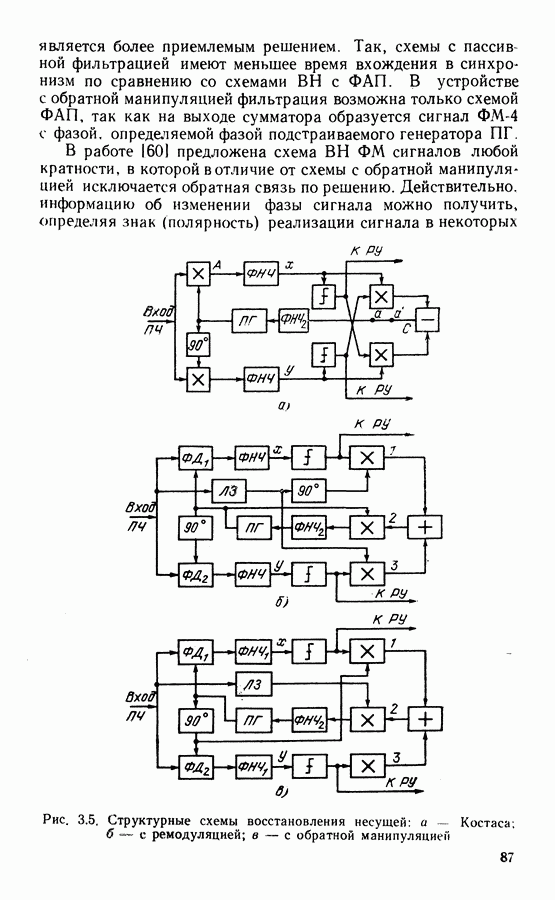
- 3.1. СТРУКТУРА МОДЕМА
- 3.2. СИСТЕМЫ ВОССТАНОВЛЕНИЯ НЕСУЩЕЙ
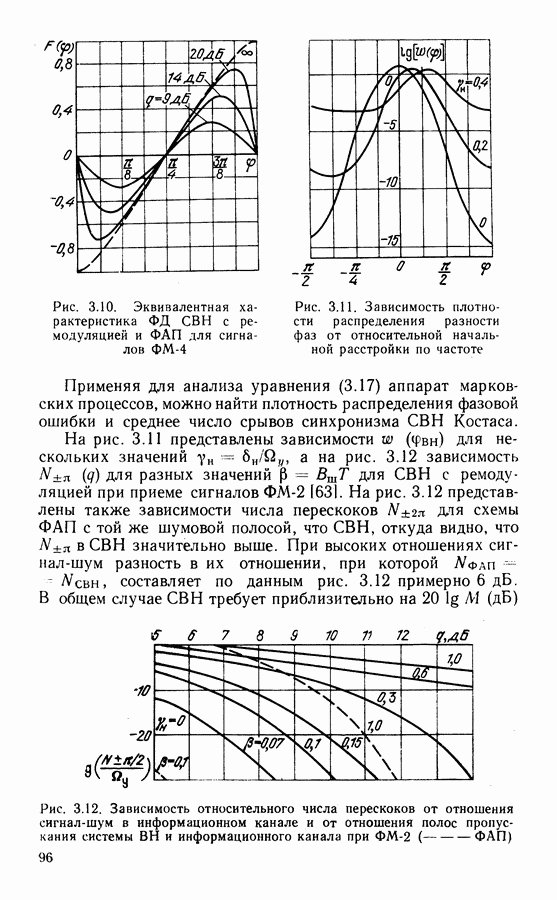
- Требования к точности работы системы ВН.
- Анализ точности систем ВН.
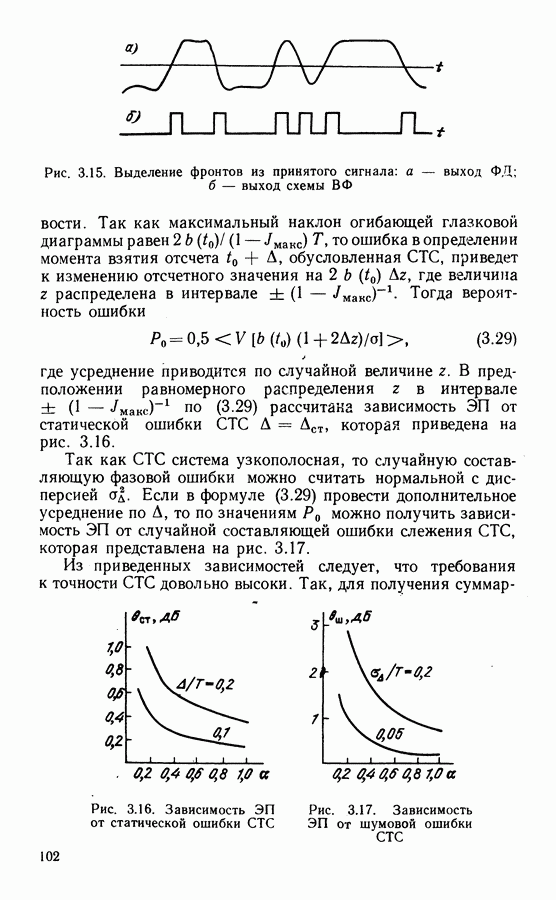
- Переходные процессы.
- 3.3. ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 3.4. ОТНОСИТЕЛЬНОЕ КОДИРОВАНИЕ
- 3.5. ПРИМЕРЫ РЕАЛИЗАЦИИ МОДЕМОВ В ЦССС
- РАЗДЕЛ III. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ
- 4.2. АЛГЕБРАИЧЕСКОЕ ОПИСАНИЕ КОДОВ
- 4.3. БЛОКОВЫЕ КОДЫ И АЛГОРИТМЫ ИХ ДЕКОДИРОВАНИЯ
- 4.4. СТРУКТУРА И ХАРАКТЕРИСТИКИ СВЕРТОЧНЫХ КОДОВ
- 4.5. АЛГОРИТМЫ ДЕКОДИРОВАНИЯ СК
- 4.6. ПОМЕХОУСТОЙЧИВОСТЬ И ЭФФЕКТИВНОСТЬ СИСТЕМ С КОДИРОВАНИЕМ
- ГЛАВА 5. КОДЕКИ
- 5.1. СОГЛАСОВАНИЕ МОДЕМА И КОДЕКА
- 5.2. ДЕКОДЕРЫ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ СК
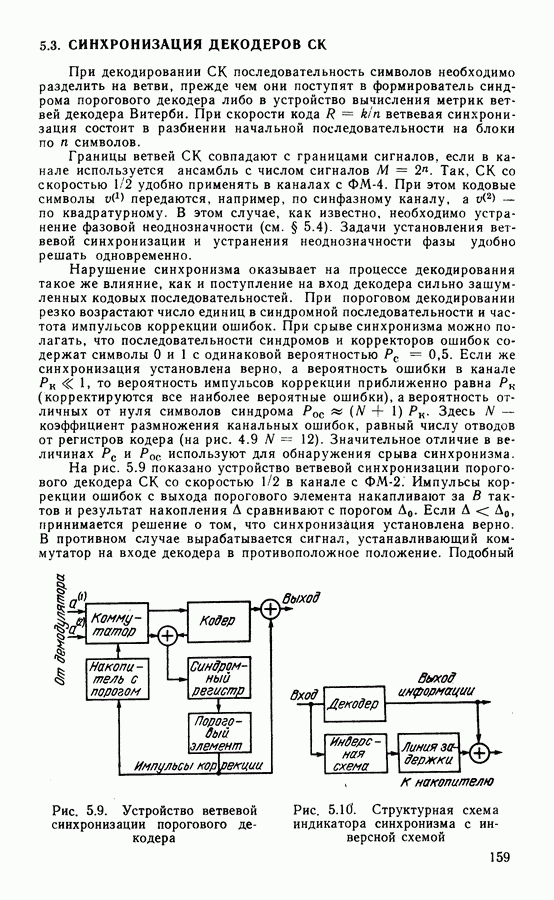
- 5.3. СИНХРОНИЗАЦИЯ ДЕКОДЕРОВ СК
- 5.4. КОДИРОВАНИЕ В КАНАЛАХ С НЕОДНОЗНАЧНОСТЬЮ
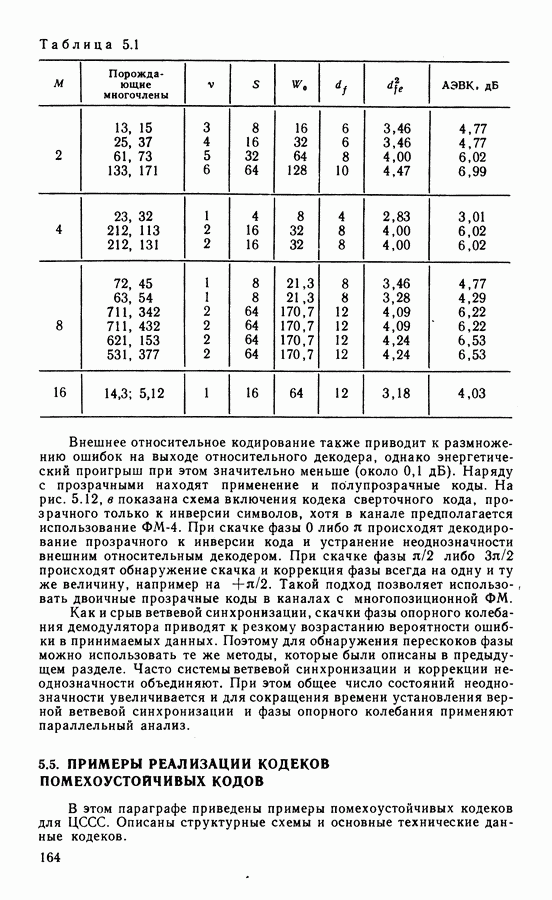
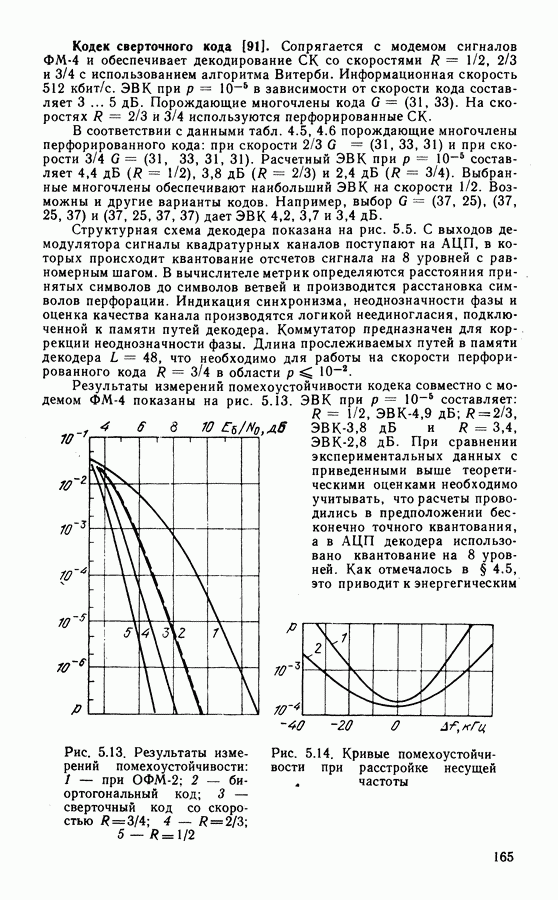
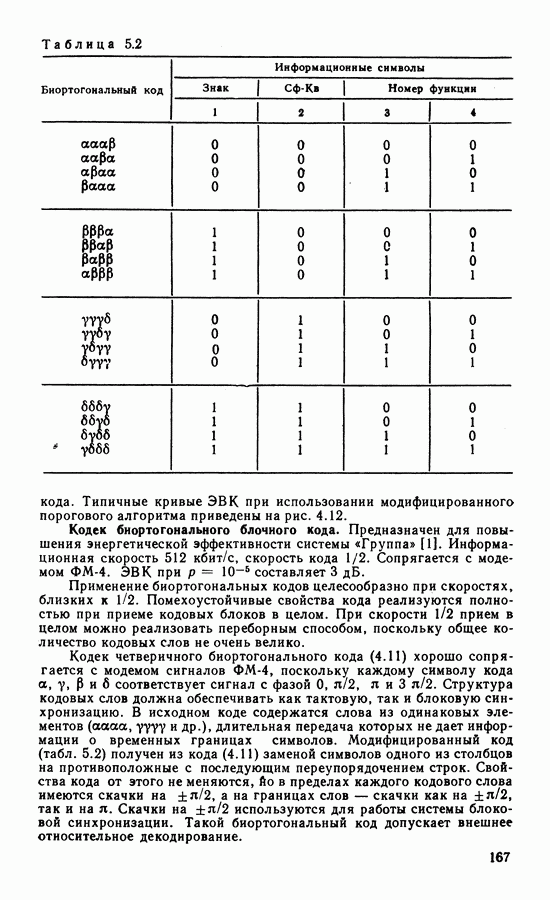
- 5.5. ПРИМЕРЫ РЕАЛИЗАЦИИ КОДЕКОВ ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Кодек биортогонального блочного кода.
- 5.6. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
- РАЗДЕЛ IV. ЦИФРОВЫЕ СИСТЕМЫ СПУТНИКОВОЙ СВЯЗИ
- ГЛАВА 6. ВЗАИМНЫЕ ПОМЕХИ В ЦИФРОВЫХ СПУТНИКОВЫХ СИСТЕМАХ
- 6.2. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ГАРМОНИЧЕСКИХ ПОМЕХ НА ДЕМОДУЛЯТОР ФМ СИГНАЛОВ
- 6.3. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ ФМ ПОМЕХ
- 6.4. АНАЛИЗ МЕШАЮЩЕГО ДЕЙСТВИЯ ЧМ—ТВ СИГНАЛА С ДИСПЕРСИЕЙ
- 6.5. ОЦЕНКА МЕШАЮЩЕГО ДЕЙСТВИЯ СИГНАЛОВ ЧУ-ЧМ
- ГЛАВА 7. СИСТЕМЫ С МДВР И МДЧР
- 7.1. ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ ПЕРЕДАЧИ В ЦССС С МДЧР
- 7.2. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДЧР
- 7.3. ЦИФРОВЫЕ СПУТНИКОВЫЕ СИСТЕМЫ С МДВР
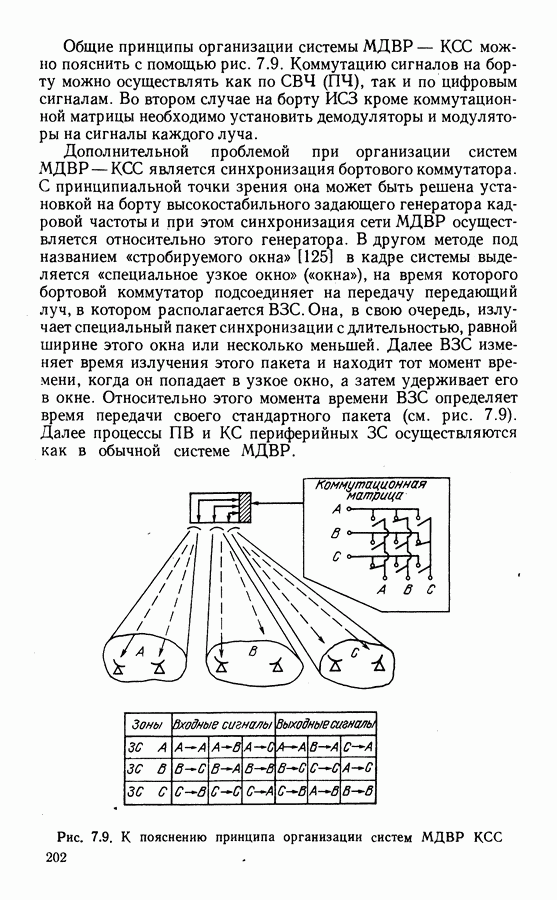
- Синхронизация систем МДВР.
- Организация кадра систем МДВР.
- Система МДВУ-40.
- ЦСС с ДВР ТДМА-120-(«Интелсат»/«Евросат»).
- МДВР с коммутацией сигналов на спутнике (КСС).
- Сопряжение систем МДВР с цифровыми наземными линиями.
- ГЛАВА 8. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МЕТОДОВ МОДУЛЯЦИИ И КОДИРОВАНИЯ В ЦССС
- 8.2. СОГЛАСОВАНИЕ СИСТЕМ МОДУЛЯЦИИ И КОДИРОВАНИЯ
- Согласование кодом Грея.
- Кодирование с разбиением ансамбля на подклассы.
- Применение недвоичных кодов.
- 8.3. СВЕРТОЧНОЕ КОДИРОВАНИЕ В КАНАЛЕ С МНОГОПОЗИЦИОННОИ ФМ
- 8.4. ОБОБЩЕННОЕ КАСКАДНОЕ КОДИРОВАНИЕ
- 8.5. ПРИМЕРЫ РЕАЛИЗАЦИИ ЭФФЕКТИВНЫХ КОДЕМОВ
- СПИСОК ЛИТЕРАТУРЫ